Abstract
We consider a system of fractional-order differential equations to analyze breast cancer growth in the immune-chemotherapeutic treatment process under some control parameters: ketogenic diet, immune booster, and anti-cancer drugs. The established model assumes the growth of the tumor density under chemotherapy treatment and the immune response during the interaction between the normal cells and tumor cells. For the local stability of the critical points (tumor-free critical point, dead critical point, and co-existing critical point), we used the Routh-Hurwitz criteria to show the necessary effect of the immune booster; moreover, we addressed the ketogenic rate in the treatment process. Our theoretical and numerical studies pointed out that on early detection of the tumor density (with weak Allee effect) the treatment should be supported by ketogenic nutrition. Several examples are shown to present our theoretical findings.
Similar content being viewed by others
1 Introduction
According to the National Cancer Registry, cancer kills more people than tuberculosis, AIDS, and malaria combined. Statistics show that cancer mortality is estimated at 13 million deaths by 2030 [1–3]. Breast cancer is the most widely recognized and obstructive disease in females around the world. Breast cancer is a disease that affects the breast’s cells and causes an uncontrolled division of abnormal cells that can be malignant in the breast tissues [4]. Some of the breast cancer risk factors are hormonal imbalance, genetics, and environmental; however, there is still little information on this disease as regards the leading cause of a malignant form [5, 6]. Various mathematical and analytical approaches have been developed to understand the interaction between the tumor cells and the immune response during the treatment process that was mainly established as integer-order differential equations (IDEs) [7–9].
However, it is seen that many problems in biology, as well as in other fields such as engineering, finance, economics, and neural networks, can be formulated successfully by fractional-order differential equations (FDEs); see, for instance, Refs. [10–15]. The nonlocal property of models of FDEs is not only depending on the current state but also provides an adequate description for the historical ones. The transformation of models governed by IDES into models of FDE needs to be precise due to the peculiarity of the order of differentiation α, where a small change in α may cause a significant change in the result. FDEs can model certain phenomena that cannot be modeled by IDEs. Thus, FDEs mainly use biological models since they are relevant to memory and the hereditary feature [16–20].
2 Mathematical model
Over the years, modeling breast cancer has become a valuable tool to understand tumor growth’s dynamical behavior in the treatment process. D’Onofrio et al. explored the role of mathematical modeling in combination therapy for tumors [21]. Studies of Kermack and McKendrick [22, 23] and some other investigations in [24–30] have shown that modeling mathematically the biological phenomena is a useful tool to solve epidemical problems.
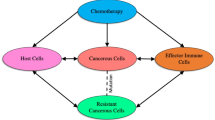
However, these studies did not include a nutritional diet (ketogenic diet) in their mathematical model. Oke et al. improved the model of Mudufza [28] in [3]. They incorporated the control parameters such as ketogenic diet, immune booster, and anti-cancer drug to emphasize the point that there is an interaction between the cells due to the mutation in the tumor cell’s DNA.
In this paper, we establish a system of FDEs in the form
where the parameters denote positive real numbers.
The first equation in system (2.1) represents the normal cell population \(N ( t )\). \(r_{1}\) is the growth rate, while \(K_{1}\) is the carrying capacity of the population. \(\mu _{1}\) represents the logistic rate and \(\beta _{1}\) denotes the inhibition rate of \(N(t)\). \(\phi _{1}\) is the tumor formation rate resulting from DNA mutation caused by the presence of excess estrogen, while \(( 1-k )\) represents the effectiveness of anti-cancer drugs.
In the second equation of (2.1), we show the luminal type (having estrogen receptors, ESR1 + ve) tumor cells that are denoted by \(T ( t )\). \(K_{2}\) is the carrying capacity of the population, and it depends on the rate of d, which is the ketogenic diet. \(r_{2}\) is the growth rate of the \(T ( t )\) population. Any mutation in DNA that is caused by excess estrogen repopulate the tumor cells by \(\phi _{1} N ( t ) E ( t )\). \(\mu _{2}\) represents the logistic rate of the tumor cell population. \(\beta _{2}\) is the rate of the effectiveness of the immune system to the tumor cells, δ is the result of the tumor starvation nutrients during the ketogenic diet.
The third equation in (2.1) shows the class of immune response as \(I ( t ) \), where ρ denotes the source rate of immune response fully infused in the body daily. The immune booster γ assists the immune response whenever tumor cells overpower immune cells to activate the immune response and fight against the tumor cells. \(\mu _{3}\) represents the logistic rate of the immune cell population, while \(\phi _{2}\) is the immune suppression rate. \(K_{3}\) is the carrying capacity and \(\beta _{3}\) is the rate of interaction between \(T(t)\) and \(I(t)\).
Finally, the last equation of system (2.1) is the estrogen compartment, which is denoted by \(E ( t ) \). It should be known that an increase in estrogen level can lead to the growth of the tumor cells. The process of constantly replenishing excess estrogen is denoted by ε. We assume that the majority of cancer cells are estrogen-receptor positive and only a small proportion of epithelial cells are estrogen-receptor positive, which can only be blocked by the anti-cancer drug \(( 1-k )\) tamoxifen. \(\beta _{4}\) is the rate at which estrogen is being washed out from the body [3, 22]. According to the information on the parameters, all parametric values are stated in Table 1.
Definition 2.1
([31])
Given a function \(\varphi (x)\), the fractional integral with order \(\alpha >0\) is given by Abdel’s formula by
Definition 2.2
([31])
Let \(\varphi : R^{+} \rightarrow R\) be a continuous function. The Caputo fractional derivative of order \(\alpha \in ( n-1, n )\), where n is a positive integer is defined as
When \(\alpha =n\), the derivatives are defined to be the usual nth order derivatives.
Definition 2.3
([32])
The Mittag-Leffler function of one variable is
3 The equilibrium points
Consider the system
To analyze the stability of the system (3.1), we perturb the equilibrium point by adding \(\varepsilon _{i} ( t ) >0\), \(i=1, 2, 3, 4\), that is,
Thus, we have
and
This perturbation around the equilibrium point is to linearize the system since we established a nonlinear fractional-order system based on the Lotka-Volterra logistic equation. Moreover, since we are working with the Caputo derivative, the constant function is here zero.
We use the fact that \(f ( \overline{N}, \overline{T}, \overline{I}, \overline{E} ) =g ( \overline{N}, \overline{T}, \overline{I}, \overline{E} ) =h ( \overline{N}, \overline{T}, \overline{I}, \overline{E} ) =j ( \overline{N}, \overline{T}, \overline{I}, \overline{E} ) =0\) and obtain, therefore, a linearized system about the equilibrium point such as
where \(Z= ( \varepsilon _{1} ( t ), \varepsilon _{2} ( t ), \varepsilon _{3} ( t ), \varepsilon _{4} ( t ) )\). Moreover, J is the Jacobian matrix at equilibrium:
We have \(B^{-1} JB=C\), where C is the diagonal matrix of the eigenvalues \(\lambda _{i}\) (\(i=1, 2, 3, 4 \)) and B, the eigenvectors of J. Therefore, we get
whose solutions are given by the Mittag-Leffler functions,
and
Matington studied in [33], a fractional differential system involving the Caputo derivative
with initial values \(x ( 0 ) = x_{0} = ( x_{10}, x_{20},\dots , x_{n0} )^{T}\), where \(x= ( x_{1}, x_{2},\dots , x_{n} )^{T}\), \(\alpha \in ( 0,1 )\) and \(A \in \mathbb{R}^{n\times n}\). The stability of system (3.10) was defined by Matington as follows.
Definition 3.1
The autonomous system (3.10) is said to be
-
(i)
stable if and only if for any \(x_{0}\), there exists \(\varepsilon >0\) such that \(\Vert x \Vert \leq \varepsilon \) for \(t \geq 0\),
-
(ii)
asymptotically stable if and only if \(\lim_{t \rightarrow \infty } \Vert x \Vert =0\).
Theorem A
([34])
The autonomous system (3.10) is
-
(i)
asymptotically stable if and only if if \(\vert \arg ( \lambda _{i} ) \vert > \frac{\alpha \pi }{2}\), in this case, the components of the state decay towards 0 like \(t^{-\alpha } \),
-
(ii)
stable if and only if either it is asymptotically stable, or those critical values which satisfy \(\vert \arg ( \lambda _{i} ) \vert = \frac{\alpha \pi }{2}\) have geometric multiplicity one.
(Here, \(\arg ( \lambda _{i} )\) denotes the arguments of the eigenvalues of the square matrix A.)
The proof of Theorem A was sketched by Matington in [33], while Zeng et al. proved the theorem in detail by using the Mittag-Leffler functions in [35]. Therefore, considering system (3.3) we can say that if \(\vert \arg ( \lambda _{i} ) \vert > \frac{\alpha \pi }{2}\) (\(i=1, 2, 3, 4 \)), then \(\eta _{i} ( t ) \) (\(i=1, 2, 3, 4 \)) are decreasing and therefore also \(\varepsilon _{i} ( t ) \) (\(i=1, 2, 3, 4 \)) are decreasing. Thus, let the solution \(( \varepsilon _{1} ( t ), \varepsilon _{2} ( t ), \varepsilon _{3} ( t ), \varepsilon _{4} ( t ) )\) of (3.3) exist. If the solution of (3.3) is increasing, then \(( \overline{N}, \overline{T}, \overline{I}, \overline{E} )\) is unstable and if \(( \varepsilon _{1} ( t ), \varepsilon _{2} ( t ), \varepsilon _{3} ( t ), \varepsilon _{4} ( t ) )\) is decreasing, then \(( \overline{N}, \overline{T}, \overline{I}, \overline{E} )\) is locally asymptotically stable.
There are four critical points; two of them are the dead critical points, one is a tumor-free critical point, and the other one is the co-existing critical point. These are given as follows:
Tumor-free critical point: \(\Lambda _{1} = ( \overline{N}_{1},0, \overline{I}_{1}, \overline{E}_{1} ) = ( \frac{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon }{\mu _{1} r_{1} \beta _{4}},0, \frac{\rho \gamma \beta _{4}}{ ( 1-k )^{2} \phi _{2} \varepsilon - \beta _{4} ( K_{3} -\delta )}, \frac{ ( 1-k ) \varepsilon }{\beta _{4}} )\), where \(\phi _{1} < \frac{K_{1} r_{1} \beta _{4}}{\varepsilon ( 1-k )^{2}}\) and \(\phi _{2} > \frac{ ( K_{3} -\delta ) \beta _{4}}{\varepsilon ( 1-k )^{2}}\) for \(K_{3} >\delta \).
Dead critical point 1: \(\Lambda _{2} = ( 0,0, \overline{I}_{2}, \overline{E}_{2} ) = ( 0, 0, \frac{\rho \gamma \beta _{4}}{ ( 1-k )^{2} \phi _{2} \varepsilon - \beta _{4} ( K_{3} -\delta )}, \frac{ ( 1-k ) \varepsilon }{\beta _{4}} )\), where \(\phi _{2} > \frac{ ( K_{3} -\delta ) \beta _{4}}{\varepsilon ( 1-k )^{2}}\) for \(K_{3} >\delta \).
Dead critical point 2: \(\Lambda _{3} = ( 0, \overline{T}_{3}, \overline{I}_{3}, \overline{E}_{3} ) = ( 0, \overline{T}_{3}, \overline{I}_{3}, \frac{ ( 1-k ) \varepsilon }{\beta _{4}} )\), where \(\phi _{2} > \frac{ ( K_{3} -\delta ) \beta _{4}}{\varepsilon ( 1-k )^{2}}\) for \(K_{3} >\delta \).
Co-existing critical point: \(\Lambda _{4} = ( \overline{N}_{4}, \overline{T}_{4}, \overline{I}_{4}, \overline{E}_{4} )\), where all classes are positive, where \(\phi _{1} < \frac{K_{1} r_{1} \beta _{4}}{\varepsilon ( 1-k )^{2}}\) and \(\phi _{2} > \frac{ ( K_{3} -\delta ) \beta _{4}}{\varepsilon ( 1-k )^{2}}\) for \(K_{3} >\delta \).
4 Stability, existence, and uniqueness
This section analyzes the local stability of (3.1) around each obtained critical point. The Jacobian matrix of the tumor-free critical point \(\Lambda _{1} = ( \overline{N}_{1},0, \overline{I}_{1}, \overline{E}_{1} )\) is given as
where
On the other hand, the characteristic equation of \(\Lambda _{1}\) is given by
Theorem 4.1
Let \(\Lambda _{1}\) be the tumor-free critical point of system (3.1) and assume that \(\phi _{1} < \frac{K_{1} r_{1} \beta _{4}}{\varepsilon ( 1-k )^{2}}\) and \(\phi _{2} > \frac{ ( K_{3} -\delta ) \beta _{4}}{\varepsilon ( 1-k )^{2}}\) hold. Then \(\Lambda _{1}\) is stable local asymptotic if and only if
where \(r_{2} < \frac{\delta }{K_{2} d}\).
Proof
From (4.2), it follows that
-
(i)
\(\lambda _{1} = r_{1} K_{1} -2 \mu _{1} \overline{N}_{1} - \frac{ ( 1-k )^{2} \phi _{1} \varepsilon }{\beta _{4}} <0\) since \(\phi _{1} < \frac{K_{1} r_{1} \beta _{4}}{\varepsilon ( 1-k )^{2}}\),
-
(ii)
\(\lambda _{2} = r_{2} K_{2} d-\delta - \beta _{2} r_{2} \overline{I}_{1} + \frac{ ( 1-k )^{2} \phi _{1} \varepsilon }{\beta _{4}} \overline{N}_{1} <0\Rightarrow \overline{N}_{1} < \frac{ ( \delta - r_{2} K_{2} d ) \beta _{4}}{ ( 1-k )^{2} \phi _{1} \varepsilon }\), where \(r_{2} < \frac{\delta }{K_{2} d}\),
-
(iii)
\(\lambda _{3} =- \frac{ ( ( 1-k )^{2} \phi _{2} \varepsilon -\beta _{4} ( K_{3} - \mu _{3} ) )}{\beta _{4}} <0\), since \(\phi _{2} > \frac{ ( K_{3} -\delta ) \beta _{4}}{\varepsilon ( 1-k )^{2}}\),
-
(iv)
\(\lambda _{4} =- \beta _{4} <0\).
□
Remark 4.1
In Theorem 4.1. it is seen that any increase in the ketogenic rate affects the growth of the tumor population. It is assumed here that the invasion of the tumor cells into the normal cells is small. Thus, the tumor cell population can be eliminated from the breast tissues, since \(\Lambda _{1}\) depends on the immune response and the estrogen level.
The Jacobian matrix of the dead critical point \(\Lambda _{2} = ( 0, 0, \frac{\rho \gamma \beta _{4}}{ ( 1-k )^{2} \phi _{2} \varepsilon - \beta _{4} ( K_{3} -\delta )}, \frac{ ( 1-k ) \varepsilon }{\beta _{4}} )\) is given as
where
Theorem 4.2
Assume that \(\phi _{1} > \frac{K_{1} r_{1} \beta _{4}}{\varepsilon ( 1-k )^{2}}\) and \(\phi _{2} > \frac{ ( K_{3} -\delta ) \beta _{4}}{\varepsilon ( 1-k )^{2}}\) holds. The dead critical point \(\Lambda _{2}\) of system (3.1) is stable local asymptotic if and only if
where \(r_{2} > \frac{\delta }{K_{2} d}\).
Proof
From (4.4), we obtain the following:
-
(i)
\(\lambda _{1} = r_{1} K_{1} - \frac{ ( 1-k )^{2} \phi _{1} \varepsilon }{\beta _{4}} <0\) if \(\phi _{1} > \frac{K_{1} r_{1} \beta _{4}}{\varepsilon ( 1-k )^{2}}\),
-
(ii)
\(\lambda _{2} = r_{2} K_{2} d-\delta - \beta _{2} r_{2} \overline{I}_{2} <0\Rightarrow \overline{I}_{2} > \frac{ ( r_{2} K_{2} d-\delta ) \beta _{4}}{ ( 1-k )^{2} \phi _{1} \varepsilon }\), where \(r_{2} > \frac{\delta }{K_{2} d}\),
-
(iii)
\(\lambda _{3} =- \frac{ ( ( 1-k )^{2} \phi _{2} \varepsilon -\beta _{4} ( K_{3} - \mu _{3} ) )}{\beta _{4}} <0\), since \(\phi _{2} > \frac{ ( K_{3} -\delta ) \beta _{4}}{\varepsilon ( 1-k )^{2}}\),
-
(iv)
\(\lambda _{4} =- \beta _{4} <0\).
□
Remark 4.2
In Theorem 4.2. it is shown that applying a low ketogenic diet increases the growth of the tumor population. In this scenario, the damage of DNA causes a malignant class in the breast tissues. The competition between the tumor cells and the immune system is intense, and the effect of the anti-cancer drug tamoxifen decreases the tumor population. However, the increase of the estrogen level also affected the healthy cell population to extinct as well.
Now, we consider the Jacobian matrix of dead critical point 2; \(\Lambda _{3} = ( 0, \overline{T}_{3}, \overline{I}_{3}, \frac{ ( 1-k ) \varepsilon }{\beta _{4}} )\), now we have
where
The characteristic equation of the dead critical point 2 is given by
Thus, the local stability for \(\Lambda _{3} = ( 0, \overline{T}_{3}, \overline{I}_{3}, \overline{E}_{3} )\) is obtained in Theorem 4.3 as follows.
Theorem 4.3
Let \(\Lambda _{3}\) be the critical point of system (3.1) and assume that \(\phi _{1} > \frac{K_{1} r_{1} \beta _{4}}{\varepsilon ( 1-k )^{2}} \). Then the following statements are true:
(i) Let \(r_{2} > \frac{\delta }{K_{2} d}\) and \(R_{0} <1\). If
and
then both roots are real or complex conjugates with negative real parts and \(\vert \arg ( \lambda _{i} ) \vert > \frac{\alpha \pi }{2}\) (\(i=1, 2, 3, 4 \)) is equivalent to the Routh-Hurwitz criteria. This implies that \(\Lambda _{3}\) is locally asymptotically stable.
(ii) Let \(r_{2} > \frac{\delta }{K_{2} d}\) and \(R_{0} <1\). If
and
then both roots are complex conjugate with positive real parts and
This implies that \(\Lambda _{3}\) is locally asymptotically stable.
Proof
From (4.7), we obtain
and \(\lambda _{4} =- \beta _{4} <0 \). In this case, we need to consider only the characteristic equation
Equation (4.9) shows the basic reproductive number, which is
for the characteristic equation
which implies
(i) Let us consider the case where \(\Delta = ( a_{22} + a_{33} )^{2} -4 a_{22} a_{33} ( 1- R_{0} ) >0\). For \(R_{0} <1\) and \(r_{2} > \frac{\delta }{K_{2} d}\), we have
which implies that \(\Delta >0\). Moreover, computations show that
where
and
Considering (4.12)–(4.14), we obtain
and
where
From (4.15) and (4.18), we get
(ii) Let us consider the case of complex roots with positive real parts. First of all, if
then we obtain positive real parts. Thus, for the inequality
where
and
we end up with (4.20).
Considering the condition \(\Delta = ( a_{22} + a_{33} )^{2} -4 a_{22} a_{33} ( 1- R_{0} ) <0\), we have
Moreover, computations reveal that \(4 a_{22} a_{33} > ( a_{22} + a_{33} )^{2}\), if
and
where
From (4.22), (4.25), and (4.27), we get
and
□
Remark 4.3
It is shown in Theorem 4.3 that the reproduction number has a dominant role to play in the dynamical system’s stability. In this scenario, we assumed a weak immune response with low ketogenic support. It is seen that without the control parameters, the immune system is not strong enough to defend the tissues and the human body from the invasion of the malignant population.
Let us consider the Jacobian matrix of the co-existing critical point: \(\Lambda _{4} = ( \overline{N}_{4}, \overline{T}_{4}, \overline{I}_{4}, \overline{E}_{4} )\), which has the form
where
The characteristic equation of (4.30) around \(\Lambda _{4}\) is given by
and
while (4.31) is a cubic equation of the form
Theorem 4.4
Let \(\Lambda _{4}\) be the equilibrium point of system (3.1) and assume that \(R_{0} <1\), \(\phi _{1} < \frac{K_{1} r_{1} \beta _{4}}{\varepsilon ( 1-k )^{2}}\) and \(\frac{ ( K_{3} -\delta ) \beta _{4}}{\varepsilon ( 1-k )^{2}} < \phi _{2} < \frac{ ( K_{3} - \mu _{3} ) \beta _{4}}{\varepsilon ( 1-k )^{2}}\). Then the following statements are true:
-
(i)
Let \(r_{1} > \frac{ ( 1-k )^{2} \phi _{1} \varepsilon }{2 \beta _{4} \mu _{1}}\) and \(r_{2} > \frac{\delta }{K_{2} d} \). If
$$ \overline{T}_{4} > \frac{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon }{ ( r_{1} \beta _{1} +2 r_{2} \mu _{2} ) \beta _{4}}\quad \textit{and}\quad \overline{I}_{4} > \frac{K_{2} d r_{2} -\delta }{\beta _{2} r_{2}}, $$where \(\beta _{3} > \frac{ ( r_{1} \beta _{1} +2 r_{2} \mu _{2} ) ( ( K_{3} - \mu _{3} ) \beta _{4} - ( 1-k )^{2} \phi _{2} \varepsilon )}{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon }\) then all the roots of (4.33) are real. This implies that \(\Lambda _{4}\) is locally asymptotically stable.
-
(ii)
Let \(r_{1} \geq \frac{ ( 1-k )^{2} \phi _{1} \varepsilon }{2 \beta _{4} \mu _{1}}\) and \(r_{2} > \frac{\delta }{K_{2} d} \). If
$$\begin{aligned}& \overline{N}_{4} \in \biggl( \frac{ ( r_{1} K_{1} - r_{1} \beta _{1} \overline{T}_{4} ) \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon }{\beta _{4} r_{1} ( 2 \mu _{1} + \beta _{1} )}, \infty \biggr), \\& \overline{T}_{4} \in \biggl[ \frac{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon }{ ( r_{1} \beta _{1} +2 r_{2} \mu _{2} ) \beta _{4}} , \frac{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon }{r_{1} \beta _{1} \beta _{4}} \biggr),\\& \overline{I}_{4} \in \biggl[ \frac{K_{2} d r_{2} -\delta }{\beta _{2} r_{2}} , \infty \biggr) \end{aligned}$$and
$$ \biggl( \frac{ ( 1-k ) \phi _{1} \overline{E}_{4} +2 r_{2} \mu _{2}}{ ( 1-k ) \phi _{1} \overline{E}_{4}} \biggr) > \frac{\overline{N}_{4}}{\overline{T}_{4}}, $$where \(\beta _{3} = \frac{ ( r_{1} \beta _{1} +2 r_{2} \mu _{2} ) ( ( K_{3} - \mu _{3} ) \beta _{4} - ( 1-k )^{2} \phi _{2} \varepsilon )}{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon } \), then there is one real root and one complex root with its complex conjugate, which implies that \(\Lambda _{4}\) is locally asymptotically stable.
Proof
(i) If the discriminant of (4.33) is positive, then the Routh-Hurwitz conditions are necessary and sufficient conditions for locally asymptotically stability of \(\Lambda _{4} \). Thus, we first consider the conditions for a positive discriminant of the cubic polynomial (4.33):
If
and
then the discriminant of (4.33) is positive.
Because of (4.34), we have
where we obtain
and
Since \(\Lambda _{4}\) is a positive critical point for \(\phi _{2} > \frac{ ( K_{3} -\delta ) \beta _{4}}{\varepsilon ( 1-k )^{2}}\), we see from (4.41) that \(\mu _{3} <\delta \). Considering both (4.39) and (4.41), we have
where \(\beta _{3} > \frac{ ( r_{1} \beta _{1} +2 r_{2} \mu _{2} ) ( ( K_{3} - \mu _{3} ) \beta _{4} - ( 1-k )^{2} \phi _{2} \varepsilon )}{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon } \).
On the other side, it is evident that (4.35) holds, since \(a_{33} <0\). Moreover, considering (4.36) and (4.37), we obtain the result that it is satisfied with the conditions in (4.38)–(4.42). This completes the proof of (i).
(ii) If the discriminant of (4.33) is negative, then there is only one real root and one complex root with its complex conjugate. Let us assume that
Then
and
By the result in [36], since \(a-2b>0\) and \(b \geq 0\),
which holds for
and
for \(\frac{ ( K_{3} -\delta ) \beta _{4}}{\varepsilon ( 1-k )^{2}} < \phi _{2} < \frac{ ( K_{3} - \mu _{3} ) \beta _{4}}{\varepsilon ( 1-k )^{2}}\) where \(\mu _{3} <\delta \). Considering both (4.46) and (4.48), we have
where \(\beta _{3} = \frac{ ( r_{1} \beta _{1} +2 r_{2} \mu _{2} ) ( ( K_{3} - \mu _{3} ) \beta _{4} - ( 1-k )^{2} \phi _{2} \varepsilon )}{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon } \).
On the other side, from [36] we have
which implies that \(\vert \arg ( \lambda ) \vert =\theta \geq \frac{\pi }{3}\) and from \(\vert \arg ( \lambda ) \vert > \frac{\alpha \pi }{2}\), we have \(\alpha < \frac{2}{3} \). Thus,
which holds for the conditions in (4.45)–(4.49).
At last, we consider
which implies
we have
where
and
□
Remark 4.4
In Theorem 4.4, it is shown that, if the source rate of estrogen is low, then the interaction between the normal cells and tumor cells continues. At the same time, the growth of both populations has an inverse relation. According to the ketogenic assistance and supplements of an immune booster, a robust immune response is expected in this competition.
Example 4.1
In this example, the theoretical results are demonstrated by using numerical simulations. For this purpose, we wrote code and ran it using the MATLAB version 2019. The initial values of (3.1) are \(N ( 0 ) =200\), \(T ( 0 ) =50\), \(I ( 0 ) =50\), \(E ( 0 ) =2\).
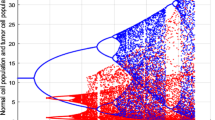
Figure 1 shows the limited competition between cancer and normal cell populations. After the cancer cells appear, some immune booster supplements support the normal cells in the interaction. The red graph is the cancer cell population \(T ( t )\), while the blue graph shows the normal cell population \(N ( t ) \). It is seen that after a specific time, the tumor population becomes so strong that the immune system needs additional support from the control parameters. Therefore, to stabilize only the immune system is not sufficient for interaction against the malignant tumor.
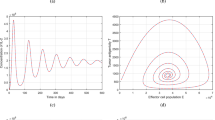
In Figs. 2 and 3, we notice that introducing a ketogenic diet reduces the cancer cells. In this case, applying for the ketogenic program during the mixed-immunotherapy shows an effect on the per capita growth of the cancer cells and stabilizes the treatment to support the normal cells.
However, it is also known that increasing the rate of the ketogenic diet leads to keto-acidosis. Keto-acidosis is a composition of ketosis and acidosis. Ketosis is a substance known as ketone bodies, and acidosis is the acid of the blood, causing frequent polyuria, poor appetite, and loss of consciousness. Therefore, a rate at \(d=0.3\) is reasonable, and the interaction can be supported by anti-cancer drugs such as tamoxifen. The tumor cell is given in red, while the normal cells are denoted in blue.
5 Existence and uniqueness
Considering system (3.1) with the initial conditions \(N ( 0 ) >0\), \(T ( 0 ) >0\), \(I ( 0 ) >0\) and \(E ( 0 ) >0\), the IVP can be written in matrix form as
where and and .
Let us assume that \(N ( 0 ) \leq \upsilon _{1}\), and \(T ( 0 ) >0\), \(I ( 0 ) >0\), \(E ( 0 ) >0\), when \(t>\sigma \geq 0\).
In this case, the following definitions can be applied to the main theorems in this section.
Definition 5.1
Let \(C^{*} [0, T]\) be the class of continuous column vector \(U(t)\) whose components \(N ( t ), T ( t ), I ( t ), E(t)\in C[0, T]\) are the class of continuous functions on the interval \([ 0, T ] \). The norm of \(U\in C^{*} [0, T]\) is given by
When \(t>\sigma \geq 0\), we write \(C_{\sigma }^{*} [0, T]\) and \(C_{\sigma } [0, T]\).
Definition 5.2
Let the IVP of (5.1) have a solution given by \(U\in C^{*} [0, T]\), if
-
(i)
\(( t, U(t) ) \in D\), \(t\in [ 0, T ]\) where \(D= [ 0,T ] \times K\) and
$$ K= \bigl\{ \bigl( N ( t ), T ( t ),I ( t ),E(t) \bigr): \bigl\vert N ( t ) \bigr\vert \leq \upsilon _{1}, \bigl\vert T ( t ) \bigr\vert \leq \upsilon _{2}, \bigl\vert I ( t ) \bigr\vert \leq \upsilon _{3}, \bigl\vert E ( t ) \bigr\vert \leq \upsilon _{4} \bigr\} . $$ -
(ii)
\(U(t)\) satisfies (5.1).
Theorem 5.1
The IVP of (5.1) has a unique solution \(U\in C^{*} [ 0, T ] \).
Proof
Let us write
Operating with \(I^{\alpha } \), we obtain
Now let \(F: C^{*} [0, T]\rightarrow C^{*} [0, T]\) be defined by
Then we get
This implies that \(\Vert FU-FV \Vert \leq \frac{ ( A+ \upsilon _{1} B+ \upsilon _{2} C+ \upsilon _{3} D+ \upsilon _{4} G )}{W^{\alpha }} \Vert U-V \Vert \). If we choose W such that \(W^{\alpha } >A+ \upsilon _{1} B+ \upsilon _{2} C+ \upsilon _{3} D+ \upsilon _{4} G\), then we obtain \(\Vert FU-FV \Vert \leq \Vert U-V \Vert \). Moreover, the operator F given by (4.4) has a unique fixed point.
Consequently, (5.3) has a unique solution \(U\in C^{*} [ 0, T ] \). From (5.3), we have
and
which implies
from which we can deduce that \(U ' \in C_{\sigma }^{*} [ 0, T ] \). Thus, we have
which implies
or
and
Therefore, this IVP is equivalent to (5.1), which completes the proof. □
6 An analysis of the tumor growth at low density
In 1838, Verhulst considered the logistic growth function to explain mono-species growth. Later on, it was demonstrated that the logistic equation needs modifications to explain the growth of the population in low density-size, which is known as the Allee effect.
The Allee effect can be divided into two main types:
-
strong Allee effect and
-
weak Allee effect.
A population with a strong Allee effect will have a critical population size, the population’s threshold. Any size that is less than the threshold will go to extinction without any further aid. However, a population with a weak Allee effect will reduce the per capita growth rate at a lower population density or size [37–41].
Based on the above discussion, we apply the weak Allee function at time t to the system (3.1), such as
where \(t>0\) and \(( N ( 0 ), T ( 0 ),I ( 0 ),E(0) ) = ( N_{0}, T_{0}, I_{0}, E_{0} ) \). Moreover, we define \(\varpi >0\) as the Allee coefficient of the tumor population and \(a ( T(t) ) = \frac{T(t)}{\varpi +T(t)}\) is the Allee function.
Considering the density of class \(T(t)\), we can see that the Allee function is useful for the malignant class if
where the immune system is also dependent on the Allee coefficient,
For a low population size of the tumor population, let us consider the stability conditions around \(\Lambda _{4}\). The characteristic equation is given by
and
while (6.4) is a cubic equation of the form
and
Theorem 6.1
Let \(\Lambda _{4}\) be the positive equilibrium point of system (6.1) and assume that \(R_{0} <1\), \(\phi _{1} < \frac{K_{1} r_{1} \beta _{4}}{\varepsilon ( 1-k )^{2}}\) and \(\frac{ ( K_{3} -\delta ) \beta _{4}}{\varepsilon ( 1-k )^{2}} < \phi _{2} < \frac{ ( K_{3} - \mu _{3} ) \beta _{4}}{\varepsilon ( 1-k )^{2}}\). Then the following statements are true:
-
(i)
Let \(r_{1} > \frac{ ( 1-k )^{2} \phi _{1} \varepsilon a ( \overline{T}_{4} )}{2 \beta _{4} \mu _{1}}\) and \(r_{2} > \frac{\delta }{K_{2} d} \). If
$$ \overline{T}_{4} > \frac{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon }{ ( r_{1} \beta _{1} +2 r_{2} \mu _{2} a ( \overline{T}_{4} ) ) \beta _{4}}\quad \textit{and} \quad \overline{I}_{4} > \frac{K_{2} d r_{2} -\delta }{\beta _{2} r_{2}}, $$where \(\beta _{3} > \frac{ ( r_{1} \beta _{1} +2 r_{2} \mu _{2} a ( \overline{T}_{4} ) ) ( ( K_{3} - \mu _{3} ) \beta _{4} - ( 1-k )^{2} \phi _{2} \varepsilon )}{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon } \) then all the roots are real. This implies that \(\Lambda _{4}\) is locally asymptotically stable.
-
(ii)
Let \(r_{1} \geq \frac{ ( 1-k )^{2} \phi _{1} \varepsilon a ( \overline{T}_{4} )}{2 \beta _{4} \mu _{1}}\) and \(r_{2} > \frac{\delta }{K_{2} d} \). If
$$\begin{aligned}& \overline{N}_{4} \in \biggl( \frac{ ( r_{1} K_{1} - r_{1} \beta _{1} \overline{T}_{4} ) \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon }{\beta _{4} r_{1} ( 2 \mu _{1} + \beta _{1} )}, \infty \biggr), \\& \overline{T}_{4} \in \biggl[ \frac{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon }{ ( r_{1} \beta _{1} +2 r_{2} \mu _{2} a ( \overline{T}_{4} ) ) \beta _{4}} , \frac{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon }{r_{1} \beta _{1} \beta _{4}} \biggr),\\& \overline{I}_{4} \in \biggl[ \frac{K_{2} d r_{2} -\delta }{\beta _{2} r_{2}} , \infty \biggr) \end{aligned}$$and
$$ \biggl( \frac{ ( 1-k ) \phi _{1} \overline{E}_{4} +2 r_{2} \mu _{2} a ( \overline{T}_{4} )}{ ( 1-k ) \phi _{1} \overline{E}_{4}} \biggr) > \frac{\overline{N}_{4}}{\overline{T}_{4}}, $$where \(\beta _{3} = \frac{ ( r_{1} \beta _{1} +2 r_{2} \mu _{2} a ( \overline{T}_{4} ) ) ( ( K_{3} - \mu _{3} ) \beta _{4} - ( 1-k )^{2} \phi _{2} \varepsilon )}{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon } \), then there are only one real root and one complex root with its complex conjugate, which imply that \(\Lambda _{4}\) is locally asymptotically stable.
Proof
(i) Let us consider the conditions for a positive discriminant of (6.6). Thus,
where we obtain
and
Considering both (6.9) and (6.11), we have
where \(\beta _{3} > \frac{ ( r_{1} \beta _{1} +2 r_{2} \mu _{2} a ( \overline{T}_{4} ) ) ( ( K_{3} - \mu _{3} ) \beta _{4} - ( 1-k )^{2} \phi _{2} \varepsilon )}{r_{1} K_{1} \beta _{4} - ( 1-k )^{2} \phi _{1} \varepsilon } \). This completes the proof of (i).
Since Theorem 4.4/(ii) is similar to (i), it is given without proof. □
Remark 6.1
Theorem 6.1 shows that the ketogenic diet affects the growth rate of the tumor population. Decreasing the ketogenic rate is increasing the tumor growth rate, which leads to a weak immune response. On the other side, increasing the ketogenic program in continuous time restricts the tumor population’s capacity, supporting the immune system. Additionally, we noticed that other complement control parameters such as anti-cancer drugs decrease the estrogen level caused by damage to the DNA.
Example 6.1
In this example, we wrote code and ran it using the MATLAB version 2019. The initial values of (3.1) are \(N ( 0 ) =200\), \(T ( 0 ) =50\), \(I ( 0 ) =50\), \(E ( 0 ) =2\). Figure 4 shows the graph of the tumor cells and the normal cells, where \(T ( t )\) is given in red and \(N ( t )\) in blue for mixed therapy in the case of early detection. All control parameters are included in the treatment with low dosages, which drive the tumor density extinct in a short discrete time. This simulation demonstrates the weak Allee effect, where the Allee coefficient is \(\varpi =0.4\). Therefore, it is seen that the ketogenic assistance and supplements of an immune booster are essential in all stages of cancer treatment.
7 Conclusions
This study analyzed a mathematical model of breast cancer as a fractional-order system to analyze tumor growth under chemotherapeutic treatment and immune response. We incorporated sensitive control parameters (ketogenic diet, immune booster, and anti-cancer drugs). Further, we assumed in the model that the majority of the malignant cells are ESR1 + ve.
In Sect. 2, we established the model, and in Sect. 3, we obtained four essential equilibrium points: the tumor-free equilibrium point, the death equilibrium point 1-2, and the co-existing equilibrium point. We proved in Sect. 4 that if the tumor cells’ invasion of the healthy cells is small, then the malignant tumor size can be eliminated from the breast tissues because of the immune response and estrogen level seen for the tumor-free equilibrium point. We found that the ketogenic diet rate supports the immune response to fight against tumor growth but cannot stop the estrogen level for the death equilibrium points. For the co-existing positive equilibrium point, it is shown that if we have a low rate of the estrogen level, then the normal cells and the cancer cells are interactional stables. This occurs with a robust immune system relevant to the support of ketogenic assistance and the immune booster’s supplements. After that, we considered the existence and uniqueness of the initial value problem in Sect. 5.
Finally, in Sect. 6, we considered the early detection case of the tumor population by applying the weak Allee effect at a discrete-time of t. We show that the Allee coefficient affects the normal cell population growth. We emphasized that the DNA damage caused by the estrogen level is still low in the early stages of the malignant population. The essential point was that the ketogenic diet rate was not related to the malignant class density, while the immune response was concerning the tumor growth and the Allee coefficient.
Availability of data and materials
All data generated or analyzed during this study are included in this published article.
References
El-Gohary, A.: Chaos and optimal control of cancer self-remission and tumor system steady states. Chaos Solitons Fractals 37, 1305–1316 (2008)
World Health Organization: Organization, Global Action Plan for the Prevention and Control on NCDs. World Health Organization, Geneva (2014)
Oke, S.I., Matadi, M.B., Xulu, S.S.: Optimal control analysis of a mathematical model for breast cancer. Math. Comput. Appl. 23, 21 (2018)
Olayebi, O.O., Agbobu, S.C., Wauton, I., Olufemi, A.S.: Mathematical modelling of breast cancer thermo-therapy treatment: ultrasound-based approach. J. Multidiscip. Eng. Sci. Stud. 2(12), 1158–1164 (2016)
Patel, M.I., Nagl, S.: The Role of the Model Integration in Complex Systems Modeling: An Example of Cancer Biology. Springer, Berlin (2010)
Sethi, M., Chakravarti, S.K.: Hyperthermia techniques for cancer treatment: a review. Int. J. PharmTech Res. 8(6), 292–299 (2015)
Wei, H.C.: Mathematical modeling of ER-positive breast cancer treatment with AZD9496 and palbociclib. AIMS Math. 5(4), 3446–3455 (2020)
Botasteanu, D.A., Lipkuwitz, S., Lee, J.M., Levy, D.: Mathematical models of breast and ovarian cancers. Wiley Interdiscip. Rev., Syst. Biol. Med. 8(4), 337–362 (2016)
Dey, S.K., Charlies, S.: Mathematical model of breast cancer treatment. Springer Proc. Math. Stat. 146, 149–160 (2015)
Solis-Perez, J.E., Gomez-Agilar, J.F., Atangana, A.: A fractional mathematical model of breast cancer competition model. Chaos Solitons Fractals 127, 38–54 (2019)
Valentim, C.A. Jr., Oliveira, N.A., Rabi, J.A., David, S.A.: Can fractional calculus help improve tumor growth models? J. Comput. Appl. Math. 379, 1–15 (2020)
Sweilam, N.H., Al-Mekhlafi, S.M., Assiri, T., Atangana, A.: Optimal control for cancer treatment mathematical model using Atangana–Baleanu–Caputo fractional derivative. Adv. Differ. Equ. 2020, 334 (2020)
Huang, C., Xiao, M., Alsaedi, A., Hayat, T.: Bifurcations in a delayed fractional complex-valued neural network. Appl. Math. Comput. 292, 210–227 (2017)
Huang, C., Cao, J., Xiao, M., Alsaedi, A., Alsaadi, F.E.: Controlling bifurcation in a delayed fractional predator-prey system with incommensurate orders. Appl. Math. Comput. 293, 293–310 (2017)
Huang, C., Cao, J.D., Xiao, M., Alsaedi, A., Hayat, T.: Effects of time delays on stability and Hopf bifurcation in a fractional-order ring-structured network with arbitrary neurons. Commun. Nonlinear Sci. Numer. Simul. 57, 1–13 (2018)
Solis-Perez, J.E., Gomez-Aguilar, J.F.: Variable-order fractal-fractional time delay equations with power, exponential and Mittag-Leffler laws and their numerical solutions. Eng. Comput. 1, 1–23 (2020)
Atangana, A., Gomez-Aguilar, J.F.: Numerical approximation of Riemann–Liouville definition of fractional derivative: from Riemann–Liouville to Atangana–Baleanu. Numer. Methods Partial Differ. Equ. 34(5), 1502–1523 (2017)
Yousef, A., Bozkurt, F.: Bifurcation and stability analysis of a system of fractional-order differential equations for a plant-herbivore model with Allee effect. Mathematics 7(5), 454 (2019)
Al-Khaled, K., Alquran, M.: An approximate solution for a fractional-order model of generalized Harry Dym equation. Math. Sci. 8, 125–130 (2014)
Ahmad, W.M., Sprott, J.C.: Chaos in fractional order autonomous nonlinear systems. Chaos Solitons Fractals 16, 339–351 (2003)
d’Ornafrio, A., Ledzewicz, U., Maurer, H., Schaettler, H.: On optimal delivery of combination therapy for tumors. Math. Biosci. 222, 13–26 (2009)
Kermarck, W.O., Mc Kendrick, A.G.: Contributions to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A 115, 700–721 (1927)
Kermarck, W.O., Mc Kendrick, A.G.: Contributions to the mathematical theory of epidemics. V. Analysis of experimental epidemics of mouse-typhoid; a bacterial disease conferring incomplete immunity. Epidemiol. Infect. 39, 271–288 (1939)
Sweilam, N.H., Al-Mekhlafi, S.M., Albalawi, A.O., Tenreiro Machado, J.A.: Optimal control of variable-order fractional model for delay cancer treatments. Appl. Math. Model. 89(2), 1557–1574 (2021)
Sowndarrajan, P.T., Manimaran, J., Debbouche, A., Shangerganesh, L.: Distributed optimal control of a tumor growth treatment model with cross-diffusion effect. Eur. Phys. J. Plus 134, 463 (2019)
Ozdemir, N., Ucar, E.: Investigating of an immune system-cancer mathematical model with Mittag-Leffler kernel. AIMS Math. 5(2), 1519–1531 (2019)
De Pillis, L.G., Radunskaya, A.E., Wiseman, C.L.: A validated mathematical model of the cell-mediated immune response to the tumor growth. Cancer Res. 65, 7950–7958 (2005)
Mufudza, C., Walter, S., Chiyaka, E.T.: Assessing the effects of estrogen on the dynamics of chemo-virotherapy cancer. Comput. Math. Methods Med. 2012, 473572 (2012)
Abernathy, K., Abernathy, Z., Baxter, A., Stevens, M.: Global dynamics of a brest cancer competition model. Differ. Equ. Dyn. Syst. 3, 1–15 (2017)
Jarret, A.M., et al.: Experimentally-driven mathematical modeling to improve combination targeted and cytotoxic therapy for HERZ + breast cancer. Sci. Rep. 9, Article ID 12830 (2019)
Li, L., Liu, J.G.: A generalized definition of Caputo derivatives and its application to fractional ODEs. SIAM J. Math. Anal. 50(3), 2867–2900 (2016)
Abdeljawad, T., Baleanu, D.: On fractional derivatives with generalized Mittag-Leffler kernels. Adv. Differ. Equ. 2018, 468 (2018)
Matignon, D.: Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 2, 1–6 (1996)
Qian, D., Li, C., Agarwal, R.P., Wang, P.J.Y.: Stability analysis of fractional differential system with Riemann–Liouville derivatives. Math. Comput. Model. 52, 862–874 (2010)
Zeng, Q.S., Cao, G.Y., Zhu, X.J.: The asymptotic stability on sequential fractional order systems. J. Shanghai Jiaotong Univ. 39, 346–348 (2005)
Ahmad, E., El-Sayed, A.M.A., El-Saka, H.A.A.: On some Routh–Hurwitz conditions for fractional-order differential equations and their applications in Lorenz, Rossler, Chua, and Chen systems. Phys. Lett. A 358, 1–4 (2006)
Courchamp, F., Berec, L., Gascoigne, J.: Allee Effects in Ecology and Conservation. Oxford University Press, Oxford (2008)
Bozkurt, F., Yousef, A.: Flip bifurcation and stability analysis of a fractional-order differential equation with Allee effect. J. Interdiscip. Math. 22(6), 1009–1029 (2019)
Allee, W.C.: Animal Aggregations: A Study in General Sociology. University of Chicago Press, Chicago (1931)
Lande, R.: Extinction threshold in demographic models of territorial populations. Am. Nat. 130(4), 624–635 (1987)
Li, X., Mou, C., Niu, W., Wang, D.: Stability analysis for discrete biological models using algebraic methods. Math. Comput. Sci. 5, 247–262 (2011)
Acknowledgements
The Scientific Research Council supports this work at Erciyes University with the project code FBA-2014-5336.
Funding
There is no financial support from any private or public organization. There is no financial relationship with any individuals (friends, spouse, relatives, …).
Author information
Authors and Affiliations
Contributions
FB and AY conceived of the study and were in charge of overall direction and planning. They designed the model and set up the main parts of the study. All authors set up the theorems and proved them. FB did the simulation results using Matlab 2019. The authors wrote the manuscript and revised it to the submitted form. There is no ghost-writing. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yousef, A., Bozkurt, F. & Abdeljawad, T. Mathematical modeling of the immune-chemotherapeutic treatment of breast cancer under some control parameters. Adv Differ Equ 2020, 696 (2020). https://doi.org/10.1186/s13662-020-03151-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-03151-5