1 Introduction

Chaotic systems have received more attention due to their potential applications in economics and management, such as equity market indices: cases from the United Kingdom [1], monetary aggregates [2], business cycle [3], firm growth and R&D investment [4], chaotic behavior in foreign direct investment, and foreign capital investments [5, 6].

Some nonlinear models have been established to investigate the complex economic dynamics such as Goodwin’s accelerate model [7], Van der Pol’s models [8], Duffing–Holmes model [9], Kaldoria model [10], and IS-LM model [11]. In recent years, chaotic economics has obtained intensive attention and has been raised to engineering applications for understanding the complex behavior of the real financial market. In [12], Chen studied the chaos behavior in a financial system with the help of fractional order. In [13], Gao and Ma introduced a new finance chaotic system and exhibited Hopf bifurcation in the qualitative analysis of the finance system. In [14], Wang et al. described a finance chaotic system with delayed fractional order. In [15], Yu et al. used speed feedback control and linear feedback control for stabilizing hyperchaotic finance system to unstable equilibrium. In [16], Wang et al. designed the sliding mode controller (SMC) for an uncertain chaotic fractional-order economic system. In [17], Vaidyanathan et al. devised a new finance chaotic system and discussed its passivity-based synchronization with circuit realization of the system. The study of economic dynamics with the approach fractional order can be seen in references [18, 19].

In this work, a financial risk chaotic system is proposed and its properties are elucidated. In Sect. 2, we present the properties and dynamics of a new fractional-order financial risk chaotic system and investigate the properties numerically via Lyapunov exponents and bifurcation diagram. Section 2 also contains the results of simulation and analysis of the new fractional-order financial risk chaotic system. Section 3 describes the adaptive fuzzy control for the fractional-order financial risk chaotic system. Section 4 contains the conclusions of this work.

2 Model of fractional-order financial risk system

At present, there are many different definitions for the fractional calculus, such as G-L definition, R-L definition, and Caputo definition. The Caputo fractional derivative is widely used in the engineering application fields. The main reason is that this definition is in the order of differential and integral, thus it a clearer physical meaning. In this work, we utilized the Caputo definition, which is defined by [20]

$$ \begin{gathered} D^{q}f =\frac{1}{\Gamma (n-q)} \int _{0}^{t}(t-\tau )^{n-q-1}f^{(n)}( \tau )\,d\tau \quad (m-1< q< m), \\ D^{q}f =\frac{d^{n}}{dt^{n}}f(t)\quad (q=n) , \end{gathered} $$
(1)

where q is the order of fractional derivative, m is the lowest integer which is not less than q, and Γ is the gamma function

$$ \Gamma (x)= \int _{0}^{\infty }t^{x-1}e^{-t}\,dt. $$
(2)

In 2013, Xiao-Dan et al. [21] reported a financial risk chaotic system:

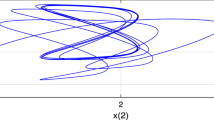
$$ \textstyle\begin{cases} \dot{x}=\delta (y-x)+yz, \\ \dot{y}=rx-y-xz, \\ \dot{z}=xy-bz. \end{cases} $$
(3)

In (3), x, y, z describe occurrence value risk, analysis value risk, and control value risk in the current market, respectively. The parameter δ denotes the analysis risk efficiency, r denotes the transmission rate of previous risk, and b denotes the distortion coefficient of risk control. Three state variables x, y, and z must be positive, because risk in financial markets always exists as the market occurs. The system (3) is chaotic when the parameter values are taken as \(\delta = 10\), \(r = 28\), and \(b = \frac{8}{3}\). We take the initial conditions of system (3) as \((10, 10, 10)\).

The mathematical description of the commensurate fractional-order model of the financial risk chaotic system (3) can be expressed as follows:

$$ \textstyle\begin{cases} \frac{d^{q_{1}}x}{dt^{q_{1}}}=\delta (y-x)+yz, \\ \frac{d^{q_{2}}y}{dt^{q_{2}}}=rx-y-xz, \\ \frac{d^{q_{3}}z}{dt^{q_{3}}}=xy-bz. \end{cases} $$
(4)

In (4), \(q_{1}\), \(q_{2}\), and \(q_{3}\) are the fractional orders of the respective states. a, b, c are constant positive parameters of the system. For numerical simulation of fractional-order model (4) of the financial risk chaotic systems, the Adams–Bashforth–Moulton predictor-corrector scheme is used [22–27].

The dynamic evolution graphs of the system are obtained by means of bifurcation diagram and Lyapunov exponents. They show dynamics of the system with the variation of system parameters. Particularly, Lyapunov exponents in the q-r parameter plane can give us a clear view of the state of the system.

The dynamical behavior of the financial risk chaotic system can be characterized by its Lyapunov exponents which are computed numerically by Wolf algorithm [28]. The Lyapunov exponents of the financial risk chaotic system are obtained as \(L1 = 1.251\), \(L2 = 0\), and \(L3 = -14.9197\), while the Kaplan–Yorke dimension of the financial risk chaotic system is obtained as \(D_{KY} = 3.0839\).

In this study, we analyze bifurcation behavior of the fractional-order financial risk system (4) in many cases.

Case (A)

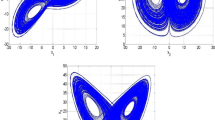
Here, we fix \(q_{2} = 1\), \(q_{3} = 1\), and \(q_{1}\) varies from 0.4 to 1. The bifurcation diagram is shown in Fig. 1(a). According to Fig. 1(a), chaotic behavior can be seen for \(q_{1} \in [0.63, 1]\) and for \(q_{1}\leq 0.62\), system (4) exhibits periodic motion.

Figure 1
figure 1

Bifurcation diagrams of the fractional-order financial risk system with derivative order varying (a) \(q_{1}\) varying, \(q_{2} =1\), \(q_{3}=1\) and \(r=28\); (b) \(q_{2}\) varying, \(q_{1}=1\), \(q_{3}=1\) and \(r=28\); (c) \(q_{3}\) varying, \(q_{1}=1\), \(q_{2}=1\) and \(r=28\); (d) \(q_{1}= q_{2}=q_{3}=q\) varying and \(r=28\)

Full size image

Case (B)

Here, we fix \(q_{1} = 1\), \(q_{3} = 1\), and \(q_{2}\) varies from 0.7 to 1. The system exhibits chaotic behavior for \(q_{1}\in [0.9, 1]\). The system shows periodic behavior for \(q_{1}< 0.9\). This has been confirmed in the bifurcation diagram analysis (see Fig. 1(b)).

Case (C)

Here, we fix \(q_{1} = 1\), \(q_{2} = 1\). Let the derivative order \(q_{3}\) vary from 0.7 to 1. It is shown in Fig. 1(c) that the system is chaotic over the interval \(q_{3}\in [0.9, 1]\) and the system behavior becomes periodic motion for \(q_{3}< 0.9\).

Case (D)

Here, we fix \(q_{1}= q_{2} = q_{3}= q\). The dynamical properties of the system with r and q varying are analyzed. The bifurcation diagram and LEs for derivative order \(q \in [0.9, 1]\) are shown in Figs. 1(d) and 2(a). The chaotic zone covers most of the range \(q \in [0.944, 1]\), excepting a periodic window near \(q \leq 0.943\). In addition, for \(q_{1}=q_{2}=q_{3}=0.98\) and vary the system parameter r from 5 to 30. The resulting bifurcation diagram is shown in Fig. 3(a), and LCE result is presented in Fig. 2(b). The largest increases with the increase of r, and when r is larger than 10.18, the system is chaotic. Also, \(q_{1}=q_{2}=q_{3}=0.95\) and r varying from 5 to 30 are shown in Fig. 3(b).

Figure 2
figure 2

LEs of the fractional-order financial risk system (a) LEs with q varying; (b) LEs with r varying

Full size image
Figure 3
figure 3

Bifurcation diagrams of the fractional-order financial risk system with parameter r varying (a) \(q_{1}=q_{2}=q_{3}=0.98\) and r varying; (b) \(q_{1}=q_{2}=q_{3}=0.95\) and r varying

Full size image

Complexity of the fractional-order financial risk chaotic system with derivative q and control parameter r varying is analyzed, where the step size of q is 0.001 and in the range of \(q \in [0.9, 1]\). In addition, step size of r is 0.25 and in the range of \(r \in [5, 30]\). LEs in the \(q-r\) plane are shown in Fig. 4(a)–4(d).

Figure 4
figure 4

\(q-r\) plane of the fractional-order financial risk system (a) LEs 1, r, q plane, (b) r, q plane, (c) LEs 2, r, q plane, and (d) LEs 3, r, q plane

Full size image

3 Adaptive fuzzy control for the fractional-order financial risk chaotic system

3.1 Fuzzy logic system

Fuzzy logic system includes singleton fuzzification, sum-product inference, and center off-sets defuzzification, which can be expressed by

$$ f(x)= \frac{\sum^{N}_{j=1}\theta _{j}\prod^{n}_{i=1}\mu _{F_{i}^{j}}(x_{i})}{ \sum^{N}_{j=1} [\prod^{n}_{i=1}\mu _{F_{i}^{j}}(x_{i}) ] }, $$
(5)

where x is the input, \(f(x)\) is the output. The membership of jth rule is \(\mu _{F_{i}^{j}}(x_{i})\), and the centroid of the jth consequent set is \(\theta _{j}\). Then (5) can be rewritten as follows:

$$ f(x)=\theta ^{T}\psi (x), $$
(6)

where \(\theta = [\theta _{1},\ldots,\theta _{N}]\), \(\psi (x)=[p_{1}(x),p_{2}(x),\ldots,p_{N}(x)]^{T}\) and the fuzzy basis function is \(p_{j}(x)= \frac{\prod^{n}_{i=1}\mu _{F_{i}^{j}}(x_{i})}{\sum^{N}_{j=1} [\prod^{n}_{i=1}\mu _{F_{i}^{j}}(x_{i}) ] }\).

Lemma 1

([29])

Suppose that \(f(x)\) is a continuous function and \(x\in \Omega \), where Ω is a compact set. For (6), there exists a fuzzy system such that

$$ \sup_{x\in \Omega } \bigl\vert f(x)-\theta ^{T}\psi (x) \bigr\vert \leq \varepsilon , $$
(7)

where \(\varepsilon >0\).

3.2 Controller design and stability analysis

Adaptive fuzzy control of the commensurate fractional-order model of financial risk chaotic system (4) is as follows:

$$ \textstyle\begin{cases} \frac{d^{q_{1}}x}{dt^{q_{1}}}=\delta (y-x)+yz+u_{1}, \\ \frac{d^{q_{2}}y}{dt^{q_{2}}}=rx-y-xz+u_{2}, \\ \frac{d^{q_{3}}z}{dt^{q_{3}}}=xy-bz+u_{3}. \end{cases} $$
(8)

Let \(f_{1}(x_{1})=\delta y+yz\), \(f_{2}(y_{2})=-xz+rx\), and \(f_{3}(z_{3})=xy\) be unknown as nonlinear functions, respectively. Then system (8) can be rewritten as

$$ \textstyle\begin{cases} \frac{d^{q_{1}}x}{dt^{q_{1}}}=-\delta x+f_{1}(x_{1})+u_{1}, \\ \frac{d^{q_{2}}y}{dt^{q_{2}}}=-y+f_{2}(y_{2})+u_{2}, \\ \frac{d^{q_{3}}z}{dt^{q_{3}}}=-bz+f_{3}(z_{3})+u_{3}. \end{cases} $$
(9)

Based on Lemma 1, the unknown functions can be respectively approximated by a fuzzy logic system as follows:

$$ \hat{f_{i}}(,\theta _{i})=\theta ^{T}_{i}\psi _{i},\quad i=1,2,3. $$
(10)

Let the optimal parameter estimation of fuzzy systems be \(\theta ^{\ast }_{i}=\min [\sup \vert f_{i}-\hat{f_{i}}(, \theta _{i}) \vert ]\), where \(\theta ^{\ast }_{i}\) is a constant.

Let the parameter error and optimal estimation error of the fuzzy system be respectively

$$\begin{aligned}& \tilde{\theta _{i}}=\theta _{i}-\theta ^{\ast }_{i}, \end{aligned}$$
(11)
$$\begin{aligned}& \varepsilon _{i}=f_{i}-\hat{f_{i}}\bigl(,\theta ^{\ast }_{i}\bigr). \end{aligned}$$
(12)

Based on [30], we can suppose that \(\vert \varepsilon _{i} \vert \leq \varepsilon ^{\ast }_{i}\), where \(\varepsilon ^{\ast }_{i}\) is a positive constant.

The estimation error of the unknown nonlinear function can be written as

$$ \begin{aligned} \hat{f}(,\theta )-f &= \hat{f}(,\theta )-\hat{f}\bigl(,\theta ^{\ast }\bigr)+ \hat{f}\bigl(,\theta ^{\ast }\bigr)-f \\ &=\hat{f}(,\theta )-\hat{f}\bigl(,\theta ^{\ast }\bigr)-\varepsilon \\ &=\theta ^{T}\psi -\theta ^{\ast T}\psi -\varepsilon \\ &=\tilde{\theta ^{T}}\psi -\varepsilon . \end{aligned} $$
(13)

Based on the above discussion, the controllers can be designed as

$$\begin{aligned}& u_{1}=-k_{1}x-\theta ^{T}_{1} \psi _{1}(x_{1})-\hat{\varepsilon }^{\ast }_{1} \operatorname{sign}(x), \end{aligned}$$
(14)
$$\begin{aligned}& u_{2}=-k_{2}y-\theta ^{T}_{2} \psi _{2}(y_{2})-\hat{\varepsilon }^{\ast }_{2} \operatorname{sign}(y), \end{aligned}$$
(15)
$$\begin{aligned}& u_{3}=-k_{3}y-\theta ^{T}_{3} \psi _{3}(z_{3})-\hat{\varepsilon }^{\ast }_{3} \operatorname{sign}(z), \end{aligned}$$
(16)

where \(k_{i}>0\), \(\hat{\varepsilon }^{\ast }_{i} \) is an estimate of the unknown constant \(\varepsilon ^{\ast }_{i}\) for \(i=1,2,3\).

In this subsection, we propose the fractional-order parameters adaptive laws as follows:

$$\begin{aligned}& \frac{d^{q}\hat{\theta _{1}}}{dt^{q}}=\mu _{1}x\psi _{1}(x_{1}), \end{aligned}$$
(17)
$$\begin{aligned}& \frac{d^{q}\hat{\varepsilon _{1}^{\ast }}}{dt^{q}}=\sigma _{1} \bigl\vert x^{T} \bigr\vert , \end{aligned}$$
(18)
$$\begin{aligned}& \frac{d^{q}\hat{\theta _{2}}}{dt^{q}}=\mu _{2}y\psi _{2}(y_{2}), \end{aligned}$$
(19)
$$\begin{aligned}& \frac{d^{q}\hat{\varepsilon _{2}^{\ast }}}{dt^{q}}=\sigma _{2} \bigl\vert y^{T} \bigr\vert , \end{aligned}$$
(20)
$$\begin{aligned}& \frac{d^{q}\hat{\theta _{3}}}{dt^{q}}=\mu _{3}z\psi _{3}(z_{3}), \end{aligned}$$
(21)
$$\begin{aligned}& \frac{d^{q}\hat{\varepsilon _{3}^{\ast }}}{dt^{q}}=\sigma _{3} \bigl\vert z^{T} \bigr\vert , \end{aligned}$$
(22)

where \(\mu _{i},\sigma _{i}>0\), \(i=1,2,3\).

To check the stability of the controlled system, some results of stability analysis of fractional-order systems are given in advance as follows.

Lemma 2

([30])

Let \(V=\frac{1}{2}x^{2}+\frac{1}{2}y^{2}\), where \(x,y \in R\) and x, y have a continuous first derivative, respectively. If there exists a constant \(h>0\) satisfying

$$ \frac{d^{q}V}{dt^{q}}\leq -hx^{2}, $$
(23)

then one has

$$ x^{2}\leq 2V(0)E_{q}\bigl(-2ht^{q} \bigr), $$
(24)

where \(E^{q}(-2ht^{q})\) is the Mittag-Leffler function.

Lemma 3

([30])

Let \(V=\frac{1}{2}x^{T}x+\frac{1}{2}y^{T}y\), where \(x,y \in R^{n}\) and x, y have a continuous first derivative, respectively. There exists a constant \(k>0\) such that

$$ \frac{d^{q}V}{dt^{q}}\leq -kx^{T}x. $$
(25)

Then \(\Vert x \Vert \), \(\Vert y \Vert \) are bounded and x asymptotically approaches zero, where \(\Vert \varepsilon \Vert \) represents Euclid from.

Lemma 4

([31–34])

If \(x \in R^{n}\) is a continuous differentiable function, one holds

$$ \frac{1}{2}\frac{d^{q}x^{T}x}{dt{q}}\leq x^{T} \frac{d^{q}x}{dt^{q}}. $$
(26)

In order to facilitate, we write the fractional order of system (8) as q. From what has been discussed above we can obtain the following:

$$ \begin{aligned} \frac{d^{q}x}{dt^{q}} &= -\delta x+f_{1}(x_{1})+u_{1} \\ &=-\delta x+f_{1}(x_{1})-\hat{f}_{1}(x_{1}, \theta _{1})+\hat{f}_{1}(x_{1}, \theta _{1})+u_{1} \\ &=-\delta x-\tilde{\theta }^{T}_{1}\psi _{1}(x_{1})+\varepsilon _{1}(x_{1})-k_{1}x- \theta _{1}^{T}\psi _{1}(x_{1})-\hat{ \varepsilon }^{\ast }_{1}\operatorname{sign}(x)+ \theta ^{T}_{1}\psi _{1}(x_{1}) \\ &=-a_{1}x-\tilde{\theta }^{T}_{1}\psi _{1}(x_{1})+\varepsilon _{1}(x_{1})- \hat{\varepsilon }^{\ast }_{1}\operatorname{sign}(x), \end{aligned} $$
(27)

where \(a_{1}=\delta +k_{1}\).

Multiply both sides of the equation (26) by \(x^{T}\), one has

$$ \begin{aligned} x^{T}\frac{d^{q}x}{dt^{q}} &=-a_{1}x^{T}x-x^{T}\tilde{\theta }^{T}_{1} \psi _{1}(x_{1})+x^{T} \varepsilon _{1}(x_{1})-x^{T}\hat{\varepsilon }^{ \ast }_{1}\operatorname{sign}(x) \\ &\leq -a_{1}x^{T}x+\varepsilon ^{\ast }_{1} \bigl\vert x^{T} \bigr\vert - \hat{\varepsilon }^{\ast }_{1} \bigl\vert x^{T} \bigr\vert -x^{T}\tilde{\theta }^{T}_{1} \psi _{1}(x_{1}) \\ &=-a_{1}x^{T}x-\tilde{\varepsilon }^{\ast }_{1} \bigl\vert x^{T} \bigr\vert -x^{T} \tilde{\theta }^{T}_{1}\psi _{1}(x_{1}). \end{aligned} $$
(28)

Similar, we can obtain

$$\begin{aligned}& y^{T}\frac{d^{q}y}{dt^{q}}=-a_{2}y^{T}y- \tilde{\varepsilon }^{\ast }_{2} \bigl\vert y^{T} \bigr\vert -y^{T}\tilde{\theta }^{T}_{2}\psi _{2}(x_{2}), \end{aligned}$$
(29)
$$\begin{aligned}& z^{T}\frac{d^{q}z}{dt^{q}}=-a_{3}z^{T}z- \tilde{\varepsilon }^{\ast }_{3} \bigl\vert z^{T} \bigr\vert -z^{T}\tilde{\theta }^{T}_{3}\psi _{3}(z_{3}), \end{aligned}$$
(30)

where \(a_{2}=1+k_{2}\), \(a_{3}=b+k_{3}\).

Theorem 1

Under given initial conditions, the variables x, y, and z of fractional-order system (8) converge to zero under the action of adaptive controller (14), (15), (16) and fractional-order parameter adaptive laws (17), (18), (19), (20), (21), (22), and all variables in the closed-loop system are bounded.

Proof

Let the Lyapunov function be

$$ V_{1}=\frac{1}{2}x^{T}x+ \frac{1}{2\mu _{1}}\tilde{\theta }^{T}_{1} \tilde{\theta }_{1}+\frac{1}{2\sigma _{1}}\tilde{\varepsilon }^{\ast T}_{1} \tilde{\varepsilon }^{\ast }_{1}, $$
(31)

where \(\tilde{\theta }_{1}=\hat{\theta }_{1}-\theta ^{\ast }_{1}\) and \(\tilde{\varepsilon }^{\ast }_{1}=\hat{\varepsilon }^{\ast }_{1}- \varepsilon ^{\ast }_{1}\).

Based on Lemma 4, (17), (18), and (28), we can obtain

$$ \begin{aligned} \frac{d^{q}V_{1}}{dt^{q}} &= x^{T} \frac{d^{q}x}{dt^{q}}+ \frac{1}{\mu _{1}}\tilde{\theta }^{T}_{1} \frac{d^{q}\tilde{\theta }_{1}}{dt^{q}}+\frac{1}{\sigma _{1}} \tilde{\varepsilon }^{\ast T}_{1} \frac{d^{q}\tilde{\varepsilon }^{\ast }_{1}}{dt^{q}} \\ &\leq -a_{1}x^{T}x-\tilde{\varepsilon }^{\ast }_{1} \bigl\vert x^{T} \bigr\vert - x^{T} \tilde{\theta }^{T}_{1}\psi _{1}(x_{1})+x^{T} \tilde{\theta }^{T}_{1} \psi _{1}(x_{1})+ \tilde{\varepsilon }^{\ast T}_{1} \bigl\vert x^{T} \bigr\vert \\ &\leq -a_{1}x^{T}x, \end{aligned} $$
(32)

where \(a_{1}>0\). We know from Lemma 3 that x asymptotically approaches zero, namely \(\lim_{t\to \infty } \Vert x \Vert =0\).

Choose the Lyapunov function as

$$ V_{2}=\frac{1}{2}y^{T}y+ \frac{1}{2\mu _{2}}\tilde{\theta }^{T}_{2} \tilde{\theta }_{2}+\frac{1}{2\sigma _{2}}\tilde{\varepsilon }^{\ast T}_{2} \tilde{\varepsilon }^{\ast }_{2}, $$
(33)

where \(\tilde{\theta }_{2}=\hat{\theta }_{2}-\theta ^{\ast }_{2}\) and \(\tilde{\varepsilon }^{\ast }_{2}=\hat{\varepsilon }^{\ast }_{2}- \varepsilon ^{\ast }_{2}\).

Based on Lemma 4, (19), (20), and (29), we can obtain

$$ \begin{aligned} \frac{d^{q}V_{2}}{dt^{q}} &= y^{T} \frac{d^{q}y}{dt^{q}}+ \frac{1}{\mu _{2}}\tilde{\theta }^{T}_{2} \frac{d^{q}\tilde{\theta }_{2}}{dt^{q}}+\frac{1}{\sigma _{2}} \tilde{\varepsilon }^{\ast T}_{2} \frac{d^{q}\tilde{\varepsilon }^{\ast }_{2}}{dt^{q}} \\ &\leq -a_{2}y^{T}y-\tilde{\varepsilon }^{\ast }_{2} \bigl\vert y^{T} \bigr\vert - y^{T} \tilde{\theta }^{T}_{2}\psi _{2}(y_{2})+y^{T} \tilde{\theta }^{T}_{2} \psi _{2}(y_{2})+ \tilde{\varepsilon }^{\ast T}_{2} \bigl\vert y^{T} \bigr\vert \\ &\leq -a_{2}y^{T}y, \end{aligned} $$
(34)

where \(a_{2}>0\). We know from Lemma 3 that y asymptotically approaches zero, namely \(\lim_{t\to \infty } \Vert y \Vert =0\).

Consider the Lyapunov function

$$ V_{3}=\frac{1}{2}z^{T}z+ \frac{1}{2\mu _{3}}\tilde{\theta }^{T}_{3} \tilde{\theta }_{3}+\frac{1}{2\sigma _{3}}\tilde{\varepsilon }^{\ast T}_{3} \tilde{\varepsilon }^{\ast }_{3}, $$
(35)

where \(\tilde{\theta }_{3}=\hat{\theta }_{3}-\theta ^{\ast }_{3}\) and \(\tilde{\varepsilon }^{\ast }_{3}=\hat{\varepsilon }^{\ast }_{3}- \varepsilon ^{\ast }_{3}\).

Based on Lemma 4, (21), (22), and (30), we can obtain

$$ \begin{aligned} \frac{d^{q}V_{3}}{dt^{q}} &= z^{T} \frac{d^{q}z}{dt^{q}}+ \frac{1}{\mu _{3}}\tilde{\theta }^{T}_{3} \frac{d^{q}\tilde{\theta }_{3}}{dt^{q}}+\frac{1}{\sigma _{3}} \tilde{\varepsilon }^{\ast T}_{3} \frac{d^{q}\tilde{\varepsilon }^{\ast }_{3}}{dt^{q}} \\ &\leq -a_{3}z^{T}z-\tilde{\varepsilon }^{\ast }_{3} \bigl\vert z^{T} \bigr\vert - z^{T} \tilde{\theta }^{T}_{3}\psi _{3}(x_{3})+z^{T} \tilde{\theta }^{T}_{3} \psi _{3}(z_{3})+ \tilde{\varepsilon }^{\ast T}_{3} \bigl\vert z^{T} \bigr\vert \\ &\leq -a_{3}z^{T}z, \end{aligned} $$
(36)

where \(a_{3}>0\). We know from Lemma 3 that z asymptotically approaches zero, namely \(\lim_{t\to \infty } \Vert z \Vert =0\). □

Noting that \(\tilde{\varepsilon }^{\ast }_{i} \in R\), \(i=1,2,3\), so it has \(\tilde{\varepsilon }^{\ast }_{i}=\tilde{\varepsilon }^{\ast T}_{i}\).

We know from Lemma 2 that \(\tilde{\theta }_{i}\), \(\tilde{\varepsilon }^{\ast }_{i}\) are bounded, and \(\hat{\theta }_{i}\), \(\hat{\varepsilon }^{\ast }_{i}\) are also bounded. From the above proof, x, y, and z are bounded, and the construction of controllers (14), (15), and (16) shows that \(u_{i}\) is bounded for \(i=1,2,3\). So, all signals in a closed loop system (8) are bounded.

3.3 Simulation studies

In this subsection, we choose fractional-order system (8) as an example.

Let the parameters of the financial risk chaotic system (8) be \(\delta =10\), \(r=28\), \(b=\frac{8}{3}\), with the initial conditions of system (8) being \((2.5,0.5,4)\) and \(q=0.95\). In the simulation, x, y, z are the inputs of the fuzzy systems. We choose four Gaussian membership functions on \([-3,3]\). \(k_{1}=15\), \(k_{2}=15\), \(k_{3}=10\) and \(\mu _{i}=700\), \(\sigma _{i}=0.8\) for \(i=1,2,3\). The estimated value of the approximation error of the fuzzy system is \(\hat{\varepsilon }^{\ast }_{1}(0)=1\), \(\hat{\varepsilon }^{\ast }_{2}(0)=1\), \(\hat{\varepsilon }^{\ast }_{3}(0)=1.5\). The simulation results are shown in Fig. 5, Fig. 6, and Fig. 7. In Fig. 5, the system variables have a rapid convergence. Figure 6 shows the smoothness of the control inputs, and Fig. 7 indicates the convergence of the fuzzy parameters under the proposed fractional-order adaptation laws. It has been shown that good control performance has been obtained.

Figure 5
figure 5

Time response of system variables

Full size image
Figure 6
figure 6

Control inputs

Full size image
Figure 7
figure 7

Fuzzy parameters

Full size image

4 Conclusion

In this paper, the numerical solution of a fractional-order financial risk chaotic system was investigated and all parameter values of the system were determined. Dynamical analysis of the new fractional-order financial risk chaotic system was described by the phase portraits, Lyapunov exponents spectrum, and bifurcation diagram. We found that the chaotic behavior exists for the new fractional-order financial risk system in the range \(q_{1}\in [0.63, 1]\), \(q_{2} \in [0.9, 1]\), \(q_{3} \in [0.9, 1]\), and \(q \in [0.944, 1]\). Also, periodic behavior exists for the fractional-order financial risk system in the range of \(q_{1} \leq 0.62\), \(q_{2} < 0.9\), \(q_{3} < 0.9\), and \(q \leq 0.943\). An adaptive fuzzy approach has been presented in this study to handle the control problem for the fractional-order financial risk system. Based on the proposed method, simulation results were given to indicate the effectiveness of the proposed scheme.