Projective synchronization of different uncertain fractional-order multiple chaotic systems with input nonlinearity via adaptive sliding mode control

Abstract

This paper introduces the projective synchronization of different fractional-order multiple chaotic systems with uncertainties, disturbances, unknown parameters, and input nonlinearities. A fractional adaptive sliding surface is suggested to guarantee that more slave systems synchronize with one master system. First, an adaptive sliding mode controller is proposed for the synchronization of fractional-order multiple chaotic systems with unknown parameters and disturbances. Then, the synchronization of fractional-order multiple chaotic systems in the presence of uncertainties and input nonlinearity is obtained. The developed method can be used for many of fractional-order multiple chaotic systems. The bounds of the uncertainties and disturbances are unknown. Suitable adaptive rules are established to overcome the unknown parameters. Based on the fractional Lyapunov theorem, the stability of the suggested technique is proved. Finally, the simulation results demonstrate the feasibility and robustness of our suggested scheme.

1 Introduction

In the last few years, chaos synchronization of multiple chaotic systems has received considerable attention among scholars in various fields of research. Chaos synchronization has been used in a wide range of physics and engineering sciences [1,2,3]. Various control methods, such as fuzzy control [4,5,6,7], sliding mode control [8,9,10,11], backstepping control [12,13,14], active control [15, 16], observer-based control [17], impulsive control [18, 19], etc., have been suggested for synchronizing chaotic systems. Nevertheless, all of the aforementioned works are limited to studying two different chaotic systems without the presence of uncertainties and disturbances, and all the parameters of the systems are known; while in real-world applications, unmodified dynamics, structural changes in the system, and noise measurements cause uncertainties and disturbances to chaotic systems and it is difficult to determine the exact parameters of the system in practical situations. So, an important issue, which is the central idea of this paper, is to synchronize multiple chaotic systems in the presence of uncertainties, disturbances, and unknown parameters.

Fortunately, adaptive control [20,21,22] is an effective way to overcome these uncertainties and the lack of accurate information. Using this type of controller helps to synchronize master and slave systems even in the presence of uncertainties, disturbances, and unknown parameters. The major idea of the adaptive rule is the estimation of the uncertain parameters. Generally, the choice of matching control rule may be complex, but the analysis of convergence properties, which is another idea of this paper, is simple.

Fractional computing [23,24,25,26], a field of mathematics, has attracted a lot of researchers in recent years. Nowadays, it has been shown that chaotic behavior exists in many fractional-order systems such as fractional-order Chen system [27], fractional-order financial system [28], fractional-order Liu system [29], fractional-order Lu system [30], etc. The fractional computation, which is a generalization of classical computing, enables us to model nonlinear phenomena more accurately. The advantages of a fractional controller include a fractional sliding surface instead of a traditional sliding surface, the existence of a degree of freedom at the sliding surface, robustness and convergence in limited time. So far, some methods have been studied to synchronize fractional-order chaotic systems. For example, Huang et al. in [31] presented an active control scheme to achieve synchronization for a fractional chaotic financial system. In [32], a controller for a class of uncertain fractional-order chaotic systems based on adaptive backstepping control strategy was investigated. The problem of chaos synchronization of fractional-order time-delayed chaotic systems was developed in [33]. The scholars of [34], using a sliding mode control strategy, designed a fractional-order disturbance observer for synchronization of fractional-order chaotic systems with disturbances. Qin et al. in [35] reported a procedure to synchronize unknown fractional-order time-delayed chaotic systems based on adaptive fuzzy control. However, all of the above works only address the issue of synchronization between two fractional-order chaotic systems. Until now, there has been no work based on the synchronization of fractional-order multiple chaotic systems, which motivates us to write this paper.

On the other hand, sliding mode [36] is a control technique that is used for nonlinear systems with uncertainties in the model. This method of control uses a switching control rule to move the state of the system to a predetermined level, which is called a sliding surface, then, after moving the states on the surface, it tries to keep them on the surface. The use of this controller has many advantages including simple implementation, fast response, robustness, and good performance. Various articles have been presented to synchronize chaotic systems using a sliding mode controller. For instance, Liu et al. in [37] developed an adaptive sliding mode control method for synchronization of fractional-order chaotic systems. The authors of [38] focused on the construction, dynamic analysis, and control of a new fractional-order financial system. Furthermore, an efficient adaptive sliding mode controller technique was used to stabilize the suggested hyperchaotic fractional system with disturbances. In [39], the finite-time robust control of uncertain nonlinear fractional-order Hopfield neural networks was studied via adaptive sliding mode control. All of these works only examined the synchronization of two chaotic systems. In [40], the delay-dependent robust dissipative sampled-data control problem for a class of uncertain nonlinear systems with both differentiable and non-differentiable time-varying delays was investigated. Sakthivel et al. in [41] addressed the tracking performance of a class of singular systems with time-varying delay via a repetitive controller based on the equivalent-input disturbance approach. So far, studies based on design fractional sliding surface have not been published to synchronize fractional-order multiple chaotic systems, which is the greatest motivation behind this work.

In addition, when the controller is implemented in physical systems, due to the physical limitations of the actuator, there are nonlinearities in control input. Input nonlinearity can lead to poor performance or even instability of synchronization control systems. Also, input nonlinearity can lead the chaotic system to unpredictable results because the chaotic system is highly sensitive to parameter. Therefore, its effect cannot be ignored in analyzing the design of the controller and detecting the chaos synchronization. Consequently, it is important to obtain a controller in the presence of nonlinear input to synchronize chaos [42, 43]. In this paper, we consider the nonlinear input effect for controller design.

Considering the above discussion, in this paper, with the application of the fractional version of Lyapunov stability theory, a fractional sliding surface is developed. First, the projective synchronization of fractional-order multiple chaotic systems with unknown parameters and disturbances, where more slave systems synchronize with one master system, is studied. Then, using the proposed controller, the projective synchronization of fractional-order multiple chaotic systems in the presence of uncertainties, disturbances, and nonlinear input is investigated. In addition, proper adaptive rules are proposed to deal with uncertain parameters. At the end, based on the Lyapunov theorem, the convergence and stability of the suggested technique is demonstrated.

The advantages of our proposed method are as follows:

• A factional adaptive sliding surface is presented. The fractional derivative increases the degree of freedom at the sliding surface.

• Adaptive rules are used to deal with uncertain parameters. The suggested technique does not require information from disturbance bounds.

• The control strategy is used for synchronizing more slave systems with one master system.

• The suggested approach is used for a wide range of systems.

• Our proposed technique has well overcome the phenomenon of chattering.

• The suggested method has been successfully used to synchronize fractional-order multiple chaotic systems with uncertainties, disturbances, uncertain parameters, and nonlinear inputs.

• It is in favor of its potential applications in multilateral communications, secret signaling, complex networks, and many other engineering fields.

The organization of this research paper is as follows: in Sect. 2, the basic definitions of fractional calculus are mentioned. The projective synchronization of fractional-order multiple chaotic systems via the suggested controller in the presence of uncertain parameters and disturbances is investigated in Sect. 3. Section 4 describes the projective synchronization of fractional-order multiple chaotic systems in the presence of uncertainties, disturbances, and nonlinear input. Section 5 gives three illustrative examples. The concluding part of our discussion is in Sect. 6.

2 Fractional calculus

Definition 1

The Riemann–Liouville fractional integration of order α of a continuous function $f ( t )$ is represented as follows:

$$ {}_{t_{0}} I_{t}^{\alpha } f ( t ) = \frac{1}{\varGamma ( \alpha )} \int _{t_{0}}^{t} \frac{f(\tau )}{(t-\tau )^{1-\alpha }}\,d\tau , $$

(1)

where $\varGamma (\alpha )$ is the well-known gamma function [44].

Definition 2

The α-order Riemann–Liouville fractional derivative of function $f ( t )$ is expressed by

$$ {}_{t_{0}} D_{t}^{\alpha } f ( t ) = \frac{d^{\alpha } f(t)}{d t^{\alpha }} = \frac{1}{\varGamma (m-\alpha )} \frac{d^{m}}{d t ^{m}} \int _{t_{0}}^{t} \frac{f(\tau )}{(t-\tau )^{\alpha -m+1}}\,d\tau , $$

(2)

where $m-1<\alpha \leq m$, $m\in N$ [44].

Definition 3

The α-order Caputo fractional derivative of function $f ( t )$ is given by

$$ {}_{t_{0}} D_{t}^{\alpha } f ( t ) = \textstyle\begin{cases} \frac{1}{\varGamma (m-\alpha )} \int _{t_{0}}^{t} \frac{f^{(m)} (\tau )}{(t- \tau )^{\alpha -m+1}}\,d\tau ,& m-1< \alpha < m, \\ \frac{d^{m} f ( t )}{d t^{m}}, &\alpha =m, \end{cases} $$

(3)

where m is the smallest integer number larger than α [44].

Theorem 1

([45, 46])

Let $x=0$be an equilibrium point for either Caputo or Riemann–Liouville fractional non-autonomous system

$$ D^{q} x ( t ) =f ( x,t ), $$

(4)

where $f(x,t)$satisfies the Lipschitz condition with Lipschitz constant $l>0$and $\alpha \in (0,1)$. Assume that there exists a Lyapunov function $V(t,x(t))$satisfying

$$\begin{aligned}& \alpha _{1} \Vert x \Vert ^{a} \leq V ( t,x ) \leq \alpha _{2} \Vert x \Vert , \end{aligned}$$

(5)

$$\begin{aligned}& \dot{V} ( t,x ) \leq - \alpha _{3} \Vert x \Vert , \end{aligned}$$

(6)

where $\alpha _{1}$, $\alpha _{2}$, $\alpha _{3}$, andaare positive constants and $\Vert . \Vert$denotes an arbitrary norm. Then the equilibrium point of system (4) is Mittag-Leffler stable.

Remark 1

Mittag-Leffler stability implies asymptotic stability [46].

Remark 2

In this paper, the notation $D^{q}$ is used to represent the Riemann–Liouville fractional derivative.

3 Projective synchronization of fractional-order multiple chaotic systems with unknown parameters and disturbances

3.1 Problem statement

In this section, we utilize the adaptive sliding mode control technique to obtain projective synchronization of fractional-order multiple chaotic systems in the presence of uncertain parameters and disturbances.

Here the aim is that more slave systems synchronize with one master system, i.e., the synchronization error moves toward zero.

A master system is given as follows:

$$ \textstyle\begin{cases} D^{q} x_{11} ( t ) = g_{11} ( x_{11} ( t ), \dots , x_{1n} ( t ) ) + G_{11} ( x_{11} ( t ), \dots , x_{1n} ( t ) ) \xi _{11} + d_{11} (t), \\ D^{q} x_{12} ( t ) = g_{12} ( x_{11} ( t ), \dots , x_{1n} ( t ) ) + G_{12} ( x_{11} ( t ),\dots , x_{1n} ( t ) ) \xi _{12} + d_{12} (t), \\ \vdots \\ D^{q} x_{1n} ( t ) = g_{1n} ( x_{11} ( t ), \dots , x_{1n} ( t ) ) + G_{1n} ( x_{11} ( t ),\dots , x_{1n} ( t ) ) \xi _{1n} + d_{1n} (t), \end{cases} $$

(7)

where $0< q<1$. $x_{1} ( t ) = [ x_{11} ( t ), \dots , x_{1n} ( t ) ]^{T}$ and $d_{1} ( t ) = [ d_{11} ( t ), \dots , d_{1n} (t) ]^{T}$ are the vectors of the states and disturbances of the master system, respectively. $g_{1} ( x_{1} ( t ) ) = [ g _{11}, \dots , g_{1n} ]^{T}$ is a continuous nonlinear function, $G_{1} ( x_{1} ( t ) ) = [ G_{11}, \dots , G_{1n} ]^{T}$ is a continuous nonlinear function matrix, and $\xi _{1} = [ \xi _{11}, \dots , \xi _{1n} ]^{T}$ is the uncertain parameter vector of the master system.

Remark 3

Most of the famous fractional-order chaotic systems, such as fractional-order Lorenz system, fractional-order Chen system, fractional-order Rossler system, fractional-order Lu system, fractional-order Liu system, fractional-order Arneodo system, fractional-order Genesio system, fractional-order Duffing oscillator, and fractional-order Van der Pol oscillator, as paradigms in the research of chaos can be expressed by Eq. (7).

We describe the other $N -1$ slave systems with control signals as follows:

$$\begin{aligned}& \textstyle\begin{cases} D^{q} x_{j1} ( t ) = g_{j1} ( x_{j1} ( t ), \dots , x_{jn} ( t ) ) + G_{j1} ( x_{j1} ( t ), \dots , x_{jn} ( t ) ) \xi _{j1} + d_{j1} ( t ) + u_{j-1,1}, \\ D^{q} x_{j2} ( t ) = g_{j2} ( x_{j1} ( t ), \dots , x_{jn} ( t ) ) + G_{j2} ( x_{j1} ( t ), \dots , x_{jn} ( t ) ) \xi _{j2} + d_{j2} ( t ) + u_{j-1,2}, \\ \vdots \\ D^{q} x_{jn} ( t ) = g_{jn} ( x_{j1} ( t ), \dots , x_{jn} ( t ) ) + G_{jn} ( x_{j1} ( t ),\dots , x_{jn} ( t ) ) \xi _{jn} + d_{jn} ( t ) + u_{j-1,n}, \end{cases}\displaystyle \\& \quad j=2, \dots , N, \end{aligned}$$

(8)

where $0< q<1$. $x_{j} (t)= [ x_{j1} ( t ), \dots , x _{jn} ( t ) ]^{T}$ and $d_{j} ( t ) = [ d_{j1} ( t ), \dots , d_{jn} ( t ) ]^{T}$ are the vectors of the states and disturbances of the slave system, respectively. $g_{j} ( x_{j} (t))= [ g_{j1},\dots , g_{jn} ]^{T}$ is a continuous nonlinear function, $G_{j} ( x_{j} (t) )= [ G_{j1},\dots , G_{jn} ]^{T}$ is a continuous nonlinear function matrix, $\xi _{j} = [ \xi _{j1},\dots , \xi _{jn} ]^{T}$ is the uncertain parameter vector of the slave system, and $u_{j-1} = [ u_{j-1,1},\dots , u_{j-1,n} ]^{T}$ is the vector of the control inputs. The fractional-order multiple chaotic systems can be rewritten in the general form

$$ \textstyle\begin{cases} D^{q} x_{1} (t)= g_{1} ( x_{1} ( t ) ) + G _{1} ( x_{1} ( t ) ) \xi _{1} + d_{1} ( t ), \\ D^{q} x_{2} (t)= g_{2} ( x_{2} ( t ) ) + G _{2} ( x_{2} ( t ) ) \xi _{2} + d_{2} ( t ) + u_{1}, \\ \vdots \\ D^{q} x_{N} (t)= g_{N} ( x_{N} ( t ) ) + G _{N} ( x_{N} ( t ) ) \xi _{N} + d_{N} ( t ) + u_{N-1}, \end{cases} $$

(9)

Remark 4

If $x_{j} ( t ) =0$, $j=2, \dots ,N$, so the synchronization issue of fractional-order multiple chaotic systems (7) is converted to the stabilization issue.

Remark 5

If the functions $g_{r} ( x_{r} ) = g _{z} ( x_{z} )$ ($r,z=1,2, \dots ,N$, $r\neq z$) and $G_{r} ( x_{r} ) = G_{z} ( x_{z} )$ ($r,z=1,2, \dots ,N$, $r\neq z$), the projective synchronization of different fractional-order multiple chaotic systems is converted into the projective synchronization of identical fractional-order multiple chaotic systems with different initial conditions.

Definition 4

The aim of the control issue is to choose a suitable controller $u_{1}, u_{2}, \dots , u_{n-1}$ which $\lim_{t\rightarrow \infty } \Vert e_{j-1} (t) \Vert = \lim_{t\rightarrow \infty } \Vert x_{1} ( t ) - C _{j} x_{j} ( t ) \Vert =0$, $j =2, \dots , N$, i.e., the state of more slave systems (8) tends to that of one master system (7). This kind of synchronization is called projective synchronization [47].

The dynamics of the error system are formed by

$$\begin{array}{c}\left[\begin{array}{c}{D}^q{e}_1(t)\\ D^q{e}_2(t)\\ ⋮\\ D^q{e}_{N-1}(t)\end{array}\right]\hfill \\ =\left[\begin{array}{c}{D}^q{x}_1-C_2{D}^q{x}_2\\ D^q{x}_1-C_3{D}^q{x}_3\\ ⋮\\ D^q{x}_1-C_N{D}^q{x}_N\end{array}\right]\hfill \\ =\left[\begin{array}{c}{g}_1(x_1(t))+G_1(x_1(t)){\xi }_1+d_1(t)-C_2[g_2(x_2(t))+G_2(x_2(t)){\xi }_2+d_2(t)+u_1]\\ g_1(x_1(t))+G_1(x_1(t)){\xi }_1+d_1(t)-C_3[g_3(x_3(t))+G_3(x_3(t)){\xi }_3+d_3(t)+u_2]\\ ⋮\\ g_1(x_1(t))+G_1(x_1(t)){\xi }_1+d_1(t)-C_N[g_N(x_N(t))+G_N(x_N(t)){\xi }_N+d_N(t)+u_{N-1}]\end{array}\right].\hfill \end{array}$$

(10)

Remark 6

The definition of the desired scaling factor C means that there exists projective synchronization among N chaotic systems, then it is easy to know that complete synchronization [48], anti-synchronization [49], and another proposed synchronization [50] can be considered as special cases in our model.

The error system dynamics can be rewritten as follows:

$$\begin{aligned} D^{q} e_{j-1,i} ( t ) =& g_{1i} ( x_{1i} ) + G_{1i} ( x_{1i} ) \xi _{1} + d_{1i} ( t ) - C _{j} g_{ji} ( x_{ji} ) \\ &{}- C_{j} G_{ji} ( x_{ji} ) \xi _{j} - C_{j} d_{ji} ( t ) - C_{j} u_{j-1,i}. \end{aligned}$$

(11)

Considering the above discussion, it can be said that the synchronization issue has been converted into stabilization of error system. The purpose of this section is to design a proper control signal in such a way that the asymptotic stability of the error system ensures the convergence to zero.

Assumption 1

We can assume that $d_{1i} ( t )$ and $C_{j} d_{ji} ( t )$ are bounded by some positive constants, i.e., $\vert d_{1i} ( t ) \vert < \sigma _{1i}$ and $\vert C_{j} d_{ji} ( t ) \vert < \vartheta _{ji}$.

So, one obtains

$$ \bigl\vert d_{1i} ( t ) - C_{j} d_{ji} ( t ) \bigr\vert \leq \rho _{i}. $$

(12)

Assumption 2

The constants $\sigma _{1i}$, $\vartheta _{ji}$, and $\rho _{i}$ are unknown positive.

3.2 Design of controller

Sliding mode controller design consists of two steps: 1) suitable sliding surface design 2) designing a controller to assure that the system’s state tends to the sliding surface.

$$ S_{j-1} = D^{q-1} e_{j-1} ( t ) + D^{-1} \sum_{j=2}^{N} l _{j-1,i} e_{j-1,i} ( t ), $$

(13)

where $S_{j-1} = [ S_{j-1,1}, S_{j-1,2}.,\dots , S_{j-1,n} ]^{T}$ and $l_{j-1} =\operatorname{diag} ( l_{j-1,1}, \dots , l_{j-1,n} ) >0$, $j=2, \dots ,N$.

When the system is in sliding mode, it is clear that

$$ S_{j-1,i} = D^{q-1} e_{j-1,i} ( t ) + D^{-1} \sum_{j=2} ^{N} l_{j-1,i} e_{j-1,i} ( t ) =0 $$

(14)

and

$$ \dot{S}_{j-1,i} = D^{q} e_{j-1,i} ( t ) + \sum _{j=2}^{N} l_{j-1,i} e_{j-1,i} ( t ) =0. $$

(15)

So, the control rule is as follows:

$$\begin{aligned} u_{j-1,i} ( t ) =& C_{j}^{-1} \Biggl[ g_{1i} ( x _{1i} ) + G_{1i} ( x_{1i} ) \hat{\xi }_{1} - C _{j} g_{ji} ( x_{ji} ) - C_{j} G_{ji} ( x_{ji} ) \hat{\xi }_{j} \\ &{} + ( \hat{\rho }_{j-1,i} + \hat{\delta } _{j-1,i} ) \operatorname{sgn} ( S_{j-1,i} ) + \sum_{j=2}^{N} l_{j-1,i} e_{j-1,i} ( t ) \Biggr], \end{aligned}$$

(16)

where $\hat{\xi }_{1} >0$, $\hat{\xi }_{j} >0$, $\hat{\rho }_{j-1,i} >0$, and $\hat{\delta }_{j-1,i} >0$ are the adaptive parameters to overcome the uncertain parameters $\xi _{1}$, $\xi _{j}$, $\rho _{j-1,i}$, and $\delta _{j-1,i}$, respectively.

The adaptive rules are designed as follows:

$$\begin{aligned}& \dot{\hat{\xi }}_{1} = G_{1}^{T} \bigl( x_{1} ( t ) \bigr) S_{j-1}, \qquad \hat{\xi }_{1} ( 0 ) = \hat{\xi }_{10} >0, \end{aligned}$$

(17)

$$\begin{aligned}& \dot{\hat{\xi }}_{j} =- C_{j} G_{j}^{T} \bigl( x_{j} ( t ) \bigr) S_{j-1}, \qquad \hat{\xi }_{j} ( 0 ) = \hat{\xi }_{j0} >0, \end{aligned}$$

(18)

$$\begin{aligned}& \dot{\hat{\rho }}_{j-1,i} = \vert S_{j-1,i} \vert , \end{aligned}$$

(19)

$$\begin{aligned}& \dot{\hat{\delta }}_{j-1,i} = \vert S_{j-1,i} \vert . \end{aligned}$$

(20)

The initial values of the adaptive parameters $\hat{\xi }_{1}$, $\hat{\xi }_{j}$, $\hat{\rho }_{j}$, and $\hat{\delta }_{j}$ are $\hat{\xi }_{10}$, $\hat{\xi }_{j0}$, $\hat{\rho }_{j0}$, and $\hat{\delta }_{j0}$, respectively.

Theorem 2

By using controller (16) and adaptive rules (17)–(20), the projective synchronization error converges to zero, i.e., the slave system trajectories (8) converge to the master system trajectory (7).

Proof

We select the Lyapunov function candidate $V_{j-1} ( t )$ as follows:

$$\begin{aligned} V_{j-1} ( t ) =& \frac{1}{2} \sum _{i=1}^{n} \bigl[ S_{j-1,i} ^{2} + ( \hat{\rho }_{j-1,i} - \rho _{j-1,i} )^{2} + ( \hat{\delta }_{j-1,i} - \delta _{j-1,i} )^{2} \bigr] \\ &{} + \frac{1}{2} \bigl[ \Vert \hat{\xi }_{1} - \xi _{1} \Vert _{2}^{2} + \Vert \hat{\xi } _{j} - \xi _{j} \Vert _{2}^{2} \bigr]. \end{aligned}$$

(21)

Differentiating (21), we get

$$\begin{aligned} \dot{V}_{j-1,i} ( t ) =& \sum_{i=1}^{n} \bigl[ S_{j-1,i} \dot{S}_{j-1,i} + ( \hat{\rho }_{j-1,i} - \rho _{j-1,i} ) \dot{\hat{\rho }}_{j-1,i} + ( \hat{\delta }_{j-1,i} - \delta _{j-1,i} ) \dot{\hat{\delta }}_{j-1,i} \bigr] + ( \hat{\xi }_{1} - \xi _{1} )^{T} \dot{\hat{\xi }}_{1} \\ &{} + ( \hat{\xi }_{j} - \xi _{j} )^{T} \dot{\hat{\xi }}_{j}. \end{aligned}$$

(22)

Introducing (15) into (22), we obtain

$$\begin{aligned} \dot{V}_{j-1,i} ( t ) =& \sum_{i=1}^{n} \Biggl[ S_{j-1,i} \Biggl( D^{q} e_{j-1,i} ( t ) + \sum_{j=2}^{N} l_{j-1,i} e_{j-1,i} ( t ) \Biggr) \\ &{} + ( \hat{\rho }_{j-1,i} - \rho _{j-1,i} ) \dot{\hat{\rho }}_{j-1,i} + ( \hat{\delta }_{j-1,i} - \delta _{j-1,i} ) \dot{\hat{\delta }} _{j-1,i} \Biggr] \\ &{}+ ( \hat{\xi }_{1} - \xi _{1} )^{T} \dot{\hat{\xi }}_{1} + ( \hat{\xi }_{j} - \xi _{j} )^{T} \dot{\hat{\xi }}_{j}. \end{aligned}$$

(23)

Combining (11), (16), and (23), we get

$$\begin{aligned} \dot{V}_{j-1,i} ( t ) =& \sum_{i=1}^{n} \Biggl[ S_{j-1,i} \Biggl( - G_{1i} ( x_{1i} ) ( \hat{\xi }_{1} - \xi _{1} ) + C_{j} G_{ji} ( x_{ji} ) ( \hat{\xi }_{j} - \xi _{j} ) \\ &{} + \bigl( d_{1i} ( t ) - C_{j} d_{ji} ( t ) \bigr) - ( \hat{\rho }_{j-1,i} + \hat{\delta }_{j-1,i} ) \operatorname{sgn} ( S_{j-1} )- \sum_{j=2}^{N} l_{j-1,i} e_{j-1,i} ( t ) \\ &{} + \sum_{j=2}^{N} l_{j-1,i} e_{j-1,i} ( t ) \Biggr) + ( \hat{\rho }_{j-1,i} - \rho _{j-1,i} ) \dot{\hat{\rho }} _{j-1,i} + ( \hat{\delta }_{j-1,i} - \delta _{j-1,i} ) \dot{\hat{\delta }}_{j-1,i} \Biggr] \\ &{} + ( \hat{\xi }_{1} - \xi _{1} )^{T} \dot{\hat{\xi }}_{1} + ( \hat{\xi }_{j} - \xi _{j} )^{T} \dot{\hat{\xi }}_{j}. \end{aligned}$$

(24)

It is clear that

$$\begin{aligned} \dot{V}_{j-1,i} ( t ) \leq& \sum_{i=1}^{n} \bigl[ \vert S _{j-1,i} \vert \bigl\vert d_{1i} ( t ) - C_{j} d _{ji} ( t ) \bigr\vert \\ &{} + S_{j-1,i} \bigl( - G_{1i} ( x_{1i} ) ( \hat{\xi }_{1} - \xi _{1} ) + C _{j} G_{ji} ( x_{ji} ) ( \hat{\xi }_{j} - \xi _{j} ) \\ &{} - ( \hat{\rho }_{j-1,i} + \hat{\delta }_{j-1,i} ) \operatorname{sgn} ( S_{j-1} ) \bigr) + ( \hat{\rho }_{j-1,i} - \rho _{j-1,i} ) \dot{\hat{\rho }}_{j-1,i} + ( \hat{\delta }_{j-1,i} - \delta _{j-1,i} ) \dot{\hat{\delta }}_{j-1,i} \bigr] \\ &{} + ( \hat{\xi }_{1} - \xi _{1} )^{T} \dot{\hat{\xi }}_{1} + ( \hat{\xi }_{j} - \xi _{j} )^{T} \dot{\hat{\xi }}_{j}. \end{aligned}$$

(25)

Utilizing Assumption 1, we get

$$\begin{aligned} \dot{V}_{j-1,i} ( t ) \leq& \sum_{i=1}^{n} \bigl[ \rho _{j-1,i} \vert S_{j-1,i} \vert - S_{j-1,i} G_{1i} ( x_{1i} ) ( \hat{\xi }_{1} - \xi _{1} ) \\ &{} + C _{j} S_{j-1,i} G_{ji} ( x_{ji} ) ( \hat{\xi }_{j} - \xi _{j} ) - ( \hat{\rho }_{j-1,i} + \hat{\delta }_{j-1,i} ) \vert S_{j-1,i} \vert + ( \hat{\rho }_{j-1,i} - \rho _{j-1,i} ) \dot{\hat{\rho }}_{j-1,i} \\ &{} + ( \hat{\delta }_{j-1,i} - \delta _{j-1,i} ) \dot{\hat{ \delta }}_{j-1,i} \bigr] + ( \hat{\xi }_{1} - \xi _{1} )^{T} \dot{\hat{\xi }}_{1} + ( \hat{ \xi }_{j} - \xi _{j} )^{T} \dot{\hat{\xi }}_{j}. \end{aligned}$$

(26)

The following equations are equivalent:

$$\begin{aligned}& \sum_{i=1}^{n} \bigl[- S_{j-1,i} G_{1i} ( x_{1i} ) \bigr] ( \hat{\xi }_{1} - \xi _{1} ) =- ( \hat{\xi }_{1} - \xi _{1} )^{T} G_{1}^{T} \bigl( x_{1} ( t ) \bigr) S _{j-1}, \\& \sum_{i=1}^{n} \bigl[ C_{j} S_{j-1,i} G_{ji} ( x_{ji} ) \bigr] ( \hat{\xi }_{j} - \xi _{j} ) = C_{j} ( \hat{\xi } _{j} - \xi _{j} )^{T} G_{j}^{T} \bigl( x_{j} ( t ) \bigr) S_{j-1}. \end{aligned}$$

By replacing adaptive rules (17)–(20) into (26), we have

$$\begin{aligned} \dot{V}_{j-1,i} ( t ) \leq& \sum_{i=1}^{n} \bigl[ - ( \hat{\rho }_{j-1,i} - \rho _{j-1,i} ) \vert S_{j-1,i} \vert - \hat{\delta }_{j-1,i} \vert S _{j-1,i} \vert + ( \hat{\rho }_{j-1,i} - \rho _{j-1,i} ) \vert S_{j-1,i} \vert \\ &{} + ( \hat{\delta } _{j-1,i} - \delta _{j-1,i} ) \vert S_{j-1,i} \vert \bigr] - ( \hat{\xi }_{1} - \xi _{1} )^{T} G_{1}^{T} \bigl( x_{1} ( t ) \bigr) S_{j-1} \\ &{}+ C_{j} ( \hat{\xi }_{j} - \xi _{j} )^{T} G_{j}^{T} \bigl( x_{j} ( t ) \bigr) S_{j-1} + ( \hat{\xi }_{1} - \xi _{1} )^{T} G_{1}^{T} \bigl( x_{1} ( t ) \bigr) S_{j-1} \\ &{} - C_{j} ( \hat{\xi }_{j} - \xi _{j} )^{T} G_{j} ^{T} \bigl( x_{j} ( t ) \bigr) S_{j-1}. \end{aligned}$$

(27)

Thus, (27) implies that

$$ \dot{V}_{j-1,i} ( t ) \leq - \sum_{i=1}^{n} \delta _{j-1,i} \vert S_{j-1,i} \vert \leq 0. $$

(28)

Therefore, one can get

$$ V_{j-1,i} ( 0 ) \geq V_{j-1,i} ( t ) + \int _{0}^{t} \delta _{j-1,i} \bigl\vert S_{j-1,i} ( \tau ) \bigr\vert \,d \tau . $$

(29)

With the help of Barbalat’s lemma [51], it is easily obtained that

$$ \lim_{t\rightarrow \infty } \int _{0}^{t} \delta _{j-1,i} \bigl\vert S _{j-1,i} (\tau ) \bigr\vert \,d \tau =0, $$

(30)

which can conclude that $S_{j-1,i} ( t ) =0$. So, using the suggested controller, we can correctly obtain the projective synchronization between the first system and the jth system for all initial conditions, i.e., the synchronization error converges to zero. Thus, Theorem 2 is proved. □

Remark 7

Theorem 1 shows the possibility of sliding mode control (13) and adaptive laws (17)–(20), and the designed controller (16) can compensate the disturbances. Then it is easy to get that $\dot{V}_{j-1,i} ( t ) \leq 0$ by reducing the inequalities, then we get $S_{j-1,i} ( t ) =0$, i.e. $S_{j-1,i} ( t ) \dot{S}_{j-1,i} ( t ) <0$, i.e., $e_{j-1,i} ( t )$ can move to $S_{j-1,i} ( t ) =0$, then the asymptotic stability of (11) is obtained based on sliding mode control theory.

4 Projective synchronization of fractional-order multiple chaotic systems with uncertainties, disturbances, and input nonlinearity

4.1 Problem statement

Here, we utilize our suggested technique for projective synchronization of fractional-order multiple chaotic systems with uncertainties, disturbances, and nonlinear input. The master chaotic system is formulated as follows:

$$ \textstyle\begin{cases} D^{q} y_{11} ( t ) = h_{11} ( y_{1} ( t ) ) +\Delta h_{11} ( y_{1} ( t ),t)+ \omega _{11} (t), \\ D^{q} y_{12} ( t ) = h_{12} ( y_{1} ( t ) ) +\Delta h_{12} ( y_{1} ( t ),t)+ \omega _{12} (t), \\ \vdots \\ D^{q} y_{1n} ( t ) = h_{1n} ( y_{1} ( t ) ) +\Delta h_{1n} ( y_{1} ( t ),t)+ \omega _{1n} (t), \end{cases} $$

(31)

where $0< q<1$. $y_{1} ( t ) = [ y_{11} ( t ), \dots , y_{1n} ( t ) ]^{T}$, $\Delta h_{1} ( y_{1} ( t ),t ) = [\Delta h_{11} ( y_{1} ( t ),t ), \dots , \Delta h_{1n} ( y_{1} ( t ),t)]^{T}$, and $\omega _{1} ( t ) = [ \omega _{11} ( t ),\dots , \omega _{1n} (t) ]^{T}$ are the vectors of the states, uncertainties, and disturbances of the master system, respectively. $h_{1} ( y_{1} ( t ) ) = [ h _{11}, \dots , h_{1n} ]^{T}$ is a continuous nonlinear function. We describe the other $N -1$ slave systems with the control signals as follows:

$$ \textstyle\begin{cases} D^{q} y_{i1} ( t ) = h_{i1} ( y_{i} ( t ) ) +\Delta h_{i1} ( y_{i} ( t ),t)+ \omega _{i1} (t)+ \phi _{i-1,1} ( v_{i-1,1} ), \\ D^{q} y_{i2} ( t ) = h_{i2} ( y_{i} ( t ) ) +\Delta h_{i2} ( y_{i} ( t ),t)+ \omega _{i2} (t)+ \phi _{i-1,2} ( v_{i-1,2} ), \\ \vdots \\ D^{q} y_{in} ( t ) = h_{in} ( y_{i} ( t ) ) +\Delta h_{in} ( y_{i} ( t ),t)+ \omega _{in} (t)+ \phi _{i-1,n} ( v_{i-1,n} ), \end{cases}\displaystyle \quad i=2, \dots , N, $$

(32)

where $i =2, \dots ,N$ and $0< q<1$. $y_{i} (t)= [ y_{i1} ( t ), \dots , y_{in} ( t ) ]^{T}$, $\Delta h_{i} ( y_{i} ( t ),t ) = [ \Delta h_{i1} ( y_{i} ( t ),t ), \dots , \Delta h_{in} ( y_{i} ( t ),t) ]^{T}$, and $\omega _{i} ( t ) = [ \omega _{i1} ( t ), \dots , \omega _{in} (t)]^{T}$ are the vectors of the states, uncertainties, and disturbances of the slave system, respectively. $h_{i} ( y_{i} (t))= [ h_{i1}, \dots , h_{in} ]^{T}$ is a continuous nonlinear function, and $\phi _{i-1} ( v_{i-1} )= [ \phi _{i-1,1} ( v_{i-1,1} ), \dots , \phi _{i-1,n} ( v _{i-1,n} )]^{T}$ is the vector of the nonlinear control inputs. In (32), $\phi (v(t))$ is a continuous nonlinear function with $\phi ( 0 ) =0$ belonging to the sector $[\alpha ,\beta ]$, where α is a nonzero scalar, i.e.,

$$ \alpha _{i-1,p} v_{i-1,p}^{2} \leq v_{i-1,p} \phi _{i-1,p} ( v _{i-1,p} ) \leq \beta _{i-1,p} v_{i-1,p}^{2};\quad \alpha _{i-1,p} >0. $$

(33)

Figure 1 depicts the nonlinear function $\phi (v(t))$.

Figure 1

Input nonlinearity

The fractional-order multiple chaotic systems can be written in a general form:

$$ \textstyle\begin{cases} D^{q} y_{1} ( t ) = h_{1} ( y_{1} ( t ) ) +\Delta h_{1} ( y_{1} ( t ),t)+ \omega _{1} (t), \\ D^{q} y_{2} ( t ) = h_{2} ( y_{2} ( t ) ) +\Delta h_{2} ( y_{2} ( t ),t)+ \omega _{2} (t)+ \phi _{1} ( v_{1} ), \\ \vdots \\ D^{q} y_{N} ( t ) = h_{N} ( y_{N} ( t ) ) +\Delta h_{N} ( y_{N} ( t ),t)+ \omega _{N} (t)+ \phi _{N-1} ( v_{N-1} ). \end{cases} $$

(34)

To achieve the projective synchronization issue, the error among one master and more slave systems is defined as $e_{i-1} = y_{1} ( t ) - J_{i} y_{i} ( t )$, $i=2, \dots , N$. So, the aim is to synchronize system (31) with system (32) via the suggested control strategy, i.e.,

$$ \lim_{t\rightarrow \infty } \bigl\Vert e_{i-1} ( t ) \bigr\Vert = \lim_{t\rightarrow \infty } \bigl\Vert y_{1} ( t ) - J_{i} y_{i} ( t ) \bigr\Vert =0,\quad i =2, \dots , N. $$

(35)

Subtracting (32) from (31), we obtain the synchronization error dynamics as follows:

$$\begin{array}{c}\left[\begin{array}{c}{D}^q{e}_1(t)\\ D^q{e}_2(t)\\ ⋮\\ D^q{e}_{N-1}(t)\end{array}\right]\hfill \\ =\left[\begin{array}{c}{D}^q{y}_1-J_2{D}^q{y}_2\\ D^q{y}_1-J_3{D}^q{y}_3\\ ⋮\\ D^q{y}_1-J_N{D}^q{y}_N\end{array}\right]\hfill \\ =\left[\begin{array}{c}{h}_1(y_1(t))+\mathrm{\Delta }{h}_1(y_1(t),t)+{\omega }_1(t)-J_2[h_2(y_2(t))+\mathrm{\Delta }{h}_2(y_2(t),t)+{\omega }_2(t)+{\varphi }_1(v_1)]\\ h_1(y_1(t))+\mathrm{\Delta }{h}_1(y_1(t),t)+{\omega }_1(t)-J_3[h_3(y_3(t))+\mathrm{\Delta }{h}_3(y_3(t),t)+{\omega }_3(t)+{\varphi }_2(v_2)]\\ ⋮\\ h_1(y_1(t))+\mathrm{\Delta }{h}_1(y_1(t),t)+{\omega }_1(t)-J_N[h_N(y_N(t))+\mathrm{\Delta }{h}_N(y_N(t),t)+{\omega }_N(t)+{\varphi }_{N-1}(v_{N-1})]\end{array}\right].\hfill \end{array}$$

(36)

The error system dynamics can be rewritten as follows:

$$\begin{aligned} D^{q} e_{i-1,p} ( t ) =& h_{1p} \bigl( y_{1p} ( t ) \bigr) + \Delta h_{1p} \bigl( y_{1p} ( t ),t \bigr) + \omega _{1p} ( t ) - J_{i} h_{ip} \bigl( y _{ip} ( t ) \bigr) \\ &{}- J_{i} \Delta h_{ip} \bigl( y_{ip} ( t ),t \bigr)- J_{i} \omega _{ip} ( t ) - J_{i} \phi _{i-1,p} ( v_{i-1,p} ). \end{aligned}$$

(37)

Assumption 3

Suppose $\vert \Delta h_{1p} \vert < \varphi _{1p}$ and $\vert J_{i} \Delta h_{ip} \vert < \mu _{ip}$. So, we get

$$ \bigl\vert \Delta h_{1p} \bigl( y_{1p} ( t ),t \bigr) - J_{i} \Delta h_{ip} \bigl( y_{ip} ( t ),t \bigr) \bigr\vert \leq \gamma _{p}. $$

(38)

Assumption 4

We can also assume that $\omega _{1p} ( t )$ and $J_{i} \omega _{ip} ( t )$ are bounded. As a result, we have

$$ \bigl\vert \omega _{1p} ( t ) - J_{i} \omega _{ip} ( t ) \bigr\vert \leq \theta _{p}. $$

(39)

Assumption 5

The constants $\varphi _{1p}$, $\mu _{ip}$, $\gamma _{p}$, and $\theta _{p}$ are unknown positive.

4.2 Design of a controller

Here, we choose the sliding surface in the following form:

$$ S_{i-1} = D^{q-1} e_{i-1} ( t ) + D^{-1} \sum_{i=2}^{N} l _{i-1,p} e_{i-1,p} ( t ), $$

(40)

where $S_{i-1} = [ S_{i-1,1}, S_{i-1,2}, \dots , S_{i-1,n} ]^{T}$ and $l_{i-1} =\operatorname{diag} ( l_{i-1,1}, \dots , l_{i-1,n} ) >0$, $i=2, \dots ,N$.

The sliding surface can be rewritten as follows:

$$ S_{i-1,p} = D^{q-1} e_{i-1,p} ( t ) + D^{-1} \sum_{i=2} ^{N} l_{i-1,p} e_{i-1,p} ( t ). $$

(41)

Differentiating $S_{i-1,p}$ in (41) yields

$$\begin{aligned}& \dot{S}_{i-1,p} = D^{q} e_{i-1,p} ( t ) + \sum _{i=2} ^{N} l_{i-1,p} e_{i-1,p} ( t ). \end{aligned}$$

(42)

The control rule is selected as

$$\begin{aligned} v_{i-1,p} ( t ) =& \Biggl[ \frac{1}{J_{i} \alpha _{i-1,p}} \Biggl( \Biggl\vert \sum_{i=2}^{N} l_{i-1,p} e_{i-1,p} ( t ) \Biggr\vert + \bigl\vert h_{1p} \bigl( y_{1p} ( t ) \bigr) - J_{i} h_{ip} \bigl( y_{ip} ( t ) \bigr) \bigr\vert \\ &{} + \hat{\gamma }_{i-1,p} + \hat{\theta }_{i-1,p} + k_{i-1,p} \Biggr) \Biggr] \operatorname{sgn} ( S_{i-1,p} ) \\ =& \lambda _{i-1,p} \operatorname{sgn} ( S_{i-1,p} ), \end{aligned}$$

(43)

where $\hat{\gamma }_{i-1,p} >0$ and $\hat{\theta }_{i-1,p} >0$ are two adaptive parameters to overcome the uncertain parameters $\gamma _{j-1,i}$ and $\theta _{j-1,i}$, respectively. $k_{i-1,p} >0$ is a switching gain.

The adaptive rules are the following:

$$\begin{aligned}& \dot{\hat{\gamma }}_{i-1,p} = \vert S_{i-1,p} \vert , \end{aligned}$$

(44)

$$\begin{aligned}& \dot{\hat{\theta }}_{i-1,p} = \vert S_{i-1,p} \vert . \end{aligned}$$

(45)

Theorem 3

By using controller (43) and adaptive rules (44), (45), the projective synchronization error converges to zero, i.e., the slave system trajectories (32) converge to the master system trajectory (31).

Proof

The Lyapunov function $V_{i-1} ( t )$ can be selected as

$$ V_{i-1} ( t ) = \frac{1}{2} \sum _{p=1}^{n} \bigl[ S_{i-1,p} ^{2} + ( \hat{\gamma }_{i-1,p} - \gamma _{i-1,p} )^{2} + ( \hat{\theta }_{i-1,p} - \theta _{i-1,p} )^{2} \bigr]. $$

(46)

Its derivative is

$$ \dot{V}_{i-1} ( t ) = \sum_{p=1}^{n} \bigl[ S_{i-1,p} \dot{S} _{i-1,p} + ( \hat{\gamma }_{i-1,p} - \gamma _{i-1,p} ) \dot{\hat{\gamma }}_{i-1,p} +( \hat{\theta }_{i-1,p} - \theta _{i-1,p} ) \dot{\hat{\theta }}_{i-1,p} \bigr]. $$

(47)

Substituting (42) into (47), we have

$$\begin{aligned} \dot{V}_{i-1} ( t ) =& \sum_{p=1}^{n} \Biggl[ S_{i-1,p} \Biggl( D^{q} e_{i-1,p} ( t ) + \sum_{i=2}^{N} l_{i-1,p} e_{i-1,p} ( t ) \Biggr) \\ &{} + ( \hat{\gamma }_{i-1,p} - \gamma _{i-1,p} ) \dot{\hat{ \gamma }}_{i-1,p} +( \hat{\theta } _{i-1,p} - \theta _{i-1,p} ) \dot{\hat{\theta }}_{i-1,p} \Biggr]. \end{aligned}$$

(48)

By using (37) and (44), (45), we get

$$\begin{aligned} \dot{V}_{i-1} ( t ) =& \sum_{p=1}^{n} \Biggl[ S_{i-1,p} \Biggl( h_{1p} \bigl( y_{1p} ( t ) \bigr) + \Delta h _{1p} \bigl( y_{1p} ( t ),t \bigr) + \omega _{1p} ( t ) - J_{i} h_{ip} \bigl( y_{ip} ( t ) \bigr) \\ &{}- J_{i} \Delta h_{ip} \bigl( y_{ip} ( t ),t \bigr) - J_{i} \omega _{ip} ( t ) - J_{i} \phi _{i-1,p} ( v_{i-1,p} ) + \sum _{i=2}^{N} l_{i-1,p} e_{i-1,p} ( t ) \Biggr) \\ &{} + ( \hat{\gamma }_{i-1,p} - \gamma _{i-1,p} ) \vert S_{i-1,p} \vert + ( \hat{\theta } _{i-1,p} - \theta _{i-1,p} ) \vert S_{i-1,p} \vert \Biggr]. \end{aligned}$$

(49)

It is clear that

$$\begin{aligned} \dot{V}_{i-1} ( t ) \leq& \sum_{p=1}^{n} \Biggl[ \vert S _{i-1,p} \vert \bigl\vert \Delta h_{1p} \bigl( y_{1p} ( t ) \bigr) - J_{i} \Delta h_{ip} \bigl( y_{ip} ( t ) \bigr) \bigr\vert \\ &{}+ \vert S_{i-1,p} \vert \bigl\vert \omega _{1p} ( t ) - J_{i} \omega _{ip} ( t ) \bigr\vert + \vert S_{i-1,p} \vert \bigl\vert h _{1p} \bigl( y_{1p} ( t ) \bigr) - J_{i} h_{ip} \bigl( y_{ip} ( t ) \bigr) \bigr\vert \\ &{} + \vert S_{i-1,p} \vert \Biggl\vert \sum _{i=2}^{N} l_{i-1,p} e_{i-1,p} ( t ) \Biggr\vert - J_{i} S_{i-1,p} \phi _{i-1,p} ( v_{i-1,p} ) + ( \hat{\gamma }_{i-1,p} - \gamma _{i-1,p} ) \vert S_{i-1,p} \vert \\ &{}+ ( \hat{\theta }_{i-1,p} - \theta _{i-1,p} ) \vert S_{i-1,p} \vert \Biggr]. \end{aligned}$$

(50)

Utilizing (33), it is easily obtained that $- S_{i-1,p} \phi _{i-1,p} ( v_{i-1,p} ) \leq - \alpha _{i-1,p} \lambda _{i-1,p} \vert S_{i-1,p} \vert$. Furthermore, the following result can be achieved:

$$\begin{aligned} \dot{V}_{i-1} ( t ) \leq& \sum_{p=1}^{n} \Biggl[ \vert S _{i-1,p} \vert \bigl\vert h_{1p} \bigl( y_{1p} ( t ) \bigr) - J_{i} h_{ip} \bigl( y_{ip} ( t ) \bigr) \bigr\vert + \vert S_{i-1,p} \vert \Biggl\vert \sum_{i=2}^{N} l_{i-1,p} e_{i-1,p} ( t ) \Biggr\vert \\ &{}- J _{i} \alpha _{i-1,p} \lambda _{i-1,p} \vert S_{i-1,p} \vert + \hat{\gamma }_{i-1,p} \vert S_{i-1,p} \vert + \hat{\theta }_{i-1,p} \vert S_{i-1,p} \vert \Biggr]. \end{aligned}$$

(51)

By replacing

$$\begin{aligned} \lambda _{i-1,p} =& \frac{1}{J_{i} \alpha _{i-1,p}} \Biggl( \Biggl\vert \sum _{i=2}^{N} l_{i-1,p} e_{i-1,p} ( t ) \Biggr\vert + \bigl\vert h_{1p} \bigl( y_{1p} ( t ) \bigr) - J_{i} h_{ip} \bigl( y_{ip} ( t ) \bigr) \bigr\vert \\ &{} + \hat{\gamma }_{i-1,p} + \hat{\theta }_{i-1,p} + k_{i-1,p} \Biggr) \end{aligned}$$

into (51), we obtain

$$\begin{aligned} \dot{V}_{i-1} ( t ) \leq& \sum_{p=1}^{n} \Biggl[ \vert S _{i-1,p} \vert \bigl\vert h_{1p} \bigl( y_{1p} ( t ) \bigr) - J_{i} h_{ip} \bigl( y_{ip} ( t ) \bigr) \bigr\vert + \vert S_{i-1,p} \vert \Biggl\vert \sum_{i=2}^{N} l_{i-1,p} e_{i-1,p} ( t ) \Biggr\vert \\ &{} - J _{i} \alpha _{i-1,p} \times \frac{1}{J_{i} \alpha _{i-1,p}} \Biggl( \Biggl\vert \sum_{i=2}^{N} l_{i-1,p} e_{i-1,p} ( t ) \Biggr\vert \\ &{}+ \bigl\vert h_{1p} \bigl( y_{1p} ( t ) \bigr) - J_{i} h_{ip} \bigl( y_{ip} ( t ) \bigr) \bigr\vert + \hat{\gamma }_{i-1,p} + \hat{\theta }_{i-1,p} + k_{i-1,p} \Biggr) \vert S_{i-1,p} \vert \\ &{}+ \hat{\gamma }_{i-1,p} \vert S_{i-1,p} \vert + \hat{ \theta }_{i-1,p} \vert S _{i-1,p} \vert \Biggr]. \end{aligned}$$

(52)

It is clear that

$$ \dot{V}_{i-1} ( t ) \leq - \sum_{p=1}^{n} k_{i-1,p} \vert S_{i-1,p} \vert \leq 0. $$

(53)

Using Barbalat’s lemma [51] in the Lyapunov stability theorem, it can be concluded that the synchronization error moves toward zero and the projective synchronization is realized. Thus, Theorem 3 is proved. □

5 Simulation results

Here, three examples are presented to examine the usefulness of the technique suggested in the previous sections. Simulations are performed using MATLAB software.

5.1 Example 1

Consider the three fractional-order chaotic systems, Chen, Lorenz, and Liu, and assume the Chen system to be the master system and the Lorenz and Liu systems to be the slave systems, which are expressed by the following nonlinear equations:

$$\begin{array}{c}\mathit{\text{Chen system:}}\hfill \\ \left[\begin{array}{c}{D}^q{x}_{11}\\ D^q{x}_{12}\\ D^q{x}_{13}\end{array}\right]=\underset{g_1(x_1(t))}{\underbrace{\left[\begin{array}{c}0\\ -x_{11}{x}_{13}\\ x_{11}{x}_{12}\end{array}\right]}}+\underset{G_1(x_1(t))}{\underbrace{\left[\begin{array}{ccc}{x}_{12}-x_{11}& 0& 0\\ -x_{11}& x_{12}+x_{11}& 0\\ 0& 0& -x_{13}\end{array}\right]}}\underset{{\xi }_1}{\underbrace{\left[\begin{array}{c}{\xi }_{11}\\ {\xi }_{12}\\ {\xi }_{13}\end{array}\right]}}+\underset{D_1}{\underbrace{\left[\begin{array}{c}{d}_{11}\\ d_{12}\\ d_{13}\end{array}\right]}},\hfill \end{array}$$

(54)

$$\begin{array}{c}\mathit{\text{Lorenz system:}}\hfill \\ \left[\begin{array}{c}{D}^q{x}_{21}\\ D^q{x}_{22}\\ D^q{x}_{23}\end{array}\right]=\underset{g_2(x_2(t))}{\underbrace{\left[\begin{array}{c}0\\ -x_{21}{x}_{23}-x_{22}\\ x_{21}{x}_{22}\end{array}\right]}}+\underset{G_2(x_2(t))}{\underbrace{\left[\begin{array}{ccc}{x}_{22}-x_{21}& 0& 0\\ 0& x_{21}& 0\\ 0& 0& -x_{23}\end{array}\right]}}\underset{{\xi }_2}{\underbrace{\left[\begin{array}{c}{\xi }_{21}\\ {\xi }_{22}\\ {\xi }_{23}\end{array}\right]}}+\underset{D_2}{\underbrace{\left[\begin{array}{c}{d}_{21}\\ d_{22}\\ d_{23}\end{array}\right]}}\hfill \\ \phantom{\left[\begin{array}{c}{D}^q{x}_{21}\\ D^q{x}_{22}\\ D^q{x}_{23}\end{array}\right]=}+\underset{u_1}{\underbrace{\left[\begin{array}{c}{u}_{11}\\ u_{12}\\ u_{13}\end{array}\right]}},\hfill \end{array}$$

(55)

and

$$\begin{array}{c}\mathit{\text{Liu system:}}\hfill \\ \left[\begin{array}{c}{D}^q{x}_{31}\\ D^q{x}_{32}\\ D^q{x}_{33}\end{array}\right]=\underset{g_3(x_3(t))}{\underbrace{\left[\begin{array}{c}0\\ -x_{31}{x}_{33}\\ 4x_{31}^2\end{array}\right]}}+\underset{G_3(x_3(t))}{\underbrace{\left[\begin{array}{ccc}{x}_{32}-x_{31}& 0& 0\\ 0& x_{31}& 0\\ 0& 0& -x_{33}\end{array}\right]}}\underset{{\xi }_3}{\underbrace{\left[\begin{array}{c}{\xi }_{31}\\ {\xi }_{32}\\ {\xi }_{33}\end{array}\right]}}+\underset{D_3}{\underbrace{\left[\begin{array}{c}{d}_{31}\\ d_{32}\\ d_{33}\end{array}\right]}}+\underset{u_2}{\underbrace{\left[\begin{array}{c}{u}_{21}\\ u_{22}\\ u_{23}\end{array}\right]}},\hfill \end{array}$$

(56)

where $q=0.98$. $\xi _{11}$, $\xi _{12}$, $\xi _{13}$, $\xi _{21}$, $\xi _{22}$, $\xi _{23}$, $\xi _{31}$, $\xi _{32}$, and $\xi _{33}$ are the unknown parameters. $u_{1} = [ u_{11}, u_{12}, u_{13} ]^{T}$ and $u_{2} = [ u_{21}, u_{22}, u_{23} ]^{T}$ are the vectors of the control inputs. The disturbances are selected as follows:

$$D_1=\left[\begin{array}{c}-0.1cos(t)\\ -0.1cos(t)\\ -0.1cos(t)\end{array}\right],D_2=D_3=\left[\begin{array}{c}0.1cos(t)\\ 0.1cos(t)\\ 0.1cos(t)\end{array}\right].$$

(57)

Utilizing the suitable coefficients $C_{1} =\operatorname{diag} \{ 1,-1,-2 \}$ and $C_{2} =\operatorname{diag} \{ -1,1,2 \}$, we have

$$ \textstyle\begin{cases} e_{11} ( t ) = x_{11} ( t ) - x_{21} ( t ), \\ e_{12} ( t ) = x_{12} ( t ) + x_{22} ( t ), \\ e_{13} ( t ) = x_{13} ( t ) +2 x_{23} ( t ), \end{cases}\displaystyle \qquad \textstyle\begin{cases} e_{21} ( t ) = x_{11} ( t ) + x_{31} ( t ), \\ e_{22} ( t ) = x_{12} ( t ) - x_{32} ( t ), \\ e_{23} ( t ) = x_{13} ( t ) -2 x_{33} ( t ). \end{cases} $$

(58)

Vectors $[1,-1,1]$, $[2,1,1]$, and $[2,1,1]$ are chosen as the initial values of $[x_{11} ( 0 ), x_{12} ( 0 ), x_{13} ( 0 )]$, $[x_{21} ( 0 ), x_{22} ( 0 ), x_{23} ( 0 )]$, and $[x_{31} ( 0 ), x _{32} ( 0 ), x_{33} ( 0 )]$, respectively. The initial conditions of the adaptive vector parameters are supposed as $[\hat{\xi }_{11} (0),\hat{\xi }_{12} (0),\hat{\xi }_{13} (0)]=[6, 0, -8]$, $[\hat{\xi }_{21} (0),\hat{\xi }_{22} (0),\hat{\xi }_{23} (0)]=[0, 6, 4]$; $[\hat{\xi }_{11} (0),\hat{\xi } _{12} (0),\hat{\xi }_{13} (0)]=[24, 0, -2]$, $[\hat{\xi }_{31} (0), \hat{\xi }_{32} (0),\hat{\xi }_{33} (0)]=[0, 24, 1]$; $[ \hat{\rho }_{11} ( 0 ), \hat{\rho }_{12} ( 0 ), \hat{\rho }_{13} ( 0 )]=[0.5, 0.5, 0.5]$, $[ \hat{\rho }_{21} ( 0 ), \hat{\rho }_{22} ( 0 ), \hat{\rho }_{23} ( 0 )]=[0.3, 0.3, 0.3]$; $[ \hat{\delta }_{11} ( 0 ), \hat{\delta }_{12} ( 0 ), \hat{\delta }_{13} ( 0 )]=[0.5, 0.5, 0.5]$, $[ \hat{\delta }_{21} ( 0 ), \hat{\delta }_{22} ( 0 ), \hat{\delta }_{23} ( 0 )]=[0.3, 0.3, 0.3]$. It is supposed $l_{1} = l_{2} =\operatorname{diag}\{25, 5, 1\}$. The control strategy in Theorem 2 is given to projectively synchronize one fractional-order Chen system (54) and two fractional-order Lorenz (55) and fractional-order Liu (56) systems with unknown parameters and disturbances. Figure 2 depicts the projective synchronization error of systems (54), (55), and (56) in the presence of suggested controller (16). It is represented that error via the suggested controller tends to zero, which shows that the projective synchronization is realized between fractional-order multiple chaotic systems with uncertain parameters and disturbances. Figure 3 displays the estimate of the master and slave system parameters. The uncertain parameters of fractional-order multiple chaotic systems are identified correctly, and the adaptive parameters move toward some true values. The trajectories of sliding surface (13) are shown in Fig. 4.

Figure 2

State trajectories of the error system: (a) $e_{11} (t)$, $e _{12} (t)$, $e_{13} (t)$ and (b) $e_{21} (t)$, $e_{22} (t)$, $e_{23} (t)$

Figure 3

Estimation of master and slave system parameters: (a) $\xi _{11} (t)$, $\xi _{12} (t)$, $\xi _{13} (t)$, $\xi _{21} (t)$, $\xi _{22} (t)$, $\xi _{23} (t)$ and (b) $\xi _{11} (t)$, $\xi _{12} (t)$, $\xi _{13} (t)$, $\xi _{31} (t)$, $\xi _{32} (t)$, $\xi _{33} (t)$

Figure 4

State trajectories of the sliding surface: (a) $S_{11} ( t )$, $S_{12} ( t )$, $S_{13} ( t )$ and (b) $S_{21} ( t )$, $S_{22} ( t )$, $S_{23} ( t )$

5.2 Example 2: economical system

One of the real physical systems that have chaotic behavior is the economy and finance. But the chaotic behavior in financial systems is undesirable due to the threat of investment safety. Therefore, in order to improve economic performance, the phenomenon of chaos should be reduced in financial systems. The model examined in this paper is a fractional-order financial system consisting of three nonlinear differential equations. The system has three variables $x_{11}$, $x_{12}$, and $x_{13}$ that represent the interest rate, the investment demand, and the price index, respectively.

Consider the three fractional-order financial systems as follows:

$$\begin{array}{c}\text{master system:}\hfill \\ \left[\begin{array}{c}{D}^q{x}_{11}\\ D^q{x}_{12}\\ D^q{x}_{13}\end{array}\right]=\underset{g_1(x_1(t))}{\underbrace{\left[\begin{array}{c}{x}_{13}+x_{12}{x}_{11}\\ 1-x_{11}^2\\ -x_{11}\end{array}\right]}}+\underset{G_1(x_1(t))}{\underbrace{\left[\begin{array}{ccc}-x_{11}& 0& 0\\ 0& -x_{12}& 0\\ 0& 0& -x_{13}\end{array}\right]}}\underset{{\xi }_1}{\underbrace{\left[\begin{array}{c}{\xi }_{11}\\ {\xi }_{12}\\ {\xi }_{13}\end{array}\right]}}+\underset{D_1}{\underbrace{\left[\begin{array}{c}-0.2cos(t)\\ -0.2cos(t)\\ -0.2cos(t)\end{array}\right]}},\hfill \end{array}$$

(59)

$$\begin{array}{c}\text{slave systems:}\hfill \\ \left[\begin{array}{c}{D}^q{x}_{21}\\ D^q{x}_{22}\\ D^q{x}_{23}\end{array}\right]=\underset{g_2(x_2(t))}{\underbrace{\left[\begin{array}{c}{x}_{23}+x_{22}{x}_{21}\\ 1-x_{21}^2\\ -x_{21}\end{array}\right]}}+\underset{G_2(x_2(t))}{\underbrace{\left[\begin{array}{ccc}-x_{21}& 0& 0\\ 0& -x_{22}& 0\\ 0& 0& -x_{23}\end{array}\right]}}\underset{{\xi }_2}{\underbrace{\left[\begin{array}{c}{\xi }_{21}\\ {\xi }_{22}\\ {\xi }_{23}\end{array}\right]}}+\underset{D_2}{\underbrace{\left[\begin{array}{c}0.2cos(t)\\ 0.2cos(t)\\ 0.2cos(t)\end{array}\right]}}\hfill \\ \phantom{\left[\begin{array}{c}{D}^q{x}_{21}\\ D^q{x}_{22}\\ D^q{x}_{23}\end{array}\right]=}+\underset{u_1}{\underbrace{\left[\begin{array}{c}{u}_{11}\\ u_{12}\\ u_{13}\end{array}\right]}}\hfill \end{array}$$

(60)

and

$$\begin{array}{rcl}\left[\begin{array}{c}{D}^q{x}_{31}\\ D^q{x}_{32}\\ D^q{x}_{33}\end{array}\right]& =& \underset{g_3(x_3(t))}{\underbrace{\left[\begin{array}{c}{x}_{33}+x_{32}{x}_{31}\\ 1-x_{31}^2\\ -x_{31}\end{array}\right]}}+\underset{G_3(x_3(t))}{\underbrace{\left[\begin{array}{ccc}-x_{31}& 0& 0\\ 0& -x_{32}& 0\\ 0& 0& -x_{33}\end{array}\right]}}\underset{{\xi }_3}{\underbrace{\left[\begin{array}{c}{\xi }_{31}\\ {\xi }_{32}\\ {\xi }_{33}\end{array}\right]}}+\underset{D_3}{\underbrace{\left[\begin{array}{c}0.2cos(t)\\ 0.2cos(t)\\ 0.2cos(t)\end{array}\right]}}\\ & & +\underset{u_2}{\underbrace{\left[\begin{array}{c}{u}_{21}\\ u_{22}\\ u_{23}\end{array}\right]}},\end{array}$$

(61)

where $q=0.98$. $\xi _{11}$, $\xi _{12}$, $\xi _{13}$, $\xi _{21}$, $\xi _{22}$, $\xi _{23}$, $\xi _{31}$, $\xi _{32}$, and $\xi _{33}$ are the unknown parameters. $u_{1} = [ u_{11}, u_{12}, u_{13} ]^{T}$ and $u_{2} = [ u_{21}, u_{22}, u_{23} ]^{T}$ are the vectors of the control inputs.

Figure 5 illustrates the chaotic behavior of financial system (59) for $\xi _{11} = 1$, $\xi _{12} = 0.1$, and $\xi _{13} = 1$.

Figure 5

The chaos attractor of system (59) with $x_{11} ( 0 ) =2$, $x_{12} ( 0 ) =-3$, $x_{13} ( 0 ) =2$

Using the suitable coefficients $C_{1} =\operatorname{diag} \{ 1,-1,-2 \}$ and $C_{2} =\operatorname{diag} \{ -1,1,2 \}$, we have

$$ \textstyle\begin{cases} e_{11} ( t ) = x_{11} ( t ) - x_{21} ( t ), \\ e_{12} ( t ) = x_{12} ( t ) + x_{22} ( t ), \\ e_{13} ( t ) = x_{13} ( t ) +2 x_{23} ( t ), \end{cases}\displaystyle \qquad \textstyle\begin{cases} e_{21} ( t ) = x_{11} ( t ) + x_{31} ( t ), \\ e_{22} ( t ) = x_{12} ( t ) - x_{32} ( t ), \\ e_{23} ( t ) = x_{13} ( t ) -2 x_{33} ( t ). \end{cases} $$

(62)

The initial conditions can be selected as $[ x_{11} ( 0 ), x_{12} ( 0 ), x_{13} ( 0 ) ]^{T} = [2,-1,1]^{T}$, $[ x_{21} ( 0 ), x_{22} ( 0 ), x_{23} ( 0 ) ]^{T} = [1,2,1]^{T}$, and $[ x_{31} ( 0 ), x_{32} ( 0 ), x_{33} ( 0 ) ]^{T} = [1,2,1]^{T}$.

Applying controller (16), the trajectories of the projective synchronization error are shown in Fig. 6. It can be seen that the synchronization errors converge to zero, which indicates that more slave systems and one master system are indeed synchronized. Figure 7 shows the trajectories of sliding surface (13). Obviously, the control signal is practical.

Figure 6

State trajectories of the error system: (a) $e_{11} (t)$, $e _{12} (t)$, $e_{13} (t)$ and (b) $e_{21} (t)$, $e_{22} (t)$, $e_{23} (t)$

Figure 7

State trajectories of the sliding surface: (a) $S_{11} ( t )$, $S_{12} ( t )$, $S_{13} ( t )$ and (b) $S_{21} ( t )$, $S_{22} ( t )$, $S_{23} ( t )$

5.3 Example 3

Consider the master system and two slave systems as follows:

$$\begin{array}{c}\text{master system:}\hfill \\ \left[\begin{array}{c}{D}^q{y}_{11}\\ D^q{y}_{12}\\ D^q{y}_{13}\end{array}\right]=\underset{h_1(y_1(t))}{\underbrace{\left[\begin{array}{c}-36y_{11}+36y_{12}\\ 20y_{12}-y_{11}{y}_{13}\\ -36y_{13}+y_{11}{y}_{12}\end{array}\right]}}+\underset{\mathrm{\Delta }{h}_1(y_1(t))}{\underbrace{\left[\begin{array}{c}\mathrm{\Delta }{h}_{11}(y_{11}(t))\\ \mathrm{\Delta }{h}_{12}(y_{12}(t))\\ \mathrm{\Delta }{h}_{13}(y_{13}(t))\end{array}\right]}}+\underset{{\omega }_1}{\underbrace{\left[\begin{array}{c}{\omega }_{11}(t)\\ {\omega }_{12}(t)\\ {\omega }_{13}(t)\end{array}\right]}},\hfill \end{array}$$

(63)

$$\begin{array}{c}\text{slave systems:}\hfill \\ \left[\begin{array}{c}{D}^q{y}_{21}\\ D^q{y}_{22}\\ D^q{y}_{23}\end{array}\right]=\underset{h_2(y_2(t))}{\underbrace{\left[\begin{array}{c}-10y_{21}+10y_{22}\\ 28y_{21}-y_{22}-y_{21}{y}_{23}\\ -\frac{8}{3}{y}_{23}+y_{21}{y}_{22}\end{array}\right]}}+\underset{\mathrm{\Delta }{h}_2(y_2(t))}{\underbrace{\left[\begin{array}{c}\mathrm{\Delta }{h}_{21}(y_{21}(t))\\ \mathrm{\Delta }{h}_{22}(y_{22}(t))\\ \mathrm{\Delta }{h}_{23}(y_{23}(t))\end{array}\right]}}+\underset{{\omega }_2}{\underbrace{\left[\begin{array}{c}{\omega }_{21}(t)\\ {\omega }_{22}(t)\\ {\omega }_{23}(t)\end{array}\right]}}+\underset{{\phi }_1(v_1)}{\underbrace{\left[\begin{array}{c}{\phi }_{11}(v_{11})\\ {\phi }_{12}(v_{12})\\ {\phi }_{13}(v_{13})\end{array}\right]}}\hfill \end{array}$$

(64)

and

$$\begin{array}{c}\left[\begin{array}{c}{D}^q{y}_{31}\\ D^q{y}_{32}\\ D^q{y}_{33}\end{array}\right]=\underset{h_3(y_3(t))}{\underbrace{\left[\begin{array}{c}-35y_{31}+35y_{32}\\ -7y_{31}+28y_{32}-y_{31}{y}_{33}\\ -3y_{33}+y_{31}{y}_{32}\end{array}\right]}}+\underset{\mathrm{\Delta }{h}_3(y_3(t))}{\underbrace{\left[\begin{array}{c}\mathrm{\Delta }{h}_{31}(y_{31}(t))\\ \mathrm{\Delta }{h}_{32}(y_{32}(t))\\ \mathrm{\Delta }{h}_{33}(y_{33}(t))\end{array}\right]}}+\underset{{\omega }_3}{\underbrace{\left[\begin{array}{c}{\omega }_{31}(t)\\ {\omega }_{32}(t)\\ {\omega }_{33}(t)\end{array}\right]}}\hfill \\ \phantom{\left[\begin{array}{c}{D}^q{y}_{31}\\ D^q{y}_{32}\\ D^q{y}_{33}\end{array}\right]=}+\underset{{\phi }_2(v_2)}{\underbrace{\left[\begin{array}{c}{\phi }_{21}(v_{21})\\ {\phi }_{22}(v_{22})\\ {\phi }_{23}(v_{23})\end{array}\right],}}\hfill \end{array}$$

(65)

where $q=0.98$. $\phi _{1} ( v_{1} ) = [ \phi _{11} ( v_{11} ), \phi _{12} ( v_{12} ), \phi _{13} ( v_{13} ) ]^{T}$, and $\phi _{2} ( v_{2} )= [ \phi _{21} ( v_{21} ), \phi _{22} ( v_{22} ), \phi _{23} ( v_{23} )]^{T}$ are the vectors of the nonlinear control inputs. $\varphi _{i-1,p} =[3+2\sin t]v_{i-1,p}$ ($i=2,3$, $p=1,2,3$) is selected as the nonlinear control inputs. The uncertainties and disturbances are chosen as follows:

$$\begin{array}{rl}& \mathrm{\Delta }{h}_1(y_1(t))=\left[\begin{array}{c}0.5sin(\pi y_{11})\\ 0.5sin(2\pi y_{12})\\ 0.5sin(3\pi y_{13})\end{array}\right],\\ & \mathrm{\Delta }{h}_2(y_2(t))=\left[\begin{array}{c}-0.5sin(\pi y_{21})\\ -0.5sin(2\pi y_{22})\\ -0.5sin(3\pi y_{23})\end{array}\right],\text{and}\\ & \mathrm{\Delta }{h}_3(y_3(t))=\left[\begin{array}{c}0.5sin(\pi y_{31})\\ 0.5sin(2\pi y_{32})\\ 0.5sin(3\pi y_{33})\end{array}\right]\end{array}$$

(66)

$${\omega }_1=\left[\begin{array}{c}0.1cost\\ 0.1cost\\ 0.1cost\end{array}\right],{\omega }_2=\left[\begin{array}{c}-0.1cost\\ -0.1cost\\ -0.1cost\end{array}\right],\text{and}{\omega }_3=\left[\begin{array}{c}0.1cost\\ 0.1cost\\ 0.1cost\end{array}\right].$$

(67)

Utilizing the suitable coefficients $J_{1} =\operatorname{diag} \{ 1,-1,-2 \}$ and $J_{2} =\operatorname{diag} \{ -1,1,2 \}$, we have

$$ \textstyle\begin{cases} e_{11} ( t ) = x_{11} ( t ) - x_{21} ( t ), \\ e_{12} ( t ) = x_{12} ( t ) + x_{22} ( t ), \\ e_{13} ( t ) = x_{13} ( t ) +2 x_{23} ( t ), \end{cases}\displaystyle \qquad \textstyle\begin{cases} e_{21} ( t ) = x_{11} ( t ) + x_{31} ( t ), \\ e_{22} ( t ) = x_{12} ( t ) - x_{32} ( t ), \\ e_{23} ( t ) = x_{13} ( t ) -2 x_{33} ( t ). \end{cases} $$

(68)

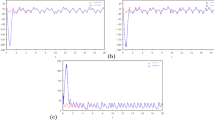
Vectors $[4,-1,6]$, $[1,2,3]$, and $[3,1,2]$ are chosen as the initial values of $[y_{11} ( 0 ), y_{12} ( 0 ), y_{13} ( 0 )]$, $[y_{21} ( 0 ), y_{22} ( 0 ), y_{23} ( 0 )]$, and $[y_{31} ( 0 ), y _{32} ( 0 ), y_{33} ( 0 )]$, respectively. The initial conditions of the adaptive vector parameters are supposed as $[\hat{\gamma }_{11} ( 0 ),\hat{\gamma }_{12} ( 0 ),\hat{\gamma }_{13} ( 0 )]=[0.03, 0.03, 0.03]$, $[\hat{\gamma }_{21} ( 0 ),\hat{\gamma } _{22} ( 0 ),\hat{\gamma }_{23} ( 0 )]=[0.02, 0.01, 0.01]$, $[\hat{\theta }_{11} ( 0 ), \hat{\theta }_{12} ( 0 ),\hat{\theta }_{13} ( 0 )]=[0.03, 0.03, 0.03]$, and $[\hat{\theta }_{21} ( 0 ),\hat{\theta }_{22} ( 0 ),\hat{\theta } _{23} ( 0 )]=[0.02, 0.01, 0.01]$. It is supposed $l_{1} = l_{2} =\operatorname{diag}\{25, 5, 1\}$. So, the control strategy under the conditions of Theorem 3 is applied to the synchronization of one master system (63) and two slave systems (64) and (65) with uncertainties, disturbances, and input nonlinearity. Figure 8 demonstrates the trajectories of the projective synchronization error, when controller (43) is used. As it can be seen, the suggested controller has been able to synchronize more slave systems with one master system even with uncertainties and disturbances. The estimate of the master and slave systems parameters is displayed in Fig. 9. Figure 10 shows the trajectories of sliding surface (40).

Figure 8

State trajectories of the error system: (a) $e_{11} (t)$, $e _{12} (t)$, $e_{13} (t)$ and (b) $e_{21} (t)$, $e_{22} (t)$, $e_{23} (t)$

Figure 9

Estimation of adaptive parameters: (a) $\gamma _{11} (t)$, $\gamma _{12} (t)$, $\gamma _{13} (t)$, $\gamma _{21} (t)$, $\gamma _{22} (t)$, $\gamma _{23} (t)$ and (b) $\theta _{11} (t)$, $\theta _{12} (t)$, $\theta _{13} (t)$, $\theta _{21} (t)$, $\theta _{22} (t)$, $\theta _{23} (t)$

Figure 10

State trajectories of the sliding surface: (a) $S_{11} ( t )$, $S_{12} ( t )$, $S_{13} ( t )$ and (b) $S_{21} ( t )$, $S_{22} ( t )$, $S_{23} ( t )$

6 Conclusion

This work attempts to study the issue of projective synchronization of different fractional-order multiple chaotic systems with fully uncertain parameters, uncertainties, disturbances, and nonlinear input. In the initial part of the discussion, an adaptive sliding mode controller is suggested for projective synchronization in the presence of uncertain parameters and disturbances. Then, the projective synchronization via an adaptive sliding mode controller is studied with input nonlinearity. It should be noted that the suggested method is simple and practical. The stability of the proposed technique is investigated via the fractional Lyapunov stability theorem and adaptive rules. Simulation results show that the suggested technique is effective and applicable to the synchronization of different fractional-order multiple chaotic systems. Eventually, it is worthy of consideration to tackle the problems of optimal control and the time-delay of these systems as the future research topics.