1 Introduction

Fractional partial differential equations as generalizations of classical partial differential equations, and they have been proposed and applied to many applications in various fields of physical sciences and engineering such as electromagnetic, acoustics, visco-elasticity and electro-chemistry. Recently, the solution of fractional partial differential equations has been obtained through a double Laplace decomposition method by the authors [1–3]. The natural transform decomposition method has been successfully used to handle linear and nonlinear problems appearing in physical and engineering disciplines [4, 5]. The Navier–Stokes equations are the fluid dynamics identical to Newton’s second law, force equals mass times acceleration, and they are of crucial significance in fluid dynamics. Also the Navier–Stokes equations are vector equations. Recently, many powerful methods have been used to obtain different type solution of time-fractional Navier–Stokes equation such as the Adomian decomposition method [6], the q-homotopy analysis transform scheme [7], the modified Laplace decomposition method [8, 9], the natural homotopy perturbation method [10] and a reliable algorithm based on the new homotopy perturbation transform method [11]. The one-dimensional Navier–Stokes equation with time-fractional derivative has been given in operator form [12]. The main objective of this work is to find the exact and approximate solution of time-fractional Navier–Stokes equations by using the double and triple Laplace Adomian decomposition methods, respectively.

2 Basic definitions and preliminaries concepts

In this section, we give some essential definitions, properties and theorems of fractional calculus and double Laplace transform, which should be used in the present study.

Definition 1

In [13] Let f be a function of three variables x, y and t, where \(x,y,t>0\). The triple Laplace transform of f is defined by

$$ L_{x}L_{y}L_{t} \bigl[ f(x,y,t) \bigr] =F(p,q,s)= \int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }e^{-px-qy-st}f(x,y,t)\,dt \,dy\,dx, $$

where p, q, s are complex variables, and further triple Laplace transforms of the partial derivatives are shown by

$$\begin{aligned}& L_{x}L_{y}L_{t} \bigl[ u_{x} ( x,y,t ) \bigr] =pU(p,q,s)-U(0,q,s), \\& L_{x}L_{y}L_{t} \bigl[ u_{t} ( x,y,t ) \bigr] =sU(p,q,s)-U(p,q,0). \end{aligned}$$

Likewise, the triple Laplace transform for the second partial derivative with respect to x, y and t are defined by

$$\begin{aligned}& L_{x}L_{y}L_{t} \bigl[ u_{tt} ( x,y,t ) \bigr] =p^{2}U(p,q,s)-pU(0,q,s)- \frac{\partial U(0,q,s)}{\partial x}, \\& L_{x}L_{y}L_{t} \bigl[ u_{yy} ( x,y,t ) \bigr] =q^{2}U(p,q,s)-qU(p,0,s)- \frac{\partial U(p,0,s)}{\partial y}, \\& L_{x}L_{y}L_{t} \bigl[ u_{tt} ( x,y,t ) \bigr] =s^{2}U(p,q,s)-sU(p,q,0)- \frac{\partial U(p,q,0)}{\partial t}. \end{aligned}$$

The inverse triple Laplace transform \(L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} [ F ( p,q,s ) ] =f(x,y,t)\) is defined [13] as follows:

$$ f(x,y,t)=\frac{1}{2\pi i} \int _{e-i\infty }^{e+i\infty }e^{px}\,dp \frac{1}{2\pi i} \int _{c-i\infty }^{c+i\infty }e^{qy}\,dq \frac{1}{2\pi i} \int _{d-i\infty }^{d+i\infty }e^{st}\,ds. $$

Definition 2

([14–16])

The Caputo time-fractional derivative operator of order \(\alpha >0\) is determined by

$$ D_{t}^{\alpha }u(r,t)= \textstyle\begin{cases} \frac{1}{\Gamma ( m-\alpha ) }\int _{0}^{t} ( t- \tau ) ^{m-\alpha -1} \frac{\partial ^{m}u(r,\tau )}{\partial \tau ^{m}}\,d\tau , \quad m-1< \alpha < m, \\ \frac{\partial ^{m}u(r,t)}{\partial t^{m}},\quad \text{for }m=\alpha \in \mathbb{N.} \end{cases} $$

In the next theorem, one can introduce the triple Laplace transform of the partial fractional Caputo derivatives.

Theorem 1

([17])

Let \(\alpha , \beta ,\gamma >0\), \(n-1<\alpha \leq n\), \(m-1<\beta \leq m\), \(r-1<\gamma \leq r\)and \(n,m,p\in \mathbb{N} \), so that \(f\in C^{l} ( \mathbb{R} ^{+}\times \mathbb{R} ^{+}\times \mathbb{R} ^{+} ) \), \(l=\max \{n,m,p\}\), \(f^{ ( l ) }\in L_{1} [ ( 0,a ) \times ( 0,b ) \times ( 0,c ) ] \)for any \(a,b,c >0\), \(\vert f(x,y,t) \vert \leq we^{x\tau _{1}+y\tau _{2}+t \tau _{3}}\), \(x >a>0\), \(y>b>0\)and \(t>c>0\)the triple Laplace transforms of Caputo’s fractional derivatives \(D_{t}^{\alpha }u(x,y,t)\), \(D_{t}^{\alpha }u(x,y,t)\)and \(D_{t}^{\alpha }u(x,y,t)\)are defined by

$$\begin{aligned}& L_{x}L_{y}L_{t} \bigl[ D_{t}^{\alpha }u(x,y,t) \bigr] \\& \quad =s^{\alpha }U ( p,q,s ) -\sum_{i=0}^{n-1}s^{\alpha -1-i}L_{y}L_{t} \bigl[ D_{t}^{i}u ( x,y,0 ) \bigr] ,\quad n-1< \alpha < n, \end{aligned}$$
(2.1)
$$\begin{aligned}& L_{x}L_{y}L_{t} \bigl[ D_{y}^{\beta }u(x,y,t) \bigr] \\& \quad =q^{\beta }U ( p,q,s ) -\sum_{j=0}^{m-1}q^{\beta -1-j}L_{y}L_{t} \bigl[ D_{y}^{j}u ( x,0,t ) \bigr] ,\quad m-1< \beta < m, \end{aligned}$$
(2.2)

and

$$\begin{aligned}& L_{x}L_{y}L_{t} \bigl[ D_{x}^{\gamma }u(x,y,t) \bigr] \\& \quad =p^{\gamma }U ( p,q,s ) -\sum_{k=0}^{r-1}p^{\gamma -1-k}L_{y}L_{t} \bigl[ D_{x}^{k}u ( 0,y,t ) \bigr] ,\quad r-1< \gamma < r. \end{aligned}$$
(2.3)

In the following part, the relations between Mittag-Leffler function and Laplace transform are considered, which are helpful in the in the current study. The Mittag-Leffler function is defined by the following series:

$$ E_{\beta } ( z ) =\sum_{k=0}^{\infty } \frac{z^{k}}{\Gamma ( \beta k+1 ) },\quad z\in \mathbb{C} , \Re (\beta )>0, $$
(2.4)

the Mittag-Leffler function with two parameters is defined by

$$ E_{\beta ,\gamma } ( z ) =\sum_{k=0}^{\infty } \frac{z^{k}}{\Gamma ( \beta k+\gamma ) }, \quad z \in \mathbb{C} , \Re (\alpha )>0, $$
(2.5)

see [18, 19]. If we put \(\beta =1\) in Eq. (2.5) we obtain Eq. (2.4). It follows from Eq. (2.5) that

$$\begin{aligned}& E_{1,1} ( z ) =\sum_{k=0}^{\infty } \frac{z^{k}}{\Gamma ( k+1 ) }=\sum_{k=0}^{\infty } \frac{z^{k}}{k!}=e^{z}, \end{aligned}$$
(2.6)
$$\begin{aligned}& E_{1,2} ( z ) =\sum_{k=0}^{\infty } \frac{z^{k}}{\Gamma ( k+2 ) }=\sum_{k=0}^{\infty } \frac{z^{k}}{ ( k+1 ) !}=\frac{1}{z}\sum_{k=0}^{\infty } \frac{z^{k+1}}{ ( k+1 ) }= \frac{e^{z}-1}{z}, \end{aligned}$$
(2.7)

and

$$ E_{1,3} ( z ) =\sum_{k=0}^{\infty } \frac{z^{k}}{\Gamma ( k+3 ) }=\sum_{k=0}^{\infty } \frac{z^{k}}{ ( k+2 ) !}=\frac{1}{z^{2}}\sum_{k=0}^{\infty } \frac{z^{k+2}}{ ( k+2 ) }= \frac{e^{z}-1-1}{z^{2}}, $$
(2.8)

in general

$$ E_{1,m} ( z ) =\frac{1}{z^{m-1}} \Biggl[ e^{z}-\sum _{k=0}^{m-2} \frac{z^{k}}{k!} \Biggr] . $$
(2.9)

Triple Laplace transforms of some Mittag-Leffler functions are given by

$$\begin{aligned}& L_{x}L_{y}L_{t} \bigl[ x^{2}t^{\alpha }E_{1,\alpha +1}(t) \bigr] = \frac{2!}{p^{3}qs^{\alpha } ( s-1 ) }, \\& L_{x}L_{y}L_{t} \bigl[ t^{\alpha }E_{1,\alpha +1}(t) \bigr] =\frac{1}{pqs^{\alpha } ( s-1 ) }, \\& L_{x}L_{y}L_{t} \bigl[ t^{2\alpha }E_{1,2\alpha +1}(t) \bigr] =\frac{1}{pqs^{2\alpha } ( s-1 ) }. \end{aligned}$$

3 Analysis of the double Laplace decomposition method

In this secction, we give the essential idea of the double Laplace Adomian decomposition method (DLADM) for the time-fractional Navier–Stokes equations. With a view to showing the fundamental scheme of the double Laplace Adomian decomposition method, we consider the following time-fractional Navier–Stokes equations:

$$\begin{aligned}& D_{t}^{\alpha }u(x,t)=D_{x}^{2}u(x,t)+ \frac{1}{x}D_{x}u(x,t)+f(x,t), \quad x,t>0, \\& n-1< \alpha < n; \end{aligned}$$
(3.1)

subject to the condition

$$ u(x,0)=f(x), $$

where \(D_{t}^{\alpha }=\frac{\partial ^{\alpha }}{\partial t^{\alpha }}\) is the fractional Caputo derivative, \(D_{x}^{2}= \frac{\partial ^{2}}{\partial x^{2}}\), \(D_{x}=\frac{\partial }{\partial x} \) and the right-hand-side function \(f(x,t)\) is the source term. In order to apply the double Laplace Adomian decomposition method, we multiply first Eq. (3.1) by x, we obtain

$$ xD_{t}^{\alpha }u=xD_{x}^{2}u+D_{x}u+xf(x,t),\quad x,t>0, $$
(3.2)

implementing the double Laplace transform on both sides of Eq. (3.2), we have

$$ L_{x}L_{t} \bigl[ xD_{t}^{\alpha }u \bigr] =L_{x}L_{t} \bigl[ xD_{x}^{2}u+D_{x}u+xf(x,t) \bigr] ,\quad x,t>0, $$
(3.3)

by using Theorem 1, we get

$$ -\frac{d}{dp} \bigl( L_{x}L_{t} \bigl[ D_{t}^{\alpha }u \bigr] \bigr) =L_{x}L_{t} \bigl[ xD_{x}^{2}u+D_{x}u+xf(x,t) \bigr] . $$

Immediately, implementing the differentiation property of the Laplace transform, we get

$$ -\frac{d}{dp} \bigl[ s^{\alpha } \bigl( L_{x}L_{t} \bigl[ u(x,t) \bigr] \bigr) -s^{\alpha -1}u ( p,0 ) \bigr] =L_{x}L_{t} \bigl[ xD_{x}^{2}u+D_{x}u \bigr] -\frac{d}{dp} \bigl( L_{x}L_{t} \bigl[ f ( x,t ) \bigr] \bigr) , $$
(3.4)

after an algebraic manipulation, we obtain

$$ \frac{d}{dp} \bigl( L_{x}L_{t} \bigl[ u(x,t) \bigr] \bigr) = \frac{1}{s}\frac{d}{dp}F ( p ) - \frac{1}{s^{\alpha }}L_{x}L_{t} \bigl[ xD_{x}^{2}u+D_{x}u \bigr] + \frac{1}{s^{\alpha }}\frac{d}{dp} \bigl( L_{x}L_{t} \bigl[ f ( x,t ) \bigr] \bigr) . $$
(3.5)

By taking the integral for both sides of Eq. (3.5) from 0 to p with respect to p, we get

$$\begin{aligned} L_{x}L_{t} \bigl[ u(x,t) \bigr] =&\frac{1}{s} \int _{0}^{p} \biggl( \frac{d}{dp}F ( p ) \biggr)\,dp-\frac{1}{s^{\alpha }} \int _{0}^{p} \bigl( L_{x}L_{t} \bigl[ xD_{x}^{2}u+D_{x}u \bigr] \bigr)\,dp \\ &{}+ \frac{1}{s^{\alpha }}\int _{0}^{p} \biggl( \frac{d}{dp} \bigl( L_{x}L_{t} \bigl[ f ( x,t ) \bigr] \bigr) \biggr)\,dp, \end{aligned}$$
(3.6)

the double Laplace Adomian decomposition solution \(u(x,t)\) is defined by the following infinite series:

$$ u ( x,t ) = \sum_{m=0}^{\infty }u_{n} ( x,t ) , $$
(3.7)

by substituting Eq. (3.7) into Eq. (3.6), we get

$$\begin{aligned}& L_{x}L_{t} \Biggl[ \sum_{m=0}^{\infty }u_{m} ( x,t ) \Biggr] \\& \quad =\frac{1}{s} \int _{0}^{p} \biggl( \frac{d}{dp}F ( p ) \biggr)\,dp+\frac{1}{s^{\alpha }} \int _{0}^{p} \biggl( \frac{d}{dp} \bigl( L_{x}L_{t} \bigl[ f ( x,t ) \bigr] \bigr) \biggr)\,dp \\& \qquad {}-\frac{1}{s^{\alpha }} \int _{0}^{p} \Biggl( L_{x}L_{t} \Biggl[ x \Biggl( \sum_{m=0}^{\infty }u_{m} ( x,t ) \Biggr) _{xx}+ \Biggl( \sum_{m=0}^{ \infty }u_{m} ( x,t ) \Biggr) _{x} \Biggr] \Biggr)\,dp, \end{aligned}$$
(3.8)

by using DLADM, we introduce the iterative relations

$$ L_{x}L_{t} \bigl[ u_{0} ( x,t ) \bigr] = \frac{1}{s}\int _{0}^{p} \biggl( \frac{d}{dp}F ( p ) \biggr)\,dp+ \frac{1}{s^{\alpha }} \int _{0}^{p} \biggl( \frac{d}{dp} \bigl( L_{x}L_{t} \bigl[ f ( x,t ) \bigr] \bigr) \biggr)\,dp, $$
(3.9)

and the remaining components can be written as

$$ L_{x}L_{t} \bigl[ u_{m+1} ( x,t ) \bigr] =- \frac{1}{s^{\alpha }}\int _{0}^{p} \bigl( L_{x}L_{t} \bigl[ xD_{x}^{2}u_{m}+D_{x}u_{m} \bigr] \bigr)\,dp,\quad m\geq 1. $$
(3.10)

Hence, \(u_{0} ( x,t ) \) and \(u_{m} ( x,t ) \) can be obtained by applying the inverse double Laplace transform to Eqs. (3.9) and (3.10), respectively, and we have

$$ u_{0} ( x,t ) =L_{p}^{-1}L_{s}^{-1} \biggl( \frac{1}{s}\int _{0}^{p} \biggl( \frac{d}{dp}F ( p ) \biggr)\,dp+ \frac{1}{s^{\alpha }} \int _{0}^{p} \biggl( \frac{d}{dp} \bigl( L_{x}L_{t} \bigl[ f ( x,t ) \bigr] \bigr) \biggr)\,dp \biggr) $$
(3.11)

and

$$ u_{m+1} ( x,t ) =-L_{p}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}\int _{0}^{p} \bigl( L_{x}L_{t} \bigl[ xD_{x}^{2}u_{m}+D_{x}u_{m} \bigr] \bigr)\,dp \biggr) ,\quad m\geq 1, $$
(3.12)

where \(L_{x}L_{t}\) is the double Laplace transform with respect to x, t and the double inverse Laplace transform denoted by \(L_{p}^{-1}L_{s}^{-1}\) is with respect to p, s. We supposed that the double inverse Laplace transform exists for Eqs. (3.11) and (3.12).

4 Analysis of the triple Laplace decomposition method

In this part of the paper, we give the fundamental idea of the triple Laplace Adomian decomposition method (TLADM) for the two-dimensional time-fractional Navier–Stokes equations. In order to show the fundamental plan of the triple Laplace Adomian decomposition method, we consider the following system of two-dimensional time-fractional Navier–Stokes equations:

$$\begin{aligned}& D_{t}^{\alpha }u+uu_{x}+vu_{y} = \rho _{0} ( u_{xx}+u_{yy} ) -\frac{1}{\rho }\frac{\partial r}{\partial x},\quad x,y,t>0, \\& D_{t}^{\alpha }v+uv_{x}+vv_{y} = \rho _{0} ( v_{xx}+v_{yy} ) -\frac{1}{\rho }\frac{\partial r}{\partial y},\quad x,y,t>0, \\& n-1 < \alpha < n; \end{aligned}$$
(4.1)

subject to

$$ u(x,y,0)=f_{1}(x,y),\qquad v(x,y,0)=g_{1}(x,y), $$

where \(D_{t}^{\alpha }=\frac{\partial ^{\alpha }}{\partial t^{\alpha }}\) is the fractional Caputo derivative, r is the pressure; in addition if r is known, then \(h_{1}= \frac{1}{\rho }\frac{\partial r}{\partial x}\) and \(h_{2}=-\frac{1}{\rho }\frac{\partial r}{\partial y}\). Applying the triple Laplace transform for Eq. (4.1), we obtain

$$\begin{aligned}& \begin{aligned}&s^{\alpha }L_{x}L_{y}L_{t} \bigl[ u(x,y,t) \bigr] -s^{\alpha -1}U ( p,q,0 ) \\ &\quad =-L_{x}L_{y}L_{t} ( uu_{x}+vu_{y} ) +L_{x}L_{y}L_{t} \bigl( \rho _{0} ( u_{xx}+u_{yy} ) -h_{1} \bigr) ,\\ &s^{\alpha }L_{x}L_{y}L_{t} \bigl[ v(x,y,t) \bigr] -s^{\alpha -1}U ( p,q,0 ) \\ &\quad =-L_{x}L_{y}L_{t} ( uv_{x}+vv_{y} ) +L_{x}L_{y}L_{t} \bigl( \rho _{0} ( v_{xx}+v_{yy} ) \bigr) +L_{x}L_{y}L_{t} ( h_{2} ) . \end{aligned} \end{aligned}$$
(4.2)

On using the differentiation property of the Laplace transform, we get

$$\begin{aligned}& \begin{aligned}&L_{x}L_{y}L_{t} \bigl[ u(x,y,t) \bigr] =\frac{1}{s}F_{1} ( p,q ) -\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( uu_{x}+vu_{y} ) \\ &\hphantom{L_{x}L_{y}L_{t} \bigl[ u(x,y,t) \bigr] =}{}+\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( u_{xx}+u_{yy} ) \bigr) - \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( h_{1} ) , \\ &L_{x}L_{y}L_{t} \bigl[ v(x,y,t) \bigr] =\frac{1}{s}G_{1} ( p,q ) -\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( uv_{x}+vv_{y} ) \\ &\hphantom{L_{x}L_{y}L_{t} \bigl[ v(x,y,t) \bigr] =}{}+\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( v_{xx}+v_{yy} ) \bigr) + \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( h_{2} ) . \end{aligned} \end{aligned}$$
(4.3)

By applying the triple inverse Laplace transformation for Eq. (4.3), we get

$$\begin{aligned}& \begin{aligned}&u(x,y,t) =L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s}F_{1} ( p,q ) \biggr) - \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( uu_{x}+vu_{y} ) \\ &\hphantom{u(x,y,t) =}{}+\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( u_{xx}+u_{yy} ) \bigr) - \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( h_{1} ) , \\ &L_{x}L_{y}L_{t} \bigl[ v(x,y,t) \bigr] =\frac{1}{s}G_{1} ( p,q ) -\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( uv_{x}+vv_{y} ) \\ &\hphantom{L_{x}L_{y}L_{t} \bigl[ v(x,y,t) \bigr] =}{}+\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( v_{xx}+v_{yy} ) \bigr) + \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( h_{2} ) , \end{aligned} \end{aligned}$$
(4.4)

the solutions \(u(x,y,t)\) and \(v(x,y,t)\) are defined by the following series:

$$ u(x,y,t)= \sum_{n=0}^{\infty }u_{n}(x,y,t),\qquad v(x,y,t)= \sum_{n=0}^{\infty }v_{n}(x,y,t); $$
(4.5)

moreover, the nonlinear terms \(uu_{x}\), \(vu_{y}\), \(uv_{x}\) and \(vv_{y}\) are determined by

$$ uu_{x}= \sum_{n=0}^{\infty }A_{n},\qquad vu_{y}= \sum_{n=0}^{\infty }B_{n},\qquad uv_{x}= \sum_{n=0}^{ \infty }C_{n},\qquad vv_{y}= \sum_{n=0}^{\infty }D_{n}, $$
(4.6)

by substituting Eq. (4.5) into Eq. (4.3), we get

$$\begin{aligned} L_{x}L_{y}L_{t} \Biggl[ \sum _{n=0}^{\infty }u_{n}(x,y,t) \Biggr] =&\frac{1}{s}F_{1} ( p,q ) - \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \Biggl( \sum_{n=0}^{\infty } ( A_{n}+B_{n} ) \Biggr) \\ &{}+\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \Biggl( \rho _{0} \Biggl( \sum_{n=0}^{\infty }u_{xxn}+ \sum_{n=0}^{\infty }u_{yyn} \Biggr) \Biggr) \\ &{}-\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( h_{1} ) \end{aligned}$$
(4.7)

and

$$\begin{aligned} L_{x}L_{y}L_{t} \Biggl[ \sum _{n=0}^{\infty }v_{n}(x,y,t) \Biggr] =&\frac{1}{s}G_{1} ( p,q ) - \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \Biggl( \sum_{n=0}^{\infty } ( C_{n}+D_{n} ) \Biggr) \\ &{}+\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \Biggl( \rho _{0} \Biggl( \sum_{n=0}^{\infty }v_{xxn}+ \sum_{n=0}^{\infty }v_{yyn} \Biggr) \Biggr) \\ &{}-\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( h_{2} ) . \end{aligned}$$
(4.8)

Taking the inverse Laplace transformation to Eqs. (4.7) and (4.8) we have

$$\begin{aligned} \sum_{n=0}^{\infty }u_{n}(x,y,t) =&L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s}F_{1} ( p,q ) \biggr) \\ &{}-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \Biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \Biggl( \sum_{n=0}^{\infty } ( A_{n}+B_{n} ) \Biggr) \Biggr) \\ &{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \Biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \Biggl( \rho _{0} \Biggl( \sum_{n=0}^{ \infty }u_{xxn}+ \sum_{n=0}^{\infty }u_{yyn}-h_{1} \Biggr) \Biggr) \Biggr) \end{aligned}$$
(4.9)

and

$$\begin{aligned} \sum_{n=0}^{\infty }v_{n}(x,y,t) =&L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s}G_{1} ( p,q ) \biggr) \\ &{}-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \Biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \Biggl( \sum_{n=0}^{\infty } ( C_{n}+D_{n} ) \Biggr) \Biggr) \\ &{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \Biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \Biggl( \rho _{0} \Biggl( \sum_{n=0}^{ \infty }v_{xxn}+ \sum_{n=0}^{\infty }v_{yyn}-h_{2} \Biggr) \Biggr) \Biggr) , \end{aligned}$$
(4.10)

by using DLADM, we introduce the recursive relations

$$\begin{aligned}& \begin{aligned}&u_{0}(x,y,t)=L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s}F_{1} ( p,q ) \biggr) , \\ &v_{0}(x,y,t)=L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s}G_{1} ( p,q ) \biggr) , \end{aligned} \end{aligned}$$
(4.11)

and the remaining components \(u_{n+1}\) and \(v_{n+1}\), \(n\geq 0\) are given by

$$\begin{aligned} u_{n+1}(x,y,t) =&-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( ( A_{n}+B_{n} ) \bigr) \biggr) \\ &{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( u_{nxx}+u_{nyy}-h_{1} ) \bigr) \biggr) \end{aligned}$$
(4.12)

and

$$\begin{aligned} v_{n+1}(x,y,t) =&-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( C_{n}+D_{n} ) \biggr) \\ &{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( v_{nxx}+v_{nyy}-h_{2} ) \bigr) \biggr) , \end{aligned}$$
(4.13)

where \(L_{x}L_{y}L_{t}\) is the triple Laplace transform with respect to x, y, t and triple inverse Laplace transform denoted by \(L_{p}^{-1}L_{q}^{-1}L_{s}^{-1}\) is with respect to p, q, s. We assume that the triple inverse Laplace transform with respect to p, q and s exist for Eqs. (4.11), (4.12) and (4.13).

5 Numerical examples

In this part of paper, we discuss the achievement of our present methods and examine its accuracy by using the decomposition method with connection of the Laplace transform. Three problems are given.

Problem 1

Consider the homogeneous one-dimensional motion of a viscous fluid in a tube given by

$$ D_{t}^{\alpha }u=-\frac{\partial r}{\rho \partial z}+ \frac{1}{x} \frac{\partial }{\partial x} ( xD_{x}u ) ,\quad x, t>0, $$
(5.1)

subject to the initial condition

$$ u ( x,0 ) =1-x^{2}. $$
(5.2)

One can write Eq. (5.1) in the form

$$ D_{t}^{\alpha }u=K+\frac{1}{x} \frac{\partial }{\partial x} ( xD_{x}u ) x,\quad x, t>0, $$
(5.3)

where \(K= -\frac{\partial r}{\rho \partial z}\), multiplying the above equation with x, we have

$$ xD_{t}^{\alpha }u=Kx+\frac{\partial }{\partial x} ( xD_{x}u ) ,\quad x, t>0. $$
(5.4)

Implementing the double Laplace transform on both sides of Eq. (5.4), we get

$$ L_{x}L_{t} \bigl[ xD_{t}^{\alpha }u \bigr] =L_{x}L_{t} [ Kx ] +L_{x}L_{t} \biggl[ \frac{\partial }{\partial x} ( xD_{x}u ) \biggr] , $$
(5.5)

using the differentiation property of the Laplace transform and Theorem 1, we obtain

$$ -\frac{d}{dp} \bigl[ s^{\alpha }U(p,s)-s^{\alpha -1}U(p,0) \bigr] = \frac{K}{p^{2}s}+L_{x}L_{t} \biggl[ \frac{\partial }{\partial x} ( xD_{x}u ) \biggr] , $$
(5.6)

substituting the initial condition and arranging Eq. (5.6), we have

$$\begin{aligned} \frac{dU(p,s)}{dp} =&\frac{1}{s}\frac{d}{dp} \biggl[ \frac{1}{p}- \frac{2!}{p^{3}} \biggr] -\frac{K}{p^{2}s^{\alpha +1}} \\ &{}-\frac{1}{s^{\alpha }}L_{x}L_{t} \biggl[ \frac{\partial }{\partial x} ( xD_{x}u ) \biggr] , \end{aligned}$$
(5.7)

by integrating both sides of Eq. (5.7) from 0 to p with respect to p, we have

$$ U(p,s)=\frac{1}{ps}-\frac{2!}{p^{3}s}+\frac{K}{ps^{\alpha +1}}- \frac{1}{s^{\alpha }} \int _{0}^{p}L_{x}L_{t} \biggl[ \frac{\partial }{\partial x} ( xD_{x}u ) \biggr]\,dp. $$
(5.8)

The inverse double Laplace transform of Eq. (5.8) is denoted by

$$ u ( x,t ) =1-x^{2}+ \frac{Kt^{\alpha }}{\Gamma ( \alpha +1 ) }-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{1}{s^{\alpha }}\int _{0}^{p}L_{x}L_{t} \biggl[ v\frac{\partial }{\partial x} ( xD_{x}u ) \biggr]\,dp \biggr] , $$
(5.9)

we assume an infinite series solution of the unknown function \(u(x,t)\) is given by

$$ u ( x,t ) = \sum_{m=0}^{\infty }u_{m} ( x,t ) , $$
(5.10)

substituting Eq. (5.10) into Eq. (5.9), we get

$$\begin{aligned} \sum_{m=0}^{\infty }u_{m} ( x,t ) =&1-x^{2}+ \frac{Kt^{\alpha }}{\Gamma ( \alpha +1 ) } \\ &{}-L_{p}^{-1}L_{s}^{-1} \Biggl[ \frac{1}{s^{\alpha }} \int _{0}^{p}L_{x}L_{t} \Biggl[ v \frac{\partial }{\partial x} \Biggl( x\frac{\partial }{\partial x} \sum _{m=0}^{\infty }u_{m} ( x,t ) \Biggr) \Biggr]\,dp \Biggr] . \end{aligned}$$
(5.11)

The zeroth component \(u_{0}\) is proposed by Adomian method, is constantly contains initial condition and the nonhomogeneous term, both of which are assumed to be known. Accordingly, we put

$$ u_{0}=1-x^{2}+\frac{Kt^{\alpha }}{\Gamma ( \alpha +1 ) }. $$

The remaining components \(u_{m+1}\), \(m\geq 0\) are given by using the relation

$$ u_{m+1} ( x,t ) =-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{1}{s^{\alpha }}\int _{0}^{p}L_{x}L_{t} \biggl[ \frac{\partial }{\partial x} ( xD_{x}u_{m} ) \biggr]\,dp \biggr] , $$
(5.12)

by substituting \(m=0\), into Eq. (5.12), we get

$$\begin{aligned}& u_{1} ( x,t ) =-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{1}{s^{\alpha }}\int _{0}^{p}L_{x}L_{t} \biggl[ v\frac{\partial }{\partial x} ( xD_{x}u_{0} ) \biggr]\,dp \biggr] \\& \hphantom{u_{1} ( x,t )}=-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{1}{s^{\alpha }} \int _{0}^{p} \biggl[ -\frac{4v}{p^{2}s} \biggr]\,dp \biggr] =-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{4v}{ps^{\alpha +1}} \biggr] , \\& u_{1} ( x,t ) =- \frac{4t^{\alpha }}{\Gamma ( \alpha +1 ) }, \end{aligned}$$
(5.13)

similarly at \(m=1\),

$$\begin{aligned} u_{2} ( x,t ) =&-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{1}{s^{\alpha }}\int _{0}^{p}L_{x}L_{t} \biggl[ \frac{\partial }{\partial x} ( xD_{x}u_{1} ) \biggr]\,dp \biggr] \\ =&-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{1}{s^{\alpha }} \int _{0}^{p} [ 0 ]\,dp \biggr] =0, \end{aligned}$$
(5.14)

at \(m=2\), we have

$$ u_{3} ( x,t ) =0. $$

Hence, the solution of Eq. (5.1) can be can be found to be

$$ u(x,t)=1-x^{2}+ \frac{ ( K-4 ) t^{\alpha }}{\Gamma ( \alpha +1 ) }. $$

The result is the same as given by [6, 10].

Problem 2

The nonhomogeneous time-fractional Navier–Stokes equation

$$ D_{t}^{\alpha }u=D_{x}^{2}u+ \frac{1}{x}D_{x}u+x^{2}e^{t}-4e^{t},\quad x,t>0, $$
(5.15)

subject to the initial condition

$$ u ( x,0 ) =x^{2}. $$
(5.16)

Applying the double Laplace transform on both sides of Eq. (5.15), subject to the initial condition Eq. (5.16), we have

$$ U(p,s)=\frac{2!}{p^{3}s}+ \frac{2!}{p^{3}s^{\alpha } ( s-1 ) }- \frac{4}{ps^{\alpha } ( s-1 ) }- \frac{1}{s^{\alpha }}\int _{0}^{p}L_{x}L_{t} \biggl[ \frac{\partial }{\partial x} ( xD_{x}u ) \biggr]\,dp. $$
(5.17)

Working with the double Laplace inverse on both sides of Eq. (5.17) gives

$$\begin{aligned} u(x,t) =&x^{2}+x^{2}t^{\alpha }E_{1,\alpha +1}(t)-4t^{\alpha }E_{1, \alpha +1}(t) \\ &{}-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{1}{s^{\alpha }} \int _{0}^{p}L_{x}L_{t} \biggl[ \frac{\partial }{\partial x} ( xD_{x}u ) \biggr]\,dp \biggr]. \end{aligned}$$
(5.18)

By using the above-mentioned method the solution of Eq. (3.7), is given by

$$\begin{aligned} \sum_{m=0}^{\infty }u_{m} ( x,t ) =&x^{2}+x^{2}t^{ \alpha }E_{1,\alpha +1}(t)-4t^{\alpha }E_{1,\alpha +1}(t) \\ &{}-L_{p}^{-1}L_{s}^{-1} \Biggl[ \frac{1}{s^{\alpha }} \int _{0}^{p}L_{x}L_{t} \Biggl[ \frac{\partial }{\partial x} \Biggl( x \frac{\partial }{\partial x} \sum _{m=0}^{\infty }u_{m} ( x,t ) \Biggr) \Biggr]\,dp \Biggr] , \end{aligned}$$
(5.19)

the first few terms of the double Laplace decomposition series are given by

$$ u_{0}=x^{2}+x^{2}t^{\alpha }E_{1,\alpha +1}(t)-4t^{\alpha }E_{1, \alpha +1}(t) $$

and

$$ u_{m+1} ( x,t ) =-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{1}{s^{\alpha }}\int _{0}^{p}L_{x}L_{t} \biggl[ \frac{\partial }{\partial x} ( xD_{x}u_{m} ) \biggr]\,dp \biggr]. $$

Hence, at \(m=0\), we get

$$\begin{aligned}& u_{1}=-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{1}{s^{\alpha }}\int _{0}^{p}L_{x}L_{t} \biggl[ \frac{\partial }{\partial x} ( xD_{x}u_{0} ) \biggr]\,dp \biggr] \\& \hphantom{u_{1}}=-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{1}{s^{\alpha }} \int _{0}^{p}L_{x}L_{t} \bigl[ 4x+4xt^{\alpha }E_{1,\alpha +1}(t) \bigr]\,dp \biggr] \\& \hphantom{u_{1}}=L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{4}{ps^{\alpha +1}}+ \frac{4}{ps^{2\alpha } ( s-1 ) } \biggr] , \\& u_{1} =\frac{4t^{\alpha }}{\Gamma ( \alpha +1 ) }+4t^{2 \alpha }E_{1,2\alpha +1}(t). \end{aligned}$$

In the same manner,

$$\begin{aligned} u_{2} =&-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{1}{s^{\alpha }}\int _{0}^{p}L_{x}L_{t} \biggl[ \frac{\partial }{\partial x} ( xD_{x}u_{1} ) \biggr]\,dp \biggr] \\ &{}-L_{p}^{-1}L_{s}^{-1} \biggl[ \frac{1}{s^{\alpha }} \int _{0}^{p}L_{x}L_{t} [ 0 ]\,dp \biggr] , \\ u_{2} =&0, \end{aligned}$$

and

$$ u_{3}=0,\qquad u_{4}=0, \ldots. $$

The series solution is therefore given by

$$\begin{aligned}& u(x,t) =u_{0}+u_{1}+u_{2}+\cdots, \\& u(x,t) =x^{2}+x^{2}t^{\alpha }E_{1,\alpha +1}(t)-4t^{\alpha }E_{1, \alpha +1}(t)+ \frac{4t^{\alpha }}{\Gamma ( \alpha +1 ) }+4t^{2 \alpha }E_{1,2\alpha +1}(t), \end{aligned}$$

where E denotes the Mittag-Leffler function. On setting \(\alpha =1\) in Eq. (5.15), we get the exact solution of the non-time-fractional Navier–Stokes equation

$$ D_{t}u=D_{x}^{2}u+\frac{1}{x}D_{x}u+x^{2}e^{t}-4e^{t},\quad x,t>0, $$

under the same condition \(u ( x,0 ) =x^{2}\). The solution is given by

$$ u(x,t)=x^{2}e^{t}. $$

In the following problem, the suggested method is applied to the two-dimensional time-fractional model of the Navier–Stokes equation, in Eq. (5.20). We let \(h_{1}=\frac{1}{\rho }\frac{\partial r}{\partial x} =- h_{2}=-\frac{1}{\rho }\frac{\partial r}{\partial y}=h\) as follows.

Problem 3

Consider the time-fractional order two-dimensional Navier–Stokes equation [9, 13]

$$\begin{aligned}& D_{t}^{\alpha }u+uu_{x}+vu_{y} = \rho _{0} ( u_{xx}+u_{yy} ) +h,\quad x,y,t>0, \\& D_{t}^{\alpha }v+uv_{x}+vv_{y}= \rho _{0} ( v_{xx}+v_{yy} ) -h,\quad x,y,t>0, \\& n-1 < \alpha < n; \end{aligned}$$
(5.20)

subject to the condition

$$ u(x,y,0)=-\sin (x+y),\qquad v(x,y,0)=\sin (x+y), $$

by taking the triple Laplace transform for both sides of Eq. (5.20), we get

$$\begin{aligned}& L_{x}L_{y}L_{t} \bigl[ D_{t}^{\alpha }u+uu_{x}+vu_{y}=\rho _{0} ( u_{xx}+u_{yy} ) +h \bigr], \\& L_{x}L_{y}L_{t} \bigl[ D_{t}^{\alpha }v+uv_{x}+vv_{y}=\rho _{0} ( v_{xx}+v_{yy} ) -h \bigr] , \end{aligned}$$

on using the differentiation property of the Laplace transform, we have

$$\begin{aligned}& L_{x}L_{y}L_{t} \bigl[ u(x,y,t) \bigr] =\frac{1}{s}L_{x}L_{y} \bigl[ u(x,y,0) \bigr] -\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( uu_{x}+vu_{y} ) \\& \hphantom{L_{x}L_{y}L_{t} \bigl[ u(x,y,t) \bigr] =}{}+\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( u_{xx}+u_{yy} ) \bigr) + \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( h ) , \\& L_{x}L_{y}L_{t} \bigl[ v(x,y,t) \bigr] =\frac{1}{s}L_{x}L_{y} \bigl[ v(x,y,0) \bigr] -\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( uv_{x}+vv_{y} ) \\& \hphantom{L_{x}L_{y}L_{t} \bigl[ v(x,y,t) \bigr] =}{}+\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( v_{xx}+v_{yy} ) \bigr) - \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( h ) , \end{aligned}$$
(5.21)

substituting the initial condition and arranging Eq. (5.21), we have

$$\begin{aligned}& L_{x}L_{y}L_{t} \bigl[ u(x,y,t) \bigr] =- \frac{p+q}{s ( p^{2}+1 ) ( q^{2}+1 ) }-\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( uu_{x}+vu_{y} ) \\& \hphantom{L_{x}L_{y}L_{t} \bigl[ u(x,y,t) \bigr] =}{}+\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \bigl( \rho _{0} ( u_{xx}+u_{yy} ) +h \bigr) \bigr) , \\& L_{x}L_{y}L_{t} \bigl[ v(x,y,t) \bigr] =\frac{p+q}{s ( p^{2}+1 ) ( q^{2}+1 ) }-\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( uv_{x}+vv_{y} ) \\& \hphantom{L_{x}L_{y}L_{t} \bigl[ v(x,y,t) \bigr] =}{}+\frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( v_{xx}+v_{yy} ) -h \bigr) . \end{aligned}$$
(5.22)

Now, implementing the inverse triple Laplace transform for Eq. (5.22)

$$\begin{aligned}& u(x,y,t) =-\sin (x+y)-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( uu_{x}+vu_{y} ) \biggr) \\& \hphantom{u(x,y,t)}{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( u_{xx}+u_{yy} ) +h \bigr) \biggr) , \\& v(x,y,t) =\sin (x+y)-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( uv_{x}+vv_{y} ) \biggr) \\& \hphantom{v(x,y,t)}{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( v_{xx}+v_{yy} ) -h \bigr) \biggr). \end{aligned}$$
(5.23)

The zeroth components \(u_{0}\) and \(v_{0}\) are found by the Adomian method. Always it contains initial condition and the source term, both of which are assumed to be known. Accordingly, we set

$$ u_{0}=-\sin (x+y),\qquad v_{0}=\sin (x+y). $$

The remaining components \(u_{n+1}\), \(u_{n+1}\), \(n\geq 0\) are given by using the relations

$$\begin{aligned} u_{n+1} =&-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( ( A_{n}+B_{n} ) \bigr) \biggr) \\ &{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( u_{nxx}+u_{nyy} ) +h \bigr) \biggr) \end{aligned}$$
(5.24)

and

$$\begin{aligned} v_{n+1} =&-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( C_{n}+D_{n} ) \biggr) \\ &{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( v_{nxx}+v_{nyy} ) -h \bigr) \biggr) \end{aligned}$$
(5.25)

the first few terms of the Adomian polynomials \(A_{n}\), \(B_{n}\), \(C_{n}\) and \(D_{n}\) are given by

$$\begin{aligned}& A_{0} =u_{0}u_{0x},\qquad A_{1}=u_{0}u_{1x}+u_{1}u_{0x}, \\& A_{2} =u_{0}u_{2x}+u_{1}u_{1x}+u_{2}u_{0x}, \\& A_{3} =u_{0}u_{3x}+u_{1}u_{2x}+u_{2}u_{1x}+u_{3}u_{0x}, \end{aligned}$$
(5.26)
$$\begin{aligned}& B_{0} =v_{0}u_{0y},\qquad B_{1}=v_{0}u_{1y}+v_{1}u_{0y}, \\& B_{2} =v_{0}u_{2y}+v_{1}u_{1y}+v_{2}u_{0y}, \\& B_{3} =v_{0}u_{3y}+v_{1}u_{2y}+v_{2}u_{1y}+v_{3}u_{0y}, \end{aligned}$$
(5.27)
$$\begin{aligned}& C_{0} =u_{0}v_{0x},\qquad C_{1}=u_{0}v_{1x}+u_{1}v_{0x}, \\& C_{2}=u_{0}v_{2x}+u_{1}v_{1x}+u_{2}v_{0x}, \\& C_{3} =u_{0}v_{3x}+u_{1}v_{2x}+u_{2}v_{1x}+u_{3}v_{0x}, \end{aligned}$$
(5.28)
$$\begin{aligned}& D_{0} =v_{0}v_{0y},\qquad D_{1}=v_{0}v_{1y}+v_{1}v_{0y}, \\& D_{2} =v_{0}v_{2y}+v_{1}v_{1y}+v_{2}v_{0y}, \\& D_{3} =v_{0}v_{3y}+v_{1}v_{2y}+v_{2}v_{1y}+v_{3}v_{0y}, \end{aligned}$$
(5.29)

by putting \(n=0\), into Eqs. (5.24) and (5.25), we get

$$\begin{aligned} u_{1} =&-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( ( A_{0}+B_{0} ) \bigr) \biggr) \\ &{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( u_{0xx}+u_{0yy} ) +h \bigr) \biggr) \\ =&L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} \bigl( 2\sin (x+y) \bigr) \bigr) +h \biggr) \\ =&L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{\rho _{0}}{s^{\alpha }} \frac{p+q}{ ( p^{2}+1 ) ( q^{2}+1 ) }- \frac{h}{s^{\alpha }} \biggr) \\ =&2\frac{\rho _{0}t^{\alpha }}{\Gamma ( \alpha +1 ) } \sin (x+y)+\frac{ht^{\alpha }}{\Gamma ( \alpha +1 ) }, \end{aligned}$$

in the same way, we have

$$\begin{aligned} v_{1} =&-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( C_{0}+D_{0} ) \biggr) +L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( v_{0xx}+v_{0yy} ) -h \bigr) \biggr) \\ =&-2\frac{\rho _{0}t^{\alpha }}{\Gamma ( \alpha +1 ) } \sin (x+y)-\frac{ht^{\alpha }}{\Gamma ( \alpha +1 ) }, \end{aligned}$$

similarly at \(n=1\),

$$\begin{aligned} u_{2} =&-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( ( u_{0}u_{1x}+u_{1}u_{0x}+v_{0}u_{1y}+v_{1}u_{0y} ) \bigr) \biggr) \\ &{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( u_{1xx}+u_{1yy}+q ) \bigr) \biggr) \\ =&L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \biggl( \frac{-4\rho _{0}^{2}\sin (x+y)t^{\alpha }}{\Gamma ( \alpha +1 ) } \biggr) \biggr) \\ =&- \frac{ ( 2\rho _{0} ) ^{2}\sin (x+y)t^{2\alpha }}{\Gamma ( 3\alpha +1 ) } \end{aligned}$$

and

$$\begin{aligned} v_{2} =&-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( u_{0}v_{1x}+u_{1}v_{0x}+v_{0}v_{1y}+v_{1}v_{0y} ) \biggr) \\ &{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( v_{1xx}+v_{1yy}-q ) \bigr) \biggr) \\ =&\frac{ ( 2\rho _{0} ) ^{2}\sin (x+y)t^{2\alpha }}{\Gamma ( 3\alpha +1 ) } \end{aligned}$$

at \(n=2\), we have

$$\begin{aligned} u_{3} =&-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( ( u_{0}u_{2x}+u_{1}u_{1x}+u_{2}u_{0x}+v_{0}u_{2y}+v_{1}u_{1y}+v_{2}u_{0y} ) \bigr) \biggr) \\ &{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( u_{2xx}+u_{2yy} ) +h \bigr) \biggr) \\ =&\frac{-8\rho _{0}^{3}\sin (x+y)t^{3\alpha }}{\Gamma ( 3\alpha +1 ) }= \frac{ ( 2\rho _{0} ) ^{3}\sin (x+y)t^{3\alpha }}{\Gamma ( 3\alpha +1 ) } \end{aligned}$$

and

$$\begin{aligned} v_{3} =&-L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} ( u_{0}v_{2x}+u_{1}v_{1x}+u_{2}v_{0x}+v_{0}v_{2y}+v_{1}v_{1y}+v_{2}v_{0y} ) \biggr) \\ &{}+L_{p}^{-1}L_{q}^{-1}L_{s}^{-1} \biggl( \frac{1}{s^{\alpha }}L_{x}L_{y}L_{t} \bigl( \rho _{0} ( v_{2xx}+v_{2yy} ) -h \bigr) \biggr) \\ =&- \frac{8\rho _{0}^{3}\sin (x+y)t^{3\alpha }}{\Gamma ( 3\alpha +1 ) }=- \frac{ ( 2\rho _{0} ) ^{3}\sin (x+y)t^{3\alpha }}{\Gamma ( 3\alpha +1 ) }. \end{aligned}$$

In the same manner, we have

$$ u_{n}=- \frac{ ( -2\rho _{0} ) ^{n}\sin (x+y)t^{n\alpha }}{\Gamma ( n\alpha +1 ) },\qquad v_{n}= \frac{ ( -2\rho _{0} ) ^{n}\sin (x+y)t^{n\alpha }}{\Gamma ( n\alpha +1 ) },\quad \forall n\geq 2. $$

The solution of Eq. (5.20) is given by

$$\begin{aligned}& u(x,y,t) =u_{0}+u_{1}+u_{2}+ \cdots+u_{n} , \\& v(x,y,t) =v_{0}+v_{1}+v_{2}+ \cdots+v_{n}, \\& u(x,y,t) =-\sin (x+y) \sum_{n=0}^{\infty } \frac{ ( -2\rho _{0} ) ^{n}t^{n\alpha }}{\Gamma ( n\alpha +1 ) }+ \frac{ht^{\alpha }}{\Gamma ( \alpha +1 ) } , \\& v(x,y,t) =\sin (x+y) \sum_{n=0}^{\infty } \frac{ ( -2\rho _{0} ) ^{n}t^{n\alpha }}{\Gamma ( n\alpha +1 ) }- \frac{ht^{\alpha }}{\Gamma ( \alpha +1 ) }, \end{aligned}$$

at \(\alpha =1\) and \(h=0\), we obtain the exact solution of the classical Navier–Stokes equation for the velocity:

$$\begin{aligned}& u(x,y,t) =-\sin (x+y)e^{-2\rho _{0}t} , \\& v(x,y,t) =\sin (x+y)e^{-2\rho _{0}t}. \end{aligned}$$

6 Numerical result

In this section, we clarify the accuracy and efficiency of the double Laplace Adomian decomposition method by numerical results of \(u(x,t)\) for the exact solution when \(\alpha =1\) and approximate solutions with α using different fractional values for the time-fractional Navier–Stokes equation. The solutions of Eqs. (5.1) and (5.15) are represented through Figs. 1–4, respectively.

Figure 1
figure 1

Plot of \(u(r,t)\) vs. r, for problem (1), when \(k=v=t=1\) for different values of α

Full size image

Figure 1 compares the approximate solutions of Eq. (5.1) at \(t=1\). It shows that besides the approximate solution at \(\alpha =1\) we get the exact solution, and the function \(u(x,t)\) decreases as the fractional derivative decreases at \(\alpha =0.75,0.50,0.25\).

The three-dimensional surface in Fig. 2(a) shows the solution of Eqs. (5.1) at (\(\alpha =0.5\)) and Fig. 2(b) shows the exact solution of the time-fractional Navier–Stokes equation with \(\alpha =1\) in normal form.

Figure 2
figure 2

The surface shows the solution \(u(r,t)\) for problem (1), when \(k=v=1\). (a) \(\alpha =0.5\); (b) \(\alpha =1\)

Full size image

In the same manner, the exact solution and approximate solution of Eq. (5.15) were demonstrated in Figs. 3 and 4. Figures 3 gives plots of the behavior of Eq. (5.15) when \(t=1\) and \(\alpha =0.75,0.50,0.25\), in this case the function \(u(x,t)\) increases quickly and gets far from the exact solution.

Figure 3
figure 3

Plot of \(u(r,t)\) vs. r, for problem (2), when \(k=v=t=1\) for different values of α

Full size image
Figure 4
figure 4

The surface shows the solution \(u(r,t)\) for problem (2), when \(k=v=1\). (a) \(\alpha =0.5\); (b) \(\alpha =1\)

Full size image

The three-dimensional surface in Fig. 4(a) shows the solution of Eqs. (5.15) at (\(\alpha =0.5\)) and Fig. 4(b) shows the exact solution of the time-fractional Navier–Stokes equation at \(\alpha =1\) in standard form equal to \(x^{2}e^{t}\).

It is clear from the solutions of Eqs. (5.1) and (5.15) that the double Laplace transform decomposition method shows good agreement with the exact solutions of the problems.

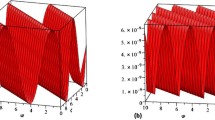
Figure 5 consists of two graphs, namely Fig. 5(a) and Fig. 5(b). Figures 5(a) and 5(b) represent the functions \(u(x,y,t)\) and \(u(x,y,t)\) of the Navier–Stokes equation, respectively, of Eq. (5.20) when \(\rho =0.5\), \(\alpha =0.5\) and \(t=0.5\).

Figure 5
figure 5

The surface shows the solution for problem (3), when \(\rho =0.5\), \(\alpha =0.5\) and \(t=0.5\)

Full size image

Figure 6 consists of two graphs, namely Fig. 6(a) and Fig. 6(b). Figures 6(a) and 6(b) represent the functions \(u(x,y,t)\) and \(u(x,y,t)\) of the Navier–Stokes equation, respectively, of Eq. (5.20) when \(\rho =0.5\), \(\alpha =0.5\) and \(t=0.05\).

Figure 6
figure 6

The surface shows the solution for problem (3), when \(\rho =0.5\), \(\alpha =0.5\) and \(t=0.05\)

Full size image

Conclusion 1

In this work, double and triple Laplace Adomian decomposition methods are suggested for solving one- and two-dimensional time-fractional Navier–Stokes equations. These methods have been proved to be a powerful tool which enable us to manage fractional order differential equations and allow one to reach the desired accuracy. All we have to do is to increase the number of iterations. Therefore, it can be found that DLADM and TLADM are very effective in the search of exact and numerical solutions for the fractional Navier–Stokes equation.