1 Introduction

Burger’s equation is one of the fundamental and essential nonlinear partial differential equations (PDE) containing diffusive properties and nonlinear expansion effects. Burger’s equation was improved as a model of disorderly fluid movement. The fractional Burger’s equation has received much interest and the solution to this problem becomes essential for mathematicians and physical phenomena. This problem has been found to demonstrate various types of events, for instance, a mathematical model of turbulence and an approximate theorem of flow through a trauma wave traveling in a viscous liquid [1, 2]. The authors in [3] introduced a semianalytical method that is called the local fractional Laplace homotopy analysis method to solve wave equations with local fractional derivatives and the authors used the same method to solve differential equations involving local fractional derivatives based on the local fractional calculus [4]. The Shehu transform and a semianalytical method have been used to solve multidimensional fractional diffusion equations [5]. The numerical solution of three-dimensional coupled Burger’s Equations has been studied by the Laplace decomposition method in [6, 7]. In recent years, substantial confirmation was offered on the Laplace decomposition method and its changes for discussing mathematical problems [8, 9]. In a previous study, the authors recommended various kinds of approximation and exact technique to solve fractional Burger’s equation methods [10–12]. The researchers in [13] suggested the variational iteration method to gain Burger’s equation. In [14], the Laplace decomposition method (LDM) was applied to determine the solution of two-dimensional nonlinear Burger’s equations. The authors in [15] proposed a modification of the double Laplace decomposition method to obtain an analytical approximation solution of a coupled system of Burger’s equation. There are many approaches where one can obtain a series of solutions, such as the Modified Laplace variational iteration method [16], and the He–Laplace method [17]. The approximate solution of wave problems in multidimensional orders was studied by applying the Aboodh homotopy integral transform method (AHITM), see [18]. The authors in [19] used the Yang Transform to obtain the approximation solution of nonlinear time-fractional Klein–Gordon equations. The authors in [20] employed the Fountain theorem and the symmetric Mountain-Pass theorem to study the novel trinonlocal Kirchhoff problem. The main aim of this paper is to offer a new hybrid of a double Sumudu-Generalized Laplace Transform to determine the exact solutions of the time-fractional regular and singular coupled Burger’s equations. Finally, examples are given to clarify the proposed technique. Definitions will be recalled; the double Sumudu transform and the Generalized Laplace Transform that are useful in this article.

The Double Sumudu transform of the function \(\psi (\chi ,\sigma )\) is determined by \(\Psi (\mu _{1},\mu _{2})\) in the following definition.

Definition 1

[21] let \(\psi (\chi ,\sigma )\) be a function we define as the double Sumudu Transform of function \(\psi (\chi ,\sigma ) \), \(\sigma ,\chi \in \mathbb{R} ^{+}\) is given by

$$ \Psi (\mu _{1},\mu _{2})=S_{2} \bigl[ \psi ( \chi ,\sigma ) \bigr] = \int ^{\infty }_{0} \int ^{\infty }_{0} \frac{1}{uv}e^{-(\frac{\chi }{u}+\frac{\sigma }{v})}\psi ( \chi ,\sigma )\,d\chi \,d \sigma . $$

The generalized Laplace transform of the function \(\psi (t)\) is given by \(G_{\alpha }\) in the following definition.

Definition 2

If \(\psi (t)\) is an integrable function defined for all \(t\geq 0\), its generalized Laplace transform \(G_{\alpha }\) is the integral of \(\psi (t)\) times \(s^{\alpha }e^{-\frac{t}{s}}\) from \(t=0\) to ∞. It is a function of s, say \(\Psi ( s ) \), and is denoted by \(G_{\alpha } ( \psi ) \); thus

$$ \Psi ( s ) =G_{t} ( \psi ) =s^{\alpha } \int _{0}^{\infty }\psi ( t ) e^{-\frac{t}{s}}\,dt, $$

where, \(s\in \mathbb{C} \) and \(\alpha \in Z\), for more details see [22].

Definition 3

[23–25]. The Caputo time-fractional derivative operator of order \(\beta >0\) is presented by

$$ D_{t}^{\beta }\psi (\chi ,t)= \textstyle\begin{cases} \frac{1}{\Gamma ( m-\beta ) }\int _{0}^{t} ( t-\tau ) ^{m-\beta -1} \frac{\partial ^{m}\psi (\chi ,\tau )}{\partial \tau ^{m}}\,d\tau , \\ \frac{\partial ^{m}\psi (\chi ,t)}{\partial t^{m}},\quad \text{for }m= \beta \in \mathbb{N} \end{cases}\displaystyle \quad m-1< \beta < m. $$

2 Main results of double Sumudu-generalized Laplace transform

The definitions and existence condition of the double Sumudu-generalized Laplace transform are presented in this section. Here, we work with the double Sumudu-generalized Laplace transform, which is defined by

$$\begin{aligned} S_{\chi }S_{\sigma }G_{t} \bigl( f ( \chi ,\sigma ,t ) \bigr) &=F ( \mu _{1},\mu _{2},s ) \\ & = \frac{s^{\alpha }}{\mu _{1}\mu _{2}}\int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }e^{- ( \frac{\chi }{\mu _{1}}+\frac{\sigma }{\mu _{2}}+\frac{t}{s} ) }f ( \chi ,\sigma ,t ) \,dt\,d\sigma \,d\chi \end{aligned}$$
(1)

and we note that the double Sumudu-generalized Laplace transform is a hybrid between the double Sumudu transform and the generalized Laplace transform. From the definition of the double Sumudu-generalized Laplace transform, we conclude the following:

1. if we put \(\alpha =0\) and \(s=\frac{1}{s}\) we obtain the double Sumudu–Laplace transform

$$\begin{aligned} S_{\chi }S_{\sigma }L_{t} \bigl( f ( \chi ,\sigma ,t ) \bigr) &=F ( \mu _{1},\mu _{2},s ) \\ & = \frac{1}{\mu _{1}\mu _{2}}\int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }f ( \chi ,\sigma ,t ) e^{- ( \frac{\chi }{\mu _{1}}+\frac{\sigma }{\mu _{2}}+st ) } \,dt\,d\sigma \,d \chi ; \end{aligned}$$
(2)

2. if we put \(\alpha =0\) and replacing s by ϖ we obtain the double Sumudu–Yang Transform

$$\begin{aligned} S_{\chi }S_{\sigma }Y \bigl( f ( \chi ,\sigma ,t ) \bigr) &=F ( \mu _{1},\mu _{2},\varpi ) \\ & = \frac{1}{\mu _{1}\mu _{2}}\int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }f ( \chi ,\sigma ,t ) e^{- ( \frac{\chi }{\mu _{1}}+\frac{\sigma }{\mu _{2}}+\frac{t}{\varpi } ) } \,dt\,d \sigma \,d\chi ; \end{aligned}$$
(3)

3. At \(\alpha =-1\) and replacing s by \(\mu _{3}\) we obtain the triple Sumudu Transform

$$\begin{aligned} S_{\chi }S_{\sigma }S_{t} \bigl( f ( \chi ,\sigma ,t ) \bigr) &=F ( \mu _{1},\mu _{2},\mu _{3} ) \\ &= \frac{1}{\mu _{1}\mu _{2}\mu _{3}} \int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }f ( \chi ,\sigma ,t ) e^{- ( \frac{\chi }{\mu _{1}}+\frac{\sigma }{\mu _{2}}+\frac{t}{\mu _{3}} ) } \,dt\,d \sigma \,d\chi ; \end{aligned}$$
(4)

4. At \(\alpha =1\) we obtain the double Sumudu-Elzaki transform

$$\begin{aligned} S_{\chi }S_{\sigma }E_{t} \bigl( f ( \chi ,\sigma ,t ) \bigr) &=F ( \mu _{1},\mu _{2},s ) \\ & = \frac{s}{\mu _{1}\mu _{2}}\int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }f ( \chi ,\sigma ,t ) e^{- ( \frac{\chi }{\mu _{1}}+\frac{\sigma }{\mu _{2}}+\frac{t}{s} ) } \,dt\,d \sigma \,d\chi ; \end{aligned}$$
(5)

5. At \(\alpha =-1\) and \(\frac{1}{v}=\frac{1}{s}\) we obtain the double Sumudu–Aboodh transform

$$\begin{aligned} S_{\chi }S_{\sigma }E_{t} \bigl( f ( \chi ,\sigma ,t ) \bigr) &=F ( \mu _{1},\mu _{2},v ) \\ & = \frac{1}{\mu _{1}\mu _{2}v}\int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }f ( \chi ,\sigma ,t ) e^{- ( \frac{\chi }{\mu _{1}}+\frac{\sigma }{\mu _{2}}+vt ) } \,dt\,d\sigma \,d \chi . \end{aligned}$$
(6)

From the analysis above concerning the double Sumudu-generalized Laplace transform, we note that the hybrid of the double Sumudu-generalized Laplace transform is more generic than the above transforms. Hence, the double Sumudu-generalized Laplace decomposition method is considered the most generic amongst other related methods.

2.1 Existence condition for the double Sumudu-generalized Laplace transform

In this section, the existence conditions and definitions of the double Sumudu-generalized Laplace transform are addressed as follows:

If \(f ( \chi ,\sigma ,t ) \) is an exponential order \(a_{1}\), \(a_{2}\), and b as \(\chi \rightarrow \infty \), \(\sigma \rightarrow \infty \), \(t\rightarrow \infty \), and if \(\exists R>0\) thence \(\forall \chi >\chi \), \(\forall \sigma >\sigma \) and \(\forall t>T\)

$$ \bigl\vert f ( \chi ,\sigma ,t ) \bigr\vert \leq \operatorname{Re}^{a_{1} \chi +a_{2}\sigma +bt}, $$
(7)

for some χ, σ and T, we can write \(f ( \chi ,\sigma ,t ) \) as follows:

$$ f ( \chi ,\sigma ,t ) =O \bigl( e^{a_{1}\chi +a_{2}\sigma +bt} \bigr)\quad \text{as }\sigma \rightarrow \infty , \sigma \rightarrow \infty , t\rightarrow \infty , $$

equally,

$$ \lim_{ \substack{ \chi \rightarrow \infty \\ \sigma \rightarrow \infty \\ t\rightarrow \infty }}e^{- \frac{1}{\mu }\chi -\frac{1}{\eta }\sigma -\frac{1}{\varepsilon }t} \bigl\vert f ( \chi ,\sigma ,t ) \bigr\vert =R\lim_{ \substack{ \chi \rightarrow \infty \\ \sigma \rightarrow \infty \\ t\rightarrow \infty }}e^{- ( \frac{1}{\lambda _{1}}-a_{1} ) \chi - ( \frac{1}{\lambda _{2}}-a_{2} ) \sigma - ( \frac{1}{\eta }-c ) t}=0, $$
(8)

whenever \(\frac{1}{\lambda _{1}}>a\), \(\frac{1}{\eta }>c\) and \(\frac{1}{\lambda _{2}}>b\). The function \(f ( \chi ,\sigma ,t ) \) does not expand quicker than \(R ( \chi ,\sigma ,t ) e^{a_{1}\chi +a_{2}\sigma +bt}\) as \(\chi \rightarrow \infty \), \(\sigma \rightarrow \infty \), \(t\rightarrow \infty \).

Theorem 1

The function \(f ( \chi ,\sigma ,t ) \) is defined on \((0,\chi )\), \(( 0,\sigma ) \), and \((0,T)\) and of exponential order \(( \chi ,\sigma ,t ) \), then the double Sumudu-generalized Laplace transform of \(f ( \chi ,\sigma ,t ) \) exists for all \(\operatorname{Re}\frac{1}{\mu _{1}}>\frac{1}{\lambda _{1}}\), \(\operatorname{Re}\frac{1}{\mu _{2}}> \frac{1}{\lambda _{2}}\), \(\operatorname{Re}\frac{1}{s}>\frac{1}{\eta }\).

Proof

By utilizing Eq. (1) and Eq. (7), we obtain

$$\begin{aligned} \bigl\vert F ( \mu _{1},\mu _{2},s ) \bigr\vert =& \biggl\vert \frac{s^{\alpha }}{\mu _{1}\mu _{2}} \int _{0}^{\infty } \int _{0}^{\infty }e^{- ( \frac{\chi }{\mu _{1}}+ \frac{\sigma }{\mu _{2}}+\frac{t}{s} ) }f ( \chi ,\sigma ,t ) \,d\chi \,d\sigma \,dt \biggr\vert \\ \leq &R \biggl\vert \frac{s^{\alpha }}{\mu _{1}\mu _{2}} \int _{0}^{ \infty } \int _{0}^{\infty } \int _{0}^{\infty }e^{ ( \frac{1}{\psi _{1}}-a ) \chi - ( \frac{1}{\psi _{2}}-b ) \sigma - ( \frac{1}{v}-c ) t}\,d\chi \,d\sigma \,dt \biggr\vert \\ =& \frac{Rs^{\alpha +1}}{ ( 1-a\mu _{1} ) ( 1-c\mu _{2} ) ( 1-bs ) }. \end{aligned}$$
(9)

On using the condition \(\operatorname{Re}\frac{1}{\mu _{1}}>\frac{1}{\lambda _{1}}\), \(\operatorname{Re}\frac{1}{\mu _{2}}>\frac{1}{\lambda _{2}}\), \(\operatorname{Re}\frac{1}{s}>\frac{1}{\eta }\), and Eq. (8), we obtain

$$ \lim_{ \substack{ \chi \rightarrow \infty \\ \sigma \rightarrow \infty \\ t\rightarrow \infty }} \bigl\vert F(\psi _{1},\psi _{2},v) \bigr\vert =0\quad \text{or}\quad \lim_{{{ \substack{ \chi \rightarrow \infty \\ \sigma \rightarrow \infty \\ t\rightarrow \infty }}}}F( \psi _{1},\psi _{2},v)=0. $$

 □

The inverse double Sumudu-generalized Laplace transform \(S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} [ S_{\chi }S_{ \sigma }G_{t} ( \psi ( \chi , \sigma ,t ) ) ] =\psi ( \chi ,\sigma ,t ) \) is denoted by the following formula

$$\begin{aligned} &\psi ( \chi ,\sigma ,t ) \\ &\quad = \frac{1}{ ( 2\pi i ) ^{3}}\int _{\tau -i\infty }^{\tau -i\infty } \int _{\delta -i\infty }^{ \delta -i\infty } \int _{\sigma -i\infty }^{\sigma -i\infty }e^{ \frac{1}{\mu _{1}}\chi +\frac{1}{\mu _{1}}\sigma +\frac{1}{s}t}S_{\chi }S_{\sigma }G_{t} \bigl[ \psi ( \chi ,\sigma ,t ) \bigr]\,ds \,d\mu _{2}\,d\mu _{1}. \end{aligned}$$

Theorem 2

If the double Sumudu-generalized Laplace transform of the function \(f ( \chi ,\sigma ,t ) \) is presented by \(S_{\chi }S_{\sigma }G_{t} ( f ( \chi ,\sigma ,t ) ) =F(\mu _{1},\mu _{2},s)\), then the double Sumudu-generalized Laplace transform of the functions

$$ \chi \sigma f ( \chi ,\sigma ,t ) , $$

is determined by

$$ S_{\chi }S_{\sigma }G_{t} \bigl[ \chi \sigma f ( \chi , \sigma ,t ) \bigr] =\mu _{1}\mu _{2} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}F(\mu _{1},\mu _{2},s) \bigr) . $$
(10)

Proof

By applying partial derivatives according to \(\mu _{1}\) for Eq. (10), we yield

$$\begin{aligned} \frac{\partial F(\mu _{1},\mu _{2},s)}{\partial \mu _{1}} =& \frac{\partial }{\partial \mu _{1}} \int _{0}^{\infty } \int _{0}^{ \infty } \int _{0}^{\infty }\frac{s^{\alpha }}{\mu _{1}\mu _{2}}e^{- ( \frac{1}{\mu _{1}} \chi +\frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) }f ( \chi ,\sigma ,t )\,d\chi \,d\sigma \,dt, \\ =& \int _{0}^{\infty } \int _{0}^{\infty } \frac{s^{\alpha }}{\mu _{2}}e^{- ( \frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) } \\ &{}\times \biggl( \int _{0}^{\infty }\frac{\partial }{\partial \mu _{1}} \frac{1}{\mu _{1}}e^{-\frac{1}{\mu _{1}}\chi }f ( \chi ,\sigma ,t )\,d\chi \biggr)\,d\sigma \,dt, \end{aligned}$$
(11)

by handling the partial derivative inside the brackets, we obtain

$$\begin{aligned} \int _{0}^{\infty }\frac{\partial }{\partial \mu _{1}} \frac{1}{\mu _{1}}e^{-\frac{1}{\mu _{1}}\chi }f ( \chi ,\sigma ,t )\,d\chi =& \int _{0}^{\infty } \biggl( \frac{1}{\mu _{1}^{3}}\chi - \frac{1}{\mu _{1}^{2}} \biggr) e^{-\frac{1}{\mu _{1}}\chi }f ( \chi ,\sigma ,t )\,d\chi \\ =& \int _{0}^{\infty }\frac{1}{\mu _{1}^{3}}\chi e^{- \frac{1}{\mu _{1}}\chi }f ( \chi ,\sigma ,t )\,d\chi \\ &{}- \int _{0}^{\infty }\frac{1}{\mu _{1}^{2}}e^{-\frac{1}{\mu _{1}} \chi }f ( \chi ,\sigma ,t )\,d\chi , \end{aligned}$$
(12)

substituting Eq. (12) into Eq. (11), one can obtain the following equation

$$\begin{aligned} \frac{\partial F(\mu _{1},\mu _{2},s)}{\partial \mu _{1}} =& \int _{0}^{\infty } \int _{0}^{\infty }\frac{s^{\alpha }}{\mu _{2}}e^{- ( \frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) } \biggl( \int _{0}^{\infty } \frac{1}{\mu _{1}^{3}}\chi e^{-\frac{1}{\mu _{1}}\chi }f ( \chi , \sigma ,t )\,d\chi \biggr)\,d\sigma \,dt \\ &{}- \int _{0}^{\infty } \int _{0}^{\infty } \frac{s^{\alpha }}{\mu _{2}}e^{- ( \frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) } \biggl( \int _{0}^{\infty }\frac{1}{\mu _{1}^{2}}e^{-\frac{1}{\mu _{1}}\chi }f ( \chi ,\sigma ,t )\,d\chi \biggr)\,d\sigma \,dt \end{aligned}$$
(13)

and by taking derivatives according to \(\mu _{2}\) for Eq. (13), we achieve

$$\begin{aligned} \frac{\partial ^{2}F(\mu _{1},\mu _{2},s)}{\partial \mu _{1}\partial \mu _{2}} =&\frac{s^{\alpha }}{\mu _{1}^{3}} \int _{0}^{\infty } \int _{0}^{ \infty }\chi e^{- ( \frac{1}{\mu _{1}}\chi +\frac{1}{s}t ) } \\ &{}\times \biggl( \int _{0}^{\infty }e^{-\frac{1}{\mu _{2}}\sigma } \biggl( \frac{1}{\mu _{2}^{3}}\sigma -\frac{1}{\mu _{2}^{2}} \biggr) f ( \chi ,\sigma ,t ) \biggr)\,d\chi \,d\sigma \,dt \\ &{}-\frac{s^{\alpha }}{\mu _{1}} \int _{0}^{\infty } \int _{0}^{\infty }e^{- ( \frac{1}{\mu _{1}}\chi +\frac{1}{s}t ) } \\ &{}\times \biggl( \int _{0}^{ \infty }e^{-\frac{1}{\mu _{2}}\sigma } \biggl( \frac{1}{\mu _{2}^{3}}\sigma -\frac{1}{\mu _{2}^{2}} \biggr) f ( \chi ,\sigma ,t ) \biggr)\,d\chi \,d\sigma \,dt. \end{aligned}$$
(14)

After the arrangement, Eq. (14), becomes

$$\begin{aligned} \frac{\partial ^{2}F(\mu _{1},\mu _{2},s)}{\partial \mu _{1}\partial \mu _{2}} =&\frac{1}{\mu _{1}^{2}\mu _{2}^{2}}S_{\chi }S_{\sigma }G_{t} \bigl[ \chi \sigma f ( \chi ,\sigma ,t ) \bigr] - \frac{1}{\mu _{1}^{2}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl[ \chi f ( \chi ,\sigma ,t ) \bigr] \\ &{}-\frac{1}{\mu _{1}\mu _{2}^{2}}S_{\chi }S_{\sigma }G_{t} \bigl[ \sigma f ( \chi ,\sigma ,t ) \bigr] + \frac{1}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl[ f ( \chi ,\sigma ,t ) \bigr] , \end{aligned}$$
(15)

by arranging the above equation, we obtain

$$\begin{aligned} S_{\chi }S_{\sigma }G_{t} \bigl[ \chi \sigma ( \chi , \sigma ,t ) \bigr] =&\mu _{1}^{2}\mu _{2}^{2} \frac{\partial ^{2}F(\mu _{1},\mu _{2},s)}{\partial \mu _{1}\partial \mu _{2}}+\mu _{1}^{2}\mu _{2} \frac{\partial F(\mu _{1},\mu _{2},s)}{\partial \mu _{1}} \\ &{}+\mu _{1}\mu _{2}^{2} \frac{\partial F(\mu _{1},\mu _{2},s)}{\partial \mu _{2}}+ \mu _{1} \mu _{2}F(\mu _{1},\mu _{2},s), \end{aligned}$$

thence,

$$ S_{\chi }S_{\sigma }G_{t} \bigl[ \chi \sigma f ( \chi , \sigma ,t ) \bigr] =\mu _{1}\mu _{2} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}F(\mu _{1},\mu _{2},s) \bigr) . $$

The proof is completed. □

The double Sumudu-generalized Laplace transform of the function \(\psi (\chi ,\sigma ,t)\) is determined by \(S_{\chi }S_{\sigma }G_{t} [ \psi ( \chi ,\sigma ,t ) ] =\Psi (\mu _{1},\mu _{2},s)\) then, the double Sumudu-generalized Laplace transform of \(\frac{\partial \psi }{\partial \chi }\), \(\frac{\partial ^{2}\psi }{\partial \chi ^{2}}\), \(D_{t}^{\beta }\psi \) is presented as

$$\begin{aligned}& S_{\chi }S_{\sigma }G_{t} \biggl[ \frac{\partial \psi }{\partial \chi } \biggr] = \frac{\Psi (\mu _{1},\mu _{2},s)-\Psi (0,\mu _{2},s)}{\mu _{1}}, \end{aligned}$$
(16)
$$\begin{aligned}& S_{\chi }S_{\sigma }G_{t} \biggl( \frac{\partial ^{2}\psi }{\partial \chi ^{2}} \biggr) = \frac{\Psi (\mu _{1},\mu _{2},s)}{\mu _{1}^{2}}- \frac{\psi ( 0,\mu _{2},s ) }{\mu _{1}^{2}}- \frac{\psi _{t}(0,\mu _{2},s)}{\mu _{1}}, \end{aligned}$$
(17)
$$\begin{aligned}& S_{\chi }S_{\sigma }G_{t} \biggl[ \frac{\partial \psi }{\partial \sigma } \biggr] = \frac{\Psi (\mu _{1},\mu _{2},s)-\Psi (\mu _{1},0,s)}{\mu _{2}}, \\& S_{\chi }S_{\sigma }G_{t} \biggl( \frac{\partial ^{2}\psi }{\partial \sigma ^{2}} \biggr) = \frac{\Psi (\mu _{1},\mu _{2},s)}{\mu _{2}^{2}}- \frac{\Psi (\mu _{1},0,s)}{\mu _{2}^{2}}- \frac{\psi _{t}(\mu _{1},0,s)}{\mu _{2}} \end{aligned}$$
(18)

and

$$ S_{\chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta } \psi \bigr] = \frac{\Psi (\mu _{1},\mu _{2},s)}{s^{\beta }}-s^{\alpha -\beta +1} \Psi (\mu _{1},\mu _{2},0). $$
(19)

The next theorem offers the double Sumudu-generalized Laplace transform of the partial derivatives \(\chi D_{t}^{\beta }\psi \) and \(\sigma D_{t}^{\beta }\psi \).

Theorem 3

The double Sumudu-generalized Laplace transform of the fractional partial derivatives \(\chi D_{t}^{\beta }\psi \) and \(\sigma D_{t}^{\beta }\psi \) is achieved by

$$\begin{aligned} S_{\chi }S_{\sigma }G_{t} \bigl[ \chi D_{t}^{\beta } \psi \bigr] =& \frac{\mu _{1}\mu _{2}}{s^{\beta }} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}\Psi (\mu _{1},\mu _{2},s) \bigr) \\ &{}-\mu _{1}\mu _{2}s^{\alpha -\beta +1} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}\Psi (\mu _{1},\mu _{2},0) \bigr) \end{aligned}$$
(20)

and

$$\begin{aligned} S_{\chi }S_{\sigma }G_{t} \bigl[ \sigma D_{t}^{\beta }\psi \bigr] =& \frac{\mu _{2}}{s^{\beta }}\frac{\partial }{\partial \mu _{1}} \bigl( \mu _{2} \Psi (\mu _{1},\mu _{2},s) \bigr) \\ &{}-\mu _{2}s^{\alpha -\beta +1}\frac{\partial }{\partial \mu _{2}} \bigl( \mu _{1}\Psi (\mu _{1},\mu _{2},0) \bigr) . \end{aligned}$$
(21)

Proof

By employing partial derivatives according to \(\mu _{1 }\) for Eq. (1), we obtain

$$\begin{aligned}& \frac{\partial }{\partial \mu _{1}} \bigl( S_{\chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta }\psi \bigr] \bigr) \\& \quad = \frac{\partial }{\partial \mu _{1}}\int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty } \frac{s^{\alpha }}{\mu _{1}\mu _{2}}e^{- ( \frac{1}{\mu _{1}} \chi +\frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) }D_{t}^{\beta } \psi \,d\chi \,d\sigma \,dt, \\& \quad = \int _{0}^{\infty } \int _{0}^{\infty } \frac{s^{\alpha }}{\mu _{2}}e^{- ( \frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) } \biggl( \int _{0}^{\infty }\frac{\partial }{\partial \mu _{1}} \frac{1}{\mu _{1}}e^{-\frac{1}{\mu _{1}}\chi }D_{t}^{\beta }\psi \,d\chi \biggr)\,d\sigma \,dt \end{aligned}$$
(22)

and the partial derivative within the brackets can be calculated as follows:

$$\begin{aligned} \int _{0}^{\infty }\frac{\partial }{\partial \mu _{1}} \frac{1}{\mu _{1}}e^{-\frac{1}{\mu _{1}}\chi }D_{t}^{\beta }\psi \,d\chi =& \int _{0}^{ \infty } \biggl( \frac{1}{\mu _{1}^{3}}\chi - \frac{1}{\mu _{1}^{2}} \biggr) e^{-\frac{1}{\mu _{1}}\chi }D_{t}^{\beta }\psi \,d \chi \\ =& \int _{0}^{\infty }\frac{1}{\mu _{1}^{3}}\chi e^{- \frac{1}{\mu _{1}}\chi }D_{t}^{\beta }\psi \,d\chi \\ &{}- \int _{0}^{\infty }\frac{1}{\mu _{1}^{2}}e^{-\frac{1}{\mu _{1}} \chi }D_{t}^{\beta } \psi \,d\chi , \end{aligned}$$
(23)

by putting Eq. (23) into Eq. (22), we obtain

$$\begin{aligned}& \frac{\partial }{\partial \mu _{1}} \bigl( S_{\chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta }\psi \bigr] \bigr) \\& \quad = \int _{0}^{\infty } \int _{0}^{\infty }\frac{s^{\alpha }}{\mu _{2}}e^{- ( \frac{1}{\mu _{2}}\sigma + \frac{1}{s}t ) } \biggl( \int _{0}^{\infty }\frac{1}{\mu _{1}^{3}}\chi e^{- \frac{1}{\mu _{1}}\chi }D_{t}^{\beta }\psi \,d\chi \biggr)\,d\sigma \,dt \\& \qquad {}- \int _{0}^{\infty } \int _{0}^{\infty } \frac{s^{\alpha }}{\mu _{2}}e^{- ( \frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) } \biggl( \int _{0}^{\infty }\frac{1}{\mu _{1}^{2}}e^{-\frac{1}{\mu _{1}}\chi }D_{t}^{ \beta } \psi \,d\chi \biggr)\,d\sigma \,dt, \end{aligned}$$
(24)

therefore, Eq. (24) becomes

$$\begin{aligned}& \frac{\partial }{\partial \mu _{1}} \bigl( S_{\chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta }\psi \bigr] \bigr) \\& \quad = \frac{1}{\mu _{1}^{2}} \biggl( \frac{s^{\alpha }}{\mu _{1}\mu _{2}} \int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }e^{- ( \frac{1}{\mu _{1}}\chi + \frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) }\chi D_{t}^{\beta }\psi \,d\chi \,d\sigma \,dt \biggr) \\& \qquad {}-\frac{1}{\mu _{1}} \biggl( \frac{s^{\alpha }}{\mu _{1}\mu _{2}}\int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }e^{- ( \frac{1}{\mu _{1}}\chi +\frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) }D_{t}^{ \beta } \psi \,d\chi \,d\sigma \,dt \biggr), \end{aligned}$$
(25)

hence,

$$\begin{aligned} \frac{\partial }{\partial \mu _{1}} \bigl( S_{\chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta }\psi \bigr] \bigr) =& \frac{1}{\mu _{1}^{2}}S_{\chi }S_{\sigma }G_{t} \bigl[ \chi D_{t}^{ \beta }\psi \bigr] -\frac{1}{\mu _{1}}S_{\chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta }\psi \bigr] \end{aligned}$$
(26)

and by arranging the above equation, we will obtain the proof of Eq. (20) as follows

$$\begin{aligned} S_{\chi }S_{\sigma }G_{t} \bigl[ \chi D_{t}^{\beta } \psi \bigr] =& \frac{\mu _{1}}{s^{\beta }}\frac{\partial }{\partial \mu _{1}} \bigl( \mu _{1} \Psi (\mu _{1},\mu _{2},s) \bigr) \\ &{}-\mu _{1}s^{\alpha -\beta +1}\frac{\partial }{\partial \mu _{1}} \bigl( \mu _{1}\Psi (\mu _{1},\mu _{2},0) \bigr). \end{aligned}$$

Similarly, we can prove Eq. (21). □

The double Sumudu-generalized Laplace transform of the partial derivatives is presented in the upcoming theorem:

Theorem 4

The double Sumudu-generalized Laplace transform of the fractional partial derivatives \(\chi \sigma D_{t}^{\beta }\psi \) is determined by

$$\begin{aligned} S_{\chi }S_{\sigma }G_{t} \bigl[ \chi \sigma D_{t}^{\beta }\psi \bigr] =&\frac{\mu _{1}\mu _{2}}{s^{\beta }} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}\Psi (\mu _{1},\mu _{2},s) \bigr) \\ &{}-\mu _{1}\mu _{2}s^{\alpha -\beta +1} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}\Psi (\mu _{1},\mu _{2},0) \bigr) . \end{aligned}$$
(27)

Proof

By taking partial derivatives according to \(\mu _{1 }\) for Eq. (1), we have

$$\begin{aligned}& \frac{\partial }{\partial \mu _{1}} \bigl( S_{\chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta }\psi \bigr] \bigr) \\& \quad = \frac{\partial }{\partial \mu _{1}}\int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty } \frac{s^{\alpha }}{\mu _{1}\mu _{2}}e^{- ( \frac{1}{\mu _{1}} \chi +\frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) }D_{t}^{\beta } \psi \,d\chi \,d\sigma \,dt, \\& \quad = \int _{0}^{\infty } \int _{0}^{\infty } \frac{s^{\alpha }}{\mu _{2}}e^{- ( \frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) } \biggl( \int _{0}^{\infty }\frac{\partial }{\partial \mu _{1}} \frac{1}{\mu _{1}}e^{-\frac{1}{\mu _{1}}\chi }D_{t}^{\beta }\psi \,d\chi \biggr)\,d\sigma \,dt \end{aligned}$$
(28)

and we calculate the partial derivative inside brackets as follows:

$$\begin{aligned} \int _{0}^{\infty }\frac{\partial }{\partial \mu _{1}} \frac{1}{\mu _{1}}e^{-\frac{1}{\mu _{1}}\chi }D_{t}^{\beta }\psi \,d\chi =& \int _{0}^{ \infty } \biggl( \frac{1}{\mu _{1}^{3}}\chi - \frac{1}{\mu _{1}^{2}} \biggr) e^{-\frac{1}{\mu _{1}}\chi }D_{t}^{\beta }\psi \,d \chi \\ =& \int _{0}^{\infty }\frac{1}{\mu _{1}^{3}}\chi e^{- \frac{1}{\mu _{1}}\chi }D_{t}^{\beta }\psi \,d\chi \\ &{}- \int _{0}^{\infty }\frac{1}{\mu _{1}^{2}}e^{-\frac{1}{\mu _{1}} \chi }D_{t}^{\beta } \psi \,d\chi . \end{aligned}$$
(29)

Putting Eq. (29) into Eq. (28), we obtain

$$\begin{aligned}& \frac{\partial }{\partial \mu _{1}} \bigl( S_{\chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta }\psi \bigr] \bigr) \\& \quad = \int _{0}^{\infty } \int _{0}^{\infty }\frac{s^{\alpha }}{\mu _{2}}e^{- ( \frac{1}{\mu _{2}}\sigma + \frac{1}{s}t ) } \biggl( \int _{0}^{\infty }\frac{1}{\mu _{1}^{3}}\chi e^{- \frac{1}{\mu _{1}}\chi }D_{t}^{\beta }\psi \,d\chi \biggr)\,d\sigma \,dt \\& \qquad {}- \int _{0}^{\infty } \int _{0}^{\infty } \frac{s^{\alpha }}{\mu _{2}}e^{- ( \frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) } \biggl( \int _{0}^{\infty }\frac{1}{\mu _{1}^{2}}e^{-\frac{1}{\mu _{1}}\chi }D_{t}^{ \beta } \psi \,d\chi \biggr)\,d\sigma \,dt, \end{aligned}$$
(30)

the partial derivative with respect to \(\mu _{2}\) for Eq. (30) is calculated as the following:

$$\begin{aligned}& \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( S_{ \chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta }\psi \bigr] \bigr) \\& \quad = \frac{\partial }{\partial \mu _{2}} \biggl( \int _{0}^{\infty } \int _{0}^{ \infty }\frac{s^{\alpha }}{\mu _{2}}e^{- ( \frac{1}{\mu _{2}}\sigma + \frac{1}{s}t ) } \biggl( \int _{0}^{\infty }\frac{1}{\mu _{1}^{3}}\chi e^{- \frac{1}{\mu _{1}}\chi }D_{t}^{\beta }\psi \,d\chi \biggr)\,d\sigma \,dt \biggr) \\& \qquad {}-\frac{\partial }{\partial \mu _{2}} \biggl( \int _{0}^{\infty } \int _{0}^{\infty }\frac{s^{\alpha }}{\mu _{2}}e^{- ( \frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) } \biggl( \int _{0}^{\infty } \frac{1}{\mu _{1}^{2}}e^{-\frac{1}{\mu _{1}}\chi }D_{t}^{\beta } \psi \,d\chi \biggr)\,d\sigma \,dt \biggr) , \end{aligned}$$
(31)

therefore, Eq. (31) becomes

$$\begin{aligned}& \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( S_{ \chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta }\psi \bigr] \bigr) \\& \quad = \frac{1}{\mu _{1}^{2}\mu _{2}^{2}} \biggl( \frac{s^{\alpha }}{\mu _{1}\mu _{2}}\int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }e^{- ( \frac{1}{\mu _{1}}\chi +\frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) }\chi \sigma D_{t}^{\beta }\psi \,d\chi \,d\sigma \,dt \biggr) \\& \qquad {}+\frac{1}{\mu _{1}\mu _{2}} \biggl( \frac{s^{\alpha }}{\mu _{1}\mu _{2}}\int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }e^{- ( \frac{1}{\mu _{1}}\chi +\frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) }D_{t}^{ \beta } \psi \,d\chi \,d\sigma \,dt \biggr) \\& \qquad {}-\frac{1}{\mu _{1}\mu _{2}^{2}} \biggl( \frac{s^{\alpha }}{\mu _{1}\mu _{2}}\int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }e^{- ( \frac{1}{\mu _{1}}\chi +\frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) } \sigma D_{t}^{\beta }\psi \,d\chi \,d\sigma \,dt \biggr) \\& \qquad {}-\frac{1}{\mu _{1}^{2}\mu _{2}} \biggl( \frac{s^{\alpha }}{\mu _{1}\mu _{2}}\int _{0}^{\infty } \int _{0}^{\infty } \int _{0}^{\infty }e^{- ( \frac{1}{\mu _{1}}\chi +\frac{1}{\mu _{2}}\sigma +\frac{1}{s}t ) }\chi D_{t}^{ \beta }\psi \,d\chi \,d\sigma \,dt \biggr) , \end{aligned}$$
(32)

thence

$$\begin{aligned}& \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( S_{ \chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta }\psi \bigr] \bigr) \\& \quad = \frac{1}{\mu _{1}^{2}\mu _{2}^{2}}S_{\chi }S_{\sigma }G_{t} \bigl[ \chi \sigma D_{t}^{\beta }\psi \bigr] +\frac{1}{\mu _{1}\mu _{2}}S_{ \chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta }\psi \bigr] \\& \qquad {}-\frac{1}{\mu _{1}\mu _{2}^{2}}S_{\chi }S_{\sigma }G_{t} \bigl[ \sigma D_{t}^{\beta }\psi \bigr] -\frac{1}{\mu _{1}^{2}\mu _{2}}S_{ \chi }S_{\sigma }G_{t} \bigl[ \chi D_{t}^{\beta }\psi \bigr] \end{aligned}$$
(33)

and one can rearrange Eq. (33), to prove Eq. (27)

$$\begin{aligned} S_{\chi }S_{\sigma }G_{t} \bigl[ \chi \sigma D_{t}^{\beta }\psi \bigr] =&\frac{\mu _{1}\mu _{2}}{s^{\beta }} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}\Psi (\mu _{1},\mu _{2},s) \bigr) \\ &{}-\mu _{1}\mu _{2}s^{\alpha -\beta +1} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}\Psi (\mu _{1},\mu _{2},0) \bigr). \end{aligned}$$

 □

3 Double Sumudu-generalized Laplace decomposition method and two-dimensional time-fractional coupled Burger’s equation

This section aims to make use of the double Sumudu-generalized Laplace decomposition method (DSGLTDM) to solve the two-dimensional time-fractional coupled Burger’s equation. In the upcoming analysis, we deem the two-dimensional fractional coupled Burger’s equation to be:

$$\begin{aligned}& D_{t}^{\beta }\psi +\psi \psi _{\chi }+\phi \psi _{\sigma } = \frac{1}{\Re } ( \psi _{\chi \chi }+\psi _{\sigma \sigma } ) \\& D_{t}^{\beta }\phi +\psi \phi _{\chi }+\phi \phi _{\sigma } = \frac{1}{\Re } ( \phi _{\chi \chi }+\phi _{\sigma \sigma } ) \\& n-1 < \beta < n; \end{aligned}$$
(34)

with the following conditions

$$ \psi ( \chi ,\sigma ,0 ) =f_{1} ( \chi ,\sigma ) ,\qquad \phi ( \chi ,\sigma ,0 ) =g_{1} ( \chi ,\sigma ) , $$
(35)

where \(D_{t}^{\beta }=\frac{\partial ^{\beta }}{\partial t^{\beta }}\) stands for the fractional Caputo derivative, ℜ is the Reynolds number, and the velocity components are determined by \(\psi ( \chi ,\sigma ,t ) \) and \(\phi ( \chi , \sigma ,t ) \) in the χ and σ directions, respectively. The two-dimensional coupled Burger’s equations are the same as the incompressible Navier–Stokes equations with the pressure-gradient terms removed. With the purpose to gain the solution of Eq. (34), first, operating the double Sumudu-generalized Laplace for Eq. (34) and using the double Sumudu transform for Eq. (35) we gain

$$\begin{aligned} S_{\chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta } \psi \bigr] =&S_{ \chi }S_{\sigma }G_{t} \biggl[ \frac{1}{\Re } ( \psi _{\chi \chi }+ \psi _{\sigma \sigma } ) \biggr] \\ &{}-S_{\chi }S_{\sigma }G_{t} [ \psi \psi _{\chi }+\phi \psi _{ \sigma } ] \end{aligned}$$
(36)

and

$$\begin{aligned} S_{\chi }S_{\sigma }G_{t} \bigl[ D_{t}^{\beta } \phi \bigr] =&S_{ \chi }S_{\sigma }G_{t} \biggl[ \frac{1}{\Re } ( \phi _{ \chi \chi }+ \phi _{\sigma \sigma } ) \biggr] \\ &{}-S_{\chi }S_{\sigma }G_{t} [ \psi \phi _{\chi }+\phi \phi _{\sigma } ] , \end{aligned}$$
(37)

by putting Eq. (19) into Eq. (36) and Eq. (37), we obtain

$$\begin{aligned} \frac{\Psi (\mu _{1},\mu _{2},s)}{s^{\beta }} =&s^{\alpha -\beta +1}F_{1}( \mu _{1},\mu _{2}) \\ &{}+S_{\chi }S_{\sigma }G_{t} \biggl[ \frac{1}{\Re } ( \psi _{\chi \chi }+\psi _{\sigma \sigma } ) \biggr] \\ &{}-S_{\chi }S_{\sigma }G_{t} [ \psi \psi _{\chi }+\phi \psi _{\sigma } ] \end{aligned}$$
(38)

and

$$\begin{aligned} \frac{\Phi (\mu _{1},\mu _{2},s)}{s^{\beta }} =&s^{\alpha -\beta +1}G_{1}( \mu _{1},\mu _{2}) \\ &{}+S_{\chi }S_{\sigma }G_{t} \biggl[ \frac{1}{\Re } ( \phi _{\chi \chi }+ \phi _{\sigma \sigma } ) \biggr] \\ &{}-S_{\chi }S_{\sigma }G_{t} [ \psi \phi _{\chi }+\phi \phi _{\sigma } ] , \end{aligned}$$
(39)

therefore, by rearranging Eq. (38) and Eq. (39) we obtain

$$\begin{aligned} \Psi (\mu _{1},\mu _{2},s) =&s^{\alpha +1}F_{1}( \mu _{1},\mu _{2}) \\ &{}+s^{\beta }S_{\chi }S_{\sigma }G_{t} \biggl[ \frac{1}{\Re } ( \psi _{\chi \chi }+\psi _{\sigma \sigma } ) \biggr] \\ &{}-s^{\beta }S_{\chi }S_{\sigma }G_{t} [ \psi \psi _{ \chi }+\phi \psi _{\sigma } ] , \end{aligned}$$
(40)

and

$$\begin{aligned} \Phi (\mu _{1},\mu _{2},s) =&s^{\alpha +1}G_{1}( \mu _{1},\mu _{2}) \\ &{}+s^{\beta }S_{\chi }S_{\sigma }G_{t} \biggl[ \frac{1}{\Re } ( \phi _{\chi \chi }+ \phi _{\sigma \sigma } ) \biggr] \\ &{}-s^{\beta }S_{\chi }S_{\sigma }G_{t} [ \psi \phi _{ \chi }+\phi \phi _{\sigma } ] \end{aligned}$$
(41)

and by employing the inverse double Sumudu-generalized Laplace for Eq. (38) and Eq. (39), we yield

$$\begin{aligned} \psi ( \chi ,\sigma ,t ) =&f_{1} ( \chi ,\sigma ) \\ &{}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} \biggl[ \frac{1}{\Re } ( \psi _{ \chi \chi }+\psi _{\sigma \sigma } ) \biggr] \biggr] \\ &{}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} [ A_{n}+B_{n} ] \bigr] \end{aligned}$$
(42)

and

$$\begin{aligned} \phi ( \chi ,\sigma ,t ) =&g_{1} ( \chi ,\sigma ) \\ &{}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} \biggl[ \frac{1}{\Re } ( \phi _{ \chi \chi }+\phi _{\sigma \sigma } ) \biggr] \biggr] \\ &{}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} [ C_{n}+D_{n} ] \bigr], \end{aligned}$$
(43)

where some terms of the Adomian polynomials \(A_{n}\) \(B_{n}\), \(C_{n} \), and \(D_{n}\) are determined by

$$\begin{aligned}& A_{0} = \psi _{0}\psi _{0\chi }, \qquad A_{1}=\psi _{0}\psi _{1 \chi }+\psi _{1} \psi _{0\chi }, \\& A_{2} = \psi _{0}\psi _{2\chi }+\psi _{1}\psi _{1\chi }+\psi _{2} \psi _{0\chi }, \\& A_{3} = \psi _{0}\psi _{3\chi }+\psi _{1}\psi _{2\chi }+\psi _{2} \psi _{1\chi }+ \psi _{3}\psi _{0\chi }, \end{aligned}$$
(44)
$$\begin{aligned}& B_{0} = \phi _{0}\psi _{0\sigma },\qquad B_{1}=\phi _{0}\psi _{1 \sigma }+\phi _{1} \psi _{0\sigma }, \\& B_{2} = \phi _{0}\psi _{2\sigma }+\phi _{1}\psi _{1\sigma }+\phi _{2} \psi _{0\sigma }, \\& B_{3} = \phi _{0}\psi _{3\sigma }+\phi _{1}\psi _{2\sigma }+\phi _{2} \psi _{1\sigma }+ \phi _{3}\psi _{0\sigma }, \end{aligned}$$
(45)
$$\begin{aligned}& C_{0} = \psi _{0}\phi _{0\chi },\qquad C_{1}=\psi _{0}\phi _{1 \chi }+\psi _{1} \phi _{0\chi }, \\& C_{2} = \psi _{0}\phi _{2\chi }+\psi _{1}\phi _{1\chi }+\psi _{2} \phi _{0\chi }, \\& C_{3} = \psi _{0}\phi _{3\chi }+\psi _{1}\phi _{2\chi }+\psi _{2} \phi _{1\chi }+ \psi _{3}\phi _{0\chi }. \end{aligned}$$
(46)
$$\begin{aligned}& D_{0} = \phi _{0}\phi _{0\sigma },\qquad D_{1}=\phi _{0}\phi _{1 \sigma }+\phi _{1} \phi _{0\sigma }, \\& D_{2} = \phi _{0}\phi _{2\sigma }+\phi _{1}\phi _{1\sigma }+\phi _{2} \phi _{0\sigma }, \\& D_{3} = \phi _{0}\phi _{3\sigma }+\phi _{1}\phi _{2\sigma }+\phi _{2} \phi _{1\sigma }+ \phi _{3}\phi _{0\sigma } \end{aligned}$$
(47)

and \(S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1}\) denotes the inverse double Sumudu-generalized Laplace. The double Sumudu-generalized Laplace decomposition method (DSGLTDM) defines the solutions \(\psi (\chi ,\sigma ,t)\) and \(\psi (\chi ,\sigma ,t)\) and is represented by the following infinite series.

$$\begin{aligned}& \psi ( \chi ,\sigma ,t ) =\sum_{n=0}^{\infty } \psi _{n} ( \chi ,\sigma ,t ) \end{aligned}$$
(48)
$$\begin{aligned}& \phi ( \chi ,\sigma ,t ) =\sum_{n=0}^{\infty } \phi _{n} ( \chi ,\sigma ,t ) . \end{aligned}$$
(49)

Moreover, the nonlinear terms \(\psi \psi _{\chi }\), \(\phi \frac{\partial \psi }{\partial \sigma }\), \(\psi \frac{\partial \phi }{\partial \chi }\) and \(\phi \frac{\partial \phi }{\partial \sigma }\) are presented by:

$$ \psi \psi _{\chi }=\sum_{n=0}^{\infty }A_{n}, \qquad \phi \frac{\partial \psi }{\partial \sigma }=\sum_{n=0}^{\infty }B_{n}, \qquad \psi \frac{\partial \phi }{\partial \chi }=\sum_{n=0}^{ \infty }C_{n}, \qquad \phi \frac{\partial \phi }{\partial \sigma }=\sum_{n=0}^{\infty }D_{n}. $$
(50)

By substituting Eq. (48) and Eq. (49) into Eq. (42) and Eq. (43), we obtain

$$\begin{aligned} \sum_{n=0}^{\infty }\psi _{n} ( \chi ,\sigma ,t ) =&f_{1} ( \chi ,\sigma ) +S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \Biggl[ s^{\beta }S_{\chi }S_{\sigma }G_{t} \Biggl[ \frac{1}{\Re } \Biggl( \sum_{n=0}^{\infty } ( \psi _{n \chi \chi }+\psi _{n\sigma \sigma } ) \Biggr) \Biggr] \Biggr] \\ &{}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \Biggl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} \Biggl[ \sum_{n=0}^{\infty } ( A_{n}+B_{n} ) \Biggr] \Biggr] \end{aligned}$$
(51)

and

$$\begin{aligned} \sum_{n=0}^{\infty }\phi _{n} ( \chi ,\sigma ,t ) =&g_{1} ( \chi ,\sigma ) +S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \Biggl[ s^{\beta }S_{\chi }S_{\sigma }G_{t} \Biggl[ \frac{1}{\Re } \Biggl( \sum_{n=0}^{\infty } ( \phi _{n \chi \chi }+\phi _{n\sigma \sigma } ) \Biggr) \Biggr] \Biggr] \\ &{}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \Biggl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} \Biggl[ \sum_{n=0}^{\infty } ( C_{n}+D_{n} ) \Biggr] \Biggr]. \end{aligned}$$
(52)

By comparing both sides of Eq. (51) and Eq. (52), we obtain

$$\begin{aligned}& \psi _{0} ( \chi ,\sigma ,t ) = f_{1} ( \chi , \sigma ) , \\& \phi _{0} ( \chi ,\sigma ,t ) = g_{1} ( \chi , \sigma ) . \end{aligned}$$
(53)

Generally, the remnant terms are presented by

$$\begin{aligned} \psi _{n+1} ( \chi ,\sigma ,t ) =&S_{\mu _{1}}^{-1}S_{ \mu _{2}}^{-1}G_{s}^{-1} \biggl[ s^{\beta }S_{\chi }S_{\sigma }G_{t} \biggl[ \frac{1}{\Re } \bigl( ( \psi _{n\chi \chi }+\psi _{n\sigma \sigma } ) \bigr) \biggr] \biggr] \\ &{}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} \bigl[ ( A_{n}+B_{n} ) \bigr] \bigr] \end{aligned}$$
(54)

and

$$\begin{aligned} \phi _{n+1} ( \chi ,\sigma ,t ) =&S_{\mu _{1}}^{-1}S_{ \mu _{2}}^{-1}G_{s}^{-1} \biggl[ s^{\beta }S_{\chi }S_{\sigma }G_{t} \biggl[ \frac{1}{\Re } \bigl( ( \phi _{n\chi \chi }+\phi _{n\sigma \sigma } ) \bigr) \biggr] \biggr] \\ &{}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} \bigl[ ( C_{n}+D_{n} ) \bigr] \bigr], \end{aligned}$$
(55)

where the inverse double Sumudu-generalized Laplace transform is determined by \(S_{\zeta _{1}}^{-1}S_{\zeta _{2}}^{-1}G_{s}^{-1}\). We assume that the inverse exists for Eqs. (54) and (55). For the goal of illustrating the advantages and the reliability of the (DSGLTDM) we solve the two-dimensional fractional coupled Burger’s equations.

Example 1

[13, 26, 27] Consider the singular two-dimensional time-fractional coupled Burger’s equations to be determined by

$$\begin{aligned}& D_{t}^{\alpha }\psi +\psi \psi _{\chi }+\phi \psi _{\sigma } = \psi _{ \chi \chi }+\psi _{\sigma \sigma },\qquad \chi , \sigma ,t>0, \\& D_{t}^{\alpha }\phi +\psi \phi _{\chi }+\phi \phi _{\sigma } = \phi _{ \chi \chi }+\phi _{\sigma \sigma },\qquad \chi , \sigma ,t>0, \\& n-1 < \alpha < n, \end{aligned}$$
(56)

with the following conditions

$$ \psi (\chi ,\sigma ,0)=\chi +\sigma ,\qquad \phi (\chi ,\sigma ,0)= \chi -\sigma . $$
(57)

Utilizing the previous steps one can obtain

$$\begin{aligned}& \psi (\chi ,\sigma ,t) = \chi +\sigma +S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ s^{\beta }S_{\chi }S_{\sigma }G_{t} \biggl[ \frac{1}{\Re } ( \psi _{\chi \chi }+\psi _{\sigma \sigma } ) \biggr] \biggr] \\& \hphantom{\psi (\chi ,\sigma ,t) =} {}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} [ A_{n}+B_{n} ] \bigr] , \\& \phi (\chi ,\sigma ,t) = \chi -\sigma +S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ s^{\beta }S_{\chi }S_{\sigma }G_{t} \biggl[ \frac{1}{\Re } ( \phi _{\chi \chi }+\phi _{\sigma \sigma } ) \biggr] \biggr] \\& \hphantom{\phi (\chi ,\sigma ,t) =}{}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} [ C_{n}+D_{n} ] \bigr] . \end{aligned}$$
(58)

The zeroth components \(\psi _{0}\) and \(\phi _{0}\) are proposed by the Adomian method; combining the initial conditions and the sources terms as follows:

$$\begin{aligned}& \psi _{0} ( \chi ,\sigma ,t ) = \chi +\sigma \\& \phi _{0} ( \chi ,\sigma ,t ) = \chi -\sigma . \end{aligned}$$
(59)

The remainder components \(\psi _{n+1}\), \(\phi _{n+1}\), \(n\geq 0\) are determined by utilizing the relation

$$\begin{aligned} \psi _{n+1} ( \chi ,\sigma ,t ) =&S_{\mu _{1}}^{-1}S_{ \mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{\chi }S_{\sigma }G_{t} \bigl[ ( \psi _{n\chi \chi }+\psi _{n\sigma \sigma } ) \bigr] \bigr] \\ &{}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} \bigl[ ( A_{n}+B_{n} ) \bigr] \bigr] \end{aligned}$$
(60)

and

$$\begin{aligned} \phi _{n+1} ( \chi ,\sigma ,t ) =&S_{\mu _{1}}^{-1}S_{ \mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{\chi }S_{\sigma }G_{t} \bigl[ ( \phi _{n\chi \chi }+\phi _{n\sigma \sigma } ) \bigr] \bigr] \\ &{}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} \bigl[ ( C_{n}+D_{n} ) \bigr] \bigr] , \end{aligned}$$
(61)

for \(n=0,1,2,\ldots\) , so, at \(n=0\)

$$\begin{aligned}& \psi _{1} ( \chi ,\sigma ,t ) = S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{\chi }S_{\sigma }G_{t} \bigl[ \bigl( ( \psi _{0\chi \chi }+\psi _{0\sigma \sigma } ) \bigr) \bigr] \bigr] \\& \hphantom{\psi _{1} ( \chi ,\sigma ,t ) =} {}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} \bigl[ ( A_{0}+B_{0} ) \bigr] \bigr] \\& \hphantom{\psi _{1} ( \chi ,\sigma ,t )} = -S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} \bigl[ ( 2 \chi ) \bigr] \bigr] \\& \hphantom{\psi _{1} ( \chi ,\sigma ,t ) } = -S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ 2s^{\alpha + \beta +1}\mu _{1} \bigr] \\& \psi _{1} ( \chi ,\sigma ,t ) = \frac{-2\chi t^{\beta }}{\Gamma ( \alpha +1 ) } \end{aligned}$$

and

$$\begin{aligned}& \phi _{1} ( \chi ,\sigma ,t ) = S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{\chi }S_{\sigma }G_{t} \bigl[ \bigl( ( \phi _{0\chi \chi }+\phi _{0\sigma \sigma } ) \bigr) \bigr] \bigr] \\& \hphantom{\phi _{1} ( \chi ,\sigma ,t )=} {}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} \bigl[ ( C_{0}+D_{0} ) \bigr] \bigr] \\& \hphantom{\phi _{1} ( \chi ,\sigma ,t )} = -S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ s^{\beta }S_{ \chi }S_{\sigma }G_{t} \bigl[ ( 2 \chi ) \bigr] \bigr] \\& \hphantom{\phi _{1} ( \chi ,\sigma ,t )} = -S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl[ 2s^{\alpha + \beta +1}\mu _{2} \bigr] \\& \phi _{1} ( \chi ,\sigma ,t ) = \frac{-2\sigma t^{\beta }}{\Gamma ( \alpha +1 ) }, \end{aligned}$$

likely, at \(n=1\), we have

$$\begin{aligned} \psi _{2} =&-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl( s^{ \beta }S_{\chi }S_{\sigma }G_{t} \bigl( ( \psi _{0}\psi _{1 \chi }+\psi _{1}\psi _{0\chi }+\phi _{0}\psi _{1\sigma }+\phi _{1} \psi _{0\sigma } ) \bigr) \bigr) \\ &{}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl( s^{\beta }S_{ \chi }S_{\sigma }G_{t} \bigl( ( \psi _{1\chi \chi }+\psi _{1 \sigma \sigma } ) \bigr) \bigr) , \\ =&-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl( s^{\beta }S_{ \chi }S_{\sigma }G_{t} \biggl( \frac{-t^{\beta }}{\Gamma ( \alpha +1 ) } ( 4\chi +4\sigma ) \biggr) \biggr) \\ =&S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl( ( 4\mu _{1}+4 \mu _{2} ) s^{\alpha +2\beta +1} \bigr) \\ =& \frac{4 ( \chi +\sigma ) t^{2\beta }}{\Gamma ( 2\alpha +1 ) } \end{aligned}$$

and

$$\begin{aligned} \phi _{2} =&-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl( s^{ \beta }S_{\chi }S_{\sigma }G_{t} ( D_{1}+E_{1} ) \bigr) \\ &{}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl( s^{\beta }S_{ \chi }S_{\sigma }G_{t} ( \phi _{1\chi \chi }+\phi _{1\sigma \sigma } ) \bigr) \\ =&S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl( s^{\beta }S_{ \chi }S_{\sigma }G_{t} \biggl( \frac{-t^{\beta }}{\Gamma ( \beta +1 ) } ( -4\chi +4\sigma ) \biggr) \biggr) \\ =&S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl( ( -4\mu _{1}+4 \mu _{2} ) s^{\alpha +2\beta +1} \bigr) \\ =& \frac{4 ( \chi -\sigma ) t^{2\beta }}{\Gamma ( 2\alpha +1 ) }, \end{aligned}$$

at \(n=2\), we produce

$$\begin{aligned} \psi _{3} =&-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl( s^{ \beta }S_{\chi }S_{\sigma }G_{t} ( \psi _{0\chi }\psi _{2}+\psi _{1 \chi }\psi _{1}+ \psi _{\chi 2}\psi _{0}+\phi _{0}\psi _{\sigma 2}+ \phi _{1}\psi _{\sigma 1}+\phi _{2} \psi _{\sigma 0} ) \bigr) \\ &{}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl( s^{\beta }S_{ \chi }S_{\sigma }G_{t} \bigl( ( \psi _{\chi \chi 2}+\psi _{ \sigma \sigma 2} ) \bigr) \bigr) , \\ =&-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl( s^{\beta }S_{ \chi }S_{\sigma }G_{t} \biggl( \biggl( 16\chi + \frac{4\chi \Gamma ( 2\beta +1 ) }{ ( \Gamma ( \beta +1 ) ) ^{2}} \biggr) \frac{t^{2\beta }}{\Gamma ( 2\beta +1 ) } \biggr) \biggr) \\ =&-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl( 16\mu _{1}s^{ \alpha +3\beta +1}+ \frac{4\Gamma ( 2\beta +1 ) \mu _{1}s^{\alpha +3\beta +1}}{ ( \Gamma ( \beta +1 ) ) ^{2}} \biggr) \\ =& \biggl( -16\chi - \frac{4\Gamma ( 2\beta +1 ) \chi }{ ( \Gamma ( \beta +1 ) ) ^{2}} \biggr) \frac{t^{3\beta }}{\Gamma ( 3\beta +1 ) }, \end{aligned}$$

similar to

$$\begin{aligned} \phi _{3} =&-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl( s^{ \beta }S_{\chi }S_{\sigma }G_{t} ( D_{2}+E_{2} ) \bigr) \\ &{}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \bigl( s^{\beta }S_{ \chi }S_{\sigma }G_{t} \bigl( ( \phi _{2\chi \chi }+\phi _{2 \sigma \sigma } ) \bigr) \bigr) \\ =&-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl( s^{\beta }S_{ \chi }S_{\sigma }G_{t} \biggl( \biggl( 16\sigma + \frac{4\sigma \Gamma ( 2\beta +1 ) }{ ( \Gamma ( \beta +1 ) ) ^{2}} \biggr) \frac{t^{2\beta }}{\Gamma ( 2\beta +1 ) } \biggr) \biggr) \\ =& \biggl( -16\sigma - \frac{4\sigma \Gamma ( 2\beta +1 ) }{ ( \Gamma ( \beta +1 ) ) ^{2}} \biggr) \frac{t^{3\beta }}{\Gamma ( 3\beta +1 ) }. \end{aligned}$$

Thus, the solution of Eq. (56) is

$$\begin{aligned}& \psi (\chi ,\sigma ,t) = \sum_{n=0}^{\infty }u_{n}= \psi _{0}+ \psi _{1}+\psi _{2}+\psi _{3}+\cdots \\& \psi (\chi ,\sigma ,t) = \chi +\sigma - \frac{2\chi t^{\beta }}{\Gamma ( \beta +1 ) }+ \frac{4 ( \chi +\sigma ) t^{2\beta }}{\Gamma ( 2\beta +1 ) }- \biggl( 16\chi + \frac{4\chi \Gamma ( 2\beta +1 ) }{ ( \Gamma ( \beta +1 ) ) ^{2}} \biggr) \frac{t^{3\beta }}{\Gamma ( 3\beta +1 ) }+\cdots \end{aligned}$$

and

$$\begin{aligned}& \phi (\chi ,\sigma ,t) = \sum_{n=0}^{\infty }v_{n}= \phi _{0}+ \phi _{1}+\phi _{2}+\phi _{3}+\cdots \\& \phi (\chi ,\sigma ,t) = \chi -\sigma - \frac{2\sigma t^{\beta }}{\Gamma ( \beta +1 ) }+ \frac{4 ( \chi +\sigma ) t^{2\beta }}{\Gamma ( 2\beta +1 ) } \\& \hphantom{\phi (\chi ,\sigma ,t) =}{}- \biggl( 16\sigma + \frac{4\sigma \Gamma ( 2\beta +1 ) }{ ( \Gamma ( \beta +1 ) ) ^{2}} \biggr) \frac{t^{3\alpha }}{\Gamma ( 3\alpha +1 ) }+ \cdots, \end{aligned}$$

at \(\beta =1\) the solution of the above equation becomes

$$\begin{aligned}& \psi (\chi ,\sigma ,t) = \chi +\sigma -2\chi t+2 ( \chi + \sigma ) t^{2}-4\chi t^{3}+4 ( \chi +\sigma ) t^{4}-8 \chi t^{5} \\& \hphantom{\psi (\chi ,\sigma ,t) =} {}+8 ( \chi +\sigma ) t^{6}-16\chi t^{7}+16 ( \chi + \sigma ) t^{8}\cdots \\& \hphantom{\psi (\chi ,\sigma ,t) } = \chi \bigl( 1+2t^{2}+4t^{4}+8t^{6}+\cdots \bigr) +\sigma \bigl( 1+2t^{2}+4t^{4}+8t^{6}+ \cdots \bigr) \\& \hphantom{\psi (\chi ,\sigma ,t) =} {}-2\chi t \bigl( 1+2t^{2}+4t^{4}+8t^{6}+ \cdots \bigr) \\& \psi (\chi ,\sigma ,t) = \frac{ ( \chi +\sigma -2\chi t ) }{1-2t^{2}} \end{aligned}$$

and

$$\begin{aligned}& \phi (\chi ,\sigma ,t) = \chi -\sigma - \frac{2\sigma t^{\alpha }}{\Gamma ( \alpha +1 ) }+ \frac{4 ( \chi -\sigma ) t^{2\alpha }}{\Gamma ( 2\alpha +1 ) } \\& \hphantom{\phi (\chi ,\sigma ,t) =}{}+ \biggl( -16\sigma - \frac{4\sigma \Gamma ( 2\alpha +1 ) }{ ( \Gamma ( \alpha +1 ) ) ^{2}} \biggr) \frac{t^{3\alpha }}{\Gamma ( 3\alpha +1 ) }+\cdots \\& \hphantom{\phi (\chi ,\sigma ,t)} = ( \chi -\sigma ) -2\sigma t+2 ( \chi -\sigma ) t^{2}-4\sigma t^{3}+4 ( \chi -\sigma ) t^{4}-8 \sigma t^{5}+8 ( \chi -\sigma ) t^{6} \\& \hphantom{\phi (\chi ,\sigma ,t)=}{}-16\sigma t^{7}+16 ( \chi -\sigma ) t^{8}\cdots \\& \hphantom{\phi (\chi ,\sigma ,t)} = \chi \bigl( 1+2t^{2}+4t^{4}+8t^{6}+\cdots \bigr) -\sigma \bigl( 1+2t^{2}+4t^{4}+8t^{6}+ \cdots \bigr) \\& \hphantom{\phi (\chi ,\sigma ,t)=} {}-2\sigma t \bigl( 1+2t^{2}+4t^{4}+8t^{6}+ \cdots \bigr) \\& \phi (\chi ,\sigma ,t) = \frac{ ( \chi -\sigma -2\sigma t ) }{1-2t^{2}}. \end{aligned}$$

We achieved the same results that were presented in [13, 26, 27].

Table 1 and Table 2 above show the comparison between exact and approximate solutions of Example 1.

Table 1 Comparison between the exact and approximation solutions for \(\psi (\chi ,\sigma ,t)\)
Full size table
Table 2 Comparison between the exact and approximation solutions for \(\phi (\chi ,\sigma ,t)\)
Full size table

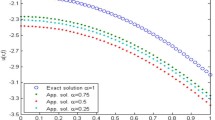
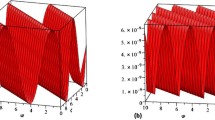
The comparison between the exact and numerical solutions for the Eq. (56) is shown in Figs. 1 and 2. We obtain the exact solution at \(\beta =1\) and the different values of β such as (\(\beta =0.95\), \(\beta =0.99\)) shows the approximate solution. The surfaces in Figs. 3 and 4 show the exact solution of the functions \(\psi (\chi ,\sigma ,t)\) and \(\phi (\chi ,\sigma ,t)\) at \(\chi =0\), respectively.

Figure 1
figure 1

The comparison between the exact and numerical solutions for \(\psi (\chi ,\sigma ,t)\)

Full size image
Figure 2
figure 2

The comparison between the exact and numerical solutions for \(\phi (\chi ,\sigma ,t)\)

Full size image
Figure 3
figure 3

The surface shows the function \(\psi (\chi ,\sigma ,t)\)

Full size image
Figure 4
figure 4

The surface shows the function \(\phi (\chi ,\sigma ,t)\)

Full size image

4 Double Sumudu-generalized Laplace decomposition method and singular two-dimensional time-fractional coupled Burger’s equation

The objective of this section is to interpret the utilization of the double Sumudu-generalized Laplace decomposition method for solving the singular two-dimensional time-fractional coupled Burger’s equations in the following form

$$\begin{aligned}& D_{t}^{\alpha }\psi +\frac{1}{\chi }\psi \psi _{\chi }+ \frac{1}{\sigma }\phi \phi _{\sigma }-\frac{1}{\chi } ( \chi \psi _{\chi } ) _{\chi }-\frac{1}{\sigma } ( \sigma \psi _{\sigma } ) _{\sigma } = f ( \chi ,\sigma ,t ) ,\qquad \\& D_{t}^{\alpha }\phi +\frac{1}{\chi }\psi \phi _{\chi }+ \frac{1}{\sigma }\phi \phi _{\sigma }-\frac{1}{\chi } ( \chi \phi _{\chi } ) _{\chi }-\frac{1}{\sigma } ( \sigma \phi _{\sigma } ) _{\sigma } = g ( \chi ,\sigma ,t ) , \\& \chi ,\sigma ,t > 0, \end{aligned}$$
(62)

with the initial condition

$$ \psi (\chi ,\sigma ,0)=f_{1}(\chi ,\sigma ),\qquad \phi (\chi , \sigma ,0)=g_{1}(\chi ,\sigma ), $$
(63)

where \(D_{t}^{\alpha }=\frac{\partial ^{\alpha }}{\partial t^{\alpha }}\) is the fractional Caputo derivative and \(\frac{1}{\chi } ( \chi \psi _{\chi } ) _{\chi }\), \(\frac{1}{\sigma } ( \sigma \psi _{\sigma } ) _{\sigma }\), \(\frac{1}{\chi } ( \chi \phi _{\chi } ) _{\chi }\), \(\frac{1}{\sigma } ( \sigma \phi _{\sigma } ) _{\sigma }\) are the so-called Bessel operators, \(\psi (\chi ,\sigma ,t)\) and \(\phi (\chi ,\sigma ,t)\) are the velocity components to be presented, f \(( \chi ,\sigma ,t ) \), \(g ( \chi ,\sigma ,t ) \), \(f_{1}(\chi ,\sigma )\), and \(g_{1}(\chi ,\sigma )\) are given functions. For the purpose of obtaining the solution of Eq. (62), we apply the next steps:

Step 1: Multiply both sides of Eq. (62) by χσ to yield

$$\begin{aligned}& \chi \sigma D_{t}^{\alpha }\psi +\sigma \psi \psi _{\chi }+ \chi \phi \psi _{\sigma }-\sigma ( \chi \psi _{\chi } ) _{\chi }- \chi ( \sigma \psi _{\sigma } ) _{\sigma } = \chi \sigma f ( \chi ,\sigma ,t ) , \\& \chi \sigma D_{t}^{\alpha }\phi +\sigma \psi \phi _{\chi }+ \chi \phi \phi _{\sigma }-\sigma ( \chi \phi _{\chi } ) _{\chi }- \chi ( \sigma \phi _{\sigma } ) _{\sigma } = \chi \sigma g ( \chi ,\sigma ,t ) , \\& \chi ,\sigma ,t > 0. \end{aligned}$$
(64)

Step 2: Taking the double Sumudu-generalized Laplace transform for either side of Eq. (64) we gain

$$\begin{aligned} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}\Psi (\mu _{1},\mu _{2},s) \bigr) =&s^{\alpha +1} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1}\mu _{2}F_{1}( \mu _{1}, \mu _{2}) \bigr) \\ &{}+\frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \sigma ( \chi \psi _{\chi } ) _{\chi }+\chi ( \sigma \psi _{\sigma } ) _{\sigma } \bigr) \\ &{}-\frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} ( \sigma \psi \psi _{\chi }+\chi \phi \psi _{\sigma } ) \\ &{}+\frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \chi \sigma f ( \chi ,\sigma ,t ) \bigr) \end{aligned}$$
(65)

and

$$\begin{aligned} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}\Phi (\mu _{1},\mu _{2},s) \bigr) =&s^{\alpha +1} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1}\mu _{2}G_{1}( \mu _{1}, \mu _{2}) \bigr) \\ &{}+\frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \sigma ( \chi \phi _{\chi } ) _{\chi }+\chi ( \sigma \phi _{\sigma } ) _{\sigma } \bigr) \\ &{}-\frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} ( \sigma \psi \phi _{\chi }+\chi \phi \phi _{\sigma } ) \\ &{}+\frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \chi \sigma g ( \chi ,\sigma ,t ) \bigr) . \end{aligned}$$
(66)

Step 3: By taking the double integral for both sides of Eq. (65) and Eq. (66) from 0 to \(\mu _{1}\) and 0 to \(\mu _{2}\) according to \(\mu _{1}\) and \(\mu _{2}\), respectively, we obtain

$$\begin{aligned} \Psi (\mu _{1},\mu _{2},s) =&\frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( s^{\alpha +1} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1}\mu _{2}F_{1}( \mu _{1}, \mu _{2}) \bigr) \biggr)\,d\mu _{1}\,d \mu _{2} \\ &{}+\frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \sigma ( \chi \psi _{\chi } ) _{\chi }+\chi ( \sigma \psi _{\sigma } ) _{ \sigma } \bigr) \biggr)\,d\mu _{1}\,d\mu _{2} \\ &{}-\frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} ( \sigma \psi \psi _{\chi }+\chi \phi \psi _{\sigma } ) \biggr)\,d\mu _{1}\,d\mu _{2} \\ &{}+\frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}}\frac{s^{\beta }}{\mu _{1}\mu _{2}} \bigl( S_{ \chi }S_{\sigma }G_{t} \bigl( \chi \sigma f ( \chi , \sigma ,t ) \bigr) \bigr)\,d\mu _{1}\,d\mu _{2} \end{aligned}$$
(67)

and

$$\begin{aligned} \Phi (\mu _{1},\mu _{2},s) =&\frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( s^{\alpha +1} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1}\mu _{2}G_{1}( \mu _{1}, \mu _{2}) \bigr) \biggr)\,d\mu _{1}\,d \mu _{2} \\ &{}+\frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \sigma ( \chi \phi _{\chi } ) _{\chi }+\chi ( \sigma \phi _{\sigma } ) _{ \sigma } \bigr) \biggr)\,d\mu _{1}\,d\mu _{2} \\ &{}-\frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} ( \sigma \psi \phi _{\chi }+\chi \phi \phi _{\sigma } ) \biggr)\,d\mu _{1}\,d\mu _{2} \\ &{}+\frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}}\frac{s^{\beta }}{\mu _{1}\mu _{2}} \bigl( S_{ \chi }S_{\sigma }G_{t} \bigl( \chi \sigma g ( \chi , \sigma ,t ) \bigr) \bigr)\,d\mu _{1}\,d\mu . \end{aligned}$$
(68)

Step 4: On using the inverse double Sumudu-generalized Laplace decomposition method for Eqs. (67) and (68), we obtain

$$\begin{aligned} \psi (\chi ,\sigma ,t) =&S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( s^{\alpha +1} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}F_{1}( \mu _{1},\mu _{2}) \bigr) \biggr)\,d\mu _{1}\,d \mu _{2} \biggr] \\ &{}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \\ &{}\times \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \sigma ( \chi \psi _{\chi } ) _{\chi }+\chi ( \sigma \psi _{ \sigma } ) _{\sigma } \bigr) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr] \\ &{}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \\ &{}\times \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} ( \sigma \psi \psi _{\chi }+\chi \phi \psi _{\sigma } ) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr] \\ &{}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \\ &{}\times \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}}\frac{s^{\beta }}{\mu _{1}\mu _{2}} \bigl( S_{\chi }S_{\sigma }G_{t} \bigl( \chi \sigma f ( \chi , \sigma ,t ) \bigr) \bigr)\,d\mu _{1}\,d\mu _{2} \biggr] \end{aligned}$$
(69)

and

$$\begin{aligned} \phi (\chi ,\sigma ,t) =&S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( s^{\alpha +1} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}G_{1}( \mu _{1},\mu _{2}) \bigr) \biggr)\,d\mu _{1}\,d \mu _{2} \biggr] \\ &{}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \\ &{}\times \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \sigma ( \chi \phi _{\chi } ) _{\chi }+\chi ( \sigma \phi _{ \sigma } ) _{\sigma } \bigr) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr] \\ &{}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} ( \sigma \psi \phi _{\chi }+\chi \phi \phi _{\sigma } ) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr] \\ &{}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \\ &{}\times \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}}\frac{s^{\beta }}{\mu _{1}\mu _{2}} \bigl( S_{\chi }S_{\sigma }G_{t} \bigl( \chi \sigma g ( \chi , \sigma ,t ) \bigr) \bigr)\,d\mu _{1}\,d\mu _{2} \biggr] . \end{aligned}$$
(70)

Step 5: Substituting Eqs. (48), (50), and Eq. (49) into Eqs. (69) and (70), we have

$$\begin{aligned}& \sum_{n=0}^{\infty }\psi _{n}(\chi , \sigma ,t) \\& \quad = S_{\mu _{1}}^{-1}S_{ \mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}}\int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( s^{ \alpha +1}\frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}F_{1}( \mu _{1},\mu _{2}) \bigr) \biggr)\,d\mu _{1}\,d \mu _{2} \biggr] \\& \qquad {}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \Biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \Biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \Biggl( \sigma \Biggl( \chi \sum_{n=0}^{\infty } \psi _{n\chi } \Biggr) _{ \chi } \\& \qquad {}+\chi \Biggl( \sigma \sum _{n=0}^{\infty }\psi _{n \sigma } \Biggr) _{\sigma } \Biggr) \Biggr)\,d\mu _{1}\,d\mu _{2} \Biggr] \\& \qquad {}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \\& \qquad {}\times \Biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \Biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \Biggl( \sigma \sum_{n=0}^{\infty }A_{n}+ \chi \sum_{n=0}^{\infty }B_{n} \Biggr) \Biggr)\,d\mu _{1}\,d\mu _{2} \Biggr] \\& \qquad {}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}}\frac{s^{\beta }}{\mu _{1}\mu _{2}} \bigl( S_{\chi }S_{\sigma }G_{t} \bigl( \chi \sigma f ( \chi , \sigma ,t ) \bigr) \bigr)\,d\mu _{1}\,d\mu _{2} \biggr] \end{aligned}$$

and

$$\begin{aligned}& \sum_{n=0}^{\infty }\phi _{n}(\chi , \sigma ,t) \\& \quad = S_{\mu _{1}}^{-1}S_{ \mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}}\int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( s^{ \alpha +1}\frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1} \mu _{2}G_{1}( \mu _{1},\mu _{2}) \bigr) \biggr)\,d\mu _{1}\,d \mu _{2} \biggr] \\& \qquad {}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \Biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \Biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \Biggl( \sigma \Biggl( \chi \sum_{n=0}^{\infty } \phi _{n\chi } \Biggr) _{ \chi } \\& \qquad {}+\chi \Biggl( \sigma \sum _{n=0}^{\infty }\phi _{n \sigma } \Biggr) _{\sigma } \Biggr) \Biggr)\,d\mu _{1}\,d\mu _{2} \Biggr] \\& \qquad {}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \\& \qquad {}\times \Biggl( \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \Biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \Biggl( \sigma \sum_{n=0}^{\infty }C_{n}+ \chi \sum_{n=0}^{\infty }D_{n} \Biggr) \Biggr)\,d\mu _{1}\,d\mu _{2} \Biggr) \\& \qquad {}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}}\frac{s^{\beta }}{\mu _{1}\mu _{2}} \bigl( S_{\chi }S_{\sigma }G_{t} \bigl( \chi \sigma g ( \chi , \sigma ,t ) \bigr) \bigr)\,d\mu _{1}\,d\mu _{2} \biggr] . \end{aligned}$$

Step 6: On utilizing the double Sumudu-generalized Laplace decomposition method, we present the recursive relations to obtain:

$$\begin{aligned}& \psi _{0}(\chi ,\sigma ,t) \\& \quad = S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( s^{\alpha +1} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1}\mu _{2}F_{1}( \mu _{1}, \mu _{2}) \bigr) \biggr)\,d\mu _{1}\,d \mu _{2} \biggr] \\& \qquad {}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}}\frac{s^{\beta }}{\mu _{1}\mu _{2}} \bigl( S_{\chi }S_{\sigma }G_{t} \bigl( \chi \sigma f ( \chi , \sigma ,t ) \bigr) \bigr)\,d\mu _{1}\,d\mu _{2} \biggr] \end{aligned}$$
(71)

and

$$\begin{aligned}& \phi _{0}(\chi ,\sigma ,t) \\& \quad = S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( s^{\alpha +1} \frac{\partial ^{2}}{\partial \mu _{1}\partial \mu _{2}} \bigl( \mu _{1}\mu _{2}G_{1}( \mu _{1}, \mu _{2}) \bigr) \biggr)\,d\mu _{1}\,d \mu _{2} \biggr] \\& \qquad {}+S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}}\frac{s^{\beta }}{\mu _{1}\mu _{2}} \bigl( S_{\chi }S_{\sigma }G_{t} \bigl( \chi \sigma g ( \chi , \sigma ,t ) \bigr) \bigr)\,d\mu _{1}\,d\mu _{2} \biggr] . \end{aligned}$$
(72)

The remainder components \(\psi _{n+1}\) and \(\phi _{n+1}\), \(n\geq 0\) are determined by

$$\begin{aligned}& \psi _{n+1}(\chi ,\sigma ,t) \\& \quad = S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \sigma ( \chi \psi _{n\chi } ) _{\chi }+\chi ( \sigma \psi _{n\sigma } ) _{ \sigma } \bigr) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr] \\& \qquad {}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} ( \sigma A_{n}+ \chi B_{n} ) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr] \end{aligned}$$
(73)

and

$$\begin{aligned}& \phi _{n+1}(\chi ,\sigma ,t) \\& \quad = S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \sigma ( \chi \phi _{n\chi } ) _{\chi }+\chi ( \sigma \phi _{n\sigma } ) _{ \sigma } \bigr) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr] \\& \qquad {}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl( \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} ( \sigma C_{n}+ \chi D_{n} ) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr) \end{aligned}$$
(74)

and \(S_{\chi }S_{\sigma }G_{t}\) is the double Sumudu-generalized Laplace transform with respect to χ, σ, t and the inverse double Sumudu-generalized Laplace transform is denoted by \(S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1}\) according to \(\mu _{1}\), \(\mu _{2}\), s. We assumed that the inverse double Sumudu-generalized Laplace transform with respect to \(\mu _{1}\), \(\mu _{2}\), and s exists for Eqs. (71), (72), (73), and (74). In the following example, we use the double Sumudu-generalized Laplace transform Adomain decomposition method to solve singular two-dimensional time-fractional coupled Burger’s equations.

Example 2

[26] Consider that the singular two-dimensional time-fractional coupled Burger’s equations are presented by

$$\begin{aligned}& D_{t}^{\alpha }\psi +\frac{1}{\chi }\psi \psi _{\chi }+ \frac{1}{\sigma }\phi \psi _{\sigma }-\frac{1}{\chi } ( \chi \psi _{\chi } ) _{\chi }-\frac{1}{\sigma } ( \sigma \psi _{\sigma } ) _{\sigma } = \bigl( \chi ^{2}-\sigma ^{2} \bigr) e^{t},\qquad \\& D_{t}^{\alpha }\phi +\frac{1}{\chi }\psi \phi _{\chi }+ \frac{1}{\sigma }v\phi \phi _{\sigma }-\frac{1}{\chi } ( \chi \phi _{\chi } ) _{\chi }-\frac{1}{\sigma } ( \sigma \phi _{\sigma } ) _{\sigma } = \bigl( \chi ^{2}-\sigma ^{2} \bigr) e^{t}, \\& \chi ,\sigma ,t > 0, \end{aligned}$$
(75)

with the initial condition

$$ \psi (\chi ,\sigma ,0)=\chi ^{2}-\sigma ^{2},\qquad \phi (\chi , \sigma ,0)=\chi ^{2}-\sigma ^{2}. $$

By using our method above, we successfully obtain

$$\begin{aligned}& \psi _{0} ( \chi ,\sigma ,t ) = \chi ^{2}-\sigma ^{2}+ \bigl( \chi ^{2}-\sigma ^{2} \bigr) \biggl( \frac{t^{\beta }}{\Gamma ( \beta +1 ) }+ \frac{t^{\beta +1}}{\Gamma ( \beta +2 ) }+ \frac{t^{\beta +2}}{\Gamma ( \beta +3 ) }+\cdots \biggr), \\& \phi _{0} ( \chi ,\sigma ,t ) = \chi ^{2}-\sigma ^{2}+ \bigl( \chi ^{2}-\sigma ^{2} \bigr) \biggl( \frac{t^{\beta }}{\Gamma ( \beta +1 ) }+ \frac{t^{\beta +1}}{\Gamma ( \beta +2 ) }+ \frac{t^{\beta +2}}{\Gamma ( \beta +3 ) }+\cdots \biggr) , \end{aligned}$$

and the remainder components \(\psi _{n+1}\) and \(\phi _{n+1}\), \(n\geq 0\) are given by

$$\begin{aligned}& \psi _{n+1}(\chi ,\sigma ,t) \\& \quad = S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \sigma ( \chi \psi _{n\chi } ) _{\chi }+\chi ( \sigma \psi _{n\sigma } ) _{ \sigma } \bigr) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr] \\& \qquad {}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} ( \sigma A_{n}+ \chi B_{n} ) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr] \end{aligned}$$
(76)

and

$$\begin{aligned}& \phi _{n+1}(\chi ,\sigma ,t) \\& \quad = S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \sigma ( \chi \phi _{n\chi } ) _{\chi }+\chi ( \sigma \phi _{n\sigma } ) _{ \sigma } \bigr) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr] \\& \qquad {}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl( \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} ( \sigma C_{n}+ \chi D_{n} ) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr) . \end{aligned}$$
(77)

By substituting \(n=0\), into Eqs. (76) and (77) we have

$$\begin{aligned}& \psi _{1}(\chi ,\sigma ,t) \\& \quad = S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \sigma ( \chi \psi _{0\chi } ) _{\chi }+\chi ( \sigma \psi _{0\sigma } ) _{ \sigma } \bigr) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr] \\& \qquad {}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} ( \sigma A_{0}+ \chi B_{0} ) \biggr)\,d\mu _{1} \,d\mu _{2} \biggr] , \\& \psi _{1}(\chi ,\sigma ,t) = 0 \end{aligned}$$

and

$$\begin{aligned}& \phi _{1}(\chi ,\sigma ,t) \\& \quad = S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl[ \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{\mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} \bigl( \sigma ( \chi \phi _{0\chi } ) _{\chi }+\chi ( \sigma \phi _{0\sigma } ) _{ \sigma } \bigr) \biggr)\,d\mu _{1}\,d\mu _{2} \biggr] \\& \qquad {}-S_{\mu _{1}}^{-1}S_{\mu _{2}}^{-1}G_{s}^{-1} \biggl( \frac{1}{\mu _{1}\mu _{2}} \int _{0}^{\mu _{1}} \int _{0}^{ \mu _{2}} \biggl( \frac{s^{\beta }}{\mu _{1}\mu _{2}}S_{\chi }S_{\sigma }G_{t} ( \sigma C_{0}+ \chi D_{0} ) \biggr)\,d\mu _{1} \,d\mu _{2} \biggr) , \\& \phi _{1}(\chi ,\sigma ,t) = 0. \end{aligned}$$

In a similar way, at \(n=1\), we have

$$ \psi _{2}(\chi ,\sigma ,t)=0, \qquad \phi _{2}(\chi ,\sigma ,t)=0. $$

The solution of Eq. (75) is determined by

$$\begin{aligned}& \psi (\chi ,\sigma ,t) = \psi _{0}+\psi _{1}+\psi _{2}+\cdots, \\& \phi (\chi ,\sigma ,t) = \phi _{0}+\phi _{1}+\phi _{2}+\cdots+. \end{aligned}$$

Thence, the exact solution is denoted by

$$\begin{aligned}& \psi (\chi ,\sigma ,t) = \chi ^{2}-\sigma ^{2}+ \bigl( \chi ^{2}- \sigma ^{2} \bigr) \biggl( \frac{t^{\beta }}{\Gamma ( \beta +1 ) }+ \frac{t^{\beta +1}}{\Gamma ( \beta +2 ) }+ \frac{t^{\beta +2}}{\Gamma ( \beta +3 ) }+\cdots \biggr) , \\& \phi (\chi ,\sigma ,t) = \chi ^{2}-\sigma ^{2}+ \bigl( \chi ^{2}- \sigma ^{2} \bigr) \biggl( \frac{t^{\beta }}{\Gamma ( \beta +1 ) }+ \frac{t^{\beta +1}}{\Gamma ( \beta +2 ) }+ \frac{t^{\beta +2}}{\Gamma ( \beta +3 ) }+\cdots \biggr) , \end{aligned}$$

when we put \(\alpha =1\), we obtain the exact solution of Eq. (75) as follows:

$$\begin{aligned}& \psi (\chi ,\sigma ,t) = \bigl( \chi ^{2}-\sigma ^{2} \bigr) \biggl( 1+t+\frac{t^{2}}{2!}+\frac{t^{3}}{3!}+ \frac{t^{4}}{4!}\cdots \biggr) = \bigl( \chi ^{2}-\sigma ^{2} \bigr) e^{t}, \\& \phi (\chi ,\sigma ,t) = \bigl( \chi ^{2}-\sigma ^{2} \bigr) \biggl( 1+t+\frac{t^{2}}{2!}+\frac{t^{3}}{3!}+ \frac{t^{4}}{4!}\cdots \biggr) = \bigl( \chi ^{2}-\sigma ^{2} \bigr) e^{t}. \end{aligned}$$

Table 3 and Table 4 below shows the comparison between exact and approximate solutions of Example 2.

Table 3 Comparison between the exact and approximation solutions for \(\psi (\chi ,\sigma ,t)\)
Full size table
Table 4 Comparison between the exact and approximation solutions for \(\phi (\chi ,\sigma ,t)\)
Full size table

The comparison between the exact and numerical solutions for the Eq. (75) is shown in Figs. 5 and 6. We obtain the exact solution at \(\beta =1\) and the different values of β such as (\(\beta =0.95\), \(\beta =0.99\)) shows the approximate solution. The surfaces in Figs. 7 and 8 show the exact solution of the functions \(\psi (\chi ,\sigma ,t)\) and \(\phi (\chi ,\sigma ,t)\) at \(\chi =0\), respectively.

Figure 5
figure 5

The comparison between the exact and numerical solutions for \(\psi (\chi ,\sigma ,t)\)

Full size image
Figure 6
figure 6

The comparison between the exact and numerical solutions for \(\phi (\chi ,\sigma ,t)\)

Full size image
Figure 7
figure 7

The surface shows the function \(\psi (\chi ,\sigma ,t)\)

Full size image
Figure 8
figure 8

The surface shows the function \(\phi (\chi ,\sigma ,t)\)

Full size image

5 Conclusions

In this research paper, double Sumudu-generalized Laplace transforms and Adomian decomposition have been profitably joined to obtain a new potent method called the double Sumudu-generalized Laplace Adomian decomposition method (DSGLTDM). This technique has been employed to solve regular and singular two-dimensional time-fractional coupled Burger’s equations. By involving this approach in some examples we have obtained new effective relations to solve our problems. Our method shows that the series solution can converge very quickly to the solutions. In this study, the technique utilized to obtain exact and approximation solutions can also be expanded to solve other nonlinear partial differential equations of physical interest. We see that the results of Examples 1 and 2 are the same as those of applying the Laplace–Adomian decomposition method, variational iteration method (VIM), and Triple Laplace–Adomian Decomposition Method, [13, 26, 27]. The advantage of DSGLTDM is that it generates other methods, such as the double Sumudu–Laplace transform decomposition method, see Eq. (2), the double Sumudu–Yang Transform decomposition method, see Eq. (3), the triple Sumudu Transform decomposition method, see Eq. (4), the double Sumudu–Elzaki transform decomposition method, see Eq. (5), and double Sumudu–Aboodh transform, see Eq. (6).