1 Introduction

As everyone knows, there are a lot of interacting components in a paddy ecosystem, such as weeds, inorganic salts, light intensity, herbivore, especially human activities, which make it become a complex nonlinear system. Recently, some mathematical models of paddy ecosystem have been proposed and some valuable results have been achieved [1,2,3,4,5].

In [1], the following differential equation model of the paddy ecosystem in the fallow season was put forward and the interaction between weeds and inorganic fertilizers in the system was investigated by Xiang and Zhou:

$$ \textstyle\begin{cases} {\dot{p}(t) = cf(I)H(u(t),p(t)) - ({d_{2}} + {d_{3}})p(t), }\\ {\dot{u}(t) = b - {d_{1}}u(t) + r{d_{2}}p(t) - f(I)H(u(t),p(t)),} \end{cases} $$
(1)

where \(p(t)\) denotes the weed biomass per unit area at time t, and \(u(t)\) denotes the inorganic fertilizer content per unit area at time t. In system (1), the first term on the right-hand side of the first equation represents weeds growth rate, which is related to the light intensity I and the inorganic fertilizer u. The constant c is the conversion coefficient of inorganic fertilizer and light energy converted by weeds to their biomass. The term \(d_{2}p(t)\) is the mortality of weeds. Considering the presence of weeds harvesting and herbivore consumption in the paddy field at fallow time, system (1) uses the item \(d_{3}p(t)\) to indicate the weeds removal rate. On the right-hand side of the second equation, the first term b denotes artificial fertilizer rate, the second item \(d_{1}u(t)\) indicates the loss of inorganic fertilizer in a paddy field. The coefficient r is the conversion rate of microbes transforming dead weeds to inorganic fertilizer. The last term \(f(I)H(u(t),p(t))\) is the consumption of inorganic fertilizer \(u(t)\) caused by the growth of weeds \(p(t)\). They obtained the conditions for the existence and the stability of a weeds extinction equilibrium and a positive equilibrium. They found a fact that in order not to let the inorganic fertilizer content tend to zero, the artificial fertilizer rate b should not be allowed to be 0. That is to say, some measures should be taken to avoid the exhaustion of inorganic fertilizers due to the growth of weeds. Considering herbivores in paddy fields can eat some weeds and increase fertilizer by excreting feces, Xiang, Wu, and Zhou proposed a differential equations model of the paddy ecosystem in the fallow season to reveal the effects of herbivores on inorganic fertilizer and weeds. The results show that the introduction of some herbivores into a paddy ecosystem in the fallow season can increase the content of inorganic fertilizer and makes it possible for a Hopf bifurcation phenomenon to emerge in the system [2].

Fractional differential equations can exactly describe many nonlinear phenomena. Ecosystems generally have three characteristics: first, they have greater freedom; second, most of them have memory; third, they have extensive fractal characteristics. These characteristics of ecosystems make them more suitable for establishing fractional differential equation models to study their dynamic properties. Recently, the research on the qualitative properties of fractional biological models has attracted a great deal of attention from researchers [6,7,8,9,10,11]. Rivero et al. discussed the biological significance of fractional order in [7]. They thought that the model \(D^{\alpha}x(t)=kx(t)\) reflects that the growth of population x follows the generalized exponential growth rule \(x(t)=CE_{\alpha }(kt^{\alpha})\), where \(E_{\alpha}(z)\) is the Mittag-Leffler function as follows:

$$E_{\alpha}(z)=\sum_{{n}=0}^{\infty} \frac{z^{n}}{\varGamma(\alpha{n}+1)}. $$

The Mittag-Leffler function \(E_{\alpha}(z)\) is a generalization of the classical exponential function, but it has one more parameter α, so there is one more degree of freedom. They extended several classical population models to fractional order models. By comparing the numerical solutions of different fractional order, they found that the order of fractional derivative is a good speed controller, which can control how those trajectories of system approach (or far from) the critical point. This characteristic helps to faithfully represent the anomalous reality of interaction among certain species.

The dynamic relationship between predators and predators is a very common form of population interactions. Many researchers have studied the properties of fractional order predator-prey systems [6, 8, 9, 12]. In [10], the authors studied the dynamics of a fractional order toxic-phytoplankton-phytoplankton-zooplankton system. The Routh–Hurwitz criterion was applied to discuss the stability analysis of biologically feasible equilibria for the system in terms of reproduction numbers. Local stability properties of the toxic-phytoplankton-free equilibrium were also investigated. In addition to studying the stability of equilibria for fractional order systems, many scholars have also discussed the existence of Hopf bifurcations [13,14,15,16,17]. By extending the integer order paddy ecosystem discussed in [3] to fractional order case, Zhou et al. established a fractional order paddy ecosystem with time delay [4]. They obtained the sufficient conditions of the stability of equilibria and the existence of Hopf bifurcation, which are the generalization of the corresponding conditions of integer order systems in [3].

The existence of bifurcation in a nonlinear system will cause changes in system stability [18,19,20]. Therefore, controlling the occurrence of bifurcation becomes an important research topic. Some of controllers are designed to suppress or reduce some of the existing bifurcation dynamics of a given nonlinear system [21,22,23,24]. A linear delayed feedback controller was introduced to adjust the occurrence of Hopf bifurcation for a delayed fractional gene regulatory network [21] and for a fractional predator-prey system [22]. They found that the feedback gain significantly affects the effect of bifurcation control. The polynomial function controller also was chosen to control Hopf bifurcation [23, 25]. One may obtain the desired behavior of a Hopf bifurcation effectively by choosing appropriate values of the coefficients of a polynomial controller [23]. Some other nonlinear functions were also used as bifurcation controllers. For example, a parametric delay feedback controller was added to a small-world network system [24], which is a modification of polynomial controllers whose coefficients are reduced exponentially with the time delay as \(k_{i} e^{-p(\tau)}\). The results showed that the small-world network model of the controller with delay-dependent parameters changes the dynamic characteristics of the system with delay-independent parameters controller.

It is difficult to manage rice production for an unstable paddy ecosystem. However, a Hopf bifurcation may occur in a paddy ecosystem, which will lead to instability of the system [4]. Therefore, we want to delay or eliminate the Hopf bifurcation in a paddy ecosystem by using the methods of bifurcation control. It is generally known that microbes need time to transform dead weeds into inorganic fertilizers, so time delay is inevitable. But from the term \(rd_{2}p(t)\) in the second equation of system (1), it is easy to find that model (1) did not consider the time delay. Based on the above, the main purpose of this paper is to extend system (1) to a fractional form with delay and give a detailed analysis of controlling Hopf bifurcation.

2 Preliminaries

We firstly give some basic concepts and lemmas. Consider the linear fractional order delayed system

$$ {D^{\alpha}}X(t) = AX(t) + BX(t - \tau), $$
(2)

where \(X(t) = {({x_{1}}(t),{x_{2}}(t), \ldots,{x_{n}}(t))^{T}} \in \mathbf{C}([-\tau,\infty), \mathbb{R}^{n})\), and the time delay \(\tau >0\). \(D^{\alpha}\) is the Caputo fractional derivative defined as follows:

$${D^{\alpha}}f(t) = \frac{1}{{\varGamma(m - \alpha)}} \int_{0}^{t} {{{(t - s)}^{m - \alpha - 1}}} {f^{(m)}}(s)\,ds, $$

where \(\varGamma(q) = \int_{0}^{\infty}{{e^{ - t}}{t^{q - 1}}} \,dt\) is the gamma function, \(m \in\mathbb{N}\), and \(m - 1 \le\alpha \le m\). In this paper, we suppose \(0 < \alpha\le1\). The characteristic equation of system (2) is

$$\Delta(\lambda) = \det\bigl({\lambda^{\alpha}}E - A - B{e^{ - \lambda \tau}}\bigr) = 0. $$

We will employ the following result to discuss the stability of the fractional order delayed system (2) [26].

Lemma 1

If \(\alpha\in(0, 1)\), all the eigenvalues λs of \(M=A+B\) satisfy \(\vert {\arg(\lambda)} \vert > \frac{\pi}{2}\), and the characteristic equation \(\Delta(\lambda) = 0\) has no purely imaginary roots for any \(\tau> 0\), then the zero solution of system (2) is Lyapunov globally asymptotically stable.

We still need the following Hopf bifurcation conditions proposed in [27] for a general fractional order delayed system

$$ D^{\alpha}Y(t)= F\bigl(Y(t),Y(t-\tau)\bigr): $$
(3)
  1. (a)

    All the eigenvalues of the coefficient matrix M of the linearized system of (3) at the equilibrium \(Y^{*}\) satisfy \(|\arg(\lambda)| > \alpha\pi/2\).

  2. (b)

    The characteristic equation \(\Delta(\lambda)=0\) of the linearized system of (3) has a pair of purely imaginary roots \(\pm i\omega_{0}\) when \(\tau= \tau_{0}\).

  3. (c)

    \(\frac{d\operatorname {Re}(\lambda(\tau))}{d\tau} \vert _{\tau=\tau _{0}} > 0\), where \(\operatorname {Re}(\cdot)\) denotes the real part of the complex number.

If the above conditions hold, then system (3) undergoes a Hopf bifurcation at the equilibrium \(Y^{*}\) when \(\tau= \tau_{0}\).

Next we introduce some notations defined in [4] and a polynomial of degree 4 with real coefficients \(a=(1, a_{1}, a_{2}, a_{3}, a_{4})\),

$$f_{a}(\xi) = \xi^{4} + {a_{1}} { \xi^{3}} + {a_{2}} {\xi^{2}} + {a_{3}} {\xi} + {a_{4}}, $$

where \(a_{1}>0\), \(a_{3}>0\), and \(a_{4}>0\).

If \(a_{2} \geq0\), then there is not a positive real root for equation \(f_{a}(\xi)=0\). Next, we consider the case of \(a_{2}<0\). The polynomial \(f_{a}(\xi)\) can be decomposed into the product of the following two quadratic polynomials:

$$ f_{1}(\xi) = {\xi^{2}} + \biggl( { \frac{{{a_{1}}}}{2} - M_{a}} \biggr)\xi + \frac{v_{a} }{2} - { \mathop{\operatorname{sgn}}} \biggl(\frac {{{a_{1}}v_{a}}}{2} - a_{3} \biggr)N_{a} $$
(4)

and

$$f_{2}(\xi) = {\xi^{2}} + \biggl( { \frac{{{a_{1}}}}{2} + M_{a}} \biggr)\xi + \frac{v_{a}}{2} + { \mathop{\operatorname{sgn}}} \biggl(\frac {{{a_{1}}v_{a}}}{2} - a_{3} \biggr)N_{a}, $$

where

$$M_{a} = \sqrt{\frac{{a_{1}^{2}}}{4} - {a_{2}} + v_{a} }, \qquad N_{a} = \sqrt {\frac{v_{a} ^{2}}{4} - {a_{4}}} $$

and \(v_{a}\) is any positive real root of equation

$${\nu^{3}} - {a_{2}} {\nu}^{2} + ( {{a_{1}} {a_{3}} - 4{a_{4}}} )\nu+ 4{a_{2}} {a_{4}} - a_{1}^{2}{a_{4}} - a_{3}^{2} = 0. $$

Denote the discriminants of the polynomial \(f_{1}(\xi)\) and \(f_{2}(\xi )\) by

$$ {\Delta_{a}} = \frac{{a_{1}^{2}}}{2} - {a_{2}} - v_{a} - {a_{1}}M_{a} + {\mathop{\operatorname{sgn}}} \biggl(\frac{{{a_{1}}v_{a}}}{2} - {a_{3}} \biggr)4N_{a} $$
(5)

and \({\Delta_{2}} = \frac{{a_{1}^{2}}}{2} - {a_{2}} - v_{a} + {a_{1}}M_{a} - {\mathop{\operatorname{sgn}}} (\frac{{{a_{1}}v_{a}}}{2} - {a_{3}})4N_{a}\).

As for the existence of positive roots of equation \(f_{a}(\xi)=0\), we have the following conclusion [4].

Lemma 2

Suppose that \(a_{i}>0\) (\(i=1,3,4\)). If \(a_{2}<0\) and \(\Delta_{a} \geq 0\), then there are only two positive real roots in the equation \(f_{a}(\xi) = {\xi^{4}} + {a_{1}}{\xi^{3}} + {a_{2}}{\xi^{2}} + {a_{3}}\xi + {a_{4}} = 0\). If \(a_{2}\geq0\), or \(a_{2}<0\) and \(\Delta _{a} < 0\), there is no positive real root in the equation \(f_{a}(\xi)=0\).

3 The modeling of a delayed fractional paddy ecosystem with feedback control

According to the analysis in Sect. 1, we extend the integer order system (1) to the fractional order form, introduce delay τ into the item \(rd_{2}p(t)\), and put a time delay force \(k(u(t)-u(t-\tau))\) in the second equation. Thus we obtain the fractional order paddy ecosystem with delay feedback control as follows:

$$ \textstyle\begin{cases} D^{\alpha}p(t)=cf(I)h(u(t))p(t) - {d_{2}}p(t) - {d_{3}}p(t),\\ D^{\alpha}u(t)=b - {d_{1}}u(t) + r{d_{2}}p(t - \tau) - f(I)h(u(t))p(t) + k(u(t)-u(t-\tau)), \end{cases} $$
(6)

where k is a feedback gain parameter, the meanings of the variables and other parameters are the same as those of system (1). We suppose that the uptake of inorganic fertilizer by weeds complies with the general Michaelis–Menten uptake kinetics as follows:

$$h(u) =\frac{{au}}{{m + u}}, $$

where a is the maximum uptake rate of inorganic fertilizer u and m is its half-saturation concentration. Taking into account actual requirements, the parameters in system (6) are nonnegative and satisfy the following conditions: \(0< c<1\), \(0< r<1\), and \(d_{i}>0\) (\(i=1, 2\)).

The equilibrium \((p^{*}, u^{*})\) of system (6) satisfies the following equations:

$$ \textstyle\begin{cases} F_{1}(p^{*}, u^{*}) = cf(I)h(u^{*})p^{*} - ({d_{2}} + {d_{3}}){p^{*}} = 0,\\ F_{2}(p^{*}, u^{*}) = b - d_{1}u^{*} + r{d_{2}}{p^{*}} - f(I)h(u^{*}){p^{*}}= 0. \end{cases} $$
(7)

Obviously, when \(\frac{{caf(I)}}{{{d_{2}}{+}{d_{3}}}} > 1 + \frac {{m{d_{1}}}}{b}\), system (6) has a unique positive equilibrium \((p^{*}, u^{*})\), which is defined as

$${p^{*} } = \frac{{c(b - {d_{1}}{u^{*} })}}{{(1 - rc){d_{2}} + {d_{3}}}}, \qquad {u^{*} } = \frac{{m({d_{2}} + {d_{3}})}}{{caf(I) - {d_{2}} - {d_{3}}}}. $$

From (7), for the positive equilibrium \((p^{*}, u^{*})\), the following relations hold:

$$\begin{aligned} &cf(I)h\bigl({u^{*}}\bigr) - {d_{2}} - {d_{3}} = 0,\qquad f(I)h\bigl({u^{*}}\bigr) = \frac {{{d_{2}} + {d_{3}}}}{c},\\ & h'\bigl({u^{*}}\bigr) = \frac{am}{(m + {u^{*}})^{2}} = \frac{{(a - h(u^{*}))}^{2}}{am} > 0. \end{aligned}$$

4 Control of bifurcation for a fractional paddy ecosystem

Through the coordinate transformation \(x(t)= p(t)-p^{*}\), \(y(t)=u(t)-u^{*}\), we can turn system (6) into the following form:

$$ \textstyle\begin{cases} D^{\alpha}x(t)= - ({d_{2}} + {d_{3}})x(t) + cf(I) [ {h(y + u^{*})(x + {p^{*} }) - h({u^{*} }){p^{*} }} ],\\ D^{\alpha}y(t)= r{d_{2}}x(t - \tau) - {d_{1}}y(t) - f(I) [ {h(y + u^{*})(x + {p^{*} }) - h({u^{*} }){p^{*} }} ] \\ \phantom{D^{\alpha}x(t)=}{}+ k(y(t)-y(t-\tau)). \end{cases} $$
(8)

Using the following Taylor expansion of \(h(y+u^{*})\) at the point \(u^{*}\)

$$h\bigl(y + u^{*}\bigr) = h\bigl(u^{*}\bigr) + h'\bigl(u^{*}\bigr)y + O\bigl(y^{2} \bigr), $$

where \(O(y^{2})\) represents the remaining items whose orders are greater than or equal to 2, system (8) can be written as

$$ \textstyle\begin{cases} {D^{\alpha}}x(t) = c f(I)p^{ * }h'(u^{ * })y(t) + c f(I)h'(u^{ * })x(t)y(t) + cf(I)(x(t) + p^{ * })O({y^{2}}(t)),\\ {D^{\alpha}}y(t) = r d_{2}x(t - \tau) - f(I)h(u^{*})x(t) - ( d_{1} + f(I)p^{*}h'(u^{*}) - k )y(t) - k y(t-\tau)\\ \phantom{{D^{\alpha}}y(t) =}{}- f(I)h'({u^{*} })x(t)y(t) - f(I)(x(t) + {p^{*} })O({y^{2}}(t)). \end{cases} $$
(9)

Then the linearized system of (9) at the equilibrium \((0, 0)\) is as follows:

$$ \textstyle\begin{cases} {D^{\alpha}}x(t) =cf(I){p^{*} }h'({u^{*} })y(t),\\ {D^{\alpha}}y(t) = r d_{2}x(t - \tau) - f(I)h(u^{*})x(t) - ( d_{1} + f(I)p^{*}h'(u^{*}) - k )y(t)-k y(t-\tau). \end{cases} $$
(10)

It is written in matrix form as

$$ D^{\alpha}X(t)=AX(t)+BX(t-\tau), $$
(11)

where

A=(0cf(I)p∗h′(u∗)−f(I)h(u∗)−(d1+f(I)p∗h′(u∗)−k)),B=(00rd2−k).

For simplicity, we introduce parameters

$$ \textstyle\begin{cases} {b_{1}} = {d_{1}} + f(I){p^{*} }h'({u^{*} }),\qquad b_{2} = f(I){p^{*} }h'({u^{*} })({d_{2}} + {d_{3}}),\\ {b_{3}} = rc{d_{2}}f(I){p^{*} }h'({u^{*} }),\qquad b_{4} = b_{2} - b_{3}, \end{cases} $$
(12)

and

$$ \textstyle\begin{cases} a_{1}(k,\alpha) = 2({b_{1}} - k)\cos\frac{{\alpha\pi}}{2},\qquad a_{2}(k,\alpha) = {b_{1}}({b_{1}} - 2k) + 2{b_{2}}\cos\alpha\pi,\\ a_{3}(k,\alpha) = 2[{b_{1}}{b_{2}} - k({b_{2}} - {b_{3}})]\cos\frac {{\alpha\pi}}{2},\qquad a_{4} = b_{2}^{2} - b_{3}^{2}. \end{cases} $$
(13)

Obviously, \(b_{i}>0\) (\(i=1,2,3,4\)) and \(a_{4}>0\). From \(0<\alpha\leq1\) and \(k \leq b_{1}\), we have \(a_{1}(k,\alpha) \geq0\) and \(a_{3}(k,\alpha) \geq0\). If \(2{b_{2}} \cos\alpha\pi\ge- {b_{1}}({b_{1}} - 2k)\), then \(a_{2}(k,\alpha) \geq0\).

Define

$$ \alpha_{k}=\textstyle\begin{cases} \frac{1}{\pi}\arccos\frac{{{b_{1}}(2k - {b_{1}})}}{{2{b_{2}}}},\quad \frac{b_{1}}{2} \leq k \leq\min\{b_{1},\frac{b_{1}}{2}+\frac {b_{2}}{b_{1}}\}, \\ 1 - \frac{1}{\pi}\arccos\frac{{{b_{1}}({b_{1}} - 2k)}}{{2b_{2}}},\quad \frac{b_{1}}{2}-\frac{b_{2}}{b_{1}}< k< \frac{b_{1}}{2},\\ 1,\quad k \leq\frac{b_{1}}{2}-\frac{b_{2}}{b_{1}}. \end{cases} $$
(14)

If \(\frac{b_{1}}{2}+\frac{b_{2}}{b_{1}}< b_{1}\), let \(\alpha_{k}=0\) when \(\frac{b_{1}}{2}+\frac{b_{2}}{b_{1}}< k \leq b_{1}\). Thus, if \(0 < \alpha \le{\alpha_{k}}\), then \(a_{2}(k) \geq0\). Otherwise, if \(\alpha_{k}<\alpha<1\), then \(a_{2}(k,\alpha)<0\).

Theorem 1

Suppose that \(\frac {{caf(I)}}{{{d_{2}}+ {d_{3}}}} > 1 + \frac {{m{d_{1}}}}{b}\) and \(k \leq b_{1}\).

  1. (i)

    If \(0 < \alpha\le{\alpha_{k}}\), or \({\alpha_{k}} < \alpha \le 1\) and \(\Delta_{a} < 0\), then the positive equilibrium \((p^{*}, u^{*})\) of the paddy ecosystem (6) is locally asymptotically stable for \(\tau\geq0\).

  2. (ii)

    If \({\alpha_{k}} < \alpha \le1\) and \(\Delta_{a} \geq0\), then there exists a positive number \(\tau_{k,\alpha}\) such that the positive equilibrium \((p^{*}, u^{*})\) of the paddy ecosystem (6) is locally asymptotically stable for \(\tau\in[0, \tau _{k,\alpha})\), but it is unstable for \(\tau\geq\tau_{k,\alpha}\), and a Hopf bifurcation emerges at \(\tau=\tau_{k,\alpha}\).

Proof

When \(\tau=0\), the coefficient matrix of system (11) becomes

A+B=(0cf(I)p∗h′(u∗)rd2−f(I)h(u∗)−(d1+f(I)p∗h′(u∗))).

Its characteristic equation is \(\lambda^{2}+b_{1}\lambda+b_{4}=0\). It has two eigenvalues as follows:

$${\lambda_{1,2}} = \frac{1}{2} \bigl( - {b_{1}} \pm\sqrt{b_{1}^{2} - 4{b_{4}}} \bigr). $$

Obviously, the real parts of \(\lambda_{1,2}\) are less than zero. So the eigenvalues \(\lambda_{1,2}\) of \(A+B\) satisfy \(\vert {\arg (\lambda)} \vert > \frac{\pi}{2}\).

Next we consider the existence of pure imaginary roots of the characteristic equation of linearized system (10). Its characteristic equation of system (10) is as follows:

$$ {\lambda^{2\alpha}} + (b_{1}-k) \lambda^{\alpha}+ b_{2} - \bigl(b_{3}-k \lambda^{\alpha}\bigr){e^{ - \lambda\tau}} = 0. $$
(15)

Assume that equation (15) has a pair of purely imaginary roots \(\pm i\xi\) (\(\xi>0\)). Substituting

$$\lambda=i\xi=\xi \biggl( {\cos\frac{\pi}{2} + i\sin\frac{\pi}{2}} \biggr) $$

into equation (15) and using the Euler formula \(e^{iz}=\cos z + i\sin z\), we have

$$\begin{aligned} & {\xi^{2\alpha}}(\cos\alpha\pi + i\sin\alpha\pi) + (b_{1}-k){ \xi^{\alpha}} \biggl(\cos\frac{{\alpha\pi}}{2} + i\sin \frac {{\alpha\pi}}{2} \biggr) + {b_{2}} \\ &\quad{} - \biggl[b_{3}-k\xi^{\alpha} \biggl(\cos \frac{{\alpha\pi}}{2} + i\sin\frac{{\alpha\pi}}{2} \biggr) \biggr](\cos\xi\tau - i \sin \xi\tau) = 0. \end{aligned}$$

Its real part and imaginary part are respectively

$${\xi^{2\alpha}}\cos\alpha\pi + (b_{1}-k){ \xi^{\alpha}}\cos\frac {{\alpha\pi}}{2} + {b_{2}} - \biggl(b_{3}-k\xi^{\alpha}\cos\frac{{\alpha \pi}}{2}\biggr)\cos \xi\tau+ k\xi^{\alpha}\sin\frac{{\alpha\pi}}{2} \sin\xi\tau= 0 $$

and

$${\xi^{2\alpha}}\sin\alpha\pi + (b_{1}-k){ \xi^{\alpha}}\sin\frac {{\alpha\pi}}{2} + \biggl(b_{3}-k \xi^{\alpha}\cos\frac{{\alpha\pi }}{2}\biggr)\sin\xi\tau+ k \xi^{\alpha}\sin\frac{{\alpha\pi}}{2} \cos \xi\tau= 0. $$

Denote

$$\begin{aligned} &\phi(k,\alpha) = {b_{3}} - k{\xi^{\alpha}}\cos \frac{\alpha\pi }{2},\qquad\psi(k,\alpha)= k{\xi^{\alpha}}\sin \frac{\alpha\pi}{2}, \\ &w_{1}(k,\alpha) = {\xi^{2\alpha}}\cos\alpha\pi + ({b_{1}} - k){\xi^{\alpha}}\cos\frac{\alpha\pi}{2} + {b_{2}}, \\ &w_{2}(k,\alpha) = {\xi^{2\alpha}}\sin\alpha\pi + ({b_{1}} - k){\xi^{\alpha}}\sin\frac{\alpha\pi}{2}. \end{aligned}$$

So we get the sine and cosine values of τξ as follows:

$$ \textstyle\begin{cases} \cos\tau\xi = \frac{w_{1}(k,\alpha)\phi(k,\alpha) - w_{2}(k,\alpha)\psi(k,\alpha)}{{\phi}^{2}(k,\alpha) + {\psi }^{2}(k,\alpha)},\\ \sin\tau\xi = -\frac{w_{1}(k,\alpha)\psi(k,\alpha )+w_{2}(k,\alpha)\phi(k,\alpha)}{{\phi}^{2}(k,\alpha) + {\psi }^{2}(k,\alpha)}. \end{cases} $$
(16)

Because they satisfy \(\sin^{2}\tau\xi+ \cos^{2}\tau\xi= 1\), we have

$$w_{1}^{2}(k,\alpha) + w_{2}^{2}(k, \alpha) = \phi^{2}(k,\alpha) + \psi^{2}(k,\alpha). $$

Sorting the power of ξ, one obtains

$$ f_{a}\bigl({\xi^{\alpha}}\bigr) = { \xi^{{{4}}\alpha}} + a_{1}(k,\alpha )\xi^{3\alpha} + a_{2}(k,\alpha)\xi^{2\alpha} + a_{3}(k,\alpha ) \xi^{\alpha}+ a_{4} = 0, $$
(17)

where \(a_{i}(k,\alpha)\) (\(i=1,2,3,4\)) are defined in (13).

(i) If \(0<\alpha\leq\alpha_{k}\), then \(a_{2}(k,\alpha) = b_{1}(b_{1}-2k) + 2{b_{2}}\cos\alpha\pi\ge0\). Therefore, equation (17) has no positive real root. If \(\alpha_{k} < \alpha\leq 1\) and \(\Delta_{a}<0\), we know the equation \(f_{a}(\xi)=0\) has no positive real root by Lemma 2. Then equation (17) also has no positive real root. Therefore, the equilibrium \((p^{*}, u^{*})\) is locally asymptotically stable for any \(\tau\geq0\) by Lemma 1.

(ii) If \(\alpha_{k} < \alpha\leq1\) and \(\Delta_{a} \geq0\) hold, then the equation \(f_{a}(\xi)=0\) has two positive real roots \(\xi _{1}\) and \(\xi_{2}\) by Lemma 2. Suppose \(\xi_{1} \leq\xi_{2}\), then equation (17) has a positive real root \(\xi_{a}\) such that \(\xi_{a}^{\alpha}=\xi_{2}\).

If \(\sin{\tau}{\xi} > 0\), then we have

$$ \tau_{k,\alpha} = \frac{1}{\xi_{a}}\arccos \frac{w_{1}(k,\alpha )\phi(k,\alpha) - w_{2}(k,\alpha)\psi(k,\alpha)}{{\phi }^{2}(k,\alpha) + {\psi}^{2}(k,\alpha)} $$
(18)

from the first equation of (16). If \(\sin{\tau}{\xi} < 0\), then we get

$$ \tau_{k,\alpha} = \frac{2\pi}{\xi_{a}} - \frac{1}{\xi_{a}}\arccos \frac{w_{1}(k,\alpha)\phi(k,\alpha) - w_{2}(k,\alpha)\psi(k,\alpha )}{{\phi}^{2}(k,\alpha) + {\psi}^{2}(k,\alpha)}. $$
(19)

Thus, conditions (a) and (b) are satisfied. Next, we verify that the transversal condition (c) holds. Computing the derivative of λ with respect to τ in (15) yields

$$\frac{{d\lambda}}{{d\tau}} = - \frac{{({b_{3}} - k{\lambda^{\alpha}})\lambda{e^{ - \lambda\tau}}}}{{2\alpha{\lambda^{ {{2}}\alpha{- 1}}} + \alpha({b_{1}} - k){\lambda ^{\alpha - 1}} + (k\alpha{\lambda^{\alpha - 1}} + \tau({b_{3}} - k{\lambda^{\alpha}})){e^{ - \lambda\tau}}}}. $$

Substituting \(\lambda=i\xi_{a}\) and \(\tau=\tau_{k,\alpha}\) gives

$$\begin{aligned} { \biggl( {\frac{d\lambda}{d\tau}} \biggr)}^{-1} \bigg|_{\lambda= i \xi_{a}} & = { - \biggl[ {\frac{\alpha((2 {\lambda^{2\alpha}} +(b_{1}-k) {\lambda^{\alpha}}){e^{\lambda\tau}} + k \lambda ^{\alpha})}{\lambda^{2}(b_{3} - k\lambda^{\alpha})} + \frac{\tau }{\lambda}} \biggr]} \bigg|_{\lambda= i \xi_{a}} \\ & = {\frac{\alpha ((2 {(i\xi_{a}) ^{2\alpha}} + (b_{1}-k) {(i\xi_{a}) ^{\alpha}}){e^{i\xi_{a} \tau_{k,\alpha} }} + k(i\xi _{a})^{\alpha-2} )}{\xi_{a}^{2} (b_{3} - k(i\xi _{a})^{\alpha} )} - \frac{\tau_{k,\alpha} }{i\xi_{a}}}. \end{aligned}$$

For convenience sake, we use the following two notations:

$$\begin{aligned} &w_{3} =2\xi_{a}^{2\alpha}\cos\alpha\pi + ({b_{1}} - k)\xi _{a}^{\alpha}\cos \frac{\alpha\pi}{2}, \\ &w_{4} =2\xi_{a}^{2\alpha}\sin\alpha\pi + ({b_{1}} - k)\xi _{a}^{\alpha}\sin \frac{\alpha\pi}{2}. \end{aligned}$$

Then we obtain its real part as follows:

$$\begin{aligned} {\mathop{\operatorname{Re}} } \biggl\{ {{{ \biggl( {\frac{{d\lambda }}{{d\tau_{k,\alpha}}}} \biggr)}^{ - 1}}} \bigg|_{\lambda = i{\xi_{a}}} \biggr\} & = \frac{\alpha}{\xi_{a}^{2}(\phi^{2}(k,\alpha)+\psi^{2}(k,\alpha ))}\bigl[ \bigl(\phi(k,\alpha)w_{3}- \psi(k, \alpha)w_{4}\bigr) \cos{\xi _{a}}\tau_{k,\alpha} \\ &\quad {}- \bigl(\phi(k,\alpha)w_{4} + \psi(k,\alpha)w_{3} \bigr)\sin{\xi_{a}}\tau _{k,\alpha} +b_{3}\phi(k, \alpha) \\ &\quad {} -\phi^{2}(k,\alpha)-\psi^{2}(k,\alpha)\bigr]. \end{aligned}$$

Substituting (16) into the above expression, we obtain that

$$\begin{aligned} {\mathop{\operatorname{Re}} } \biggl\{ \biggl( \frac{{d\lambda }}{{d\tau}} \biggr)^{ - 1} \bigg|_{\lambda = i{\xi_{a}}} \biggr\} &= \frac{\alpha [ w_{1}w_{3}+w_{2} w_{4}+b_{3}\phi(k,\alpha )-\phi^{2}(k,\alpha)-\psi^{2}(k,\alpha) ]}{\xi_{a}^{2}(\phi ^{2}(k,\alpha)+\psi^{2}(k,\alpha))} \\ & = \frac{\alpha}{\xi_{a}^{2}(\phi^{2}(k,\alpha)+\psi^{2}(k,\alpha ))}\biggl[ 2\xi_{a}^{4\alpha} + 3({b_{1}-k})\cos\frac{\alpha\pi }{2}\xi_{a}^{3\alpha} \\ &\quad {} + \bigl( 2b_{2}\cos\alpha\pi+b_{1}(b_{1}-2k) \bigr)\xi_{a}^{2\alpha} \\ &\quad {} + \bigl(b_{1}b_{2}-(b_{2}-b_{3})k \bigr)\cos\frac{\alpha\pi}{2}\xi _{a}^{\alpha} \biggr] \\ &=\frac{\alpha [ {4\xi_{a}^{3\alpha} + 3{a_{1}(k,\alpha)}\xi _{a}^{2\alpha} + 2{a_{2}(k,\alpha)}\xi_{a}^{\alpha} + {a_{3}(k,\alpha)}} ]}{2\xi_{a}^{2-\alpha}(\phi^{2}(k,\alpha )+\psi^{2}(k,\alpha))} \\ & = \frac{\alpha{{f}_{a}'}(\xi_{a}^{\alpha})}{2\xi_{a}^{2-\alpha }(\phi^{2}(k,\alpha)+\psi^{2}(,\alpha))}. \end{aligned}$$

Notice that \(\xi_{a}^{\alpha}\) is the larger positive real root of equation \(f_{a}(\xi)=0\) and the coefficient of the highest power \(\xi ^{4}\) in the polynomial \(f_{a}(\xi)\) is equal to 1, it is easy to derive \(f_{a}'(\xi_{a}^{\alpha})>0\). So the transversal condition (c) holds. Therefore, a Hopf bifurcation emerges at the positive equilibrium \((p^{*}, u^{*})\) when \(\tau=\tau_{k,\alpha}\). □

Taking α and k as variable parameters, but fixing other parameters, \(f(I)=12\), \(m=4\), \(a=0.1\), \(b=5\), \(r=0.9\), \(c=0.9\), \(d_{1}=0.01\), \(d_{2}=0.8\), and \(d_{3}=0.1\), we draw two curves \(\alpha _{k}\) and \(\Delta_{a} = 0\) in the \(k-\alpha\) coordinate system (Fig. 1). From the proof of Theorem 1, we can see that the coefficient \(a_{2}(k,\alpha)\geq0\) at the lower left of the curve \(\alpha_{k}\), while \(a_{2}(k,\alpha)<0\) at its upper right. From Theorem 1, the lower left of the curve \(\Delta_{a} = 0\) is the stable region of system (6), while the stability at its upper right region is determined by the time delay τ.

Figure 1
figure 1

The stable region of system (6). The curve \(\alpha_{k}\) is defined by (14). The \(\Delta_{a}\) defined in (5) is the discriminant of polynomial (4)

Full size image

Remark 1

Consider the uncontrolled fractional paddy ecosystem with delay

$$ \textstyle\begin{cases} {D^{\alpha}}p(t) = cf(I)h(u(t))p(t) - {d_{2}}p(t) - {d_{3}}p(t),\\ {D^{\alpha}}u(t) = b - {d_{1}}u(t) + r{d_{2}}p(t - \tau) - f(I)h(u(t))p(t). \end{cases} $$
(20)

That is the case of \(k=0\) in system (6).

From (13), we have

$$ \textstyle\begin{cases} a_{1}(0,\alpha) = 2{b_{1}} \cos\frac{{\alpha\pi}}{2},\qquad a_{2}(0,\alpha) = {b_{1}^{2}} + 2{b_{2}}\cos\alpha\pi,\\ a_{3}(0,\alpha) = 2{b_{1}}{b_{2}}\cos\frac{{\alpha\pi}}{2},\qquad a_{4} = b_{2}^{2} - b_{3}^{2}. \end{cases} $$
(21)

Because \(k=0< b_{1}/2\), by definition (14), we get

$$ \alpha_{0}=\textstyle\begin{cases} 1 - \frac{1}{\pi}\arccos\frac{b_{1}^{2}}{2b_{2}},& b_{1}^{2}< 2b_{2},\\ 1,&b_{1}^{2} \geq2b_{2}. \end{cases} $$

From (16), we know

$$ \sin\tau\xi = - \frac{{{\xi^{2\alpha}}\sin\alpha\pi + {b_{1}}{\xi^{\alpha}}\sin\frac{{\alpha\pi}}{2}}}{{{b_{3}}}}< 0. $$

So we have from (19)

$$ \tau_{0,\alpha} = \frac{2\pi}{\xi_{a}} - \frac{1}{\xi_{a}}\arccos \frac{\xi_{a}^{2\alpha}\cos\alpha\pi + {b_{1}}\xi_{a}^{\alpha}\cos \frac{{\alpha\pi}}{2} + b_{2}}{b_{3}}. $$
(22)

Therefore, we obtain the stability and bifurcation existence of the uncontrolled fractional paddy ecosystem (20) from Theorem 1.

Corollary 1

Suppose that \(\frac {{caf(I)}}{{{d_{2}} + {d_{3}}}} > 1 + \frac{{m{d_{1}}}}{b}\).

  1. (i)

    If \(0 < \alpha\le{\alpha_{0}}\), or \({\alpha_{0}} < \alpha \le 1\) and \(\Delta_{a} < 0\), then the positive equilibrium \((p^{*}, u^{*})\) of the paddy ecosystem (20) is locally asymptotically stable for \(\tau\geq0\).

  2. (ii)

    If \({\alpha_{0}} < \alpha \le1\) and \(\Delta_{a} \geq0\), then there exists a positive number \(\tau_{0}\) as (22) such that the positive equilibrium \((p^{*}, u^{*})\) of the paddy ecosystem (20) is locally asymptotically stable for \(\tau\in[0, \tau _{0,\alpha})\), but it is unstable for \(\tau\geq\tau_{0,\alpha}\), and a Hopf bifurcation emerges at \(\tau=\tau_{0,\alpha}\).

5 Numerical examples

In this section, we provide two numerical examples to verify the efficiency and feasibility of our results. In systems (6) and (20), let \(f(I)=12\), \(m=4\), \(a=0.1\), \(r=0.9\), \(c=0.9\), \(d_{1}=0.01\), \(d_{2}=0.8\), and \(d_{3}=0.1\).

5.1 Example for uncontrolled system

Firstly, we take \(\alpha=0.98\) and \(b=20\). The uncontrolled system (20) has a positive equilibrium \((70.7142, 20)\). By computing, we get \(\alpha_{0} \approx0.6099\) and \(\Delta_{a} \approx-0.0913\). By Corollary 1, the equilibrium \((70.7142, 20)\) is locally asymptotically stable for any \(\tau\geq0\).

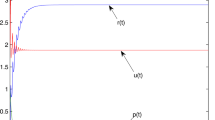
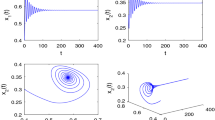
Let us take \(b=5\) and \(\alpha=0.98\) again. System (20) also has a positive equilibrium \((17.1429, 20)\). For this case, we have \(\alpha_{0} \approx0.5290\) and \(\Delta_{a} \approx0.0475\). We further get the Hopf bifurcation critical value \(\tau_{0,\alpha} \approx9.8065\) by using (22). According to Corollary 1, the equilibrium \((17.1429, 20)\) is locally asymptotically stable when \(\tau\in[0, \tau_{0,\alpha})\); otherwise, the equilibrium \((17.1429, 20)\) is unstable and a Hopf bifurcation emerges at \(\tau= \tau_{0,\alpha}\). Figure 2 depicts the asymptotic stability of the positive equilibrium \((17.1429, 20)\) when the time delay \(\tau= 8 < \tau_{0,\alpha}\). Figure 3 indicates that system (20) has a periodic oscillation bifurcating from the equilibrium \((17.1429, 20)\) when the time delay \(\tau= 11 > \tau_{0,\alpha}\).

Figure 2
figure 2

The asymptotical stability of \((p^{*}, u^{*}) \approx (17.1429, 20)\) in uncontrolled system (20) with \(\alpha=0.98\), \(b=5\), and \(\tau=8<\tau_{0,0.98} \approx9.8065\)

Full size image
Figure 3
figure 3

Waveform diagram of uncontrolled system (20) with \(\alpha=0.98\), \(b=5\), and \(\tau=11>\tau_{0,0.98} \approx9.8065\)

Full size image

5.2 Example for controlled system

We discuss the influence of feedback gain k and fractional order α on the bifurcation of controlled system (6) by numerical calculation. Let \(b=5\). We firstly obtain \(b_{1} \approx0.1529\) from (12) and \(b_{1}/2-b_{2}/b_{1} \approx-0.7647\). Let the feedback gain k take different values between \(b_{1}/2-b_{2}/b_{1}\) and \(b_{1}\), then we can get the \(\alpha _{k}\) from (14). For any \(k\in(b_{1}/2-b_{2}/b_{1},b_{1})\) and \(\alpha\in(\alpha_{k},1]\), we calculate the corresponding critical threshold \(\xi_{a}\) by solving equation (17) and bifurcation point \(\tau_{k,\alpha}\) from (18) or (19). We draw the contours of time delay \(\tau_{k,\alpha}\) in the \(k-\alpha\) coordinate system (Fig. 4). Table 1 lists some critical frequency \(\xi_{a}\) and bifurcation point \(\tau _{k,\alpha}\) for different \(k\in[-0.14,0.15]\) when \(\alpha=0.98\). From Fig. 4 or Table 1, we can find that the \(\tau_{k,\alpha}\) value is increasing as the feedback gain k or the fractional order α decreases. Therefore, it verifies the result that the occurrence of the Hopf bifurcation is delayed by taking smaller k or α.

Figure 4
figure 4

Contours of the Hopf bifurcation critical time delay function \(\tau_{k,\alpha}\)

Full size image
Table 1 Effect of feedback control gain on the Hopf bifurcation critical value
Full size table

The above two examples show that if the paddy ecosystem is not controlled, a Hopf bifurcation may occur in the system, which will be disadvantageous to paddy management. However, by introducing feedback control to inorganic fertilizers, we can effectively expand the stable range of equilibrium and suppress the occurrence of bifurcation.

6 Conclusion

In this paper, our model generalizes the existing integer order model (1) to fractional order case, which is much closer to the real complex paddy ecosystem. We have obtained two important results. Firstly, the time delay τ required for the transformation of dead weeds into inorganic fertilizers affects the dynamics of the paddy ecosystem. In system (6), by introducing time delay τ to the item \(r{d_{2}}p(t)\), we have analyzed how the stability of the system is affected by time delay τ. Theorem 1 tells us that the stability of system (6) is independent of time delay only when conditions \(0 < \alpha\le{\alpha _{k}}\), or \({\alpha_{k}} < \alpha \le1\) and \(\Delta_{a}<0\) hold. Otherwise, there exists a critical value \(\tau_{k,\alpha}\), when the delay τ increases from zero to \(\tau_{k,\alpha}\), system (6) will change from stable to unstable and Hopf bifurcation phenomena will arise. Secondly, the delay feedback controller and the fractional order can effectively control the occurrence of Hopf bifurcation in the fractional paddy ecosystem with time delay. In the proof of Theorem 1, we give a formula (18) or (19) for calculating the critical point of bifurcation, which is related to the feedback gain k and fractional order α. From the numerical results, we have observed that the bifurcation critical value \(\tau_{k,\alpha}\) increases as the feedback gain k and fractional order α become smaller and smaller. But when α becomes smaller, there exists a lower bound of α, which is determined by inequalities \(\alpha> \alpha _{k}\) and \(\Delta_{a} \geq0\).

We make it clear that although the time delay leads to instability and bifurcation, the bifurcation can be controlled by the feedback controller or fractional order. Therefore, our conclusions can guide the management of complex dynamic phenomena in the paddy ecosystem.