1 Introduction

Fractional calculus is used to describe several problems in biology, physics, engineering, and applied mathematics. Fractional derivatives are investigated in two major ways: as local and nonlocal derivatives. There are several definitions for the local derivatives. These definitions are considered as a direct generalization of the ordinary derivatives; see [1, 2]. However, these definitions do not consider the history of the functions during computing the derivative. Other definitions are the nonlocal fractional derivatives such as the Caputo and ABFD definitions; see [3, 4]. The fractional Ricatti equation (FRE) is investigated based on different definitions of fractional derivatives. For example, see [5,6,7]. Akgul, et al., discussed several fractional problems using different methods such as the reproducing kernel Hilbert space method [8,9,10,11,12,13,14,15,16], while Alquran, et al., used a fractional power series method [17,18,19,20,21,22,23,24]. In this article, we consider the following class of equations:

where \(u \in H^{1}(0,1)\), μ, ν, ξ are continuous functions on [0,1] We organize our paper as follows. In Sect. 2, we present the preliminaries which we used in this paper. Method of the solution is given in Sect. 3. Some numerical results are presented in Sect. 4 to show the efficiency of the proposed method. Finally, we draw some conclusions and closing remarks.

2 Preliminaries

We present the basic definitions and theorems which we use in this article.

Definition 1

([4])

Let \(u\in H^{1}(0,1)=\{u\in L^{2}(0,1): u ^{\prime }\in L^{2}(0,1)\}\) and \(0<\gamma \leq 1\). The ABFD in the Caputo sense of u of order γ is defined by

(1)

For simplicity, we choose \(B(\gamma )=1\). The fractional integral is defined as follows.

Definition 2

([4])

The fractional integral is given by

$$ I^{\gamma }u(x)=\frac{1-\gamma }{B(\gamma )}u(x)+\frac{\gamma }{B( \gamma )\varGamma (\gamma )} \int _{0}^{x}u(s) (x-s)^{\gamma -1}\,ds. $$
(2)

Theorem 3

Let \(u\in H^{1}(0,1)\) such that exists. Then

(3)

Proof

See [2]. □

The fractional Legendre polynomials are \(\{FL_{r}(x):r=0,1,2,\ldots\}\) which are defined by

$$ FL_{r}(x)=L_{r}\bigl(2x^{\gamma }-1\bigr),\quad r=0,1,2, \ldots, $$
(4)

where \(\{L_{r}(x):r=0,1,2,\ldots\}\) are the Legendre polynomials. Then

$$ \int _{0}^{1}FL_{r}(x)\, FL_{s}(x) w(x)\,dx= \textstyle\begin{cases} \frac{1}{(2r+1)\gamma }, & r=s, \\ 0, & r\neq s, \end{cases} $$
(5)

where \(w(x)=x^{\gamma -1}\). Also, \(FL_{r}(x)\) is given as

$$ FL_{r}(x)=\sum_{j=0}^{r}(-1)^{j+r} \frac{(r+j)!}{(r-j)!}\frac{x ^{j\gamma }}{(j!)^{2}}. $$
(6)

Theorem 4

Let \(g\in C^{1}[0,1]\). Then

$$ g(x)=\sum_{r=0}^{\infty }g_{r}\, FL_{r}(x), $$
(7)

where

$$ g_{r}=(2r+1)\gamma \int _{0}^{1}g(x)\,FL_{r}(x)w(x)\,dx. $$
(8)

For the proof of these properties, see [6].

Theorem 5

\(I^{\gamma }\,FL_{r}(x)\) is a linear combination of \(\{FL_{0}(x),FL_{1}(x),\ldots,FL_{r+1}(x)\}\).

Proof

Simple calculations imply that

$$\begin{aligned} I^{\gamma }\,FL_{r}(x) =&\frac{1-\gamma }{B(\gamma )}\,FL_{r}(x)+ \frac{ \gamma }{B(\gamma )\varGamma (\gamma )} \int _{0}^{x}\,FL_{r}(s) (x-s)^{ \gamma -1}\,ds \\ =&\frac{1-\gamma }{B(\gamma )}\,FL_{r}(x)+\frac{\gamma }{B(\gamma ) \varGamma (\gamma )} \int _{0}^{x}\sum_{j=0}^{r}(-1)^{j+r} \frac{(r+j)!}{(r-j)!}\frac{s^{j\gamma }}{(j!)^{2}}(x-s)^{\gamma -1}\,ds \\ =&\frac{1-\gamma }{B(\gamma )}\,FL_{r}(x)+\frac{\gamma }{B(\gamma ) \varGamma (\gamma )}\sum _{j=0}^{r}(-1)^{j+r}\frac{(r+j)!}{(r-j)!} \frac{1}{(j!)^{2}} \int _{0}^{x}s^{j\gamma }(x-s)^{\gamma -1}\,ds \\ =&\frac{1-\gamma }{B(\gamma )}\,FL_{r}(x)+\frac{\gamma }{B(\gamma )} \sum _{j=0}^{r}(-1)^{j+r}\frac{(r+j)!}{(r-j)!} \frac{1}{(j!)^{2}} \frac{\varGamma (1+j \gamma )}{\varGamma (1+\gamma (1+j))}x^{(j+1)r}. \end{aligned}$$
(9)

Thus, \(I^{\gamma }\,FL_{r}(x)\) is a linear combination of \(\{FL_{0}(x),FL _{1}(x),\ldots,FL_{r+1}(x)\}\). □

3 Method of solution

We want to investigate the operational matrix of \(I^{\gamma }\). Define the set of k block pulse functions on \([0,1) \) by

$$ \bigl\{ p_{0}(x),p_{1}(x),\ldots,p_{k-1}(x)\bigr\} , $$

where

$$ p_{r}(x)=\textstyle\begin{cases} 1, & \frac{r}{k}\leq x< \frac{r+1}{k}, \\ 0, & x\in {}[ 0,1)-[\frac{r}{k},\frac{r+1}{k}), \end{cases}\displaystyle \quad r=0,1,\ldots,k-1. $$
(10)

Then

$$ p_{r}(x)p_{s}(x)=\textstyle\begin{cases} p_{r}(x), & r=s, \\ 0, & r\neq s, \end{cases} $$
(11)

and

$$ \int _{0}^{1}p_{r}(x)p_{s}(x) \,dx=\textstyle\begin{cases} \frac{1}{k}, & r=s, \\ 0, & r\neq s, \end{cases} $$
(12)

where \(0\leq r\), \(s\leq k-1\). If \(g\in L_{2}[0,1]\), then

$$ g(x)=\sum_{r=0}^{k-1}g_{k} p_{r}(x). $$
(13)

Multiply both sides by \(p_{s}(x)\) then integrate from 0 to 1 to get

$$\begin{aligned} \int _{0}^{1}g(x)p_{s}(x)\,dx =&\sum _{r=0}^{k-1}g_{r} \int _{0}^{1}p_{r}(x)p_{s}(x) \,dx \\ =&\frac{g_{s}}{k} , \end{aligned}$$
(14)

which implies that

$$ g_{s}=k \int _{0}^{1}g(x)p_{s}(x)\,dx. $$
(15)

Thus,

$$ g(x)=G^{T}P(x), $$
(16)

where

$$ G=k \begin{pmatrix} \int _{0}^{1}g(x)p_{0}(x)\,dx \\ \int _{0}^{1}g(x)p_{1}(x)\,dx \\ \vdots \\ \int _{0}^{1}g(x)p_{k-1}(x)\,dx \end{pmatrix} ,\qquad p= \begin{pmatrix} p_{0}(x) \\ p_{1}(x) \\ \vdots \\ p_{k-1}(x) \end{pmatrix} . $$

Theorem 6

\(I^{\gamma }P=\varOmega P \) where

$$ \varOmega = \begin{pmatrix} a & b & b & \cdots & b \\ b & a & b & \cdots & b \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ b & b & b & \cdots & a \end{pmatrix}, $$

where

$$ a=\frac{1-\gamma }{B(\gamma )}+\frac{1}{B(\gamma )\varGamma (\gamma )k ^{\gamma }},\qquad b=\frac{1}{B(\gamma )\varGamma (\gamma )k^{\gamma }}. $$

Proof

For any \(0\leq r\leq k-1\)

$$\begin{aligned} I^{\gamma }p_{r}(x) =&\frac{1-\gamma }{B(\gamma )}p_{r}(x)+ \frac{ \gamma }{B(\gamma )\varGamma (\gamma )} \int _{0}^{x}p_{r}(s) (x-s)^{ \gamma -1} \,ds \\ =&\frac{1-\gamma }{B(\gamma )}p_{r}(x)+\frac{\gamma }{B(\gamma ) \varGamma (\gamma )} \int _{\frac{r}{k}}^{\frac{r+1}{k}}\biggl( \frac{r+1}{k}-s \biggr)^{\gamma -1}\,ds \\ =&\frac{1-\gamma }{B(\gamma )}p_{r}(x)+\frac{1}{B(\gamma )\varGamma ( \gamma )k^{\gamma }} \\ =&\frac{1-\gamma }{B(\gamma )}p_{r}(x)+\frac{1}{B(\gamma )\varGamma ( \gamma )k^{\gamma }}\sum _{r=0}^{k-1} p_{r}(x). \end{aligned}$$
(17)

Thus,

$$ I^{\gamma }P=\varOmega P, $$
(18)

where

$$ \varOmega = \begin{pmatrix} a & b & b & \cdots & b \\ b & a & b & \cdots & b \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ a & a & a & \cdots & a \end{pmatrix} $$
(19)

and

$$ a=\frac{1-\gamma }{B(\gamma )}+\frac{1}{B(\gamma )\varGamma (\gamma )k ^{\gamma }},\qquad b=\frac{1}{B(\gamma )\varGamma (\gamma )k^{\gamma }}. $$
(20)

 □

Theorem 7

Let

$$FL(x)= \begin{pmatrix} FL_{0}(x) \\ FL_{1}(x) \\ \vdots \\ FL_{k-1}(x) \end{pmatrix} . $$

Then

$$ FL(x)=FP\, P(x), $$
(21)

where FP is a \(k\times k\) matrix with

$$ (FP)_{r,s}=\sum_{j=0}^{r}(-1)^{j+r} \frac{(r+j)!}{(r-j)!} \frac{1}{(j!)^{2}} \biggl( \frac{(s+1)^{j\gamma +1}-s^{{j\gamma +1}}}{(j \gamma +1)k^{{j\gamma }}} \biggr) . $$
(22)

Proof

For any \(r\in \{0,1,\ldots,k-1\}\), \(FL_{r}(x)\in L_{2}[0,1]\). Thus from Eq. (14), we get

$$ FL_{r}(x)=\sum_{s=0}^{k-1}(FP)_{r,s} p_{s}(x). $$
(23)

Hence, from Eq. (15), we get

$$\begin{aligned} (FP)_{r,s} =&k \int _{0}^{1}FL_{r}(x) \,p_{s}(x)\,dx \\ =&k\sum_{j=0}^{r}(-1)^{j+r} \frac{(r+j)!}{(r-j)!} \frac{1}{(j!)^{2}} \int _{\frac{s}{k}}^{\frac{s+1}{k}}x^{j\gamma }\,dx \\ =&\sum_{j=0}^{r}(-1)^{j+r} \frac{(r+j)!}{(r-j)!} \frac{1}{(j!)^{2}} \biggl( \frac{(s+1)^{j\gamma +1}-s^{{j\gamma +1}}}{(j \gamma +1)k^{{j\gamma }}} \biggr) . \end{aligned}$$
(24)

 □

Theorem 8

FP is an invertible matrix.

Proof

From Theorem 7,

$$ FL(x) \bigl(FL(x)\bigr)^{T}=FP\, P(x) \bigl(P(x)\bigr)^{T} \,FP^{T}. $$
(25)

Hence,

$$ \int _{0}^{1}FL(x) \bigl(FL(x)\bigr)^{T}x^{\gamma -1} \,dx=FP \int _{0} ^{1}P(x) \bigl(P(x)\bigr)^{T}x^{\gamma -1} \,dx\,FP^{T}. $$
(26)

From Eqs. (6) and (12), we have

$$\begin{aligned} \int _{0}^{1}FL(x) \bigl(FL(x)\bigr)^{T}x^{\gamma -1} \,dx =&\frac{1}{\gamma } \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & \frac{1}{3} & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & \frac{1}{2k-1} \end{pmatrix} \\ =&\varLambda _{1} \end{aligned}$$
(27)

and

$$\begin{aligned} \int _{0}^{1}P(x) \bigl(P(x)\bigr)^{T}x^{\gamma -1} \,dx =&\frac{1}{\gamma k^{\gamma }} \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 2^{\gamma }-1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & k^{\gamma }-(k-1)^{\gamma } \end{pmatrix} \\ =&\varLambda _{2}. \end{aligned}$$
(28)

Therefore,

$$ \varLambda _{1}=FP \varLambda _{2} \,FP^{T}. $$
(29)

Thus,

$$ \det (FP)=\sqrt{\frac{\prod_{r=0}^{k-1} \frac{1}{\gamma (2r+1)}}{\prod_{r=0}^{k-1}\frac{(r+1)^{\gamma }-r^{\gamma }}{\gamma k^{\gamma }}}}\neq 0. $$
(30)

Hence, FP is invertible. □

Theorem 9

\(I^{\gamma }\,FL(x)=\varPsi \, FL(x)\) where

$$ \varPsi =FP\, \varOmega\, FP^{-1}. $$
(31)

Proof

Let

$$ I^{\gamma }\,FL(x)=\varPsi \,FL(x). $$
(32)

From Eqs. (19) and (22)

$$ I^{\gamma }\,FL(x)=\varPsi \, FP\, P(x) $$
(33)

and

$$\begin{aligned} I^{\gamma }\,FL(x) =&FP\, I^{\gamma } P(x) \\ =&FP\, \varOmega\, P(x). \end{aligned}$$
(34)

Hence,

$$ \varPsi\, FP\, P(x)=FP \,\varOmega\, P(x), $$
(35)

which implies that

$$ \varPsi \, FP=FP\, \varOmega $$
(36)

or

$$ \varPsi =FP\, \varOmega\, FP^{-1}. $$
(37)

Now, let \(u\in C^{1}[0,1]\), then

$$ u(x)=\sum_{r=0}^{\infty }u_{r} \,FL_{r}(x), $$
(38)

where

$$ u_{r}=(2r+1)\gamma \int _{0}^{1}u(x)\,FL_{r}(x)x^{\gamma -1} \,dx. $$
(39)

Let

$$ U_{k}(x)=\sum_{r=0}^{k-1}u_{r} \,FL_{r}(x)=U^{T} \,FL(x), $$
(40)

where

$$ U= \begin{pmatrix} u_{0} \\ u_{1} \\ \vdots \\ u_{k-1} \end{pmatrix} . $$

Thus,

(41)

Using Theorem 3, we get

$$\begin{aligned} u(x)-\alpha =&I^{\gamma }U^{T}\,FL(x) \\ =&U^{T}I^{\gamma }\,FL(x) \\ =&U^{T} \,\varPsi \, FL(x) \\ =&U^{T}\, \varPsi \, FP\, P(x), \end{aligned}$$
(42)

which implies that

$$ u(x)=U^{T} \varPsi \,FP\, P(x)+\alpha . $$
(43)

Thus, Eq. (1) implies that

$$ U^{T}\,FP\, P(x)+\mu (x) \bigl( U^{T} \varPsi \, FP\, P(x)+ \alpha \bigr) + \nu (x) \bigl(U^{T} \varPsi \, FP\, P(x)+\alpha \bigr)^{2}=\varXi\, FP\, P(x), $$
(44)

where \(\xi (x)=\varXi \,FP\, P(x)\). If

$$ U^{T}\, \varPsi \, FP= \begin{pmatrix} \varkappa _{1} & \varkappa _{2} & \cdots & \varkappa _{k} \end{pmatrix} , $$
(45)

then

$$ \bigl(U^{T} \varPsi \, FP\, P(x)+\alpha \bigr)^{2}= \begin{pmatrix} \varkappa _{1}^{2}+2\varkappa _{1}\alpha & \varkappa _{2}^{2}+2\varkappa _{2} \alpha & \cdots & \varkappa _{k}^{2}+2\varkappa _{k}\alpha \end{pmatrix} P(x)+\alpha ^{2}. $$
(46)

Hence,

$$ \bigl( \digamma _{1}(U)+\mu (x) \digamma _{2}(U)+\nu (x) \digamma _{3}(U) \bigr) P(x)= \digamma _{4}(x), $$
(47)

where

$$\begin{aligned}& \digamma _{1}(U) = U^{T}\,FP, \end{aligned}$$
(48)
$$\begin{aligned}& \digamma _{2}(U) = U^{T} \,\varPsi\, FP, \end{aligned}$$
(49)
$$\begin{aligned}& \digamma _{3}(U) = \begin{pmatrix} \varkappa _{1}^{2}+2\varkappa _{1}\alpha \varkappa _{2}^{2}+2\varkappa _{2} \alpha \cdots \varkappa _{k}^{2}+2\varkappa _{k}\alpha \end{pmatrix} , \end{aligned}$$
(50)
$$\begin{aligned}& \digamma _{4}(x) = \varXi \, FP\, P(x)-\alpha \mu (x)-\alpha ^{2}\nu (x). \end{aligned}$$
(51)

To solve Eq. (48), we use the collocation points

$$ t_{r}=\frac{r+1}{k+1},\quad r=0,1,\ldots,k-1. $$
(52)

Then we solve the generated nonlinear system to find U using Mathematica. □

4 Numerical results

We present two examples to show the efficiency of the proposed method.

Example 1

Consider the following problem:

where

$$\begin{aligned} f(x) =&x^{2}+1+ \bigl( x^{2}+1 \bigr) ^{2}-4-4x \\ &{}+\frac{8\sqrt{x}(3+2x)}{3\sqrt{\pi }}+4e^{x}Erfc(\sqrt{x}). \end{aligned}$$

The exact solution is

$$ u(x)=x^{2}+1. $$

Let \(k=7\). Let \(Q=\{p_{0}(x),p_{0}(x),\ldots,p_{6}(x)\}\) be the set of block pulse functions on \([0,1)\) where

$$ p_{r}(x)=\textstyle\begin{cases} 1, & \frac{r}{7}\leq x< \frac{r+1}{7}, \\ 0, & \text{otherwise}, \end{cases}\displaystyle \quad r=0,1,\ldots,6. $$

Let

$$ f(x)=\sum_{r=0}^{6}g_{r} p_{r}(x)=G^{T}P(x). $$

From Eq. (22), we have

$$ G= \begin{pmatrix} 2.03186 \\ 2.21914 \\ 2.59375 \\ 3.16995 \\ 3.97389 \\ 5.04267 \\ 6.42401 \end{pmatrix} ,\qquad P(x)= \begin{pmatrix} p_{0}(x) \\ p_{1}(x) \\ p_{2}(x) \\ p_{3}(x) \\ p_{4}(x) \\ p_{5}(x) \\ p_{6}(x) \end{pmatrix} . $$

From Eqs. (23) and (24), we have

$$ \varOmega = \begin{pmatrix} \frac{1}{2}+\frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6 \pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6 \pi }} & \frac{1}{\sqrt{6\pi }} \\ \frac{1}{\sqrt{6\pi }} & \frac{1}{2}+\frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6 \pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6 \pi }} & \frac{1}{\sqrt{6\pi }} \\ \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{2}+\frac{1}{\sqrt{6 \pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6 \pi }} & \frac{1}{\sqrt{6\pi }} \\ \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6 \pi }} & \frac{1}{2}+\frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6 \pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} \\ \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6 \pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{2}+\frac{1}{\sqrt{6 \pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} \\ \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6 \pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{2}+\frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} \\ \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6 \pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6\pi }} & \frac{1}{\sqrt{6 \pi }} & \frac{1}{2}+\frac{1}{\sqrt{6\pi }} \end{pmatrix} . $$

From Eq. (32), we have

$$ FP= \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ -0.496 & -0.079 & 0.193 & 0.413 & 0.603 & 0.772 & 0.927 \\ -0.083 & -0.479 & -0.437 & -0.239 & 0.049 & 0.3977 & 0.791 \\ 0.313 & 0.112 & -0.265 & -0.433 & -0.345 & 0.005 & 0.613 \\ -0.158 & 0.324 & 0.228 & -0.135 & -0.395 & -0.280 & 0.416 \\ -0.076 & -0.126 & 0.280 & 0.235 & -0.155 & -0.384 & 0.227 \\ 0.125 & -0.228 & -0.083 & 0.281 & 0.146 & -0.309 & 0.068 \end{pmatrix}. $$

It is easy to see that FP is invertible, since \(\det (FP)=1.4895\times 10^{-3}\neq 0\). From Eq. (37), we have

$$\begin{aligned} \varPsi =&FP \,\varOmega\, FP^{-1} \\ =& \begin{pmatrix} 2.1 & -6.3\times 10^{-4} & 2.1\times 10^{-4} & 1.1\times 10^{-2} & 4.2\times 10^{-4} & -7.6\times 10^{-4} & -8.2\times 10^{-4} \\ 0.5 & 0.50 & 6.6\times 10^{-4} & 3.5\times 10^{-3} & 5.4\times 10^{-4} & -4.5\times 10^{-4} & -2.3\times 10^{-4} \\ 4.5\times 10^{-5} & -4.4\times 10^{-5} & 0.50 & -6.4\times 10^{-4} & 5.3\times 10^{-5} & 2.3\times 10^{-5} & 1.8\times 10^{-5} \\ 3.7\times 10^{-5} & 2\times 10^{-4} & -2.3\times 10^{-5} & 0.50 & -1.4\times 10^{-4} & 1.4\times 10^{-4} & 4.4\times 10^{-5} \\ -8\times 10^{-5} & 1.1\times 10^{-4} & -2.1\times 10^{-4} & -3.5\times 10^{-4} & 0.50 & 8.6\times 10^{-5} & 9.9\times 10^{-6} \\ 1.4\times 10^{-4} & -1.1\times 10^{-4} & -9.7\times 10^{-5} & 5.3\times 10^{-4} & 6.3\times 10^{-5} & 0.50 & -3.4\times 10^{-5} \\ 1.2\times 10^{-5} & -1.4\times 10^{-4} & 4.0\times 10^{-5} & 6.2\times 10^{-4} & 1.1\times 10^{-4} & -1.1\times 10^{-4} & 0.50 \end{pmatrix}. \end{aligned}$$

By Eq. (47), we get

$$ U= \begin{pmatrix} 1.2 \\ 0.4 \\ 0.28571428569 \\ 0.1 \\ 0.01428571428 \\ 0 \\ 0 \end{pmatrix} . $$

Thus,

$$ u_{7}(x)=\sum_{r=0}^{6}u_{r} \,FL_{r}(x)=1+x^{2}. $$

Hence, we get the exact solution.

Example 2

Consider the following problem:

where

$$ f(x)=x^{\gamma +1}+x^{2\gamma +2}+\frac{1+\gamma }{1-\gamma }\varGamma (1+ \gamma )x^{1+\gamma }E_{\gamma ,\gamma +2} \biggl( \frac{-\gamma x^{ \gamma }}{1-\gamma } \biggr) . $$

The exact solution is

$$ u(x)=x^{\gamma +1}. $$

Let

$$ R(\gamma )=\max_{r=0,1,\ldots,100} \biggl\vert u_{30}\biggl( \frac{r}{100}\biggr)-u\biggl(\frac{r}{100}\biggr) \biggr\vert . $$

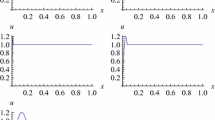
Then the absolute errors for different choices of γ are given in Table 1.

Table 1 Absolute errors
Full size table

The graph of the exact and the approximate solutions for \(\gamma =0.3,0.6,0.9 \), and 0.99 are given in Fig. 1.

Figure 1
figure 1

The exact and the approximate solutions for \(\gamma = 0.3,0.6,0.9\), and 0.99, dots: approximate solutions, joint lines: exact solutions

Full size image

5 Closing remarks

In this article, we present a method to approximate the solution of FRE based on the ABFD in Caputo sense. The numerical method is based on the fractional operational matrix of the fractional derivative. We present two examples. In the first example, we get the exact solution. In the second one, the absolute error is of order 10−13. Results are given in Table 1. Figure 1 presents the agreement between the exact and the approximate solutions in Example 2 for different choices of γ. From the numerical results, we see that the proposed method gives accurate results. It is advisable to use it for other nonlinear fractional differential equations.