1 Introduction

Nowadays, the mathematical models involving fractional order derivative were given noticeable importance because they are more accurate and realistic as compared to the classical order models [22, 26, 28]. Motivated by the advancement of fractional calculus, many researchers have focused to investigate the solutions of nonlinear differential equations with the fractional operator by developing quite a few analytical or numerical techniques to find approximate solutions [6, 10, 19, 29, 30]. These differential equations involves several fractional differential operators like Riemann–Liouville, Caputo, Hilfer etc. [4, 15, 32].

However, these operators possess a power law kernel and have limitations in modeling physical problems. To overcome this difficulty, recently an alternate fractional differential operator having a kernel with exponential decay has been introduced by Caputo and Fabrizio [9]. This novel approach of fractional derivative is known as the Caputo–Fabrizio (C–F) operator which has attracted many research scholars due to the fact that it has a non-singular kernel. Also the C–F operator is most appropriate for modeling some class of real-world problem which follows the exponential decay law. With the passage of time, developing a mathematical model using the C–F fractional order derivative became a remarkable field of research. In recent times, several mathematicians were busy in development and simulation of CFFDE. One can read the articles of the aforementioned derivative to see further characteristics and applications [3, 8, 11, 16,17,18, 20, 25, 34].

In the present study, we analyze the following Caputo–Fabrizio fractional differential equations (C-FFDE) to obtain uniqueness and existence criteria of solutions [5, 7, 35]:

$$ \textstyle\begin{cases} {}^{\mathrm{CF}}D^{\gamma }_{t}u(t)= f(t, u(t)), \quad 0< \gamma < 1, \\ u(0) = u_{0}. \end{cases} $$
(1)

Here \({}^{\mathrm{CF}}D^{\gamma }_{t}\) is for the CFFDE. \(f: [0,1] \times \mathbb{R} \rightarrow \mathbb{R} \) is continuous and \(u_{0} \in \mathbb{R}\), \(t \in [0,1]\).

Fractional reaction–diffusion equations have been broadly examined as of lately. These equations emerge normally as description models of numerous evolution processes in various branches of science [12, 21, 33]. Furthermore by continuation to the above literature, we demonstrate the utility of the C–F operator on one- and two-dimensional reaction–diffusion equations, namely the Fitzhugh–Nagumo (FN) equation and the Fisher equation, respectively given by

$$\begin{aligned}& {}^{\mathrm{CF}}D^{\gamma }_{t}u(t)= \beta u_{xx}+g(u)+h(x,t), \end{aligned}$$
(2)
$$\begin{aligned}& {}^{\mathrm{CF}}D^{\gamma }_{t}u(t)= \beta (u_{xx}+u_{yy})+g(u)+h(x,t), \end{aligned}$$
(3)

where the nonlinear function \(g(u)\) represents the reaction kinetics, \(h(x,t)\) is a source term and β denotes the diffusion coefficient.

By considering \(g(u) = \lambda u^{\alpha }(1-u^{\nu })(u-\theta)\) and \(h(x,t)=0\), Eqs. (2) and (3) reduce to

$$\begin{aligned}& {}^{\mathrm{CF}}D^{\gamma }_{t}u(t)= \beta u_{xx}+\lambda u^{\alpha }\bigl(1-u^{ \nu }\bigr) (u-\theta), \end{aligned}$$
(4)
$$\begin{aligned}& {}^{\mathrm{CF}}D^{\gamma }_{t}u(t)= \beta (u_{xx}+u_{yy})+\lambda u^{\alpha }\bigl(1-u ^{\nu }\bigr) (u-\theta), \end{aligned}$$
(5)

If we put \(\lambda =1\), \(\beta =1\), \(\alpha =1\) and \(\nu =1\), then Eq. (4) reduces to a time fractional FN equation which is one of the most significant reaction–diffusion equation, used to display the transmission of nerve driving forces [14]. The mathematical model of population genetics is also described by using the FN equation [1]. Next, if we take \(\lambda =\frac{1}{2}\), \(\beta =1\), \(\alpha =1\), \(\nu =1\) and \(\theta =0\), then Eq. (5) becomes a time fractional Fisher equation in an infinite domain as suggested by Fisher [13] as a model for the spatial transient propagation of a virile gene. In [2], Atangana studied a nonlinear Fisher reaction–diffusion equation.

In [24] Khan et al. used the homotopy analysis method (HAM) to find approximate analytical solutions of fractional reaction–diffusion equations. The residual power series method (RPSM) was applied by Tchier et al. [31] to find a numerical solution of fractional reaction–diffusion equations. The series solutions of reaction–diffusion equations were obtained by Merdan [27] by using a fractional variational iteration method (FVIM). Motivated by this, in the present manuscript, we compute approximate solutions of nonlinear fractional reaction–diffusion equations by using a reliable and efficient approach known as the iterative Laplace transform method (ILTM). The proposed technique is an amalgamation of the Laplace transform and the new iterative method (NIM) proposed by Jafari et al. [23].

In the light of the above examined writing, the present study concentrates on establishing the uniqueness and existence criteria of solutions of the nonlinear C-FFDE. Also, we demonstrate the effectiveness of the iterative Laplace transform method by obtaining the approximate solutions and 3D plots of the time fractional reaction–diffusion equations.

2 Preliminaries of fractional calculus

Definition 2.1

([9])

Let \(u\in H^{1}(0,b)\), \(b > 0\), \(0<\gamma <1 \), then the time fractional Caputo–Fabrizio fractional differential operator (C-FFDO) is defined as

$$ {}^{\mathrm{CF}}D^{\gamma }_{t}u(t)= \frac{(2-\gamma)M(\gamma)}{2(1-\gamma)} \int _{0}^{t}\exp \biggl[-\frac{\gamma (t-s)}{1-\gamma } \biggr] u'(\tau)\,d\tau, \quad t \geq 0, 0< \gamma < 1, $$
(6)

with a normalization function \(M(\gamma)\) which is depending on \(\gamma \ni M(0)=M(1)=1\).

Definition 2.2

([8])

The C-FFDO of order \(0<\gamma <1\) is given by

$$ {}^{\mathrm{CF}}J^{\gamma }_{t}u(t)= \frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}u(t) + \frac{2 \gamma)}{(2-\gamma)M(\gamma)} \int _{0}^{t} u(\tau)\,d\tau, $$
(7)

like the usual Caputo derivative, this new operator gives \({}^{\mathrm{CF}}D^{ \gamma }_{t}u(t)=0\), if u is a constant function.

The main advantage of the Caputo–Fabrizio operator over the old operator of Caputo is that there is no singularity for \(t= s\) in the new kernel.

Definition 2.3

([9])

The Laplace transform for the C-FFDO of order \(0<\gamma \leq 1 \) and \(m\in \mathbb{N}\) is given by

$$\begin{aligned} \mathbb{L} \bigl({}^{\mathrm{CF}}D^{m+\gamma }_{t}u(t) \bigr) (s) & =\frac{1}{1-\gamma }\mathbb{L}\bigl(u^{(m+1)}(t)\bigr)\mathbb{L} \biggl(\exp \biggl( -\frac{\gamma }{1- \gamma }t \biggr) \biggr) \\ & = \frac{s^{m+1}\mathbb{L}(u(t))-s^{m}u(0)-s^{m-1}u'(0)-\cdots -u^{(m)}(0)}{s+\gamma (1-s)}. \end{aligned}$$
(8)

In particular, we have

$$\begin{aligned} &\mathbb{L} \bigl({}^{\mathrm{CF}}D^{\gamma }_{t}u(t) \bigr) (s) = \frac{s\mathbb{L}(u(t))}{s+ \gamma (1-s)}, \quad m=0, \\ &\mathbb{L} \bigl({}^{\mathrm{CF}}D^{\gamma +1}_{t}u(t) \bigr) (s) = \frac{s^{2} \mathbb{L}(u(t))-su(0)-u'(0)}{s+\gamma (1-s)},\quad m=1. \end{aligned}$$

Lemma 2.1

The IVP

$$ \textstyle\begin{cases} {}^{\mathrm{CF}}D^{\gamma }_{t}u(t)=f(t), \quad t\geq 0, 0 < \gamma < 1, \\ u(0)=u_{0} \in R, \end{cases} $$
(9)

has a solution in terms of the integral given by

$$ u(t)= u_{0}+\frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}\bigl(f(t)-f(0)\bigr)+\frac{2 \gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} f(\tau)\,d\tau. $$
(10)

3 Main results

Prior to expressing and demonstrating the fundamental outcomes, we present the following lemma and notations.

Let \(\mathbb{\mu } = [0, 1]\) and \(C(\mu) \) denote the space of all continuous functions on μ.

Considering the set \(\mathbb{B} = \{u(t) |u(t) \in C(\mu)\} \), endowed with the norm \(\Vert u(t) \Vert _{\mathbb{B}}= \max_{t\in \mu } |u(t)|\), is a Banach space. By Lemma (9), IVP (1) is expressed as an integral equation given by

$$ u(t)= u_{0}+\frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}\bigl(f\bigl(t, u(t)\bigr)-f\bigl(0, u(0)\bigr)\bigr)+\frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} f\bigl(\tau, u( \tau)\bigr)\,d\tau. $$
(11)

Let the operator \(T:\mathbb{B} \rightarrow \mathbb{B} \) be defined by

$$\begin{aligned} Tu(t) =& u_{0}+\frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}\bigl(f\bigl(t, u(t) \bigr)-f\bigl(0, u(0)\bigr)\bigr) \\ &{}+\frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} f\bigl(\tau, u( \tau)\bigr)\,d\tau, \end{aligned}$$
(12)

then the fixed point of operator T is equivalent to the solution of IVP (1).

$$ \text{In this article, let us denote} \quad A = \frac{2}{M(\gamma)}. $$
(13)

Theorem 3.1

Let \(f: \mu \times R \rightarrow R \) be a continuous function. Assume that at least one of the following conditions is fulfilled:

(H1):

A non-negative function \(g(t) \in L[0,1]\) exists, such that \(|f(t, x) | \leq g(t) + c_{0} | x |^{\delta }\), where \(c_{0} \geq 0\), \(0 < \delta < 1\).

(H2):

The function f satisfies \(|f(t, x) | \leq c_{0} | x |^{ \delta }\), where \(c_{0} > 0\), \(\delta > 1\). Then IVP (1) has a solution.

Proof

We make use of the Schauder fixed point theorem. For this purpose, assume that condition (H1) is satisfied.

Define \(G = \{ u(t) | u(t) \in \mathbb{B}, \Vert u(t) \Vert _{\mathbb{B}} \leq K, t \in \mu \}\), where \(K \geq \max \{ (2\operatorname{Ac}_{0})^{\frac{1}{1-\delta }}, 2l \}\) and

$$ l = \max_{t\in \mu } \biggl(u_{0} + \frac{4(1-\gamma)}{(2- \gamma)M(\gamma)}g(t)+ \frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} \bigl\vert g(\tau) \bigr\vert \,d \tau \biggr). $$

Obviously, in the Banach space \(\mathbb{B}\), G is a ball. Next, we show that T: \(G\rightarrow G\).

For all \(u\in G \), we have

$$\begin{aligned} \bigl\vert Tu(t) \bigr\vert =& \biggl\vert u_{0}+\frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}\bigl(f\bigl(t, u(t)\bigr)-f\bigl(0, u(0)\bigr) \bigr)+\frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} f\bigl( \tau, u(\tau)\bigr)\,d\tau \biggr\vert \\ \leq& u_{0}+\frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}\big|(f\bigl(t, u(t)\bigr) \big\vert + \frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}\big|(f\bigl(0, u(0)\bigr) \big\vert \\ &{} +\frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} \bigl\vert f\bigl( \tau, u(\tau) \bigr) \bigr\vert \,d\tau \\ \leq& u_{0}+\frac{4(1-\gamma)}{(2-\gamma)M(\gamma)} \bigl( g(t) + c _{0}K^{\delta } \bigr) + \frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} \bigl( \bigl\vert g(\tau) \bigr\vert +c_{0}K^{\delta }\bigr)\,d\tau \\ \leq& u_{0}+\frac{4(1-\gamma) ( g(t) + c_{0}K^{\delta } )}{(2- \gamma)M(\gamma)} + \frac{2\gamma c_{0}K^{\delta }t}{(2-\gamma)M( \gamma)}+ \frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} \bigl\vert g( \tau) \bigr\vert \,d \tau \\ \leq& u_{0}+\frac{4(1-\gamma)}{(2-\gamma)M(\gamma)}g(t) + \frac{2 \gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} \bigl\vert g(\tau) \bigr\vert \,d \tau \\ &{} + \biggl(\frac{4(1-\gamma)}{(2-\gamma)M(\gamma)}+\frac{2 \gamma t}{(2-\gamma)M(\gamma)} \biggr)c_{0}K^{\delta } \\ \leq& u_{0}+\frac{4(1-\gamma)}{(2-\gamma)M(\gamma)}g(t) + \frac{2 \gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} \bigl\vert g(\tau) \bigr\vert \,d \tau +\frac{2 c _{0}K^{\delta } }{M(\gamma)}. \end{aligned}$$

Therefore,

$$\begin{aligned} \bigl\Vert Tu(t) \bigr\Vert _{\mathbb{B}} =& \max _{t\in \mu } \bigl\vert Tu(t) \bigr\vert \\ \leq& l+\frac{2 c_{0}K^{\delta } }{M(\gamma)}= l+ Ac_{0}K^{\delta } \leq \frac{K}{2}+\frac{K}{2}=K. \end{aligned}$$

Here \(Tu(t)\) is continuous on μ.

Now, assume that condition (H2) is satisfied. Select \(0< K \leq (\frac{1}{\operatorname{Ac}_{0}} )^{\frac{1}{\delta -1}}\).

Similarly, repeating the above arguments we get

$$ \bigl\Vert Tu(t) \bigr\Vert _{\mathbb{B}} \leq \operatorname{Ac}_{0}K^{\delta } \leq K. $$

Consequently, we get \(T : G \rightarrow G \).

Obviously, the operator T is continuous because of the continuity of f. □

Further, we set up the complete continuity of the operator T. Let \(R = \max_{t\in \mu } |f (t, u(t))|\), for any \(u\in G \), let \(t_{1}, t_{2} \in \mu \) be such that \(t_{1} < t_{2}\).

Also, let \(U_{1}=\frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}\) and \(U_{2}=\frac{2\gamma }{(2-\gamma)M(\gamma)}\), then we get

$$\begin{aligned} \bigl\vert Tu(t_{2})-Tu(t_{1}) \bigr\vert =& \biggl\vert u_{0}+U_{1}\bigl[f \bigl(t_{2}, u(t_{2})\bigr)-f\bigl(0, u(0)\bigr)\bigr]+U _{2} \int _{0}^{t_{2}} f\bigl(\tau, u(\tau)\bigr)\,d\tau \\ &{} - u_{0}-U_{1}\bigl[f\bigl(t_{1}, u(t_{1})\bigr)-f\bigl(0, u(0)\bigr)\bigr]-U_{2} \int _{0}^{t_{1}} f\bigl(\tau, u(\tau)\bigr)\,d\tau \biggr\vert \\ =& \biggl\vert U_{1}\bigl[f\bigl(t_{2}, u(t_{2})\bigr)-f\bigl(t_{1}, u(t_{1})\bigr) \bigr]+U_{2} \int _{t _{1}}^{t_{2}} f\bigl(\tau, u(\tau)\bigr)\,d\tau \biggr\vert \\ \leq& U_{1} \bigl\vert f\bigl(t_{2}, u(t_{2}) \bigr) \bigr\vert + U_{1} \bigl\vert f\bigl(t_{1}, u(t_{1})\bigr) \bigr\vert +U_{2} \int _{t_{1}}^{t_{2}} \bigl\vert f\bigl(\tau, u(\tau) \bigr) \bigr\vert \,d\tau \\ \leq& 2RU_{1} + R U_{2} \int _{t_{1}}^{t_{2}}\,d\tau \\ =&R\bigl(2U_{1} + U_{2}(t_{2}-t_{1}) \bigr). \end{aligned}$$

In view of the uniform continuity of the function \((t_{2}-t_{1})\) on the interval μ, we see that TG is an equicontinuous set. Also, this function is uniformly bounded as \(TG \subseteq G\); hence T is completely continuous. As a result of Schauder’s fixed point theorem, there exists a solution of IVP (1) in G.

Corollary 3.1

Suppose the function f is continuous and bounded on \(\mu \times \mathbb{R}\), then IVP (1) has a solution.

Proof

As f is continuous and bounded on \(\mu \times \mathbb{R}\), there exists \(L>0\) which satisfies \(|f| < L \). Let \(g(t) = L\), \(c_{0} = 0 \) in condition (H1) of Theorem 3.1, then IVP (1) has a solution.

Next, we establish the uniqueness criteria for solutions of IVP (1) with the help of Banach contraction principle. □

Theorem 3.2

Let \(f: \mu \times \mathbb{R} \rightarrow \mathbb{R} \) be continuous function and let the conditions given below be satisfied:

(H3):

There exists a non-negative function \(\eta (t) \in L[0,1] \) which gives

$$ \bigl\vert f(t, x) - f(t, y) \bigr\vert \leq \eta \vert x -y \vert , \quad t \in [0,1], $$

also the function f satisfies \(f(t, 0) = 0\).

(H4):

Suppose that \(\sigma = \max_{t\in \mu } | \frac{2(1- \gamma)}{(2-\gamma)M(\gamma)} \eta (t) + \frac{2\gamma }{(2-\gamma)M(\gamma)}\int _{0}^{t} \eta (\tau)\,d\tau | < 1\), then IVP (1) has a unique solution.

Proof

We denote the operator T by

$$ Tu(t) = \phi + \frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}f\bigl(t, u(t)\bigr)+ \frac{2 \gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} f\bigl(\tau, u(\tau)\bigr)\,d\tau, $$

where \(\phi = u_{0}-\frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}f(0, u _{0})\). For \(u(t) \in \mathbb{B} \), we get

$$\begin{aligned} \bigl\vert Tu(t) \bigr\vert = & \biggl\vert \phi + \frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}f\bigl(t, u(t)\bigr)+\frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} f\bigl(\tau, u( \tau)\bigr)\,d\tau \biggr\vert \\ \leq& \vert \phi \vert + \frac{2(1-\gamma)}{(2-\gamma)M(\gamma)} \bigl\vert f\bigl(t, u(t) \bigr)-f(t, 0) \bigr\vert \\ &{} +\frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} \bigl\vert f\bigl( \tau, u(\tau) \bigr)-f(\tau, 0) \bigr\vert \,d\tau \\ \leq& \vert \phi \vert + \frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}\eta (t) \bigl\vert u(t) \bigr\vert +\frac{2 \gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t}\eta (\tau) \bigl\vert u(\tau) \bigr\vert \,d\tau \\ \leq& \vert \phi \vert + \biggl(\frac{2(1-\gamma)}{(2-\gamma)M(\gamma)} \eta (t)+ \frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t}\eta ( \tau)\,d\tau \biggr) \Vert u \Vert , \end{aligned}$$

hence, we have

$$\begin{aligned} \bigl\Vert Tu(t) \bigr\Vert _{\mathbb{B}} &\leq \vert \phi \vert + \biggl(\frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}\eta (t)+\frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t}\eta (\tau)\,d\tau \biggr) \Vert u \Vert \\ &\leq \vert \phi \vert + \sigma \Vert u \Vert \leq \Vert u \Vert , \end{aligned}$$

therefore, \(T:\mathbb{B} \rightarrow \mathbb{B}\). Let \(u(t), v(t) \in \mathbb{B}\), then we have

$$\begin{aligned} \bigl\vert Tu(t)-Tv(t) \bigr\vert = & \biggl\vert \phi +\frac{2(1-\gamma)}{(2-\gamma)M( \gamma)} f\bigl(t, u(t)\bigr)+\frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0} ^{t} f\bigl(\tau, u(\tau)\bigr)\,d\tau \\ &{} -\phi -\frac{2(1-\gamma)}{(2-\gamma)M(\gamma)}f\bigl(t, v(t)\bigr)-\frac{2 \gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} f\bigl(\tau, v(\tau)\bigr)\,d\tau \biggr\vert \\ \leq& \frac{2(1-\gamma)}{(2-\gamma)M(\gamma)} \bigl\vert f\bigl(t, u(t)\bigr)-f\bigl(t, v(t)\bigr) \bigr\vert \\ &{} + \frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} \bigl\vert f\bigl(\tau, u( \tau) \bigr)-f\bigl(\tau, v(\tau)\bigr) \bigr\vert \,d\tau \\ \leq& \frac{2(1-\gamma)}{(2-\gamma)M(\gamma)} \eta (t) \bigl\vert u(t)-v(t) \bigr\vert + \frac{2\gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} \eta ( \tau) \bigl\vert u(\tau)- v( \tau) \bigr\vert \,d\tau \\ \leq& \biggl(\frac{2(1-\gamma)}{(2-\gamma)M(\gamma)} \eta (t) + \frac{2 \gamma }{(2-\gamma)M(\gamma)} \int _{0}^{t} \eta (\tau)\,d\tau \biggr) \bigl\Vert u(\tau)- v(\tau) \bigr\Vert \\ \leq &\sigma \bigl\Vert u(\tau)- v(\tau) \bigr\Vert \leq \bigl\Vert u( \tau)- v(\tau) \bigr\Vert . \end{aligned}$$

In view of \(\sigma < 1\), T is a contraction. Consequently, T has only one fixed point as a result of Banach contraction principle, hence it gives a solution of IVP (1). □

4 Applications

In this section, we shall propose an algorithm to solve a general non-homogeneous C-FFDE and demonstrate it by solving time fractional FN and Fisher equations.

4.1 Iterative Laplace transform method

We take a general non-homogeneous C-FFDE of the form

$$ {}^{\mathrm{CF}}D^{m+\gamma }_{t}u(x,t) = f (x,t) + \phi u(x,t) + \psi u(x,t),\quad n-1 < \gamma \leq n, n\in N, $$
(14)

with the initial conditions

$$ \frac{\partial ^{k}u(x,0)}{\partial t^{k}}= \theta _{k}(x), \quad k=0,1,2,\ldots,n-1. $$

Here \(f (x,t)\) is a source term, ϕ and ψ are given linear and nonlinear operator, respectively. Applying the Laplace transform (8) on two sides of (14) yields

$$ \mathbb{L}\bigl(u(x,t)\bigr)= \chi (x,s) + \biggl( \frac{s+\gamma (1-s)}{s^{m+1}} \biggr)\mathbb{L}\bigl(\phi u(x,t) + \psi u(x,t)\bigr), $$
(15)

where

$$ \chi (x,s) = \frac{1}{s^{m+1}} \bigl( s^{m}\theta _{0}(x) + s^{m-1}\theta _{1}(x)+\cdots +\theta _{m}(x) \bigr)+ \frac{s+\gamma (1-s)}{s ^{m+1}}\widetilde{f}(x,s). $$

Next, we apply the inverse Laplace transform on (15) then we have

$$ u(x,t)= \chi (x,t) + \mathbb{L}^{-1} \biggl[ \biggl( \frac{s+\gamma (1-s)}{s ^{m+1}} \biggr)\mathbb{L}\bigl(\phi u(x,t) + \psi u(x,t)\bigr) \biggr], $$
(16)

where the term obtained from the source term is denoted by \(\chi (x,t)\). Further, we apply the new iterative method introduced in [10]. We consider the solution as an infinite series given as

$$ u(x,t) = \sum_{j=0}^{\infty }u_{j}(x,t); $$
(17)

since ϕ is linear,

$$ \phi \Biggl(\sum_{j=0}^{\infty }u_{j}(x,t) \Biggr) = \sum_{j=0}^{\infty }\phi \bigl(u_{j}(x,t) \bigr). $$
(18)

The nonlinear operator ψ is decomposed as

$$ \psi \Biggl(\sum_{j=0}^{\infty }u_{j} \Biggr) = \psi \bigl(u_{0}(x,t)\bigr) + \sum _{j=1}^{\infty } \Biggl\{ \psi \Biggl(\sum _{i=0}^{j}u_{i}(x,t) \Biggr)- \psi \Biggl( \sum_{i=0}^{j-1}u_{i}(x,t) \Biggr) \Biggr\} . $$
(19)

In view of (17), (18) and (19), Eq. (16) is equivalent to

$$\begin{aligned} \sum_{j=0}^{\infty }u_{j}(x,t) =& \chi (x,t) + \mathbb{L}^{-1} \Biggl[ \biggl( \frac{s+\gamma (1-s)}{s^{m+1}} \biggr) \mathbb{L} \Biggl( \sum_{j=0} ^{\infty }\phi \bigl(u_{j}(x,t) \bigr) \Biggr) \Biggr] \\ &{} + \mathbb{L}^{-1} \Biggl[ \biggl( \frac{s+\gamma (1-s)}{s ^{m+1}} \biggr) \mathbb{L} \Biggl( \psi \bigl(u_{0}(x,t) \bigr) + \sum _{j=1} ^{\infty } \Biggl\{ \psi \Biggl(\sum _{i=0}^{j}u_{i}(x,t) \Biggr) \\ &{} - \psi \Biggl(\sum_{i=0}^{j-1}u_{i}(x,t) \Biggr) \Biggr\} \Biggr) \Biggr], \end{aligned}$$
(20)

furthermore, we consider the recurrence relation as given by

$$\begin{aligned} \begin{aligned} & u_{ 0}(x,t) =\chi (x,t), \\ &u_{ 1}(x,t) = \mathbb{L}^{-1} \biggl[ \biggl( \frac{s+\gamma (1-s)}{s ^{m+1}} \biggr)\mathbb{L} \bigl( \phi \bigl(u_{0}(x,t) \bigr)+ \psi \bigl(u _{0}(x,t) \bigr) \bigr) \biggr], \\ &u_{p+1}(x,t) = \mathbb{L}^{-1} \Biggl[ \biggl( \frac{s+\gamma (1-s)}{s ^{m+1}} \biggr)\mathbb{L} \Biggl( \phi \bigl(u_{r}(x,t) \bigr)+ \Biggl\{ \psi \Biggl(\sum_{i=0}^{p}u_{i}(x,t) \Biggr) \\ &\hphantom{u_{p+1}(x,t) =}{} - \psi \Biggl(\sum_{i=0}^{p-1}u_{i}(x,t) \Biggr) \Biggr\} \Biggr) \Biggr]. \end{aligned} \end{aligned}$$
(21)

The p-term approximate solution is given by

$$ u = u_{0}+u_{1}+u_{2}+\cdots +u_{p-1}. $$
(22)

4.2 Illustrative examples

The efficiency of ILTM is validated by simulating time fractional reaction–diffusion equations in this section.

Example 4.1

The time fractional Fitzhugh–Nagumo equation is

$$ {}^{\mathrm{CF}}D^{\gamma }_{t}u(x,t)= u_{xx}+u(1-u) (u-\theta),\quad t>0, 0< \gamma \leq 1, $$
(23)

with initial condition

$$ u(x, 0)= \frac{1}{1+ e^{-\frac{x}{\sqrt{2}}}}. $$

Here \(x\in \mathbb{R}\), \(\theta \in (0,1)\) and the exact solution of Eq. (26) for \(\gamma =1\) is

$$ u(x, t)= \frac{1}{1+ e^{(-\frac{1}{2}) (x+ (\frac{1+2\theta }{ \sqrt{2}} )t )}}. $$

Taking the Laplace transform on (8) to (23), we get

$$ \mathbb{L}\bigl(u(x,t)\bigr)= \frac{ u(x, 0)}{s}+ \biggl( \frac{s+\gamma (1-s)}{s} \biggr)\mathbb{L} \bigl( u_{xx}+u(1-u) (u-\theta) \bigr). $$
(24)

Applying the inverse Laplace transform on (24)

$$ u(x,t)= u(x, 0)+ \mathbb{L}^{-1} \biggl[ \biggl( \frac{s+\gamma (1-s)}{s} \biggr)\mathbb{L} \bigl( u_{xx}+u(1-u) (u-\theta) \bigr) \biggr]. $$
(25)

In view of Eq. (21), we get

$$\begin{aligned} &u_{0} =\frac{1}{e^{-\frac{x}{\sqrt{2}}}+1}, \\ &u_{1} = -\frac{(2 \theta -1) e^{\frac{x}{\sqrt{2}}} (\gamma (t-1)+1)}{2 (e^{\frac{x}{\sqrt{2}}}+1 )^{2}}, \\ &u_{2}= \frac{e^{\frac{x}{\sqrt{2}}} }{96 (e^{\frac{x}{ \sqrt{2}}}+1 )^{6}} \big(24 \theta (2 \theta -1) \bigl(\gamma ^{2} \bigl(t^{2}-4 t+2 \bigr)+4 \gamma (t-1)+2 \bigr)-24 \bigl(2 \theta ^{2}-3 \theta +1 \bigr) \\ &\hphantom{u_{2}=}{}\times e^{2 \sqrt{2}x} \bigl(\gamma ^{2} \bigl(t^{2}-4 t+2 \bigr)+4 \gamma (t-1)+2 \bigr)-12 (2 \theta -1) \bigl(-4 e^{\frac{x}{\sqrt{2}}}+e^{\sqrt{2} x}+1 \bigr) \\ &\hphantom{u_{2}=}{}\times \bigl(e^{\frac{x}{\sqrt{2}}}+1 \bigr)^{2} \bigl( \gamma ^{2} \bigl(t^{2}-4 t+2 \bigr)+4 \gamma (t-1)+2 \bigr)+8 (2 \theta -1) e^{ \frac{x}{\sqrt{2}}} \bigl(3 \bigl(2 \theta ^{2}+5 \theta -5 \bigr) \\ &\hphantom{u_{2}=}{} +3 \gamma ^{2} \bigl(6 \theta ^{2}+7 \theta +4 \bigl(\theta ^{2}+\theta -1 \bigr) t^{2}-2 \bigl(6 \theta ^{2}+7 \theta -7 \bigr) t-7 \bigr)+\gamma ^{3} \bigl(2 \theta ^{2}+\theta -1 \bigr) \\ &\hphantom{u_{2}=}{}\times \bigl(t^{3}-6 t^{2}+9 t-3 \bigr)+3 \gamma \bigl(6 \theta ^{2}+11 \theta -11 \bigr) (t-1) \bigr)+8 (2 \theta -1) e^{\frac{3 x}{ \sqrt{2}}} \bigl(6 \theta ^{2}-27 \theta \\ &\hphantom{u_{2}=}{} +3 \gamma ^{2} \bigl(6 \theta ^{2}-19 \theta +4 \bigl(\theta ^{2}-3 \theta +1 \bigr) t^{2}-2 \bigl(6 \theta ^{2}-19 \theta +6 \bigr) t+6 \bigr)+\gamma ^{3} \bigl(2 \theta ^{2}-5 \theta +2 \bigr) \\ &\hphantom{u_{2}=}{}\times \bigl(t^{3}-6 t^{2}+9 t-3 \bigr)+3 \gamma \bigl(6 \theta ^{2}-23 \theta +6 \bigr) (t-1)+6 \bigr) \\ &\hphantom{u_{2}=}{}+e^{\sqrt{2} x} \bigl(36 \bigl(8 \theta ^{3}-12 \theta ^{2}-2 \theta +3 \bigr) \\ &\hphantom{u_{2}=}{} +6 \gamma ^{2} (2 \theta -1) \bigl(96 (\theta -1) \theta + \bigl(68 \theta ^{2}-68 \theta +5 \bigr) t^{2}-192 (\theta -1) \theta t \bigr)+4 \gamma ^{3} (2 \theta -1)^{3} \\ &\hphantom{u_{2}=}{}\times \bigl(8 t^{3}-39 t^{2}+54 t-18 \bigr)+3 \gamma ^{4} (2 \theta -1)^{3} \bigl(t^{4}-8 t^{3}+18 t^{2}-16 t+4 \bigr) \\ &\hphantom{u_{2}=}{} +24 \gamma \bigl(40 \theta ^{3}-60 \theta ^{2}+6 \theta +7 \bigr) (t-1) \bigr) \big). \end{aligned}$$

Example 4.2

We consider the time fractional two-dimensional Fisher equation

$$ {}^{\mathrm{CF}}D^{\gamma }_{t}u(x,y,t)= \frac{1}{2}(u_{xx}+u_{yy})+u^{2}(1-u), \quad t>0, 0< \gamma \leq 1, $$
(26)

with initial condition

$$ u(x, y, 0)= \frac{1}{1+ e^{\frac{x+y}{\sqrt{2}}}}, $$

for \(\Delta = \{(x,y): x, y\in [0,1]\} \). The exact solution of Eq. (26) for \(\gamma =1\) is

$$ u(x,y,t)= \frac{1}{1+ e^{\frac{x+y- (\frac{t}{\sqrt{2}} )}{ \sqrt{2}}}}. $$

Applying the Laplace transform on (8) to (26), we get

$$ \mathbb{L}\bigl(u(x,y,t)\bigr)= \frac{ u(x, y, 0)}{s}+ \biggl( \frac{s+\gamma (1-s)}{s} \biggr)\mathbb{L} \biggl(\frac{1}{2}(u_{xx}+u _{yy})+u^{2}(1-u) \biggr), $$
(27)

taking the inverse Laplace transform of (27)

$$ u(x,t)= u(x, 0)+ \mathbb{L}^{-1} \biggl[ \biggl( \frac{s+\gamma (1-s)}{s} \biggr)\mathbb{L} \biggl( \frac{1}{2}(u_{xx}+u _{yy})+u^{2}(1-u) \biggr) \biggr]. $$
(28)

In view of Eq. (21), we get

$$\begin{aligned} &u_{0} = \frac{1}{e^{\frac{x+y}{\sqrt{2}}}+1}, \\ &u_{1} = \frac{(\gamma (t-1)+1) e^{\frac{x+y}{\sqrt{2}}}}{2 (e^{\frac{x+y}{\sqrt{2}}}+1 )^{2}}, \\ &u_{2}=\frac{e^{\frac{x+y}{\sqrt{2}}}}{96 (e^{\frac{x+y}{ \sqrt{2}}}+1 )^{6}} \bigl(-24 \bigl(\gamma ^{2} \bigl(t^{2}-4 t+2 \bigr)+4 \gamma (t-1)+2 \bigr)+12 \bigl(\gamma ^{2} \bigl(t^{2}-4 t+2 \bigr) \\ &\hphantom{u_{2}=}{} +4 \gamma (t-1)+2 \bigr) \bigl(-4 e^{ \frac{x+y}{\sqrt{2}}}+e^{\sqrt{2} (x+y)}+1 \bigr) \bigl(e^{\frac{x+y}{ \sqrt{2}}}+1 \bigr)^{2}-16 \bigl(3 \gamma ^{2} \bigl(2 t^{2}-6 t+3 \bigr) \\ &\hphantom{u_{2}=}{} +\gamma ^{3} \bigl(t^{3}-6 t^{2}+9 t-3 \bigr)+9 \gamma (t-1)+3 \bigr) e^{\frac{x+y}{ \sqrt{2}}}+8 \bigl(3 \gamma ^{2} \bigl(4 t^{2}-14 t+7 \bigr) \\ &\hphantom{u_{2}=}{} +\gamma ^{3} \bigl(t^{3}-6 t^{2}+9 t-3 \bigr)+33 \gamma (t-1)+15 \bigr) e^{\frac{3 (x+y)}{\sqrt{2}}}+ \bigl(-30 \gamma ^{2} t^{2}-4 \gamma ^{3} \bigl(8 t^{3} \\ &\hphantom{u_{2}=}{} -39 t^{2}+54 t-18 \bigr)-3 \gamma ^{4} \bigl(t^{4}-8 t^{3}+18 t^{2}-16 t+4 \bigr) \\ &\hphantom{u_{2}=}{}+168 \gamma (t-1)+108 \bigr) e^{\sqrt{2} (x+y)} \bigr). \end{aligned}$$

5 Numerical results and discussion

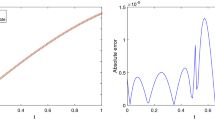
Figures 1 and 2 show the numerical simulations of three term approximate solutions of (23) for \(\gamma = 1, 0.8\) using ILTM from which one infers that this technique can describe the conduct of said variables precisely for the considered region. The intervals \([-10, 10]\) and \([0, 10]\) give the validity region of convergence of solutions for \(\gamma = 1\) and the intervals \([-10, 10]\), \([0, 12]\) for \(\gamma = 0.8\). The non-integer order has negligible effect in the dynamics of the FN equation. Also, Figs. 3 and 4 show the numerical simulations of three term approximate solutions of (26) for \(\gamma = 1, 0.8\) and the validity region of convergence of solutions given by intervals \([-5, 5]\) and \([0, 10]\) for \(\gamma =1\) and \(\gamma = 0.8\).

Figure 1
figure 1

Approximate solution of (23) for \(\gamma = 1\)

Full size image
Figure 2
figure 2

Approximate solution of (23) \(\gamma = 0.8\)

Full size image
Figure 3
figure 3

Approximate solution of (26) for \(\gamma = 1\), \(y=x\)

Full size image
Figure 4
figure 4

Approximate solution of (26) for \(\gamma = 0.8\), \(y=x\)

Full size image

Likewise, Tables 1 and 2 display the comparison among approximate solutions of (23) and (26), respectively, using ILTM with known results obtained by RPSM [31] and FVIM [27] for \(\gamma = 1, 0.8\). The numerical values demonstrate that the region of convergence of approximate solutions depend continuously on the time fractional derivative γ. These tables clarify convergence of the approximate solutions to the exact solutions, and as the value of the t decreases the absolute error becomes smaller. Hence, it is observed that the proposed technique is most suitable in terms of computational cost and accuracy for obtaining approximate solutions of nonlinear fractional reaction–diffusion equations.

Table 1 Numerical comparison between approximate solutions \(u_{\mathrm{ILTM}}\), \(u_{\mathrm{RPSM}}\), \(u_{\mathrm{FVIM}}\) and exact solution of (23) for \(x=0.01\), \(\theta =0.8\)
Full size table
Table 2 Numerical comparison between approximate solutions \(u_{\mathrm{ILTM}}\), \(u_{\mathrm{RPSM}}\) and exact solution of (26) for \(y=x=0.5\)
Full size table

6 Conclusions

This manuscript presents the existence and uniqueness criteria for nonlinear fractional differential equations involving the Caputo–Fabrizio differential operator. Further, we have developed ILTM to obtain approximate solutions of the Caputo–Fabrizio fractional differential equations successfully. The approximate solutions are compared with exact solutions and also with other existing solutions by other methods. It is observed that the obtained approximate series solutions for the first three terms are very precise and converge very rapidly to the solutions of real physical problems. The proposed approach is reliable, simple and effective to find approximate solutions of many nonlinear reaction–diffusion equations of fractional order.