1 Introduction

Many dynamical phenomena can be represented by Liénard equations, such as biological, mechanical, and electrical systems. In [1–3], the reader can find a broad list of contributions in mathematics and engineering which are based on such equations. In particular, the authors in [3] presented a Liénard type model in terms of the flow rate that was derived from the water hammer equations and subsequently used for parameter estimation purposes. The contribution presented in this article can be considered as an extension of this work, because we present another space-temporal Liénard type model for pipelines but governed by fractional derivatives, which gives the opportunity to model unknown dynamics associated to fluid phenomena in the pipeline. Another feature of the proposed model is that it can be conveniently expressed in terms of the flow rate or in terms of the pressure head as required.

In the last decades fractional calculus (FC) allowed the investigation of the nonlocal response of multiple phenomena [4–10], the fractional derivatives may be memory operators which usually represent dissipative effects or damage [11]. The fractional derivative considers the history and nonlocal distributed effects of any physical system. Some fundamental definitions in the context of FC are Erdelyi-Kober, Riesz, Riemann-Liouville, Hadamard, Grünwald-Letnikov, Weyl, Jumarie and Caputo [12–14]. Some advantages and disadvantages of these fractional derivatives are reviewed by Abdon in [15]. The Riemann-Liouville definition entails physically unacceptable initial conditions (fractional order initial conditions) [16]; conversely for the Caputo representation, the initial conditions are expressed in terms of integer-order derivatives having direct physical significance [17], these definitions have the disadvantage that their kernel has a singularity [18], this kernel includes memory effects and therefore both definitions cannot accurately describe the full effect of the memory. Due to this inconvenience, Caputo and Fabrizio in [19] presented a new definition of fractional operator without a singular kernel, the Caputo-Fabrizio (CF) fractional operator; this operator possesses very interesting properties, for instance, the possibility to describe fluctuations and structures with different scales [19]. Furthermore, this definition allows for a description of mechanical properties related with damage, fatigue, and material heterogeneities. The properties of this new fractional operator are reviewed in detail in Lozada and Nieto [20]. Other applications of the CF fractional operator are given in [21–30].

In 1992, based on the homotopy in topology, Liao [31] proposed a method, named homotopy analysis method (HAM), which transforms a nonlinear problem into an infinite number of linear problems without using perturbation techniques [32]. An account of the recent developments of HAM was given in [33]. The HAM has been applied to solve linear and nonlinear fractional partial differential equations [34]. The fractional KdV-Burgers-Kuramoto equation was solved using the HAM [35]. Also the nonlinear Riccati differential equations of fractional order were solved with this method [36]. Hashim et al. [37] employed the homotopy analysis method to solve some fractional initial value problems (fIVPs). In [38] the applicability of HAM was extended to construct a numerical solution for the fractional BBM-Burgers equation. This method has also been employed for solving the fractional Klein-Gordon equation [39]. The HAM was applied to a linear homogeneous one and two-dimensional fractional heat-like partial differential equations subject to the Neumann boundary conditions [40]. The HAM was also applied to linear and nonlinear homogeneous fractional diffusion-wave equations [41]. Recently, the HAM was shown to be capable of solving linear and nonlinear systems of fractional partial differential equations (FPDEs) [42].

The aim of this paper is to apply the Laplace homotopy analysis method (LHAM) to provide analytical solutions of a Liénard type models of a pipeline, the Caputo-Fabrizio fractional operator is applied. The current paper is organized as follows: In Section 2, we describe the Liénard representation. In Section 3, the water hammer equations are obtained. Section 4 describes the fractional Liénard Model of a fluid transmission line and the general description of the LHAM is presented. Section 5 presents the application of the LHAM using the Caputo-Fabrizio fractional derivative, and a conclusion is given in Section 6.

2 Liénard equation

A generalization of differential equations that describes the behavior of second-order mechanical systems is the so-called Liénard system [43], corresponding to the following equation:

$$ \ddot{x}(t)+F_{0}\bigl(x(t)\bigr)\dot{x}(t)+G_{0} \bigl(x(t)\bigr)=0,\quad \mbox{where } \dot {x}(t)=\frac{\partial}{\partial t}, \ddot{x}(t)= \frac{\partial ^{2}}{\partial t^{2}}, $$
(1)

for given functions \(F_{0}\), \(G_{0}\) and position \(x(t)\). On the one hand, a particular case of Eq. (1) is the equation of damped oscillations: \(\ddot{x}(t)+\gamma\dot{x}(t)+\omega^{2}x(t)=0\), where \(\ddot{x}(t)\) is the acceleration, \(\dot{x}(t)\) is the velocity, and γ, ω are constant parameters. For \(\gamma=0\), the equation of the linear harmonic oscillator is obtained, which represents one of the fundamental equations of both classical and quantum physics. Generally, a linear oscillation can be described by the equation \(\ddot{x}(t)+F_{0}(t)\dot{x}(t)+G_{0}(t)x(t)=0\). On the other hand, the Liénard equation is a generalization of the Levinson-Smith type equation [44]

$$ \ddot{x}(t)+F_{0}\bigl(x(t),\dot{x}(t)\bigr) \dot{x}(t)+G_{0}\bigl(x(t)\bigr)=0. $$
(2)

The Liénard type equation (1), for representing non-scalar systems, can be rewritten in a state space representation by considering \(x(t)\), \(\dot{x}(t)\) as state variables \(x_{1}(t),x_{2}(t)\in X\) (X, being an adequate Banach space), leading to

$$ \dot{x}_{1}(t)=x_{2}(t); \qquad \dot{x}_{2}(t)=-F_{0}\bigl(x_{1}(t) \bigr)x_{2}(t)-G_{0}\bigl(x_{1}(t)\bigr). $$
(3)

Therefore \(F_{0}:X\rightarrow\mathcal{L}(X)\) (where \(\mathcal{L}(X)\) is the space of bounded linear functions from X to X) and \(G_{0}:X\rightarrow X\). Now, if there exists a function \(F:X\rightarrow X\) such that \(F_{0}(\xi(t))\) is the Fréchet derivative of F at \(\xi (t)\) for all \(\xi(t)\in X\) and \(F(0_{X})=0_{X}\) (where \(0_{X}\) is the zero element of X), then the change of variables

$$ \bigl( \textstyle\begin{array}{@{}c@{\quad}c@{}} \zeta_{1}(t)&\zeta_{2}(t) \end{array}\displaystyle \bigr)=\Phi\bigl( \textstyle\begin{array}{@{}c@{\quad}c@{}} x_{1}(t)&x_{2}(t) \end{array}\displaystyle \bigr), $$
(4)

defined as

$$ \Phi:\bigl( \textstyle\begin{array}{@{}c@{\quad}c@{}} x_{1}(t)&x_{2}(t) \end{array}\displaystyle \bigr)\rightarrow \bigl( \textstyle\begin{array}{@{}c@{\quad}c@{}} x(t)&\dot{x}(t)+F(x(t)) \end{array}\displaystyle \bigr), $$
(5)

transform system (3) into

$$ \dot{\zeta}_{1}(t)=\zeta_{2}(t)-F\bigl(\zeta_{1}(t) \bigr);\qquad \dot{\zeta}_{2}(t)=-G_{0}\bigl( \zeta_{1}(t)\bigr). $$
(6)

3 Water hammer equations

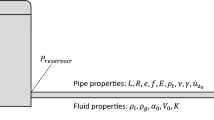
By assuming that convective changes in velocity are negligible, as well as that both the liquid density and the cross-sectional area are constant, the momentum and continuity equations governing the dynamics of the fluid in a horizontal pipeline can be expressed as [45]

$$\begin{aligned}& \frac{\partial Q(z,t)}{\partial t} +gA_{r}\frac {\partial H(z,t)}{\partial z}+ \frac{f}{2\phi A_{r}}Q(z,t)\bigl\vert Q(z,t)\bigr\vert =0, \end{aligned}$$
(7)
$$\begin{aligned}& \frac{\partial H(z,t)}{\partial t} +\frac {b^{2}}{gA_{r}}\frac{\partial Q(z,t)}{\partial z}=0, \end{aligned}$$
(8)

where \((z,t) \in(0,L)\times(0,\infty)\) are the space (m) and time (s) coordinates, respectively, L is the length of the pipe, \(H(z,t)\) is the pressure head (m), \(Q(z,t)\) is the flow rate (m3/s), b is the wave speed in the fluid (m/s), g is the gravitational acceleration (m/s2), \(A_{r}\) is the cross-sectional area of the pipe (m2), ϕ is the inside diameter of the pipe (m), and f is the Darcy-Weisbach friction factor.

In this work, the initial conditions expressing the spatial profiles of \(Q(z,t)\) and \(H(z,t)\) at the instant \(t=0\) are denoted \(H(z,0)={{H}^{0}}(z)\), \(Q(z,0)={{Q}^{0}}(z)\); and the following Dirichlet conditions can be imposed at the boundaries of the pipeline: (i) upstream pressure head, \(H(0,t)={{H}_{\mathrm{in}}(t)}\), (ii) downstream pressure head, \(H(L,t)={{H}_{\mathrm{out}}(t)}\), (iii) upstream flow rate, \(Q ( 0,t )={{Q}_{\mathrm{in}}(t)}\) and (iv) downstream flow rate, \(Q ( L,t )={{Q}_{\mathrm{out}}(t)}\).

3.1 Linearized version of the water hammer equations

In [45] and [46], Eq. (7) and Eq. (8) were linearized for using two common procedures in making flow studies: the impedance approach and the matrix method, which utilize transfer functions for the pressure and flow. Such a linear version of equations (7) and (8) is given as follows:

$$\begin{aligned}& \frac{\partial h(z,t)}{\partial z} +\frac {1}{A_{r}}\frac{\partial q(z,t)}{\partial t}+ \frac{fq_{0}}{2g\phi A_{r}^{2}}q(z,t)=0, \end{aligned}$$
(9)
$$\begin{aligned}& \frac{\partial q(z,t)}{\partial z} +\frac {gA_{r}}{b^{2}}\frac{\partial h(z,t)}{\partial t}=0, \end{aligned}$$
(10)

where \(q_{0}\) and \(h_{0}\) are the flow and pressure in equilibrium, \(q(z,t)\) and \(h(z,t)\) are the flow rate and pressure head around the equilibrium \((q_{0},h_{0})\), respectively. The physical parameters of the pipeline can be redefined in terms of electrical parameters as follows:

$$ \mathcal{L}=\frac{1}{gA_{r}}, \qquad \mathcal{C}= \frac{gA_{r}}{b^{2}},\qquad \mathcal {R}=\frac{fq_{0}}{g\phi A_{r}^{2}}, $$
(11)

such that Eq. (9) and Eq. (10) can be rewritten as

$$\begin{aligned}& \frac{\partial h(z,t)}{\partial z} +\mathcal {L}\frac{\partial q(z,t)}{\partial t}+ \mathcal{R}q(z,t)=0, \end{aligned}$$
(12)
$$\begin{aligned}& \frac{\partial q(z,t)}{\partial z} +\mathcal{C}\frac{\partial h(z,t)}{\partial t}=0. \end{aligned}$$
(13)

Notice that Eq. (12) and Eq. (13) are the telegrapher equations without the admittance term \(\mathcal{G}\). In a pipeline, the meaning of this admittance term is distributed outflow. Hence, the following equations represent a pipeline with outflow:

$$\begin{aligned}& \frac{\partial h(z,t)}{\partial z} +\mathcal{L}\frac{\partial q(z,t)}{\partial t}+ \mathcal{R}q(z,t)=0, \end{aligned}$$
(14)
$$\begin{aligned}& \frac{\partial q(z,t)}{\partial z} +\mathcal{C}\frac{\partial h(z,t)}{\partial t}+ \mathcal{G}h(z,t)=0. \end{aligned}$$
(15)

3.2 Liénard model of a fluid transmission line (integer order)

By differentiating equations (12) and (13) and applying some algebraic manipulation, we obtain a pair of hyperbolic partial differential equations that involve only one variable

$$\begin{aligned}& \frac{\partial^{2}h(z,t)}{\partial z^{2}}=\mathcal{LC}\frac{\partial ^{2}h(z,t)}{\partial t^{2}}+(\mathcal{RC}+ \mathcal{GL})\frac{\partial h(z,t)}{\partial t}+\mathcal{GR}h(z,t), \end{aligned}$$
(16)
$$\begin{aligned}& \frac{\partial^{2}q(z,t)}{\partial z^{2}}=\mathcal{LC}\frac{\partial ^{2}q(z,t)}{\partial t^{2}}+(\mathcal{RC}+ \mathcal{GL})\frac{\partial q(z,t)}{\partial t}+\mathcal{GR}q(z,t). \end{aligned}$$
(17)

Either using the Liénard transform in terms of the flow

$$ \Phi:\bigl( \textstyle\begin{array}{@{}c@{\quad}c@{}} x_{1}(t)&x_{2}(t) \end{array}\displaystyle \bigr) \rightarrow\bigl( \textstyle\begin{array}{@{}c@{\quad}c@{}} q(z,t)&\dot{q}(z,t)+F(q(z,t)) \end{array}\displaystyle \bigr), $$
(18)

or in terms of the pressure head

$$ \Phi:\bigl( \textstyle\begin{array}{@{}c@{\quad}c@{}} x_{1}(t)&x_{2}(t) \end{array}\displaystyle \bigr) \rightarrow\bigl( \textstyle\begin{array}{@{}c@{\quad}c@{}} h(z,t)&\dot{h}(z,t)+F(h(z,t)) \end{array}\displaystyle \bigr), $$
(19)

the couple of equations (12) and (13) becomes

$$ \begin{aligned} &\frac{\partial x_{1}(z,t)}{\partial t}=x_{2}(z,t)- \biggl( \frac{\mathcal {RC}+\mathcal{GL}}{\mathcal{LC}} \biggr)x_{1}(z,t), \\ &\frac{\partial x_{2}(z,t)}{\partial t}=- \biggl(\frac{\mathcal {GR}}{\mathcal{LC}} \biggr)x_{1}(z,t)+ \biggl(\frac{1}{\mathcal{LC}} \biggr)\frac{\partial^{2}x_{1}(z,t)}{\partial z^{2}}. \end{aligned} $$
(20)

4 Liénard model of a fluid transmission line (fractional order)

The CF fractional operator is defined as follows [19, 20]:

$$ {}_{0}^{\mathrm{CF}}\mathcal{D}_{t}^{\alpha}f (t )= \frac{1}{1-\alpha } \int_{0}^{t}f ' (\tau )\exp \biggl(- \frac{\alpha (t-\tau )}{1-\alpha} \biggr)\, d\tau,\quad 0< \alpha\leq1, $$
(21)

where \({}_{0}^{\mathrm{CF}}\mathcal{D}_{t}^{\alpha}f (t )\) is the CF fractional operator with respect to t, \(M (\alpha )\) is a normalization function, such that \(M(0)=M(1)=1\); in this definition, the derivative of a constant is equal to zero, but unlike the usual Caputo definition [14], the kernel does not have a singularity at \(t=\tau\).

The Laplace transform (\(\mathscr{L}\)) of this novel definition (21) is defined as follows [19, 20]:

$$\begin{aligned} \mathscr{L} \bigl[{}_{0}^{\mathrm{CF}}\mathcal{D}_{t}^{ (\alpha+n )}f (t ) \bigr] & =\frac{1}{1-\alpha}\mathscr{L} \bigl[f^{ (\alpha +n )} (t ) \bigr] \mathscr{L} \biggl[\exp \biggl(-\frac{\alpha }{\alpha-1} t \biggr) \biggr] \\ & =\frac{s^{n+1}\mathscr{L} [f (t ) ]-s^{n}f (0 )-s^{n-1}f' (0 )-\cdots-f^{ (n )} (0 )}{s+\alpha (1-s )}. \end{aligned}$$
(22)

From this expression we have

$$ \begin{aligned} &\mathscr{L} \bigl[{}_{0}^{\mathrm{CF}} \mathcal{D}_{t}^{\alpha}f (t ) \bigr] =\frac{s\mathscr{L} [f (t ) ]-f (0 )}{s+\alpha (1-s )}, \quad n=0, \\ &\mathscr{L} \bigl[{}_{0}^{\mathrm{CF}}\mathcal{D}_{t}^{ (\alpha+1 )}f (t ) \bigr] =\frac{s^{2}\mathscr{L} [f (t ) ]-sf (0 )-f' (0 )}{s+\alpha (1-s )},\quad n=1. \end{aligned} $$
(23)

4.1 Description of the LHAM

An alternative procedure for constructing fractional differential equation was reported in [47], and successfully applied in [6–10]. In this context, to keep the dimensionality of the fractional differential equation a new parameter σ is introduced in the following way:

$$ \frac{d }{d t} \to\frac{1}{\sigma^{1 - \alpha}}\cdot{{}^{\mathrm{CF}}_{0}} { \mathcal{D}}_{t}^{\alpha}, \quad m - 1 < \alpha \leq m, m \in M=1,2,3,\ldots , $$
(24)

and

$$ \frac{d^{2} }{d t^{2}} \to\frac{1}{\sigma^{2(1 - \alpha)}}\cdot{{}^{\mathrm{CF}}_{0}} { \mathcal{D}}_{t}^{2\alpha},\quad m - 1 < \alpha \leq m, m \in M=1,2,3,\ldots , $$
(25)

where α represents the order of the fractional temporal operator and σ has the dimension of seconds, this auxiliary parameter is associated with the temporal components in the system (these components change the time constant of the system) [47]. In this context, the authors of [48] used the Planck time, \(t_{p}=5.39106\times10^{-44}\) seconds, with the finality to preserve the dimensional compatibility. Following [48] the σ parameter corresponds to the \(t_{p}\) in our calculations. For the case \(\alpha= 1\) the expressions (24) and (25) become ordinary temporal operators. Following this idea, we consider the following coupled linear fractional partial differential equations:

$$ \begin{aligned} &{{}^{\mathrm{CF}}_{0}} { \mathcal{D}}_{t}^{\alpha}x_{1} (z,t )-t_{p}^{1-\alpha}x_{2} (z,t )+t_{p}^{1-\alpha} \biggl(\frac {\mathcal{RC}+\mathcal{GL}}{\mathcal {LC}} \biggr)x_{1} (z,t )=0, \\ &{{}^{\mathrm{CF}}_{0}} {\mathcal{D}}_{t}^{\alpha}x_{2} (z,t )+t_{p}^{1-\alpha} \biggl(\frac{\mathcal{RG }}{\mathcal{LC}} \biggr)x_{1} (z,t )-t_{p}^{1-\alpha} \biggl( \frac{1}{\mathcal{LC}} \biggr)\frac {\partial^{2}x_{1} (z,t )}{\partial z^{2}}=0, \end{aligned} $$
(26)

with the initial conditions

$$ \frac{\partial^{k}x_{i} (z,0 )}{\partial t^{k}}=x_{i,k} (z,0 ) , \quad k=0,1,\ldots,n-1 , $$
(27)

and the boundary conditions

$$ x_{i} (0,t )=x_{i,0} (t ) ,\quad t\geq0. $$
(28)

The Laplace transform satisfies

$$ \mathscr{L} \bigl[{{}^{\mathrm{CF}}_{0}} {\mathcal{D}}_{t}^{\alpha}f(t) \bigr] (s )=\frac{1}{ (s+\alpha (1-s ) )} \bigl(s\mathscr {L} \bigl[f(t) \bigr] (s )-f (0 ) \bigr), \quad s>0, $$
(29)

we can define \(\Phi (x,s )=L [f(x,t) ] (s )\), for equation (26), we can write

$$\begin{aligned}& X_{1} (z,s ) =\mathscr{L} \bigl[x_{1}(z,t) \bigr] (s ) \\& \hphantom{X_{1} (z,s )}=\frac{x_{1} (z,0 )}{s} + (t_{p} )^{1-\alpha} \biggl(\frac{ (s+\alpha (1-s ) )}{s} \biggr) \biggl[X_{2} (z,s )- \biggl(\frac {\mathcal{RC}+\mathcal{GL}}{\mathcal{LC}} \biggr)X_{1} (z,s ) \biggr], \end{aligned}$$
(30)
$$\begin{aligned}& X_{2} (z,s )=\mathscr{L} \bigl[x_{2}(z,t) \bigr] (s ) \\& \hphantom{X_{2} (z,s )}=\frac{x_{2} (z,0 )}{s} + (t_{p} )^{1-\alpha} \biggl(\frac{ (s+\alpha (1-s ) )}{s} \biggr) \biggl[ \biggl(\frac{\mathcal{RG}}{\mathcal{LC}} \biggr)+ \biggl(\frac{1}{\mathcal {LC}} \biggr)\frac{\partial^{2}}{\partial z^{2}} \biggr]X_{1} (z,s ). \end{aligned}$$
(31)

According to LHAM, we construct the homotopy for Eq. (30) as follows:

$$ \begin{aligned} &X_{1} (z,s )=\frac{x_{1} (z,0 )}{s}+p (t_{p} )^{1-\alpha} \biggl(\frac{ (s+\alpha (1-s ) )}{s} \biggr) \biggl[X_{2} (z,s )- \biggl(\frac{\mathcal {RC}+\mathcal{GL}}{\mathcal{LC}} \biggr)X_{1} (z,s ) \biggr], \\ &X_{2} (z,s )=\frac{x_{2} (z,0 )}{s}+p (t_{p} )^{1-\alpha} \biggl(\frac{ (s+\alpha (1-s ) )}{s} \biggr) \biggl[ \biggl(\frac{\mathcal{RG}}{\mathcal{LC}} \biggr)+ \biggl(\frac{1}{\mathcal{LC}} \biggr)\frac{\partial^{2}}{\partial z^{2}} \biggr]X_{1} (z,s ), \end{aligned} $$
(32)

where \(X_{i} (z,s )\) denote the Laplace transform of \(x_{i} (z,t )\).

Applying the LHAM to obtain the solution of Eq. (32), we can start by the hypothesis that the solution \(\Phi (x,z )\) is expressed as

$$ X_{i} (z,s )=\sum_{j=0}^{\infty}p^{j}X_{i , j} (z,s ) , $$
(33)

where \(X_{i j} (z,s )\), \(j=0,1,2,\ldots\) , are the unknown functions. Substituting (33) into (32), we get

$$ \begin{aligned} &\sum_{j=0}^{\infty}p^{j}X_{1,j} (z,s ) \\ &\quad =\frac{x_{1} (z,0 )}{s}+p (t_{p} )^{1-\alpha} \biggl( \frac{ (s+\alpha (1-s ) )}{s} \biggr) \\ &\qquad {}\times\Biggl[\sum_{j=0}^{\infty}p^{j}X_{2,j} (z,s )- \biggl(\frac{\mathcal{RC} +\mathcal{GL}}{\mathcal{LC}} \biggr)\sum_{j=0}^{\infty}p^{j}X_{1,j} (z,s ) \Biggr], \\ &\sum_{j=0}^{\infty}p^{j}X_{2,j} (z,s ) \\ &\quad =\frac{x_{2} (z,0 )}{s}+p (t_{p} )^{1-\alpha } \biggl( \frac{ (s+\alpha (1-s ) )}{s} \biggr) \\ &\qquad {}\times\biggl[ \biggl(\frac{\mathcal{RG}}{\mathcal{LC}} \biggr)+ \biggl( \frac{1}{\mathcal{LC}} \biggr)\frac{\partial^{2}}{\partial z^{2}} \biggr]\sum _{j=0}^{\infty}p^{j}X_{1,j} (z,s ), \end{aligned} $$
(34)

which, on comparing the coefficients of powers of p, yields

$$\begin{aligned}& p^{0}: X_{1,0} (z,s ) =\frac{x_{1} (z,0 )}{s}, \\& \hphantom{p^{0}:{}} X_{2,0} (z,s ) =\frac{x_{2} (z,0 )}{s}, \\& p^{1}: X_{1,1} (z,s ) = (t_{p} )^{1-\alpha} \biggl(\frac{ (s+\alpha (1-s ) )}{s} \biggr) \biggl[X_{2,0} (z,s )- \biggl( \frac{\mathcal{RC}+\mathcal {GL}}{\mathcal{LC}} \biggr)X_{1,0} (z,s ) \biggr], \\& \hphantom{p^{1}:{}} X_{2,1} (z,s ) = (t_{p} )^{1-\alpha} \biggl(\frac { (s+\alpha (1-s ) )}{s} \biggr) \biggl[ \biggl(\frac {\mathcal{RG}}{\mathcal{LC}} \biggr)+ \biggl(\frac {1}{\mathcal{LC}} \biggr)\frac{\partial^{2}}{\partial z^{2}} \biggr]X_{1,0} (z,s ), \\& \ldots, \\& p^{n+1}: X_{1, n+1} (z,s ) = (t_{p} )^{1-\alpha } \biggl(\frac{ (s+\alpha (1-s ) )}{s} \biggr) \biggl[X_{2, n} (z,s )- \biggl( \frac{\mathcal{RC}+\mathcal {GL}}{\mathcal{LC}} \biggr)X_{1, n} (z,s ) \biggr], \\& \hphantom{p^{n+1}:{}} X_{2, n+1} (z,s ), = (t_{p} )^{1-\alpha} \biggl(\frac{ (s+\alpha (1-s ) )}{s} \biggr) \biggl[ \biggl(\frac {\mathcal{RG}}{\mathcal{LC}} \biggr)+ \biggl(\frac {1}{\mathcal{LC}} \biggr)\frac{\partial^{2}}{\partial z^{2}} \biggr]X_{1, n} (z,s ). \end{aligned}$$
(35)

In the limit \(p\rightarrow1\), we note that (35) becomes the approximate solution for the problem of (26)-(27) and is given by

$$ \begin{aligned} &H_{1, n} (z,s )= \sum_{i=0}^{n}X_{1, n} (z,s ), \\ &H_{2, n} (z,s )= \sum_{i=0}^{n}X_{2, n} (z,s ). \end{aligned} $$
(36)

Taking the inverse Laplace transform of (36), we obtain

$$ \begin{aligned} &x_{1} (z,t )\approx \mathscr{L}^{-1} \bigl[H_{1 ,n} (z,s ) \bigr] , \\ &x_{2} (z,t )\approx \mathscr{L}^{-1} \bigl[H_{2 ,n} (z,s ) \bigr]. \end{aligned} $$
(37)

5 Applications

Consider the coupled linear fractional partial differential equation (26) with initial condition

$$ \begin{aligned} &x_{1} (z,0 ) = \biggl(\frac{2\sqrt{\mathcal{LC}} (\mathcal{CR}+\mathcal{GL} )}{ (\mathcal{CR}-\mathcal{GL} )} \biggr)\sin \biggl(\frac{ (\mathcal{CR}-\mathcal{GL} )}{2\sqrt{\mathcal{LC}}}z \biggr), \\ &x_{2} (z,0 ) = \biggl(\frac{ (\mathcal{CR}+\mathcal{GL} )}{\sqrt{\mathcal{LC}} (\mathcal{CR}-\mathcal{GL} )} \biggr)\sin \biggl( \frac{ (\mathcal{CR}-\mathcal{GL} )}{2\sqrt{\mathcal{LC}}}z \biggr), \end{aligned} $$
(38)

the exact solution of the given problem (26) is given by

$$\begin{aligned}& \begin{aligned} &x_{1} (z,t )= \biggl(\frac{4\sqrt{ (\mathcal{L C} )^{3}}t_{p}^{\alpha}\exp (\frac{ (\mathcal{CR}+\mathcal{GL} )t\alpha t_{p}}{ (-2\mathcal {LC}t_{p}^{\alpha}+(-1+\alpha)t_{p} (\mathcal{GL}+\mathcal{CR} ) )} )}{ (2\mathcal {LC}t_{p}^{\alpha}-(-1+\alpha) (\mathcal{GL}+\mathcal{CR} )t_{p} ) (\mathcal {CR}-\mathcal{GL} )} \biggr) \\ &\hphantom{x_{1} (z,t )={}}{}\times\sin \biggl(\frac { (\mathcal{CR}-\mathcal{GL} )}{2\sqrt {\mathcal{LC}}}z \biggr), \\ &x_{2} (z,t ) = \biggl(\frac{2\sqrt{\mathcal{LC}} t_{p}^{\alpha} (\mathcal{CR}+\mathcal{GL} )\exp (\frac{ (\mathcal{CR}+\mathcal {GL} )t\alpha t_{p}}{ (-2\mathcal{LC}t_{p}^{\alpha}+(-1+\alpha)t_{p} (\mathcal{GL}+\mathcal {CR} ) )} )}{ (2\mathcal{LC}t_{p}^{\alpha}-(-1+\alpha) (\mathcal{GL}+\mathcal {CR} )t_{p} ) (\mathcal{CR}-\mathcal{GL} )} \biggr) \\ &\hphantom{x_{2} (z,t ) ={}}{}\times\sin \biggl( \frac{ (\mathcal{CR}-\mathcal{GL} )}{2\sqrt {\mathcal{LC}}}z \biggr), \end{aligned} \end{aligned}$$
(39)
$$\begin{aligned}& X_{i,j} (z,s )=L \bigl[x_{i,j} (z,t ) \bigr]=0 , \end{aligned}$$
(40)

therefore we can apply the LHAM method, which yields

$$\begin{aligned}& p^{1}: X_{1,0} (z,s ) =\mathscr{L} \bigl[x_{1} (z,0 ) \bigr], \\& p^{1}: X_{2,0} (z,s ) =\mathscr{L} \bigl[x_{2} (z,0 ) \bigr], \\& p^{1}: X_{1,1} (z,t ) =\mathscr{L}^{-1} \biggl[ (t_{p} )^{1-\alpha} \biggl(\frac{ (s+\alpha (1-s ) )}{s} \biggr) \biggl[X_{2,0} (z,s )- \biggl(\frac{\mathcal{RC}+\mathcal{GL}}{\mathcal{LC}} \biggr)X_{1,0} (z,s ) \biggr] \biggr] \\& \hphantom{p^{1}: X_{1,1} (z,t )}= \biggl(\frac{t_{p}^{1-\alpha} (\mathcal{CR}+\mathcal {GL} ) (1+(-1+t)\alpha )}{\sqrt{\mathcal{L C}} (\mathcal{GL}-\mathcal{CR} )} \biggr)\sin \biggl( \frac { (\mathcal{CR}-\mathcal{GL} )}{2\sqrt {\mathcal{LC}}}z \biggr), \\& \hphantom{p^{1}:{}}X_{2,1} (z,t ) =\mathscr{L}^{-1} \biggl[ (t_{p} )^{1-\alpha} \biggl(\frac{ (s+\alpha (1-s ) )}{s} \biggr) \biggl[ \biggl( \frac{\mathcal{RG}}{\mathcal{LC}} \biggr)+ \biggl(\frac{1}{\mathcal{LC}} \biggr)\frac{\partial ^{2}}{\partial z^{2}} \biggr]X_{1,0} (z,s ) \biggr] \\& \hphantom{p^{1}: X_{2,1} (z,t )}= \biggl(\frac{t_{p}^{1-\alpha} (\mathcal{CR}+\mathcal{GL} )^{2} (1+(-1+t)\alpha )}{2\sqrt{ (\mathcal{LC} )^{3}} (\mathcal{GL}-\mathcal{CR} )} \biggr)\sin \biggl( \frac { (\mathcal{CR}-\mathcal{GL} )}{2\sqrt {\mathcal{LC}}}z \biggr), \\& p^{1}: X_{1,2} (z,t ) =\mathscr{L}^{-1} \biggl[ (t_{p} )^{1-\alpha} \biggl(\frac{ (s+\alpha (1-s ) )}{s} \biggr) \biggl[X_{2,1} (z,s )- \biggl(\frac{\mathcal{RC}+\mathcal{GL}}{\mathcal{LC}} \biggr)X_{1,1} (z,s ) \biggr] \biggr] \\& \hphantom{p^{1}: X_{1,2} (z,t )}=- \biggl(\frac{t_{p}^{2-2\alpha} (\mathcal{CR}+\mathcal{GL} )^{2} (2+4(-1+t)\alpha+(2+ (-4+t )t)\alpha^{2} )}{4\sqrt{ (\mathcal{LC} )^{3}} (\mathcal {GL}-\mathcal{CR} )} \biggr) \\& \hphantom{p^{1}: X_{1,2} (z,t )={}}{}\times\sin \biggl( \frac{ (\mathcal{CR}-\mathcal{GL} )}{2\sqrt{\mathcal{LC}}}z \biggr), \\& \hphantom{p^{1}:{}}X_{2,2} (z,t ) =\mathscr{L}^{-1} \biggl[ (t_{p} )^{1-\alpha} \biggl(\frac{ (s+\alpha (1-s ) )}{s} \biggr) \biggl[ \biggl(\frac{\mathcal{RG}}{\mathcal{LC}} \biggr)+ \biggl(\frac{1}{\mathcal{LC}} \biggr) \frac{\partial ^{2}}{\partial z^{2}} \biggr]X_{1,1} (z,s ) \biggr] \\& \hphantom{p^{1}:: X_{1,2} (z,t )}=- \biggl(\frac{t_{p}^{2-2\alpha} (\mathcal{CR}+\mathcal{GL} )^{3} (2+4(-1+t)\alpha+(2+ (-4+t )t)\alpha^{2} )}{8\sqrt{ (\mathcal{LC} )^{5}} (\mathcal {GL}-\mathcal{CR} )} \biggr) \\& \hphantom{p^{1}:: X_{1,2} (z,t )={}}{}\times\sin \biggl( \frac{ (\mathcal{CR}-\mathcal{GL} )}{2\sqrt{\mathcal{LC}}}z \biggr), \\& \ldots \end{aligned}$$
(41)

and so on. Here \(X_{i,j}(z,s)=\mathscr{L} [x_{i,j} (z,t ) ]\) are the Laplace transforms of the approximated solution \(x_{i,j} (z,t )\). By (36), we get

$$ \begin{aligned} &x_{1,n} (z,t )=\sum _{i=0}^{n}X_{1,i} (z,t ) \\ &\hphantom{x_{1,n} (z,t )} = \biggl[ - \biggl(\frac{2\sqrt{\mathcal{LC}} (\mathcal{CR}+\mathcal {GL} )}{ (\mathcal{GL}-\mathcal{CR} )} \biggr) + \biggl( \frac{t_{p}^{1-\alpha} (\mathcal{CR}+\mathcal {GL} ) (1+(-1+t)\alpha )}{\sqrt{\mathcal{LC}} (\mathcal{GL}-\mathcal{CR} )} \biggr) \\ &\hphantom{x_{1,n} (z,t )={}}{}- \biggl(\frac{t_{p}^{2-2\alpha} (\mathcal{CR}+\mathcal{GL} )^{2} (2+4(-1+t)\alpha+(2+ (-4+t )t)\alpha^{2} )}{4\sqrt{ (\mathcal{LC} )^{3}} (\mathcal {GL}-\mathcal{CR} )} \biggr) \biggr] \\ &\hphantom{x_{1,n} (z,t )={}}{}\times\sin \biggl( \frac{ (\mathcal{CR}-\mathcal{GL} )}{2\sqrt{\mathcal{LC}}}z \biggr)+\cdots, \\ &x_{2,n} (z,t )=\sum_{i=0}^{n}X_{2,i} (z,t ) \\ &\hphantom{x_{2,n} (z,t )}= \biggl[ - \biggl(\frac{ (\mathcal{CR}+\mathcal{GL} )}{\sqrt{\mathcal{LC}} (\mathcal{GL}-\mathcal {CR} )} \biggr) + \biggl( \frac{t_{p}^{1-\alpha} (\mathcal{CR}+\mathcal{GL} )^{2} (1+(-1+t)\alpha )}{2\sqrt{ (\mathcal{LC} )^{3}} (\mathcal{GL}-\mathcal{CR} )} \biggr) \\ &\hphantom{x_{2,n} (z,t )={}}{}- \biggl(\frac{t_{p}^{2-2\alpha} (\mathcal{CR}+\mathcal{GL} )^{3} (2+4(-1+t)\alpha+(2+ (-4+t )t)\alpha^{2} )}{8\sqrt{ (\mathcal{LC} )^{5}} (\mathcal {GL}-\mathcal{CR} )} \biggr) \biggr] \\ &\hphantom{x_{2,n} (z,t )={}}{}\times\sin \biggl( \frac{ (\mathcal{CR}-\mathcal{GL} )}{2\sqrt{\mathcal{LC}}}z \biggr)+\cdots, \end{aligned} $$
(42)

which, on taking the limit \(n\rightarrow\infty\), yields

$$ \begin{aligned} &x_{1} (z,t )=\lim_{n\rightarrow\infty}x_{1,n} (z,t )=\lim_{n\rightarrow\infty}\sum_{i=0}^{n}X_{1,i} (z,t ) \\ &\hphantom{x_{1} (z,t )}= \biggl(\frac{4\sqrt{ (\mathcal{LC} )^{3}}t_{p}^{\alpha}\exp (\frac{ (\mathcal{CR}+\mathcal{GL} )t\alpha t_{p}}{ (-2\mathcal {LC}t_{p}^{\alpha}+(-1+\alpha)t_{p} (\mathcal{GL}+\mathcal{CR} ) )} )}{ (2\mathcal {LC}t_{p}^{\alpha}-(-1+\alpha) (\mathcal{GL}+\mathcal{CR} )t_{p} ) (\mathcal {CR}-\mathcal{GL} )} \biggr) \\ &\hphantom{x_{1} (z,t )={}}{}\times\sin \biggl( \frac { (\mathcal{CR}-\mathcal{GL} )}{2\sqrt {\mathcal{LC}}}z \biggr), \\ &x_{2} (z,t )=\lim_{n\rightarrow\infty}x_{2,n} (z,t )= \lim_{n\rightarrow\infty}\sum_{i=0}^{n}X_{2,i} (z,t ) \\ &\hphantom{x_{2} (z,t )}= \biggl(\frac{2\sqrt{\mathcal{LC}} t_{p}^{\alpha} (\mathcal {CR}+\mathcal{GL} )\exp (\frac{ (\mathcal{CR}+\mathcal{GL} )t\alpha t_{p}}{ (-2\mathcal{LC}t_{p}^{\alpha}+(-1+\alpha )t_{p} (\mathcal{GL}+\mathcal{CR} ) )} )}{ (2\mathcal{LC}t_{p}^{\alpha }-(-1+\alpha) (\mathcal{GL}+\mathcal{CR} )t_{p} ) (\mathcal{CR}-\mathcal {GL} )} \biggr) \\ &\hphantom{x_{2} (z,t )={}}{}\times\sin \biggl( \frac{ (\mathcal{CR}-\mathcal{GL} )}{2\sqrt{\mathcal{L C}}}z \biggr), \end{aligned} $$
(43)

where these functions \(x_{1} (z,t )\) and \(x_{2} (z,t ) \) are the analytical solutions (39) to the original problem (26).

5.1 Analysis of the limit case \(\alpha=1\)

Consider the limit of the coupled linear fractional partial differential (26) equation when \(\alpha=1\) (classical case), i.e.

$$ \begin{aligned} &\frac{\partial x_{1} (z,t )}{\partial t}-x_{2} (z,t )+ \biggl( \frac{\mathcal{RC}+\mathcal{GL}}{\mathcal{LC}} \biggr)x_{1} (z,t )=0, \\ &\frac{\partial x_{2} (z,t )}{\partial t}+ \biggl(\frac {\mathcal{RG}}{\mathcal{LC}} \biggr)x_{1} (z,t )- \biggl(\frac{1}{\mathcal{LC}} \biggr)\frac {\partial^{2}x_{1} (z,t )}{\partial z^{2}}=0 , \end{aligned} $$
(44)

if we take the limit \(\alpha=1\) in the exact solutions (43) we obtain the following solutions:

$$ \begin{aligned} &x_{1} (z,t )= \biggl(\frac{2\sqrt{\mathcal{LC}}\exp (-\frac{ (\mathcal{CR} +\mathcal{GL} )t}{2\mathcal{LC}} )}{ (\mathcal {CR}-\mathcal{GL} )} \biggr)\sin \biggl(\frac{ (\mathcal {CR}-\mathcal{GL} )}{2\sqrt{\mathcal{LC}}}z \biggr), \\ &x_{2} (z,t )= \biggl(\frac{ (\mathcal{CR}+\mathcal {GL} )\exp (-\frac{ (\mathcal{CR}+\mathcal {GL} )t}{2\mathcal{LC}} )}{\sqrt {\mathcal{LC}} (\mathcal{CR}-\mathcal{GL} )} \biggr)\sin \biggl( \frac{ (\mathcal{CR}-\mathcal{GL} )}{2\sqrt{\mathcal {LC}}}z \biggr), \end{aligned} $$
(45)

which are actually the correct solutions to the coupled equation (44).

5.2 Simulation and comparison of the models

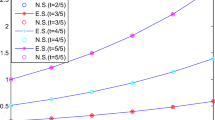
Table 1 shows the physical parameters considered in the simulations.

Table 1 Physical parameters
Full size table

Figures 1(a) and 1(b) show the numerical simulations for the approximate and exact solutions for arbitrarily chosen α values.

Figure 1
figure 1

Numerical simulations for the approximate and exact solutions.

Full size image

6 Conclusions

The Liénard equation is used in many fields of science for representing the dynamical behavior of physical systems. For this reason it is very important to analyze its solutions under different conditions as well as explore different ways to solve it. In this article, we presented the procedure to solve a Liénard equation by using the Laplace homotopy analysis method using a new fractional derivative without singular kernel. In particular, this equation represents the fluid dynamics of a pipeline. The solution obtained by the aforementioned method is valid for the equation governed by both integer and fractional derivatives.

This results may relate to, or may be extended to relate to a class of fractional oscillators based on fractional Langevin equation, which have interesting behavior in the locations of the characteristic [49] as well as roots stability [50].