1 Introduction

In order to understand the Human Immunodeficiency Virus (HIV) dynamics within-host and the drug therapy strategies, many mathematical models have been constructed and developed (see [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]). Some of these models assume that HIV infects one category of target cells, that is, CD4+ T cells [1, 29, 40]. Among these models, the basic model which has been developed by Nowak and Bangham [1] is considered the most popular. The model is a three-dimensional system of ODEs which characterize the interaction between HIV (v), uninfected CD4+ T cells (x), and infected CD4+ T cells (u). Other HIV dynamics models assume that HIV has categories of target cells, CD4+ T cells and macrophages [30,31,32,33,34,35,36,37,38,39,40]. The basic model describing the HIV interaction with two categories of target cells is presented in [30] and [32] as:

$$\begin{aligned} &\dot{x}_{1}(t) =\lambda_{1}-d_{1}x_{1}(t)- \beta_{1}x_{1}(t)v(t), \end{aligned}$$
(1)
$$\begin{aligned} &\dot{u}_{1}(t) =\beta_{1}x_{1}(t)v(t)- \mu_{1}u_{1}(t), \end{aligned}$$
(2)
$$\begin{aligned} &\dot{x}_{2}(t) =\lambda_{2}-d_{2}x_{2}(t)- \beta_{2}x_{2}(t)v(t), \end{aligned}$$
(3)
$$\begin{aligned} &\dot{u}_{2}(t) =\beta_{2}x_{2}(t)v(t)- \mu_{2}u_{2}(t), \end{aligned}$$
(4)
$$\begin{aligned} &\dot{v}(t) =k_{1}u_{1}(t)+k_{2}u_{2}(t)-rv(t). \end{aligned}$$
(5)

The variables describe the concentrations of \(x_{i}\), the uninfected and infected cells and free HIV, respectively; \(i=1\) and \(i=2\) represent the CD4+ T cells and macrophages, respectively; \(\lambda_{i}\) represents the generation rate of the uninfected cells; \(d_{i}\) are the death rate constants; and \(\beta_{i}\) are the infection rate constants. Equations (2) and (4) represent the population dynamics of the activated infected cells and show that they die with the same constant rate \(\mu_{i}\). The HIV particles are generated from infected CD4+ T cells and infected macrophages at rates \(k_{1}u_{1}\) and \(k_{2}u_{2}\), respectively. The HIV particles are cleared at rate rv.

A lot of considerations have been added that aim to get the best representation of the HIV infection. Most notable are latent HIV reservoirs which serve as a major barrier in curing HIV infection. Despite the fact that the antiretroviral therapy significantly limits the level of HIV in the blood, there is still a low viral load due to ongoing reactivation of latent infected cells reservoirs. Variant models have been developed to study the dynamics of HIV in the presence of latent reservoirs (see, e.g., [23,24,25,26,27,28,29,30,31,32,33,34]).

Cytotoxic T Lymphocyte (CTL) cells play a prominent role in achieving the best representation of the HIV dynamics. CTL cells attack the HIV infected cells and hence try to eliminate or control the infection. The first mathematical model describing the interaction between CTL immune response and viral infection had been presented by Nowak and Bangham [1], since then many mathematical models have been presented to study the effect of CTL immune response on virus dynamics (see, e.g., [41,42,43,44]). However, it has been reported in [45] that during the infection, HIV causes an impairment in the CTL job. Virus dynamics models with CTL immune impairment have been studied in many papers (see, e.g., [45,46,47,48,49,50,51,52]). All the HIV dynamics models with CTL immune impairment presented in the literature consider one category of target cells, CD4+ T cells.

In the present paper we investigate the global stability of an HIV dynamics model with CTL immune impairment and two categories of target cells, CD4+ T cells and macrophages. The importance of considering such a model is due to the observation of Perleson el al. that after the rapid first phase of decay during the initial 1–2 weeks of an antiretroviral treatment, plasma virus levels declined at a considerably slower rate [31]. This second phase of viral decay was attributed to the turnover of a longer-lived virus reservoir of infected cell population. Therefore, the two target cells model is more accurate than the one target cell model, and then more accurate drug efficacy is determined when using the model with two classes of target cells. Moreover, a better understanding of the mechanisms behind this immune impairment in HIV infection may help to devise better therapeutic regimens and to identify patients more responsive to certain drugs [53]. We consider both latently and actively infected cells. We incorporate multiple discrete or distributed time delays to describe the time between the HIV contacts of target cells and the emission of new mature HIV particles. We study global stability of the two steady states of the model using Lyapunov method. The theoretical results are supported by numerical simulations.

2 HIV model with discrete delays

We study the following HIV model:

$$\begin{aligned} &\dot{x}_{1}(t) =\lambda_{1}-d_{1}x_{1}(t)- \beta_{1}x_{1}(t)v(t), \end{aligned}$$
(6)
$$\begin{aligned} &\dot{y}_{1}(t) =\rho_{1}\beta_{1}e^{-\alpha_{1}\tau_{1}}x_{1}(t- \tau _{1})v(t-\tau_{1})-ay_{1}(t)-\delta y_{1}(t), \end{aligned}$$
(7)
$$\begin{aligned} &\dot{u}_{1}(t) =(1-\rho_{1})\beta_{1}e^{-\alpha_{2}\tau_{2}}x_{1}(t- \tau_{2})v(t-\tau_{2})+\delta y_{1}(t)-pu_{1}(t)z(t)- \mu u_{1}(t), \end{aligned}$$
(8)
$$\begin{aligned} &\dot{x}_{2}(t) =\lambda_{2}-d_{2}x_{2}(t)- \beta_{2}x_{2}(t)v(t), \end{aligned}$$
(9)
$$\begin{aligned} &\dot{y}_{2}(t) =\rho_{2}\beta_{2}e^{-\alpha_{3}\tau_{3}}x_{2}(t- \tau _{3})v(t-\tau_{3})-ay_{2}(t)-\delta y_{2}(t), \end{aligned}$$
(10)
$$\begin{aligned} &\dot{u}_{2}(t) =(1-\rho_{2})\beta_{2}e^{-\alpha_{4}\tau_{4}}x_{2}(t- \tau_{4})v(t-\tau_{4})+\delta y_{2}(t)-pu_{2}(t)z(t)- \mu u_{2}(t), \end{aligned}$$
(11)
$$\begin{aligned} &\dot{v}(t) =ke^{-\alpha_{5}\tau_{5}} \bigl( u_{1}(t-\tau_{5})+u_{2}(t- \tau_{5}) \bigr) -rv(t), \end{aligned}$$
(12)
$$\begin{aligned} &\dot{z}(t) =c \bigl( u_{1}(t)+u_{2}(t) \bigr) -m \bigl( u_{1}(t)+u_{2}(t) \bigr) z(t)-bz(t). \end{aligned}$$
(13)

Here \(u_{i}\), \(y_{i}\) and z are the concentrations of the latent infected, actively infected and CTL cells, respectively. The fractions \(\rho_{i}\) and \(1-\rho_{i}\) with \(0<\rho_{i}<1\) where \(i=1,2\) are the probabilities that upon infection, uninfected cell will become either latently or actively infected. Equations (7) and (10) describe the population dynamics of the latent infected CD4+ T and macrophages cells and shows that they die with the same constant rate a and become active with constant rate \(\delta y_{i}\). The actively infected cells are removed by the CTL at rate \(pu_{i}z\). The CTLs are proliferated at the rate of \(c(u_{1}+u_{2})\) and decay at rate of bz. The term \(m ( u_{1}+u_{2} ) z\) represents the immune impairment rate. Here \(\tau_{1}\) and \(\tau_{3}\) are the times between HIV entry of CD4+ T cells and macrophages, respectively, to become latent infected; \(\tau_{2}\) and \(\tau_{4}\) are the times between HIV entry of CD4+ T cells and macrophages, respectively, to produce immature HIV. The immature HIVs need time \(\tau_{5}\) to become mature. The factors \(e^{-\alpha _{j}\tau_{j}}\), \(j=1,\dots,5\), represent the probability of surviving to the age of \(\tau_{i}\), where \(\alpha_{j}\) are positive constants.

To ensure the uniqueness of the solution of system (6)–(13), we take the following initial conditions [54]:

$$\begin{aligned} \begin{aligned} &x_{1}(\eta) =\omega_{1}(\eta),\qquad y_{1}(\eta)= \omega_{2}(\eta),\qquad u_{1}(\eta)= \omega_{3}(\eta),\\ & x_{2}(\eta)=\omega_{4}(\eta),\qquad y_{2}(\eta)=\omega _{5}(\eta),\qquad u_{2}(\eta)= \omega_{6}(\eta), \\ &v(\eta) =\omega_{7}(\eta), \qquad z(\eta)=\omega_{8}( \eta), \qquad\omega_{i}(\eta) \geq0,\quad \eta \in {}[-\kappa,0], i=1,\dots,8, \end{aligned} \end{aligned}$$
(14)

where \(\kappa=\max \{ \tau_{1},\tau_{2},\tau_{3},\tau_{4},\tau_{5}\}\), \((\omega_{1}(\eta),\dots,\omega_{8}(\eta))\in C([-\kappa,0],\mathbb{R}_{\geq 0}^{8})\), C is the Banach space of continuous functions mapping the interval \([-\kappa,0] \) into \(\mathbb{R}_{\geq0}\).

2.1 Nonnegativity and boundedness

Proposition 1

The solutions of system (6)–(13) are nonnegative and ultimately bounded.

Proof

From Eqs. (6)–(13) of the system, we have

$$\begin{aligned} &x_{i}(t) \geq \omega_{3i-2}(0)e^{-\int_{0}^{t} ( d_{i}+\beta _{i}v(s) ) \,ds},\quad i=1,2, \\ &y_{i}(t) \geq \omega_{3i-1}(0)e^{-(a+\delta)t},\quad i=1,2, \\ &u_{i}(t) \geq \omega_{3i}(0)e^{-\int_{0}^{t} ( \mu+pz(s) ) \,ds}, \quad i=1,2, \\ &v(t) \geq \omega_{7}(0)e^{-rt}, \\ &z(t) \geq \omega_{8}(0)e^{-\int_{0}^{t} ( m ( u_{1}(s)+u_{2}(s) ) +b ) \,ds}, \end{aligned}$$

therefore \(x_{i}(t),y_{i}(t),u_{i}(t),v(t)\),\(z(t)\geq0\) for all \(t\geq0\) and \(i=1,2\).

From Eqs. (6) and (9), we have sup\(_{t\rightarrow \infty}x_{i}(t)\leq \frac{\lambda_{i}}{d_{i}}\). Let us define

$$\begin{aligned} L_{1}(t) ={}&\rho_{1}e^{-\alpha_{1}\tau_{1}}x_{1}(t- \tau_{1})+ ( 1-\rho_{1} ) e^{-\alpha_{2}\tau_{2}}x_{1}(t- \tau_{2})+\rho_{2}e^{-\alpha_{3}\tau_{3}}x_{2}(t- \tau_{3}) \\ & {}+ ( 1-\rho_{2} ) e^{-\alpha_{4}\tau_{4}}x_{2}(t- \tau_{4})+y_{1}(t)+u_{1}(t)+y_{2}(t)+u_{2}(t)+ \frac{\mu}{2c}z(t). \end{aligned}$$

Then

$$\begin{aligned} \dot{L}_{1}(t) ={}&\rho_{1}e^{-\alpha_{1}\tau_{1}} \bigl[ \lambda_{1}-d_{1}x_{1}(t- \tau_{1})-\beta_{1}x_{1}(t-\tau_{1})v(t- \tau_{1}) \bigr] \\ &{} + ( 1-\rho_{1} ) e^{-\alpha_{2}\tau_{2}} \bigl[ \lambda _{1}-d_{1}x_{1}(t-\tau_{2})- \beta_{1}x_{1}(t-\tau_{2})v(t- \tau_{2}) \bigr] \\ &{} +\rho_{2}e^{-\alpha_{3}\tau_{3}} \bigl[ \lambda_{2}-d_{2}x_{2}(t- \tau _{3})-\beta_{2}x_{2}(t- \tau_{3})v(t- \tau_{3}) \bigr] \\ &{} + ( 1-\rho_{2} ) e^{-\alpha_{4}\tau_{4}} \bigl[ \lambda _{2}-d_{2}x_{2}(t-\tau_{4})- \beta_{2}x_{2}(t-\tau_{4})v(t- \tau_{4}) \bigr] \\ &{} +\rho_{1}\beta_{1}e^{-\alpha_{1}\tau_{1}}x_{1}(t- \tau_{1})v(t-\tau _{1})-ay_{1}(t)-\delta y_{1}(t) \\ &{} +(1-\rho_{1})\beta_{1}e^{-\alpha_{2}\tau_{2}}x_{1}(t- \tau_{2})v(t-\tau _{2})+\delta y_{1}(t)-pu_{1}(t)z(t)- \mu u_{1}(t) \\ &{} +\rho_{2}\beta_{2}e^{-\alpha_{3}\tau_{3}}x_{2}(t- \tau_{3})v(t-\tau _{3})-ay_{2}(t)-\delta y_{2}(t) \\ & {}+(1-\rho_{2})\beta_{2}e^{-\alpha_{4}\tau_{4}}x_{2}(t- \tau_{4})v(t-\tau _{4})+\delta y_{2}(t)-pu_{2}(t)z(t)- \mu u_{2}(t) \\ &{} +\frac{\mu}{2} \bigl( u_{1}(t)+u_{2}(t) \bigr) - \frac{\mu m}{2c} \bigl( u_{1}(t)+u_{2}(t) \bigr) z(t)- \frac{\mu b}{2c}z(t) \\ ={}&\rho_{1}e^{-\alpha_{1}\tau_{1}}\lambda_{1}+ ( 1- \rho_{1} ) e^{-\alpha_{2}\tau_{2}}\lambda_{1}+\rho_{2}e^{-\alpha_{3}\tau_{3}} \lambda _{2}+ ( 1-\rho_{2} ) e^{-\alpha_{4}\tau_{4}} \lambda_{2} \\ &{} - \biggl( p+\frac{\mu m}{2c} \biggr) \bigl( u_{1}(t)+u_{2}(t) \bigr) z(t)-\rho_{1}e^{-\alpha_{1}\tau_{1}}d_{1}x_{1}(t- \tau_{1})\\ &{}- ( 1-\rho _{1} ) e^{-\alpha_{2}\tau_{2}}d_{1}x_{1}(t- \tau_{2}) \\ & {}-\rho_{2}e^{-\alpha_{3}\tau_{3}}d_{2}x_{2}(t- \tau_{3})- ( 1-\rho _{2} ) e^{-\alpha_{4}\tau_{4}}d_{2}x_{2}(t- \tau_{4})-ay_{1}(t)-ay_{2}(t) \\ &{} -\frac{\mu}{2}u_{1}(t)-\frac{\mu}{2}u_{2}(t)- \frac{\mu b}{2c}z(t) \\ \leq{}& \lambda_{1}+\lambda_{2}-\delta_{1}L_{1}(t), \end{aligned}$$

\(\delta_{1}=\min \{d_{1},d_{2},a,\frac{\mu}{2},b\}\). Hence \(\limsup_{t\rightarrow \infty}L_{1}(t)\leq M_{1}\), \(\limsup_{t\rightarrow \infty }y_{i}(t)\leq M_{1}\), \(\limsup_{t\rightarrow \infty}u_{i}(t)\leq M_{1}\) and \(\limsup_{t\rightarrow \infty}z(t)\leq M_{2}\), for all \(t\geq0\) where \(i=1,2\), where, \(M_{1}=\frac{\lambda_{1}+\lambda_{2}}{\delta_{1}}\) and \(M_{2}=\frac{2c}{\mu}\). From Eq. (12) we have

$$\begin{aligned} \dot{v}(t) & =ke^{-\alpha_{5}\tau_{5}} \bigl( u_{1}(t-\tau_{5})+u_{2}(t- \tau_{5}) \bigr) -rv(t) \\ & \leq2kM_{1}-rv(t), \end{aligned}$$

which yields \(\limsup_{t\rightarrow \infty}v(t)\leq M_{3}\) where \(M_{3}=\frac{2kM_{1}}{r}\). □

2.2 Steady states

The basic reproduction number of system (6)–(13) is given as:

$$R_{0}=\frac{\delta k}{\mu r(a+\delta)} \bigl( \gamma_{1} \beta_{1}x_{1}^{0}+ \gamma_{2}\beta_{2}x_{2}^{0} \bigr), $$

where

$$\begin{aligned} &\gamma_{1} =\rho_{1}e^{-\alpha_{1}\tau_{1}-\alpha_{5}\tau_{5}}+ \frac{(a+\delta)}{\delta}(1-\rho_{1})e^{-\alpha_{2}\tau_{2}-\alpha_{5}\tau_{5}}, \\ &\gamma_{2} =\rho_{2}e^{-\alpha_{3}\tau_{3}-\alpha_{5}\tau_{5}}+ \frac{(a+\delta)}{\delta}(1-\rho_{2})e^{-\alpha_{4}\tau_{4}-\alpha_{5}\tau_{5}}, \\ & x_{1}^{0} =\frac{\lambda_{1}}{d_{1}}, \qquad x_{2}^{0}=\frac {\lambda_{2}}{d_{2}}. \end{aligned}$$

Lemma 1

For system (6)–(13) (i) if \(R_{0}\leq1\), then there exists an infection-free steady state \(E_{0}\), and (ii) if \(R_{0}>1\), then there exist two steady states, \(E_{0}\) and a chronic steady state \(E^{\ast}\).

Proof

The steady states of model (6)–(13) satisfy

$$\begin{aligned} &\lambda_{1}-d_{1}x_{1}-\beta_{1}x_{1}v =0, \end{aligned}$$
(15)
$$\begin{aligned} &\rho_{1}\beta_{1}e^{-\alpha_{1}\tau_{1}}x_{1}v-ay_{1}- \delta y_{1} =0, \end{aligned}$$
(16)
$$\begin{aligned} &(1-\rho_{1})\beta_{1}e^{-\alpha_{2}\tau_{2}}x_{1}v+ \delta y_{1}-pu_{1}z-\mu u_{1} =0, \end{aligned}$$
(17)
$$\begin{aligned} &\lambda_{2}-d_{2}x_{2}-\beta_{2}x_{2}v =0, \end{aligned}$$
(18)
$$\begin{aligned} &\rho_{2}\beta_{2}e^{-\alpha_{3}\tau_{3}}x_{2}v-ay_{2}- \delta y_{2} =0, \end{aligned}$$
(19)
$$\begin{aligned} &(1-\rho_{2})\beta_{2}e^{-\alpha_{4}\tau_{4}}x_{2}v+ \delta y_{2}-pu_{2}z-\mu u_{2} =0, \end{aligned}$$
(20)
$$\begin{aligned} &ke^{-\alpha_{5}\tau_{5}} ( u_{1}+u_{2} ) -rv =0, \end{aligned}$$
(21)
$$\begin{aligned} &c ( u_{1}+u_{2} ) -m ( u_{1}+u_{2} ) z-bz =0. \end{aligned}$$
(22)

One solution of Eqs. (15)–(22) yields an infection-free steady state \(E_{0}=(x_{1}^{0},0,0,x_{2}^{0},0,0, 0,0)\). Moreover, we have

$$A_{1}v^{3}+B_{1}v^{2}+C_{1}v+D_{1}=0, $$

where

$$\begin{aligned} &A_{1} =\beta_{1}\beta_{2} ( \mu m+pc ) r^{2}, \\ &B_{1} =\beta_{1}\beta_{2}\mu rbke^{-\alpha_{5}\tau_{5}}+ ( \beta _{1}d_{2}+\beta_{2}d_{1} ) ( \mu m+pc ) r^{2}-\frac {\beta_{1}\beta_{2}mr\delta k}{a+\delta} ( \lambda_{1} \gamma_{1}+\lambda_{2}\gamma_{2} ), \\ &C_{1} =\mu rbke^{-\alpha_{5}\tau_{5}} ( \beta_{1}d_{2}+ \beta_{2}d_{1} ) +\mu mr^{2}d_{1}d_{2} ( 1-R_{0} ) +pcr^{2}d_{1}d_{2}\\ &\phantom{C_{1} =}{}- \frac{\beta_{1}\beta_{2}bk^{2}\delta e^{-\alpha_{5}\tau_{5}}}{a+\delta } ( \lambda_{1}\gamma_{1}+ \lambda_{2}\gamma_{2} ), \\ &D_{1} =\mu rbkd_{1}d_{2}e^{-\alpha_{5}\tau_{5}} ( 1-R_{0} ). \end{aligned}$$

Let

$$\varPsi_{1}(v)=A_{1}v^{3}+B_{1}v^{2}+C_{1}v+D_{1}=0. $$

If \(R_{0}>1\), then \(\varPsi_{1}(0)=D_{1}<0\); moreover, \({\lim_{v\rightarrow \infty }}\varPsi_{1}(v)=\infty\), which implies that there exists \(v^{\ast}>0\) such that \(\varPsi_{1}(v^{\ast})=0\). Thus a chronic steady state \(E^{\ast}=(x_{1}^{\ast },y_{1}^{\ast},u_{1}^{\ast},x_{2}^{\ast},y_{2}^{\ast},u_{2}^{\ast},v^{\ast },z^{\ast})\) exists when \(R_{0}>1\), where

$$\begin{aligned} &x_{i}^{\ast} =\frac{\lambda_{i}}{d_{i}+\beta_{i}v^{\ast}},\quad i=1,2, \\ &y_{1}^{\ast} =\frac{\rho_{1}\beta_{1}e^{-\alpha_{1}\tau_{1}}x_{1}^{\ast }v^{\ast}}{a+\delta},\qquad y_{2}^{\ast}= \frac{\rho_{2}\beta_{2}e^{-\alpha_{3}\tau_{3}}x_{2}^{\ast}v^{\ast}}{a+\delta }, \\ &u_{i}^{\ast} =\frac{\gamma_{i}\beta_{i}x_{i}^{\ast}v^{\ast}\delta }{e^{-\alpha_{5}\tau_{5}} ( \mu+pz^{\ast} ) (a+\delta )},\qquad \sum _{i=1}^{2}u_{i}^{\ast}= \frac{rv^{\ast}}{e^{-\alpha _{5}\tau_{5}}k}, \\ &z^{\ast} =\frac{crv^{\ast}}{bke^{-\alpha_{5}\tau_{5}}+mrv^{\ast}}. \end{aligned}$$

 □

2.3 Global stability

We use Lyapunov method to investigate the global stability of the steady states. Let \(f(\eta)=\eta-1-\ln(\eta) \) and \((x_{1},y_{1},u_{1},x_{2},y_{2},u_{2},v,z)=(x_{1}(t),y_{1}(t),u_{1}(t),x_{2}(t),y_{2}(t),u_{2}(t),v(t),z(t))\).

Theorem 1

If \(R_{0}\leq1\), then \(E_{0}\) for system (6)–(13) is globally asymptotically stable.

Proof

We consider \(W_{1}(x_{1},y_{1},u_{1},x_{2},y_{2},u_{2},v,z)\) as

$$\begin{aligned} W_{1} ={}&\sum_{i=1}^{2} \biggl[ \gamma_{i}x_{i}^{0}f \biggl( \frac{x_{i}}{x_{i}^{0}} \biggr) +e^{-\alpha_{5}\tau_{5}}y_{i}+\frac{a+\delta}{\delta }e^{-\alpha_{5}\tau_{5}}u_{i} \biggr] +\frac{\mu(a+\delta)}{\delta k}v+\frac{p(a+\delta)}{2\delta c}e^{-\alpha_{5}\tau_{5}}z^{2} \\ &{} +\rho_{1}e^{-\alpha_{1}\tau_{1}-\alpha_{5}\tau_{5}} \int_{0}^{\tau_{1}}\beta_{1}x_{1}(t- \vartheta)v(t-\vartheta)\,d\vartheta\\ &{}+\frac{(a+\delta)}{\delta } ( 1-\rho_{1} ) e^{-\alpha_{2}\tau_{2}-\alpha_{5}\tau_{5}} \int _{0}^{\tau_{2}}\beta_{1}x_{1}(t- \vartheta)v(t-\vartheta)\,d\vartheta \\ &{} +\rho_{2}e^{-\alpha_{3}\tau_{3}-\alpha_{5}\tau_{5}} \int_{0}^{\tau_{3}}\beta_{2}x_{2}(t- \vartheta)v(t-\vartheta)\,d\vartheta\\ &{}+\frac{(a+\delta)}{\delta } ( 1-\rho_{2} ) e^{-\alpha_{4}\tau_{4}-\alpha_{5}\tau_{5}} \int _{0}^{\tau_{4}}\beta_{2}x_{2}(t- \vartheta)v(t-\vartheta)\,d\vartheta \\ &{} +\frac{\mu(a+\delta)}{\delta}e^{-\alpha_{5}\tau_{5}} \int_{0}^{\tau_{5}} \bigl[ u_{1}(t- \vartheta)+u_{2}(t-\vartheta) \bigr] \,d\vartheta. \end{aligned}$$

It is seen that \(W_{1}>0\) for all \(x_{1},y_{1},u_{1},x_{2},y_{2},u_{2},v,z>0\), and \(W_{1}(x_{1}^{0},0,0,x_{2}^{0},0,0,0,0)=0\). Calculating \(\dot {W}_{1}\) along system (6)–(13), we obtain

$$\begin{aligned} \dot{W}_{1} ={}&\sum_{i=1}^{2} \biggl[ \gamma_{i} \biggl( 1-\frac{x_{i}^{0}}{x_{i}} \biggr) \dot{x}_{i}+e^{-\alpha_{5}\tau_{5}}\dot{y}_{i}+\frac {a+\delta}{\delta}e^{-\alpha_{5}\tau_{5}} \dot{u}_{i} \biggr] \\ &{} +\frac {\mu(a+\delta)}{\delta k}\dot{v}+\frac{p(a+\delta)}{\delta c}e^{-\alpha _{5}\tau_{5}}z \dot{z} \\ & {}+\rho_{1}e^{-\alpha_{1}\tau_{1}-\alpha_{5}\tau_{5}}\beta_{1} \bigl[ x_{1}v-x_{1}(t-\tau_{1})v(t-\tau_{1}) \bigr] \\ &{}+\frac{(a+\delta) ( 1-\rho_{1} ) }{\delta}e^{-\alpha_{2}\tau_{2}-\alpha_{5}\tau_{5}}\beta_{1} \bigl[ x_{1}v-x_{1}(t-\tau_{2})v(t-\tau_{2}) \bigr] \\ &{} +\rho_{2}e^{-\alpha_{3}\tau_{3}-\alpha_{5}\tau_{5}}\beta_{2} \bigl[ x_{2}v-x_{2}(t-\tau_{3})v(t-\tau_{3}) \bigr] \\ &{} +\frac{(a+\delta) ( 1-\rho_{2} ) }{\delta}e^{-\alpha_{4}\tau_{4}-\alpha_{5}\tau_{5}}\beta_{2} \bigl[ x_{2}v-x_{2}(t-\tau_{4})v(t-\tau_{4}) \bigr] \\ &{} +\frac{\mu(a+\delta)}{\delta}e^{-\alpha_{5}\tau_{5}} \bigl[ u_{1}+u_{2}-u_{1}(t- \tau_{5})-u_{2}(t-\tau_{5}) \bigr]. \end{aligned}$$
(23)

Equation (23) can be simplified as

$$\begin{aligned} \dot{W}_{1} ={}&\sum_{i=1}^{2} \biggl[ \gamma_{i} \biggl( 1-\frac{x_{i}^{0}}{x_{i}} \biggr) ( \lambda_{i}-d_{i}x_{i}-\beta_{i}x_{i}v ) \biggr] -\frac{\mu(a+\delta)}{\delta k}rv\\ &{} +\frac{p(a+\delta)}{\delta c}e^{-\alpha_{5}\tau_{5}}z \bigl[ -m(u_{1}+u_{2})z-bz \bigr] +\gamma_{1}\beta_{1}x_{1}v+ \gamma_{2}\beta_{2}x_{2}v. \end{aligned}$$

Since \(\lambda_{i}=d_{i}x_{i}^{0}\),

$$\begin{aligned} \dot{W}_{1} ={}&\sum_{i=1}^{2} \biggl[ \gamma_{i} \biggl( 1-\frac{x_{i}^{0}}{x_{i}} \biggr) \bigl( d_{i}x_{i}^{0}-d_{i}x_{i} \bigr) -\gamma_{i}\beta_{i}x_{i}v \biggl( 1-\frac{x_{i}^{0}}{x_{i}} \biggr) +\gamma_{i}\beta _{i}x_{i}v \biggr] -\frac{\mu(a+\delta)}{\delta k}rv \\ &{} -\frac{pm(a+\delta)}{\delta c}e^{-\alpha_{5}\tau_{5}} ( u_{1}+u_{2} ) z^{2}-\frac{pb(a+\delta)}{\delta c}e^{-\alpha_{5}\tau_{5}}z^{2} \\ ={}&\sum_{i=1}^{2}\frac{-d_{i}\gamma_{i} ( x_{i}-x_{i}^{0} ) ^{2}}{x_{i}}+ \frac{\mu r(a+\delta)}{\delta k} ( R_{0}-1 ) v\\ &{}-\frac{pm(a+\delta)e^{-\alpha_{5}\tau_{5}}}{\delta c}\sum _{i=1}^{2}u_{i}z^{2}- \frac{pb(a+\delta)e^{-\alpha_{5}\tau_{5}}}{\delta c}z^{2}. \end{aligned}$$

It follows that \(\dot{W}_{1}\leq0\) if \(R_{0}\leq1\). Therefore, \(\dot{W}_{1}=0\) implies that \(x_{i}=x_{i}^{0}\), \(v=0\) and \(z=0\). One can easily show that the largest invariant set \(\varOmega_{0}\subseteq \varOmega=\{(x_{1},y_{1},u_{1},x_{2},y_{2},u_{2},v,z)|\dot{W}_{1}=0\}\) is the singleton \(\{E_{0}\}\). By LaSalle’s invariance principle, \(E_{0}\) is globally asymptotically stable. □

Theorem 2

If \(R_{0}>1\), then \(E^{\ast}\) for system (6)–(13) is globally asymptotically stable.

Proof

Consider \(W_{2}(x_{1},y_{1},u_{1},x_{2},y_{2},u_{2},v,z)\) as

$$\begin{aligned} W_{2} ={}&\sum_{i=1}^{2} \biggl[ \gamma_{i}x_{i}^{\ast}f \biggl( \frac{x_{i}}{x_{i}^{\ast}} \biggr) +e^{-\alpha_{5}\tau_{5}}y_{i}^{\ast}f \biggl( \frac{y_{i}}{y_{i}^{\ast}} \biggr) +\frac{(a+\delta)}{\delta}e^{-\alpha _{5}\tau_{5}}u_{i}^{\ast}f \biggl( \frac{u_{i}}{u_{i}^{\ast}} \biggr) \biggr]\\ &{} +\frac{(a+\delta) ( \mu+pz^{\ast} ) }{\delta k}v^{\ast}f \biggl( \frac{v}{v^{\ast}} \biggr) \\ &{} +\frac{p(a+\delta)}{2\delta ( c-mz^{\ast} ) }e^{-\alpha_{5}\tau_{5}} \bigl( z-z^{\ast} \bigr) ^{2}+\rho_{1}\beta_{1}e^{-\alpha_{1}\tau_{1}-\alpha_{5}\tau_{5}}x_{1}^{\ast}v^{\ast} \int_{0}^{\tau_{1}}f \biggl( \frac{x_{1}(t-\vartheta)v(t-\vartheta)}{x_{1}^{\ast}v^{\ast}} \biggr) \,d\vartheta \\ & {}+\frac{(a+\delta)}{\delta}(1-\rho_{1})\beta_{1}e^{-\alpha_{2}\tau _{2}-\alpha_{5}\tau_{5}}x_{1}^{\ast}v^{\ast} \int_{0}^{\tau_{2}}f \biggl( \frac{x_{1}(t-\vartheta)v(t-\vartheta)}{x_{1}^{\ast}v^{\ast}} \biggr) \,d\vartheta \\ &{} +\rho_{2}\beta_{2}e^{-\alpha_{3}\tau_{3}-\alpha_{5}\tau_{5}}x_{2}^{\ast }v^{\ast} \int_{0}^{\tau_{3}}f \biggl( \frac{x_{2}(t-\vartheta)v(t-\vartheta )}{x_{2}^{\ast}v^{\ast}} \biggr) \,d\vartheta \\ &{} +\frac{(a+\delta)}{\delta}(1-\rho_{2})\beta_{2}e^{-\alpha_{4}\tau _{4}-\alpha_{5}\tau_{5}}x_{2}^{\ast}v^{\ast} \int_{0}^{\tau_{4}}f \biggl( \frac{x_{2}(t-\vartheta)v(t-\vartheta)}{x_{2}^{\ast}v^{\ast}} \biggr) \,d\vartheta \\ & {}+\frac{(a+\delta)(\mu+pz^{\ast})}{\delta}e^{-\alpha_{5}\tau_{5}} \int _{0}^{\tau_{5}} \biggl[ u_{1}^{\ast}f \biggl( \frac{u_{1}(t-\vartheta)}{u_{1}^{\ast}} \biggr) +u_{2}^{\ast}f \biggl( \frac{u_{2}(t-\vartheta)}{u_{2}^{\ast}} \biggr) \biggr] \,d\vartheta. \end{aligned}$$

Calculating \(\dot{W}_{2}\) along system (6)–(13), we obtain

$$\begin{aligned} \dot{W}_{2} ={}&\sum_{i=1}^{2} \biggl[ \gamma_{i} \biggl( 1-\frac{x_{i}^{\ast}}{x_{i}} \biggr) \dot{x}_{i}+e^{-\alpha_{5}\tau_{5}} \biggl( 1-\frac {y_{i}^{\ast}}{y_{i}} \biggr) \dot{y}_{i}+\frac{(a+\delta)}{\delta}e^{-\alpha_{5}\tau_{5}} \biggl( 1- \frac{u_{i}^{\ast}}{u_{i}} \biggr) \dot {u}_{i} \biggr] \\ &{}+\frac{(a+\delta) ( \mu+pz^{\ast} ) }{\delta k} \biggl( 1-\frac{v^{\ast}}{v} \biggr) \dot{v} \\ &{} +\frac{p(a+\delta)}{\delta ( c-mz^{\ast} ) }e^{-\alpha_{5}\tau_{5}} \bigl( z-z^{\ast} \bigr) \dot{z}\\ &{}+ \rho_{1}\beta_{1}e^{-\alpha _{1}\tau_{1}-\alpha_{5}\tau_{5}}x_{1}^{\ast}v^{\ast} \biggl[ \frac{x_{1}v}{x_{1}^{\ast}v^{\ast}}-\frac{x_{1}(t-\tau_{1})v(t-\tau_{1})}{x_{1}^{\ast }v^{\ast}}+\operatorname{ln}\frac{x_{1}(t-\tau_{1})v(t-\tau_{1})}{x_{1}v} \biggr] \\ &{} +\frac{(a+\delta)}{\delta}(1-\rho_{1})\beta_{1}e^{-\alpha_{2}\tau _{2}-\alpha_{5}\tau_{5}}x_{1}^{\ast}v^{\ast}\\ &{}\times\biggl[ \frac{x_{1}v}{x_{1}^{\ast }v^{\ast}}-\frac{x_{1}(t-\tau_{2})v(t-\tau_{2})}{x_{1}^{\ast}v^{\ast}}+\operatorname{ln}\frac{x_{1}(t-\tau_{2})v(t-\tau_{2})}{x_{1}v} \biggr] \\ &{} +\rho_{2}\beta_{2}e^{-\alpha_{3}\tau_{3}-\alpha_{5}\tau_{5}}x_{2}^{\ast }v^{\ast} \biggl[ \frac{x_{2}v}{x_{2}^{\ast}v^{\ast}}-\frac{x_{2}(t-\tau _{3})v(t-\tau_{3})}{x_{2}^{\ast}v^{\ast}}+\operatorname{ln}\frac{x_{2}(t-\tau_{3})v(t-\tau_{3})}{x_{2}v} \biggr] \\ &{} +\frac{(a+\delta)}{\delta}(1-\rho_{2})\beta_{2}e^{-\alpha_{4}\tau _{4}-\alpha_{5}\tau_{5}}x_{2}^{\ast}v^{\ast}\\ &{}\times\biggl[ \frac{x_{2}v}{x_{2}^{\ast }v^{\ast}}-\frac{x_{2}(t-\tau_{4})v(t-\tau_{4})}{x_{2}^{\ast}v^{\ast}}+\operatorname{ln}\frac{x_{2}(t-\tau_{4})v(t-\tau_{4})}{x_{2}v} \biggr] \\ &{} +\frac{(a+\delta)(\mu+pz^{\ast})}{\delta}e^{-\alpha_{5}\tau_{5}} \biggl[ u_{1}^{\ast} \biggl( \frac{u_{1}}{u_{1}^{\ast}}-\frac{u_{1}(t-\tau_{5})}{u_{1}^{\ast}}+\operatorname{ln}\frac{u_{1}(t-\tau_{5})}{u_{1}} \biggr) \\ &{}+u_{2}^{\ast} \biggl( \frac{u_{2}}{u_{2}^{\ast}}-\frac{u_{2}(t-\tau_{5})}{u_{2}^{\ast}}+\operatorname{ln} \frac{u_{2}(t-\tau_{5})}{u_{2}} \biggr) \biggr]. \end{aligned}$$

Using the following chronic steady state conditions:

$$\begin{aligned} &\lambda_{i} =d_{i}x_{i}^{\ast}+ \beta_{i}x_{i}^{\ast}v^{\ast},\qquad (a+ \delta)y_{1}^{\ast }=\rho_{1}\beta_{1}e^{-\alpha_{1}\tau_{1}}x_{1}^{\ast}v^{\ast}, \\ &\lambda_{i} =d_{i}x_{i}^{\ast}+ \beta_{i}x_{i}^{\ast}v^{\ast}, \qquad (a+ \delta)y_{1}^{\ast }=\rho_{1}\beta_{1}e^{-\alpha_{1}\tau_{1}}x_{1}^{\ast}v^{\ast}, \\ &(a+\delta)y_{2}^{\ast} =\rho_{2} \beta_{2}e^{-\alpha_{3}\tau_{3}}x_{2}^{\ast}v^{\ast}, \qquad (a+\delta) \bigl(\mu+pz^{\ast } \bigr)e^{-\alpha_{5}\tau_{5}}u_{i}^{\ast}= \delta \gamma_{i}\beta_{i}x_{i}^{\ast }v^{\ast}, \\ &rv^{\ast} =ke^{-\alpha_{5}\tau_{5}} \bigl( u_{1}^{\ast}+u_{2}^{\ast } \bigr),\qquad c \bigl( u_{1}^{\ast}+u_{2}^{\ast} \bigr) =m \bigl( u_{1}^{\ast}+u_{2}^{\ast} \bigr) z^{\ast}+bz^{\ast}, \end{aligned}$$

we can simplify:

$$\begin{aligned} &\frac{p}{ ( c-mz^{\ast} ) } \bigl( z-z^{\ast} \bigr) \dot{z} \\ & \quad = \frac{p ( z-z^{\ast} ) }{ ( c-mz^{\ast} ) } \bigl( c ( u_{1}+u_{2} ) -m ( u_{1}+u_{2} ) z-bz \bigr) \\ &\quad =\frac{p ( z-z^{\ast} ) }{ ( c-mz^{\ast} ) } \bigl( c ( u_{1}+u_{2} ) -m ( u_{1}+u_{2} ) z-bz-c \bigl( u_{1}^{\ast}+u_{2}^{\ast} \bigr) +m \bigl( u_{1}^{\ast}+u_{2}^{\ast} \bigr) z^{\ast}+bz^{\ast} \bigr) \\ &\quad =-\frac{pb}{ ( c-mz^{\ast} ) } \bigl( z-z^{\ast} \bigr) ^{2}- \frac{pm ( u_{1}+u_{2} ) }{ ( c-mz^{\ast} ) } \bigl( z-z^{\ast} \bigr) ^{2} \\ & \qquad{}+p \bigl( u_{1}-u_{1}^{\ast} \bigr) \bigl( z-z^{\ast} \bigr) +p \bigl( u_{2}-u_{2}^{\ast} \bigr) \bigl( z-z^{\ast} \bigr) \\ &\quad =p \Biggl[ \sum_{i=1}^{2}u_{i}^{\ast}z^{\ast}- \sum_{i=1}^{2}u_{i}^{\ast }z- \sum_{i=1}^{2}u_{i}z^{\ast}+ \sum_{i=1}^{2}u_{i}z- \frac{ [ b+m ( u_{1}+u_{2} ) ] }{ ( c-mz^{\ast} ) } \bigl( z-z^{\ast } \bigr) ^{2} \Biggr]. \end{aligned}$$

Due to steady state conditions, we can rewrite

$$\begin{aligned} \dot{W}_{2} ={}&\sum_{i=1}^{2} \frac{-\gamma_{i}d_{i} ( x_{i}-x_{i}^{\ast} ) ^{2}}{x_{i}}+\rho_{1}\beta_{1}e^{-\alpha_{1}\tau_{1}-\alpha_{5}\tau_{5}}x_{1}^{\ast}v^{\ast} \biggl[ 4-\frac{x_{1}^{\ast}}{x_{1}}-\frac{y_{1}^{\ast}x_{1}(t-\tau_{1})v(t-\tau_{1})}{y_{1}(t)x_{1}^{\ast }v^{\ast}} \\ &{}-\frac{y_{1}u_{1}^{\ast}}{y_{1}^{\ast}u_{1}}- \frac{u_{1}(t-\tau _{5})v^{\ast}}{u_{1}^{\ast}v} +\operatorname{ln}\frac{x_{1}(t-\tau_{1})v(t-\tau_{1})}{x_{1}v}+\operatorname{ln}\frac {u_{1}(t-\tau_{5})}{u_{1}} \biggr] \\ &{} + \frac{(a+\delta)}{\delta}(1- \rho_{1})\beta_{1}e^{-\alpha_{2}\tau_{2}-\alpha_{5}\tau_{5}}x_{1}^{\ast}v^{\ast } \biggl[ 3-\frac{x_{1}^{\ast}}{x_{1}}-\frac{u_{1}(t-\tau_{5})v^{\ast}}{u_{1}^{\ast}v} \\ &{} -\frac{u_{1}^{\ast}x_{1}(t-\tau_{2})v(t-\tau_{2})}{u_{1}x_{1}^{\ast}v^{\ast}}+\operatorname{ln}\frac{x_{1}(t-\tau_{2})v(t-\tau_{2})}{x_{1}v}+\operatorname{ln}\frac {u_{1}(t-\tau_{5})}{u_{1}} \biggr] \\ &{} + \rho_{2}\beta_{2}e^{-\alpha_{3}\tau _{3}-\alpha_{5}\tau_{5}}x_{2}^{\ast}v^{\ast} \biggl[ 4-\frac{x_{2}^{\ast}}{x_{2}} -\frac{y_{2}^{\ast}x_{2}(t-\tau_{3})v(t-\tau_{3})}{y_{2}x_{2}^{\ast}v^{\ast}}-\frac{y_{2}u_{2}^{\ast}}{y_{2}^{\ast}u_{2}}-\frac {u_{2}(t-\tau_{5})v^{\ast}}{u_{2}^{\ast}v} \\ &{}+\operatorname{ln} \frac{x_{2}(t-\tau_{3})v(t-\tau_{3})}{x_{2}v}+\operatorname{ln}\frac{u_{2}(t-\tau_{5})}{u_{2}} \biggr] \\ &{} +\frac{(a+\delta)}{\delta}(1-\rho_{2})\beta_{2}e^{-\alpha_{4}\tau _{4}-\alpha_{5}\tau_{5}}x_{2}^{\ast}v^{\ast} \biggl[ 3-\frac{x_{2}^{\ast}}{x_{2}}-\frac{u_{2}(t-\tau_{5})v^{\ast}}{u_{2}^{\ast}v}-\frac{u_{2}^{\ast }x_{2}(t-\tau_{4})v(t-\tau_{4})}{u_{2}x_{2}^{\ast}v^{\ast}}\\ &{}+\operatorname{ln} \frac {u_{2}(t-\tau_{5})}{u_{2}} +\operatorname{ln}\frac{x_{2}(t-\tau_{4})v(t-\tau_{4})}{x_{2}v} \biggr]\\ &{} -\frac{(a+\delta)}{\delta}e^{-\alpha_{5}\tau_{5}} \frac{p [ b+m ( u_{1}+u_{2} ) ] }{ ( c-mz^{\ast} ) } \bigl( z-z^{\ast } \bigr) ^{2}. \end{aligned}$$

Consider the following relations:

ln ( x 1 ( t − τ 1 ) v ( t − τ 1 ) x 1 v ) + ln ( u 1 ( t − τ 5 ) u 1 ) = ln ( x 1 ∗ x 1 ) + ln ( y 1 ∗ x 1 ( t − τ 1 ) v ( t − τ 1 ) y 1 x 1 ∗ v ∗ ) + ln ( y 1 u 1 ∗ y 1 ∗ u 1 ) + ln ( u 1 ( t − τ 5 ) v ∗ u 1 ∗ v ) , ln ( x 1 ( t − τ 2 ) v ( t − τ 2 ) x 1 v ) + ln ( u 1 ( t − τ 5 ) u 1 ) = ln ( x 1 ∗ x 1 ) + ln ( x 1 ( t − τ 2 ) v ( t − τ 2 ) u 1 ∗ x 1 ∗ v ∗ u 1 ) + ln ( u 1 ( t − τ 5 ) v ∗ u 1 ∗ v ) .

Using similar relations for the terms containing \(\tau_{3}\) and \(\tau_{4}\), we finally obtain

$$\begin{aligned} \dot{W}_{2} ={}&\sum_{i=1}^{2} \biggl[ \frac{-\gamma_{i}d_{i} ( x_{i}-x_{i}^{\ast} ) ^{2}}{x_{i}} \\ &{}-\gamma_{i}\beta_{i}x_{i}^{\ast}v^{\ast}f \biggl( \frac{x_{i}^{\ast}}{x_{i}} \biggr) \biggr] -\rho_{1}\beta_{1}e^{-\alpha_{1}\tau_{1}-\alpha_{5}\tau_{5}}x_{1}^{\ast}v^{\ast} \biggl[ f \biggl( \frac{y_{1}^{\ast}x_{1}(t-\tau_{1})v(t-\tau_{1})}{y_{1}x_{1}^{\ast }v^{\ast}} \biggr) +f \biggl( \frac{y_{1}u_{1}^{\ast}}{y_{1}^{\ast}u_{1}} \biggr) \\ &{} +f \biggl( \frac{u_{1}(t-\tau_{5})v^{\ast}}{u_{1}^{\ast}v} \biggr) \biggr] -\frac{(a+\delta)}{\delta}(1- \rho_{1})\beta_{1}e^{-\alpha_{2}\tau _{2}-\alpha_{5}\tau_{5}}x_{1}^{\ast}v^{\ast} \\ &{}\times\biggl[ f \biggl( \frac {x_{1}(t-\tau_{2})v(t-\tau_{2})u_{1}^{\ast}}{x_{1}^{\ast}v^{\ast}u_{1}} \biggr) +f \biggl( \frac{u_{1}(t-\tau_{5})v^{\ast}}{u_{1}^{\ast}v} \biggr) \biggr] \\ &{} -\rho_{2}\beta_{2}e^{-\alpha_{3}\tau_{3}-\alpha_{5}\tau_{5}}x_{2}^{\ast }v^{\ast} \biggl[ f \biggl( \frac{y_{2}^{\ast}x_{2}(t-\tau_{3})v(t-\tau_{3})}{y_{2}(t)x_{2}^{\ast}v^{\ast}} \biggr) +f \biggl( \frac{y_{2}u_{2}^{\ast}}{y_{2}^{\ast}u_{2}} \biggr) +f \biggl( \frac{u_{2}(t-\tau_{5})v^{\ast}}{u_{2}^{\ast}v} \biggr) \biggr] \\ &{} -\frac{(a+\delta)}{\delta}(1-\rho_{2})\beta_{2}e^{-\alpha_{4}\tau _{4}-\alpha_{5}\tau_{5}}x_{2}^{\ast}v^{\ast} \biggl[ f \biggl( \frac {x_{2}(t-\tau_{4})v(t-\tau_{4})u_{2}^{\ast}}{x_{2}^{\ast}v^{\ast}u_{2}} \biggr) +f \biggl( \frac{u_{2}(t-\tau_{5})v^{\ast}}{u_{2}^{\ast}v} \biggr) \biggr] \\ &{} -\frac{(a+\delta)}{\delta}\frac{p [ b+m ( u_{1}+u_{2} ) ] }{ ( c-mz^{\ast} ) }e^{-\alpha_{5}\tau_{5}} \bigl( z-z^{\ast} \bigr) ^{2}. \end{aligned}$$
(24)

It follows that \(\dot{W}_{2}\leq0\). Now LaSalle’s invariance principle implies that \(E^{\ast}\) is globally asymptotically stable. □

3 HIV model with distributed delays

We study the HIV infection model with distributed time delays:

$$\begin{aligned} &\dot{x}_{1}(t) =\lambda_{1}-d_{1}x_{1}(t)- \beta_{1}x_{1}(t)v(t), \end{aligned}$$
(25)
$$\begin{aligned} &\dot{y}_{1}(t) =\rho_{1}\beta_{1} \int_{0}^{s_{1}}h_{1}(\tau)e^{-m_{1}\tau }x_{1}(t- \tau)v(t-\tau)\,d\tau-ay_{1}(t)-\delta y_{1}(t), \end{aligned}$$
(26)
$$\begin{aligned} & \dot{u}_{1}(t) =(1-\rho_{1})\beta_{1} \int_{0}^{s_{2}}h_{2}(\tau )e^{-m_{2}\tau}x_{1}(t-\tau)v(t-\tau)\,d\tau \\ &\phantom{\dot{u}_{1}(t) =}{}+\delta y_{1}(t)-pu_{1}(t)z(t)-\mu u_{1}(t), \end{aligned}$$
(27)
$$\begin{aligned} &\dot{x}_{2}(t) =\lambda_{2}-d_{2}x_{2}(t)- \beta_{2}x_{2}(t)v(t), \end{aligned}$$
(28)
$$\begin{aligned} &\dot{y}_{2}(t) =\rho_{2}\beta_{2} \int_{0}^{s_{3}}h_{3}(\tau)e^{-m_{3}\tau }x_{2}(t- \tau)v(t-\tau)\,d\tau-ay_{2}(t)-\delta y_{2}(t), \end{aligned}$$
(29)
$$\begin{aligned} &\dot{u}_{2}(t) =(1-\rho_{2})\beta_{2} \int_{0}^{s_{4}}h_{4}(\tau )e^{-m_{4}\tau}x_{2}(t-\tau)v(t-\tau)\,d\tau \\ &\phantom{\dot{u}_{2}(t) =}{}+\delta y_{2}(t)-pu_{2}(t)z(t)-\mu u_{2}(t), \end{aligned}$$
(30)
$$\begin{aligned} &\dot{v}(t) =k \int_{0}^{s_{5}}g(\tau)e^{-n\tau} \bigl( u_{1}(t-\tau )+u_{2}(t-\tau) \bigr) \,d \tau-rv(t), \end{aligned}$$
(31)
$$\begin{aligned} &\dot{z}(t) =c \bigl( u_{1}(t)+u_{2}(t) \bigr) -m \bigl( u_{1}(t)+u_{2}(t) \bigr) z(t)-bz(t). \end{aligned}$$
(32)

The factors \(h_{2i-1}(\tau)e^{-m_{2i-1}\tau}\), \(i=1,2\) are the probabilities that uninfected cells contacted by HIV at time \(t-\tau\) survived τ time units and become latently infected at time t, where \(i=1\) and \(i=2\) represent the CD4+ T cells and macrophages, respectively; \(h_{2i}(\tau)e^{-m_{2i}\tau}\), \(i=1,2\) are the probabilities that the uninfected cells contacted by HIV at time \(t-\tau\) survived τ time units and become actively infected at time t; \(g(\tau)e^{-n\tau}\) is the probability that an immature pathogen at time \(t-\tau\) survived τ time units to become mature at time t. The probability distribution function \(h_{i}(\tau)\), \(i=1,\dots,4\) and \(g(\tau)\) are assumed to satisfy \(h_{i}(\tau)>0, i=1,\dots,4\) and \(g(\tau)>0\), as well as

$$\begin{aligned} &\int_{0}^{s_{j}}h_{j}(\tau)\,d\tau= \int_{0}^{s_{5}}g(\tau)\,d\tau=1,\qquad \int_{0}^{s_{j}}h_{j}(\tau)e^{\varepsilon r} \,dr< \infty,\\ & \int _{0}^{s_{5}}g(\tau)e^{\varepsilon r}\,dr< \infty,\quad i=1,\dots,4,\varepsilon>0. \end{aligned}$$

Let

$$H_{j}= \int_{0}^{s_{j}}h_{j}(\tau)e^{-m_{j}\tau} \,d\tau=,\qquad G= \int _{0}^{s_{5}}g(\tau)e^{-n\tau}\,d\tau=G, \quad j=1, \dots,4. $$

Then \(0< H_{j}\leq1\) and \(0< G\leq1\),\(j=1,\dots,4\).

The initial conditions for system (25)–(32) are the same as given by (14) where \(\kappa=\max \{s_{1},s_{2},s_{3},s_{4},s_{5}\}\).

3.1 Nonnegativity and boundedness

Proposition 2

The solutions of system (25)–(32) are nonnegative and ultimately bounded.

Proof

The nonnegativity can be shown as in Proposition 1. To show the boundedness, let us define

$$\begin{aligned} U_{1}(t) ={}&\rho_{1} \int_{0}^{s_{1}}h_{1}(\tau)e^{-m_{1}\tau}x_{1}(t- \tau)\,d\tau+ ( 1-\rho_{1} ) \int_{0}^{s_{2}}h_{2}(\tau )e^{-m_{2}\tau}x_{1}(t-\tau)\,d\tau \\ &{} +\rho_{2} \int_{0}^{s_{3}}h_{3}(\tau)e^{-m_{3}\tau}x_{2}(t- \tau )\,d\tau+ ( 1-\rho_{2} ) \int_{0}^{s_{4}}h_{4}(\tau)e^{-m_{4}\tau }x_{2}(t- \tau)\,d\tau \\ &{} +y_{1}(t)+u_{1}(t)+y_{2}(t)+u_{2}(t)+ \frac{\mu}{2c}z(t). \end{aligned}$$

Then

$$\begin{aligned} \dot{U}_{1}(t) ={}&\rho_{1}H_{1} \lambda_{1}+ ( 1-\rho_{1} ) H_{2} \lambda_{1}+\rho_{2}H_{3}\lambda_{2}+ ( 1-\rho_{2} ) H_{4}\lambda_{2} \\ &{} - \biggl( p+\frac{\mu m}{2c} \biggr) \bigl( u_{1}(t)+u_{2}(t) \bigr) z(t)-\rho_{1}e^{-\alpha_{1}\tau_{1}}d_{1}x_{1}(t- \tau_{1})\\ &{}- ( 1-\rho _{1} ) e^{-\alpha_{2}\tau_{2}}d_{1}x_{1}(t- \tau_{2}) \\ &{} -\rho_{2}e^{-\alpha_{3}\tau_{3}}d_{2}x_{2}(t- \tau_{3})- ( 1-\rho _{2} ) e^{-\alpha_{4}\tau_{4}}d_{2}x_{2}(t- \tau_{4})-ay_{1}(t)-ay_{2}(t) \\ &{} -\frac{\mu}{2}u_{1}(t)-\frac{\mu}{2}u_{2}(t)- \frac{\mu b}{2c}z(t) \\ \leq{}& \lambda_{1}+\lambda_{2}-\delta_{1}U_{1}(t). \end{aligned}$$

Then \(\limsup_{t\rightarrow \infty}x_{i}(t)\leq M_{1}\), \(\limsup_{t\rightarrow \infty}y_{i}(t)\leq M_{1}\), \(\limsup_{t\rightarrow \infty}u_{i}(t)\leq M_{1}\), \(\limsup_{t\rightarrow \infty}z(t)\leq M_{2} \) and \(\limsup_{t\rightarrow \infty}v(t)\leq M_{3}\), where \(M_{1}\), \(M_{2}\) and \(M_{3}\) are defined in the previous section. □

3.2 Steady states

The basic reproduction number \(R_{0}\) for system (25)–(32) is as follows:

$$R_{0}=\frac{\delta kG}{\mu r(a+\delta)} \bigl( \xi_{1} \beta_{1}x_{1}^{0}+\xi_{2} \beta_{2}x_{2}^{0} \bigr), $$

where

$$\xi_{1}=\rho_{1}H_{1}+\frac{(a+\delta)}{\delta}(1- \rho_{1})H_{2}, \qquad \xi_{2}= \rho_{2}H_{3}+\frac{(a+\delta)}{\delta}(1-\rho_{2})H_{4}. $$

Lemma 2

For system (25)–(32) (i) if \(R_{0}\leq1\), then there exists an infection-free steady state \(E_{0}\), and (ii) if \(R_{0}>1\), then there exist two steady states, \(E_{0}\) and a chronic steady state \(E^{\ast}\).

Proof

The steady states of model (25)–(32) satisfy:

$$\begin{aligned} &\lambda_{1}-d_{1}x_{1}-\beta_{1}x_{1}v =0, \end{aligned}$$
(33)
$$\begin{aligned} &\rho_{1}\beta_{1}H_{1}x_{1}v-ay_{1}- \delta y_{1} =0, \end{aligned}$$
(34)
$$\begin{aligned} &(1-\rho_{1})\beta_{1}H_{2}x_{1}v+ \delta y_{1}-pu_{1}z-\mu u_{1} =0, \end{aligned}$$
(35)
$$\begin{aligned} & \lambda_{2}-d_{2}x_{2}-\beta_{2}x_{2}v =0, \end{aligned}$$
(36)
$$\begin{aligned} &\rho_{2}\beta_{2}H_{3}x_{2}v-ay_{2}- \delta y_{2} =0, \end{aligned}$$
(37)
$$\begin{aligned} &(1-\rho_{2})\beta_{2}H_{4}x_{2}v+ \delta y_{2}-pu_{2}z-\mu u_{2} =0, \end{aligned}$$
(38)
$$\begin{aligned} &kG ( u_{1}+u_{2} ) -rv =0, \end{aligned}$$
(39)
$$\begin{aligned} &c ( u_{1}+u_{2} ) -m ( u_{1}+u_{2} ) z-bz =0. \end{aligned}$$
(40)

We find that system (25)–(32) admits an infection-free steady state \(E_{0}=(x_{1}^{0},0,0,x_{2}^{0},0,0, 0,0) \) where \(x_{1}^{0}=\frac {\lambda_{1}}{d_{1}}\), \(x_{2}^{0}=\frac{\lambda_{2}}{d_{2}}\). In addition, from Eqs. (33)–(40) we get

$$A_{2}v^{3}+B_{2}v^{2}+C_{2}v+D_{2}=0, $$

where

$$\begin{aligned} &A_{2} =\beta_{1}\beta_{2} ( \mu m+pc ) r^{2}, \\ &B_{2} =\beta_{1}\beta_{2}\mu rbGk+ ( \beta_{1}d_{2}+\beta_{2}d_{1} ) ( \mu m+pc ) r^{2}-\frac{\beta_{1}\beta_{2}mr\delta Gk}{a+\delta} ( \lambda_{1} \xi_{1}+\lambda_{2}\xi_{2} ), \\ &C_{2} =\mu rbGk ( \beta_{1}d_{2}+ \beta_{2}d_{1} ) +\mu mr^{2}d_{1}d_{2} ( 1-R_{0} ) +pcr^{2}d_{1}d_{2}- \frac{\beta _{1}\beta_{2}\delta bG^{2}k^{2}}{a+\delta} ( \lambda_{1}\xi_{1}+ \lambda_{2}\xi_{2} ), \\ &D_{2} =\mu rbkd_{1}d_{2}G ( 1-R_{0} ). \end{aligned}$$

Let

$$\varPsi_{2}(v)=A_{2}v^{3}+B_{2}v^{2}+C_{2}v+D_{2}=0. $$

If \(R_{0}>1\), then \(\varPsi_{2}(0)=D_{2}<0\); moreover, \({\lim_{v\rightarrow \infty}}\varPsi_{2}(v)=\infty\). Then there exits \(v^{\ast}\in(0,\infty)\) such that \(\varPsi_{2}(v^{\ast})=0\). Therefore, a chronic steady state \(E^{\ast }=(x_{1}^{\ast},y_{1}^{\ast},u_{1}^{\ast},x_{2}^{\ast},y_{2}^{\ast},u_{2}^{\ast},v^{\ast},z^{\ast})\) exists if \(R_{0}>1\), where

$$\begin{aligned} &x_{i}^{\ast} =\frac{\lambda_{i}}{d_{i}+\beta_{i}v^{\ast}}, \quad i =1,2, \\ &y_{1}^{\ast} =\frac{\rho_{1}\beta_{1}H_{1}x_{1}^{\ast}v^{\ast}}{a+\delta }, \qquad y_{2}^{\ast} =\frac{\rho_{2}\beta_{2}H_{3}x_{2}^{\ast}v^{\ast}}{a+\delta}, \\ &u_{i}^{\ast} =\frac{\xi_{i}\beta_{i}x_{i}^{\ast}v^{\ast}\delta}{ ( \mu+pz^{\ast} ) (a+\delta)}, \qquad \sum _{i=1}^{2}u_{i}^{\ast} = \frac{rv^{\ast}}{Gk}, \\ & z^{\ast} =\frac{crv^{\ast}}{bkG+mrv^{\ast}}. \end{aligned}$$

 □

3.3 Global stability

Theorem 3

If \(R_{0}\leq1\), then \(E_{0}\) for system (25)–(32) is globally asymptotically stable.

Proof

Define

$$\begin{aligned} V_{1} ={}&\sum_{i=1}^{2} \biggl[ \xi_{i}x_{i}^{0}f \biggl( \frac{x_{i}}{x_{i}^{0}} \biggr) +y_{i}+\frac{a+\delta}{\delta}u_{i} \biggr] + \frac {\mu(a+\delta)}{\delta Gk}v+\frac{p(a+\delta)}{2\delta c}z^{2} \\ &{} +\rho_{1}\beta_{1} \int_{0}^{s_{1}}h_{1}(\tau)e^{-m_{1}\tau} \int_{0}^{\tau }x_{1}(t-\vartheta)v(t- \vartheta)\,d\vartheta \,d\tau \\ &{}+\frac{(a+\delta)}{\delta } ( 1-\rho_{1} ) \int_{0}^{s_{2}}h_{2}(\tau)e^{-m_{2}\tau} \int _{0}^{\tau}\beta_{1}x_{1}(t- \vartheta)v(t-\vartheta)\,d\vartheta \,d\tau \\ &{} +\rho_{2}\beta_{2} \int_{0}^{s_{3}}h_{3}(\tau)e^{-m_{3}\tau} \int_{0}^{\tau }x_{2}(t-\vartheta)v(t- \vartheta)\,d\vartheta \,d\tau \\ &{}+\frac{(a+\delta)}{\delta } ( 1-\rho_{2} ) \beta_{2} \int_{0}^{s_{4}}h_{4}(\tau)e^{-m_{4}\tau } \int_{0}^{\tau}x_{2}(t-\vartheta)v(t- \vartheta)\,d\vartheta \,d\tau \\ & {}+\frac{\mu(a+\delta)}{\delta G} \int_{0}^{s_{5}}g(\tau)e^{-n\tau} \int _{0}^{\tau} \bigl[ u_{1}(t- \vartheta)+u_{2}(t-\vartheta) \bigr] \,d\vartheta \,d\tau. \end{aligned}$$
(41)

Calculating \(\dot{V}_{1}\) along system (25)–(32), we obtain

$$\begin{aligned} \dot{V}_{1} ={}&\sum_{i=1}^{2} \biggl[ \xi_{i} \biggl( 1-\frac{x_{i}^{0}}{x_{i}} \biggr) \dot{x}_{i}+\dot{y}_{i}+\frac{a+\delta}{\delta} \dot{u}_{i} \biggr] +\frac{\mu(a+\delta)}{\delta Gk}\dot{v}+ \frac{p(a+\delta)}{\delta c}z\dot{z} \\ &{} +\rho_{1}\beta_{1} \int_{0}^{s_{1}}h_{1}(\tau)e^{-m_{1}\tau} \bigl[ x_{1}(t)v(t)-x_{1}(t-\tau)v(t-\tau) \bigr] \,d\tau \\ &{} +\frac{(a+\delta) ( 1-\rho_{1} ) }{\delta}\beta_{1} \int _{0}^{s_{2}}h_{2}(\tau)e^{-m_{2}\tau} \bigl[ x_{1}(t)v(t)-x_{1}(t-\tau )v(t-\tau) \bigr] \,d\tau \\ & {}+\rho_{2}\beta_{2} \int_{0}^{s_{3}}h_{3}(\tau)e^{-m_{3}\tau} \bigl[ x_{2}v-x_{2}(t-\tau)v(t-\tau) \bigr] \,d\tau \\ &{}+\frac{(a+\delta) ( 1-\rho_{2} ) }{\delta}\beta_{2} \int _{0}^{s_{4}}h_{4}(\tau)e^{-m_{4}\tau} \bigl[ x_{2}v-x_{2}(t-\tau )v(t-\tau) \bigr] \,d\tau \\ &{} +\frac{\mu(a+\delta)}{\delta G} \int_{0}^{s_{5}}g(\tau)e^{-n\tau} \bigl[ u_{1}+u_{2}-u_{1}(t-\tau)-u_{2}(t- \tau) \bigr] \,d\tau. \end{aligned}$$

Since \(\lambda_{i}=d_{i}x_{i}^{0}\), we get

$$\begin{aligned} \dot{V}_{1} ={}&\sum_{i=1}^{2} \biggl[ \xi_{i} \biggl( 1-\frac{x_{i}^{0}}{x_{i}} \biggr) \bigl( d_{i}x_{i}^{0}-d_{i}x_{i} \bigr) -\xi_{i}\beta _{i}x_{i}v \biggl( 1- \frac{x_{i}^{0}}{x_{i}} \biggr) +\xi_{i}\beta_{i}x_{i}v \biggr] -\frac{\mu(a+\delta)}{\delta Gk}rv \\ &{} -\frac{pm(a+\delta)}{\delta c} ( u_{1}+u_{2} ) z^{2}- \frac{pb(a+\delta)}{\delta c}z^{2} \\ ={}& \sum_{i=1}^{2}\frac{-d_{i}\xi_{i} ( x_{i}-x_{i}^{0} ) ^{2}}{x_{i}}+ \frac{\mu r(a+\delta)}{\delta Gk} ( R_{0}-1 ) v-\frac{pm(a+\delta)}{\delta}\sum _{i=1}^{2}u_{i}z^{2}- \frac{pb(a+\delta )}{\delta c}z^{2}. \end{aligned}$$

Similar to the proof of Theorem 1, \(E_{0}\) is globally asymptotically stable if \(R_{0}\leq1\). □

Theorem 4

If \(R_{0}>1\), then \(E^{\ast}\) for system (25)–(32) is globally asymptotically stable.

Proof

Define

$$\begin{aligned} V_{2} ={}&\sum_{i=1}^{2} \biggl[ \xi_{i}x_{i}^{\ast}f \biggl( \frac{x_{i}}{x_{i}^{\ast}} \biggr) +y_{i}^{\ast}f \biggl( \frac{y_{i}}{y_{i}^{\ast}} \biggr) + \frac{(a+\delta)}{\delta}u_{i}^{\ast}f \biggl( \frac{u_{i}}{u_{i}^{\ast}} \biggr) \biggr] +\frac{(a+\delta) ( \mu+pz^{\ast} ) }{\delta Gk}v^{\ast}f \biggl( \frac{v}{v^{\ast}} \biggr) \\ &{} +\frac{p(a+\delta)}{2\delta ( c-mz^{\ast} ) } \bigl( z-z^{\ast } \bigr) ^{2}\\ &{}+ \rho_{1}\beta_{1}x_{1}^{\ast}v^{\ast} \int_{0}^{s_{1}}h_{1}( \tau)e^{-m_{1}\tau} \int_{0}^{\tau}f \biggl( \frac{x_{1}(t-\vartheta )v(t-\vartheta)}{x_{1}^{\ast}v^{\ast}} \biggr) \,d\vartheta \,d\tau \\ &{} +\frac{(a+\delta)}{\delta}(1-\rho_{1})\beta_{1}x_{1}^{\ast}v^{\ast} \int _{0}^{s_{2}}h_{2}(\tau)e^{-m_{2}\tau} \int_{0}^{\tau}f \biggl( \frac {x_{1}(t-\vartheta)v(t-\vartheta)}{x_{1}^{\ast}v^{\ast}} \biggr) \,d\vartheta \,d\tau \\ &{} +\rho_{2}\beta_{2}x_{2}^{\ast}v^{\ast} \int_{0}^{s_{3}}h_{3}(\tau )e^{-m_{3}\tau} \int_{0}^{\tau}f \biggl( \frac{x_{2}(t-\vartheta)v(t-\vartheta )}{x_{2}^{\ast}v^{\ast}} \biggr) \,d\vartheta \,d\tau \\ &{} +\frac{(a+\delta)}{\delta}(1-\rho_{2})\beta_{2}x_{2}^{\ast}v^{\ast} \int _{0}^{s_{4}}h_{4}(\tau)e^{-m_{4}\tau} \int_{0}^{\tau}f \biggl( \frac {x_{2}(t-\vartheta)v(t-\vartheta)}{x_{2}^{\ast}v^{\ast}} \biggr) \,d\vartheta \,d\tau \\ &{} +\frac{(a+\delta)(\mu+pz^{\ast})}{\delta G} \int_{0}^{s_{5}}g(\tau )e^{-n\tau} \int_{0}^{\tau} \biggl[ u_{1}^{\ast}f \biggl( \frac{u_{1}(t-\vartheta)}{u_{1}^{\ast}} \biggr) +u_{2}^{\ast}f \biggl( \frac {u_{2}(t-\vartheta)}{u_{2}^{\ast}} \biggr) \biggr] \,d\vartheta \,d\tau. \end{aligned}$$

It is seen that function \(V_{2} \) is positive definite. The time derivative of \(V_{2}\) is given by the following:

$$\begin{aligned} \dot{V}_{2} ={}&\sum_{i=1}^{2} \biggl[ \xi_{i} \biggl( 1-\frac{x_{i}^{\ast}}{x_{i}} \biggr) \dot{x}_{i}+ \biggl( 1-\frac{y_{i}^{\ast}}{y_{i}} \biggr) \dot{y}_{i}+\frac{(a+\delta)}{\delta} \biggl( 1-\frac{u_{i}^{\ast}}{u_{i}} \biggr) \dot{u}_{i} \biggr]\\ &{}+\frac{(a+\delta) ( \mu+pz^{\ast} ) }{\delta Gk} \biggl( 1-\frac{v^{\ast}}{v} \biggr) \dot{v} \\ &{} +\frac{p(a+\delta)}{\delta ( c-mz^{\ast} ) } \bigl( z-z^{\ast } \bigr) \dot{z}+ \rho_{1}\beta_{1}x_{1}^{\ast}v^{\ast} \int_{0}^{s_{1}}h_{1}( \tau)e^{-m_{1}\tau} \biggl[ \frac{x_{1}v}{x_{1}^{\ast}v^{\ast}}-\frac{x_{1}(t-\tau)v(t-\tau)}{x_{1}^{\ast}v^{\ast}}\\ &{}+\operatorname{ln} \frac{x_{1}(t-\tau)v(t-\tau)}{x_{1}v} \biggr] \,d\tau \\ &{} +\frac{(a+\delta)}{\delta}(1-\rho_{1})\beta_{1}x_{1}^{\ast}v^{\ast} \int _{0}^{s_{2}}h_{2}(\tau)e^{-m_{2}\tau} \biggl[ \frac{x_{1}v}{x_{1}^{\ast}v^{\ast}}-\frac{x_{1}(t-\tau)v(t-\tau)}{x_{1}^{\ast}v^{\ast}}\\ &{}+\operatorname{ln}\frac {x_{1}(t-\tau)v(t-\tau)}{x_{1}v} \biggr] \,d \tau \\ &{} +\rho_{2}\beta_{2}x_{2}^{\ast}v^{\ast} \int_{0}^{s_{3}}h_{3}(\tau )e^{-m_{3}\tau} \biggl[ \frac{x_{2}v}{x_{2}^{\ast}v^{\ast}}-\frac{x_{2}(t-\tau)v(t-\tau)}{x_{2}^{\ast}v^{\ast}}+\operatorname{ln}\frac{x_{2}(t-\tau)v(t-\tau)}{x_{2}v} \biggr] \,d \tau \\ &{} +\frac{(a+\delta)}{\delta}(1-\rho_{2})\beta_{2}x_{2}^{\ast}v^{\ast} \int _{0}^{s_{4}}h_{4}(\tau)e^{-m_{4}\tau} \biggl[ \frac{x_{2}v}{x_{2}^{\ast}v^{\ast}}-\frac{x_{2}(t-\tau)v(t-\tau)}{x_{2}^{\ast}v^{\ast}}\\ &{}+\operatorname{ln}\frac {x_{2}(t-\tau)v(t-\tau)}{x_{2}v} \biggr] \,d \tau \\ &{} +\frac{(a+\delta)(\mu+pz^{\ast})}{\delta G}u_{1}^{\ast} \int_{0}^{s_{5}}g(\tau)e^{-n\tau} \biggl[ \frac{u_{1}}{u_{1}^{\ast}}-\frac{u_{1}(t-\tau )}{u_{1}^{\ast}}+\operatorname{ln}\frac{u_{1}(t-\tau)}{u_{1}} \biggr] \,d\tau \\ &{} +\frac{(a+\delta)(\mu+pz^{\ast})}{\delta G}u_{2}^{\ast} \int_{0}^{s_{5}}g(\tau)e^{-n\tau} \biggl[ \frac{u_{2}}{u_{2}^{\ast}}-\frac{u_{2}(t-\tau )}{u_{2}^{\ast}}+\operatorname{ln}\frac{u_{2}(t-\tau)}{u_{2}} \biggr] \,d\tau. \end{aligned}$$

Using chronic steady state conditions

$$\begin{aligned} &\lambda_{i} =d_{i}x_{i}^{\ast}+ \beta_{i}x_{i}^{\ast}v^{\ast},\qquad (a+\delta)y_{1}^{\ast}=\rho_{1} \beta_{1}H_{1}x_{1}^{\ast}v^{\ast}, \\ &(a+\delta)y_{2}^{\ast} =\rho_{2} \beta_{2}H_{3}x_{2}^{\ast}v^{\ast },\qquad (a+\delta) \bigl(\mu+pz^{\ast} \bigr)u_{i}^{\ast}= \xi_{i}\beta_{i}\delta x_{i}^{\ast}v^{\ast}, \\ &rv^{\ast} =kG \bigl( u_{1}^{\ast}+u_{2}^{\ast} \bigr) ,\qquad 0=c \bigl( u_{1}^{\ast}+u_{2}^{\ast} \bigr) -m \bigl( u_{1}^{\ast}+u_{2}^{\ast} \bigr) z^{\ast}-bz^{\ast }, \end{aligned}$$

we can simplify:

$$\begin{aligned} &\frac{p}{ ( c-mz^{\ast} ) } \bigl( z-z^{\ast} \bigr) \dot{z} \\ &\quad= \frac{p(a+\delta) ( z-z^{\ast} ) }{\delta ( c-mz^{\ast } ) } \bigl( c ( u_{1}+u_{2} ) -m ( u_{1}+u_{2} ) z-bz \bigr) \\ &\quad =p \Biggl[ \sum_{i=1}^{2}u_{i}^{\ast}z^{\ast}- \sum_{i=1}^{2}u_{i}^{\ast }z- \sum_{i=1}^{2}u_{i}z^{\ast}+ \sum_{i=1}^{2}u_{i}z- \frac{ [ b+m\sum_{i=1}^{2}u_{i} ] }{ ( c-mz^{\ast} ) } \bigl( z-z^{\ast} \bigr) ^{2} \Biggr]. \end{aligned}$$
(42)

The following relations will be used:

$$\begin{aligned} &\ln \biggl( \frac{x_{1}(t-\tau)v(t-\tau)}{x_{1}v} \biggr) =\ln \biggl( \frac{x_{1}^{\ast}v^{\ast}y_{1}}{x_{1}vy_{1}^{\ast}} \biggr) +\ln \biggl( \frac{y_{1}^{\ast}x_{1}(t-\tau)v(t-\tau)}{y_{1}x_{1}^{\ast}v^{\ast}} \biggr) , \\ &\ln \biggl( \frac{x_{1}(t-\tau)v(t-\tau)}{x_{1}v} \biggr) =\ln \biggl( \frac{x_{1}^{\ast}v^{\ast}u_{1}}{x_{1}vu_{1}^{\ast}} \biggr) +\ln \frac {u_{1}^{\ast}x_{1}(t-\tau)v(t-\tau)}{u_{1}x_{1}^{\ast}v^{\ast}}, \\ &\ln \biggl( \frac{u_{i}(t-\tau)}{u_{i}} \biggr) =\ln \biggl( \frac {vu_{i}^{\ast}}{v^{\ast}u_{i}} \biggr) +\ln \biggl( \frac{u_{i}(t-\tau)v^{\ast }}{u_{i}^{\ast}v} \biggr). \end{aligned}$$

Now using the last relations with steady state conditions and Eq. (42), we can rewrite

$$\begin{aligned} \dot{V}_{2}(t) ={}&\sum_{i=1}^{2} \biggl[ \frac{-\xi_{i}\,d_{i} ( x_{i}-x_{i}^{\ast} ) ^{2}}{x_{i}}+\xi_{i}\beta_{i}x_{i}^{\ast}v^{\ast } \biggl( 1-\frac{x_{i}^{\ast}}{x_{i}} \biggr)\\ &{} -\frac{\xi_{i}\beta_{i}x_{i}^{\ast}v^{\ast}}{G} \int_{0}^{s_{5}}g(\tau)e^{-n\tau}f \biggl( \frac{v^{\ast}u_{i}(t-\tau)}{vu_{i}^{\ast}} \biggr) \,d\tau \\ &{} +\frac{\xi_{i}\beta_{i}x_{i}^{\ast}v^{\ast}}{G} \int_{0}^{s_{5}}g(\tau)e^{-n\tau}\operatorname{ln} \frac{vu_{i}^{\ast}}{v^{\ast}u_{i}}\,d\tau \biggr] -\rho _{1}\beta_{1}H_{1}x_{1}^{\ast}v^{\ast} \biggl( \frac{y_{1}u_{1}^{\ast}}{y_{1}^{\ast}u_{1}}-1 \biggr) \\ &{}-\rho_{2}\beta_{2}H_{3}x_{2}^{\ast}v^{\ast } \biggl( \frac{y_{2}u_{2}^{\ast}}{y_{2}^{\ast}u_{2}}-1 \biggr) \\ &{} -\rho_{1}\beta_{1}x_{1}^{\ast}v^{\ast} \int_{0}^{s_{1}}h_{1}(\tau )e^{-m_{1}\tau}f \biggl( \frac{y_{1}^{\ast}x_{1}(t-\tau)v(t-\tau)}{y_{1}x_{1}^{\ast}v^{\ast}} \biggr) \,d\tau\\ &{}+ \rho_{1}\beta_{1}x_{1}^{\ast}v^{\ast}\int_{0}^{s_{1}}h_{1}(\tau)e^{-m_{1}\tau}\operatorname{ln} \frac{y_{1}x_{1}^{\ast}v^{\ast}}{y_{1}^{\ast}x_{1}v}\,d\tau \\ &{} -\rho_{2}\beta_{2}x_{2}^{\ast}v^{\ast} \int_{0}^{s_{3}}h_{3}(\tau )e^{-m_{3}\tau}f \biggl( \frac{y_{2}^{\ast}x_{2}(t-\tau)v(t-\tau)}{y_{2}x_{2}^{\ast}v^{\ast}} \biggr) \,d\tau\\ &{}+ \rho_{2}\beta_{2}x_{2}^{\ast}v^{\ast}\int_{0}^{s_{3}}h_{3}(\tau)e^{-m_{3}\tau}\operatorname{ln} \frac{y_{2}x_{2}^{\ast}v^{\ast}}{y_{2}^{\ast}x_{2}v}\,d\tau \\ & {}+\frac{a+\delta}{\delta}(1-\rho_{1})\beta_{1}x_{1}^{\ast}v^{\ast} \int _{0}^{s_{2}}h_{2}(\tau)e^{-m_{2}\tau}\operatorname{ln} \frac{u_{1}x_{1}^{\ast}v^{\ast}}{u_{1}^{\ast}x_{1}v}\,d\tau\\ &{}+\frac{a+\delta}{\delta}\rho_{2} \beta_{2}x_{2}^{\ast }v^{\ast} \int_{0}^{s_{4}}h_{4}(\tau)e^{-m_{4}\tau}\operatorname{ln} \frac{u_{2}x_{2}^{\ast }v^{\ast}}{u_{2}^{\ast}x_{2}v}\,d\tau \\ &{} -\frac{a+\delta}{\delta}(1-\rho_{1})\beta_{1}x_{1}^{\ast}v^{\ast} \int _{0}^{s_{2}}h_{2}(\tau)e^{-m_{2}\tau}f \biggl( \frac{u_{1}^{\ast}x_{1}(t-\tau)v(t-\tau)}{u_{1}x_{1}^{\ast}v^{\ast}} \biggr) \,d\tau \\ &{} -\frac{a+\delta}{\delta}(1-\rho_{2})\beta_{2}x_{2}^{\ast}v^{\ast} \int _{0}^{s_{4}}h_{4}(\tau)e^{-m_{4}\tau}f \biggl( \frac{u_{2}^{\ast}x_{2}(t-\tau)v(t-\tau)}{u_{2}x_{2}^{\ast}v^{\ast}} \biggr) \,d\tau \\ &{} -\frac{p(a+\delta) [ b+m ( u_{1}+u_{2} ) ] }{\delta ( c-mz^{\ast} ) } \bigl( z-z^{\ast} \bigr) ^{2}. \end{aligned}$$

Finally, we obtain

$$\begin{aligned} \dot{V}_{2}(t) ={}& {-}\sum_{i=1}^{2} \biggl[ \frac{\xi_{i}d_{i} ( x_{i}-x_{i}^{\ast} ) ^{2}}{x_{i}}+\xi_{i}\beta_{i}x_{i}^{\ast}v^{\ast }f \biggl( \frac{x_{i}^{\ast}}{x_{i}} \biggr)\\ &{} +\frac{\xi_{i}\beta_{i}x_{i}^{\ast}v^{\ast}}{G} \int_{0}^{s_{5}}g(\tau)e^{-n\tau}f \biggl( \frac{v^{\ast}u_{i}(t-\tau)}{vu_{i}^{\ast}} \biggr) \,d\tau \biggr] \\ & {}-\rho_{1}\beta_{1}H_{1}x_{1}^{\ast}v^{\ast}f \biggl( \frac{y_{1}u_{1}^{\ast }}{y_{1}^{\ast}u_{1}} \biggr) -\rho_{1}\beta_{1}x_{1}^{\ast}v^{\ast} \int _{0}^{s_{1}}h_{1}(\tau)e^{-m_{1}\tau}f \biggl( \frac{y_{1}^{\ast}x_{1}(t-\tau)v(t-\tau)}{y_{1}x_{1}^{\ast}v^{\ast}} \biggr) \,d\tau \\ &{} -\rho_{2}\beta_{2}H_{3}x_{2}^{\ast}v^{\ast}f \biggl( \frac{y_{2}u_{2}^{\ast }}{y_{2}^{\ast}u_{2}} \biggr) -\rho_{2}\beta_{2}x_{2}^{\ast}v^{\ast} \int _{0}^{s_{3}}h_{3}(\tau)e^{-m_{3}\tau}f \biggl( \frac{y_{2}^{\ast}x_{2}(t-\tau)v(t-\tau)}{y_{2}x_{2}^{\ast}v^{\ast}} \biggr) \,d\tau \\ &{} -\frac{a+\delta}{\delta}(1-\rho_{1})\beta_{1}x_{1}^{\ast}v^{\ast} \int _{0}^{s_{2}}h_{2}(\tau)e^{-m_{2}\tau}f \biggl( \frac{u_{1}^{\ast}x_{1}(t-\tau)v(t-\tau)}{u_{1}x_{1}^{\ast}v^{\ast}} \biggr) \,d\tau \\ &{} -\frac{a+\delta}{\delta}(1-\rho_{2})\beta_{2}x_{2}^{\ast}v^{\ast} \int _{0}^{s_{4}}h_{4}(\tau)e^{-m_{4}\tau}f \biggl( \frac{u_{2}^{\ast}x_{2}(t-\tau)v(t-\tau)}{u_{2}x_{2}^{\ast}v^{\ast}} \biggr) \,d\tau \\ &{} -\frac{p(a+\delta) [ b+m ( u_{1}+u_{2} ) ] }{\delta ( c-mz^{\ast} ) } \bigl( z-z^{\ast} \bigr) ^{2}. \end{aligned}$$

Applying LaSalle’s invariance principle to the last equation, we get \(\dot{V}_{2}\leq0\), leading to the global asymptotic stability of the chronic steady state \(E^{\ast}\). □

4 Numerical simulations

In this section, we perform numerical simulation for model (6)–(13) with values of the parameters given in Table 1. Let us consider for simplicity that \(\tau_{1}=\tau_{2}=\tau_{3}=\tau_{4}=\tau_{5}=\tau_{c}\), and chose the initial conditions as:

  1. (IC1)

    \(\omega_{1}(\eta )=700, \omega_{2}(\eta)=20, \omega_{3}(\eta)=15, \omega_{4}(\eta )=15, \omega_{5}(\eta)=0.0005, \omega_{6}(\eta)=0.0005, \omega_{7}(\eta)=15 \) and \(\omega_{8}(\eta)=1.5\);

  2. (IC2)

    \(\omega_{1}(\eta)=500, \omega_{2}(\eta)=15, \omega_{3}(\eta)=10, \omega_{4}(\eta)=10, \omega_{5}(\eta)=0.001, \omega_{6}(\eta)=0.001, \omega_{7}(\eta)=12 \) and \(\omega_{8}(\eta)=1\);

  3. (IC3)

    \(\omega_{1}(\eta)=300, \omega_{2}(\eta)=5, \omega_{3}(\eta)=5, \omega_{4}(\eta)=1, \omega_{5}(\eta)=0.3, \omega_{6}(\eta)=0.3, \omega_{7}(\eta )=8 \) and \(\omega_{8}(\eta)=0.5\), \(\eta \in {}[-\max \{ \tau_{1},\tau_{2},\tau_{3},\tau_{4},\tau_{5}\},0]\).

Table 1 The parameter values of model (6)–(13)
Full size table

Case I. Stability of the steady states

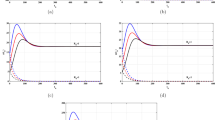
Let \(\tau_{c}=0.7\) and \(\rho_{1}=\rho_{2}=0.5\). We have two subcases shown in Fig. 1:

Figure 1
figure 1

The evolution of model (6)–(13) with varied infection rates

Full size image

(a) if \(\beta_{1}=2.4\times10^{-5}\) and \(\beta_{2}=2\times10^{-5}\), then \(R_{0}=0.0264<1\). It follows that \(E_{0}\) is globally asymptotically stable. In this case the concentration of the uninfected cells is increasing and returns to its normal value \(\lambda_{i}/d_{i}\), while the concentrations of infected cells, HIV particles and CTLs are decaying and approach zero.

(b) if \(\beta_{1}=0.002\) and \(\beta_{2}=0.001\) then \(R_{0}=2.1955>1\). Therefore, \(E^{\ast}\) exists and is globally asymptotically stable. In this case the concentration of the uninfected cells is decreasing, while the concentrations of infected cells, HIV particles and CTLs are increasing. In this situation HIV infection will be chronic.

From the above, one can see that the infection rate parameters \(\beta_{1}\) and \(\beta_{2}\) have significant effects on stabilizing the infection-free steady state. This is because \(R_{0}\) can be decreased by decreasing the values of \(\beta_{1}\) and \(\beta_{2}\). The values of the parameters \(\beta_{1}\) and \(\beta_{2}\) can be reduced when an HIV infected patient is treated by reverse transcriptase inhibitor (RTI) drugs which prevent HIV from infecting the uninfected target cells. When incorporating the RTI drugs into the HIV dynamics model, the parameters \(\beta_{1}\) and \(\beta_{2}\) will be replaced by \((1-\epsilon)\beta_{1}\) and \((1-\epsilon)\beta_{2}\), respectively, where ϵ is the drug efficacy with \(0\leq \epsilon<1\). In this case, the basic reproduction number is given by

$$R_{0}(\epsilon)=\frac{(1-\epsilon)\delta k}{\mu r(a+\delta)} \bigl( \gamma _{1} \beta_{1}x_{1}^{0}+\gamma_{2} \beta_{2}x_{2}^{0} \bigr). $$

Therefore, one can find the minimum drug efficacy \(\epsilon_{m}\), which makes \(R_{0}(\epsilon)\leq1\) and then stabilizes the system around the infection-free steady state \(E_{0}\), as:

$$ \epsilon_{m}=\max \biggl\{ 1-\frac{\mu r(a+\delta)}{\delta k ( \gamma _{1}\beta_{1}x_{1}^{0}+\gamma_{2}\beta_{2}x_{2}^{0} ) },0 \biggr\} . $$
(43)

Case II. Effect of the time delay on the HIV dynamics

In this case, we fix the parameters \(\beta_{1}=0.002\), \(\beta_{2}=0.001\) and \(\rho_{1}=\rho_{2}=0.5\). We consider initial conditions IC1. Figure 2 shows that the stability of the steady states has been changed by changing the values of the delay parameter \(\tau_{c}\). It can be seen that as \(\tau_{c}\) is increased the concentration of the uninfected cells is increased, while the concentrations of infected cells, free HIV particles and CTLs are decreased. From Fig. 2 we can see that, in case of smaller values of \(\tau_{c}\), trajectories of the system will converge to \(E^{\ast}\). If the value of \(\tau_{c}\) is increased, trajectories will converge to \(E^{\ast}\) and finally approach \(E_{0}\). Using the values of the parameters given in Table 1, we have the following:

Figure 2
figure 2

The evolution of model (6)–(13) with varied \(\tau_{c}\)

Full size image
  1. (i)

    if \(0.0\leq \tau_{c}<1.0932\), then \(E^{\ast}\) exists and is globally asymptotically stable;

  2. (ii)

    if \(\tau_{c}\geq1.0932\), then \(E_{0}\) is globally asymptotically stable.

This result support the results of Theorems 1 and 2.

From a biological point of view, the intracellular delay plays a similar role as an antiviral treatment in eliminating the virus. We observe that sufficiently large delay suppresses viral replication and clears the virus from the body. This gives us some suggestions on new drugs to prolong the increase of the intracellular delay period.

Case III. Effect of latency on the dynamical behavior of the system

In this case, we show the HIV dynamics for different values of \(\rho_{i}\), the fraction of uninfected cells that become latently infected cells. We take \(\beta_{1}=0.002\), \(\beta_{2}=0.001\), \(\tau_{c}=0.8\) and the initial conditions IC1. For simplicity we let \(\rho_{1}=\rho_{2}=\rho_{c}\). Figure 4 shows the effect of \(\rho_{c}\) on the the evolution of system states. When \(\rho_{c}\) increases, we observe an increase in the concentration of the latently infected CD4+ T cells and macrophages. This means that the reservoirs of these cells are enlarged, which promotes an increase in the amount of virus that escapes treatment [18]. Subsequently, after activation of the latently infected cells, new HIV will be produced and released into the blood stream [55]. From Fig. 4 we can see that, when \(\rho_{c}\) is increased, the concentrations of uninfected cells, actively infected cells, free HIV particles and CTLs are decreased. Using the values of the parameters given in Table 1 we have the following:

  1. (i)

    if \(0.0\leq \rho_{c}<0.9437\), then \(R_{0}>1\) and \(E^{\ast}\) exists and is globally asymptomatically stable;

  2. (ii)

    if \(\rho_{c}\geq0.9437\), then \(R_{0}\leq1\) and \(E_{0}\) is globally asymptomatically stable.

Case IV. Effect of the immune impairment parameter m on the HIV dynamics

In this case, we choose \(\beta_{1}=2.4\times10^{-3}\), \(\beta_{2}=2\times10^{-3}\), \(\tau_{c}=0.5, \rho_{c}=0.5\) and the initial conditions IC4: \(\omega_{1}(\eta)=280, \omega_{2}(\eta )=15, \omega_{3}(\eta)=9, \omega_{4}(\eta)=1, \omega_{5}(\eta )=0.045, \omega_{6}(\eta)=0.03, \omega_{7}(\eta)=11 \) and \(\omega_{8}(\eta)=0.5\). Figure 3 shows that, as m is increased, the concentration of CTL cells is decreased and then the concentrations of latently infected cells, actively infected cells and free HIV particles are increased, while the concentration of the uninfected cells is decreased. We note that \(R_{0}\) does not depend on the parameter m; therefore, m does not change the stability properties of steady states.

Figure 3
figure 3

The evolution of model (6)–(13) with varied m

Full size image
Figure 4
figure 4

The evolution of model (6)–(13) with varied \(\rho_{c}\)

Full size image

5 Conclusion and discussion

All of the existing mathematical models of HIV infection with CTL immune impairment study the HIV infection and production in one class of target cells, CD4+ T cells. However, it has been reported in several papers that HIV can infect both CD4+ T cells and macrophages. In this paper, we have studied an HIV dynamics model with CTL immune impairment and with two classes of target cells, CD4+ T cells and macrophages. We have considered two types of infected cells, latently infected cells (such cells contain HIV but are not producing it) and actively infected cells (such cells are producing HIV). The model considers multiple discrete or distributed time delays to characterize the time between an HIV contact of an uninfected target cell and the creation of mature HIV particles. We have shown that the solutions of the model are nonnegative and ultimately bounded which ensures the well-posedness of the model. We have derived a biological threshold number \(R_{0}\) (the basic reproduction number) which fully determines the existence and stability of the two steady states of the model. We have investigated the global stability of the model steady states by using Lyapunov method and LaSalle’s invariance principle. We have proven that (i) if \(R_{0}\leq1\), then the infection-free steady state \(E_{0}\) is globally asymptotically stable and HIV is predicted to be completely cleared from the HIV infected individuals, (ii) if \(R_{0}>1\), then the chronic steady state \(E^{\ast}\) is globally asymptotically stable and a chronic HIV infection is attained. We have conducted numerical simulations and have shown that both the theoretical and numerical results are consistent.

Our analysis extends the results presented in [49], where the global stability was analyzed for a model with one target cell population. When we consider the HIV dynamics with only one class of target cells, CD4+ T cells, then model (6)–(13) under the effect of RTI drug therapy with drug efficacy ϵ leads to the following model:

$$\begin{aligned} &\dot{x}_{1}(t) =\lambda_{1}-d_{1}x_{1}(t)-(1- \epsilon)\beta_{1}x_{1}(t)v(t), \end{aligned}$$
(44)
$$\begin{aligned} &\dot{y}_{1}(t) =(1-\epsilon)\rho_{1} \beta_{1}e^{-\alpha_{1}\tau_{1}}x_{1}(t- \tau_{1})v(t-\tau_{1})-ay_{1}(t)-\delta y_{1}(t), \end{aligned}$$
(45)
$$\begin{aligned} &\dot{u}_{1}(t) =(1-\epsilon) (1-\rho_{1}) \beta_{1}e^{-\alpha_{2}\tau_{2}}x_{1}(t-\tau_{2})v(t- \tau_{2})+\delta y_{1}(t)-pu_{1}(t)z(t)-\mu u_{1}(t), \end{aligned}$$
(46)
$$\begin{aligned} &\dot{v}(t) =ke^{-\alpha_{5}\tau_{5}}u_{1}(t-\tau_{5})-rv(t), \end{aligned}$$
(47)
$$\begin{aligned} &\dot{z}(t) =cu_{1}(t)-mu_{1}(t)z(t)-bz(t). \end{aligned}$$
(48)

The basic reproduction number for system (44)–(48) is given by

$$R_{0}^{C}(\epsilon)=\frac{(1-\epsilon)\delta k\gamma_{1}\beta_{1}x_{1}^{0}}{\mu r(a+\delta)}. $$

The basic reproduction number for system (6)–(13) under the effect of RTI drug therapy can be written as:

$$\begin{aligned} &R_{0}(\epsilon) =R_{0}^{C}( \epsilon)+R_{0}^{M}(\epsilon), \\ &R_{0}^{C}(\epsilon) =\frac{(1-\epsilon)\delta k\gamma_{1}\beta_{1}x_{1}^{0}}{\mu r(a+\delta)}, \\ &R_{0}^{M}(\epsilon) =\frac{(1-\epsilon)\delta k\gamma_{2}\beta_{2}x_{2}^{0}}{\mu r(a+\delta)}, \end{aligned}$$

where \(R_{0}^{M}(\epsilon)\) is the basic reproduction number of a model that describes the HIV dynamics with only macrophages and neglects the CD4+ T cells. For system (44)–(48) one can determine the minimum drug efficacy \(\epsilon_{m}^{C}\) such that \(R_{0}^{C}(\epsilon_{m}^{C})<1\), namely

$$ \epsilon_{m}^{C}=\max \biggl\{ 1-\frac{\mu r(a+\delta)}{\delta k\gamma_{1}\beta_{1}x_{1}^{0}},0 \biggr\} . $$
(49)

Comparing Eqs. (43) and (49), we get that \(\epsilon _{m}^{C}\leq \epsilon_{m}\). Therefore, if we apply drugs with ϵ such that \(\epsilon_{m}^{C}\leq \epsilon<\epsilon_{m}\), this guarantees that \(R_{0}^{C}(\epsilon)\leq1\), and then \(E_{0}\) of system (44)–(48) is globally asymptotically stable; however, \(R_{0}(\epsilon)>1\) and so \(E_{0}\) of (6)–(13) is unstable. Therefore, more accurate drug efficacy ϵ is determined when using the model with two classes of target cells. This shows the importance of considering the effect of the macrophages in the HIV dynamics.

In the literature, fractional-order differential equations have been applied with the purpose of obtaining a deeper understanding of the complex behavioral patterns of HIV dynamical systems [53, 55,56,57]. The memory property of the fractional models allows the integration of more information from the past, which translates into more accurate predictions for the model. Clinicians can thus use the information (in terms of behavior predictions) of fractional-order systems to fit patients’ data with the most appropriate non-integer-order index [53]. As a future work it is reasonable to use a corresponding fractional modification of our models, as fractional differential equations inherently include memory.