Abstract
This paper studies the robust adaptive control of fractional-order chaotic systems with system uncertainties and bounded external disturbances. Based on a proposed lemma, quadratic Lyapunov functions are used in the stability analysis and fractional-order adaptation laws are designed to update the controller parameters. By employing the fractional-order expansion of classical Lyapunov stability method, a robust controller is designed for fractional-order chaotic systems. The system states asymptotically converge to the origin and all signals in the closed-loop system remain bounded. A counterexample is constructed to show that the fractional-order derivative of a function is less than zero does not mean that the function monotonically decreases (this property appears in many references). Finally, simulation results are presented to confirm our theoretical results.
Similar content being viewed by others
1 Introduction
Chaos phenomenon is very common in physical systems (also biology, economics, etc.), and chaotic systems have become one of the hot topics in the nonlinear systems [1–14]. Since Lorenz discovered the first chaotic attractor, the research on the control and synchronization of chaotic systems has been widely used in many fields. In the past 20 years, many chaos control and synchronization methods have been proposed [15–17]. Fractional-order calculus has almost the same long history as integer calculus. It was found that the complex chaotic behavior appeared if one introduced the fractional differential operator into the integer order chaotic systems. In fact, fractional-order calculus provides new mathematical tools for many practical systems, especially for chaotic systems in physics, because it is very suitable for describing the dynamic behavior of some physical systems that are very sensitive to the initial state values [18–28]. There are many methods (such as drive-response control, Lyapunov function method, sliding mode control, generalized synchronization control, active control, nonlinear feedback control) on synchronization and control of fractional-order chaotic systems. However, some new problems run into the case of fractional-order chaotic systems. Firstly, as the tiny initial value changes will cause the system’s trajectory shape and affect its stability, it is difficult to control or synchronize the chaotic systems. Secondly, although the Lyapunov second method of fractional-order systems is proposed in [29], and the control and stability analysis of fractional order nonlinear systems has gradually become a research focus, it is hard to use the squared Lyapunov function in the stability analysis of fractional-order systems because the fractional-order derivatives of square functions have a very complex form (as pointed out in [30, 31]). In order to get over it, many efforts have been made. In 2015, Liu et al. [32, 33] proposed a method to realize adaptive fuzzy synchronous control of uncertain fractional-order chaotic systems with unknown asymptotic control gain. This is really a relatively universal construction method which can be used in many kinds of control and synchronization of chaotic systems [26, 32, 34–50].
We must point out that the technical part of the successful use of this method is Remark 1 (i.e., Lemma 5 in [32] or Lemma 7 in [33]) which is indeed questionable. In this paper, we proposed some corrections and verified that the revised theory can still work in control of chaotic systems. Our contributions are as follows:
-
To coin a counterexample which shows that the fractional-order derivative of a function is less than zero does not mean that the function monotonically decreases. Then we correct Lemma 5 in [32] and Lemma 7 in [33] to Lemma 4 in this paper.
-
To further verify the effectiveness of the new Lemma 4 in the above relatively universal fractional-order Lyapunov second method, we study the robust adaptive control of fractional-order chaotic systems with bounded external disturbances and system uncertainties.
2 Preliminaries
In this section we present some notions and lemmas which are needed in this paper.
Definition 1
(1) Suppose \(f:[0,+\infty)\longrightarrow R\) (the set of all real numbers) and \(f'\) are bounded and continuous almost everywhere. The Caputo fractional-order derivative and Caputo fractional-order integral of f with order α (\(\alpha\in(0,1)\)) are defined by the following equalities (1) and (2), respectively [51]:
where \(\Gamma(z)=\int_{0}^{\infty}e^{-t}t^{z-1}\,dt\) (\(z\in \mathbb{C}\), \(\operatorname{Re}(z)>0\)) is the gamma function, and \(\mathbb{C}\) is the set of all complex numbers.
(2) Assume that \(f:[0,+\infty)\longrightarrow R\) is piecewise continuous and satisfies \(|f(t)|\leq Me^{ct}\) for some \(M>0\) and \(c\geq0\). Then the integral \(\int_{0}^{\infty}f(t)e^{-{z}t}\,dt\) is convergent in \({\mathbb {C}}_{c}=\{z\in{\mathbb {C}} \mid \operatorname{Re}(z)>c\}\), and hence we get a mapping \(F:{\mathbb {C}}_{c}\longrightarrow{\mathbb {C}}\) (called the Laplace transformation of f, written also as \({\mathscr{L}}(f)\)). It has been shown that there exists unique \(g:[0,+\infty)\longrightarrow R\) (called the inverse Laplace transformation of F, written as \({\mathscr{L}}^{-1}(F)\)) such that \({\mathscr{L}}(g)=F\) (i.e., \(g=f\)). It can be shown that the Laplace transform of the Caputo fractional derivative is
(3) The convolution G of two functions f and g is defined by \(G(x)=f(x)*g(x)= \int_{-\infty}^{+\infty}f(u)g(x-u)\,du\), and the Mittag-Leffler function with two parameters is defined by
where \(\alpha,\beta>0\). Note that \(E_{1,1}(s)=e^{s}\). The Laplace transform of the function \(f(t)=t^{\beta-1}E_{\alpha,\beta}(-a t^{\alpha})\) is [52]
Lemma 1
([29])
Let \(\mathbf{0}: [0,+\infty)\longrightarrow R^{n}\) be the mapping taking constant value \(\mathbf{0}=[0,0,\ldots, 0]\), where \(R^{n}\) is the ordinary n-dimensional Euclidean space. If 0 is an equilibrium of the following fractional-order nonlinear system (where \(\boldsymbol{x}: [0,+\infty)\longrightarrow R^{n}\)):
and there exist a Lyapunov function \(V(t,{\boldsymbol {x}})\) and three class-k functions \(g_{1}\), \(g_{2}\), \(g_{3}\) such that
where \(0<\beta<1\), and \(\|\cdot\|\) is the Euclidean norm, then the equilibrium point 0 of system (6) is Mittag-Leffler stable (and thus asymptotically stable).
Lemma 2
Suppose that \(x(t)\in C^{1}[0,T]\) where T is a positive constant, then the following two equations hold:
Lemma 3
([51])
If \({\boldsymbol {x}}: [0,+\infty)\longrightarrow R^{n}\) is continuously derivable, then
3 Controller design and stability analysis
In this paper, the fractional-order chaotic system model is considered. This mathematical model describes a fractional-order system by n-directional nonlinear fractional-order differential equations. The considered model can be expressed as follows:
where \(x_{i}(t)\) is the state variable. Assume that system (12) has some equilibrium points, one of them is noted as \({\boldsymbol {x}}^{*}=(x^{*}_{1},x^{*}_{2},\ldots,x^{*}_{n})^{T}\).
According to (12), the controlled model can be expressed as follows:
where \(\Delta f_{i}({\boldsymbol {x}}(t))\) is system uncertainty, \(d_{i}(t)\) is unknown external disturbance, and \(u_{i}(t)\) is the control input.
Let the error state be
In the closed-loop system, we will design the control input \(u_{i}(t)\) to make sure that the error states converge to the origin and all signals remain bounded. To reach this goal, the following assumptions are needed.
Assumption 1
The system uncertainty \(\Delta f_{i}({\boldsymbol {x}}(t))\) is Lipschitz continuous, and there exists a positive constant \(\gamma_{i}\) such that
where \(\|\cdot\|\) denotes the Euclidean norm.
Assumption 2
The external disturbance \(d_{i}(t)\) is a bounded continuous function, i.e., \(d_{i}(t)\) satisfies the following inequality:
where \(d_{i}\) is a positive constant.
Since the Caputo derivative of a constant is zero, from (13) and (14) we have
For each \(i\in\{1,2,\ldots,n\}\), multiplying \(e_{i}(t)\) to both sides of (17), by Assumptions 1 and 2, we have
Then we design a controller \(u_{i}(t)\) as follows:
where \(k_{i}\) is a positive design parameter, \(\hat{\gamma}_{i}(t)\) is the estimation of \(\gamma_{i}\), and \(\hat{\bar{d}}_{i}(t)\) is the estimation of \(\bar{d}_{i}\).
Substituting (19) into (18) yields
where
and
are the estimation errors of unknown parameters \(\gamma_{i}\) and \(\bar{d}_{i}\), respectively.
Remark 1
In [32], there exists such a result: Suppose that \(f':[0,+\infty)\longrightarrow R\) is continuous. Then \(f:[0,+\infty )\longrightarrow R\) is monotone increasing (resp., monotone decreasing) if \(D^{\alpha}(f)(t)\geq0\) (resp., \(D^{\alpha}(f)(t)\leq0\)) for all \(t\in[0,+\infty)\). However, this result is not proper. In this section we will construct a counter-example to show this and meanwhile give a corrected form (i.e., Lemma 4).
Example 1
Let \(\alpha\in(0,1)\). We are going to construct the needed counter-example in 11 steps.
Step 1. Let \(a=\max \{1,\frac{1}{4^{1-\alpha }-2^{1-\alpha}} \}\), and
From
we have
Step 2. Let
By L’Hospital’s rule, we have
From (26) and (27), we can know
Step 3. Since \(h_{2}(t)= t^{-\alpha}\) is decreasing in \((0,+\infty)\), \(\frac{1}{(t-3)^{\alpha}}\leq\frac{1}{(t-4)^{\alpha}}\) (\(\forall t\in(4,+\infty)\)), thus
and
Step 4.
Step 5. As \(I(t)\) is continuous in \([4,+\infty)\) and \(\lim_{t\rightarrow+\infty}I(t)=0\) (see (28)), there exists \(b>0\) such that \(|I(t)|\leq b\) (\(\forall t\in[4,+\infty)\)).
Step 6. Given \(t\in(4,+\infty)\), we note
As \(u''(\tau)=(-\alpha)(-\alpha-1)(t-\tau)^{-\alpha-2}\geq0\), \(u(\tau)=\frac{1}{(t-\tau)^{\alpha}}\) is convex downwards in \([0,t)\), thus
Step 7. From (29) and (33) we know (\(\forall t\in(4,+\infty)\))
Step 8. There exists \(t_{0}\in (4,+\infty)\) such that \(I(t)\geq0\) (\(\forall t\in [t_{0},+\infty)\)). In fact, \(\lim_{t\rightarrow +\infty}[2(t-4)^{\alpha}-t^{\alpha}]=+\infty\) by (27). As \(2(t-4)^{\alpha}-t^{\alpha}\) is continuous,
for some \(t_{0}\in(4,+\infty)\), which together with (34) implies \(I(t)\geq0\) (\(\forall t\in[t_{0},+\infty)\)).
Step 9. Let \(c=\max \{0, b [\int _{2.25}^{2.75}\frac{d\tau}{(t_{0}-\tau)^{\alpha}} ]^{-1} \}\),
and
Then \(g(x)\) is a piecewise linear continuous function which is negative just in \((3,4)\). From the fundamental theorem of calculus, we know the function \(f(t)=\int_{0}^{t}g(x)\,dx\) satisfies \(f'(0+)=g(0)\) and \(f'(t)=g(t)\). By the definitions of \(g(x)\) and \(f(t)\), \(f(t)\) is monotonous increasing in \([0,3]\) and \([4,+\infty)\) but monotonous decreasing in \((3,4)\), which means that \(f(t)\) is not monotone in \([0,+\infty)\).
Step 10. Now we prove
If \(t\in[0,3)\), then \((t-\tau)^{\alpha}>0\) (\(\tau\in[0,t)\)), and thus \(\frac{g(\tau)}{(t-\tau)^{\alpha}}\geq0\) (\(\tau\in [0,t)\)) by the definition of \(g(x)\), which means \(D^{\alpha}(f)(t)\geq 0\). If \(t\in[3,4]\), then \(\varphi'(t)\leq0\) (i.e., \(\varphi(t)= t^{1-\alpha}-(t-2)^{1-\alpha}\) is monotonous decreasing) by Step 3 and the minimum of \(\varphi(t)\) in \([3,4]\) is \(\varphi(4)=4^{1-\alpha}-2^{1-\alpha}\). As \(\psi(t)=(t-3)^{1-\alpha}\) is monotonous increasing, its maximum on \([3,4]\) is \(\psi(4)=1\). By Step 1,
If \(t\in(4,+\infty)\), then
If \(t\in(4,t_{0}]\), then
If \(t\in(t_{0},+\infty)\), then
Step 11. From Steps 1–10 we know \(h(t)=-f(t)\) is differentiable in \([0,+\infty)\), \(h'\) is continuous, and \(D^{\alpha}(h)(t)\leq0\) (\(t\in[0,+\infty)\)), but \(h(t)\) is not monotone in \([0,+\infty)\).
Remark 2
This example shows a difference between fractional and integer order calculus. And the results in [32] are still right because their proofs are valid as long as we replace Lemma 5 in [32] by the following Lemma 4. In many closed-loop systems, it is difficult to determine that all signals are bounded. With the following lemma, we can manage to do this. For example, the signals γ̂ and \(\hat{\bar{d}}\) in system (13).
Lemma 4
Assume that \(f'\) is continuous and bounded in \([0,+\infty)\). Then \(f(t)\geq f(0)\) if \(D^{\alpha}(f)(t)\geq0\) (\(t\in [0,+\infty)\)), and \(f(t)\leq f(0)\) if \(D^{\alpha}(f)(t)\leq0\).
Proof
We just prove the first part of this lemma.
Step 1.On \([0,+\infty)\), if f is continuous \(S_{t}=\{(u,v)\in R^{2}\mid0\le u\leq v\le t\}\) (\(t>0\)) and \(\alpha,\beta\in(0,1)\), by Fubini’s theorem [54], the following holds:
Step 2. If f is continuous on \([0,+\infty)\), we have
In fact, let
the partial derivatives of (45) are continuous and their Jacobian matrix is not 0 almost everywhere in the domain. By the definition of Caputo fractional-order integral and Step 1, we have (where B is the beta function)
Step 3. If \(f'\) is bounded and continuous in \([0,+\infty)\), then
In fact, from the definitions of Caputo derivative and integral, we know \(D^{\alpha}(f)=I^{1-\alpha}(f')\). By Step 2,
By the fundamental theorem of calculus, \(I^{1}(f')=f(t)-f(0)\).
Step 4. Since \(D^{\alpha}(f)(t)\geq0\) (\(t\in [0,+\infty)\)), \(f(t)-f(0)= I^{\alpha}\circ D^{\alpha}(f)(t)\geq0\) (\(\forall t\in[0,\infty)\)) by Step 3 and the definition of \(I^{\alpha}\), which means \(f(t)\geq f(0)\) (\(\forall t\in[0,\infty)\)). □
And we show the following lemma.
Lemma 5
Let \(V_{1}(t)=\frac{1}{2}x^{2}(t)+\frac{1}{2}y^{2}(t)\), where \(x,y: [0,+\infty)\longrightarrow R\) is a continuous function. If
where k is a positive constant, then we have
Proof
Using the fractional integral operator \({I^{\alpha}}\) to both sides of (49), it follows from Lemma 2 that
It follows from (51) that
There exists a nonnegative function \(m(t)\) such that
Taking the Laplace transform (\(\mathscr{L}\{\cdot\}\)) on (53) by (3) gives
where \({}_{2}X(s)\) and \(M(s)\) are Laplace transforms of \(x^{2}(t)\) and \(m(t)\), respectively. Using (5), the solution of (54) will be given as
where ∗ represents the convolution operator. Noting that \(m(t)\), \(E_{\alpha,0}(-2kt^{\alpha})\) and \(t^{-1}\) are nonnegative functions, it follows from (55) that (50) holds. Then this ends the proof for Lemma 5. □
Based on the above discussions, now we are ready to give the following results.
Theorem 1
Consider the fractional-order chaotic system (13). Under Assumptions 1 and 2, let the control input be (19). If \(\hat{\gamma}_{i}(t)\) and \(\hat{\bar{d}}_{i}(t)\) are updated by
and
respectively, where \(h_{i}\) and \(m_{i}\) are positive design parameters, then the tracking error \(e_{i}(t)\) will tend to the origin asymptotically, and all signals in the closed-loop system will remain bounded.
Proof
Let us consider the following Lyapunov function candidate:
Then, by using Lemma 3, we have
Noting that the fractional-order derivative of a constant is zero, from (21) and (22) we have
and
Substituting (20), (60), and (61) into (59), we have
Then substituting (56) and (57) into (62) gives
Thus, we have \(D^{\alpha}V_{i}(t) \leq-k_{i} |e_{i}(t)|^{2}\leq0\). According to Lemma 4, \(V_{i}(t) \leq V_{i}(0)\). In addition, for \(V_{i}(t)=\frac{1}{2}e_{i}^{2}(t)+\frac{1}{2h_{i}} \tilde{\gamma}_{i}^{2}(t)+\frac{1}{2m_{i}} {\tilde{\bar{d}}_{i}}^{2}(t)\), we can know that \(e_{i}(t)\), \(\tilde{\gamma}_{i}(t)\), and \({\tilde{\bar{d}}_{i}}(t)\) are all bounded. From Lemma 5 and (63), we can conclude that \(e_{i}(t)\) will asymptotically converge to the origin. This ends the proof for Theorem 1. □
Remark 3
In the stability analysis of fractional-order nonlinear systems, the Lyapunov function candidate \(V(t)=2e^{T}(t)e(t)\) is often used. The αth-order of \(V(t)\) can be given as
where
We can see that it is very hard to use the above complicated infinite series to analyze the stability of fractional-order systems. However, in this paper, by using Lemma 3 and the proposed Lemma 5, we need not tackle the above complicated infinite series.
4 Simulation studies
Consider the following fractional-order system with Caputo fractional derivative:
Let \(\alpha=0.95\), and the equilibrium point is \((2,3.2^{0.5},0.8^{0.5})^{T}\).
The system uncertainties are chosen as:
We can easily conclude that Assumption 1 is satisfied. Let the external disturbances be
Assumption 2 is satisfied, too. The controller design parameters are chosen as \(k_{1}=k_{2}=k_{3}=1\), \(h_{1}=h_{2}=h_{3}=0.1\), \(m_{1}=m_{2}=m_{3}=0.1\). The initial conditions of the fractional-order adaptation law are chosen as \(\hat{\gamma}_{1}(0) = 0.1\), \(\hat{\gamma}_{2}(0) =0.2\), \(\hat{\gamma}_{3}(0) =0.2\), \(\hat {\bar{d}}_{1}(0)=0.1\), \(\hat{\bar{d}}_{2}(0)=0.1\), \(\hat{\bar{d}}_{3}(0)=0.2\). To eliminate the chattering phenomenon, the discontinuous term \(\operatorname{sign}(\cdot)\) is replaced by \(\arctan (10\cdot)\).
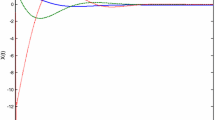
Figure 1 shows the behavior of the chaotic system. Figure 2 shows how the fractional-order system has become stable when the controller is activated since \(t=30\). Figure 3 shows the action of controllers. In this figure, the control inputs do not converge to zero because \(f_{i}(t)\) do not converge to zero. And after \(t=30\), the error states of the fractional-order system which converge to the origin are shown in Fig. 4. From the simulation results, we can see that the good control performance has been obtained, and the system variables converge to the origin rapidly when the controller is activated at \(t=30\).
5 Conclusions
Chaotic systems can be used in many fields. Controlling fractional-order chaotic systems by using an effective control method is an interesting yet challenging work. In this paper, an example is built to show that being less than zero for a fractional-order derivative does not mean that the function monotonically decreases. And the robust control of fractional-order chaotic systems by means of adaptive control is primarily discussed. The proposed method can be divided into three aspects: (1) Based on the fractional-order Lyapunov second method, analyzing the stability of general fractional-order chaotic systems; (2) Designing the fractional-order adaptation laws and uploading the controller; (3) Using the quadratic Lyapunov functions in the stability analysis of fractional-order systems. The control theorem of fractional-order systems may be enriched by our results, and the proposed control method can also be extended to other fractional-order systems.
References
Robertson, B.R., Combs, A.: Chaos Theory in Psychology and the Life Sciences. Psychology Press, Hove (2014)
Steven, S.H.: Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering, 2nd edn. CRC Press, Boca Raton (2014)
Liu, Y.J., Tong, S.C.: Barrier Lyapunov functions for Nussbaum gain adaptive control of full state constrained nonlinear systems. Automatica 76(2), 143–152 (2017)
Li, Y.M., Tong, S.C.: Adaptive fuzzy output-feedback stabilization control for a class of switched nonstrict-feedback nonlinear systems. IEEE Trans. Cybern. 47, 1007–1016 (2017)
Wu, Y.H.: Liouville-type theorem for a nonlinear degenerate parabolic system of inequalities. Math. Notes 103(1–2), 155–163 (2018)
Liu, L.S., Sun, F.L., Zhang, X.G., Wu, Y.H.: Bifurcation analysis for a singular differential system with two parameters via to topological degree theory. Nonlinear Anal., Model. Control 22(1), 31–50 (2017)
Sun, Y., Liu, L.S., Wu, Y.H.: The existence and uniqueness of positive monotone solutions for a class of nonlinear Schrödinger equations on infinite domains. J. Comput. Appl. Math. 321, 478–486 (2017)
Xu, R., Ma, X.T.: Some new retarded nonlinear Volterra–Fredholm type integral inequalities with maxima in two variables and their applications. J. Inequal. Appl. 2017(1), 187 (2017)
Peng, X.M., Shang, Y.D., Zheng, X.X.: Lower bounds for the blow-up time to a nonlinear viscoelastic wave equation with strong damping. Appl. Math. Lett. 76, 66–73 (2018)
Feng, D.X., Sun, M., Wang, X.Y.: A family of conjugate gradient methods for large-scale nonlinear equations. J. Inequal. Appl. 2017(1), 236 (2017)
Li, F.S., Gao, Q.Y.: Blow-up of solution for a nonlinear Petrovsky type equation with memory. Appl. Math. Comput. 274, 383–392 (2016)
Gao, L.J., Wang, D.D., Wang, G.: Further results on exponential stability for impulsive switched nonlinear time-delay systems with delayed impulse effects. Appl. Math. Comput. 268, 186–200 (2015)
Gu, J., Meng, F.W.: Some new nonlinear Volterra–Fredholm type dynamic integral inequalities on time scales. Appl. Math. Comput. 245, 235–242 (2014)
Lin, X.L., Zhao, Z.Q.: Existence and uniqueness of symmetric positive solutions of 2n-order nonlinear singular boundary value problems. Appl. Math. Lett. 26(7), 692–698 (2013)
Shevitz, D., Paden, B.: Lyapunov stability theory of nonsmooth systems. IEEE Trans. Autom. Control 39(9), 1910–1914 (2002)
Li, X.D., Cao, J.D.: An impulsive delay inequality involving unbounded time-varying delay and applications. IEEE Trans. Autom. Control 62, 3618–3625 (2017)
Hu, J.Q., Cao, J.D., Guerrero, J.M., Yong, T.Y., Yu, J.: Improving frequency stability based on distributed control of multiple load aggregators. IEEE Trans. Smart Grid 8, 1553–1567 (2017)
Wu, J., Zhang, X.G., Liu, L.S., Wu, Y.H.: Positive solution of singular fractional differential system with nonlocal boundary conditions. Adv. Differ. Equ. 2014(1), 323 (2014)
Zhang, X.G., Liu, L.S., Wu, Y.H.: Variational structure and multiple solutions for a fractional advection–dispersion equation. Comput. Math. Appl. 68(12), 1794–1805 (2014)
Wang, Y., Liu, L.S., Wu, Y.H.: Positive solutions for a class of higher-order singular semipositone fractional differential systems with coupled integral boundary conditions and parameters. Adv. Differ. Equ. 2014(1), 268 (2014)
Jiang, J.Q., Liu, L.S., Wu, Y.H.: Positive solutions to singular fractional differential system with coupled boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 18(11), 3061–3074 (2013)
Wang, Y.Q., Liu, L.S., Wu, Y.H.: Existence and uniqueness of positive solution to singular fractional differential equations. Bound. Value Probl. 2012(1), 81 (2012)
Hao, X.A., Wang, H.Q., Liu, L.S., Cui, Y.J.: Positive solutions for a system of nonlinear fractional nonlocal boundary value problems with parameters and p-Laplacian operator. Bound. Value Probl. 2017(1), 182 (2017)
Zhang, X.G., Mao, C.L., Liu, L.S., Wu, Y.H.: Exact iterative solution for an abstract fractional dynamic system model for bioprocess. Qual. Theory Dyn. Syst. 16(1), 205–222 (2017)
Feng, Q.H., Meng, F.W.: Traveling wave solutions for fractional partial differential equations arising in mathematical physics by an improved fractional Jacobi elliptic equation method. Math. Methods Appl. Sci. 40(10), 3676–3686 (2017)
Zhang, L.H., Zheng, Z.W.: Lyapunov type inequalities for the Riemann–Liouville fractional differential equations of higher order. Adv. Differ. Equ. 2017(1), 270 (2017)
Xu, R., Meng, F.W.: Some new weakly singular integral inequalities and their applications to fractional differential equations. J. Inequal. Appl. 2016(1), 78 (2016)
Wu, J., Zhang, X.G., Liu, L.S., Wu, Y.H.: Twin iterative solutions for a fractional differential turbulent flow model. Bound. Value Probl. 2016(1), 98 (2016)
Li, Y., Chen, Y., Podlubny, I.: Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica 45(8), 1965–1969 (2009)
Trigeassou, J.C., Maamri, N., Sabatier, J., Oustaloup, A.: A Lyapunov approach to the stability of fractional differential equations. Signal Process. 91(3), 437–445 (2011)
Shen, J., Lam, J.: \(l_{\infty}\)-Gain analysis for positive systems with distributed delays. Automatica 50(1), 175–179 (2014)
Liu, H., Li, S.G., Sun, Y.G., Wang, H.X.: Adaptive fuzzy synchronization for uncertain fractional-order chaotic systems with unknown non-symmetrical control gain. Acta Phys. Sin. 64(7), 331–334 (2015)
Liu, H., Li, S.G., Wang, H.X., Li, G.J.: Adaptive fuzzy synchronization for a class of fractional-order neural networks. Chin. Phys. B 26(3), 258–267 (2017)
Benchohra, M., Henderson, J., Ntouyas, S.K., Ouahab, A.: Existence results for fractional order functional differential equations with infinite delay. J. Math. Anal. Appl. 338(2), 1340–1350 (2008)
Liu, H., Li, S., Cao, J.D., Alsaedi, A., Alsaadi, F.E.: Adaptive fuzzy prescribed performance controller design for a class of uncertain fractional-order nonlinear systems with external disturbances. Neurocomputing 219(C), 422–430 (2017)
Liu, H., Pan, Y., Li, S., Chen, Y.: Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Trans. Syst. Man Cybern. Syst. 47(8), 2209–2217 (2017)
Xu, R., Zhang, Y.: Generalized Gronwall fractional summation inequalities and their applications. J. Inequal. Appl. 2015(1), 242 (2015)
Wang, J.X., Yuan, Y., Zhao, S.L.: Fractional factorial split-plot designs with two-and four-level factors containing clear effects. Commun. Stat., Theory Methods 44(4), 671–682 (2015)
Zhang, X.G., Liu, L.S., Benchawan, W., Wu, Y.H.: The eigenvalue for a class of singular p-Laplacian fractional differential equations involving the Riemann–Stieltjes integral boundary condition. Appl. Math. Comput. 235, 412–422 (2014)
Wang, Y.Q., Liu, L.S., Wu, Y.H.: Positive solutions for a nonlocal fractional differential equation. Nonlinear Anal., Theory Methods Appl. 74(11), 3599–3605 (2011)
Shen, T.K., Xin, J., Huang, J.H.: Time-space fractional stochastic Ginzburg–Landau equation driven by Gaussian white noise. Stoch. Anal. Appl. 36(1), 103–113 (2018)
Li, M.M., Wang, J.R.: Exploring delayed Mittag-Leffler type matrix functions to study finite time stability of fractional delay differential equations. Appl. Math. Comput. 324, 254–265 (2018)
Zhang, J., Lou, Z.L., Ji, Y.J., Shao, W.: Ground state of Kirchhoff type fractional Schrödinger equations with critical growth. J. Math. Anal. Appl. 462(1), 57–83 (2018)
Ding, X.H., Cao, J.D., Zhao, X., Alsaadi, F.E.: Finite-time stability of fractional-order complex-valued neural networks with time delays. Neural Process. Lett. 46, 561–580 (2017)
Ding, X.S., Cao, J.D., Zhao, X., Alsaadi, F.E.: Mittag-Leffler synchronization of delayed fractional-order bidirectional associative memory neural networks with discontinuous activations: state feedback control and impulsive control schemes. Proc. R. Soc. A 473, 20170322 (2017)
Chen, X.Y., Cao, J.D., Ju, H.P., Huang, T.W., Qiu, J.L.: Finite-time multi-switching synchronization behavior for multiple chaotic systems with network transmission mode. J. Franklin Inst. 355, 2892–2911 (2018)
Chen, X.Y., Ju, H.P., Cao, J.D., Qiu, J.L.: Sliding mode synchronization of multiple chaotic systems with uncertainties and disturbances. Appl. Math. Comput. 308, 161–173 (2017)
Chen, X.Y., Cao, J.D., Qiu, J.L., Alsaedi, A., Alsaadi, F.E.: Adaptive control of multiple chaotic systems with unknown parameters in two different synchronization modes. Adv. Differ. Equ. 2016, 231 (2016)
Cao, J.D., Sivasamy, R., Rakkiyappan, R.: Sampled-data \(h_{\infty}\) synchronization of chaotic Lur’e systems with time delay. Circuits Syst. Signal Process. 35, 811–835 (2016)
Bao, H.B., Cao, J.D.: Finite-time generalized synchronization of nonidentical delayed chaotic systems. Nonlinear Anal., Model. Control 21, 306–324 (2016)
Liu, H., Li, S.G., Wang, H.X., Sun, Y.G.: Adaptive fuzzy control for a class of unknown fractional-order neural networks subject to input nonlinearities and dead-zones. Inf. Sci. 454–455, 30–45 (2018)
Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Academic Press, New York (1998)
Li, G., Cao, J., Alsaedi, A., Ahmad, B.: Limit cycle oscillation in aeroelastic systems and its adaptive fractional-order fuzzy control. Int. J. Mach. Learn. Cybern. 9(8), 1297–1305 (2018)
Halmos, P.R.: Measure Theory. Springer, Berlin (2007)
Acknowledgements
The authors are grateful to the referees for their helpful suggestions which have greatly improved the presentation of this paper.
Funding
This work is supported by the National Natural Science Foundation of China (No. 11771263), the Fundamental Research Funds for the Central Universities, and the Natural Science Foundation of Anhui Province of China (No. 1808085MF181).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors conceived of the study, participated in its design and coordination, read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, S., Liu, H. & Li, S. Robust adaptive control for fractional-order chaotic systems with system uncertainties and external disturbances. Adv Differ Equ 2018, 412 (2018). https://doi.org/10.1186/s13662-018-1863-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1863-9