Abstract
In this paper, a two species amensalism model with Michaelis–Menten type harvesting and a cover for the first species that takes the form
is investigated, where \(a_{i}\), \(b_{i}\), \(i=1,2\), and \(c_{1}\) are all positive constants, k is a cover provided for the species x, and \(0< k<1\). The stability and bifurcation analysis for the system are taken into account. The existence and stability of all possible equilibria of the system are investigated. With the help of Sotomayor’s theorem, we can prove that there exist two saddle-node bifurcations and two transcritical bifurcations under suitable conditions.
Similar content being viewed by others
1 Introduction
Amensalism and commensalism are common relations between the species. Here, amensalism is an interaction where a species inflicts harm on the other species without any costs or benefits received by the other, and commensalism is a relationship which is only favorable to the one side and has no influence on the other side.
During the last decade, many scholars investigated the dynamic behaviors of a commensalism model [1–13], while only recently did scholars pay attention to the dynamic behaviors of an amensalism model [1, 14–21].
Sun [14] for the first time proposed the two species amensalism model as follows:
The stability of all equilibria of the system is investigated. Zhu and Chen [15] studied the qualitative property of the following amensalism model which is a general form of the previous system:
After that, some scholars focused on an amensalism model. Han et al. [16] investigated the two species non-autonomous amensalism model. Wu [17] investigated the dynamic behaviors of the two species amensalism symbiosis model with non-monotonic function response as follows:
With more works on the amensalism mode published, some scholars paid attention to the influence of refuge on the amensalism model. Xie et al. [18] considered a two species amensalism model with a partial cover for the first species to protect it from the second species, the model is as follows:
where \(a_{i}\), \(b_{i}\), \(i=1,2\), and \(c_{1}\) are all positive constants, k is a cover provided for the species x, and \(0< k<1\). They showed that system (1.1) has four possible equilibria \(E_{0}(0,0)\), \(E_{1}(\frac{a_{1}}{b_{1}},0)\), \(E_{2}(0,\frac{a_{2}}{b_{2}})\), and \(E_{3}(x^{*},y^{*})\), where \(x^{*}=\frac{a_{1}b_{2}-a_{2}c_{1}(1-k)}{b_{1}b_{2}}\), \(y^{*}=\frac{a_{2}}{b_{2}}\). They showed that \(E_{0}(0,0)\) and \(E_{1}(\frac{a_{1}}{b_{1}},0)\) are unstable, if \(0< k<1-\frac{a_{1}b_{2}}{a_{2}c_{1}}\), then \(E_{3}(x^{*},y^{*})\) is globally stable, if \(1-\frac{a_{1}b_{2}}{a_{2}c_{1}}< k<1\), then \(E_{3}(x^{*},y^{*})\) is globally stable. More precisely, the conditions which ensure the local stability of \(E_{2}(0,\frac{a_{2}}{b_{2}})\) are enough to ensure its global stability, and once the positive equilibrium exists, it is globally stable. After that, Wu et al. [19] proposed a two species amensalism model with Holling II functional response and a cover for the first species and investigated the local and global stability property of possible equilibria of the system.
On the other hand, to obtain the resource for the development of a human being, considering the harvesting of species is necessary. During the last decade, many scholars investigated the influence of the harvesting to predator–prey or competition system [22–24].
Recently, some scholars started to focus on the influence of the harvesting on the amensalism or commensalism model [20, 25]. Chen [20] proposed a non-selective harvesting Lotka–Volterra amensalism model incorporating partial closure for the populations, investigated the existence, local stability, and the global stability property of the equilibrium solutions of the system and discussed the influence of the parameter m. Liu et al. [25] proposed a non-autonomous non-selective harvesting Lotka–Volterra commensalism model incorporating partial closure for the populations and investigated the extinction, partial survival, persistent property, and the global stability property of the solutions of the system.
There are three types of harvesting: (1) constant harvesting [26, 27]; (2) linear harvesting [28–32]; and (3) nonlinear harvesting [22–24, 33]. As we know, nonlinear harvesting is more realistic from biological and economical points of view [22]. Clark [23] first proposed a harvesting term \(h=\frac{qEx}{cE+lx}\), which is named Michaelis–Menten type functional form of catch rate. Hu and Cao [24] studied the stability and bifurcation of the system with the Michaelis–Menten type harvesting in predator.
It brings to our attention that in [18] the dynamic behaviors of the amensalism model with a partial cover are simple and interesting; at the same time, the influence of a human actor to the nature is rising. No one has ever considered the amensalism model with a cover and nonlinear harvesting. Hence, studying the dynamic behavior of the amensalism model with cover and nonlinear harvesting is meaningful. Stimulated by the works of [18, 20], and [24], we propose the following two species amensalism model with Michaelis–Menten type harvesting and a cover for the first species:
where \(a_{i}\), \(b_{i}\), \(m_{i}\), \(i=1,2\), q, E, and \(c_{1}\) are all positive constants, where \(a_{i}\) represents the intrinsic growth rate of the ith species, \(b_{i}\) describes the intraspecific competition of the ith species, k is a cover provided for the species x, and \(0< k<1\), E is the combined fishing effort used to harvest.
We take the following transformations as [26] to simplify system (1.2):
dropping the bars, system (1.2) can be written as
where
The aim of this paper is to investigate the local stability property of the possible equilibria and bifurcation of system (1.3). We arrange the paper as follows: in the next section, we investigate the existence and local stability property of the equilibria of system (1.3). In Sect. 3, we discuss the saddle-node bifurcation and transcritical bifurcation of the system. Numeric simulations are presented in Sect. 4 to show the feasibility of the main results. We end this paper with a brief discussion.
2 The existence and stability of equilibria
2.1 The existence of equilibria
The equilibria of system (1.3) are determined by the system
The system always admits the boundary equilibria \(E_{0}(0,0)\), \(E_{1}(0, \delta \beta)\), while for other possible boundary equilibria and positive equilibria, we need to consider the following situations:
(i) If \(x\neq0\), \(y=0\), we may have another boundary equilibrium \(E_{2}(x_{2},0)\), where \(x_{2}\) is the root of the following equation:
Let the discriminant of Eq. (2.2) be denoted by \(\triangle_{1}\) and express \(\triangle_{1}\) in terms of α, i.e.,
let \(\alpha_{1}\) be the root of \(\triangle _{1} (\alpha)\). After calculating, we have
(ii) If \(x\neq0\), \(y\neq0\), we may have a positive equilibrium \(E_{3}(x_{3},\delta \beta)\), where \(x_{3}\) is the root of the following equation:
Let \(\triangle_{2}\) denote the discriminant of Eq. (2.4) and express it as follows:
let \(\alpha_{2}\) be the root of \(\triangle _{2} (\alpha)\). After calculating, we have
Concerned with the number of equilibria of system (1.3), we have the following theorem.
Theorem 2.1
For all positive parameters, there are two boundary equilibria \(E_{0}(0,0)\), \(E_{1}(0, \delta \beta) \). In system (1.3), for other possible boundary equilibria and positive equilibria, we have:
-
(i)
For other possible boundary equilibria:
-
(a)
If \(\alpha >\alpha_{1}\), then system (1.3) has no other boundary equilibrium;
-
(b)
If \(\alpha =\alpha_{1}\) and \(\gamma < 1\), then there exists another boundary equilibrium \(E_{21}(x_{21},0)\), where \(x_{21}=\frac{1-\gamma}{2}\);
-
(c)
If \(\gamma <\alpha <\alpha_{1}\) and \(\gamma < 1\), then there exist two boundary equilibria \(E_{22}(x_{22},0)\), \(E_{23}(x_{23},0)\), where \(x_{22,23}=\frac{1-\gamma\mp\sqrt{\triangle}_{1} }{2}\);
-
(d)
If \(\alpha=\gamma\) and \(\gamma < 1\), then \(E_{22}\) coincides with \(E_{0}\) and there exists another boundary equilibrium \(E_{23}(x_{23},0)\), where \(x_{23}=1-\gamma\);
-
(e)
If \(0<\alpha<\gamma\), then there exists another boundary equilibrium \(E_{23}(x_{23},0)\), where \(x_{23}\) is the same as in case (c);
-
(a)
-
(ii)
For the possible positive equilibria:
-
(a)
If \(\alpha >\alpha_{2}\), then system (1.3) has no positive equilibria;
-
(b)
If \(\alpha =\alpha_{2}\) and \(\gamma < 1-\delta\beta\), then there exists a unique positive equilibrium \(E_{31}(x_{31},\delta\beta)\), where \(x_{31}=\frac{1-\delta\beta-\gamma }{2}\);
-
(c)
If \(\gamma-\gamma\delta\beta <\alpha <\alpha_{2}\) and \(\gamma < 1-\delta\beta\), then there exist two distinct positive equilibria \(E_{32}(x_{32},\delta\beta)\), \(E_{33}(x_{33},\delta\beta)\), where \(x_{32,33}=\frac{1-\delta\beta-\gamma\mp\sqrt{\triangle}_{2} }{2}\);
-
(d)
If \(\alpha=\gamma-\gamma\delta\beta\) and \(\gamma < 1-\delta\beta\), then \(E_{32}\) coincides with \(E_{1}\) and there exists a unique positive equilibrium \(E_{33}(x_{33},\delta\beta)\), where \(x_{33}=1-\delta\beta-\gamma\);
-
(e)
If \(0<\alpha<\gamma-\gamma\delta\beta\), then there exists a unique positive equilibrium \(E_{33}(x_{33},\delta\beta)\), where \(x_{33}\) is the same as in case (c).
-
(a)
Proof
Let \(f(x)=x^{2}+(\gamma +1)x+\alpha-\gamma\), we can get that if \(\alpha>\alpha_{1}\), then \(\triangle_{1}<0\), which means that the function has no zero point.
If \(\alpha=\alpha_{1}\), then \(\triangle_{1}=0\), which means that the function has a unique positive zero point \(x_{21}=\frac{1-\gamma}{2}\), where \(\gamma<1\).
If \(0<\alpha<\alpha_{1}\), then \(\triangle_{1}>0\), which means that the function has two distinct zero points \(x_{22,23}=\frac{1-\gamma\mp\sqrt{\triangle}_{1} }{2} \), and we have to discuss the symbol of them.
If \(f(0)>0\) and the symmetry is positive, we have \(x_{22,23}>0\), as the conditions mention above, it follows that \(\gamma<\alpha<\alpha_{1}\) and \(\gamma >1\). If \(f(0)>0\) and the symmetry is negative, we have \(x_{22,23}<0\). If \(f(0)=0\) and the symmetry is positive, that is, \(\alpha=\gamma\) and \(\gamma >1\), we have \(x_{22}=0\), \(x_{23}=1-\gamma\), that is to say, \(E_{22}\) coincides with \(E_{0}\) and there exists another boundary equilibrium \(E_{23}\) where \(\alpha=\gamma\) and \(\gamma >1\). If \(f(0)=0\) and the symmetry is negative, we have \(x_{22}<0\), \(x_{23}=0\). If \(f(0)<0\), no matter what the symbol of symmetry is, we have \(x_{22}<0\), \(x_{23}>0\). In other words, there exists another boundary equilibrium \(E_{23}\) where \(0<\alpha<\gamma\).
To discuss the possible positive equilibria, we use similar methods and get the results as in Theorem 2.1(ii).
This ends the proof of Theorem 2.1. □
2.2 Stability of the equilibria \(E_{0}\), \(E_{1}\)
Then, we analyze the stability of the equilibrium of system (1.3).
Theorem 2.2
For all positive parameters, there are two boundary equilibria \(E_{0}(0,0)\), \(E_{1}(0, \delta \beta)\), then:
-
(1)
\(E_{0}(0,0)\) is always unstable;
-
(2)
For \(E_{1}(0, \delta \beta)\), we have:
-
(i)
If \(1-\delta\beta-\alpha/\gamma>0\), then \(E_{1}(0, \delta \beta)\) is a saddle;
-
(ii)
If \(1-\delta\beta-\alpha/\gamma<0\), then \(E_{1}(0, \delta \beta)\) is a stable node;
-
(iii)
If \(1-\delta\beta-\alpha/\gamma=0\), then: If \(\alpha =\gamma^{2}\), then \(E_{1}(0, \delta \beta)\) is a stable node; If \(\alpha \neq\gamma^{2}\), then \(E_{1}(0, \delta \beta)\) is a saddle node.
-
(i)
Proof
The Jacobian matrix of system (1.3) is calculated as
(i) Then the Jacobian matrix of system (1.3) about the equilibrium \(E_{0}(0,0)\) is given by
The characteristic equation of Jacobian matrix (2.7) is
from which it follows that two eigenvalues of \(J(E_{0})\) are \(\lambda_{1}=1-\frac{\alpha}{\gamma}\), \(\lambda_{2}=\delta>0\). It is obvious that \(E_{0}(0,0)\) is always unstable.
(ii) The Jacobian matrix of system (1.3) about the equilibrium \(E_{1}(0, \delta \beta)\) is given by
The characteristic equation of Jacobian matrix (2.8) is
from which it follows that two eigenvalues of \(J(E_{1})\) are \(\lambda_{1}=1-\delta\beta-\frac{\alpha}{\gamma}\), \(\lambda_{2}=-\delta<0\). One could easily see that if \(1-\delta\beta-\frac{\alpha}{\gamma}>0\), then \(E_{1}(0, \delta \beta)\) is a saddle; if \(1-\delta\beta-\alpha/\gamma<0\), then \(E_{1}(0, \delta \beta)\) is a stable node; if \(1-\delta\beta-\frac{\alpha}{\gamma}=0\), i.e., \(\lambda_{1}=0, \lambda_{2}=-\delta\), we cannot draw the conclusion easily.
In this case, Theorem 7.1 in Chap. 2 in [34] is used to determine the stability of the equilibrium \(E_{1}\). We transform the equilibrium \(E_{1}\) to the origin by translation \((X,Y)=(x,y-\delta\beta)\) at first, and then expand in power series up to the forth order around the origin, which makes the system to be of the following form:
where \(P_{1}(X,Y)\) is a power series in \((X,Y)\) with terms \(X^{i}Y^{j}\) satisfying \(i+j\ge5\).
Let \(x=X\), \(y=Y\), \(\tau =-\delta t\), where τ is a new time variable, then we have
where \(P_{2}(x,y)\) is a power series in \((x,y)\) with terms \(x^{i}y^{j}\) satisfying \(i+j\ge5\).
From \(y+\frac{1}{\delta\beta}y^{2}=0 \), we get the implicit function \(y=0\), then
According to Theorem 7.1 in Chap. 2 in [34], if the coefficient of \(x^{2}\) is \(\gamma^{2}-\alpha\neq0 \), i.e., \(m=2\), then the equilibrium \(E_{1}\) is a saddle node. If \(\gamma^{2}-\alpha=0\), then we have \(m=3\), \(a_{m}=\frac{\alpha }{\delta\gamma^{3}}>0\), by Theorem 7.1 in Chap. 2 in [34], \(E_{1}\) is an unstable node. Note that we have used the transform \(\tau =-\delta t\), which means the orbits with time going in the opposite direction. That is, \(E_{1}\) is a stable node.
This ends the proof of Theorem 2.2. □
2.3 Stability of the equilibria \(E_{21}\), \(E_{22}\), \(E_{23}\)
Theorem 2.3
Assume that \(E_{21}\), \(E_{22}\), \(E_{23}\) exist, then they are all unstable.
Proof
Note that \(E_{21}(x_{21},0)\) satisfies the equation
The Jacobian matrix about the equilibrium \(E_{21}\) is given by
The eigenvalues of the above matrix are \(\lambda_{1}= -x_{21}+\frac{\alpha x_{21}}{(\gamma+x_{21})^{2}}\), \(\lambda_{2}=\delta>0\). Hence, \(E_{21}\) is unstable. The stability of \(E_{22}\), \(E_{23}\) can be proved by the same method. Obviously, \(E_{22}\), \(E_{23}\) are unstable too.
This ends the proof of Theorem 2.3. □
2.4 Stability of the equilibrium \(E_{31}\)
Theorem 2.4
Assume that \(\alpha =\alpha_{2}\) and \(\gamma < 1-\delta\beta\) hold, system (1.3) has a unique positive equilibrium \(E_{31}(x_{31},\delta\beta)\), where \(x_{31}=\frac{1-\delta\beta-\gamma }{2}\), then \(E_{31}\) is a saddle node.
Proof
Note that \(E_{31}(x_{31},\delta\beta)\) satisfies the equation
where \(\alpha=\alpha_{2}=\frac{(\delta\beta-\gamma -1)^{2}}{4}\).
Then the Jacobian matrix about the equilibrium \(E_{31}\) is given by
The eigenvalues of the above matrix are \(\lambda_{1}= 0\), \(\lambda_{2}=-\delta<0\).
Then Theorem 7.1 in Chap. 2 in [34] is used to determine the stability of the equilibrium \(E_{31}\). Now we transform the equilibrium \(E_{31}\) to the origin by translation \((X,Y)=(x-x_{31},y-\delta\beta)\) and then expand in power series up to the forth order around the origin, which makes the system to be of the following form:
where
and \(Q_{1}(X,Y)\) is a power series in \((X,Y)\) with terms \(X^{i}Y^{j}\) satisfying \(i+j\ge5\).
In order to make the Jacobian matrix into a standard form, we use the transformation
then system (2.13) becomes
where
and \(Q_{2}(x,y)\) is a power series in \((x,y)\) with terms \(x^{i}y^{j}\) satisfying \(i+j\ge4\).
Let \(\tau =-\delta t\), where τ is a new time variable, then we have
where \(c_{ij}=-\frac{1}{\delta}b_{ij}\) and \(P_{2}(x,y)\) is a power series in \((x,y)\) with terms \(x^{i}y^{j}\) satisfying \(i+j\ge4\).
From \(y+\frac{1}{\delta\beta}y^{2}=0 \), we get the implicit function \(y=0\), then
Because of \(x_{31}>0\), \(1+\gamma -\delta \beta>2\gamma>0\), the coefficient of \(x^{2}\) is \(\frac{x_{31}}{\delta(1+\gamma -\delta \beta)}>0\) holding for all positive parameters, i.e., \(m=2,a_{m}>0\). Hence, by Theorem 7.1 in Chap. 2 in [34], \(E_{31}\) is a saddle node.
This ends the proof of Theorem 2.4. □
2.5 Stability of the equilibria \(E_{32}\), \(E_{33}\)
Theorem 2.5
-
(1)
Assume that
$$\gamma-\gamma\delta\beta < \alpha < \alpha_{2},\qquad \gamma < 1-\delta\beta $$holds, then \(E_{32}\) is unstable, \(E_{33}\) is locally asymptotically stable;
-
(2)
Assume that
$$\alpha=\gamma-\gamma\delta\beta,\qquad \gamma < 1-\gamma\delta\beta $$holds, then \(E_{33}\) is locally asymptotically stable;
-
(3)
Assume that
$$0< \alpha< \gamma-\gamma\delta\beta $$holds, then \(E_{33}\) is locally asymptotically stable if \(\gamma<1-\delta\beta\), \(E_{33}\) is unstable if \(\gamma>1-\delta\beta\).
Proof
Note that \(E_{32,33}(x_{32,33},\delta\beta)\) satisfies the equation
The Jacobian matrix about the equilibria \(E_{32,33}\) is given by
The eigenvalues of the above matrix are \(\lambda_{1}= x_{32,33}(\frac{\alpha }{(\gamma+x_{32,33})^{2}}-1)\), \(\lambda_{2}=-\delta<0\). Hence, the stability of \(E_{32,33}\) is determined by the symbol of \(\lambda_{1}\).
-
(1)
If \(\gamma-\gamma\delta\beta <\alpha <\alpha_{2}\) and \(\gamma < 1-\delta\beta\), after simple calculation, we have:
-
(a)
For the equilibrium \(E_{32}(\frac{1-\gamma-\sqrt{\triangle}_{1} }{2},\delta\beta)\), since \(\frac{\alpha }{(\gamma+x_{32,33})^{2}}>1\), it follows that \(\lambda_{1}>0\), that is, \(E_{32}\) is unstable;
-
(b)
For the equilibrium \(E_{33}(\frac{1-\gamma+\sqrt{\triangle}_{1} }{2},\delta\beta)\), since \(\frac{\alpha }{(\gamma+x_{32,33})^{2}}<1\), it follows that \(\lambda_{1}<0\), that is, \(E_{33}\) is locally asymptotically stable.
-
(a)
-
(2)
If \(\alpha=\gamma-\gamma\delta\beta\) and \(\gamma < 1-\delta\beta\), system (1.3) only has a unique equilibrium \(E_{33}(1-\delta \beta-\gamma,\delta\beta)\), after simple calculation, we have \(\lambda_{1}=\frac{(\delta\beta + \gamma -1)^{2}}{\delta \beta -1}\). And as \(\gamma < 1-\delta\beta\), we have \(\delta \beta -1<0\), \((\delta\beta + \gamma -1)^{2}>0\), that is to say, \(\lambda_{1}<0\). Hence \(E_{33}\) is locally asymptotically stable.
-
(3)
If \(0<\alpha<\gamma-\gamma\delta\beta\), as discussed in case (1), for the equilibrium \(E_{33}(\frac{1-\gamma+\sqrt{\triangle}_{1} }{2},\delta\beta)\), there are \(\frac{\alpha }{(\gamma+x_{32,33})^{2}}<1\), then:
-
(a)
If \(\gamma<1-\delta\beta\), we have \(\lambda_{1}<0\), that is, \(E_{33}\) is locally asymptotically stable;
-
(b)
If \(\gamma>1-\delta\beta\), we have \(\lambda_{1}>0\), that is, \(E_{33}\) is unstable.
-
(a)
This ends the proof of Theorem 2.5. □
The existence and stability of equilibria of system (1.3) are summarized in Table 1, where \(\gamma<1-\delta\beta \) and \(\gamma<\alpha_{2} \).
3 Bifurcation analysis
This section tries to discuss variable bifurcations of system (1.3) and obtains the conditions for the saddle-node bifurcation and the transcritical bifurcation.
3.1 Saddle-node bifurcation
The conditions which can ensure the existence of boundary equilibria \(E_{22}\), \(E_{23}\) are given in Sect. 2. After observing the change of \(E_{22}\), \(E_{23}\), we could find that these boundary equilibria are distinct if \(\gamma<\alpha<\alpha_{1}\), and \(E_{22}\) coincides with \(E_{23}\) if \(\alpha=\alpha_{1}\); finally they will all disappear if \(\alpha>\alpha_{1}\). Hence, the appearance or annihilation of equilibria may be due to the occurrence of a saddle-node bifurcation in the boundary equilibrium \(E_{21}\) which exists when
We will prove the existence of a saddle-node bifurcation as follows.
Theorem 3.1
System (1.3) undergoes a saddle-node bifurcation when the system parameters satisfy the restriction \(\alpha =\alpha_{SN1}\) along with the condition \(\gamma < 1\) which is given in Theorem 2.1. Here, \(\alpha \equiv \alpha_{SN1}=\frac{(\gamma+1)^{2}}{4}\) and α is seen as the bifurcation parameter.
Proof
In this section, we use Sotomayor’s theorem [35] to prove the occurrence of a saddle-node bifurcation with the transversality condition \(\alpha =\alpha_{SN1}\). The Jacobian matrix about the equilibrium \(E_{21}\) is given by
Obviously, \(J(E_{21})\) has a zero eigenvalue, named \(\lambda_{1}\).
Let V and W be two eigenvectors respectively corresponding to the eigenvalue \(\lambda_{1}\) for the matrices \(J(E_{21})\) and \(J(E_{21})^{T}\). After simple calculation, we have
Moreover,
One could easily see that V and W satisfy
which means that when \(\alpha =\alpha_{SN1}\), the saddle-node bifurcation occurs at \(E_{21}\).
The proof of Theorem 3.1 is finished. □
Similarly the conditions which can ensure the existence of positive equilibria \(E_{32}\), \(E_{33}\) are given in Sect. 2, and we could find that these positive equilibria are distinct if \(\gamma-\gamma\delta\beta <\alpha <\alpha_{2}\), and \(E_{32}\) coincides with \(E_{33}\) if \(\alpha=\alpha_{2}\); finally they will all disappear if \(\alpha>\alpha_{2}\). Hence, the appearance or annihilation of equilibria may be due to the occurrence of a saddle-node bifurcation at the positive equilibrium \(E_{31}\) which exists when
We will prove the occurrence of a saddle-node bifurcation at the positive equilibrium \(E_{31}\) as follows.
Theorem 3.2
System (1.3) undergoes a saddle-node bifurcation when the system parameters satisfy the restriction \(\alpha =\alpha_{SN1}\) along with the condition \(\gamma < 1\) which is given in Theorem 2.1. Here, \(\alpha \equiv \alpha_{SN1}=\frac{(\gamma+1)^{2}}{4}\) and α is seen as the bifurcation parameter.
Proof
We also use Sotomayor’s theorem [35] to prove the occurrence of a saddle-node bifurcation with the transversality condition \(\alpha =\alpha_{SN2}\). The Jacobian matrix about the equilibrium \(E_{31}\) is given by
Obviously, \(J(E_{31})\) has a zero eigenvalue, named \(\lambda_{1}\).
Let V and W be two eigenvectors respectively corresponding to the eigenvalue \(\lambda_{1}\) for the matrices \(J(E_{31})\) and \(J(E_{31})^{T}\). After simple calculation, we have
Moreover,
One could easily see that V and W satisfy
which means that when \(\alpha =\alpha_{SN2}\), the saddle-node bifurcation occurs at \(E_{31}\).
The proof of Theorem 3.2 is finished. □
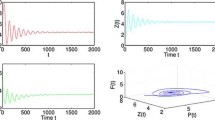
For \(\beta=0.5\), \(\gamma=0.2\), \(\delta=0.4\), we get \(\alpha_{SN1}=\alpha_{1}=0.36\). For \(0.2=\gamma <\alpha <\alpha_{SN1}\), system (1.3) has two distinct boundary equilibria \(E_{22}\), \(E_{23}\) (see Fig. 1(e), (f), (g)) which coincide with each other for \(\alpha =\alpha_{SN1}\) (see Fig. 1(h)) and no boundary equilibrium in the x-axis for \(\alpha >\alpha_{SN1}\) (see Fig. 1(i)).
(a) Dynamic behaviors of system (1.3), the parameters \((\alpha,\beta,\gamma,\delta)=(0.1,0.5,0.2,0.4)\). (b) Dynamic behaviors of system (1.3), the parameters \((\alpha,\beta,\gamma,\delta)=(0.16,0.5,0.2,0.4)\). (c) Dynamic behaviors of system (1.3), the parameters \((\alpha,\beta,\gamma,\delta)=(0.18,0.5,0.2,0.4)\). (d) Dynamic behaviors of system (1.3), the parameters \((\alpha,\beta,\gamma,\delta)=(0.2,0.5,0.2,0.4)\). (e) Dynamic behaviors of system (1.3), the parameters \((\alpha,\beta,\gamma,\delta)=(0.22,0.5,0.2,0.4)\). (f) Dynamic behaviors of system (1.3), the parameters \((\alpha,\beta,\gamma,\delta)=(0.25,0.5,0.2,0.4)\). (g) Dynamic behaviors of system (1.3), the parameters \((\alpha,\beta,\gamma,\delta)=(0.3,0.5,0.2,0.4)\). (h) Dynamic behaviors of system (1.3), the parameters \((\alpha,\beta,\gamma,\delta)=(0.36,0.5,0.2,0.4)\). (i) Dynamic behaviors of system (1.3), the parameters \((\alpha,\beta,\gamma,\delta)=(0.5,0.5,0.2,0.4)\)
Meanwhile, we get \(\alpha_{SN2}=\alpha_{2}=0.25\). For \(0.16=\gamma-\gamma\delta\beta <\alpha <\alpha_{SN2}\), system (1.3) has two distinct interior equilibria \(E_{22}\), \(E_{23}\) (see Fig. 1(c), (d), (e)) which coincide with each other for \(\alpha =\alpha_{SN1}\) (see Fig. 1(f)) and no interior equilibrium for \(\alpha >\alpha_{SN1}\) (see Fig. 1(g), (h), (i)).
3.2 Transcritical bifurcation
In Sect. 2, it was easy for us to notice an interesting phenomenon: when \(\alpha=\gamma\), \(E_{22}\) will coincide with \(E_{0}\) if \(\gamma < 1\) and \(E_{23}\) will coincide with \(E_{0}\) if \(\gamma > 1\). Hence, the appearance of the phenomenon may be due to the occurrence of a transcritical bifurcation in the boundary equilibrium \(E_{0}\). Then we have the following.
Theorem 3.3
System (1.3) undergoes a transcritical bifurcation when the system parameters satisfy the restriction \(\alpha =\alpha_{TC1}=\gamma\). Here, α is seen as the bifurcation parameter.
Proof
In this section, we also use Sotomayor’s theorem [35] to verify the occurrence of a transcritical bifurcation with the transversality condition \(\alpha =\alpha_{TC1}\). The Jacobian matrix about the equilibrium \(E_{0}\) is given by
Obviously, \(J(E_{0})\) has a zero eigenvalue, named \(\lambda_{1}\).
Let V and W be two eigenvectors respectively corresponding to the eigenvalue \(\lambda_{1}\) for the matrices \(J(E_{0})\) and \(J(E_{0})^{T}\). After simple calculation, we have
Moreover,
Therefore V and W satisfy
which means that when \(\alpha =\alpha_{TC1}\), the transcritical bifurcation occurs at \(E_{0}\).
The proof of Theorem 3.3 is finished. □
This interesting phenomenon also takes place in the boundary equilibrium \(E_{1}\): when \(\alpha=\gamma-\gamma\delta\beta\), then \(E_{32}\) will coincide with \(E_{1}\) if \(\gamma < 1-\delta\beta\) and \(E_{33}\) will coincide with \(E_{1}\) if \(\gamma > 1-\delta\beta\). Hence, the appearance of the phenomenon may be due to the occurrence of a transcritical bifurcation in the boundary equilibrium \(E_{1}\). Then we have the following.
Theorem 3.4
System (1.3) undergoes a transcritical bifurcation when the system parameters satisfy the restriction \(\alpha =\alpha_{TC2}=\gamma-\gamma\delta\beta\). Here, α is seen as the bifurcation parameter.
Proof
We also use Sotomayor’s theorem [35] to prove the occurrence of a transcritical bifurcation with the transversality condition \(\alpha =\alpha_{TC2}\).The Jacobian matrix about the equilibrium \(E_{1}\) is given by
Obviously, \(J(E_{1})\) has a zero eigenvalue, named \(\lambda_{1}\).
Let V and W be two eigenvectors respectively corresponding to the eigenvalue \(\lambda_{1}\) for the matrices \(J(E_{1})\) and \(J(E_{1})^{T}\). After simple calculation, we have
Moreover,
Therefore V and W satisfy
which means that when \(\alpha =\alpha_{TC2}\), the transcritical bifurcation also occurs at \(E_{1}\).
The proof of Theorem 3.4 is finished. □
4 Numeric simulations
Example 4.1
Consider the following system:
In this system, corresponding to system (1.3), we take \(\beta=0.5\), \(\gamma=0.2\), \(\delta=0.4\). Then we have \(0.2=\gamma<1-\delta\beta=0.8\), \(\gamma-\gamma\delta\beta=0.16\), \(\alpha_{1}=\frac{(\gamma+1)^{2}}{4}=0.36\), and \(\alpha_{2}=\frac{(\delta\beta-\gamma -1)^{2}}{4}=0.25\). From Theorem 2.1, system (4.1) has two boundary equilibria \(E_{0}(0,0)\), \(E_{1}(0, 0.2)\) for all positive parameters, and \(E_{0}(0,0)\) is unstable from Theorem 2.2(1).
-
(1)
Take \(\alpha=0.1\), then \(0<\alpha<\gamma-\gamma\delta\beta\), from Theorem 2.1(i)(e) and (ii)(e), system (4.1) has another boundary equilibrium \(E_{23}(0.9099,0)\) and a unique positive equilibrium \(E_{33}(0.6873,0.2)\). Furthermore, from Theorem 2.2(2)(i), Theorem 2.3, and Theorem 2.5(3), we have \(E_{1}\) is a saddle, \(E_{23}\) is unstable, and \(E_{33}\) is locally asymptotically stable, see Fig. 1(a);
-
(2)
Take \(\alpha=0.16\), then \(\alpha=\gamma-\gamma \delta\beta<\gamma\), \(\alpha\neq\gamma^{2}\), from Theorem 2.1(i)(e) and (ii)(d), system (4.1) has another boundary equilibrium \(E_{23}(0.8472,0)\) and a unique positive equilibrium \(E_{33^{*}}(0.6,0.2)\). Furthermore, from Theorem 2.2(2)(iii), Theorem 2.3, and Theorem 2.5(2), we have \(E_{1}\) is a saddle node, \(E_{23}\) is unstable, and \(E_{33^{*}}\) is locally asymptotically stable, see Fig. 1(b);
-
(3)
Take \(\alpha=0.18\), then \(\gamma-\gamma \delta\beta<\alpha<\gamma\), from Theorem 2.1(i)(e) and (ii)(c), system (4.1) has another boundary equilibrium \(E_{23}(0.8243,0)\) and two distinct positive equilibria \(E_{32}(0.0354,0.2)\), \(E_{33}(0.5646,0.2)\). Furthermore, from Theorem 2.2(2)(ii), Theorem 2.3, and Theorem 2.5(1), we have \(E_{1}\) is a stable node, \(E_{23}\) is unstable, \(E_{32}\) is unstable, and \(E_{33}\) is locally asymptotically stable, see Fig. 1(c);
-
(4)
Take \(\alpha=0.2\), then \(\alpha=\gamma\), from Theorem 2.1(i)(d) and (ii)(c), system (4.1) has another boundary equilibrium \(E_{23^{*}}(0.8,0)\) and two distinct positive equilibria \(E_{32}(0.0764,0.2)\), \(E_{33}(0.5236,0.2)\). Furthermore, from Theorem 2.2(2)(ii), Theorem 2.3, and Theorem 2.5(1), we have \(E_{1}\) is a stable node, \(E_{23}\) is unstable, \(E_{32}\) is unstable, and \(E_{33}\) is locally asymptotically stable, see Fig. 1(d);
-
(5)
Take \(\alpha=0.22\), then \(\gamma<\alpha<\alpha_{2}\), from Theorem 2.1(i)(c) and (ii)(c), system (4.1) has other two boundary equilibria \(E_{22}(0.0258,0)\) \(E_{23}(0.7741,0)\) and two distinct positive equilibria \(E_{32}(0.1268,0.2)\), \(E_{33}(0.4732,0.2)\). Furthermore, from Theorem 2.2(2)(ii), Theorem 2.3, and Theorem 2.5(1), we have \(E_{1}\) is a stable node, \(E_{22}\), \(E_{23}\) is unstable, \(E_{32}\) is unstable, and \(E_{33}\) is locally asymptotically stable, see Fig. 1(e);
-
(6)
Take \(\alpha=0.25\), then \(\alpha=\alpha_{2}\), from Theorem 2.1(i)(c) and (ii)(b), system (4.1) has other two boundary equilibria \(E_{22}(0.0683,0)\) \(E_{23}(0.7317,0)\) and a unique positive equilibrium \(E_{31}(0.3,0.2)\). Furthermore, from Theorem 2.2(2)(ii), Theorem 2.3, and Theorem 2.4, we have \(E_{1}\) is a stable node, \(E_{22}\), \(E_{23}\) is unstable and \(E_{31}\) is a saddle node, see Fig. 1(f);
-
(7)
Take \(\alpha=0.3\), then \(\alpha_{2}<\alpha<\alpha_{1}\), from Theorem 2.1(i)(c) and (ii)(a), system (4.1) has other two boundary equilibria \(E_{22}(0.1551,0)\) \(E_{23}(0.6450,0)\) and none positive equilibria. Furthermore, from Theorem 2.2(2)(ii), Theorem 2.3, we have \(E_{1}\) is a stable node and \(E_{22}\), \(E_{23}\) is unstable, see Fig. 1(g);
-
(8)
Take \(\alpha=0.36\), then \(\alpha=\alpha_{1}\), from Theorem 2.1(i)(b) and (ii)(a), system (4.1) has another boundary equilibrium \(E_{21}(0.4,0)\) and none positive equilibria. Furthermore, from Theorem 2.2(2)(ii), Theorem 2.3, we have \(E_{1}\) is a stable node and \(E_{21}\) is unstable, see Fig. 1(h);
-
(9)
Take \(\alpha=0.5\), then \(\alpha_{1}<\alpha\), from Theorem 2.1(i)(a) and (ii)(a), system (4.1) only has two boundary equilibria \(E_{0}(0,0)\), \(E_{1}(0, 0.2)\). Furthermore, from Theorem 2.2 (2) (ii), we have \(E_{1}\) is a stable node, see Fig. 1(i);
5 Conclusion
An amensalism model with Michaelis–Menten type harvesting and a cover for the first species is proposed and studied in this paper. Already Xie et al. [18] investigated the local and global stability property of the possible equilibria of the above model, where the harvesting term \(h=0\). By contrast, we can find some interesting phenomena about the dynamic behavior of system (1.3):
-
(a)
At most, there are six equilibria for the system including two distinct interior points. While in [18] there just four equilibria and a unique interior point;
-
(b)
With the increase in the number of equilibria, dynamic behavior of the system becomes more complex, such as the appearance of bifurcation;
-
(c)
In [18], once the positive equilibrium exists, it is globally stable. While in system (1.3), if \(\alpha=\alpha_{2}\), then there is a unique positive equilibrium \(E_{31}\); from Theorem 2.4, we have \(E_{31}\) is a saddle node (see Fig. 1(h)).
That is, by introducing the harvesting, the dynamic behaviors of the system become complicated.
References
Yang, K., Miao, Z., Chen, F., et al.: Influence of single feedback control variable on an autonomous Holling-II type cooperative system. J. Math. Anal. Appl. 435(1), 874–888 (2016)
Xie, X.D., Miao, Z.S., Xue, Y.L.: Positive periodic solution of a discrete Lotka–Volterra commensal symbiosis model. Commun. Math. Biol. Neurosci. 2015, Article ID 2 (2015)
Miao, Z.S., Xie, X.D., Pu, L.Q.: Dynamic behaviors of a periodic Lotka–Volterra commensal symbiosis model with impulsive. Commun. Math. Biol. Neurosci. 2015, Article ID 3 (2015)
Xue, Y.L., Xie, X.D., Chen, F.D., Han, R.Y.: Almost periodic solution of a discrete commensalism system. Discrete Dyn. Nat. Soc. 2015, Article ID 295483 (2015)
Chen, F.D., Pu, L.Q., Yang, L.Y.: Positive periodic solution of a discrete obligate Lotka–Volterra model. Commun. Math. Biol. Neurosci. 2015, Article ID 14 (2015)
Han, R.Y., Chen, F.D.: Global stability of a commensal symbiosis model with feedback controls. Commun. Math. Biol. Neurosci. 2015, Article ID 15 (2015)
Wu, R.X., Li, L., Lin, Q.F.: A Holling type commensal symbiosis model involving Allee effect. Commun. Math. Biol. Neurosci. 2018, Article ID 6 (2018)
Lin, Q.F.: Dynamic behaviors of a commensal symbiosis model with non-monotonic functional response and non-selective harvesting in a partial closure. Commun. Math. Biol. Neurosci. 2018, Article ID 4 (2018)
Wu, R.X., Lin, L., Zhou, X.Y.: A commensal symbiosis model with Holling type functional response. J. Math. Comput. Sci. 16, 364–371 (2016)
Chen, F., Wu, H., Xie, X.: Global attractivity of a discrete cooperative system incorporating harvesting. Adv. Differ. Equ. 2016, 268 (2016)
Georgescu, P., Maxin, D.: Global stability results for models of commensalism. Int. J. Biomath. 10(3), 33–50 (2016)
Lin, Q.: Allee effect increasing the final density of the species subject to the Allee effect in a Lotka–Volterra commensal symbiosis model. Adv. Differ. Equ. 2018, 196 (2018)
Wang, D.: Dynamic behaviors of an obligate Gilpin–Ayala system. Adv. Differ. Equ. 2016, 270 (2016)
Sun, G.C.: Qualitative analysis on two populations amensalism model. J. Jiamusi Univ. (Nat. Sci. Ed.) 21(3), 283–286 (2003)
Zhu, Z.F., Chen, Q.L.: Mathematic analysis on commensalism Lotka–Volterra model of populations. J. Jixi Univ. 8(5), 100–101 (2008)
Han, R.Y., Xue, Y.L., Yang, L.Y.: On the existence of positive periodic solution of a Lotka–Volterra amensalism model. J. Rongyang Univ. 33(2), 22–26 (2015)
Wu, R.: A two species amensalism model with non-monotonic functional response. Commun. Math. Biol. Neurosci. 2016, Article ID 19 (2016)
Xie, X.D., Chen, F.D., He, M.X.: Dynamic behaviors of two species amensalism model with a cover for the first species. J. Math. Comput. Sci. 16, 395–401 (2016)
Wu, R.X., Zhao, L., Lin, Q.X.: Stability analysis of a two species amensalism model with Holling II functional response and a cover for the first species. J. Nonlinear Sci. Appl. 2016, Article ID 46 (2016)
Chen, B.: Dynamic behaviors of a non-selective harvesting Lotka–Volterra amensalism model incorporating partial closure for the populations. Adv. Differ. Equ. 2018, Article ID 111 (2018)
Wu, R.: Dynamic behaviors of a nonlinear amensalism model. Adv. Differ. Equ. 2018, 187 (2018)
Gupta, R.P., Chandra, P.: Bifurcation analysis of modified Leslie–Gower predator-prey model with Michaelis–Menten type prey harvesting. J. Math. Anal. Appl. 398(1), 278–295 (2013)
Clark, C.W.: Aggregation and fishery dynamics: a theoretical study of schooling and the purse seine tuna fisheries. Fish. Bull. 77(2), 317–337 (1979)
Hu, D., Cao, H.: Stability and bifurcation analysis in a predator-prey system with Michaelis–Menten type predator harvesting. Nonlinear Anal., Real World Appl. 33, 58–82 (2017)
Liu, Y., Xie, X.D., Lin, Q.F.: Permanence, partial survival, extinction and global attractivity of a non-autonomous harvesting Lotka–Volterra commensalism model incorporating partial closure for the populations. Adv. Differ. Equ. 2018, 211 (2018)
Huang, J., Gong, Y., Ruan, S.: Bifurcation analysis in a predator-prey model with constant-yield predator harvesting. Discrete Contin. Dyn. Syst., Ser. B 18, 2101–2121 (2013)
Xiao, D., Jennings, L.S.: Bifurcations of a ratio-dependent predator-prey system with constant rate harvesting. SIAM J. Appl. Math. 65(3), 737–753 (2005)
Chen, L., Chen, F.: Global analysis of a harvested predator-prey model incorporating a constant prey refuge. Int. J. Biomath. 3(02), 205–223 (2010)
Zhang, N., Chen, F., Su, Q., et al.: Dynamic behaviors of a harvesting Leslie–Gower predator-prey model. Discrete Dyn. Nat. Soc. 2011, Article ID 473949 (2011)
Xie, X., Chen, F., Xue, Y.: Note on the stability property of a cooperative system incorporating harvesting. Discrete Dyn. Nat. Soc. 2014, Article ID 327823 (2014)
Wu, H., Chen, F.: Harvesting of a single-species system incorporating stage structure and toxicity. Discrete Dyn. Nat. Soc. 2009, Article ID 290123 (2009)
Liu, Y., Xie, X., Guan, X., et al.: Dynamic behaviors of a non-selective harvesting Lotka–Volterra predator-prey model incorporating partial closure for the populations. J. Biomath. 33(1), 91–97 (2018)
Liu, Y., Guan, X., Xie, X., Lin, Q.: On the existence and stability of positive periodic solution of a nonautonomous commensal symbiosis model with Michaelis–Menten type harvesting. Commun. Math. Biol. Neurosci. In press
Zhang, Z., Ding, T., Huang, W., Dong, Z.: Qualitative Theory of Differential Equation. Science Press, Beijing (1992)
Perko, L.: Differential Equations and Dynamical Systems. Springer, New York (2001)
Acknowledgements
We would like to thank Dr. Hebai Chen for useful discussion during the period of writing this paper.
Funding
The research was supported by Guangxi College Enhancing Youths Capacity Project (2017KY0599) and the Science Research Development Fund of Youths Researchers of Guangxi University of Finance and Economics (2017QNB18).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that there is no conflict of interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, Y., Zhao, L., Huang, X. et al. Stability and bifurcation analysis of two species amensalism model with Michaelis–Menten type harvesting and a cover for the first species. Adv Differ Equ 2018, 295 (2018). https://doi.org/10.1186/s13662-018-1752-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1752-2