Abstract
We consider a pathogen dynamics model with antibodies and both pathogen-to-susceptible and infected-to-susceptible transmissions. We consider two types of infected cells, latently infected cells, and actively infected cells. The model considers three types of discrete or distributed delays to characterize the time between the pathogen or the infected cell contacts a susceptible cell and the creation of mature pathogens. We deduct the basic reproduction number and antibody response activation number which determine the existence and stability of the steady states. The global stability analysis of the steady states is established using Lyapunov method. The theoretical results are confirmed by numerical simulations.
Similar content being viewed by others
1 Introduction
Modeling and analysis of within-host human pathogen dynamics have been studied in several works (see, e.g., [1–23]). These works can help researchers to better understand the pathogen dynamical behavior and to provide new suggestions for clinical treatment. A vast amount of the mathematical models presented in the literature focused on modeling the interaction between three main compartments, susceptible cells (s), infected cells (y), and pathogens (p). B cell is one of the central components of the immune system against viral infections. The B cells create antibodies to neutralize the pathogens. Murase et al. [24] considered the effect of antibodies (x) on the pathogen infection model as follows:
The susceptible cells are produced at rate ω, die at rate ds, and become infected at rate \(\pi_{1}sp\), where \(\pi_{1}\) is the pathogen-susceptible incidence rate constant. λ is the death rate constant of the infected cells, a is the neutralization rate constant of the pathogens, and c is the death rate constant of the pathogens. The infected cell releases a number n of pathogens during its lifespan. The B cells are proliferated and die at rates \(rpx\) and mx, respectively, where r and m are constants. The effect of antibody immune response on the pathogen dynamics has been studied in several works (see, e.g., [24–29]). In these works, it was assumed that the susceptible cells become infected by contacting with pathogens (pathogen-to-susceptible transmission). In [30–33], it was reported that the pathogens can also spread by infected-to-susceptible transmission. However, in these works the antibody immune response was neglected. In very recent works [34, 35], and [36], both pathogen-to-susceptible and infected-to-susceptible transmissions were incorporated in the pathogen dynamics models with antibody immune response. However, the latently infected cells were neglected in these models.
It is worth stressing that the introduction of delay equations has been widely applied to model complex systems in biology. Indeed, the introduction of delay terms can be viewed as a first step towards modeling multiscale dynamics and heterogeneity features in population dynamics [37].
In the present paper we investigate the global stability of pathogen dynamics models with antibodies and both pathogen-to-susceptible and infected-to-susceptible transmissions. We consider both latently infected cells and actively infected cells. We incorporate three types of discrete or distributed time delays to describe the time between the pathogen or the actively infected cell contacts a susceptible cell and the emission of new mature pathogens. We calculate two bifurcation parameters \(\mathcal{R}_{0}\) (the basic reproduction number) and \(\mathcal{R}_{1}\) (the antibody response activation number) which determine the existence and global stability of all steady states. Numerical simulations are performed to confirm the theoretical results.
2 Model with discrete-time delays
We investigate the following pathogen dynamics model with discrete-time delays:
The model assumes that the susceptible cells are infected by pathogens at rate \(\pi_{1}s(t)p(t)\) and by infected cells at rate \(\pi_{2}s(t)y(t)\). The fractions ρ and \((1-\rho)\) with \(0<\rho <1\) are the proportions of infection that lead to latency and activation, respectively. \(\lambda_{u}\) is the death rate constant of the latently infected cells. Latently infected cells are activated at rate \(\alpha u(t)\). Here, \(\tau_{1}\) is the time between pathogen entry a susceptible cell to become latent infected, and \(\tau_{2}\) is the time between pathogen entry a susceptible cell and the production of immature pathogens. The immature pathogens need time \(\tau_{3}\) to be mature. The factors \(e^{-\varepsilon_{1}\tau_{1}}\), \(e^{-\varepsilon_{2}\tau_{2}}\), and \(e^{-\varepsilon_{3}\tau_{3}}\) represent the probability of surviving to the age of \(\tau_{1}\), \(\tau_{2}\), and \(\tau_{3}\), respectively, where \(\varepsilon_{1}\), \(\varepsilon_{2}\), and, \(\varepsilon_{3}\) are positive constants.
We consider the initial conditions
where \(\kappa =\max \{ \tau_{1},\tau_{2},\tau_{3}\}\) and C is the Banach space of continuous functions mapping the interval \([-\kappa,0] \) into \(\mathbb{R}_{\mathbb{\geq }0}\) with norm \(\Vert \phi_{j} \Vert =\sup_{-\kappa \leq \theta \leq 0} \vert \phi _{j}(\theta) \vert \). Then system (2) has a unique solution for \(t>0\) [38].
2.1 Properties of solution
Lemma 1
The solutions of system (2) with initial conditions (3) are nonnegative and ultimately bounded for \(t>0\).
Proof
We have from Eq. (2)1 that \(\dot{s}|_{s=0}= \omega >0\). Therefore \(s(t)>0\) for all \(t\geq 0\). Moreover, for \(t\in {}[ 0,\kappa ]\), we have
By recursive argument we get \(u(t)\geq 0\), \(y(t)\geq 0\) and \(p(t)\geq 0\) \(\forall t\geq 0\). The nonnegativity of the model’s solutions implies that \(\dot{s}(t)\leq \omega -ds(t)\) and then \(\lim_{t\rightarrow \infty }\sup s(t)\leq \frac{\omega }{d}\). Let us define \(X_{1}(t)=\rho e^{-\varepsilon_{1}\tau_{1}}s(t-\tau_{1})+(1-\rho)e ^{-\varepsilon_{2}\tau_{2}}s(t-\tau_{2})+u(t)+y(t)\). Then
where \(\sigma_{1}=\min { \{ d,\lambda_{u},\lambda \} }\). It follows that \(\lim_{t\rightarrow \infty }\sup X_{1}(t) \leq M_{1}\), where \(M_{1}=\frac{\omega }{\sigma_{1}}\). Since \(s(t)>0\), \(u(t)\geq 0\), and \(y(t)\geq 0\), then \(\lim_{t\rightarrow \infty }\sup u(t)\leq M_{1}\) and \(\lim_{t\rightarrow \infty }\sup y(t)\leq M_{1}\). Moreover, let \(X_{2}(t)=p(t)+\frac{a}{r}x(t)\). Then
where \(\sigma_{2}=\min { \{ c,m \} }\). Then \(\lim_{t\rightarrow \infty }\sup X_{2}(t)\leq M_{2}\), where \(M_{2}=\frac{n \lambda M_{1}}{\sigma_{2}}\). The nonnegativity of the solution implies that \(\lim_{t\rightarrow \infty }\sup p(t)\leq M_{2}\) and \(\lim_{t\rightarrow \infty }\sup x(t)\leq M_{3}\), where \(M _{3}=\frac{r}{a}M_{2}\). This shows the ultimate boundedness of \(s(t)\), \(u(t)\), \(y(t)\), \(p(t)\), and \(x(t)\). □
2.2 Steady states and threshold parameters
In the following, we derive the basic reproduction number from system (2) by using the next-generation method and calculate the steady states. We first define the matrices \(\mathbb{F}\) and \(\mathbb{V}\) as follows:
where \(s_{0}=\frac{\omega }{d}\). Then
where
The basic reproduction number \(\mathcal{R}_{0}\) can be computed as the spectral radius of \(\mathbb{FV}^{-1}\):
where
The parameter \(\mathcal{R}_{0}\) can be written as \(\mathcal{R}_{0}= \mathcal{R}_{01}+\mathcal{R}_{02}\), where
The model has three steady states:
-
(i)
The pathogen-free steady state \(\Omega_{0}=(s_{0},0,0,0,0)\).
-
(ii)
The infected steady state without antibodies \(\Omega_{1}=(s_{1},u _{1},y_{1},p_{1},0)\), where
$$\begin{aligned} &s_{1} =\frac{s_{0}}{\mathcal{R}_{0}},\qquad y_{1}= \frac{cd}{n \pi_{1}\lambda e^{-\varepsilon_{3}\tau_{3}}+c\pi_{2}}(\mathcal{R}_{0}-1), \\ &u_{1} =\frac{\rho \omega e^{-\varepsilon_{1}\tau_{1}}}{ ( \alpha +\lambda_{u} ) \mathcal{R}_{0}}(\mathcal{R}_{0}-1),\qquad p_{1}=\frac{n\lambda e^{-\varepsilon_{3}\tau_{3}}}{c}y_{1}. \end{aligned}$$ -
(iii)
The infected steady state with antibodies \(\Omega_{2}=(s_{2},u _{2},y_{2},p_{2},x_{2})\), where
$$\begin{aligned} \begin{aligned}&s_{2} =\frac{(\alpha +\lambda_{u})u_{2}}{\rho e^{-\varepsilon_{1} \tau_{1}} ( \pi_{1}p_{2}+\pi_{2}y_{2} ) },\qquad y_{2}= \frac{-B+\sqrt{B^{2}-4AC}}{2A}, \\ &u_{2} =\frac{\omega \rho e^{-\varepsilon_{1}\tau_{1}} ( \pi _{1}m+\pi_{2}ry_{2} ) }{(\alpha +\lambda_{u})[rd+ ( \pi_{1}m+ \pi_{2}ry_{2} ) ]},\qquad p_{2}= \frac{m}{r}, \\ & x_{2}= \frac{c}{a} \biggl( \frac{n\lambda e^{-\varepsilon_{3}\tau_{3}}y_{2}}{cp _{2}}-1 \biggr), \end{aligned} \end{aligned}$$(5)and
$$ A=\lambda \pi_{2}r,\qquad B=\lambda (rd+\pi_{1}m)- \frac{\gamma \omega \pi_{2}r}{e^{-\varepsilon_{3}\tau_{3}}},\qquad C=-\frac{ \gamma \omega \pi_{1}m}{e^{-\varepsilon_{3}\tau_{3}}}. $$(6)
We note that \(\Omega_{2}\) exists if \(\frac{n\lambda e^{-\varepsilon _{3}\tau_{3}}y_{2}}{cp_{2}}>1\). Now we can define antibody immune response activation number as follows:
It follows that \(x_{2}=\frac{c}{a} ( \mathcal{R}_{1}-1 ) \). Thus, an infected steady state with antibodies \(\Omega_{2}=(s_{2},u _{2},y_{2},p_{2},x_{2})\) exists when \(\mathcal{R}_{1}>1\).
Lemma 2
Let \(\mathcal{R}_{0}>1\), then (i) if \(\mathcal{R} _{1}\leq 1\), then \(p_{1}\leq p_{2}\), and (ii) if \(\mathcal{R}_{1}>1\), then \(p_{1}>p_{2}\).
Proof
(i) Let \(\mathcal{R}_{1}\leq 1\), then \(\frac{n\lambda e^{-\varepsilon_{3}\tau_{3}}y_{2}}{cp_{2}}\leq 1\). Using Eq. (5), we obtain
which implies that
Using Eq. (6), we get
Thus \(p_{1}\leq p_{2}\). The proof of (ii) can be done in a similar way. □
2.3 Global properties
We define a function \(G(\theta)=\theta -1-\ln \theta \) and use the notation \((s,u,y,p,x)=(s(t),u(t),y(t), p(t),x(t))\).
Theorem 1
The pathogen-free steady state \(\Omega_{0}\) of system (2) is globally asymptotically stable when \(\mathcal{R} _{0}\leq 1\).
Proof
Define \(U_{0}(s,u,y,p,x)\) as follows:
where γ is defined by Eq. (4). We have \(U_{0}(s,u,y,p,x)>0\) for all \(s,u,y,p,x>0\), while \(U_{0}(s_{0},0,0,0,0)=0\). Calculate \(\frac{dU_{0}}{dt}\) along the solution of system (2) as follows:
Equation (8) can be simplified as follows:
We have
Therefore, we obtain
Thus, \(\frac{dU_{0}}{dt}\leq 0\) when \(\mathcal{R}_{0}\leq 1\) for all \(s,p,x>0\). Moreover, \(\frac{dU_{0}}{dt}=0\) if and only if \(x(t)=0\), \(p(t)=0\), and \(s(t)=s_{0}\). Let \(D_{0}=\{(s,u,y,p,x): \frac{dU_{0}}{dt}=0\}\) and \(D_{0}^{\prime }\) be the largest invariant subset of \(D_{0}\). The solutions of system (2) tend to \(D_{0}^{\prime }\) [38]. For each element in \(D_{0}^{\prime }\), we have \(p(t)=0\). Thus Eq. (2)4 yields
Then \(y(t)=0\). From Eq. (2)3 we have
Then \(u(t)=0\). It follows that \(D_{0}^{\prime }\) contains a single point that is \(\{ \Omega_{0}\}\). From LaSalle’s invariance principle, \(\Omega_{0}\) is globally asymptotically stable when \(\mathcal{R}_{0} \leq 1\). □
Theorem 2
For system (2), assume that \(\mathcal{R} _{1}\leq 1<\mathcal{R}_{0}\), then \(\Omega_{1}\) is globally asymptotically stable.
Proof
Let \(U_{1}(s,u,y,p,x)\) be given as follows:
We have \(U_{1}(s,u,y,p,x)>0\) for all \(s,u,y,p,x>0\) and \(U_{1}(s _{1},u_{1},y_{1},p_{1},0)=0\). Calculating \(\frac{dU_{1}}{dt}\), we obtain
Simplifying Eq. (9) and applying the steady state conditions for \(\Omega_{1}\)
we get
Consider the following equalities with (\(i=1 \)):
we obtain
From Lemma 2, we have \(p_{1}\leq p_{2}\) when \(\mathcal{R}_{1}\leq 1\). Thus, \(\frac{dU_{1}}{dt}\leq 0\) and \(\frac{dU_{1}}{dt}=0\) occur at the infected steady state without antibodies \(\Omega_{1}\). Let \(D_{1}^{ \prime }\) be the largest invariant subset of the set \(D_{1}= \{ ( s,u,y,p,x ):\frac{dU_{1}}{dt}=0 \} \). Thus, the solutions of system (2) tend to \(D_{1}^{\prime }\). It is clear that \(D_{1}= \{ \Omega_{1} \} \). Using LaSalle’s invariance principle, we conclude that \(\Omega_{1}\) is globally asymptotically stable when \(\mathcal{R}_{1}\leq 1\) and \(\mathcal{R}_{0}>1\). □
Theorem 3
For system (2), suppose that \(\mathcal{R} _{1}>1\), then \(\Omega_{2}\) is globally asymptotically stable.
Proof
Consider \(U_{2}(s,u,y,p,x)\):
We have \(U_{2}(s,u,y,p,x)>0\) for all \(s,u,y,p,x>0\), while \(U_{2}(s,u,y,p,x)\) reaches its global minimum at \(\Omega_{2}\). Calculate \(\frac{dU_{2}}{dt}\) as follows:
Simplifying Eq. (11) and applying the steady state conditions for \(\Omega_{2}\):
we get
Applying equalities (10) when (\(i=2 \)), we obtain
Since \(\mathcal{R}_{1}>1\), then \(s_{2}\), \(u_{2}\), \(y_{2}\), \(p_{2}\), and \(x_{2}>0\). We obtain \(\frac{dU_{2}}{dt}\leq 0\), and then the solutions of system (2) tend to \(D_{2}^{\prime }\), the largest invariant subset of \(D_{2}= \{ ( s,u,y,p,x ):\frac{dU_{2}}{dt}=0 \} \). Clearly, \(\frac{dU_{2}}{dt}=0\) when \(s=s_{2}\), \(u=u_{2}\), \(y=y_{2}\), and \(p=p_{2}\). Since \(p=p_{2} \) in \(D_{2}^{\prime }\), then
which gives \(x=x_{2}\). Therefore, \(\frac{dU_{2}}{dt}=0\) when \(s=s_{2}\), \(u=u_{2}\), \(y=y_{2}\), \(p=p_{2}\), and \(x=x_{2}\). The global asymptotic stability of \(\Omega_{2}\) is conducted from LaSalle’s invariance principle. □
3 Model with distributed delays
We consider a pathogen dynamics model with distributed delays:
where \(f_{1}(\tau)e^{-\mu_{1}\tau }\) is probability that susceptible host cells contacted by the pathogens at time \(t-\tau \) survived τ time units and became latently infected at time t, \(f_{2}(\tau)e^{-\mu_{2}\tau }\) is probability that susceptible host cells contacted by the pathogens at time \(t-\tau \) survived τ time units and became actively infected at time t, and \(f_{3}(\tau)e^{-\mu_{3}\tau }\) is the probability that an immature pathogen at time \(t-\tau \) survived τ time units to become a mature pathogen at time t. The probability distribution functions \(f_{j}(\tau)\), \(j=1,\ldots,3\), satisfy the following conditions:
(i) \(f_{j}(\tau)>0\), (ii) \(\int_{0}^{h_{j}}f_{j}(\tau)\,d\tau =1\), (iii) \(\int_{0}^{h_{j}}f_{j}(\tau)e^{\ell \tau }\,d\tau<\infty \), where \(\ell >0\).
Let \(\Theta_{j}(\tau)=f_{j}(\tau)e^{-\mu_{j}\tau }\) and \(\eta_{j}= \int_{0}^{h_{j}}\Theta_{j}(\tau)\,d\tau\), \(j=1,2,3\), thus \(0<\eta_{j} \leq 1\).
The initial conditions for system (12) are the same as given by (3) where \(\kappa = \max \{h_{1},h_{2},h_{3}\}\).
3.1 Properties of solution
Lemma 3
The solutions \((s(t),u(t),y(t),p(t),x(t))\) of system (12) with initial conditions (3) are nonnegative and ultimately bounded for \(t>0\).
Proof
From Lemma 1 we have \(s(t)>0\) for all \(t\geq 0\). For \(t\in {}[ 0,\kappa ]\), we have
We obtain by recursive argument that \(u(t)\geq 0\), \(y(t)\geq 0\), \(p(t) \geq 0\), and \(x(t)\geq 0\ \forall t\geq 0\).
Clearly \(\lim_{t\rightarrow \infty }\sup s(t)\leq \frac{ \omega }{d}\). Let us define \(Y_{1}(t)=\rho \int_{0}^{h_{1}}\Theta_{1}( \tau)s(t-\tau)\,d\tau +(1-\rho) \int_{0}^{h_{2}}\Theta_{2}(\tau)s(t- \tau)\,d\tau +u(t)+y(t)\). Then
where \(\sigma_{1}=\min { \{ d,\lambda_{u},\lambda \} }\). It follows that \(\lim_{t\rightarrow \infty }\sup Y_{1}(t) \leq \tilde{M}_{1}\), where \(\tilde{M}_{1}=\frac{\omega }{\sigma_{1}}\). Since \(s(t)>0\), \(u(t)\geq 0\), and \(y(t)\geq 0\), then \(\lim_{t\rightarrow \infty }\sup u(t)\leq \tilde{M}_{1}\) and \(\lim_{t\rightarrow \infty }\sup y(t)\leq \tilde{M}_{1}\). Further, let us consider \(Y_{2}(t)=p(t)+\frac{a}{r}x(t)\). Then
where \(\sigma_{2}=\min { \{ c,m \} }\). Then \(\lim_{t\rightarrow \infty }\sup Y_{2}(t)\leq \tilde{M}_{2}\), where \(\tilde{M}_{2}=\frac{n\lambda \tilde{M}_{1}}{\sigma_{2}}\). The nonnegativity of the solution implies that \(\lim_{t\rightarrow \infty }\sup p(t)\leq \tilde{M}_{2}\) and \(\lim_{t\rightarrow \infty }\sup x(t)\leq \tilde{M}_{3}\), where \(\tilde{M}_{3}= \frac{r}{a}\tilde{M}_{2}\). This shows the ultimate boundedness of \(s(t)\), \(u(t)\), \(y(t)\), \(p(t)\), and \(x(t)\). □
3.2 Steady states and threshold parameters
For system (12) the matrices \(\mathbb{F}\) and \(\mathbb{V}\) are given by
and then
where
Thus, \(\tilde{\mathcal{R}}_{0}\) is given by
where
The model has three steady states:
-
(i)
The pathogen-free steady state \(\Omega_{0}=(s_{0},0,0,0,0)\).
-
(ii)
The infected steady state without antibodies \(\Omega_{1}=(s_{1},u _{1},y_{1},p_{1},0)\), where
$$\begin{aligned} &s_{1} =\frac{s_{0}}{\tilde{\mathcal{R}}_{0}},\qquad y _{1}= \frac{cd}{n\pi_{1}\lambda \eta_{3}+c\pi_{2}}(\tilde{\mathcal{R}} _{0}-1), \\ &u_{1} =\frac{\omega \rho \eta_{1}}{ ( \alpha +\lambda_{u} ) \tilde{\mathcal{R}}_{0}}(\tilde{\mathcal{R}}_{0}-1), \qquad p_{1}=\frac{n\lambda \eta_{3}}{c}y_{1}. \end{aligned}$$ -
(iii)
The infected steady state with antibodies \(\Omega_{2}=(s_{2},u _{2},y_{2},p_{2},x_{2})\), where
$$\begin{aligned} \begin{aligned}&s_{2} =\frac{(\alpha +\lambda_{u})u_{2}}{\rho \eta_{1} ( \pi _{1}p_{2}+\pi_{2}y_{2} ) },\qquad y_{2}= \frac{-\tilde{B}+\sqrt{ \tilde{B}^{2}-4\tilde{A}\tilde{C}}}{2\tilde{A}}, \\ &u_{2} =\frac{\omega \rho \eta_{1} ( \pi_{1}m+\pi_{2}ry_{2} ) }{(\alpha +\lambda_{u})[rd+ ( \pi_{1}m+\pi_{2}ry_{2} ) ]},\qquad p_{2}= \frac{m}{r}, \\ & x_{2}=\frac{c}{a} \biggl( \frac{n\lambda \eta_{3}y _{2}}{cp_{2}}-1 \biggr), \end{aligned} \end{aligned}$$(14)where
$$ \begin{aligned}&\tilde{A}=\lambda \pi_{2}r, \qquad \tilde{B}=\lambda (rd+ \pi_{1}m)-\frac{ \tilde{\gamma }\omega \pi_{2}r}{\eta_{3}}, \\ & \tilde{C}=-\frac{ \tilde{\gamma }\omega \pi_{1}m}{\eta_{3}}. \end{aligned}$$(15)
We note that \(\Omega_{2}\) exists when \(\frac{n\lambda \eta_{3}y_{2}}{cp _{2}}>1\). Now we define
Hence, \(x_{2}=\frac{c}{a} ( \tilde{\mathcal{R}}_{1}-1 ) \). Thus, an infected steady state with antibodies \(\Omega_{2}=(s_{2},u _{2},y_{2}, p_{2},x_{2})\) exists when \(\tilde{\mathcal{R}}_{1}>1\).
Lemma 4
Let \(\tilde{\mathcal{R}}_{0}>1\), then (i) if \(\tilde{\mathcal{R}}_{1}\leq 1\), then \(p_{1}\leq p_{2}\), and (ii) if \(\tilde{\mathcal{R}}_{1}>1\), then \(p_{1}>p_{2}\).
Proof
(i) Let \(\tilde{\mathcal{R}}_{1}\leq 1\), then \(\frac{n\lambda \eta_{3}y_{2}}{cp_{2}}\leq 1\). Using Eq. (14), we obtain
which gives
Using Eq. (15), we get
It follows that \(p_{1}\leq p_{2}\). In a similar way, we can prove (ii). □
3.3 Global properties
Theorem 4
The pathogen-free steady state \(\Omega_{0}\) of system (12) is globally asymptotically stable when \(\tilde{\mathcal{R}}_{0}\leq 1\).
Proof
Let \(V_{0}(s,u,y,p,x)\) be given as follows:
where γ̃ is defined by Eq. (13). We get \(V_{0}(s,u,y,p,x)>0\) for all \(s,u,y,p,x>0\), \(V_{0}(s_{0},0, 0,0,0)=0\) and
Thus, \(\frac{dV_{0}}{dt}\leq 0\) when \(\tilde{\mathcal{R}}_{0}\leq 1\) for all \(s,p,x>0\). Similar to Theorem 1, we get \(\frac{dV_{0}}{dt}=0\) at \(\Omega_{0}\). Therefore, \(\Omega_{0}\) is globally asymptotically stable when \(\tilde{\mathcal{R}}_{0}\leq 1\). □
Theorem 5
For system (12), suppose that \(\tilde{\mathcal{R}}_{1}\leq 1<\tilde{\mathcal{R}}_{0}\), then \(\Omega_{1}\) is globally asymptotically stable.
Proof
Let us consider \(V_{1}(s,u,y,p,x)\):
We have \(V_{1}(s,u,y,p,x)>0\) for all \(s,u,y,p,x>0\) and \(V_{1}(s _{1},u_{1},y_{1},p_{1},0)=0\). Calculating \(\frac{dV_{1}}{dt}\), we obtain
Simplifying Eq. (17) and applying the steady state conditions for \(\Omega_{1}\)
we get
Consider the following equalities with (\(i=1\)):
we obtain
From Lemma 4, we have if \(\tilde{\mathcal{R}}_{1}\leq 1\) then \(p_{1} \leq p_{2}\). Thus \(\frac{dV_{1}}{dt}\leq 0\) and \(\frac{dV_{1}}{dt}=0\) occur at the infected steady state without antibodies \(\Omega_{1}\). Thus, \(\Omega_{1}\) is globally asymptotically stable when \(\tilde{\mathcal{R}}_{1}\leq 1\) and \(\tilde{\mathcal{R}}_{0}>1\). □
Theorem 6
For system (12), suppose that \(\tilde{\mathcal{R}}_{1}>1\), then \(\Omega_{2}\) is globally asymptotically stable.
Proof
Define \(V_{2} ( s,u,y,p,x ) \) as follows:
We have \(V_{2}(s,u,y,p,x)>0\) for all \(s,u,y,p,x>0\), while \(V_{2}(s,u,y,p,x)\) reaches its global minimum at \(\Omega_{2}\). Calculate \(\frac{dV_{2}}{dt}\) as follows:
Simplifying Eq. (19) and applying the steady state conditions for \(\Omega_{2}\)
we get
Considering equalities (18) with (\(i=2 \)), we obtain
Since \(\tilde{\mathcal{R}}_{1}>1\), then \(s_{2}\), \(u_{2}\), \(y_{2}\), \(p_{2}\), and \(x_{2}>0\). We have \(\frac{dV_{2}}{dt}\leq 0\), then following the proof of Theorem 3, one can show that \(\Omega_{2}\) is globally asymptotically stable. □
4 Numerical simulations
We present some numerical simulations to approve our theoretical results of system (2) with parameter values given in Table 1. We consider different initial values:
- IV1::
-
\(\phi_{1}(\theta)=800\), \(\phi_{2}(\theta)=2\), \(\phi_{3}(\theta)=2\), \(\phi_{4}(\theta)=6\), \(\phi_{5}(\theta)=2\),
- IV2::
-
\(\phi_{1}(\theta)=600\), \(\phi_{2}(\theta)=4\), \(\phi_{3}(\theta)=6\), \(\phi_{4}(\theta)=9\), \(\phi_{5}(\theta)=4\),
- IV3::
-
\(\phi_{1}(\theta)=400\), \(\phi_{2}(\theta)=6\), \(\phi_{3}(\theta)=9\), \(\phi_{4}(\theta)=15\), \(\phi_{5}(\theta)=6\),
- IV4::
-
\(\phi_{1}(\theta)=700\), \(\phi_{2}(\theta)=1\), \(\phi_{3}(\theta)=1\), \(\phi_{4}(\theta)=9\), \(\phi_{5}(\theta)=4\), \(\theta \in {}[ -\max \{ \tau_{1},\tau_{2},\tau_{3}\},0]\).
The stability of the steady states will be investigated by varying six parameters r, \(\pi_{1}\), \(\pi_{2}\), \(\tau_{1}\), \(\tau_{2}\), and \(\tau_{3}\) and fixing the other parameters.
Case (I) Effect of the parameters \(\pi_{1}\), \(\pi_{2}\), and r:
We choose \(\tau_{1}=\tau_{2}=\tau_{3}=0\) and \(\pi_{1}\), \(\pi_{2}\), and r are varied.
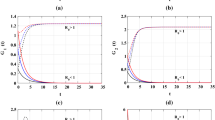
Set(1) \(\pi_{1}=0.0001\), \(\pi_{2}=0.0001\), and \(r=0.001\). This yields \(\mathcal{R}_{0}=0.3818<1\) and \(\mathcal{R}_{1}=0.1401<1\). Figure 1 shows that the concentration of susceptible cells increases and tends to the value \(\omega /d=1000\). In addition, the concentrations of infected cells, free pathogens, and antibodies are decreased and tend to zero for IV1–IV3. Therefore, there exists only one steady state that is \(\Omega_{0}\) and it is globally asymptotically stable. This shows the validity of Theorem 1.
The simulation of trajectories of system (2) for Case (I)
Set(2) \(\pi_{1}=0.0006\), \(\pi_{2}=0.0006\), and \(r=0.001\). With these values we obtain \(\mathcal{R}_{0}= 2.2909>1\) and \(\mathcal{R} _{1}=0.2367<1\). Figure 1 shows that the solutions of the system tend to the steady state \(\Omega_{1}=(436.5079,5.1227,6.1472,15.368,0)\) for all the three initial values IV1–IV3. Therefore, \(\Omega_{1}\) exists and it is globally asymptotically stable. Hence, the result of Theorem 2 is confirmed.
Set(3) \(\pi_{1}=0.0006\), \(\pi_{2}=0.0006\), and \(r=0.04\) and then \(\mathcal{R}_{0}=2.2909>1\) and \(\mathcal{R}_{1}=2.5285>1\). Figure 1 shows that the solutions of the system approach the steady state \(\Omega_{2}=(768.22,2.1071,2.5285,2.5,30.5702)\) for all the initial values IV1–IV3. Thus, \(\Omega_{2}\) exists and it is globally asymptotically stable. This validates the result of Theorem 3.
Case (II) Effect of time delay parameters:
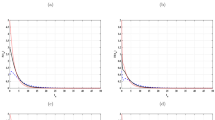
For this case, we take IV4 and choose the values \(\pi_{1}=0.0006\), \(\pi_{2}=0.0006\), and \(r=0.04\). Let us consider the case \(\tau =\tau_{1}=\tau_{2}=\tau_{3}\). We compute the values of \(\mathcal{R}_{0}\), \(\mathcal{R}_{1}\) and the steady states of system (2) as a function of τ (see Table 2).
Table 2 shows that the values of \(\mathcal{R}_{0}\) and \(\mathcal{R} _{1}\) are decreased as τ is increased. Moreover, we have the following cases:
-
(i)
\(\Omega_{2}\) exists and it is globally asymptotically stable when \(0\leq \tau <0.368091\);
-
(ii)
\(\Omega_{1}\) exists and it is globally asymptotically stable when \(0.368091\leq \tau <0.499367\);
-
(iii)
\(\Omega_{0}\) is globally asymptotically stable when \(\tau \geq 0.499367\).
Figure 2 depicts that the numerical results are also compatible with the results of Theorems 1–3.
The simulation of trajectories of system (2) with different values of τ for Case (II)
This means that the time delay can play the role of controller which can be designed to stabilize the system around the pathogen-free steady state \(\Omega_{0}\).
5 Conclusion
In this paper, we have studied two pathogen dynamics models with antibody immune response. Both pathogen-to-susceptible and infected-to-susceptible transmissions have been considered. We have considered two types of infected cells, latently infected cells, and actively infected cells. We have incorporated three types of discrete-time delays and distributed-time delays in the first and second models, respectively. We have shown that the solutions of the system are nonnegative and ultimately bounded, which ensures the well-posedness of the models. For each model, we have derived two threshold parameters \(\mathcal{R}_{0}\) (the basic reproduction number) and \(\mathcal{R} _{1}\) (the antibody response activation number), which fully determine the existence and stability of the three steady states of the model. We have investigated the global stability of all steady states of the model by using Lyapunov method and LaSalle’s invariance principle. We have proven that (i) if \(\mathcal{R}_{0}\leq 1\), then the pathogen-free steady state \(\Omega_{0}\) is globally asymptotically stable; (ii) if \(\mathcal{R}_{1}\leq 1<\mathcal{R}_{0}\), then the infected steady state without antibodies \(\Omega_{1}\) is globally asymptotically stable; and (iii) if \(\mathcal{R}_{1}>1\), then the infected steady state with antibodies \(\Omega_{2}\) is globally asymptotically stable. We have conducted numerical simulations and have shown that both the theoretical and numerical results are consistent.
References
Nowak, M.A., May, R.M.: Virus Dynamics: Mathematical Principles of Immunology and Virology. Oxford University Press, Oxford (2000)
Shu, H., Wang, L., Watmough, J.: Global stability of a nonlinear viral infection model with infinitely distributed intracellular delays and CTL immune responses. SIAM J. Appl. Math. 73(3), 1280–1302 (2013)
Huang, G., Takeuchi, Y., Ma, W.: Lyapunov functionals for delay differential equations model of viral infections. SIAM J. Appl. Math. 70(7), 2693–2708 (2010)
Hattaf, K., Yousfi, N.: A generalized virus dynamics model with cell-to-cell transmission and cure rate. Adv. Differ. Equ. 2016, 174 (2016)
Wang, J., Teng, Z., Miao, H.: Global dynamics for discrete-time analog of viral infection model with nonlinear incidence and CTL immune response. Adv. Differ. Equ. 2016, 143 (2016)
Elaiw, A.M., Raezah, A.A.: Stability of general virus dynamics models with both cellular and viral infections and delays. Math. Methods Appl. Sci. 40(16), 5863–5880 (2017)
Elaiw, A.M., Elnahary, E.K., Raezah, A.A.: Effect of cellular reservoirs and delays on the global dynamics of HIV. Adv. Differ. Equ. 2018, 85 (2018)
Elaiw, A.M., Hassanien, I.A., Azoz, S.A.: Global stability of HIV infection models with intracellular delays. J. Korean Math. Soc. 49(4), 779–794 (2012)
Elaiw, A.M.: Global dynamics of an HIV infection model with two classes of target cells and distributed delays. Discrete Dyn. Nat. Soc. 2012, Article ID 253703 (2012)
Elaiw, A.M., AlShamrani, N.H., Hattaf, K.: Dynamical behaviors of a general humoral immunity viral infection model with distributed invasion and production. Int. J. Biomath. 10(3), Article ID 1750035 (2017)
Elaiw, A.M., Raezah, A.A., Hattaf, K.: Stability of HIV-1 infection with saturated virus-target and infected-target incidences and CTL immune response. Int. J. Biomath. 10(5), Article ID 1750070 (2017)
Elaiw, A.M., AlShamrani, N.H.: Stability of latent pathogen infection model with adaptive immunity and delays. J. Integr. Neurosci. https://doi.org/10.3233/JIN-180087
Kang, C., Miao, H., Chen, X., Xu, J., Huang, D.: Global stability of a diffusive and delayed virus dynamics model with Crowley–Martin incidence function and CTL immune response. Adv. Differ. Equ. 2017, 324 (2017)
Callaway, D.S., Perelson, A.S.: HIV-1 infection and low steady state viral loads. Bull. Math. Biol. 64, 29–64 (2002)
Elaiw, A.M., AlShamrani, N.H., Alofi, A.S.: Stability of CTL immunity pathogen dynamics model with capsids and distributed delay. AIP Adv. 7, Article ID 125111 (2017)
Elaiw, A.M.: Global properties of a class of HIV models. Nonlinear Anal., Real World Appl. 11, 2253–2263 (2010)
Elaiw, A.M.: Global properties of a class of virus infection models with multitarget cells. Nonlinear Dyn. 69(1–2), 423–435 (2012)
Elaiw, A.M., Azoz, S.A.: Global properties of a class of HIV infection models with Beddington–DeAngelis functional response. Math. Methods Appl. Sci. 36, 383–394 (2013)
Elaiw, A.M., Almuallem, N.A.: Global dynamics of delay-distributed HIV infection models with differential drug efficacy in cocirculating target cells. Math. Methods Appl. Sci. 39, 4–31 (2016)
Li, B., Chen, Y., Lu, X., Liu, S.: A delayed HIV-1 model with virus waning term. Math. Biosci. Eng. 13, 135–157 (2016)
Elaiw, A.M., Raezah, A.A., Alofi, B.S.: Dynamics of delayed pathogen infection models with pathogenic and cellular infections and immune impairment. AIP Adv. 8, Article ID 025323 (2018)
Zhang, F., Li, J., Zheng, C., Wang, L.: Dynamics of an HBV/HCV infection model with intracellular delay and cell proliferation. Commun. Nonlinear Sci. Numer. Simul. 42, 464–476 (2017)
Gómez-Acevedo, H., Li, M.Y.: Backward bifurcation in a model for HTLV-I infection of CD4+ T cells. Bull. Math. Biol. 67(1), 101–114 (2005)
Murase, A., Sasaki, T., Kajiwara, T.: Stability analysis of pathogen-immune interaction dynamics. J. Math. Biol. 51, 247–267 (2005)
Wang, T., Hu, Z., Liao, F.: Stability and Hopf bifurcation for a virus infection model with delayed humoral immunity response. J. Math. Anal. Appl. 411, 63–74 (2014)
Elaiw, A.M., AlShamrani, N.H.: Global stability of humoral immunity virus dynamics models with nonlinear infection rate and removal. Nonlinear Anal., Real World Appl. 26, 161–190 (2015)
Elaiw, A.M., AlShamrani, N.H.: Global properties of nonlinear humoral immunity viral infection models. Int. J. Biomath. 8(5), Article ID 1550058 (2015)
Elaiw, A.M., AlShamrani, N.H.: Stability of a general delay-distributed virus dynamics model with multi-staged infected progression and immune response. Math. Methods Appl. Sci. 40(3), 699–719 (2017)
Xu, J., Zhou, Y., Li, Y., Yang, Y.: Global dynamics of a intracellular infection model with delays and humoral immunity. Math. Methods Appl. Sci. 39(18), 5427–5435 (2016)
Culshaw, R.V., Ruan, S., Webb, G.: A mathematical model of cell-to-cell spread of HIV-1 that includes a time delay. J. Math. Biol. 46, 425–444 (2003)
Chen, S.-S., Cheng, C.-Y., Takeuchi, Y.: Stability analysis in delayed within-host viral dynamics with both viral and cellular infections. J. Math. Anal. Appl. 442, 642–672 (2016)
Lai, X., Zou, X.: Modeling cell-to-cell spread of HIV-1 with logistic target cell growth. J. Math. Anal. Appl. 426, 563–584 (2015)
Yang, Y., Zou, L., Ruan, S.: Global dynamics of a delayed within-host viral infection model with both virus-to-cell and cell-to-cell transmissions. Math. Biosci. 270, 183–191 (2015)
Elaiw, A.M., Raezah, A., Alofi, A.: Stability of a general delayed virus dynamics model with humoral immunity and cellular infection. AIP Adv. 7(6), Article ID 065210 (2017)
Elaiw, A.M., Raezah, A., Alofi, A.S.: Effect of humoral immunity on HIV-1 dynamics with virus-to-target and infected-to-target infections. AIP Adv. 6(8), Article ID 085204 (2016)
Lin, J., Xu, R., Tian, X.: Threshold dynamics of an HIV-1 virus model with both virus-to-cell and cell-to-cell transmissions, intracellular delay, and humoral immunity. Appl. Math. Comput. 315, 516–530 (2017)
Gibelli, L., Elaiw, A., Alghamdi, M.A., Althiabi, A.M.: Heterogeneous population dynamics of active particles: progression, mutations, and selection dynamics. Math. Models Methods Appl. Sci. 27, 617–640 (2017)
Hale, J.K., Lunel, S.M.V.: Introduction to Functional Differential Equations. Springer, New York (1993)
Funding
This work was supported by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah, under grant No. (D-127-130-1438). The authors, therefore, gratefully acknowledge the DSR for technical and financial support.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hobiny, A.D., Elaiw, A.M. & Almatrafi, A.A. Stability of delayed pathogen dynamics models with latency and two routes of infection. Adv Differ Equ 2018, 276 (2018). https://doi.org/10.1186/s13662-018-1720-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1720-x