Delay-induced Hopf bifurcation of an SVEIR computer virus model with nonlinear incidence rate

Abstract

We are concerned with the Hopf bifurcation of an SVEIR computer virus model with time delay and nonlinear incident rate. First of all, by analyzing the associated characteristic equation we obtain sufficient conditions for its local stability and the existence of a Hopf bifurcation. Directly afterward, by means of the normal form theory and the center manifold theorem we derive explicit formulas that determine the direction of the Hopf bifurcation and the stability of the bifurcated periodic solutions. Finally, we carry out numerical simulations to illustrate and verify the theoretical results.

1 Introduction

With the fast development and popularization of computer networks, computer viruses have tremendous influence on our society. To predict the propagation of computer viruses in networks, in recent years many computer virus models have been proposed and investigated such as SIRS models [1–5], SEIS models [6, 7], SEIR models [8–10], SEIQRS models [11–13], SLBS models [14–16] and some other models [17–20].

The overwhelming majority of the computer virus models mentioned assume a bilinear infection rate. However, there are several reasons why bilinear infection rate requires modification [21]. Especially, the propagation of computer viruses can be dramatically affected by the topology of the underlying network, and this may lead to some specific nonlinear infection rates. In addition, the choice of the treatment function is also an important factor for the modeling of computer virus spreading. For example, the treatment rate may be slow due to the lower effectiveness of antivirus, and the treatment rate may increase slowly and attain its peak and finally settles down at its saturation value with the improved and effective antivirus technology [22]. Based on this fact, Upadhyay et al. [22] proposed the following computer virus model with nonlinear incidence rate and saturated treatment rate:

$$ \textstyle\begin{cases} \frac{dS(t)}{dt}=A-\delta_{0} S(t)- \frac{\alpha S(t)I(t)}{S(t)+I(t)+c}+\eta V(t)-\mu S(t), \\ \frac{dE(t)}{dt}=\frac{\alpha S(t)I(t)}{S(t)+I(t)+c}-(\delta_{0}+ \delta_{1})E(t), \\ \frac{dI(t)}{dt}=\delta_{1} E(t)-(\delta_{0}+\delta_{2}+\delta_{3}) I(t)-\frac{\beta I(t)}{I(t)+a}, \\ \frac{dR(t)}{dt}=\delta_{2} I(t)-\delta_{0} R(t)+ \frac{\beta I(t)}{I(t)+a}, \\ \frac{dV(t)}{dt}=\mu S(t)-(\delta_{0}+\eta) V(t), \end{cases} $$

(1)

where $S(t)$, $E(t)$, $I(t)$, $R(t)$, and $V(t)$ denote the numbers of the susceptible computers, the exposed computers, the infectious computers, the recovered computers, and the vaccinated computers at time t, respectively, A is the recruitment rate of new computers, α is the contact rate of the susceptible computers, η is the rate at which the vaccinated computers lose their immunity and join the susceptible ones, β denotes the maximal treatment capacity of a network, $\delta_{0}$ is the natural mortality rate of all the computers, $\delta_{1}$ is the rate at which the exposed computers become the infectious ones, $\delta_{2}$ is the recovery rate of the infectious computers, $\delta_{3}$ is the crashing rate of the infectious computers due to the viruses, a is the half saturation constant for the infectious computers, c is the saturation constant for the susceptible computers, and μ is the vaccination rate of the susceptible computers. Upadhyay et al. [22] studied the stability of the viral equilibrium of system (1).

It is well known that time delays of one type or another have been incorporated into computer virus models due to latent period [3, 4], temporary immunity period [5, 12], or other reasons [9], because time delays may play a complicated role on the models. For example, time delays can cause the loss of stability and can induce Hopf bifurcation and periodic solutions. As stated in [4], the occurrence of a Hopf bifurcation means that the state of computer virus prevalence changes from an equilibrium to a limit cycle, and this phenomenon is unexpected, since the periodic behavior is unpleasant from the viewpoint of epidemiology. Having this idea in mind and considering that the antivirus software may use a period to clean the viruses in the infectious computers, it is worth investigating the Hopf bifurcation of the following system with time delay:

$$ \textstyle\begin{cases} \frac{dS(t)}{dt}=A-\delta_{0} S(t)- \frac{\alpha S(t)I(t)}{S(t)+I(t)+c}+\eta V(t)-\mu S(t), \\ \frac{dE(t)}{dt}=\frac{\alpha S(t)I(t)}{S(t)+I(t)+c}-(\delta_{0}+ \delta_{1})E(t), \\ \frac{dI(t)}{dt}=\delta_{1} E(t)-(\delta_{0}+\delta_{3}) I(t)-\delta _{2} I(t-\tau)-\frac{\beta I(t-\tau)}{I(t-\tau)+a}, \\ \frac{dR(t)}{dt}=\delta_{2} I(t-\tau)-\delta_{0} R(t)+\frac{\beta I(t-\tau)}{I(t-\tau)+a}, \\ \frac{dV(t)}{dt}=\mu S(t)-(\delta_{0}+\eta) V(t), \end{cases} $$

(2)

where τ is the time delay due to the period the antivirus software uses to clean the viruses in the infectious computers.

The organization of the rest of this paper is organized as follows. In Sect. 2, the local stability and existence of a Hopf bifurcation are performed. In Sect. 3, the direction and stability of the Hopf bifurcation are determined. In Sect. 4, the obtained analytical findings are justified through computer simulations. This work is closed by Sect. 5.

2 Stability of the viral equilibrium and existence of Hopf bifurcation

By direct computation we get that if $[\alpha \delta_{1}-(\delta_{0}+ \delta_{1})(\delta_{0}+\delta_{2}+\delta_{3})](I_{*}+a)>\beta \delta _{1}(\delta_{0}+\delta_{1})$, then system (2) has a viral equilibrium $P_{*}(S_{*}, E_{*}, I_{*}, R_{*}, V_{*})$, where

$$\begin{aligned}& S_{*} =\frac{(\delta_{0}+\delta_{1})(\delta_{0}+\delta_{2}+\delta _{3})(I_{*}+a)(I_{*}+c)+\beta \delta_{1}(\delta_{0}+\delta_{1})(I_{*}+c)}{[ \alpha \delta_{1}-(\delta_{0}+\delta_{1})(\delta_{0}+\delta_{2}+\delta _{3})](I_{*}+a)-\beta \delta_{1}(\delta_{0}+\delta_{1})}, \\& E_{*} =\frac{(\delta_{0}+\delta_{2}+\delta_{3})I_{*}}{\delta_{1}}+\frac{ \beta I_{*}}{\delta_{1}(I_{*}+a)}, \\& R_{*} =\frac{\delta_{2}I_{*}}{\delta_{0}}+\frac{\beta I_{*}}{\delta _{0}(I_{*}+a)}, \\& V_{*} =\frac{\mu [(\delta_{0}+\delta_{1})(\delta_{0}+\delta_{2}+ \delta_{3})(I_{*}+a)(I_{*}+c)+\beta \delta_{1}(\delta_{0}+\delta_{1})(I _{*}+c)]}{(\delta_{0}+\eta)\{[\alpha \delta_{1}-(\delta_{0}+\delta _{1})(\delta_{0}+\delta_{2}+\delta_{3})](I_{*}+a)-\beta \delta_{1}( \delta_{0}+\delta_{1})\}}, \end{aligned}$$

and $I_{*}$ is the positive root of the equation

$$ a_{3}I^{3}+a_{2}I^{2}+a_{1}I+a_{0}=0, $$

(3)

where

$$\begin{aligned}& a_{0} =\delta_{1}B_{6}c-B_{1}c( \delta_{0}+\eta)+\delta_{1}ac\bigl[B_{7}-B _{2}(\delta_{0}+\eta)\bigr] \\& \hphantom{a_{0}=}{}+Aa\delta_{1}(\delta_{0}+\eta) (B_{3}a-B_{4}), \\& a_{1} =B_{6}a^{2}\delta_{1}-a^{2} \delta_{1}(\delta_{0}+\eta) (B_{1} \delta_{1}+B_{3}B_{5}) \\& \hphantom{a_{1}=}{}+\delta_{1}(a+c) \bigl(B_{7}-B_{2}( \delta_{0}+\eta)\bigr) \\& \hphantom{a_{1}=}{}+a(\delta_{0}+\eta) \bigl(B_{4}B_{5} \delta_{1}-B_{3}\beta (\delta_{0}+ \delta_{1})\bigr) \\& \hphantom{a_{1}=}{}+(\delta_{0}+\eta) \bigl(2AB_{3}a \delta_{1}-AB_{4}\delta_{1}+B_{4}\beta (\delta_{0}+\delta_{1})\bigr), \\& a_{2} =\delta_{1}(2B_{6}a+B_{7})+ \delta_{1}(\delta_{0}+\eta) (AB_{3}+B _{4}B_{5}-B_{2}) \\& \hphantom{a_{2}=}{}-(\delta_{0}+\eta) \bigl(B_{3}\beta ( \delta_{0}+\delta_{1})+\delta_{1}(B _{1}+B_{3}B_{5})\bigr), \\& a_{3} =\delta_{1}B_{6}-\delta_{1}( \delta_{0}+\eta) (B_{1}+B_{3}B_{5}), \end{aligned}$$

with

$$\begin{aligned}& B_{1} =(\delta_{0}+\mu) (\delta_{0}+ \delta_{1}) (\delta_{0}+\delta _{2}+ \delta_{3}), \\& B_{2} =\beta \delta_{1}(\delta_{0}+\mu) ( \delta_{0}+\delta_{1}), \\& B_{3} =\alpha \delta_{1}-(\delta_{0}+ \delta_{1}) (\delta_{0}+\delta _{2}+ \delta_{3}), \\& B_{4} =\beta \delta_{1}(\delta_{0}+ \delta_{1}), \\& B_{5} =\frac{(\delta_{0}+\delta_{1})(\delta_{0}+\delta_{2}+\delta _{3})}{\delta_{1}}, \\& B_{6} =\eta \mu (\delta_{0}+\delta_{1}) ( \delta_{0}+\delta_{2}+\delta _{3}), \\& B_{7} =\eta \mu \beta \delta_{1}(\delta_{0}+ \delta_{1}). \end{aligned}$$

For Eq. (3), we have the following results.

Lemma 1

If $a_{3}=0$, then

• (1) if $a_{2}=0$ and $a_{0}/a_{1}<0$, then there exists a unique positive root $I_{*}=-a_{0}/a_{1}$ of Eq. (3);

• (2) When $\Delta >0$, if $a_{2}/a_{1}<0$ and $a_{0}/a_{2}>0$, then there exist two positive roots $I_{*}^{(1)}=I_{*}^{+}$ and $I_{*}^{(2)}=I _{*}^{-}$; if $a_{0}/a_{2}<0$, then there is a unique positive root $I_{*}=I_{*}^{+}$ with $a_{1}>0$ or $I_{*}=I_{*}^{-}$ with $a_{2}<0$; if $a_{0}=0$ and $a_{1}/a_{2}<0$, then there is a unique positive root $I_{*}=-a_{1}/a_{2}$;

• (3) if $\Delta =0$ and $a_{1}/a_{2}<0$, then there is a unique positive root $I_{*}=-a_{1}/(2a_{2})$. Here $\Delta =a_{1}^{2}-4a_{2}a_{0}$, $I_{*}^{+}=(-a_{1}+\sqrt{ \Delta })/(2a_{2})$, and $I_{*}^{-}=-(a_{1}+\sqrt{\Delta })/(2a_{2})$.

Lemma 2

For $a_{3}\neq 0$, let $l_{2}=a_{2}/a_{3}$, $l_{1}=a_{1}/a_{3}$, and $l_{0}=a_{0}/a_{3}$. Then:

• (1) if $l_{0}<0$, then Eq. (3) has at least one positive root;

• (2) if $l_{0}\geq 0$ and $l_{2}^{2}-3l_{1}\leq 0$, then Eq. (3) has no positive root;

• (3) if $l_{0}\geq 0$ and $l_{2}^{2}-3l_{1}>0$, then Eq. (3) has a positive root if and only if $\frac{-l _{2}+\sqrt{l_{2}^{2}-3l_{1}}}{3}>0$ and $h (\frac{-l_{2}+\sqrt{l _{2}^{2}-3l_{1}}}{3} )\leq 0$, where $h(I)=I^{3}+l_{2}I^{2}+l_{1}I+l _{0}$.

Then, we can obtain the linearization of system (2). Let $u_{1}(t)=S(t)-S_{*}$, $u_{2}(t)=E(t)-E_{*}$, $u_{3}(t)=I(t)-I_{*}$, $u_{4}(t)=R(t)-R_{*}$, $u_{5}(t)=V(t)-V_{*}$. We can rewrite system (2) as follows:

$$ \textstyle\begin{cases} \dot{u}_{1}(t)=a_{11}u_{1}(t)+a_{13}u_{3}(t)+a_{15}u_{5}(t)+\sum_{i+j\geq 2}\frac{1}{i!j!}f_{ij}^{(1)}u_{1}^{i}(t)u_{3}^{j}(t), \\ \dot{u}_{2}(t)=a_{21}u_{1}(t)+a_{22}u_{2}(t)+a_{23}u_{3}(t)+\sum_{i+j\geq 2}\frac{1}{i!j!}f_{ij}^{(2)}u_{1}^{i}(t)u_{3}^{j}(t), \\ \dot{u}_{3}(t)=a_{32}u_{2}(t)+a_{33}u_{3}(t)+b_{33}u_{3}(t-\tau)+ \sum_{i\geq 2}\frac{1}{i!}f_{i}^{(3)}u_{3}^{i}(t-\tau), \\ \dot{u}_{4}(t)=a_{44}u_{4}(t)+b_{43}u_{3}(t-\tau)+\sum_{i \geq 2}\frac{1}{i!}f_{i}^{(4)}u_{3}^{i}(t-\tau), \\ \dot{u}_{5}(t)=a_{51}u_{1}(t)+a_{55}u_{5}(t), \end{cases} $$

(4)

where

$$\begin{aligned}& a_{11} =- \biggl[\delta_{0}+\mu +\frac{\alpha I_{*}(I_{*}+c)}{(S_{*}+I _{*}+c)^{2}} \biggr],\qquad a_{13}=- \frac{\alpha S_{*}(S_{*}+c)}{(S_{*}+I_{*}+c)^{2}},\qquad a_{15}=\eta, \\& a_{21} =\frac{\alpha I_{*}(I_{*}+c)}{(S_{*}+I_{*}+c)^{2}},\qquad a_{22}=-( \delta_{0}+\delta_{1}), \qquad a_{23}= \frac{\alpha S_{*}(S_{*}+c)}{(S_{*}+I _{*}+c)^{2}}, \\& a_{32} =\delta_{1},\qquad a_{33}=-( \delta_{0}+\delta_{3}),\qquad b_{33}=- \biggl[ \delta_{2}+\frac{a\beta }{(I_{*}+a)^{2}} \biggr], \\& a_{44} =-\delta_{0},\qquad a_{51}=\mu,\qquad a_{55}=-(\delta_{0}+\eta), \\& b_{43}= \biggl[ \delta_{2}+\frac{a\beta }{(I_{*}+a)^{2}} \biggr], \\& f_{ij}^{(k)} =\frac{\partial^{i+j}f^{(k)}(S_{*}, E_{*}, I_{*}, R_{*}, V_{*})}{\partial u_{1}^{i}(t)\partial u_{3}^{j}(t)}, \\& f_{i}^{(k)} =\frac{\partial^{i}f^{(k)}(S_{*}, E_{*}, I_{*}, R_{*}, V _{*})}{\partial u_{3}^{i}(t-\tau)}, \\& f^{(1)} =A-\delta_{0} u_{1}(t)-\frac{\alpha u_{1}(t)u_{3}(t)}{u_{1}(t)+u _{3}(t)+c}- \mu S(t), \\& f^{(2)} =\frac{\alpha u_{1}(t)u_{3}(t)}{u_{1}(t)+u_{3}(t)+c}-(\delta _{0}+ \delta_{1})u_{2}(t), \\& f^{(3)} =\delta_{1} u_{2}(t)-(\delta_{0}+ \delta_{3}) u_{3}(t)-\delta _{2} u_{3}(t- \tau)-\frac{\beta u_{3}(t-\tau)}{u_{3}(t-\tau)+a}, \\& f^{(4)} =\delta_{2} u_{3}(t-\tau)- \delta_{0} u_{4}(t)+\frac{\beta u _{3}(t-\tau)}{u_{3}(t-\tau)+a}. \end{aligned}$$

Then we obtain the linearized system of system (4)

$$ \textstyle\begin{cases} \dot{u}_{1}(t)=a_{11}u_{1}(t)+a_{13}u_{3}(t)+a_{15}u_{5}(t), \\ \dot{u}_{2}(t)=a_{21}u_{1}(t)+a_{22}u_{2}(t)+a_{23}u_{3}(t), \\ \dot{u}_{3}(t)=a_{32}u_{2}(t)+a_{33}u_{3}(t)+b_{33}u_{3}(t-\tau), \\ \dot{u}_{4}(t)=a_{44}u_{4}(t)+b_{43}u_{3}(t-\tau), \\ \dot{u}_{5}(t)=a_{51}u_{1}(t)+a_{55}u_{5}(t). \end{cases} $$

(5)

The characteristic equation is

$$\begin{aligned} P(\lambda) =&\lambda^{5}+p_{4} \lambda^{4}+p_{3}\lambda^{3}+p_{2}\lambda ^{2}+p_{1}\lambda +p_{0}+\bigl(q_{4} \lambda^{4}+q_{3}\lambda^{3}+q_{2} \lambda^{2}+q_{1}\lambda +q_{0} \bigr)e^{-\lambda \tau } \\ =&0, \end{aligned}$$

(6)

where

$$\begin{aligned}& p_{0} =a_{44}(a_{22}a_{33}-a_{23}a_{32}) (a_{15}a_{51}-a_{11}a_{55})-a _{13}a_{21}a_{32}a_{44}a_{55}, \\& p_{1} =a_{55}\bigl(a_{11}a_{22}(a_{33}+a_{44})+a_{33}a_{44}(a_{11}+a_{22}) \bigr)+a _{11}a_{22}a_{33}a_{44} \\& \hphantom{p_{1}=}{}-a_{23}a_{32}(a_{11}a_{44}+a_{11}a_{55}+a_{44}a_{55})+a_{15}a_{23}a _{32}a_{51} \\& \hphantom{p_{1}=}{}-a_{15}a_{51}(a_{22}a_{33}+a_{22}a_{44}+a_{33}a_{44})+a_{13}a_{21}a _{32}(a_{44}+a_{55}), \\& p_{2} =a_{23}a_{32}(a_{11}+a_{44}+a_{55})+a_{15}a_{51}(a_{22}+a_{33}+a _{44})-a_{13}a_{21}a_{32} \\& \hphantom{p_{2}=}{}-\bigl(a_{11}a_{22}(a_{33}+a_{44})+a_{33}a_{44}(a_{11}+a_{22}) \bigr) \\& \hphantom{p_{2}=}{}-a_{55}\bigl(a_{11}a_{22}+a_{33}a_{44}+(a_{11}+a_{22}) (a_{33}+a_{44})\bigr), \\& p_{3} =a_{11}a_{22}+a_{33}a_{44}+(a_{11}+a_{22}) (a_{33}+a_{44})-a _{23}a_{32}-a_{15}a_{51} \\& \hphantom{p_{3}=}{}+a_{55}(a_{11}+a_{22}+a_{33}+a_{44}), \\& p_{4} =-(a_{11}+a_{22}+a_{33}+a_{44}+a_{55}),\qquad q_{0}=a_{22}a_{44}b _{33}(a_{15}a_{51}-a_{11}a_{55}), \\& q_{1} =a_{11}a_{22}b_{33}(a_{44}+a_{55})+a_{44}a_{55}b_{33}(a_{11}+a _{22})-a_{15}a_{51}b_{33}(a_{22}+a_{44}), \\& q_{2} =a_{15}a_{51}b_{33}-b_{33} \bigl(a_{11}a_{22}+a_{44}a_{55}+(a_{11}+a _{22}) (a_{44}+a_{55})\bigr), \\& q_{3} =b_{33}(a_{11}+a_{22}+a_{44}+a_{55}), \qquad q_{4}=-b_{33}. \end{aligned}$$

When $\tau =0$, Eq. (3) reduces to

$$ \lambda^{5}+p_{04}\lambda^{4}+p_{03} \lambda^{3}+p_{02}\lambda^{2}+p _{01} \lambda +p_{00}=0 $$

(7)

with

$$ \begin{aligned}&p_{00}=p_{0}+q_{0},\qquad p_{01}=p_{1}+q_{1},\qquad p_{02}=p_{2}+q_{2}, \\ &p_{03}=p _{3}+q_{3},\qquad p_{04}=p_{4}+q_{4}. \end{aligned} $$

Obviously,

$$ p_{04}=\mu +5\delta_{0}+\delta_{1}+ \delta_{2}+\delta_{3}+\frac{\alpha I_{*}(I_{*}+c)}{(S_{*}+I_{*}+c)^{2}}+\frac{a\beta }{(I_{*}+a)^{2}}>0. $$

An application of the Routh–Hurwitz criterion gives $\operatorname{Re}( \lambda)<0$ if and only if condition ($H_{1}$) is satisfied, that is, if the following inequalities hold:

$$\begin{aligned}& \operatorname{det}_{2} = \left \vert \begin{matrix} p_{04} &{1} \\ p_{02} &p_{03} \end{matrix} \right \vert >0, \end{aligned}$$

(8)

$$\begin{aligned}& \operatorname{det}_{3} =\left \vert \begin{matrix} p_{04} &{1} &{0} \\ p_{02} &p_{03} &p_{04} \\ {0} &p_{01} &p_{02} \end{matrix} \right \vert >0, \end{aligned}$$

(9)

$$\begin{aligned}& \operatorname{det}_{4} =\left \vert \begin{matrix} p_{04} &{1} &{0} &{0} \\ p_{02} &p_{03} &p_{04} &{1} \\ p_{00} &p_{01} &p_{02} &p_{03} \\ {0} &{0} &p_{00} &p_{01} \end{matrix} \right \vert >0, \end{aligned}$$

(10)

$$\begin{aligned}& \operatorname{det}_{5} =\left \vert \begin{matrix} p_{04} &{1} &{0} &{0} &{0} \\ p_{02} &p_{03} &p_{04} &{1} &{0} \\ p_{00} &p_{01} &p_{02} &p_{03} &p_{04} \\ {0} &{0} &p_{00} &p_{01} &p_{02} \\ {0} &{0} &{0} &{0} &p_{00} \end{matrix} \right \vert >0. \end{aligned}$$

(11)

For $\tau >0$, we assume that $\lambda =i\omega$ ($\omega >0$) is a root of Eq. (6). Then

$$ \textstyle\begin{cases} (q_{1}\omega -q_{3}\omega^{3})\sin \tau \omega +(q_{4}\omega^{4}-q _{2}\omega^{2}+q_{0})\cos \tau \omega =p_{2}\omega^{2}-p_{4}\omega ^{4}-p_{0}, \\ (q_{1}\omega -q_{3}\omega^{3})\cos \tau \omega -(q_{4}\omega^{4}-q _{2}\omega^{2}+q_{0})\sin \tau \omega =p_{3}\omega^{3}-\omega^{5}-p _{1}\omega. \end{cases} $$

Thus

$$ \omega^{10}+e_{4}\omega^{8}+e_{3} \omega^{6}+e_{2}\omega^{4}+e_{1} \omega^{2}+e_{0}=0, $$

(12)

where

$$\begin{aligned}& e_{0} =p_{0}^{2}-q_{0}^{2}, \qquad e_{1}=p_{1}^{2}-2p_{0}p_{2}+2q_{0}q_{2}-q _{1}^{2}, \\& e_{2} =p_{2}^{2}-2p_{1}p_{3}+2p_{0}p_{4}-q_{2}^{2}-2q_{1}q_{3}, \\& e_{3} =p_{3}^{2}+2p_{1}-2p_{2}p_{4}+2q_{2}q_{4}-q_{3}^{2}, \\& e_{4} =p_{4}^{2}-2p_{3}-q_{4}^{2}. \end{aligned}$$

Let $v=\omega^{2}$. Then Eq. (12) becomes

$$ v^{5}+e_{4}v^{4}+e_{3}v^{3}+e_{2}v^{2}+e_{1}v+e_{0}=0. $$

(13)

Based on the discussion about the distribution of the roots of Eq. (13) in [23] and considering that all the values of parameters in system (2) are given, we can obtain all the roots of Eq. (13). Thus we make the following assumption:

($H_{2}$):

Equation (13) has at least one positive root $v_{0}$.

If condition ($H_{2}$) holds, then there exists $v_{0}>0$ such that Eq. (6) has a pair of purely imaginary roots $\pm i \omega_{0}=\pm i\sqrt{v_{0}}$. For $\omega_{0}$, we have

$$ \tau_{0}=\frac{1}{\omega_{0}}\times \biggl\{ \frac{g_{1}(\omega_{0})}{g _{2}(\omega_{0})} \biggr\} , $$

where

$$\begin{aligned}& g_{1}(\omega_{0}) =(q_{3}-p_{4}q_{4}) \omega_{0}^{8}+(p_{3}q_{3}-q _{1}+p_{2}q_{4}+p_{4}q2) \omega_{0}^{6} \\& \hphantom{g_{1}(\omega_{0}) =}{}+(p_{1}q_{3}+p_{3}q_{1}-p_{0}q_{4}-p_{2}q_{2}-p_{4}q_{0}) \omega_{0} ^{4} \\& \hphantom{g_{1}(\omega_{0}) =}{}+(p_{0}q_{2}+p_{2}q_{0}-p_{1}q_{1}) \omega_{0}^{2}-p_{0}q_{0}, \\& g_{2}(\omega_{0}) =q_{4}^{2} \omega_{0}^{8}+\bigl(q_{3}^{2}-2q_{2}q_{4} \bigr) \omega_{0}^{6}+\bigl(q_{2}^{2}+2q_{0}q_{4}+2q_{1}q_{3} \bigr)\omega_{0}^{4} \\& \hphantom{g_{2}(\omega_{0}) =}{}+\bigl(q_{1}^{2}-2q_{0}q_{2} \bigr)\omega_{0}^{2}+q_{0}^{2}. \end{aligned}$$

Next, differentiating Eq. (6) with respect to τ, we obtain

$$\begin{aligned} \biggl[\frac{d\lambda }{d\tau } \biggr]^{-1} =&-\frac{5\lambda^{4}+4p_{4} \lambda^{3}+3p_{3}\lambda^{2}+2p_{2}\lambda +p_{1}}{\lambda (\lambda ^{5}+p_{4}\lambda^{4}+p_{3}\lambda^{3}+p_{2}\lambda^{2}+p_{1}\lambda +p_{0})} \\ &{}+\frac{4q_{4}\lambda^{3}+3q_{3}\lambda^{2}+2q_{2}\lambda +q _{1}}{\lambda (q_{4}\lambda^{4}+q_{3}\lambda^{3}+q_{2}\lambda^{2}+q _{1}\lambda +q_{0})}-\frac{\tau }{\lambda }. \end{aligned}$$

Further, we have

$$ \operatorname{Re}\biggl[\frac{d\lambda }{d\tau } \biggr]_{\tau =\tau_{0}}^{-1}= \frac{f ^{\prime }(v_{0})}{(q_{1}\omega_{0}-q_{3}\omega_{0}^{3})^{2}+(q_{4} \omega_{0}^{4}-q_{2}\omega_{0}^{2}+q_{0})^{2}}, $$

where $v_{0}=\omega_{0}^{2}$ and $f(v)=v^{5}+e_{4}v^{4}+e_{3}v^{3}+e _{2}v^{2}+e_{1}v+e_{0}$.

Therefore, if condition ($H_{3}$): $f^{\prime }(v_{0})\neq 0$ holds, then $\operatorname{Re}[\frac{d\lambda }{d\tau }]_{\tau =\tau_{0}}\neq 0$. Based on the previous discussion and the Hopf bifurcation theorem in [24], we have the following:

Theorem 1

Suppose that the conditions ($H_{1}$), ($H_{2}$), and ($H_{3}$) hold for system (2). The viral equilibrium $P_{*}(S_{*}, E_{*}, I _{*}, R_{*}, V_{*})$ is locally asymptotically stable when $\tau \in [0, \tau_{0})$; a Hopf bifurcation occurs at the viral equilibrium $P_{*}(S_{*}, E_{*}, I_{*}, R_{*}, V_{*})$ when $\tau =\tau_{0}$, and a family of periodic solutions bifurcate from the viral equilibrium $P_{*}(S_{*}, E_{*}, I_{*}, R_{*}, V_{*})$ near $\tau =\tau_{0}$.

3 Direction and stability of the Hopf bifurcation

Let $u_{1}(t)=S(t)-S_{*}$, $u_{2}(t)=E(t)-E_{*}$, $u_{3}(t)=I(t)-I _{*}$, $u_{4}(t)=R(t)-R_{*}$, $u_{5}(t)=V(t)-V_{*}$. Rescale the time delay by $t\rightarrow (t/\tau)$. Let $\tau =\tau_{0}+\varrho$, $\varrho \in R$. Then the Hopf bifurcation occurs at $\varrho =0$. Thus system (2) can be transformed into

$$ \dot{u}(t)=L_{\varrho }u_{t}+F(\varrho, u_{t}), $$

(14)

where $u_{t}=(u_{1}(t), u_{2}(t), u_{3}(t), u_{4}(t), u_{5}(t))^{T}=(S, E, I, R, V)^{T} \in R^{5}$, $u_{t}(\theta)=u(t+\theta)\in C=C([-1, 0], R^{5})$, and $L_{\varrho }$: $C\rightarrow R^{5}$ and $F(\varrho, u _{t})\rightarrow R^{5}$ are given by

$$\begin{aligned}& L_{\varrho }\phi =(\tau_{0}+\varrho) \bigl(M_{\max }\phi (0)+N_{\max } \phi (-1)\bigr), \\& F(\varrho,\phi)=(F_{1}, F_{2}, F_{3}, F_{4}, 0) \end{aligned}$$

with

$$ M_{\max }= \left ( \begin{matrix} a_{11} &{0} &a_{13} &{0} &a_{15} \\ a_{21} &a_{22} &a_{23} &{0} &{0} \\ {0} &a_{32} &a_{33} &{0} &{0} \\ {0} &{0} &{0} &a_{44} &{0} \\ a_{51} &{0} &{0} &{0} &a_{55} \end{matrix} \right ) ,\qquad N_{\max }= \left ( \begin{matrix} {0} &{0} &{0} &{0} &{0} \\ {0} &{0} &{0} &{0} &{0} \\ {0} &{0} &b_{33} &{0} &{0} \\ {0} &{0} &b_{43} &{0} &{0} \\ {0} &{0} &{0} &{0} &{0} \end{matrix} \right ), $$

and

$$\begin{aligned}& F_{1} =a_{16}\phi_{1}^{2}(0)+a_{17} \phi_{3}^{2}(0)+a_{18}\phi_{1}(0) \phi_{3}(0)+a_{19}\phi_{1}^{2}(0) \phi_{3}(0) \\& \hphantom{F_{1} =}{}+a_{110}\phi_{1}(0)\phi_{3}^{2}(0)+a_{111} \phi_{1}^{3}(0)+a_{112} \phi_{3}^{3}(0)+ \cdots, \\& F_{2} =a_{24}\phi_{1}^{2}(0)+a_{25} \phi_{3}^{2}(0)+a_{26}\phi_{1}(0) \phi_{3}(0)+a_{27}\phi_{1}^{2}(0) \phi_{3}(0) \\& \hphantom{F_{2} =}{}+a_{28}\phi_{1}(0)\phi_{3}^{2}(0)+a_{29} \phi_{1}^{3}(0)+a_{210}\phi _{3}^{3}(0)+ \cdots, \\& F_{3} =a_{34}\phi_{3}^{2}(-1)+a_{35} \phi_{3}^{3}(-1)+\cdots, \\& F_{4} =a_{45}\phi_{3}^{2}(-1)+a_{46} \phi_{3}^{3}(-1)+\cdots, \\& a_{16} =\frac{\alpha I_{*}(I_{*}+c)}{(S_{*}+I_{*}+c)^{3}},\qquad a_{17}=\frac{ \alpha S_{*}(S_{*}+c)}{(S_{*}+I_{*}+c)^{3}}, \\& a_{18} =-\frac{2\alpha S_{*}I_{*}+c\alpha (S_{*}+I_{*}+c)}{(S_{*}+I _{*}+c)^{3}}, \\& a_{19}= \frac{2\alpha I_{*}(2S_{*}-I_{*})+2c\alpha (S _{*}+c)}{(S_{*}+I_{*}+c)^{4}}, \\& a_{110} =\frac{2\alpha S_{*}(2I_{*}-S_{*})+2c\alpha (I_{*}+c)}{(S _{*}+I_{*}+c)^{4}}, \\& a_{111} =-\frac{\alpha I_{*}(I_{*}+c)}{(S_{*}+I_{*}+c)^{4}},\qquad a_{112}=- \frac{ \alpha S_{*}(S_{*}+c)}{(S_{*}+I_{*}+c)^{4}}, \\& a_{24} =-\frac{\alpha I_{*}(I_{*}+c)}{(S_{*}+I_{*}+c)^{3}},\qquad a_{25}=- \frac{ \alpha S_{*}(S_{*}+c)}{(S_{*}+I_{*}+c)^{3}}, \\& a_{26} =\frac{2\alpha S_{*}I_{*}+c\alpha (S_{*}+I_{*}+c)}{(S_{*}+I _{*}+c)^{3}}, \\& a_{27}=- \frac{2\alpha I_{*}(2S_{*}-I_{*})+2c\alpha (S _{*}+c)}{(S_{*}+I_{*}+c)^{4}}, \\& a_{28} =-\frac{2\alpha S_{*}(2I_{*}-S_{*})+2c\alpha (I_{*}+c)}{(S _{*}+I_{*}+c)^{4}}, \\& a_{29} =\frac{\alpha I_{*}(I_{*}+c)}{(S_{*}+I_{*}+c)^{4}},\qquad a_{210}=\frac{ \alpha S_{*}(S_{*}+c)}{(S_{*}+I_{*}+c)^{4}}, \\& a_{34} =\frac{a\beta }{(I_{*}+a)^{3}},\qquad a_{35}=- \frac{a\beta }{(I_{*}+a)^{4}},\qquad a_{45}=-\frac{a\beta }{(I_{*}+a)^{3}},\qquad a_{46}=\frac{a\beta }{(I_{*}+a)^{4}}. \end{aligned}$$

According to the Riesz representation theorem, there is a matrix $\eta (\theta, \varrho)$ in $\theta \in [-1, 0]$ such that

$$ L_{\mu }\phi = \int_{-1}^{0}d\eta (\theta, \varrho)\phi (\theta) $$

(15)

for $\phi \in C$. In fact, we choose

$$ \eta (\theta,\varrho)=(\tau_{0}+\varrho) \bigl(M_{\max }\delta (\theta)+N _{\max }\delta (\theta +1)\bigr), $$

where $\delta (\theta)$ is the Dirac delta function.

For $\phi \in C([-1,0], R^{5})$, define

$$ A(\varrho)\phi =\textstyle\begin{cases} \frac{d\phi (\theta)}{d\theta }, \quad -1\leq \theta < 0, \\ \int_{-1}^{0}d\eta (\theta,\varrho)\phi (\theta), \quad \theta =0, \end{cases} $$

and

$$ R(\varrho)\phi =\textstyle\begin{cases} 0, \quad -1\leq \theta < 0, \\ F(\varrho,\phi), \quad \theta =0. \end{cases} $$

Then system (14) becomes

$$ \dot{u}(t)=A(\varrho)u_{t}+R(\varrho)u_{t}. $$

(16)

For $\varphi \in C^{1}([0, 1], (R^{5})^{*})$, the adjoint operator $A^{*}$ of $A(0)$ can be defined as

$$ A^{*}(\varphi)=\textstyle\begin{cases} -\frac{d\varphi (s)}{ds}, \quad 0< s\leq 1, \\ \int_{-1}^{0}d{\eta }^{T}(s,0)\varphi (-s), \quad s=0. \end{cases} $$

Next, we define the bilinear inner form for A and $A^{*}$:

$$ \bigl\langle \varphi (s),\phi (\theta)\bigr\rangle =\bar{\varphi }(0)\phi (0)- \int_{\theta =-1}^{0} \int_{\xi =0}^{\theta }\bar{\varphi }(\xi - \theta)\,d\eta ( \theta)\phi (\xi)\,d\xi, $$

(17)

where $\eta (\theta)=\eta (\theta, 0)$.

Let $\rho (\theta)=(1, \rho_{2}, \rho_{3}, \rho_{4}, \rho_{5})^{T}e ^{i\tau_{0}\omega_{0}\theta }$ and $\rho^{*}(s)=(1, \rho_{2}^{*}, \rho _{3}^{*}, \rho_{4}^{*}, \rho_{5}^{*})^{T}e^{i\tau_{0}\omega_{0}s}$ be the eigenvectors for $A(0)$ and $A^{*}(0)$ corresponding to $+i\tau_{0}\omega_{0}$ and $-i\tau_{0}\omega_{0}$, respectively. Then, we have

$$\begin{aligned}& \rho_{2} =\frac{a_{21}+a_{23}\rho_{3}}{i\omega_{0}-a_{22}}, \\& \rho_{3}= \frac{i \omega_{0}-a_{11}}{a_{13}}-\frac{a_{15}a_{51}}{a_{13}(i\omega_{0}-a _{55})}, \\& \rho_{4} =\frac{b_{43}e^{-i\tau_{0}\omega_{0}}\rho_{3}}{i\omega_{0}-a _{44}},\qquad \rho_{5}= \frac{a_{51}}{i\omega_{0}-a_{55}}, \\& \rho_{2}^{*} =\frac{a_{15}a_{51}}{a_{21}(i\omega_{0}+a_{55})}-\frac{i \omega_{0}+a_{11}}{a_{21}}, \\& \rho_{3}^{*} =-\frac{(i\omega_{0}+a_{22})\rho_{2}}{a_{32}},\qquad \rho_{5} ^{*}=-\frac{a_{15}}{i\omega_{0}+a_{55}}, \\& \rho_{4}^{*} =-\frac{(i\omega_{0}+a_{33}+b_{33}e^{i\tau_{0}\omega _{0}})\rho_{3}^{*}-a_{23}\rho_{2}^{*}+a_{13}}{b_{43}e^{i\tau_{0}\omega _{0}}}. \end{aligned}$$

From Eq. (17) we get

$$\begin{aligned} \bar{D} =&\bigl[1+\rho_{2}\bar{\rho }_{2}^{*}+ \rho_{3}\bar{\rho }_{3}^{*}+ \rho_{4} \bar{\rho }_{4}^{*}+\rho_{5}\bar{\rho }_{5}^{*}+\tau_{0}e^{-i \tau_{0}\omega_{0}} \rho_{3}\bigl(b_{33}\bar{\rho }_{3}^{*}+b_{43} \bar{ \rho }_{4}^{*}\bigr)\bigr]^{-1}, \end{aligned}$$

so that $\langle \rho^{*}, \rho \rangle =1$ and $\langle \rho^{*}, \bar{ \rho }\rangle =0$.

Next, based on the algorithms in [24] and a computation similar to that in [25–27], we obtain

$$\begin{aligned}& g_{20} =2\tau_{0}\bar{D}\bigl[a_{16}+a_{17} \rho_{3}^{2}+a_{18}\rho_{3}+\bar{ \rho }_{2}^{*}\bigl(a_{24}+a_{25} \rho_{3}^{2}+a_{26}\rho_{3}\bigr) \\& \hphantom{g_{20}=}{}+\bigl(a_{34}\bar{\rho }_{3}^{*}+a_{45} \bar{\rho }_{4}^{*}\bigr)\rho_{3}^{2}e ^{-2i\tau_{0}\omega_{0}}\bigr], \\& g_{11} =\tau_{0}\bar{D}\bigl[2a_{16}+2a_{17} \rho_{3}\bar{\rho }_{3}+2a _{18}\operatorname{Re}\{ \rho_{3}\}+\bar{\rho }_{2}^{*}\bigl(2a_{24}+2a_{25} \rho _{3}\bar{\rho }_{3}+2a_{26}\operatorname{Re}\{ \rho_{3}\}\bigr) \\& \hphantom{g_{11}=}{}+2\bigl(a_{34}\bar{\rho }_{3}^{*}+a_{45} \bar{\rho }_{4}^{*}\bigr)\rho_{3}\bar{ \rho }_{3}\bigr], \\& g_{02} =2\tau_{0}\bar{D}\bigl[a_{16}+a_{17} \bar{\rho }_{3}^{2}+a_{18}\bar{ \rho }_{3}+\bar{\rho }_{2}^{*}\bigl(a_{24}+a_{25} \bar{\rho }_{3}^{2}+a_{26}\bar{ \rho }_{3} \bigr) \\& \hphantom{g_{02}=}{}+\bigl(a_{34}\bar{\rho }_{3}^{*}+a_{45} \bar{\rho }_{4}^{*}\bigr)\bar{\rho } _{3}^{2}e^{2i\tau_{0}\omega_{0}} \bigr], \\& g_{21} =2\tau_{0}\bar{D}\biggl[a_{16} \bigl(2W_{11}^{(1)}(0)+W_{20}^{(1)}(0)\bigr)+a _{17}\bigl(2W_{11}^{(3)}(0)\rho_{3}+W_{20}^{(3)}(0) \bar{\rho }_{3}\bigr) \\& \hphantom{g_{21}=}{}+a_{18}\biggl(W_{11}^{(1)}(0) \rho_{3}+\frac{1}{2}W_{20}^{(1)}(0)\bar{ \rho }_{3}+W_{11}^{(3)}(0)+\frac{1}{2}W_{20}^{(3)}(0) \biggr) \\& \hphantom{g_{21}=}{}+a_{19}(\bar{\rho }_{3}+2 \rho_{3})+a_{110}\bigl(\rho_{3}^{2}+2 \rho_{3}\bar{ \rho }_{3}\bigr)+3a_{111}+3a_{112} \rho_{3}^{2}\bar{\rho }_{3} \\& \hphantom{g_{21}=}{}+\bar{\rho }_{2}^{*}\biggl(a_{24} \bigl(2W_{11}^{(1)}(0)+W_{20}^{(1)}(0) \bigr)+a_{25}\bigl(2W _{11}^{(3)}(0) \rho_{3}+W_{20}^{(3)}(0)\bar{\rho }_{3} \bigr) \\& \hphantom{g_{21}=}{}+a_{26}\biggl(W_{11}^{(1)}(0) \rho_{3}+\frac{1}{2}W_{20}^{(1)}(0)\bar{ \rho }_{3}+W_{11}^{(3)}(0)+\frac{1}{2}W_{20}^{(3)}(0) \biggr) \\& \hphantom{g_{21}=}{}+a_{27}(\bar{\rho }_{3}+2 \rho_{3})+a_{28}\bigl(\rho_{3}^{2}+2 \rho_{3}\bar{ \rho }_{3}\bigr)+3a_{29}+3a_{210} \rho_{3}^{2}\bar{\rho }_{3}\biggr) \\& \hphantom{g_{21}=}{}+\bar{\rho }_{3}^{*}\bigl(a_{34} \bigl(2W_{11}^{(3)}(-1)\rho_{3}e^{-i\tau_{0} \omega_{0}}+W_{20}^{(3)}(-1) \bar{\rho }_{3}e^{i\tau_{0}\omega_{0}}\bigr)+3a _{35} \rho_{3}^{2}\bar{\rho }_{3}e^{-i\tau_{0}\omega_{0}}\bigr) \\& \hphantom{g_{21}=}{}+\bar{\rho }_{4}^{*}\bigl(a_{45} \bigl(2W_{11}^{(3)}(-1)\rho_{3}e^{-i\tau_{0} \omega_{0}}+W_{20}^{(3)}(-1) \bar{\rho }_{3}e^{i\tau_{0}\omega_{0}}\bigr)+3a _{46} \rho_{3}^{2}\bar{\rho }_{3}e^{-i\tau_{0}\omega_{0}}\bigr) \biggr], \end{aligned}$$

with

$$\begin{aligned}& W_{20}(\theta) =\frac{ig_{20}\rho (0)}{\tau_{0}\omega_{0}}e^{i\tau _{0}\omega_{0}\theta }+ \frac{i\bar{g}_{02}\bar{\rho }(0)}{3\tau_{0} \omega_{0}}e^{-i\tau_{0}\omega_{0}\theta }+E_{1}e^{2i\tau_{0}\omega _{0}\theta }, \\& W_{11}(\theta) =-\frac{ig_{11}\rho (0)}{\tau_{0}\omega_{0}}e^{i\tau _{0}\omega_{0}\theta }+ \frac{i\bar{g}_{11}\bar{\rho }(0)}{\tau_{0} \omega_{0}}e^{-i\tau_{0}\omega_{0}\theta }+E_{2}, \end{aligned}$$

where $E_{1}$ and $E_{2}$ can be obtained by the following two equations:

$$\begin{aligned}& E_{1}=2\hspace{-1pt} \left ( \begin{matrix} 2i\omega_{0}-a_{11} &{0} &-a_{13} &{0} &-a_{15} \\ -a_{21} &2i\omega_{0}-a_{22} &-a_{23} &{0} &{0} \\ {0} &-a_{32} &2i\omega_{0}-a_{33}-b_{33}e^{-2i\tau_{0}\omega_{0}} &{0} &{0} \\ {0} &{0} &-b_{43}e^{-2i\tau_{0}\omega_{0}} &2i\omega_{0}-a_{44} &{0} \\ -a_{51} &{0} &{0} &{0} &2i\omega_{0}-a_{55} \end{matrix} \right ) ^{-1} \\& \hphantom{E_{1}=}{}\times \left ( \begin{matrix} E_{1}^{(1)} \\ E_{1}^{(2)} \\ E_{1}^{(3)} \\ E_{1}^{(4)} \\ {0} \end{matrix} \right ) , \\& E_{2}=- \left ( \begin{matrix} a_{11} &{0} &a_{13} &{0} &a_{15} \\ a_{21} &a_{22}& a_{23} &{0} &{0} \\ {0} &a_{32} &a_{33}+b_{33} &{0} &{0} \\ {0} &{0} &b_{43} &a_{44} &{0} \\ a_{51} &{0} &{0} &{0} &a_{55} \end{matrix} \right ) ^{-1}\times \left ( \begin{matrix} E_{2}^{(1)} \\ E_{2}^{(2)} \\ E_{2}^{(3)} \\ E_{2}^{(4)} \\ {0} \end{matrix} \right ) , \end{aligned}$$

with

$$\begin{aligned}& E_{1}^{(1)} =a_{16}+a_{17} \rho_{3}^{2}+a_{18}\rho_{3}, \\& E_{1}^{(2)} =a_{24}+a_{25} \rho_{3}^{2}+a_{26}\rho_{3}, \\& E_{1}^{(3)} =a_{34}\rho_{3}^{2}e^{-2i\tau_{0}\omega_{0}}, \qquad E_{1}^{(4)}=a _{45}\rho_{3}^{2}e^{-2i\tau_{0}\omega_{0}}, \\& E_{2}^{(1)} =2a_{16}+2a_{17} \rho_{3}\bar{\rho }_{3}+2a_{18}\operatorname{Re}\{ \rho_{3}\}, \\& E_{2}^{(2)} =2a_{24}+2a_{25} \rho_{3}\bar{\rho }_{3}+2a_{26}\operatorname{Re}\{ \rho_{3}\}, \\& E_{2}^{(3)} =2a_{34}\rho_{3}\bar{\rho }_{3}, \qquad E_{2}^{(4)}=2a_{45}\rho _{3}\bar{\rho }_{3}. \end{aligned}$$

Then we can obtain

$$\begin{aligned}& C_{1}(0) =\frac{i}{2\tau_{0}\omega_{0}} \biggl(g_{11}g_{20}-2 \vert g_{11} \vert ^{2}-\frac{ \vert g _{02} \vert ^{2}}{3} \biggr)+ \frac{g_{21}}{2}, \\& \mu_{2} =-\frac{\operatorname{Re}\{C_{1}(0)\}}{\operatorname{Re}\{\lambda '(\tau_{0}) \}}, \\& \beta_{2} =2{\operatorname{Re}\bigl\{ C_{1}(0)\bigr\} }, \\& T_{2} =-\frac{\operatorname{Im}\{C_{1}(0)\}+\mu_{2}\operatorname{Im}\{\lambda '(\tau _{0})\}}{\tau_{0}\omega_{0}}. \end{aligned}$$

(18)

Thus, based on the properties of the Hopf bifurcation discussed in [24], we can get the following:

Theorem 2

The sign of $\mu_{2}$ determines the direction of the Hopf bifurcation: if $\mu_{2}>0$ ($\mu_{2}<0$), then the Hopf bifurcation is supercritical (subcritical); the sign of $\beta_{2}$ determines the stability of the bifurcated periodic solutions: if $\beta_{2}<0$ ($\beta_{2}>0$), then the bifurcated periodic solutions are stable (unstable); and the sign of $T_{2}$ determines the period of the bifurcated periodic solutions: if $T_{2}>0$ ($T_{2}<0$), then the period of the bifurcated periodic solutions increases (decreases).

4 Numerical simulation

In this section, we try to present some numerical simulations for system (2) to validate the previous main results. By extracting some values from [22] and considering the conditions for the existence of the Hopf bifurcation, we choose a set of parameters as follows: $A=2$, $\delta_{0}=0.02$, $\alpha =0.27$, $\beta =0.003$, $c=0.01$, $\eta =0.2$, $\mu =0.003$, $\delta_{1}=0.2$, $\delta_{2}=0.045$, $\delta_{3}=0.03$, $a=0.4$. Then, we obtain the following specific case of system (2):

$$ \textstyle\begin{cases} \frac{dS(t)}{dt}=2-0.02 S(t)-\frac{0.27 S(t)I(t)}{S(t)+I(t)+0.01}+0.2V(t)-0.003 S(t), \\ \frac{dE(t)}{dt}=\frac{0.27 S(t)I(t)}{S(t)+I(t)+0.01}-0.22E(t), \\ \frac{dI(t)}{dt}=0.2 E(t)-0.05I(t)-0.045 I(t-\tau)-\frac{0.003 I(t- \tau)}{I(t-\tau)+0.4}, \\ \frac{dR(t)}{dt}=0.045 I(t-\tau)-0.02 R(t)+\frac{0.003 I(t-\tau)}{I(t- \tau)+0.4}, \\ \frac{dV(t)}{dt}=0.003 S(t)-0.22 V(t). \end{cases} $$

(19)

Then Eq. (3) becomes

$$ -1.7084e-004I^{3}+0.0028I^{2}+0.0023I+4.6141e-004=0. $$

(20)

By means of Matlab software package we can get the unique positive root $I_{*}=17.1823$ of Eq. (20). Then we get $[\alpha \delta _{1}-(\delta_{0}+\delta_{1})(\delta_{0}+\delta_{2}+\delta_{3})](I_{*}+a)=0.5820> \beta \delta_{1}(\delta_{0}+\delta_{1})=1.3200e-004$. Thus we obtain the unique viral equilibrium $P_{*}(10.8619, 8.3082, 17.1832, 38.8068, 0.1481)$ of system (19).

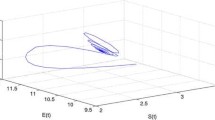
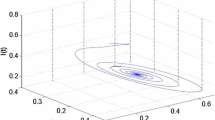
By computation we obtain $\omega_{0}=3.5844$, $\tau_{0}=81.3618$, and $\lambda^{\prime }(\tau_{0})=0.0041-0.0872i$. As is shown in Figs. 1–3, the viral equilibrium $P_{*}(10.8619, 8.3082, 17.1832, 38.8068,0.1481)$ is locally asymptotically stable when $\tau =63.65< \tau_{0}=81.3618$. However, the viral equilibrium $P_{*}(10.8619, 8.3082, 17.1832, 38.8068,0.1481)$ loses its stability, and a Hopf bifurcation occurs once $\tau >\tau_{0}=81.3618$, which can be exhibited by Figs. 4–6 with $\tau =106.79$. This is consistent with the results in Theorem 1. Therefore we can conclude that the propagation of the viruses in system (19) can be controlled by shortening the period that antivirus software uses to clean the viruses.

Figure 1

The trajectories of S, E, I, R, and V with $\tau =63.65<\tau_{0}$

Figure 2

Dynamic behavior of system (19): projection on S-E-I with $\tau =63.65<\tau_{0}$

Figure 3

Dynamic behavior of system (19): projection on E-I-V with $\tau =63.65<\tau_{0}$

Figure 4

The trajectories of S, E, I, R, and V with $\tau =106.79>\tau_{0}$

Figure 5

Dynamic behavior of system (19): projection on S-E-I with $\tau =106.79>\tau_{0}$

Figure 6

Dynamic behavior of system (19): projection on E-I-V with $\tau =106.79>\tau_{0}$

In addition, by some complex computations based on Eq. (18) we obtain $g_{20}=-3.7011+6.8056i$, $g_{11}=2.9207+0.6036i$, $g_{02}=-3.7011-6.8056i$, $g_{21}=-8.7200-3.3956i$, and $C_{1}(0)=-4.4504-1.6676i$. Further, we obtain $\beta_{2}=-8.9008<0$, $\mu_{2}=1085.5>0$, and $T_{2}=0.3303>0$. According to Theorem 2, the Hopf bifurcation is supercritical, the bifurcated periodic solutions are stable, and the period of the bifurcated periodic solutions increases. Therefore, the time delay due to the period that antivirus software uses to clean the viruses is harmful since the periodic behavior is unpleasant from the viewpoint of epidemiology. In practice, the stability of the computer virus system must be guaranteed to predict and even eliminate the viruses.

5 Conclusions

In this paper, we propose a delayed SVEIR computer virus model with nonlinear incident rate and saturated treatment rate by incorporating the time delay due to the period that antivirus software uses to clean the viruses in the infectious computers into the model considered in the literature [22]. Compared with the work in [22], the model considered in the present paper is more general, and we mainly investigate the effects of the delay on the model.

The main results are given in terms of the stability of the viral equilibrium and Hopf bifurcation. We prove that the propagation of the viruses can be controlled when the value of the delay is below the critical value $\tau_{0}$. However, a Hopf bifurcation occurs when the value of the delay passes through the critical value $\tau_{0}$, which indicates that computers of the five classes in the model may coexist in an oscillatory mode under some conditions and the viruses will be out of control in this case. Therefore, we should control the occurrence of the Hopf bifurcation by using some bifurcation control strategies, and this will be a major emphasis of our future research.