1 Introduction

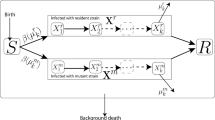
Computer viruses are major threats to Internet security, and they have led to huge economic losses [1–3]. Inspired by the compelling analogies between computer viruses and their biological counterparts, many scholars investigate computer viruses spreading on the Internet with epidemic models since the work by Kephart and White [4]. Wierman and Marchette et al. [5–7] proposed the classical SIR computer virus propagation model respectively based on the SIR epidemic model. Considering the feasibility of the loss of immunity for the recovered computers, Gan et al. [8] proposed an SIRS computer propagation model and studied the stability of the model. Yuan et al. [9–11] studied the dynamics of the SEIR computer virus propagation model based on the fact that some viruses may purposely lay dormant for a period of time prior to infecting other computers for stealth reasons. However, the SEIR model assumes that the recovered computers have a permanent immunization period with a certain probability which is not consistent with real situation. Based on this, Mishra et al. [12, 13] presented the SEIRS computer virus propagation model. In [14], Mishra and Jia paid attention to the combination of computer virus propagation model and quarantine to study the prevalence of the viruses and proposed the SEIQRS model for the transmission of malicious objects in computer network. However, all the above computer virus models focused on the internal computers and neglected the effect of the external computers on virus spread. In order to study the effect of the external computers on virus spread, Chen et al. [15] proposed the following computer virus model under the influence of external computers:

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{dS(t)}{dt}=-\delta S(t)-\eta S(t)I(t)-\gamma_{1} S(t)+\alpha_{2} I(t)+\gamma_{2} E(t), \\ \frac{dI(t)}{dt}=\eta S(t)I(t)-\delta I(t)-\alpha_{1} I(t)-\alpha_{2} I(t),\\ \frac{dE(t)}{dt}=-\delta E(t)-\gamma_{2} E(t)+\gamma_{1} S(t)+\alpha_{1} I(t)+\varepsilon, \end{array}\displaystyle \right . $$
(1)

where \(S(t)\), \(I(t)\) and \(E(t)\) denote the numbers of the susceptible computers, the infected computers and external computers, respectively. δ is the rate at which each computer dies out; εis the birth rate of external computers; \(\alpha_{1} \), \(\alpha_{2}\),\(\gamma_{1}\), \(\gamma_{2} \) and η are the states transmission rates. Chen et al. [15] studied the global stability of virus-free and viral equilibrium of system (1).

As stated in [9], some viruses may purposely lay dormant for a period of time prior to infecting other computers for stealth reasons, it may be more realistic to assume that the susceptible computers are infected at time \(t-\tau\) and then these infected computers have infection ability at time t. Therefore, we incorporate the latent period delay of the computer viruses into system (1) and get the following computer virus model with time delay:

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{dS(t)}{dt}=-\delta S(t)-\eta S(t-\tau)I(t-\tau)-\gamma_{1} S(t) +\alpha_{2} I(t)+\gamma_{2} E(t), \\ \frac{dI(t)}{dt}=\eta S(t-\tau)I(t-\tau)-\delta I(t)-\alpha_{1} I(t)-\alpha_{2} I(t), \\ \frac{dE(t)}{dt}=-\delta E(t)-\gamma_{2} E(t)+\gamma_{1} S(t)+\alpha_{1} I(t)+\varepsilon, \end{array}\displaystyle \right . $$
(2)

where τ is the latent period delay of the computer viruses. The main purpose of this paper is to investigate the effect of the latent period delay on system (2), especially the Hopf bifurcation caused by the delay. It is well known that the time delay can have important influence on a dynamical system, and dynamical systems with time delay have been investigated extensively in recent years [10, 13, 16–19].

The organization of this paper is as follows. Section 2 considers stability of the positive equilibrium and existence of the Hopf bifurcation. Section 3 is devoted to the properties of the Hopf bifurcation. Some numerical simulations are carried out to verify the theoretical results in Section 4, and this work is summarized in Section 5.

2 Stability of the positive equilibrium and existence of Hopf bifurcation

By a direct computation, we can get that if

$$R_{0}=\frac{\varepsilon\gamma_{2} \eta}{\delta(\gamma_{1} +\gamma_{2} +\delta)(\alpha_{1} +\alpha_{2} +\delta )}>1, $$

system (2) has a unique positive equilibrium \(E_{\ast}(S_{\ast}, I_{\ast}, E_{\ast})\), where

$$\begin{aligned} &S_{\ast}=\frac{\alpha_{1} +\alpha_{2} +\delta}{\eta}, \\ &I_{\ast}=\frac{\varepsilon\gamma_{2} \eta-\delta(\gamma_{1} +\gamma_{2} +\delta)(\alpha_{1} +\alpha_{2} +\delta)}{\eta\delta(\alpha_{1} +\gamma_{2} +\delta)}, \\ &E_{\ast}=\frac{\varepsilon}{\delta+\gamma_{2} }+\frac{\gamma_{1} (\alpha_{1} +\alpha_{2} +\delta)}{\eta(\delta+\gamma_{2} )}+\frac{\alpha_{1} I_{\ast}}{\delta+\gamma_{2} }. \\ &\lambda^{3}+A_{2} \lambda^{2}+A_{1} \lambda+A_{0} +\bigl(B_{2} \lambda^{2}+B_{1} \lambda+B_{0} \bigr)e^{-\lambda\tau}=0, \end{aligned}$$
(3)

where

$$\begin{aligned}& A_{0} =a_{3} a_{4} a_{5} -a_{1} a_{4} a_{7} , \\& A_{1} =a_{1} a_{4} +a_{1} a_{7} +a_{4} a_{7} -a_{3} a_{5} , \\& A_{2} =-(a_{1} +a_{4} +a_{7} ), \\& B_{0} =a_{1} a_{7} b_{4} -a_{2} a_{7} b_{3} +a_{3} a_{5} b_{4} -a_{3} a_{6} b_{3} +a_{4} a_{7} b_{1} , \\& B_{1} =a_{1} b_{4} -a_{2} b_{3} +a_{4} b_{1} +a_{7} b_{1} +a_{7} b_{4} ,\qquad B_{2} =-(b_{1} +b_{4} ), \end{aligned}$$

and

$$\begin{aligned}& a_{1} =-(\delta+\gamma_{1} ),\qquad a_{2} = \alpha_{2} ,\qquad a_{3} =\gamma_{2} , \\& a_{4} =-(\alpha_{1} +\alpha_{2} +\delta),\qquad a_{5} =\gamma_{1} ,\qquad a_{6} = \alpha_{1} ,\qquad a_{7} =-(\delta+\gamma_{2} ), \\& b_{1} =-\eta I_{\ast},\qquad b_{2} =-\eta S_{\ast},\qquad b_{3} =\eta I_{\ast},\qquad b_{4} =\eta S_{\ast}. \end{aligned}$$

When \(\tau=0\), Eq. (3) becomes

$$ \lambda^{3}+(A_{2} +B_{2} ) \lambda^{2}+(A_{1} +B_{1} )\lambda+A_{0} +B_{0} =0. $$
(4)

Based on the expressions of \(A_{2}\), \(B_{2} \) and \(a_{1}\), \(a_{4}\), \(a_{7}\), \(b_{1}\), \(b_{4} \), we can get

$$A_{2} +B_{2} =\gamma_{1} +\gamma_{2} +2 \delta+\eta I_{\ast}>0. $$

Therefore if the condition (H1) \((A_{2} +B_{2} )(A_{1} +B_{1} )>A_{0} +B_{0} >0\) holds, then system (2) is locally asymptotically stable when\(\tau=0\).

For \(\tau>0\), let \(\lambda=i\omega\) (\(\omega>0\)) be the root of Eq. (3), then

$$\left \{ \textstyle\begin{array}{@{}l} B_{1} \omega\sin\tau\omega+(B_{0} -B_{2} \omega^{2})\cos\tau\omega=A_{2} \omega^{2}-A_{0} , \\ B_{1} \omega\cos\tau\omega-(B_{0} -B_{2} \omega^{2})\sin\tau\omega =\omega ^{3}-A_{1} \omega. \end{array}\displaystyle \right . $$

Then we get

$$ \omega^{6}+c_{2} \omega^{4}+c_{1} \omega^{2}+c_{0} =0, $$
(5)

where

$$\begin{aligned}& c_{0} =A_{0}^{2} -B_{0}^{2} , \qquad c_{1} =A_{1}^{2} -B_{1}^{2} -2A_{0} A_{2} +2B_{0} B_{2} , \\& c_{2} =A_{2}^{2} -B_{2}^{2} -2A_{1} . \end{aligned}$$

Let \(\omega^{2}=v\), then Eq. (5) can be transformed into the following form:

$$ v^{3}+c_{2} v^{2}+c_{1} v+c_{0} =0. $$
(6)

Next, we assume that (H2) Eq. (6) has at least one positive root.

If the condition (H1) holds, then there exists one positive root \(v_{0}\) of Eq. (6) such that Eq. (3) has a pair of purely imaginary roots \(\pm i\omega _{0} =\pm i\sqrt{v_{0}}\).

Taking derivation on both sides of Eq. (3), we obtain

$$ { \biggl[ {\frac{{d\lambda}}{{d\tau}}} \biggr]^{ - 1}} =\frac {{3{\lambda^{2}} + 2{A_{2}}\lambda + {A_{1}}}}{{{\lambda^{4}} + {A_{2}}{\lambda^{3}} + {A_{1}}{\lambda^{2}} + {A_{0}}\lambda}} + \frac{{2{B_{2}}\lambda + {B_{1}}}}{{{B_{2}}{\lambda^{3}} + {B_{1}}{\lambda ^{2}} + {B_{0}}\lambda}} - \frac{\tau}{\lambda}. $$

Thus, we can get

$$\operatorname{Re} \biggl[ {\frac{{d\lambda}}{{d\tau}}} \biggr]_{\tau = {\tau_{0}}}^{- 1} = \frac{{f'({v_{0}})}}{{B_{1}^{2}\omega_{0}^{2} + {{({B_{0}} - {B_{2}}\omega_{0}^{2})}^{2}}}}, $$

where \(f(v)=v^{3}+c_{2} v^{2}+c_{1} v+c_{0} \) and \(v_{0} =\omega_{0}^{2}\).

It is clear that if the condition (H3) \(f'({v_{0}})\ne0\) holds, then \(\operatorname{Re} [{\frac{d\lambda}{d\tau}} ]_{\tau=\tau_{0} }^{-1}\ne0\). Therefore, according to the Hopf bifurcation theorem in [20], we have the following results.

Theorem 1

For system (2), we assume that the conditions (H1)-(H3) hold for the parameters. Then the positive equilibrium \(E_{\ast}(S_{\ast}, I_{\ast}, E_{\ast})\) is asymptotically stable for \(\tau\in[0, \tau_{0} )\) and the positive equilibrium \(E_{\ast}(S_{\ast}, I_{\ast}, E_{\ast})\) becomes unstable for τ staying in some right neighborhood of \(\tau_{0} \), with a Hopf bifurcation occurring when \(\tau =\tau_{0}\).

3 Direction and stability of the Hopf bifurcation

In this section, we shall obtain the explicit formulae for determining the direction, stability and period of these periodic solutions bifurcating from the positive equilibrium \(E_{\ast}(S_{\ast},I_{\ast},E_{\ast})\) of system (2) at the critical value \(\tau_{0} \). For convenience, let \(\tau=\tau_{0} +\upsilon\), \(\upsilon\in R\). Then \(\upsilon=0\) is the Hopf bifurcation value of system (2).

Let \(u_{1}=S(\tau t)\), \(u_{2}=I(\tau t)\), \(u_{3}=E(\tau t)\). Then system (2) is transformed into a functional differential equation in \(C=C([-1,0], R^{3})\) as

$$ \dot{u}(t)=L_{\upsilon}(u_{t} )+F( \upsilon,u_{t} ), $$
(7)

where \(u_{t} =(S(t),I(t),E(t))^{T}\in R^{3}\) and \(L_{\upsilon}: C\to R\), \(F: R\times C\to R\) are given respectively by

$$L_{\upsilon}\varphi=(\tau_{0} +\upsilon)\bigl[A_{\max} \varphi(0)+B_{\max} \varphi(-1)\bigr], $$

where

$$A_{\max} = \begin{bmatrix} {a_{1} } & {a_{2} } & {a_{3} } \\ 0 & {a_{4} } & 0 \\ {a_{5} } & {a_{6} } & {a_{7} } \end{bmatrix},\qquad B_{\max} = \begin{bmatrix} {b_{1} } & {b_{2} } & 0 \\ {b_{3} } & {b_{4} } & 0 \\ 0 & 0 & 0 \end{bmatrix} $$

and

$$F(\upsilon, u_{t} )=(\tau_{0} +\upsilon) \begin{pmatrix} {-\beta\varphi_{1} (0)\varphi_{2} (0)} \\ {\beta\varphi_{1} (0)\varphi_{2} (0)} \\ {0} \end{pmatrix}. $$

Clearly, \(L_{\upsilon}\) is a linear continuous operator from \(C=C([-1, 0], R^{3})\) to \(R^{3}\). By the Riesz representation theorem, there exists a matrix function with bounded variation components \(\eta(\theta,\upsilon)\), \(\theta \in [-1,0]\) such that

$$L_{\upsilon}\varphi=\int_{-1}^{0} {d\eta( \theta,\upsilon)} \varphi (\theta ),\quad\varphi\in C=C\bigl([-1,0],R^{3} \bigr). $$

In fact we can choose

$$\eta(\theta,\upsilon)=(\tau_{0} +\upsilon) \bigl(A_{\max} \delta(\theta )+B_{\max} \delta(\theta+1)\bigr), $$

where \(\delta(\theta)\) is the Dirac delta function.

For \(\varphi\in C([-1,0],R^{3})\), we define

$$A(\upsilon)\varphi= \left \{ \textstyle\begin{array}{@{}l@{\quad}l} \frac{d\varphi(\theta)}{d\theta},& -1\le\theta< 0, \\ \int_{-1}^{0} {d\eta(\theta,\upsilon)} \varphi(\theta), & \theta=0, \end{array}\displaystyle \right . $$

and

$$R(\upsilon)\varphi= \left \{ \textstyle\begin{array}{@{}l@{\quad}l} 0,& -1\le\theta< 0, \\ F(\upsilon,\varphi),& \theta=0. \end{array}\displaystyle \right . $$

Then system (7) is equivalent to the abstract differential equation

$$ \dot{u}(t)=A(\upsilon)u_{t}+R(\upsilon)u_{t}, $$
(8)

where \(u_{t} =u(t+\theta)\) for \(\theta\in[-1,0]\).

For \(\phi\in C([-1,0],(R^{3})^{\ast})\), define

$$A^{\ast}(\upsilon)s= \left \{ \textstyle\begin{array}{@{}l@{\quad}l} -\frac{d\phi(s)}{ds},& 0< s\le1, \\ \int_{-1}^{0} {d\eta^{T}(s,\upsilon)} \phi(-s),& s=0. \end{array}\displaystyle \right . $$

For \(\varphi\in C([-1,0],R^{3})\) and \(\phi\in C([-1,0],(R^{3})^{\ast})\), define the bilinear form

$$ \langle \phi,\varphi\rangle=\bar{\phi}(0)\varphi(0)-\int _{\theta=-1}^{0} {\int_{\xi =0}^{\theta}{ \bar{\phi}(\xi-\theta)} }\,d\eta(\theta)\varphi(\xi )\,d\xi , $$
(9)

where \(\eta(\theta)=\eta(\theta,0)\).

Thus, we can conclude that \(A(0)\) and A∗ are adjoint operators. Let \(q(\theta)=(1, q_{2}, q_{3} )^{T} e^{i\omega_{0}\tau_{0}\theta}\) be the eigenvector of \(A(0)\) corresponding to the eigenvalue \(+i\omega_{0} \tau_{0} \) and \(q^{\ast}(s)=D(1, q_{2}^{\ast}, q_{3}^{\ast})e^{i\omega_{0}\tau_{0}s}\) be the eigenvector of \(A^{\ast}\) corresponding to the eigenvalue \(-i\omega_{0}\tau_{0} \). Namely, \(A(0)q(\theta)=i\omega_{0}\tau_{0}q(\theta)\) and \(A^{\ast}q^{\ast^{T}}(s)=-i\omega_{0}\tau_{0}q^{\ast^{T}}(s)\). From the definitions of \(A(0)\) and A∗, we can obtain

$$\begin{aligned}& q_{2} =\frac{b_{3} e^{-i\omega_{0} \tau_{0} }}{i\omega_{0} -a_{4} -b_{4} e^{-i\omega_{0} \tau_{0} }}, \\& q_{3} =\frac{a_{5} }{i\omega_{0} -a_{7} }+\frac{a_{6} b_{3} e^{-i\omega_{0} \tau_{0} }}{(i\omega_{0} -a_{7} )(i\omega_{0} -a_{4} -b_{4} e^{-i\omega_{0} \tau_{0} })}, \\& q_{2}^{\ast}=\frac{i\omega_{0} -a_{1} -b_{1} e^{i\omega_{0} \tau_{0} }}{b_{3} e^{i\omega _{0} \tau_{0} }}+\frac{a_{3} a_{5} }{(i\omega_{0} +a_{7} )b_{3} e^{i\omega_{0} \tau_{0} }}, \\& q_{3}^{\ast}=-\frac{a_{3} }{i\omega_{0} +a_{7} }. \end{aligned}$$

From Eq. (9), we can obtain

$$\begin{aligned} &\bigl\langle q^{*}(s), q(\theta)\bigr\rangle \\ &\quad=\bar{D}\bar{q}^{*}(0)q(0) -\int_{-1}^{0}\int_{0}^{\theta}\bar{D}\bar{q}^{*}(0)e^{-i\omega_{0}\tau_{0}(\xi -\theta)}\,d\eta(\theta)q(0)e^{i\omega_{0}\tau_{0}\xi}\,d\xi \\ &\quad=\bar{D}\biggl[1+q_{2}\bar{q}_{2}^{*}+q_{3} \bar{q}_{3}^{*} -\int_{-1}^{0}\bar{q}^{*}(0)\theta e^{i\omega_{0}\tau_{0}\theta}\,d\eta(\theta )q(0)\biggr] \\ &\quad=\bar{D}\bigl[1+q_{2}\bar{q}_{2}^{*}+q_{3} \bar{q}_{3}^{*}+\bar {q}^{*}(0)\bigl[B_{\max}e^{-i\omega_{0}\tau_{0}} \bigr]q(0)\bigr] \\ &\quad=\bar{D}\bigl[1+q_{2}\bar{q}_{2}^{*}+q_{3} \bar{q}_{3}^{*}+\tau_{0}e^{-i\omega_{0}\tau _{0}}\bigl(b_{1}+b_{2}q_{2} +b_{3}\bar{q}_{1}^{*}+b_{4}q_{2} \bar{q}_{2}^{*}\bigr)\bigr]. \end{aligned}$$

Then we can choose

$$\begin{aligned} \bar{D}=\bigl[1+q_{2}\bar{q}_{2}^{*}+q_{3} \bar{q}_{3}^{*}+\tau_{0}e^{-i\omega_{0}\tau _{0}}\bigl(b_{1}+b_{2}q_{2} +b_{3}\bar{q}_{1}^{*}+b_{4}q_{2} \bar{q}_{2}^{*}\bigr)\bigr]^{-1} \end{aligned}$$

such that

$$\bigl\langle q^{\ast},q\bigr\rangle =1,\qquad\bigl\langle q^{\ast},\bar{q}\bigr\rangle =0. $$

Next, we use the same notations as those in Hassard et al. [20], and we first compute the coordinates to describe the center manifold \(C_{0}\) at \(\upsilon=0\). Let \(x_{t}\) be the solution of Eq. (8) when \(\upsilon=0\). Define

$$\begin{aligned}& z(t)=\bigl\langle q^{*}, x_{t}\bigr\rangle , \end{aligned}$$
(10)
$$\begin{aligned}& W(t, \theta)=x_{t}(\theta)-2\operatorname{Re}\bigl\{ z(t)q(\theta)\bigr\} \end{aligned}$$
(11)

on the center manifold \(C_{0}\), and we have

$$ W(t, \theta)=W\bigl(z(t), \bar{z}(t), \theta\bigr), $$
(12)

where

$$\begin{aligned} W\bigl(z(t), \bar{z}(t), \theta\bigr) =&W(z, \bar{z}) =W_{02}\frac{z^{2}}{2}+W_{11}z\bar{z}+W_{02} \frac{\bar{z}^{2}}{2}+\cdots \end{aligned}$$
(13)

and z and z̄ are local coordinates for center manifold \(C_{0}\) in the direction of \(q^{*}\) and \(\bar{q}^{*}\). Note that W is real if \(x_{t}\) is real, we only deal with real solutions. For the solutions \(x_{t}\) of Eq. (8),

$$\begin{aligned} \dot{z}(t) =&\bigl\langle q^{*}, \dot{x}_{t}\bigr\rangle \\ =&\bigl\langle q^{*}, A(0)x_{t}\bigr\rangle +\bigl\langle q^{*}, R(0)x_{t}\bigr\rangle \\ =&\bigl\langle A^{*}(0)q^{*}, x_{t}\bigr\rangle +\bigl\langle q^{*}, R(0)x_{t}\bigr\rangle \\ =&\bigl\langle A^{*}(0)q^{*}, x_{t}\bigr\rangle +\bar{q}^{*}(0)R(0)x_{t} -\int_{-1}^{0}\int_{0}^{\theta}\bar{q}^{*}(\xi-\theta)\,d\eta(\theta )A(0)R(0)x_{t}(\xi)\,d\xi \\ =&i\omega_{0}\tau_{0}z(t)+\bar{q}^{*}(0)f\bigl(0, x_{t}(\theta)\bigr) \\ :=&i\omega_{0}\tau_{0}z(t)+\bar{q}^{*}(0)f_{0} \bigl(z(t), \bar{z}(t)\bigr). \end{aligned}$$

That is,

$$ \dot{z}(t)=i\omega_{0}\tau_{0}z(t)+g(z, \bar{z}), $$
(14)

where

$$ g(z, \bar{z})=g_{20}\frac{z^{2}}{2}+g_{11}z \bar{z}+g_{02}\frac{\bar {z}^{2}}{2}+g_{21}\frac{z^{2}\bar{z}}{2}+ \cdots. $$
(15)

Hence, we have

$$\begin{aligned} g(z, \bar{z})=\bar{q}^{*}(0)f_{0}(z, \bar{z}) =\bar{D}\bigl(1, \bar{q}^{*}_{2}, \bar{q}^{*}_{3}\bigr) \bigl(f_{1}(0, x_{t}), f_{2}(0, x_{t}), 0\bigr)^{T}, \end{aligned}$$
(16)

where

$$\begin{aligned}& f_{1}(0, x_{t})=-\beta\tau_{0} \varphi_{1}(0)\varphi_{2}(0), \\& f_{2}(0, x_{t})=\beta\tau_{0} \varphi_{1}(0)\varphi_{2}(0). \end{aligned}$$

Since

$$x_{t}=x(t+\theta)=W(z, \bar{z}, \theta)+zq(\theta)+\bar{z}\bar{q}( \theta) $$

and

$$q(\theta)=(1, q_{2}, q_{3})^{T}e^{i\omega_{0}\tau_{0}\theta}, $$

we have

$$\begin{aligned}& \begin{aligned}[b] x_{t}={}& \begin{bmatrix} x_{1}(t+\theta)\\ x_{2}(t+\theta)\\ {0} \end{bmatrix}+ \begin{bmatrix} W^{(1)}(t+\theta)\\ W^{(2)}(t+\theta)\\ {0} \end{bmatrix} +z \begin{bmatrix} {1}\\ q_{2}\\ q_{3} \end{bmatrix} e^{i\omega_{0}\tau_{0}\theta}+\bar{z} \begin{bmatrix} {1}\\ \bar{q}_{2}\\ \bar{q}_{3} \end{bmatrix} e^{-i\omega_{0}\tau_{0}\theta}, \end{aligned} \\& \varphi_{1}(0)=z+\bar{z}+W_{20}^{(1)}(0) \frac {z^{2}}{2}+W_{11}^{(1)}(0)z\bar{z} +W_{02}^{(1)}\frac{\bar{z}^{2}}{2}+\cdots, \\& \varphi_{2}(0)=zq_{2}+\bar{z} \bar{q}_{2}+W_{20}^{(2)}(0)\frac {z^{2}}{2}+W_{11}^{(2)}(0)z \bar{z} +W_{02}^{(2)}\frac{\bar{z}^{2}}{2}+\cdots, \\& \varphi_{3}(0)=zq_{3}+\bar{z} \bar{q}_{3}+W_{20}^{(3)}(0)\frac {z^{2}}{2}+W_{11}^{(3)}(0)z \bar{z} +W_{02}^{(3)}\frac{\bar{z}^{2}}{2}+\cdots. \end{aligned}$$

From Eq. (15) and Eq. (16), we have

$$\begin{aligned} g(z, \bar{z}) =\bar{D}\bigl(1, \bar{q}_{2}^{*}, \bar{q}_{3}^{*} \bigr) \begin{bmatrix} M_{11}z^{2}+M_{12}z\bar{z}+M_{13}\bar{z}^{2}+M_{14}z^{2}\bar{z}\\ M_{21}z^{2}+M_{22}z\bar{z}+M_{23}\bar{z}^{2}+M_{24}z^{2}\bar{z}\\ {0} \end{bmatrix} +\cdots, \end{aligned}$$

where

$$\begin{aligned}& M_{11}=-\beta\tau_{0}q_{2}, \\& M_{12}=-\beta\tau_{0}(q_{2}+\bar{q}_{2}), \\& M_{13}=-\beta\tau_{0}\bar{q}_{2}, \\& M_{14}=-\beta\tau_{0}\biggl(W_{11}^{(1)}(0)q_{2}+ \frac{1}{2}W_{20}^{(1)}(0)\bar {q}_{2}+W_{11}^{(2)}(0)+ \frac{1}{2}W_{20}^{(2)}(0)\biggr), \\& M_{21}=\beta\tau_{0}q_{2}, \\& M_{22}=\beta\tau_{0}(q_{2}+\bar{q}_{2}), \\& M_{23}=\beta\tau_{0}\bar{q}_{2}, \\& M_{24}=\beta\tau_{0}\biggl(W_{11}^{(1)}(0)q_{2}+ \frac{1}{2}W_{20}^{(1)}(0)\bar {q}_{2}+W_{11}^{(2)}(0)+ \frac{1}{2}W_{20}^{(2)}(0)\biggr). \end{aligned}$$

Thus, we have

$$\begin{aligned} g(z, \bar{z}) =&\bar{D}\bigl[\bigl(M_{11}+ \bar{q}_{2}^{*}M_{21}\bigr)z^{2} +\bigl(M_{12}+\bar{q}_{2}^{*}M_{22}\bigr)z \bar{z} \\ &{} +\bigl(M_{13}+\bar{q}_{2}^{*}M_{23}\bigr) \bar{z}^{2} +\bigl(M_{14}+\bar{q}_{2}^{*}M_{24} \bigr)z^{2}\bar{z}\bigr]+\cdots. \end{aligned}$$
(17)

Comparing the coefficients in Eq. (15) and Eq. (17), we can get

$$\begin{aligned}& g_{20} =2\beta\tau_{0} \bar{D}q_{2} \bigl( \bar{q}_{2}^{\ast}-1\bigr), \\& g_{11} =\beta\tau_{0} \bar{D}(q_{2} + \bar{q}_{2} ) \bigl(\bar{q}_{2}^{\ast}-1\bigr), \\& g_{02} =2\beta\tau_{0} \bar{D}\bar{q}_{2} \bigl( \bar{q}_{2}^{\ast}-1\bigr), \\& g_{21} =2\beta\tau_{0} \bar{D}\bigl(\bar{q}_{2}^{\ast}-1 \bigr) \biggl(W_{11}^{(1)} (0)q_{2} + \frac{1}{2}W_{20}^{(1)} (0)\bar{q}_{2} +W_{11}^{(2)} (0)+\frac{1}{2}W_{20}^{(2)} (0)\biggr), \end{aligned}$$

with

$$\begin{aligned}& W_{20} (\theta)=\frac{ig_{20} q(0)}{\tau_{0} \omega_{0} }e^{i\tau_{0} \omega _{0} \theta}+ \frac{i\bar{g}_{02} \bar{q}(0)}{3\tau_{0} \omega_{0} }e^{-i\tau _{0} \omega_{0} \theta}+E_{1} e^{2i\tau_{0} \omega_{0} \theta}, \\& W_{11} (\theta)=-\frac{ig_{11} q(0)}{\tau_{0} \omega_{0} }e^{i\tau_{0} \omega _{0} \theta}+ \frac{i\bar{g}_{11} \bar{q}(0)}{\tau_{0} \omega_{0} }e^{-i\tau _{0} \omega_{0} \theta}+E_{2}, \end{aligned}$$

where \(E_{1} \) and \(E_{2} \) can be determined by the following equations respectively:

$$\begin{aligned}& \begin{pmatrix} {a_{11}^{\prime}} & {a_{12}^{\prime}} & {-a_{3} } \\ {-b_{3} e^{-2i\omega_{0} \tau_{0} }} & {a_{22}^{\prime}} & 0 \\ {-a_{5} } & {-a_{6} } & {a_{33}^{\prime}} \end{pmatrix} E_{1} =2 \begin{pmatrix} {-\beta q_{3} } \\ {\beta q_{3} } \\ 0 \end{pmatrix}, \\& \begin{pmatrix} {a_{1} +b_{1} } & {a_{2} +b_{2} } & {a_{3} } \\ {b_{3} } & {a_{4} +b_{4} } & 0 \\ {a_{5} } & {a_{6} } & {a_{7} } \end{pmatrix} E_{1} =2 \begin{pmatrix} {-\beta(q_{3} +\bar{q}_{3} )} \\ {\beta(q_{3} +\bar{q}_{3} )} \\ 0 \end{pmatrix} \end{aligned}$$

with

$$\begin{aligned}& a_{11}^{\prime}2i=\omega_{0} -a_{1} -b_{1} e^{-2i\omega_{0} \tau_{0} }, \\& a_{12}^{\prime}=-a_{2} -b_{2}e^{-2i\omega_{0} \tau_{0} }, \\& a_{22}^{\prime}=2i\omega_{0} -a_{4} -b_{4} e^{-2i\omega_{0} \tau_{0} }, \\& a_{33}^{\prime}=2i\omega_{0} -a_{7}. \end{aligned}$$

Then we can get the following coefficients:

$$ \begin{aligned} &C_{1} (0)=\frac{i}{2\omega_{0} \tau_{0} } \biggl(g_{11} g_{20} -2\vert {g_{11} } \vert ^{2}-\frac{\vert {g_{02} } \vert ^{2}}{3}\biggr)+\frac{g_{21} }{2}, \\ &\mu_{2} =-\frac{\operatorname{Re}\{C_{1} (0)\}}{\operatorname{Re}\{\lambda'(\tau_{0} )\}}, \\ &\beta_{2} =2\operatorname{Re}\bigl\{ C_{1} (0)\bigr\} , \\ &T_{2} =-\frac{\operatorname{Im}\{C_{1} (0)\}+\mu_{2} \operatorname{Im}\{\lambda'(\tau_{0} )\}}{\omega_{0} \tau _{0} }. \end{aligned} $$
(18)

Theorem 2

For system (2), we assume that the conditions (H1)-(H3) hold for the parameters. Then, if \(\mu_{2} >0\) (\(\mu_{2} <0\)), then the Hopf bifurcation is supercritical (subcritical); if \(\beta_{2}<0\) (\(\beta_{2} >0\)), then the bifurcating periodic solutions are stable (unstable); if \(T_{2}>0\) (\(T_{2}<0\)), then the bifurcating periodic solutions increase (decrease).

4 Numerical simulation

In this section, we present a numerical example to validate the feasibility of the theoretical result obtained above. By extracting some values from [15] and considering the conditions for the existence of the Hopf bifurcation, we choose a set of parameters as follows: \(\alpha_{1}=0.2\), \(\alpha_{2}=0.3\), \(\gamma_{1}=0.1\), \(\gamma_{2}=0.4\), \(\eta=0.1\), \(\delta =0.12\) and \(\varepsilon=6\). Then system (2) becomes

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{dS(t)}{dt}=-0.12S(t)-0.1S(t-\tau)I(t-\tau)-0.1S(t) +0.3I(t)+0.4E(t),\\ \frac{dLI(t)}{dt}=0.1S(t-\tau)I(t-\tau)-0.12I(t)-0.2I(t)-0.3I(t), \\ \frac{dE(t)}{dt}=-0.12E(t)-0.4E(t)+0.1S(t)+0.2I(t)+6. \end{array}\displaystyle \right . $$
(19)

By Matlab 7.0, we get \(R_{0}=5.2029>1\) and the positive equilibrium \(E_{\ast}(6.2000, 22.4389, 21.3611)\) of system (19). Then we have \(A_{0}+B_{0}=0.0520>0\), \(A_{1}+B_{1}=0.5023>0\), \(A_{2}+B_{2}=1.9439>0\) and \((A_{2}+B_{2})(A_{1}+B_{1})=0.9764>A_{0}+B_{0}=0.0520>0\). That is, the condition (H1) holds. Further, we get only one critical value of the time delay \(\tau_{0}=1.1598\), \(\omega_{0}=2.0232\) and \(f'(v_{0})=0.0081>0\). That is, the conditions (H2) and (H3) hold. Therefore, according to Theorem 1, we can conclude that \(E_{\ast}(6.2000, 22.4389, 21.3611)\) is locally asymptotically stable when \(\tau\in[0, \tau _{0} )\). As can be seen from Figures 1-4, \(E_{\ast}(6.2000, 22.4389, 21.3611)\) is locally asymptotically stable when \(\tau=1.05<\tau_{0}\). When the value of the delay passes through the critical value \(\tau _{0} \), a Hopf bifurcation occurs and a family of periodic solutions bifurcate from \(E_{\ast}(6.2000, 22.4389, 21.3611)\), which can be shown by Figures 5-8. As shown in Figures 5-8, we choose \(\tau=1.65>\tau_{0}\), \(E_{\ast}(6.2000, 22.4389, 21.3611)\) become unstable and a Hopf bifurcation occurs. The Hopf bifurcation phenomenon can be also illustrated by the bifurcation diagram with respect to τ in Figure 9. Numerical simulations show that we should try to shorten the delay as much as possible so that we can control the computer viruses propagation effectively.

Figure 1
figure 1

The trajectory graph in t-S plane with \(\pmb{\tau=1.05<1.1598=\tau_{0}}\) .

Full size image
Figure 2
figure 2

The trajectory graph in t-I plane with \(\pmb{\tau=1.05<1.1598=\tau_{0}}\) .

Full size image
Figure 3
figure 3

The trajectory graph in t-E plane with \(\pmb{\tau=1.05<1.1598=\tau_{0}}\) .

Full size image
Figure 4
figure 4

The phase plot of the states S , I , E with \(\pmb{\tau=1.05<1.1598=\tau_{0}}\) .

Full size image
Figure 5
figure 5

The trajectory graph in t-S plane with \(\pmb{\tau=1.65>1.1598=\tau_{0}}\) .

Full size image
Figure 6
figure 6

The trajectory graph in t-I plane with \(\pmb{\tau=1.65>1.1598=\tau_{0}}\) .

Full size image
Figure 7
figure 7

The trajectory graph in t-E plane with \(\pmb{\tau=1.65>1.1598=\tau_{0}}\) .

Full size image
Figure 8
figure 8

The phase plot of the states S , I , E with \(\pmb{\tau=1.65>1.1598=\tau_{0}}\) .

Full size image
Figure 9
figure 9

The bifurcation diagram with respect to  τ .

Full size image

5 Conclusions

Considering that some computer viruses may purposely lay dormant for a period of time prior to infecting other computers, we incorporate the latent period delay of the computer viruses into the model considered in the literature [15] and propose a delayed SIE computer virus propagation model in this paper. Compared with the work in [15], we mainly consider the effect of the latent period delay on system (2). It is shown that the latent period delay plays an important role on the stability of system (2). When \(\tau <\tau_{0} \), system (2) is locally asymptotically stable and the characteristics of computer viruses propagation can be easily predicted and eliminated. However, when \(\tau\ge\tau_{0} \), a Hopf bifurcation occurs and the computer viruses propagation is unstable and may be out of control. Furthermore, the properties of the Hopf bifurcation are investigated by using the normal form theory and the center manifold theorem. It should be pointed out that the assumptions for the parameters of system (2) in this paper are only technical and we do not take the specific meanings of them into account. Namely, our study is restricted only to the theoretical analysis of the Hopf bifurcation phenomena of system (2). It may be helpful for field investigation or experimental studies on the propagation of computer viruses in networks. In addition, the other behaviors of system (2) out of the assumptions on the parameters have been disregarded. We leave these as our future work.