1 Introduction

During the last decade, many scholars [1–11] investigated the dynamic behavior of the mutualism model, and many excellent results were obtained. For example, Chen, Xie, and Chen [1] showed that the stage structure of the species can lead to the extinction of the mutualism model, despite the cooperation between the species; Chen, Chen, and Li [3] showed that the feedback control variables have no influence on the persistent property of a kind of mutualism model, and in this direction, some similar results was established in [6, 8]; several scholars [2, 4, 7, 10, 11] investigated the stability property of the positive equilibrium of the cooperative system, Xie, Chen, and Xue [10] showed that if the harvesting effort is limited, then the cooperative system admits a unique positive equilibrium, which is globally attractive.

Commensalism, which describes a symbiotic interaction between two populations where one population gets benefit from the other while the other is neither harmed nor benefited due to the interaction with the previous species [12], has not arisen the attention of the scholars, since the model seems simple and can be seen as a particular case of the mutualism model. Only recently scholars paid attention to such a kind of relationship; see [12–20] and the references therein. Topics such as the existence of the positive periodic solution [17], the existence of a positive almost periodic solution [14], the existence and stability of the positive equilibrium [16], the influence of the impulsive [15] were investigated, and many excellent results were obtained. However, as was pointed out by Georgescu and Maxin [20], “One would think that the stability of the coexisting equilibria for two-species models of commensalism would follow immediately from the corresponding results for models of mutualism, when these results are available, …, However, this is not actually the case”. Hence, it is necessary to do some further works on commensalism model.

Sun and Sun [18] proposed the following commensalism system:

$$ \begin{gathered} \frac{dx}{dt} = r_{1}x \biggl(1- \frac{x}{K_{1}}+\alpha \frac{y}{K_{1}} \biggr), \\ \frac{dy}{dt} = r_{2}y \biggl(1- \frac{y}{K_{2}} \biggr), \end{gathered} $$
(1.1)

where \(r_{1}\), \(r_{2}\), \(K_{1}\), \(K_{2}\), α are all positive constants. By linearizing the system at equilibrium the authors investigated the local stability property of the equilibria of the system. They showed that the unique positive equilibrium of the system is locally asymptotically stable, whereas the other three boundary equilibria are all unstable.

Recently, Xue, Han, Yang et al. [21] argued that the nonautonomous model is more suitable, since the coefficients of the system vary with time. They proposed the following two species nonautonomous commensalism model:

$$ \begin{gathered} \frac{dN_{1}}{dt} = N_{1} \bigl(a(t)-b(t)N_{1}+c(t)N_{2} \bigr), \\ \frac{dN_{2}}{dt} = N_{2} \bigl(d(t)-e(t)N_{2} \bigr). \end{gathered} $$
(1.2)

The authors gave a set of sufficient conditions that ensure the existence of a unique globally attractive positive periodic solution.

On the other hand, to obtain the resource for the development of the human being, harvest of the species is necessary. During the last decades, many scholars investigated the influence of the harvesting to predator–prey or competition system; see [22–27] and the references therein. Chakraborty, Das, and Kar [24] argued that it is necessary to harvest the population but harvesting should be regulated, so that both the ecological sustainability and conservation of the species can be implemented in a long run. They proposed the following harvesting predator–prey model:

$$ \begin{gathered} \frac{dx}{dt} = rx \biggl(1- \frac{x}{K} \biggr)- \frac{\alpha xy}{a+bx+cy}-q _{1}mEx, \\ \frac{dy}{dt} = sy \biggl(1- \frac{y}{L} \biggr)+ \frac{\beta xy}{a+bx+cy}-q _{2}mEy. \end{gathered} $$
(1.3)

Some interesting results concerned with the boundedness of the system, existence of equilibria, and local and global stability of the positive equilibrium were obtained.

Stimulated by the works of Xue, Han, Yang et al. [21] and Chakraborty, Das, and Kar [24], in this paper, we propose the following nonautonomous nonselective harvesting Lotka–Volterra commensalism model incorporating partial closure for the populations:

$$ \begin{gathered} \frac{dN_{1}(t)}{dt} = N_{1}(t) \bigl(a(t)-b(t)N_{1}(t)+c(t)N_{2}(t) \bigr)-q_{1}(t)F(t)m(t)N_{1}(t), \\ \frac{dN_{2}(t)}{dt} = N_{2}(t) \bigl(d(t)-e(t)N_{2}(t) \bigr)-q_{2}(t)F(t)m(t)N _{2}(t), \\ N_{1}(0) > 0, \quad\quad N_{2}(0)>0, \end{gathered} $$
(1.4)

where \(a(t)\), \(b(t)\), \(c(t)\), \(d(t)\), \(e(t)\), \(q_{1}(t)\), \(q_{2}(t)\), \(F(t)\), and \(m(t)\) are positive constants, and \(a(t)\), \(b(t)\), \(c(t)\), \(d(t)\), \(e(t)\) have the same meaning as in system (1.2); \(F(t)\) is the combined fishing effort used to harvest, and \(m(t)\) (\(0< m(t)<1\)) is the fraction of the stock available for harvesting.

As for as an ecosystem is concerned, there are the most important three topics: permanence, extinction, and global attractivity, which reflect the existence of the species in the long run, the extinction of the species, and the species maintained in a stable state. During the last decades, there are many excellent results on these three topics; see [28–37] and the references therein. For example, Shi, Li, and Chen [30] studied the extinction property of a competition system with infinite delay and feedback controls; Chen, Xie, and Li [31] investigated the partial extinction of the predator–prey model with stage structure; Chen, Chen, and Huang [32] investigated the extinction property of the nonlinear competition system with Beddington–DeAngelis functional response; Xie, Xue, Wu et al. [33] studied the extinction property of a nonlinear toxic substance competition system; Chen, Ma, and Zhang [34] showed that if the refuge is restricted to suitable area, then the Lotka–Volterra predato–prey system can admit a unique positive equilibrium, which is globally attractive. In this paper, we also focus our attention on the persistency, extinction, and stability of system (1.4).

The paper is arranged as follows. We will investigate the extinction, partial survival and persistency of system (1.4) in the next section. In Sect. 3, we investigate the global stability property of the solutions of the system. Two examples, together with their numeric simulations, are presented in Sect. 4 to show the feasibility of the main results. We end this paper by a brief discussion.

2 Extinction and persistency of the system

For the rest of the paper, for a bounded continuous function g defined on R, let

$$g^{L}=\inf_{t\in [0,+\infty )}g(t)\quad \text{and}\quad g^{M}= \sup_{t\in [0,+\infty )}g(t). $$

Lemma 2.1

([28])

If \(a>0\), \(b>0\), and \(\dot{x}\geq x(b-ax)\) for \(t\geq 0\) and \(x(0)>0\), then

$$\liminf_{t\rightarrow +\infty } x(t)\geq \frac{b}{a}. $$

If \(a>0\), \(b>0\), and \(\dot{x} \leq x(b-ax)\) for \(t\geq 0\) and \(x(0)>0\), then

$$\limsup_{t\rightarrow +\infty } x(t)\leq \frac{b}{a}. $$

Lemma 2.2

The domain \(R^{2}_{+}=\{(x,y)|x>0,y>0\}\) is invariant with respect to (1.4).

Proof

Since

$$\begin{gathered} N_{1}(t)=N_{1}(0)\exp \biggl\{ \int_{0}^{t}\Gamma_{1}(s) \,ds \biggr\} >0,\quad\quad N_{2}(t)= N_{2}(0)\exp \biggl\{ \int_{0}^{t} \Gamma_{2}(s) \,ds \biggr\} >0, \end{gathered} $$

where

$$\begin{gathered} \Gamma_{1}(s) = a(s)-q_{1}(s)F(s)m(s)-b(s)N_{1}(s)+c(s)N_{2}(s), \\ \Gamma_{2}(s) = d(s)-e(s)N_{2}(s)-q_{2}(s)F(s)m(s), \end{gathered} $$

the assertion of the lemma immediately follows for all \(t\in [0,+ \infty )\). □

Theorem 2.1

Let \((N_{1}(t),N_{2}(t))^{T}\) be any solution of system (1.4). Assume that

$$ d^{M}< q_{2}^{L}F^{L}m^{L},\quad\quad a^{M}< q_{1}^{L}F^{L}m^{L}. $$
(2.1)

Then

$$\begin{gathered} \lim_{t\rightarrow +\infty } N_{1}(t) = 0, \quad\quad \lim _{t\rightarrow +\infty } N_{2}(t)=0, \end{gathered} $$

that is, both species will be driven to extinction.

Proof

It follows from (2.1) that there exists a small enough \(\varepsilon >0\) such that

$$ a^{M}+c^{M}\varepsilon < q_{1}^{L}F^{L}m^{L}. $$
(2.2)

Let \((N_{1}(t),N_{2}(t))^{T}\) be any solution of system (1.4). From the second equation of system (1.4) it follows that

$$ \dot{N_{2}}(t) \leq \bigl(d^{M} -q_{2}^{L}F^{L}m^{L} \bigr)N_{2}(t). $$
(2.3)

So

$$ N_{2}(t)\leq N_{2}(0)\exp \bigl\{ \bigl(d^{M} -q_{2}^{L}F^{L}m^{L} \bigr)t \bigr\} \rightarrow 0 \quad \text{as } t\rightarrow 0. $$
(2.4)

For \(\varepsilon >0\) as in (2.2), it follows from (2.4) that there exists a large enough \(T_{1}\) such that

$$ N_{2}(t)< \varepsilon \quad {\text{for all }} t\geq T _{1}. $$
(2.5)

From the first equation and (2.5) it follows that

$$ \dot{N_{1}}(t) \leq N_{1}(t) \bigl(a^{M} + c^{M}\varepsilon -q_{1} ^{L}F^{L}m^{L}-b^{L}N_{1}(t) \bigr). $$
(2.6)

So

$$ N_{1}(t)\leq N_{1}(T_{1})\exp \bigl\{ \bigl(a^{M} + c^{M}\varepsilon -q _{1}^{L}F^{L}m^{L} \bigr) (t-T_{1}) \bigr\} \rightarrow 0 \quad {\text{as }} t\rightarrow 0. $$
(2.7)

This ends the proof of Theorem 2.1. □

Theorem 2.2

Let \((N_{1}(t),N_{2}(t))^{T}\) be any solution of system (1.4). Assume that

$$ d^{M}< q_{2}^{L}F^{L}m^{L},\quad\quad a^{L}>q_{1}^{M}F^{M}m^{M}. $$
(2.8)

Then

$$\begin{gathered} \frac{a^{L}-q_{1}^{M}F^{M}m^{M}}{b^{M}}\leq \liminf_{t\rightarrow +\infty } N_{1}(t) \leq \limsup_{t\rightarrow +\infty } N_{1}(t)\leq \frac{a^{M}-q_{1}^{L}F ^{L}m^{L}}{b^{L}}, \\ \lim_{t\rightarrow +\infty } N_{2}(t)=0, \end{gathered} $$

that is, the first species is permanent, and the second species will be driven to extinction.

Proof

From the first inequality of (2.8), similarly to the analysis of (2.3)–(2.4), for any solution \((N_{1}(t),N_{2}(t))^{T}\) of system (1.4), we obtain

$$ N_{2}(t)\leq N_{2}(0)\exp \bigl\{ \bigl(d^{M} -q_{2}^{L}F^{L}m^{L} \bigr)t \bigr\} \rightarrow 0 \quad {\text{as }} t\rightarrow 0. $$
(2.9)

For \(\varepsilon >0\) small enough, it follows from (2.9) that there exists a large enough \(T_{2}\) such that

$$ N_{2}(t)< \varepsilon\quad {\text{for all }} t\geq T _{2}. $$
(2.10)

From the first equation and (2.10) it follows that

$$ \dot{N_{1}}(t) \leq N_{1}(t) \bigl(a^{M} + c^{M}\varepsilon -q_{1} ^{L}F^{L}m^{L}-b^{L}N_{1}(t) \bigr). $$
(2.11)

It follows from Lemma 2.1 and (2.11) that

$$ \limsup_{t\rightarrow +\infty }N_{1}(t)\leq \frac{a^{M} + c ^{M}\varepsilon -q_{1}^{L}F^{L}m^{L}}{b^{L}}. $$
(2.12)

Since \(\varepsilon >0\) is an arbitrary small positive constant, letting \(\varepsilon \rightarrow 0\) in (2.12) leads to

$$ \limsup_{t\rightarrow +\infty }N_{1}(t)\leq \frac{a^{M} -q _{1}^{L}F^{L}m^{L}}{b^{L}}. $$
(2.13)

From the first equation we also have

$$ \dot{N_{1}}(t) \geq N_{1}(t) \bigl(a^{L} -q_{1}^{M}F^{M}m^{M}-b^{M}N _{1}(t) \bigr). $$
(2.14)

It follows from Lemma 2.1 and (2.14) that

$$ \liminf_{t\rightarrow +\infty }N_{1}(t)\geq \frac{a^{L} -q _{1}^{M}F^{M}m^{M}}{b^{M}}. $$
(2.15)

Relations (2.9), (2.13), and (2.15) show that the statement of Theorem 2.2 holds. This ends the proof of the theorem. □

Theorem 2.3

Let \((N_{1}(t),N_{2}(t))^{T}\) be any solution of system (1.4). Assume that

$$ d^{L}>q_{2}^{M}F^{M}m^{M},\quad\quad a^{M}+c^{M} \frac{d^{M}-q_{2}^{L}F ^{L}m^{L}}{e^{L}}< q_{1}^{L}F^{L}m^{L}. $$
(2.16)

Then

$$\begin{gathered} \lim_{t\rightarrow +\infty } N_{1}(t) = 0, \\ \frac{d^{L}-q_{2}^{M}F^{M}m^{M}}{e^{M}} \leq \liminf_{t\rightarrow +\infty } N_{2}(t)\leq \limsup_{t\rightarrow +\infty } N_{2}(t)\leq \frac{d^{M}-q_{2}^{L}F ^{L}m^{L}}{e^{L}}, \end{gathered} $$

that is, the second species is permanent, whereas the first species will be driven to extinction.

Proof

It follows from (2.16) that there exists a small enough \(\varepsilon >0\) such that

$$ a^{M}+c^{M} \biggl( \frac{d^{M}-q_{2}^{L}F^{L}m^{L}}{e^{L}}+\varepsilon \biggr)< q_{1}^{L}F^{L}m^{L}. $$
(2.17)

Let \((N_{1}(t),N_{2}(t))^{T}\) be any positive solution of system (1.4). From the second equation of system (1.4) it follows that

$$ \dot{N_{2}}(t) \leq N_{2}(t) \bigl(d^{M} -q_{2}^{L}F^{L}m^{L}-e^{L}N _{2}(t) \bigr). $$
(2.18)

It follows from Lemma 2.1 and (2.18) that

$$ \limsup_{t\rightarrow +\infty }N_{2}(t)\leq \frac{d^{M} -q _{2}^{L}F^{L}m^{L}}{e^{L}}. $$
(2.19)

For \(\varepsilon >0\) as in (2.17), it follows from (2.19) that there exists \(T_{3}>0\) such that

$$ N_{2}(t)< \frac{d^{M} -q_{2}^{L}F^{L}m^{L}}{e^{L}}+\varepsilon \quad \text{for all } t\geq T_{3}. $$
(2.20)

Again, from the second equation of system (1.4) we also have

$$ \dot{N_{2}}(t) \geq N_{2}(t) \bigl(d^{L} -q_{2}^{M}F^{M}m^{M}-e^{M}N _{2}(t) \bigr). $$
(2.21)

It follows from Lemma 2.1 and (2.21) that

$$ \liminf_{t\rightarrow +\infty }N_{2}(t)\geq \frac{d^{L} -q _{2}^{M}F^{M}m^{M}}{e^{M}}. $$
(2.22)

From the first equation and (2.20), for \(t\geq T_{3}\), it follows that

$$ \dot{N_{1}}(t) \leq \biggl(a^{M} + c^{M}\biggl( \frac{d^{M} -q_{2}^{L}F ^{L}m^{L}}{e^{L}}+\varepsilon \biggr)-q_{1}^{L}F^{L}m^{L} \biggr)N_{1}(t) . $$
(2.23)

So

$$ N_{1}(t)\leq N_{1}(T_{3})\exp \bigl\{ \Gamma_{1}^{\varepsilon }(t-T _{3}) \bigr\} \rightarrow 0 \quad \text{as } t\rightarrow +\infty , $$
(2.24)

where

$$\Gamma_{1}^{\varepsilon }= a^{M} + c^{M}\biggl( \frac{d^{M} -q_{2}^{L}F^{L}m ^{L}}{e^{L}}+\varepsilon \biggr)-q_{1}^{L}F^{L}m^{L}. $$

It immediately follows from (2.19), (2.22), and (2.24) that the statement of Theorem 2.3 holds. This ends the proof of the theorem. □

Theorem 2.4

Let \((N_{1}(t),N_{2}(t))^{T}\) be any solution of system (1.4). Assume that

$$ d^{L}>q_{2}^{M}F^{M}m^{M},\quad\quad a^{L}+c^{L} \frac{d^{L}-q_{2}^{M}F ^{M}m^{M}}{e^{M}}>q_{1}^{M}F^{M}m^{M}. $$
(2.25)

Then the system is permanent, that is, there exist positive constants \(m_{i}\), \(M_{i}\), \(i=1,2\), independent of the solutions of (1.4), such that

$$\begin{gathered} m_{1} \leq \liminf_{t\rightarrow +\infty } N_{1}(t)\leq \limsup_{t\rightarrow +\infty } N_{1}(t)\leq M_{1}, \\ m_{2} \leq \liminf_{t\rightarrow +\infty } N_{2}(t)\leq \limsup_{t\rightarrow +\infty } N_{2}(t)\leq M_{2}, \end{gathered} $$

where

$$ \begin{gathered} m_{1}= \frac{a^{L} + c^{L} \frac{d^{L} -q_{2}^{M}F^{M}m^{M}}{e^{M}} -q_{1}^{M}F^{M}m^{M}}{b^{M}}; \\ M_{1}= \frac{a^{M} + c^{M} \frac{d^{M} -q_{2}^{L}F^{L}m^{L}}{e^{L}} -q_{1}^{L}F^{L}m^{L}}{b^{L}}; \\ m_{2}= \frac{d^{L}-q_{2}^{M}F^{M}m^{M}}{e^{M}};\quad\quad M_{2}= \frac{d^{M}-q _{2}^{L}F^{L}m^{L}}{e^{L}}. \end{gathered} $$
(2.26)

Proof

It follows from (2.25) that, indeed, for enough small \(\varepsilon >0\), namely, for

$$ \varepsilon < \frac{ a^{L}+c^{L} ( \frac{d^{L}-q_{2}^{M}F^{M}m^{M}}{e ^{M}} )-q_{1}^{M}F^{M}m^{M} }{ c^{L}}, $$
(2.27)

we have the inequality

$$ a^{L}+c^{L} \biggl( \frac{d^{L}-q_{2}^{M}F^{M}m^{M}}{e^{M}}-\varepsilon \biggr)>q_{1}^{M}F^{M}m^{M}. $$
(2.28)

From (2.28) we can easily see that

$$ a^{M}+c^{M} \biggl( \frac{d^{M}-q_{2}^{L}F^{L}m^{L}}{e^{L}}+\varepsilon \biggr)>q_{1}^{L}F^{L}m^{L}. $$
(2.29)

Let \((N_{1}(t),N_{2}(t))^{T}\) be any solution of system (1.4). From the second equation of system (1.4), applying the first inequality of (2.25), similarly to the analysis of (2.18)–(2.22), we can show that

$$ \begin{aligned}[b] m_{2}&\stackrel{\mathrm{def}}{=} \frac{d^{L}-q_{2}^{M}F^{M}m^{M}}{e ^{M}} \leq \liminf_{t\rightarrow +\infty } N_{2}(t) \\ &\leq \limsup_{t\rightarrow +\infty } N_{2}(t)\leq \frac{d ^{M}-q_{2}^{L}F^{L}m^{L}}{e^{L}} \stackrel{\mathrm{def}}{=}M_{2}. \end{aligned} $$
(2.30)

For any positive constant \(\varepsilon >0\) small enough, which satisfies (2.27) and \(\varepsilon < \frac{d^{L}-q_{2}^{M}F^{M}m^{M}}{e^{M}}\), there exists a large enough \(T_{4}>0\) such that

$$ \frac{d^{L}-q_{2}^{M}F^{M}m^{M}}{e^{M}}-\varepsilon < N_{2}(t)< \frac{d ^{M}-q_{2}^{L}F^{L}m^{L}}{e^{L}}+ \varepsilon \quad \text{for all } t\geq T_{4}. $$
(2.31)

From the first equation of (1.4) and (2.31), for \(t\geq T_{4}\), it follows that

$$ \dot{N_{1}}(t) \leq \biggl(a^{M} + c^{M}\biggl( \frac{d^{M} -q_{2}^{L}F ^{L}m^{L}}{e^{L}}+\varepsilon \biggr)-q_{1}^{L}F^{L}m^{L}-b^{L}N_{1}(t) \biggr)N_{1}(t). $$
(2.32)

Applying Lemma 2.1 to (2.32) leads to

$$\limsup_{t\rightarrow +\infty }N_{1}(t)\leq \frac{a^{M} + c ^{M}( \frac{d^{M} -q_{2}^{L}F^{L}m^{L}}{e^{L}}+\varepsilon )-q_{1} ^{L}F^{L}m^{L}}{b^{L}}. $$

Setting \(\varepsilon \rightarrow 0\) in this inequality leads to

$$ \limsup_{t\rightarrow +\infty }N_{1}(t)\leq \frac{a^{M} + c ^{M} \frac{d^{M} -q_{2}^{L}F^{L}m^{L}}{e^{L}} -q_{1}^{L}F^{L}m^{L}}{b ^{L}} \stackrel{\mathrm{def}}{=}M_{1}. $$
(2.33)

From the first equation of (1.4) and (2.31), for \(t\geq T_{4}\), we also have

$$ \dot{N_{1}}(t) \geq \biggl(a^{L} + c^{L}\biggl( \frac{d^{L} -q_{2}^{M}F ^{M}m^{M}}{e^{M}}-\varepsilon \biggr)-q_{1}^{M}F^{M}m^{M}-b^{M}N_{1}(t) \biggr)N_{1}(t). $$
(2.34)

Applying Lemma 2.1 to (2.34) leads to

$$\liminf_{t\rightarrow +\infty }N_{1}(t)\geq \frac{a^{L} + c ^{L}( \frac{d^{L} -q_{2}^{M}F^{M}m^{M}}{e^{M}}-\varepsilon )-q_{1} ^{M}F^{M}m^{M} }{b^{M}}. $$

Setting \(\varepsilon \rightarrow 0\) in this inequality leads to

$$ \liminf_{t\rightarrow +\infty }N_{1}(t)\geq \frac{a^{L} + c ^{L} \frac{d^{L} -q_{2}^{M}F^{M}m^{M}}{e^{M}} -q_{1}^{M}F^{M}m^{M}}{b ^{M}} \stackrel{\mathrm{def}}{=}m_{1}. $$
(2.35)

Relations (2.30), (2.33), and (2.35) show that the statement of Theorem 2.4 holds. This ends the proof of the theorem. □

3 Global attractivity

In Sect. 2, we discussed the persistent or extinction property of the system, which means that the solutions of the system are bounded above and below by some positive constants or the species will be driven to extinction. One of the interesting problems is to give sufficient conditions to ensure the global attractivity of the positive solution of the system. Before we state the main results of this section, we need to introduce two useful lemmas.

Lemma 3.1

(Fluctuation lemma, [35, Lemma 4])

Let \(x(t)\) be a bounded differentiable function on \((\alpha , \infty )\). Then there exist sequences \(\tau_{n}\rightarrow \infty \) and \(\sigma_{n}\rightarrow \infty \) such that

$$\begin{aligned}& (\mathrm{a}) \quad \dot{x}(\tau_{n})\rightarrow 0\quad \textit{and} \quad x(\tau_{n}) \rightarrow \limsup_{t\rightarrow \infty }x(t)=\overline{x} \quad \textit{as }n\rightarrow \infty , \\& (\mathrm{b})\quad \dot{x}(\sigma_{n})\rightarrow 0 \quad \textit{and}\quad x(\sigma_{n}) \rightarrow \liminf_{t\rightarrow \infty }x(t)=\underline{x} \quad \textit{as } n\rightarrow \infty . \end{aligned}$$

For the logistic equation

$$ \dot{x}(t)=x(t) \bigl(r(t)-a(t)x(t) \bigr), $$
(3.1)

from Lemma 2.1 of Zhao and Chen [36] we have the following:

Lemma 3.2

Suppose that \(r(t)\) and \(a(t)\) are bounded above and below by positive constants. Then any positive solutions of Eq. (3.1) are defined on \([0, +\infty )\), bounded above and below by positive constants, and globally attractive.

Theorem 3.1

Under the assumptions of Theorem 2.2, let \(N(t)=(N_{1}(t),N_{2}(t))^{T}\) be any positive solution of system (1.4). Then the species \(N_{2}\) will be driven to extinction, that is, \(N_{2}(t)\rightarrow 0 \) as \(t\rightarrow +\infty \), and \(N_{1}(t)\rightarrow N_{1}^{*}(t)\) as \(t\rightarrow +\infty \), where \(N_{1}^{*}(t)\) is any positive solution of

$$ \frac{dN_{1}(t)}{dt}=N_{1}(t) \bigl(a(t)-q_{1}(t)F(t)m(t)-b(t)N_{1}(t) \bigr). $$
(3.2)

Proof

Let \(N(t)=(N_{1}(t),N_{2}(t))^{T}\) be any positive solution of system (1.4). By Theorem 2.2 the species \(N_{2}\) will be driven to extinction, that is, \(N_{2}(t)\rightarrow 0 \) as \(t\rightarrow +\infty \). To finish the proof of Theorem 3.1, it suffices to show that \(N_{1}(t)\rightarrow N_{1}^{*}(t)\) as \(t\rightarrow +\infty \), where \(N_{1}^{*}(t)\) is any positive solution of system (3.2). It follows from Theorem 2.2 and Lemma 3.2 that there exists \(T_{5}>0\) such that

$$\frac{1}{2} \frac{a^{L}-q_{1}^{M}F^{M}m^{M}}{b^{M}}< N_{1}(t)< \frac{3}{2} \frac{a^{M}-q_{1}^{L}F^{L}m^{L}}{b^{L}} $$

and

$$\eta_{1}< N_{1}^{*}(t)< \eta_{2}, $$

where \(\eta_{i}\), \(i=1, 2\), are two positive constants independent of the solution of system (3.2). Let \(w(t)=(N_{1}(t))^{-1}\), \(w^{*}(t)=(N _{1}^{*}(t))^{-1}\), and \(z(t)=w(t)-w^{*}(t)\). Then

$$\begin{aligned}& \dot{w}(t) = - \bigl(a(t)-q_{1}(t)F(t)m(t) \bigr)w(t)+b(t)+c(t)w(t)N _{2}(t), \\& \dot{w^{*}}(t) = - \bigl(a(t)-q_{1}(t)F(t)m(t) \bigr)w^{*}(t)+b(t). \end{aligned}$$

It follows that z satisfies

$$ z^{\prime}(t)= - \bigl(a(t)-q_{1}(t)F(t)m(t)\bigr)z(t)+ c(t)w(t)N_{2}(t), \quad t \ge T_{5}. $$
(3.3)

From this analysis, for \(t\geq T_{5}\), we have

$$0< \biggl(\frac{3}{2} \frac{a^{M}-q_{1}^{L}F^{L}m^{L}}{b^{L}} \biggr)^{- 1}< w(t)< \biggl(\frac{1}{2} \frac{a^{L}-q_{1}^{M}F^{M}m^{M}}{b^{M}} \biggr)^{- 1} $$

and

$$0< \eta_{2}^{- 1}\le w^{*}(t)\le \eta_{1}^{- 1}. $$

Thus \(z(t)\) is a bounded differentiable function. By the fluctuation lemma (Lemma 3.1) there exist sequences \(\tau_{n}\rightarrow \infty \) and \(\sigma_{n}\rightarrow \infty \) such that \(z(\tau_{n})\rightarrow \overline{z}\), \(z^{\prime}(\tau_{n})\rightarrow 0\); \(z(\sigma_{n})\rightarrow \underline{z}\), \(z^{\prime}(\sigma_{n})\rightarrow 0\) as \(n\rightarrow \infty \). We will show that \(\overline{z}=\underline{z}=0\). From (3.3) we have

$$z(t)= \frac{c(t)w(t)N_{2}(t)}{a(t)-q_{1}(t)F(t)m(t)}- \frac{z^{\prime}(t)}{a(t)-q _{1}(t)F(t)m(t)}. $$

Noting that

$$\begin{aligned}& 0 < \frac{c(t)w(t)}{ a(t)-q_{1}(t)F(t)m(t)} \leq \frac{c^{M} ( \frac{1}{2} \frac{a^{L}-q_{1}^{M}F^{M}m^{M}}{b^{M}} )^{- 1}}{a^{L}-q _{1}^{M}F^{M}m^{M}}, \\& 0 < \frac{1}{a(t)-q_{1}(t)F(t)m(t)}\leq \frac{1}{a^{L}-q_{1}^{M}F^{M}m ^{M}}, \end{aligned}$$

and \(\lim_{t\rightarrow \infty } N_{2}(t)=0\), we can see that

$$\begin{aligned} & \lim_{n\rightarrow \infty } \frac{c(\tau_{n})w(\tau_{n})N _{2}(\tau_{n})}{a(\tau_{n})-q_{1}(\tau_{n})F(\tau_{n})m(\tau_{n})} \\ & \quad = \lim_{n\rightarrow \infty } \frac{c(\sigma_{n})w(\sigma _{n})N_{2}(\sigma_{n})}{a(\sigma_{n})-q_{1}(\sigma_{n})F(\sigma_{n})m( \sigma_{n})} \\ &\quad = \lim_{n\rightarrow \infty } \frac{z^{\prime}(\tau_{n})}{a(\tau _{n})-q_{1}(\tau_{n})F(\tau_{n})m(\tau_{n})} \\ &\quad = \lim_{n\rightarrow \infty } \frac{z^{\prime}(\sigma_{n})}{a( \sigma_{n})-q_{1}(\sigma_{n})F(\sigma_{n})m(\sigma_{n})} = 0. \end{aligned}$$

Hence \(\overline{z}=\underline{z}=0\). Since

$$\bigl\vert N_{1}(t)-N_{1}^{*}(t) \bigr\vert = \bigl\vert w^{*}(t)-w(t) \bigr\vert \bigl(N_{1}^{*}(t)N_{1}(t) \bigr) $$

and both \(N_{1}(t)\) and \(N_{1}^{*}(t)\) are bounded functions, we have

$$\lim_{t\rightarrow \infty }N_{1}(t)=N_{1}^{*}(t), $$

as required. This completes the proof. □

Theorem 3.2

Under the assumptions of Theorem 2.3, let \(N(t)=(N_{1}(t),N_{2}(t))^{T}\) be any positive solution of system (1.4). Then the species \(N_{1}\) will be driven to extinction, that is, \(N_{1}(t)\rightarrow 0 \) as \(t\rightarrow +\infty \), and \(N_{2}(t)\rightarrow N_{2}^{*}(t)\) as \(t\rightarrow +\infty \), where \(N_{2}^{*}(t)\) is any positive solution of

$$ \frac{dN_{2}(t)}{dt}=N_{2}(t) \bigl(d(t)-q_{2}(t)F(t)m(t)-e(t)N_{2}(t) \bigr). $$
(3.4)

Proof

Let \(N(t)=(N_{1}(t),N_{2}(t))^{T}\) be any positive solution of system (1.4). By Theorem 2.3 the species \(N_{1}\) will be driven to extinction, that is, \(N_{1}(t)\rightarrow 0 \) as \(t\rightarrow +\infty \). On the other hand, noting that the second equation of system (1.4) is independent of \(N_{1}(t)\), from Lemma 3.2 it immediately follows that \(N_{2}(t)\rightarrow N_{2}^{*}(t)\) as \(t\rightarrow + \infty \), where \(N_{2}^{*}(t)\) is any positive solution of system (3.4). This ends the proof of Theorem 3.2. □

Theorem 3.3

In addition to (2.25), assume further that

$$ e^{L}>c^{M}. $$
(3.5)

Let \(N(t)=(N_{1}(t),N_{2}(t))^{T}\) and \(N^{*}(t)=(N_{1}^{*}(t), N_{2} ^{*}(t))^{T}\) be any two positive solutions of system (1.4). Then

$$\lim_{t\rightarrow +\infty } \bigl( \bigl\vert N_{1}(t)-N_{1}^{*}(t) \bigr\vert + \bigl\vert N _{2}(t)-N_{2}^{*}(t) \bigr\vert \bigr)=0. $$

Proof

Let \(N(t)=(N_{1}(t),N_{2}(t))^{T}\) and \(N^{*}(t)=(N _{1}^{*}(t), N_{2}^{*}(t))^{T}\) be any two positive solutions of system (1.4). For any small enough positive constant \(\varepsilon >0\), it then follows from Theorem 2.4 that there exists a large enough \(T_{6}\) such that, for all \(t\geq T_{6}\),

$$ \begin{gathered} N_{1}(t),N_{1}^{*}(t) < M_{1}+\varepsilon , \quad\quad N_{2}(t), N_{2}^{*}(t) < M_{2}+\varepsilon , \\ N_{1}(t), N_{1}^{*}(t) >m_{1}- \varepsilon , \quad\quad N_{2}(t), N_{2}^{*}(t) >m_{2}-\varepsilon . \end{gathered} $$
(3.6)

Now let

$$V (t)= \bigl\vert \ln N_{1}(t)-\ln N_{1}^{*}(t) \bigr\vert + \bigl\vert \ln N_{2}(t)-\ln N_{2}^{*}(t) \bigr\vert . $$

Then, by (3.5), for \(t>T_{6}\), we have

$$ \begin{aligned}[b] D^{+}V(t) &\leq - b(t) \bigl\vert N_{1}(t)-N_{1}^{*}(t)) \bigr\vert +c(t) \bigl\vert N_{2}(t)-N _{2}^{*}(t) \bigr\vert \\ &\quad{} -e(t) \bigl\vert N_{2}(t)-N_{2}^{*}(t) \bigr\vert \\ &\leq - b^{L} \bigl\vert N_{1}(t)-N_{1}^{*}(t)) \bigr\vert -\bigl(e^{L}-c^{M}\bigr) \bigl\vert N_{2}(t)-N _{2}^{*}(t) \bigr\vert . \end{aligned} $$
(3.7)

Integrating both sides of (3.7) on the interval \([T_{6},t)\), we have

$$ \begin{aligned}[b] &V(t)-V(T_{6})\\&\quad \leq \int_{T_{6}}^{t} \bigl[- b^{L} \bigl\vert N_{1}(s)-N_{1}^{*}(s) \bigr\vert -\bigl(e ^{L}-c^{M}\bigr) \bigl\vert N_{2}(s)-N_{2}^{*}(s) \bigr\vert \bigr]\,ds \quad \text{for } t \geq T_{6}.\end{aligned} $$
(3.8)

It follows from (3.8) that

$$ \begin{aligned}[b] &V(t)+\min \bigl\{ b^{L},e^{L}-c^{M} \bigr\} \int_{T_{6}}^{t} \bigl[ \bigl\vert N_{1}(s)-N _{1}^{*}(s) \bigr\vert + \bigl\vert N_{2}(s)-N_{2}(s) \bigr\vert \bigr]\,ds\\&\quad \leq V(T_{6}) \quad \text{for } t\geq T_{6}.\end{aligned} $$
(3.9)

Therefore \(V(t)\) is bounded on \([T_{6},+\infty )\), and also

$$ \int_{T_{6}}^{t} \bigl[ \bigl\vert N_{1}(s)-N_{1}^{*}(s) \bigr\vert + \bigl\vert N_{2}(s)-N_{2}(s) \bigr\vert \bigr]\,ds< +\infty . $$
(3.10)

By (3.6), \(\vert N_{1}(t)-N_{1}^{*}(t) \vert \) and \(\vert N_{2}(t)-N_{2}^{*}(t) \vert \) are bounded on \([T_{6},+\infty )\). On the other hand, it is easy to see that \(\dot{N_{1}}(t)\), \(\dot{N_{2}}(t)\), \(\dot{N}_{1}^{*}(t)\), and \(\dot{N}_{2}^{*}(t)\) are bounded for \(t\geq T_{6}\). Therefore \(\vert N_{1}(t)-N_{1}^{*}(t) \vert \), \(\vert N_{2}(t)-N_{2}^{*}(t) \vert \) are uniformly continuous on \([T_{6},+\infty )\). By the Barbălat lemma we conclude that

$$\lim_{t\rightarrow +\infty } \bigl[ \bigl\vert N_{1}(t)-N_{1}^{*}(t) \bigr\vert + \bigl\vert N _{2}(t)-N_{2}^{*}(t) \bigr\vert \bigr]=0. $$

This ends the proof of Theorem 3.3. □

4 Numerical simulations

Example 4.1

Consider the following system:

$$ \begin{gathered} \frac{dN_{1}(t)}{dt} = N_{1}(t) \biggl( \frac{1}{2}+\frac{1}{4}\cos t - N _{1}(t)+ N_{2}(t) \biggr)-\frac{1}{2}N_{1}(t), \\ \frac{dN_{2}(t)}{dt} = N_{2}(t) \biggl(\frac{1}{2}+ \frac{1}{4}\sin t - N _{2}(t) \biggr)-\frac{1}{2}N_{2}(t), \\ N_{1}(0) > 0, \quad\quad N_{2}(0)>0. \end{gathered} $$
(4.1)

Corresponding to system (1.4), here we take

$$\begin{aligned}& a(t)=\frac{1}{2}+\frac{1}{4}\cos t, \quad\quad d(t)=\frac{1}{2}+ \frac{1}{4} \sin t, \end{aligned}$$
(4.2)
$$\begin{aligned}& q_{1}(t)=q_{2}(t)=F(t)=c(t)=e(t)=1, \quad\quad m(t)= \frac{1}{2}. \end{aligned}$$
(4.3)

We can easily verify that

$$a^{M}< q_{1}^{L}F^{L}m^{L},\quad\quad d^{M}< q_{2}^{L}F^{L}m^{L}. $$

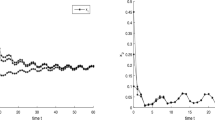
Hence, all the conditions of Theorem 2.1 hold, and it follows from Theorem 2.1 that both species will be driven to extinction. Numeric simulations (Figs. 1 and 2) also support this assertion.

Figure 1
figure 1

Numeric simulations of the first component system (4.1) with initial conditions \((x(0), y(0))=(0.5,0.1), (0.8,0.5), (0.3, 0.7)\), and \((0.7,0.9)\)

Full size image
Figure 2
figure 2

Numeric simulations of the second component of system (4.1) with initial conditions \((x(0), y(0))=(0.5,0.1), (0.8,0.5), (0.3, 0.7)\), and \((0.7,0.9)\)

Full size image

Example 4.2

Consider the following system:

$$ \begin{gathered} \frac{dN_{1}(t)}{dt} = N_{1}(t) \biggl( \frac{1}{2}+\frac{1}{4}\cos t - N _{1}(t)+ \frac{1}{4} N_{2}(t) \biggr)-\frac{1}{50}N_{1}(t), \\ \frac{dN_{2}(t)}{dt} = N_{2}(t) \biggl(\frac{1}{2}+ \frac{1}{4}\sin t - N _{2}(t) \biggr)-\frac{1}{50}N_{2}(t), \\ N_{1}(0) > 0, \quad\quad N_{2}(0)>0. \end{gathered} $$
(4.4)

Corresponding to system (1.4), here we take

$$\begin{aligned}& a(t)=\frac{1}{2}+\frac{1}{4}\cos t, \quad\quad d(t)=\frac{1}{2}+ \frac{1}{4} \sin t, \end{aligned}$$
(4.5)
$$\begin{aligned}& q_{1}(t)=q_{2}(t)=F(t)=e(t)=1,\quad\quad c(t)=\frac{1}{4}, m(t)= \frac{1}{50}. \end{aligned}$$
(4.6)

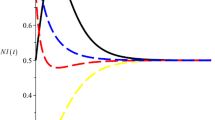
We can easily verify that all the conditions of Theorems 2.4 and 3.3 hold, and it follows from Theorems 2.4 and 3.3 that the system is permanent and that any positive solution of system (4.4) is globally attractive. Numeric simulations (Figs. 3 and 4) also support this assertion.

Figure 3
figure 3

Numeric simulations of the first component of system (4.4) with initial conditions \((x(0), y(0))=(0.5,0.1), (0.8,0.5), (0.3, 0.7)\), and \((0.7,0.9)\)

Full size image
Figure 4
figure 4

Numeric simulations of the second component of system (4.4) with initial conditions \((x(0), y(0))=(0.5,0.1), (0.8,0.5), (0.3, 0.7)\), and \((0.7,0.9)\)

Full size image

5 Discussion

Recently, many scholars [12–21] studied the dynamic behavior of the commensalism model; however, none of them consider the influence of harvesting. Stimulated by the recent works of Chakraborty, Das, and Kar [24], we propose a nonautonomous nonselective commensalism model incorporating partial closure to the population.

We focus our attention on the persistent and extinction property of the system, Theorems 2.1–2.4 show that, depending on the area that can be harvested, the the system may exhibit permanent, extinction, or partial survival phenomenon, that is, the introducing of harvesting makes the dynamic behavior of the system complicated. Theorem 2.4 shows that if the harvesting area is small enough (i.e., m is small enough), then two species can coexist in the long run. If we further assume that the intrinsic competition rate (\(e(t)\)) is larger than the cooperative between the two species (\(c(t)\)), then two species can coexist in a stable state. Such a result may help us in designing the reserve area of the species.

It seems interesting to incorporate the time delay to system (1.4) and study the influence of the time delay. We leave this for future study.