1 Introduction

Given a function \(g(t)\), let \(g_{L}\) and \(g_{M}\) denote \(\inf_{-\infty< t <\infty}g(t)\) and \(\sup_{-\infty< t<\infty}g(t)\), respectively.

The aim of this paper is to investigate the extinction property of the following two species non-autonomous competitive phytoplankton system with nonlinear inter-inhibition terms and one toxin producing phytoplankton:

$$ \begin{aligned} &\dot{x}_{1}(t) = x_{1}(t) \biggl[r_{1}(t)-a_{1}(t)x_{1}(t) - \frac{b_{1}(t)x_{2}(t)}{1+x_{2}(t)}-c_{1}(t)x_{1}(t)x_{2}(t) \biggr], \\ &\dot{x}_{2}(t) = x_{2}(t) \biggl[r_{2}(t)- \frac{b_{2}(t)x_{1}(t)}{1+x_{1}(t)} -a_{2}(t)x_{2}(t) \biggr], \end{aligned} $$
(1.1)

where \(r_{i}(t)\), \(a_{i}(t)\), \(b_{i}(t)\), \(i=1, 2\), \(c_{1}(t)\) are assumed to be continuous and bounded above and below by positive constants, and \(x_{1}(t)\), \(x_{2}(t)\) are population density of species \(x_{1}\) and \(x_{2}\) at time t, respectively. \(r_{i}(t)\), \(i=1,2\) are the intrinsic growth rates of species; \(a_{i}\) (\(i = 1,2\)) are the rates of intraspecific competition of the first and second species, respectively; \(b_{i}\) (\(i = 1,2\)) are the rates of interspecific competition of the first and second species, respectively. The second species could produce a toxic, while the first one has a non-toxic product.

The traditional two species Lotka-Volterra competition model takes the form:

$$ \begin{aligned} &\dot{x}_{1}(t)=x_{1}(t) \bigl[r_{1}-a_{1}x_{1}(t)-a_{2}x_{2}(t) \bigr], \\ &\dot{x}_{2}(t)=x_{2}(t) \bigl[r_{2}-b_{1}x_{2}(t)-b_{2}x_{2}(t) \bigr]. \end{aligned} $$
(1.2)

Chattopadhyay [2] studied a two species competition model, each species produces a substance toxic to the other only when the other is present. The model takes the form

$$ \begin{aligned} &\dot{x}_{1}(t)=x_{1}(t) \bigl[r_{1}-a_{1}x_{1}(t)-a_{2}x_{2}(t)-d_{1}x_{1}(t)x_{2}(t) \bigr], \\ &\dot{x}_{2}(t)=x_{2}(t) \bigl[r_{2}-b_{1}x_{2}(t)-b_{2}x_{2}(t)-d_{2}x_{1}(t)x_{2}(t) \bigr]. \end{aligned} $$
(1.3)

He investigated the local stability and global stability of the equilibrium. Obviously, system (1.3) is more realistic than that of (1.2). After the work of Chattopadhyay [2], the competitive system with toxic substance became one of the most important topic in the study of population dynamics, see [1–22] and the references cited therein. Li and Chen [4] studied the non-autonomous case of system (1.2), a set of sufficient conditions which guarantee the extinction of the second species and the globally attractive of the first species are obtained. Li and Chen [3] studied the extinction property of the following two species discrete competitive system:

$$ \begin{aligned} &x_{1}(n+1) = x_{1}(n)\exp \bigl[r_{1}(n)-a_{11}(n)x_{1}(n)-a_{12}(n)x_{2}(n) \\ &\hphantom{x_{1}(n+1) ={}}{}-b_{1}(n)x_{1}(n)x_{2}(n) \bigr], \\ &x_{2}(n+1) = x_{2}(n)\exp \bigl[r_{2}(n)-a_{21}(n)x_{1}(n)-a_{22}(n)x_{2}(n) \\ &\hphantom{x_{2}(n+1) ={}}{}-b_{2}(n)x_{1}(n)x_{2}(n) \bigr]. \end{aligned} $$
(1.4)

Recently, Solé et al. [17] and Bandyopadhyay [15] considered a Lotka-Volterra type of model for two interacting phytoplankton species, where one species could produce toxic, while the other one has a non-toxic product. The model takes the form

$$ \begin{aligned} &\dot{x}_{1}(t) = x_{1}(t) \bigl[r_{1}-a_{1}x_{1}(t)-a_{2}x_{2}(t)-d_{1}x_{1}(t)x_{2}(t) \bigr], \\ &\dot{x}_{2}(t) = x_{2}(t) \bigl[r_{2}-b_{1}x_{2}(t)-b_{2}x_{2}(t) \bigr]. \end{aligned} $$
(1.5)

Corresponding to system (1.5), Chen et al. [8] proposed the following two species discrete competition system:

$$\begin{aligned}& x_{1}(n+1) = x_{1}(n)\exp \bigl[r_{1}(n)-a_{11}(n)x_{1}(n)-a_{12}(n)x_{2}(n) \\& \hphantom{x_{1}(n+1) ={}}{}-b_{1}(n)x_{1}(n)x_{2}(n) \bigr], \\& x_{2}(n+1) = x_{2}(n)\exp \bigl[r_{2}(n)-a_{21}(n)x_{1}(n)-a_{22}(n)x_{2}(n) \bigr]. \end{aligned}$$
(1.6)

They investigated the extinction property of the system.

Some scholars argued that the more appropriate competition model should with nonlinear inter-inhibition terms. Indeed, Wang et al. [23] proposed the following two species competition model:

$$ \begin{aligned} &\dot{x}_{1}(t) = x_{1}(t) \biggl[r_{1}(t)-a_{1}(t)x_{1}(t) - \frac{b_{1}(t)x_{2}(t)}{1+x_{2}(t)} \biggr], \\ &\dot{x}_{2}(t) = x_{2}(t) \biggl[r_{2}(t)- \frac{b_{2}(t)x_{1}(t)}{1+x_{1}(t)} -a_{2}(t)x_{2}(t) \biggr]. \end{aligned} $$
(1.7)

By using a differential inequality, the module containment theorem, and the Lyapunov function, the authors obtained sufficient conditions which ensure the existence and global asymptotic stability of positive almost periodic solutions.

Again, corresponding to system (1.7), several scholars [24, 25] investigated the dynamic behaviors of the discrete type two species competition system with nonlinear inter-inhibition terms,

$$ \begin{aligned} &x_{1}(k+1) = x_{1}(k)\exp \biggl\{ r_{1}(k)-a_{1}(k)x_{1}(k) -\frac{b_{1}(k)x_{2}(k)}{1+x_{2}(k)} \biggr\} , \\ &{x}_{2}(k+1) = x_{2}(k)\exp \biggl\{ r_{2}(k)- \frac {b_{2}(k)x_{1}(k)}{1+x_{1}(k)} -a_{2}(k)x_{2}(k) \biggr\} . \end{aligned} $$
(1.8)

Wang and Liu [24] studied the almost periodic solution of the system (1.8). Yu [25] further incorporated the feedback control variables to the system (1.8) and investigated the persistent property of the system.

During the lase decade, many scholars [3–5, 8, 12–14, 26–33] investigated the extinction property of the competition system. Maybe stimulating by this fact, Yue [1] proposed the following two species discrete competitive phytoplankton system with nonlinear inter-inhibition terms and one toxin producing phytoplankton:

$$\begin{aligned}& x_{1}(k+1) = x_{1}(k)\exp \biggl\{ r_{1}(k)-a_{1}(k)x_{1}(k) -\frac{b_{1}(k)x_{2}(k)}{1+x_{2}(k)} \\& \hphantom{x_{1}(k+1) ={}}{}-c_{1}(k)x_{1}(k)x_{2}(k) \biggr\} , \\& {x}_{2}(k+1) = x_{2}(k)\exp \biggl\{ r_{2}(k)- \frac {b_{2}(k)x_{1}(k)}{1+x_{1}(k)} -a_{2}(k)x_{2}(k) \biggr\} . \end{aligned}$$
(1.9)

By further developing the analysis technique of Chen et al. [8], the author obtained some sufficient conditions which guarantee the extinction of one of the components and the global attractivity of the other one.

It is well known that if the amount of the species is large enough, the continuous model is more appropriate, and this motivated us to propose the system (1.1). The aim of this paper is, by developing the analysis technique of [1, 8, 9], to investigate the extinction property of the system (1.1). The remaining part of this paper is organized as follows. In Section 2, we study the extinction of some species and the stability property of the rest of the species. Some examples together with their numerical simulations are presented in Section 3 to show the feasibility of our results. We give a brief discussion in the last section.

2 Main results

Following Lemma 2.1 is a direct corollary of Lemma 2.2 of Chen [10].

Lemma 2.1

If \(a>0\), \(b>0\), and \(\dot{x}\geq x(b-ax)\), when \(t\geq{0}\) and \(x(0)>0\), we have

$$\liminf_{t\rightarrow+\infty} x(t)\geq\frac{b}{a}. $$

If \(a>0\), \(b>0\), and \(\dot{x}\leq x(b-ax)\), when \(t\geq{0}\) and \(x(0)>0\), we have

$$\limsup_{t\rightarrow+\infty} x(t)\leq \frac{b}{a}. $$

Lemma 2.2

Let \(x(t)=(x_{1}(t),x_{2}(t))^{T}\) be any solution of system (1.1) with \(x_{i}(t_{0})>0\), \(i=1,2\), then \(x_{i}(t)>0\), \(t\geq t_{0}\) and there exists a positive constant \(M_{0}\) such that

$$\limsup_{t\rightarrow+\infty} x_{i}(t)\leq M_{0},\quad i=1,2, $$

i.e., any positive solution of system (1.1) are ultimately bounded above by some positive constant.

Proof

Let \(x(t)=(x_{1}(t),x_{2}(t))^{T}\) be any solution of system (1.1) with \(x_{i}(t_{0})>0\), \(i=1,2\), then

$$\begin{aligned}& x_{1}(t) = x_{1}(t_{0})\exp \biggl\{ \int_{t_{0}}^{t} \biggl(r_{1}(s)-a_{1}(s)x_{1}(s) -\frac{b_{1}(s)x_{2}(s)}{1+x_{2}(s)} \\& \hphantom{x_{1}(t) = {}}{}-c_{1}(s)x_{1}(s)x_{2}(s) \biggr)\,ds \biggr\} >0, \\& x_{2}(t) = x_{2}(t_{0})\exp \biggl\{ \int_{t_{0}}^{t} \biggl(r_{2}(s)- \frac {b_{2}(s)x_{1}(s)}{1+x_{1}(s)} -a_{2}(s)x_{2}(s) \biggr)\,ds \biggr\} >0. \end{aligned}$$
(2.1)

From the first equation of system (1.1), we have

$$ \dot{x}_{1}(t) \leq x_{1}(t)\bigl[r_{1}(t)-a_{1}(t)x_{1}(t) \bigr]\leq x_{1}(t)\bigl[r_{1M}-a_{1L}x_{1}(t) \bigr] . $$
(2.2)

By applying Lemma 2.1 to differential inequality (2.2), it follows that

$$ \limsup_{t\rightarrow+\infty}x_{1}(t)\leq \frac{{r}_{1M}}{a_{1L}} \stackrel{\mathrm{def}}{=}M_{1}. $$
(2.3)

Similarly to the analysis of (2.2) and (2.3), from the second equation of system (1.1), we have

$$ \limsup_{t\rightarrow+\infty}x_{2}(t)\leq \frac{{r}_{2M}}{a_{2L}} \stackrel{\mathrm{def}}{=}M_{2}. $$
(2.4)

Set \(M_{0}=\max\{M_{1}, M_{2}\}\), then the conclusion of Lemma 2.2 follows. This ends the proof of Lemma 2.2. □

Lemma 2.3

(Fluctuation lemma [34])

Let \(x(t)\) be a bounded differentiable function on \((\alpha,\infty)\), then there exist sequences \(\tau_{n}\rightarrow\infty\), \(\sigma_{n}\rightarrow\infty\) such that

$$\begin{aligned} (\mathrm{a})&\quad \dot{x}(\tau_{n})\rightarrow0 \quad \textit{and} \quad x(\tau_{n})\rightarrow\limsup_{t\rightarrow\infty}x(t)= \overline {x} \quad \textit{as } n\rightarrow\infty, \\ (\mathrm{b})&\quad \dot{x}(\sigma_{n})\rightarrow0 \quad \textit{and} \quad x(\sigma_{n})\rightarrow\liminf_{t\rightarrow\infty}x(t)= \underline {x}\quad \textit{as }n\rightarrow\infty. \end{aligned}$$

For the logistic equation

$$ \dot{x}_{1}(t)=x_{1}(t) \bigl(r_{1}(t)-a_{1}(t)x_{1}(t) \bigr). $$
(2.5)

From Lemma 2.1 of Zhao and Chen [35], we have the following.

Lemma 2.4

Suppose that \(r_{1}(t)\) and \(a_{1}(t)\) are continuous functions bounded above and below by positive constants, then any positive solutions of equation (2.5) are defined on \([0, +\infty)\), bounded above and below by positive constants and globally attractive.

Our main results are Theorems 2.1-2.5.

Theorem 2.1

Assume that

$$ r_{1L}\frac{b_{2L}}{1+ M_{1} }>r_{2M}a_{1M},\qquad r_{1L}a_{2L}> r_{2M}b_{1M} $$
(2.6)

hold, further assume that the inequality

$$ c_{1M} < \frac{1}{M_{1}M_{2}}\min \biggl\{ r_{1L}- \frac{a_{1M}}{\frac{b_{2L}}{1+ M_{1} }}r_{2M} , r_{1L}-\frac{b_{1M}}{a_{2L}}r_{2M} \biggr\} $$
(2.7)

holds, then the species \(x_{2}\) will be driven to extinction, that is, for any positive solution \((x_{1}(t),x_{2}(t))^{T}\) of system (1.1), \(x_{2}(t)\rightarrow0 \) as \(t\rightarrow+\infty\).

Proof

It follows from (2.7) that one could choose a small enough positive constant \(\varepsilon_{1}>0\) such that

$$ c_{1M} < \frac{1}{(M_{1}+\varepsilon_{1})(M_{2}+\varepsilon_{1})}\min \biggl\{ r_{1L}- \frac{a_{1M}}{\frac{b_{2L} }{1+ (M_{1}+\varepsilon_{1} )}}r_{2M}, r_{1L}-\frac{b_{1M}}{a_{2L}}r_{2M} \biggr\} . $$
(2.8)

Equation (2.8) is equivalent to

$$ \begin{aligned} &\frac{a_{1M}}{\frac{b_{2L} }{1+ (M_{1}+\varepsilon_{1} )}} < \frac{r_{1L}-c_{1M} (M_{1}+\varepsilon_{1} ) (M_{2}+\varepsilon_{1} )}{r_{2M}}, \\ &\frac{b_{1M}}{a_{2L}}< \frac{r_{1L}-c_{1M} (M_{1}+\varepsilon_{1} ) (M_{2}+\varepsilon_{1} )}{r_{2M}}. \end{aligned} $$
(2.9)

Therefore, there exist two constants α, β such that

$$ \begin{aligned} &\frac{a_{1M}}{\frac{b_{2L} }{1+ (M_{1}+\varepsilon_{1} )}}< \frac{\beta}{\alpha}< \frac{r_{1L}-c_{1M} (M_{1}+\varepsilon_{1} ) (M_{2}+\varepsilon_{1} )}{r_{2M}}, \\ &\frac{b_{1M}}{a_{2L}}< \frac{\beta}{\alpha}< \frac {r_{1L}-c_{1M} (M_{1}+\varepsilon_{1} ) (M_{2}+\varepsilon_{1} )}{r_{2M}}. \end{aligned} $$
(2.10)

That is,

$$ \begin{aligned} &\alpha a_{1M}- \frac{\beta b_{2L} }{1+ (M_{1}+\varepsilon_{1} )}< 0,\qquad \alpha b_{1M}-\beta a_{2L}< 0, \\ &{-}\alpha r_{1L}+\beta r_{2M}+\alpha c_{1M} (M_{1}+\varepsilon_{1} ) (M_{2}+ \varepsilon_{1} )\stackrel{\mathrm {def}}{=}-\delta_{1}< 0. \end{aligned} $$
(2.11)

Let \(x(t)=(x_{1}(t),x_{2}(t))^{T}\) be a solution of system (1.1) with \(x_{i}(0)>0\), \(i=1,2\). For the above \(\varepsilon_{1}>0\), from Lemma 2.2 there exists a large enough \(T_{1}\) such that

$$ x_{1}(t)< M_{1}+\varepsilon_{1},\qquad x_{2}(t)< M_{2}+\varepsilon_{1} \quad \mbox{for all } t\geq T_{1}. $$
(2.12)

From (1.1) we have

$$ \begin{aligned} &\frac{\dot{x}_{1}(t)}{x_{1}(t)} = r_{1}(t)-a_{1}(t)x_{1}(t) -\frac{b_{1}(t)x_{2}(t)}{1+x_{2}(t)}-c_{1}(t)x_{1}(t)x_{2}(t), \\ &\frac{\dot{x}_{2}(t)}{x_{2}(t)} = r_{2}(t)-\frac {b_{2}(t)x_{1}(t)}{1+x_{1}(t)} -a_{2}(t)x_{2}(t). \end{aligned} $$
(2.13)

Let

$$V(t)=x_{1}^{-\alpha}(t)x_{2}^{\beta}(t). $$

From (2.11), (2.12), and (2.13), for \(t\geq T_{1}\), it follows that

$$\begin{aligned} \dot{V}(t) =&V(t) \biggl[-\alpha \biggl(r_{1}(t)-a_{1}(t)x_{1}(t) -\frac{b_{1}(t)x_{2}(t)}{1+x_{2}(t)}-c_{1}(t)x_{1}(t)x_{2}(t) \biggr) \\ &{} +\beta \biggl(r_{2}(t)-\frac{b_{2}(t)x_{1}(t)}{1+x_{1}(t)} -a_{2}(t)x_{2}(t) \biggr) \biggr] \\ =&V(t) \biggl[\bigl(-\alpha r_{1}(t)+\beta r_{2}(t) \bigr)+ \biggl( \alpha a_{1}(t)- \frac{\beta b_{2}(t) }{1+x_{1}(t)} \biggr)x_{1}(t) \\ &{} + \biggl(\alpha\frac{b_{1}(t) }{1+x_{2}(t)}-\beta a_{2}(t) \biggr)x_{2}(t)+\alpha c_{1}(t)x_{1}(t)x_{2}(t) \biggr] \\ \leq&V(t) \biggl[(-\alpha r_{1L}+\beta r_{2M})+ \biggl( \alpha a_{1M}- \frac{\beta b_{2L} }{1+ (M_{1}+\varepsilon_{1} )} \biggr)x_{1}(t) \\ &{} +(\alpha b_{1M}-\beta a_{2L})x_{2}(t)+\alpha c_{1M} (M_{1}+\varepsilon_{1} ) (M_{2}+\varepsilon_{1} ) \biggr] \\ \leq& -\delta_{1} V(t), \quad t\geq T_{1}. \end{aligned}$$

Integrating this inequality from \(T_{1}\) to t (\(\geq T_{1}\)), it follows that

$$ {V}(t)\leq V(T_{1})\exp\bigl(-\delta_{1}(t-T_{1}) \bigr). $$
(2.14)

By Lemma 2.2 we know that there exists \(M>M_{0}>0\) such that

$$ x_{i}(t)< M \quad \mbox{for all } i=1,2 \mbox{ and } t\geq T_{1}. $$
(2.15)

Therefore, (2.14) implies that

$$ x_{2}(t)< C\exp \biggl(-\frac{\delta_{1}}{\beta} (t-T_{1}) \biggr), $$
(2.16)

where

$$ C=M^{\alpha/\beta}\bigl(x_{1}(T_{1})\bigr)^{-\alpha/\beta}x_{2}(T_{1})>0. $$
(2.17)

Consequently, we have \(x_{2}(t)\rightarrow0\) exponentially as \(t\rightarrow +\infty\). □

Theorem 2.2

In addition to (2.6), further assume that the inequality

$$ c_{1M} < \frac{1}{M_{2}} \biggl(\frac{r_{1L}}{r_{2M}} \biggl( \frac{ b_{2L} }{1+ M_{1} } \biggr)-a_{1M} \biggr) $$
(2.18)

holds, then the species \(x_{2}\) will be driven to extinction, that is, for any positive solution \((x_{1}(t),x_{2}(t))^{T}\) of system (1.1), \(x_{2}(t)\rightarrow0 \) as \(t\rightarrow+\infty\).

Proof

Equation (2.18) is equivalent to

$$ c_{1M}M_{2}+ a_{1M} < \frac{r_{1L}}{r_{2M}} \biggl( \frac{ b_{2L} }{1+ M_{1} } \biggr). $$
(2.19)

It follows from (2.19) that one could choose a small enough \(\varepsilon_{2}>0\) such that

$$ c_{1M} (M_{2}+\varepsilon_{2} )+a_{1M} < \frac{r_{1L}}{r_{2M}} \biggl(\frac{ b_{2L} }{1+ ( M_{1}+\varepsilon_{2} )} \biggr). $$
(2.20)

It follows from (2.20) and (2.6) that there exist two constants α, β such that

$$ \begin{aligned} &\frac{c_{1M} (M_{2}+\varepsilon_{2} )+a_{1M}}{\frac{ b_{2L} }{1+ (M_{1}+\varepsilon_{2} )}}< \frac{\beta}{\alpha}< \frac {r_{1L}}{r_{2M}}, \\ &\frac{b_{1M}}{a_{2L}}< \frac{\beta}{\alpha}< \frac {r_{1L}}{r_{2M}}. \end{aligned} $$
(2.21)

That is,

$$ \begin{aligned} &\alpha a_{1M}-\frac{\beta b_{2L} }{1+ (M_{1}+\varepsilon_{2} )}+\alpha c_{1M}(M_{2}+\varepsilon_{2})< 0, \\ &\alpha b_{1M}-\beta a_{2L}< 0, \qquad -\alpha r_{1L}+ \beta r_{2M}\stackrel{\mathrm{def}}{=}-\delta_{2}< 0. \end{aligned} $$
(2.22)

Let \(x(t)=(x_{1}(t),x_{2}(t))^{T}\) be a solution of system (1.1) with \(x_{i}(0)>0\), \(i=1,2\). For the above \(\varepsilon_{2}>0\), from Lemma 2.2 there exists a large enough \(T_{2}\) such that

$$ x_{2}(t)< M_{2}+\varepsilon_{2} \quad \mbox{for all } t\geq T_{2}. $$
(2.23)

Let

$$V(t)=x_{1}^{-\alpha}(t)x_{2}^{\beta}(t). $$

From (2.22) and (2.23), for \(t\geq T_{2}\), it follows that

$$\begin{aligned} \dot{V}(t) =&V(t) \biggl[\bigl(-\alpha r_{1}(t)+\beta r_{2}(t)\bigr)+ \biggl( \alpha a_{1}(t)- \frac{\beta b_{2}(t) }{1+x_{1}(t)} \biggr)x_{1}(t) \\ &{} + \biggl( \frac{\alpha b_{1}(t) }{1+x_{2}(t)}-\beta a_{2}(t) \biggr)x_{2}(t)+\alpha c_{1}(t)x_{1}(t)x_{2}(t) \biggr] \\ \leq&V(t) \biggl[(-\alpha r_{1L}+\beta r_{2M})+ \biggl( \alpha a_{1M} - \frac{\beta b_{2L} }{1+ (M_{1}+\varepsilon_{2} )} \\ &{}+\alpha c_{1M}(M_{2}+\varepsilon_{2}) \biggr)x_{1}(t) +(\alpha b_{1M}-\beta a_{2L})x_{2}(t) \biggr] \\ \leq& -\delta_{2} V(t), \quad t\geq T_{2}. \end{aligned}$$

Integrating this inequality from \(T_{2}\) to t (\(\geq T_{2}\)), it follows that

$$ {V}(t)\leq V(T_{2})\exp\bigl(-\delta_{2}(t-T_{2}) \bigr). $$
(2.24)

From (2.24), similarly to the analysis of (2.15)-(2.16), we can draw the conclusion that \(x_{2}(t)\rightarrow0\) exponentially as \(t\rightarrow +\infty\). □

Theorem 2.3

In addition to (2.6), further assume that the inequality

$$ c_{1M} < \frac{1}{M_{1}} \biggl(\frac{r_{1L}}{r_{2M}}a_{2L}- b_{1M} \biggr) $$
(2.25)

holds, then the species \(x_{2}\) will be driven to extinction, that is, for any positive solution \((x_{1}(t),x_{2}(t))^{T}\) of system (1.1), \(x_{2}(t)\rightarrow0 \) as \(t\rightarrow+\infty\).

Proof

Equation (2.25) is equivalent to

$$ \frac{c_{1M}M_{1}}{a_{2L}}+\frac{b_{1M}}{a_{2L}}< \frac {r_{1L}}{r_{2M}}. $$
(2.26)

It follows from (2.26) that one could choose a small enough \(\varepsilon_{3}\) such that

$$ \frac{c_{1M} (M_{1}+\varepsilon_{3} )+b_{1M}}{a_{2L}}< \frac {r_{1L}}{r_{2M}}. $$
(2.27)

It follows from (2.6) and (2.27) that there exist two constants α, β such that

$$ \begin{aligned} &\frac{c_{1M} (M_{1}+\varepsilon_{3} )+b_{1M}}{a_{2L}}< \frac {\beta}{\alpha}< \frac{r_{1L}}{r_{2M}}, \\ &\frac{a_{1M}}{\frac{ b_{2L}}{1+M_{1}}}< \frac{\beta }{\alpha}< \frac{r_{1L}}{r_{2M}}. \end{aligned} $$
(2.28)

That is,

$$ \begin{aligned} &\alpha b_{1M}-\beta a_{2L}+\alpha c_{1M} (M_{1}+\varepsilon_{3} )< 0, \\ &\alpha a_{1M}-\frac{\beta b_{2L}}{1+M_{1}+\varepsilon_{3}}< 0, \qquad -\alpha r_{1L}+\beta r_{2M}\stackrel{\mathrm{def}}{=}-\delta_{3}< 0. \end{aligned} $$
(2.29)

Let \(x(t)=(x_{1}(t),x_{2}(t))^{T}\) be a solution of system (1.1) with \(x_{i}(0)>0\), \(i=1,2\). For the above \(\varepsilon_{3}>0\), from Lemma 2.2 there exists a large enough \(T_{3}\) such that

$$ x_{1}(t)< M_{1}+\varepsilon_{3} \quad \mbox{for all } t\geq T_{3}. $$
(2.30)

Let

$$V(t)=x_{1}^{-\alpha}(t)x_{2}^{\beta}(t). $$

From (2.29) and (2.30), for \(t\geq T_{3}\), it follows that

$$\begin{aligned} \dot{V}(t) =&V(t) \biggl[\bigl(-\alpha r_{1}(t)+\beta r_{2}(t)\bigr)+ \biggl( \alpha a_{1}(t)- \frac{\beta b_{2}(t) }{1+x_{1}(t)} \biggr)x_{1}(t) \\ &{} + \biggl( \frac{\alpha b_{1}(t) }{1+x_{2}(t)}-\beta a_{2}(t) \biggr)x_{2}(t)+\alpha c_{1}(t)x_{1}(t)x_{2}(t) \biggr] \\ \leq&V(t) \biggl[(-\alpha r_{1L}+\beta r_{2M})+ \biggl( \alpha a_{1M}- \frac{\beta b_{2L}}{1+(M_{1}+\varepsilon_{3})} \biggr)x_{1}(t) \\ &{} + \bigl(\alpha b_{1M}-\beta a_{2L}+\alpha c_{1M}(M_{1}+\varepsilon_{3}) \bigr)x_{2}(t) \biggr] \\ \leq& -\delta_{3} V(t), \quad t\geq T_{3}. \end{aligned}$$

Integrating this inequality from \(T_{3}\) to t (\(\geq T_{3}\)), it follows that

$$ {V}(t)\leq V(T_{3})\exp\bigl(-\delta_{3}(t-T_{3}) \bigr). $$
(2.31)

From (2.31), similarly to the analysis of (2.15)-(2.16), we can draw the conclusion that \(x_{2}(t)\rightarrow0\) exponentially as \(t\rightarrow +\infty\). □

Lemma 2.5

Under the assumption of Theorem  2.1 or 2.2 or 2.3, let \(x(t)=(x_{1}(t),x_{2}(t))^{T}\) be any positive solution of system (1.1), then there exists a positive constant \(m_{0}\) such that

$$\liminf_{t\rightarrow+\infty} x_{1}(t)\geq m_{0}, $$

where \(m_{0}\) is a constant independent of any positive solution of system (1.1), i.e., the first species \(x_{1}(t)\) of system (1.1) is permanent.

Proof

The proof of Lemma 2.5 is similar to that of Lemma 3.5 in [4], we omit the details here. □

Theorem 2.4

Assume that the conditions of Theorem  2.1 or 2.2 or 2.3 hold, let \(x(t)=(x_{1}(t),x_{2}(t))^{T}\) be any positive solution of system (1.1), then the species \(x_{2}\) will be driven to extinction, that is, \(x_{2}(t)\rightarrow0 \) as \(t\rightarrow +\infty\), and \(x_{1}(t)\rightarrow x_{1}^{*}(t)\) as \(t\rightarrow+\infty\), where \(x_{1}^{*}(t)\) is any positive solution of system (2.5).

Proof

By applying Lemmas 2.3 and 2.4, the proof of Theorem 2.4 is similar to that of the proof of Theorem in [4]. We omit the details here. □

Another interesting thing is to investigate the extinction property of species \(x_{1}\) in system (1.1). For this case, we have the following.

Theorem 2.5

Assume that

$$ r_{1M}b_{2M}< r_{2L}a_{1L},\qquad r_{1M}a_{2M}< r_{2L} \frac{ b_{1L}}{1+M_{2} } $$
(2.32)

hold, then the species \(x_{1}\) will be driven to extinction, that is, for any positive solution \((x_{1}(t),x_{2}(t))^{T}\) of system (1.1), \(x_{1}(t)\rightarrow0 \) as \(t\rightarrow+\infty\) and \(x_{2}(t)\rightarrow x_{2}^{*}(t)\) as \(t\rightarrow+\infty\), where \(x_{2}^{*}(t)\) is any positive solution of system \(\dot{x}_{2}(t)=x_{2}(t)(r_{2}(t)-b_{2}(t)x_{2}(t))\).

Proof

Condition (2.32) implies that there exist two constants α, β, and a small enough positive constant \(\varepsilon_{4}\), such that

$$ \begin{aligned} &\frac{r_{1M}}{r_{2L}}< \frac{\beta}{\alpha}< \frac{ \frac{ b_{1L}}{1+M_{2}+\varepsilon_{4}}}{a_{2M}}, \\ &\frac{r_{1M}}{r_{2L}}< \frac{\beta}{\alpha}< \frac {a_{1L}}{b_{2M}}. \end{aligned} $$
(2.33)

That is,

$$ \begin{aligned} &\beta b_{2M}-\alpha a_{1L}< 0,\qquad \beta a_{2M} -\frac{\alpha b_{1L}}{1+M_{2}+\varepsilon_{4}}< 0, \\ &\alpha r_{1M}-\beta r_{2L}\stackrel{\mathrm{def}}{=}- \delta_{4}< 0. \end{aligned} $$
(2.34)

For the above \(\varepsilon_{4}>0\), from Lemma 2.2 there exists a large enough \(T_{1}\) such that

$$ x_{2}(t)< M_{2}+\varepsilon_{4}\quad \mbox{for all } t\geq T_{4}. $$
(2.35)

Let

$$V_{1}(t)=x_{1}^{\alpha}(t)x_{2}^{-\beta}(t). $$

It follows from (2.34) that

$$\begin{aligned} \dot{V}_{1}(t) =&V_{1}(t) \biggl[ \alpha \biggl(r_{1}(t)-a_{1}(t)x_{1}(t) - \frac{b_{1}(t)x_{2}(t)}{1+x_{2}(t)}-c_{1}(t)x_{1}(t)x_{2}(t) \biggr) \\ &{} -\beta \biggl(r_{2}(t)-\frac{b_{2}(t)x_{1}(t)}{1+x_{1}(t)} -a_{2}(t)x_{2}(t) \biggr) \biggr] \\ =&V_{1}(t) \biggl[\bigl(\alpha r_{1}(t)-\beta r_{2}(t)\bigr)+ \biggl( -\alpha a_{1}(t)+\frac{\beta b_{2}(t)}{1+x_{1}(t)} \biggr)x_{1}(t) \\ &{} + \biggl(-\frac{\alpha b_{1}(t)}{1+x_{2}(t)}+\beta a_{2}(t) \biggr)x_{2}(t)-\alpha c_{1}(t)x_{1}(t)x_{2}(t) \biggr] \\ \leq&V_{1}(t) \biggl[(\alpha r_{1M}-\beta r_{2L}) + (- \alpha a_{1L}+\beta b_{2M} )x_{1}(t) \\ &{}+ \biggl(-\frac{\alpha b_{1L}}{1+M_{2}+\varepsilon_{4}}+\beta a_{2M} \biggr)x_{2}(t) \biggr] \\ \leq& -\delta_{4} V_{1}(t). \end{aligned}$$

Integrating this inequality from \(T_{4}\) to t (\(\geq T_{4}\)), it follows that

$$ {V}_{1}(t)\leq V_{1}(T_{4})\exp \bigl(- \delta_{4}(t-T_{4}) \bigr). $$
(2.36)

From this, similarly to the analysis of (2.15)-(2.16), we have \(x_{1}(t)\rightarrow0\) exponentially as \(t\rightarrow+\infty\). The rest of the proof of Theorem 2.5 is similar to that of the proof of Theorem in [4]. We omit the details here. □

3 Numeric example

Now let us consider the following example.

Example 1

$$ \begin{aligned} &\dot{x}(t) = x \biggl(10 - \bigl(1.5+0.5\sin(10t) \bigr)x-\frac{ 0.5y}{y+1}-0.2xy \biggr), \\ &\dot{y}(t) = y \biggl(2- \frac{11 x}{1+x}-2y \biggr). \end{aligned} $$
(3.1)

Corresponding to system (1.1), one has

$$\begin{aligned}& r_{1}(t)=10,\qquad a_{1}(t)=1.5+0.5\sin(10t), \\& b_{1}(t)=0.5,\qquad c_{1}(t)=0.2, \\& r_{2}(t)=2, \qquad a_{2}(t)=2, \qquad b_{2}(t)=11. \end{aligned}$$

And so,

$$ M_{1}=\frac{r_{1M}}{a_{1L}}=10,\qquad M_{2}= \frac {r_{2M}}{a_{2L}}=1, $$
(3.2)

consequently

$$ \begin{aligned} &r_{1L}\frac{b_{2L}}{1+ M_{1} }=10\times \frac {11}{1+10}=10>2\times2=r_{2M}a_{1M}, \\ & r_{1L}a_{2L}=10\times2>2\times0.5= r_{2M}b_{1M} \end{aligned} $$
(3.3)

hold. Also,

$$ \begin{aligned} &r_{1L}-\frac{a_{1M}}{\frac{b_{2L}}{1+ M_{1} }}r_{2M}=10-4=6, \\ &r_{1L}-\frac{b_{1M}}{a_{2L}}r_{2M} =9.5, \end{aligned} $$
(3.4)

and so

$$\begin{aligned} c_{1M} =&0.2 < \frac{1}{10}\min\{6, 9.5\} \\ =&\frac{1}{M_{1}M_{2}}\min \biggl\{ r_{1L}-\frac{a_{1M}}{\frac{b_{2L}}{1+ M_{1} }}r_{2M} , r_{1L}-\frac{b_{1M}}{a_{2L}}r_{2M} \biggr\} . \end{aligned}$$
(3.5)

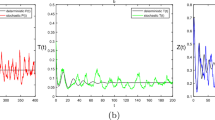
It follows from Theorem 2.1 that the first species of the system (3.1) is globally attractive, and the second species will be driven to extinction; numeric simulations (Figures 1 and 2) also support these finds.

Figure 1
figure 1

Dynamic behavior of the first component \(\pmb{x(t)}\) of the solution \(\pmb{(x(t),y(t))}\) of system ( 3.1 ) with the initial condition \(\pmb{(x(0), y(0))=(1,1), (2, 2), (3,3), (4,4), (5,5), (10,4), \mbox{and }(16, 3)}\) , respectively.

Full size image
Figure 2
figure 2

Dynamic behavior of the second component \(\pmb{y(t)}\) of the solution \(\pmb{(x(t),y(t))}\) of system ( 3.1 ) with the initial condition \(\pmb{(x(0), y(0))=(1,1), (2, 2), (3,3), (4,4), (5,5), (10,4), \mbox{and }(16, 3)}\) , respectively.

Full size image

4 Conclusion

Stimulated by the work of Yue [1], in this paper, a two species non-autonomous competitive system with nonlinear inter-inhibition terms and one toxin producing phytoplankton is proposed and studied. Series conditions which ensure the extinction of one species and the global attractivity of the other species are established.

We mention here that in system (1.1), we did not consider the influence of delay, we leave this for future investigation.