Abstract
In this paper, we propose a multi-nutrient and single microorganism chemostat model with stochastic effect and impulsive toxicant input. Firstly, for the system neglecting stochastic effect, we investigate the global dynamics including the existence and global asymptotic stability of ‘microorganism-extinction’ periodic solution, as well as the permanence of the system. Then, for the stochastic differential system with impulsive effect, we discuss the persistence and extinction of microorganisms with stochastic effect in a polluted environment. Our results indicate that the stochastic disturbance can lead to microbial extinction. Moreover, the concentration of toxicant will also affect the survival of microorganisms. Finally, numerical simulations are carried out to illustrate our theoretical results.
Similar content being viewed by others
1 Introduction
The microorganism is a very large population in the biosphere. Due to the fact that the interaction of the populations in the ecosystem is very complex and lacks strict control, it is not possible to directly investigate the interrelationships among the various groups. The chemostat is a laboratory apparatus used for the continuous culture of microorganism, and it plays an important role in exploring the growth of microorganism in a deterministic environment [1–9]. By controlling the input and output rate of the chemostat, we can investigate the interaction between microorganisms and the dynamic behavior of microbial growth in nutrition conditions. Moreover, the chemostat can be used to simulate the growth of single-cell algal phytoplankton in lakes and oceans, which is also a common model of waste-treatment and fermentation process [10, 11]. Hence, the analysis of a chemostat model is of vital importance for understanding the evolution of natural ecosystem. The model was initially proposed by Monod [12, 13] in the 1940s, then further developed by Novick and Szilard [14] in 1950 and Herbert et al. [15] in 1956.
Modeling and analyzing chemostat systems remain active in recent years. For example, Hsu et al. [16], Wolkowicz and Lu [17] and Ellermeyer [18] studied the chemostat models in which two microorganisms feed on a single nutrient. However, some experiments show that the growth of a microorganism depends on a variety of nutrition factors such as carbon, nitrogen, energy, growth factors, inorganic salts, and water [19]. Recently, the growth of microorganism species in the chemostat on continuous multi-nutrient has been investigated by many researchers [20–23]. While the species in nature are subject to short-term interference (for example, seasonal harvest, natural enemies, spraying pesticides, etc.), this short-term interference phenomenon can be described as a pulse mathematically [24–34]. Hence the chemostat models with impulsive effect have attracted wide attention [35–38].
It is generally known that species habitat is often affected by the pollutants or toxins, thus studying the effect of toxins on the species is very important. In 1983, Hallam et al. [39, 40] first studied the effects of toxic substances on the growth of a single population by means of dynamic methods, creating a new field for the study of the population pollution model. Afterwards, Ma et al. [41] considered the persistence and extinction of a population in a polluted environment. Liu et al. [42] studied the effects of impulsive toxicant input on a population in a polluted environment. In 1994, Fergola et al. [43] first introduced toxic substances into the model of the chemostat. Ma et al. [44] explored the effects of toxicants on a chemostat model with time variable nutrient input and washout. Jiao et al. [45] and Zhao et al. [46] investigated the effects of pulsed toxic substances on a microorganism. In [47], Meng et al. proposed a chemostat model with saturated growth rate and pulsed toxicant input.
Based on the above-mentioned literature, we propose a deterministic chemostat model of multi-nutrient and single microorganism with saturated growth rate and pulsed toxicant input in a polluted environment as follows:
where \(S_{1}(t) \) and \(S_{2}(t) \) denote the concentrations of a nutrient at time t, \(x(t) \) denotes the concentration of the microorganism at time t, \(P_{0}(t) \) and \(P_{e}(t) \) represent the concentration of the toxicant in the organism and in the environment at time t, respectively. \(S_{10} \) and \(S_{20} \) are positive constants and denote the concentrations of the growth-limiting nutrient, Q refers to the dilution rate. \(\mu_{1} \) and \(\mu_{2} \) are the maximum specific growth rates of the microorganism under two nutrients. \(\delta_{1} \) and \(\delta_{2} \) represent the yield of the microorganism \(x(t) \) per unit mass of substrate in two nutrients. \(a_{1} \) and \(a_{2} \) are the so-called half-saturation constants. \(r>0 \) is the rate of decrease of the intrinsic growth rate. \(kP_{e}(t) \) is the uptake of the toxicant of organism’s net from the environment at time t, \(gP_{0}(t)\) and \(mP_{0}(t)\) represent the elimination and depuration rates of a toxicant in the organism at time t, respectively. \(hP_{e}(t) \) represents the totality of losses from the system to environment at time t. u is the amount of pulsed input concentration of the toxicant at each T, and all the coefficients are positive. The functions \(\frac{\mu_{1}S _{1}(t)x(t)}{a_{1}+x(t)} \) and \(\frac{\mu_{2}S_{2}(t)x(t)}{a_{2}+x(t)} \) represent saturated growth rate of the microorganism population under two nutrients.
It is well known that in reality the natural growth of many populations is inevitably affected by random disturbances [48–54]. Many population models with random interference have been investigated [55–60]. Recently, Zhao et al. [61] and Xu et al. [62] considered the break-even concentration in a single-species stochastic chemostat model. Sun et al. [63] investigated the dynamical behavior of a stochastic two-species Monod competition chemostat model. Wang and Jiang [64] studied the stationary distribution of the stochastic chemostat model with general response functions. In [65], Xu et al. investigated a stochastic model of turbidostat in which two microorganism species compete for an inhibitory growth-limiting nutrient. Based on the stochastic sensitivity function technique, they constructed the confidence ellipse and then estimated the critical value of the intensity for noise generating a transition from coexistence to extinction. Zhang et al. [66] and Chen et al. [67, 68] studied the dynamical behaviors of stochastic models for continuous flow bioreactors. In [69], Yu et al. studied a nutrient-phytoplankton model with toxin-producing and environmental fluctuations, in which the noise interference is proportional to the variable of the system. However, in many cases, environmental noise may only affect some of the parameters of the model. The literature [70] has only considered the influence of environmental noise on the dilution rate. In this article, we consider that the growth rates of the microorganism are affected by a white noise, i.e., \(\frac{\mu_{i}S_{i}(t)x(t)}{a_{i}+x(t)} \rightarrow \frac{\mu _{i}S_{i}(t)x(t)}{a_{i}+x(t)}+ \frac{\sigma_{i}S_{i}(t)x(t)}{a_{i}+x(t)}\dot{B}_{i}(t)\) (\(i=1,2\)), where \(B(t)=(B_{1}(t),B_{2}(t)) \) is a standard Brownian motion with intensity \(\sigma^{2}_{i} \) and \(\sigma_{i}>0\) (\(i=1,2\)) is the environmental noise disturbance coefficient. Hence, the stochastic model is described by
The rest of this paper is organized as follows. Preliminaries are provided in Sect. 2. In Sect. 3, we show the existence of a unique globally asymptotically stable ‘microorganism-extinction’ periodic solution, and establish the conditions for the extinction and permanence of the microorganisms of the deterministic chemostat model (1). In Sect. 4, we investigate the impulsive stochastic chemostat model (2) and try to give criteria which can determine the extinction and persistence in mean of the microorganism. In the final section, numerical simulations are introduced to support the obtained outcomes.
2 Preliminaries
In this section, we introduce some notations, definitions, and some lemmas which are used to analyze our results.
Throughout this paper, we assume that \(S_{1}(t) \), \(S_{2}(t) \), \(x(t) \), and \(P_{0}(t) \) are continuous at \(t=nT \), and \(P_{e}(t) \) is left continuous at \(t=nT \) and \(P_{e}(nT^{+})= \lim_{t\rightarrow nT^{+}}P_{e}(t) \), and let \((\Omega ,\mathcal{F}, \{\mathcal{F}\}_{t\geq 0},\mathcal{P}) \) be a complete probability space with a filtration \(\{\mathcal{F}\}_{t\geq 0} \) satisfying the usual conditions (i.e., it is increasing and right continuous while \(\mathcal{F}_{0} \) contains all \(\mathcal{P} \)-null sets). Also, let \(R^{5}_{+}=\{z=(z_{1},z_{2},z_{3},z_{4},z_{5})\in R^{5}|z_{i}>0,i=1,2,3,4,5 \} \). For an integrable function f on \([0,+\infty ) \), define \(\langle f(t)\rangle = \frac{1}{t} \int^{t}_{0}f(\theta )\,\mathrm {d}\theta \).
Definition 2.1
-
(i)
The microorganism \(x(t) \) is said to be extinct if \(\lim_{t\rightarrow +\infty } x(t) =0 \).
-
(ii)
The microorganism \(x(t) \) is said to be permanent in mean if there exists a positive constant λ such that \(\liminf_{t\rightarrow +\infty } \langle x(t) \rangle \geq \lambda \).
Consider the following subsystem of system (1) and (2):
Lemma 2.1
([47])
System (3) has a unique positive T-periodic solution \((P^{*}_{0}(t),P^{*}_{e}(t))^{T} \), and for each solution \((P_{0}(t),P_{e}(t))^{T} \) of (3), \(P_{0}(t) \rightarrow P^{*}_{0}(t) \), \(P_{e}(t) \rightarrow P^{*}_{e}(t) \) as \(t \rightarrow +\infty \). Moreover, \(P_{0}(t) > P^{*}_{0}(t) \), \(P_{e}(t) > P^{*}_{e}(t) \) for all \(t\geq 0 \) if \(P_{0}(0) > P^{*} _{0}(0) \), \(P_{e}(0) > P^{*}_{e}(0) \), where
for \(t \in (nT,(n+1)T] \) and \(n \in Z^{+} \).
Lemma 2.2
For any positive solution \((S_{1}(t),S_{2}(t),x(t),P_{0}(t),P_{e}(t)) \) of system (1) or (2) with the initial value \((S_{1}(0),S_{2}(0),x(0),P_{0}(0),P_{e}(0^{+})) \in R^{5}_{+}\), we have
Proof
From the first and second equations of system (1) or (2), we have \(\limsup_{t\rightarrow +\infty } S_{1}(t) \leq S_{10}\), \(\limsup_{t\rightarrow +\infty } S_{2}(t) \leq S_{20} \). And, by the first three equations, one can get
This implies that \(\lim_{t\rightarrow +\infty }( \delta_{1}S_{1}(t) + \delta_{2}S_{2}(t) + x(t)) \leq \delta_{1}S_{10} + \delta_{2}S_{20} \), then \({\limsup_{t\to +\infty }} x(t) \leq \delta_{1}S_{10}+\delta_{2}S _{20}\). By Lemma 2.1, we have
This completes the proof of Lemma 2.2. □
Lemma 2.3
(cf. [71])
Suppose that \(Y(t) \in C [ \Omega \times [0,+\infty ), R_{+} = (0,+\infty )] \).
-
(1)
If there are two positive constants T and \(\lambda_{0}\) such that
$$ \log Y(t) \leq \lambda t - \lambda_{0} \int^{t}_{0} Y(s) \,\mathrm {d}s + \sum ^{m}_{j=1}\sigma_{j}B_{j}(t) $$holds for any \(t \geq T\) and constants \(\sigma_{j}\), \(j=1,2,\ldots,m\), then
$$ \textstyle\begin{cases} \limsup_{t\to +\infty } \frac{1}{t}\int^{t}_{0}Y(s)\,\mathrm {d}s \leq \lambda /\lambda_{0} \quad \textit{a.s., if }\lambda > 0, \\ \lim_{t\to +\infty } Y(t) = 0 \quad \textit{a.s., if }\lambda < 0. \end{cases} $$ -
(2)
If there are three positive constants T, λ, and \(\lambda_{0}\) such that
$$ \log Y(t) \geq \lambda t - \lambda_{0} \int^{t}_{0} Y(s) \,\mathrm {d}s + \sum ^{m}_{j=1}\sigma_{j}B_{j}(t) $$holds for all \(t \geq T\), then
$$ {\liminf_{t\to +\infty }} \frac{1}{t} \int^{t}_{0}Y(s)\,\mathrm {d}s \geq \lambda / \lambda_{0}\quad \textit{a.s.} $$
3 Dynamics of deterministic system (1)
In this section, we devote our attention to the investigation of the dynamics behavior of the deterministic model (1), to see whether the microorganism can survive. We will discuss the property of extinction and persistence.
Let
where \(a=\max \{a_{1},a_{2}\}\), \(\beta = \min \{\frac{\mu_{1}}{\delta _{1}},\frac{\mu_{2}}{\delta_{2}} \}\).
We can prove the following theorem.
Theorem 3.1
For system (1), if \(\mathcal{R}_{1} < 1 \), then the microorganism goes extinct and system (1) has a unique globally asymptotically stable ‘microorganism-extinction’ periodic solution \(( S_{10},S_{20},0,P^{*}_{0}(t),P^{*}_{e}(t) ) \).
Proof
According to Lemma 2.1, we can see that system (1) has a unique ‘microorganism-extinction’ periodic solution \(( S_{10},S _{20},0,P^{*}_{0}(t),P^{*}_{e}(t) ) \). The stability of the periodic solution \(( S_{10},S_{20},0,P^{*}_{0}(t),P^{*}_{e}(t) ) \) is determined by the eigenvalues of
which are
Then, according to Floquet theory, \(( S_{10},S_{20},0,P^{*}_{0}(t),P ^{*}_{e}(t) ) \) is locally stable if \(\lambda_{3} < 1 \), i.e., \(\mathcal{R}_{1} < 1\).
Next, we will prove the global attraction of the ‘microorganism-extinction’ periodic solution \(( S_{10},S_{20},0,P ^{*}_{0}(t),P^{*}_{e}(t) ) \) of model (1). Since the condition \(\mathcal{R}_{1} < 1 \) is satisfied, we can choose \(\varepsilon > 0 \) sufficiently small such that
In view of Lemma 2.1, we have \(\lim_{t\rightarrow +\infty } P_{0}(t) = P^{*}_{0}(t) \); therefore, there exists \(t_{1} > 0 \) such that \(P^{*}_{0}(t) - \varepsilon < P_{0}(t) < P^{*}_{0}(t) + \varepsilon \) for all \(t > t_{1} \). By the third equation of system (1) and Lemma 2.2, when \(t > t_{1} \), we have
Now we consider the comparison system
Integrating from nT to \((n+1)T \) on both sides of the first equation of (6) yields
which implies that \(y(nT) = y(0)e^{n\int^{T}_{0} (\frac{\mu_{1}S _{10}}{a_{1}} + \frac{\mu_{2}S_{20}}{a_{2}} - Q - r(P^{*}_{0}(t) - \varepsilon ) )\,\mathrm {d}t}\). By inequality (5), we get \(\lim_{n\rightarrow +\infty } y(nT) = 0\). On the other hand, from the first equations of (6), it follows
Since \(e^{\int^{t}_{nT} (\frac{\mu_{1}S_{10}}{a_{1}} + \frac{\mu _{2}S_{20}}{a_{2}} - Q - r(P^{*}_{0}(t) - \varepsilon ) ) \,\mathrm {d}t} \) is bounded on \((nT,(n+1)T] \), we obtain that \(\lim_{t\rightarrow +\infty } y(t) = 0\). Let \(( S_{1}(t), S_{2}(t), x(t), P_{0}(t), P_{e}(t)) \) be the solution of system (1) with initial conditions. By the comparison theorem, we have \({\limsup_{t\to + \infty }}x(t) \leq {\limsup_{t\to +\infty }}y(t) = 0\). Incorporating into the positivity of \(x(t) \), we know that \(\lim_{t\rightarrow +\infty } x(t) = 0\). So, the limit system of (1) is
By Lemma 2.1, it is clear that \(\lim_{t\rightarrow +\infty } S_{1}(t) = S_{10} \), \(\lim_{t\rightarrow +\infty } S_{2}(t) = S_{20} \), \(\lim_{t\rightarrow +\infty } P_{0}(t) = P^{*}_{0}(t) \), \(\lim_{t\rightarrow +\infty } P_{e}(t) = P^{*}_{e}(t)\). This gives the conclusion. □
Theorem 3.2
If \(\mathcal{R}_{2} > 1 \), then the microorganism of system (1) is permanent.
Proof
Integrating from 0 to t and dividing by t on both sides of the first three equations of (1) yields
where \(P^{*}_{0}={\max_{0\leq t \leq T}} P^{*}_{0}(t)\). Then we get
Define \(V(t) = a\ln x(t) + x(t)\). It is obvious that \(V(t) \) is bounded. Then we have
Integrating from 0 to t and dividing by t on both sides of (10) yields
According to Lemma 2.2, we know that \(0 < S_{1}(t) \leq S _{10} \), \(0 < S_{2}(t) \leq S_{20} \) and \(0 < x(t) \leq \delta_{1}S _{10}+\delta_{2}S_{20} \), then we obtain \(\lim_{t\rightarrow +\infty } \frac{V(t)}{t} = 0 \) and \(\lim_{t\rightarrow +\infty } \epsilon (t) = 0\). Finally, taking the inferior limit of both sides of (11) leads to
The proof is completed. □
From the description above, we can see that if the concentration of a toxicant is large enough then the microorganisms will be extinct.
4 Dynamics of stochastic system (2)
4.1 Extinction
In this section, we investigate the conditions which lead to the extinction of the microorganism of system (2) under the white noise stochastic disturbance. Let
then we have the following theorem.
Theorem 4.1
Let \((S_{1}(t),S_{2}(t),x(t),P_{0}(t),P_{e}(t)) \) be the solution of system (2) with the initial value \((S_{1}(0),S_{2}(0),x(0),P _{0}(0),P_{e}(0^{+})) \in R^{5}_{+}\). Then, if one of the following holds:
-
(i)
\(\sigma_{1} < \sqrt{\frac{\mu_{1}a_{1}}{S_{10}}}\), \(\sigma_{2} > \sqrt{\frac{ \mu_{2}a_{2}}{S_{20}}}\) and \(\mathcal{R}^{*}_{1} < 1\), or
-
(ii)
\(\sigma_{1} > \sqrt{\frac{\mu_{1}a_{1}}{S_{10}}}\), \(\sigma_{2} < \sqrt{\frac{ \mu_{2}a_{2}}{S_{20}}}\) and \(\mathcal{R}^{*}_{2} < 1\), or
-
(iii)
\(\sigma_{1} > \sqrt{\frac{\mu_{1}a_{1}}{S_{10}}}\), \(\sigma_{2} > \sqrt{\frac{\mu_{2}a_{2}}{S_{20}}} \) and \(\mathcal{R}^{*}_{3} < 1\), or
-
(iv)
\(\sigma_{1} < \sqrt{\frac{\mu_{1}a_{1}}{S_{10}}}\), \(\sigma_{2} < \sqrt{\frac{ \mu_{2}a_{2}}{S_{20}}}\) and \(\mathcal{R}^{*}_{4} < 1\),
the microorganism goes to extinction almost surely, i.e., \(\lim_{t\rightarrow +\infty }x(t)=0\), a.s.
Proof
Applying Itô’s formula to system (2) yields
Integrating from 0 to t and dividing by t on both sides of (12) yields
where the function \(M_{i}(t) = \int^{t}_{0}\frac{\sigma_{i}S_{i}( \theta )}{a_{i}+x(\theta )}\,\mathrm {d}B_{i}(\theta )\) (\(i=1,2\)). By the strong law of large numbers and Lemma 2.2, we get
Then there are four cases to be discussed.
Case (i): Since \(\sigma_{1} < \sqrt{\frac{\mu_{1}a_{1}}{S_{10}}}\), \(\sigma_{2} > \sqrt{\frac{\mu_{2}a_{2}}{S_{20}}}\), then we can easily see from (13) that
Taking the superior limit on both sides of (14) yields
which implies \(\lim_{t\rightarrow +\infty }x(t) = 0\), a.s.
The same discussion can be used in Case (ii), here we omit it.
Case (iii): \(\sigma_{1} > \sqrt{\frac{\mu_{1}a_{1}}{S_{10}}}\), \(\sigma_{2} > \sqrt{\frac{\mu_{2}a_{2}}{S_{20}}}\). From (13), we have
Taking the superior limit on both sides of (15) leads to
which implies \(\lim_{t\rightarrow +\infty }x(t) = 0\), a.s.
Case (iv): \(\sigma_{1} < \sqrt{\frac{\mu_{1}a_{1}}{S_{10}}}\), \(\sigma _{2} < \sqrt{\frac{\mu_{2}a_{2}}{S_{20}}}\). In this case, we can see from (13) that
Taking the superior limit on both sides of (16) yields
which implies \(\lim_{t\rightarrow +\infty }x(t) = 0\), a.s. □
This completes the proof of Theorem 4.1.
According to the magnitude of white noise intensity \(\sigma_{i}\) (\(i = 1, 2\)), Theorem 4.1 discusses the conditions under which microorganisms are extinct under different conditions (i)–(iv). The size of \(R_{i}\) (\(i=1,\ldots,4\)) depends on both nutrient and contaminant concentrations as well as on the intensity of random disturbances. Obviously, the greater the white noise intensity is, the higher the concentration of pollutants is, the smaller \(R_{i} \) is, and the more likely the microbes become extinct.
4.2 Permanence in mean
For system (2), let
then we have the following theorem.
Theorem 4.2
If \(\overline{\mathcal{R}}>1\), then for any initial value \((S_{1}(0),S _{2}(0),x(0),P_{0}(0), P_{e}(0^{+})) \in R^{5}_{+}\), system (2) is permanent in the mean; moreover, the solution \((S_{1}(t),S_{2}(t),x(t),P_{0}(t),P_{e}(t)) \) of system (2) satisfies
Proof
Integrating from 0 to t and dividing by t on both sides of the first three equations of (2) yields
then we get
Applying Itô’s formula gives
For both sides of (20), integrating from 0 to t first and then dividing by t yields
where \(M_{i}(t) = \int^{t}_{0}\sigma_{i}S_{i}(\theta ) \,\mathrm {d}B _{i}(\theta )\) (\(i=1,2\)). Inequality (21) can be rewritten as
By the strong law of large numbers and Lemma 2.2, we have \(\lim_{t\rightarrow +\infty } \frac{M_{i}(t)}{t} = 0\) (\(i=1,2\)), \(\lim_{t\rightarrow +\infty } \frac{x(t)}{t} = 0 \) and \(\lim_{t\rightarrow +\infty } \varepsilon (t) = 0\). Using Lemma 2.3, we can get
This finishes the proof of Theorem 4.2. □
5 Conclusion and simulations
In this paper, we have investigated the dynamics of a chemostat model with multi-nutrient and single microorganism in a polluted environment. On the one hand, for the system neglecting stochastic effect, we discuss the global dynamics including the existence and global asymptotic stability of ‘microorganism-extinction’ periodic solution and the permanence in mean of the system. On the other hand, for the stochastic differential system with impulsive effect, we discuss the persistence and extinction of microorganism with stochastic effect in a polluted environment. Our results show that stochastic disturbance and toxicant will affect the survival of microorganism.
Moreover, the difference between thresholds \(\mathcal{R}^{*}_{i} \) and \(\mathcal{R}_{1}\) (\(i=1,2,3,4\)) indicates that the conditions for the microorganism to go to extinction in the stochastic system (2) are weaker than those of the corresponding deterministic model (1). At the same time, since \(\mathcal{R}^{*} _{1} < 1 < \mathcal{R}_{2}\) and \(\overline{\mathcal{R}} = \mathcal{R}_{2} - \frac{\sigma^{2}_{1}S_{10}^{2}}{2a^{2}_{1}(Q+r\overline{P _{0}})}- \frac{\sigma^{2}_{2}S_{20}^{2}}{2a^{2}_{2}(Q+r\overline{P _{0}})}\), the persistent microorganism of a deterministic system may be extinct due to the white noise disturbance.
Next, computer simulations employing Euler–Maruyama (EM) method [72, 73] are presented to support the above mentioned results, illustrating extinction and persistence of the microorganism.
In our simulations for system (1) and system (2), we set
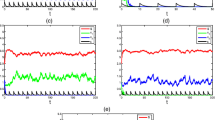
Firstly, we start with a deterministic system, direct calculation shows that \(\mathcal{R}_{2} = 1.1473 > 1\). From Theorem 3.2, the microorganism of system (1) is permanent (Fig. 1(a)). When u is increasing to \(u = 3.1 \), we have \(\mathcal{R}_{1}=0.9944 < 1\). From Theorem 3.1, the microorganism of system (1) is extinct (Fig. 1(b)). This suggests that the increase in pollutants can cause microbial extinction.
Time evolutions of the deterministic system with parameters \(S_{10}=1.5\), \(S_{20}=2\), \(Q=1.45\), \(\delta _{1}=0.9\), \(\delta _{2}=1\), \(a_{1}=1.6\), \(a_{2}=1.6\), \(\mu _{1}=0.8\), \(\mu _{2}=0.8\), \(r=0.1\), \(k=1\), \(g=0.8\), \(h=1\), \(m=0.2\), \({T=1}\). (a) Time series for \(S_{1}(t)\), \(S_{2}(t)\), \(x(t)\) with parameters \(u=0.1\), \(\mathcal{R}_{2}=1.1473\). (b) Time series for \(S_{1}(t)\), \(S_{2}(t)\), \(x(t)\) with parameters \(u=3.1\), \(\mathcal{R}_{1}=0.9944\). (c) Time series for \(P_{0}(t)\) and \(P_{e}(t)\)
Next, we consider the influence of stochastic disturbance on the above deterministic system. Let \(D =\sigma^{2}_{1} - \frac{\mu _{1}a_{1}}{S_{10}} \) and \(E = \sigma^{2}_{2} - \frac{\mu_{2}a_{2}}{S _{20}}\). We choose different parameters \(\sigma_{1} \) and \(\sigma_{2} \) as follows.
Case I. Choose \(\sigma_{1}=0.6\), \(\sigma_{2}=0.9 \), by direct calculation, we have \(D =-0.4933<0\), \(E = 0.1700>0\), \(\mathcal{R}^{*}_{1} = 0.6759 < 1\). Then, by Theorem 4.1, the microorganism eventually tends to be extinct (Fig. 2(a)).
Time evolutions of the stochastic system with parameters \(S_{10}=1.5\), \(S_{20}=2\), \(Q=1.45\), \(\delta _{1}=0.9\), \(\delta _{2}=1\), \(a_{1}=1.6\), \(a_{2}=1.6\), \(\mu _{1}=0.8\), \(\mu _{2}=0.8\), \(r=0.1\), \(k=1\), \(g=0.8\), \(h=1\), \(m=0.2\), \(u=0.1\), \({T=1}\). (a) Time series for \(S_{1}(t)\), \(S_{2}(t)\), \(x(t)\) with parameters \(\sigma_{1}=0.6\), \(\sigma_{2}=0.9\), \(\mathcal{R}^{*}_{1} = 0.6759\). (b) Time series for \(S_{1}(t)\), \(S_{2}(t)\), \(x(t)\) with parameters \(\sigma_{1}=1\), \(\sigma_{2}=0.7\), \(\mathcal{R}^{*}_{2} = 0.6419\). (c) Time series for \(S_{1}(t)\), \(S_{2}(t)\), \(x(t)\) with parameters \(\sigma_{1}=1.5\), \(\sigma_{2}=1.6\), \(\mathcal{R}^{*}_{3} = 0.1830\). (d) Time series for \(S_{1}(t)\), \(S_{2}(t)\), \(x(t)\) with parameters \(\sigma_{1}=0.5\), \(\sigma_{2}=0.5\), \(\mathcal{R}^{*}_{4} = 0.9896\)
Case II. Choose \(\sigma_{1}=1\), \(\sigma_{2}=0.7 \), by direct calculation, we have \(D = 0.1467 > 0\), \(E = -0.1500 < 0\), \(\mathcal{R}^{*}_{2} = 0.6419 < 1\). Then, by Theorem 4.1, the microorganism eventually tends to be extinct (Fig. 2(b)).
Case III. Choose \(\sigma_{1}=1.5\), \(\sigma_{2}=1.6 \), by direct calculation, we have \(D = 1.3967 > 0\), \(E = 1.9200 > 0\), \(\mathcal{R}^{*} _{3} = 0.1830 < 1\). Then, by Theorem 4.1, the microorganism eventually tends to be extinct (Fig. 2(c)).
Case IV. Choose \(\sigma_{1}=0.5\), \(\sigma_{2}=0.5 \), by direct calculation, we have \(D = -0.6033 < 0\), \(E = -0.3900 < 0\), \(\mathcal{R} ^{*}_{4} = 0.9896 < 1\). Then, by Theorem 4.1, the microorganism eventually tends to be extinct (Fig. 2(d)).
Keeping the parameters of the deterministic system constant, by adding white noise disturbance, we can get \(\mathcal{R}^{*}_{2} < 1 < \mathcal{R}_{2} \), which indicates that the persistent microorganism of a deterministic system may go to extinction under the white noise stochastic disturbance. Thus the simulation is consistent with the theoretical results of Theorem 3.2 and Theorem 4.1. Therefore, the white noise stochastic effect is harmful to the persistence of the system.
Choose \(\sigma_{1}=0.4\), \(\sigma_{2}=0.4 \), and keep all parameters unchanged as in Fig. 2, except u, the pulsed input concentration of the toxicant. When it is small, say \(u = 0.1\), we have \(\overline{ \mathcal{R}}=1.0135 > 1\). Thus, the microorganism x is persistent (Fig. 3(a)). Conversely, when it is large, say \(u=1.1\), we have \(\mathcal{R}^{*}_{4}=0.9966 < 1\). Thus, the microorganism x goes to extinction (Fig. 3(b)). This supports our theoretical results obtained in Theorem 4.1 and Theorem 4.2 as well.
Time evolutions of the stochastic system with parameters \(S_{10}=1.5\), \(S_{20}=2\), \(Q=1.45\), \(\delta _{1}=0.9\), \(\delta _{2}=1\), \(a_{1}=1.6\), \(a_{2}=1.6\), \(\mu _{1}=0.8\), \(\mu _{2}=0.8\), \(\sigma _{1}=0.4\), \(\sigma _{2}=0.4\), \(r=0.1\), \(k=1\), \(g=0.8\), \(h=1\), \(m=0.2\), \(T=1\). (a) Time series for \(S_{1}(t)\), \(S_{2}(t)\), \(x(t)\) with parameters \(u=0.1\), \(\overline{\mathcal{R}}=1.0135\). (b) Time series for \(S_{1}(t)\), \(S_{2}(t)\), \(x(t)\) with parameters \(u=1.1\), \(\mathcal{R}^{*}_{4}=0.9966\)
Numerical simulations show that the increase in pollutant emission may lead to the extinction of microbial population (Fig. 1(b)) for a deterministic chemostat model. For a persistent system with constant pollutant discharge (Fig. 1(a)), the microbial population may become extinct if disturbed by white noise (Fig. 2). And the probability of microbial extinction increases significantly with increasing noise intensity (Fig. 2(a–d)). Figure 3 shows that, for a long-lasting system with constant noise intensity (Fig. 3(a)), an increase in pollutant emissions also leads to the extinction of the microbial population (Fig. 3(b)).
References
Butler, G.J., Hsu, S.B., Waltman, P.: A mathematical model of the chemostat with periodic washout rate. SIAM J. Appl. Math. 45(3), 435–449 (1985)
Wolkowicz, G.S.K., Xia, H.: Global asymptotic behavior of a chemostat model with discrete delays. SIAM J. Appl. Math. 57(4), 1019–1043 (1997)
Meng, X., Gao, Q., Li, Z.: The effects of delayed growth response on the dynamic behaviors of the Monod type chemostat model with impulsive input nutrient concentration. Nonlinear Anal., Real World Appl. 11(5), 4476–4486 (2010)
Zhang, T., Zhang, T., Meng, X.: Stability analysis of a chemostat model with maintenance energy. Appl. Math. Lett. 68, 1–7 (2017)
Gao, J., Shen, B., Feng, E., Xiu, Z.: Modelling and optimal control for an impulsive dynamical system in microbial fed-batch culture. Comput. Appl. Math. 32(2), 275–290 (2013)
Wang, W., Ma, W., Yan, H.: Global dynamics of modeling flocculation of microorganism. Appl. Sci. 6(8), 221 (2016)
Guo, S., Ma, W.: Global dynamics of a microorganism flocculation model with time delay. Commun. Pure Appl. Anal. 16(5), 1883–1891 (2017)
Guo, S., Ma, W., Zhao, X.: Global dynamics of a time-delayed microorganism flocculation model with saturated functional responses. J. Dyn. Differ. Equ. (2017). https://doi.org/10.1007/s10884-017-9605-3
Song, K., Ma, W., Guo, S., Yan, H.: A class of dynamic models describing microbial flocculant with nutrient competition and metabolic products in wastewater treatment. Adv. Differ. Equ. 2018(1), 33 (2018)
Li, Z., Chen, L., Liu, Z.: Periodic solution of a chemostat model with variable yield and impulsive state feedback control. Appl. Math. Model. 36(3), 1255–1266 (2012)
Dong, Q., Ma, W.: Qualitative analysis of the chemostat model with variable yield and a time delay. J. Math. Chem. 51(5), 1274–1292 (2013)
Monod, J.: Recherches sur la croissance des cultures bactériennes. In: Actualites Scientifique et Industrielles, pp. 211–212. Hermann, Paris (1942)
Monod, J.: La technique de culture continue: Théorie et applications. Ann. Inst. Pasteur 79, 390–410 (1950)
Novick, A., Szilard, L.: Experiments with the chemostat on spontaneous mutations of bacteria. Proc. Natl. Acad. Sci. USA 36(12), 708–719 (1950)
Herbert, D., Elsworth, R., Telling, B.C.: The continuous culture of bacteria: a theoretical and experimental study. J. Gen. Microbiol. 14(3), 601 (1956)
Hsu, S.B., Hubbell, S., Waltman, P.: A mathematical theory for single-nutrient competition in continuous cultures of microorganisms. Bioorg. Med. Chem. Lett. 32(2), 366–383 (1977)
Wolkowicz, G.S.K., Lu, Z.: Global dynamics of a mathematical model of competition in the chemostat: general response functions and differential death rates. SIAM J. Appl. Math. 52, 222–233 (1992)
Ellermeyer, S.F.: Competition in the chemostat: global asymptotic behavior of a model with delayed response in growth. SIAM J. Appl. Math. 54(2), 456–465 (1994)
Braselton, J.P., Abell, M.L., Braselton, L.M.: Comparing the effects of interactive and noninteractive complementary nutrients on growth in a chemostat. Open J. Appl. Sci. 3(5), 323–331 (2013)
Wang, T., Chen, L., Zhang, P.: Extinction and permanence of two-nutrient and two-microorganism chemostat model with pulsed input. Commun. Nonlinear Sci. Numer. Simul. 15(10), 3035–3045 (2010)
Song, X., Zhao, Z.: Extinction and permanence of two-nutrient and one-microorganism chemostat model with pulsed input. Discrete Dyn. Nat. Soc. 2006(2), Article ID 38310 (2006)
Li, B., Smith, H.L.: Global dynamics of microbial competition for two resources with internal storage. J. Math. Biol. 55(4), 481–515 (2007)
Zhang, J., Miao, A., Zhang, T.: Threshold dynamics of a stochastic chemostat model with two nutrients and one microorganism. Math. Probl. Eng. 2017, Article ID 5217027 (2017)
Meng, X., Zhang, L.: Evolutionary dynamics in a Lotka–Volterra competition model with impulsive periodic disturbance. Math. Methods Appl. Sci. 39(2), 177–188 (2016)
Liu, M., Wang, K.: On a stochastic logistic equation with impulsive perturbations. Comput. Math. Appl. 63(5), 871–886 (2012)
Liu, Q., Chen, Q.: Dynamics of stochastic delay Lotka–Volterra systems with impulsive toxicant input and Lévy noise in polluted environments. Appl. Math. Comput. 256, 52–67 (2015)
Zhao, W., Li, J., Zhang, T., Meng, X., Zhang, T.: Persistence and ergodicity of plant disease model with Markov conversion and impulsive toxicant input. Commun. Nonlinear Sci. Numer. Simul. 48, 70–84 (2017)
Zhang, T., Ma, W., Meng, X., Zhang, T.: Periodic solution of a prey–predator model with nonlinear state feedback control. Appl. Math. Comput. 266, 95–107 (2015)
Zhang, S., Meng, X., Feng, T., Zhang, T.: Dynamics analysis and numerical simulations of a stochastic non-autonomous predator–prey system with impulsive effects. Nonlinear Anal. Hybrid Syst. 26, 19–37 (2017)
Liu, G., Wang, X., Meng, X., Gao, S.: Extinction and persistence in mean of a novel delay impulsive stochastic infected predator–prey system with jumps. Complexity 2017, Article ID 1950970 (2017)
Leng, X., Feng, T., Meng, X.: Stochastic inequalities and applications to dynamics analysis of a novel SIVS epidemic model with jumps. J. Inequal. Appl. 2017(1), 138 (2017)
Bian, F., Zhao, W., Song, Y., Yue, R.: Dynamical analysis of a class of prey–predator model with Beddington–DeAngelis functional response, stochastic perturbation, and impulsive toxicant input. Complexity 2017, Article ID 3742197 (2017)
Zhuo, X.: Global attractability and permanence for a new stage-structured delay impulsive ecosystem. J. Appl. Anal. Comput. 8(2), 457–470 (2018)
Wang, W., Zhang, T.: Caspase-1-mediated pyroptosis of the predominance for driving CD4+ T cells death: a nonlocal spatial mathematical model. Bull. Math. Biol. 80(3), 540–582 (2018)
Sun, S., Chen, L.: Dynamic behaviors of Monod type chemostat model with impulsive perturbation on the nutrient concentration. J. Math. Chem. 42(4), 837–847 (2007)
Zhao, Z., Chen, L., Song, X.: Extinction and permanence of chemostat model with pulsed input in a polluted environment. Commun. Nonlinear Sci. Numer. Simul. 14(4), 1737–1745 (2009)
Zhang, T., Ma, W., Meng, X.: Global dynamics of a delayed chemostat model with harvest by impulsive flocculant input. Adv. Differ. Equ. 2017(1), 115 (2017)
Zhang, T., Ma, W., Meng, X.: Impulsive control of a continuous-culture and flocculation harvest chemostat model. Int. J. Syst. Sci. 48(16), 3459–3469 (2017)
Hallam, T.G., Clark, C.E., Lassiter, R.R.: Effects of toxicants on populations: a qualitative approach I. Equilibrium environmental exposure. Ecol. Model. 18(3–4), 291–304 (1983)
Hallam, T.G., Clark, C.E., Jordan, G.S.: Effects of toxicants on populations: a qualitative approach II. First order kinetics. J. Math. Biol. 18(1), 25–37 (1983)
Ma, Z., Cui, G., Wang, W.: Persistence and extinction of a population in a polluted environment. Math. Biosci. 101(1), 75–97 (1990)
Liu, B., Chen, L., Zhang, Y.: The effects of impulsive toxicant input on a population in a polluted environment. J. Biol. Syst. 11(3), 265–274 (2003)
Fergola, P., Tenneriello, C., Ma, Z., Wen, X.: Effects of toxicants on chemostat models. Cybern. Syst. 94, 887–894 (1994)
Ma, Z., Guo, S., Fergola, P., Tenneriello, C.: Effects of toxicants on chemostat model with time variable nutrient input and washout. J. Syst. Sci. Math. Sci. 11(4), 342–350 (1998)
Jiao, J., Ye, K., Chen, L.: Dynamical analysis of a five-dimensioned chemostat model with impulsive diffusion and pulse input environmental toxicant. Chaos Solitons Fractals 44(1), 17–27 (2011)
Zhao, Z., Song, X.: On the study of chemostat model with pulsed input in a polluted environment. Discrete Dyn. Nat. Soc. 2007(1), 207–210 (2007)
Meng, X., Wang, L., Zhang, T.: Global dynamics analysis of a nonlinear impulsive stochastic chemostat system in a polluted environment. J. Appl. Anal. Comput. 6(3), 865–875 (2016)
Liu, Y., Liu, Q., Liu, Z.: Dynamical behaviors of a stochastic delay logistic system with impulsive toxicant input in a polluted environment. J. Theor. Biol. 329, 1–5 (2013)
Liu, Q., Chen, Q.: Analysis of the deterministic and stochastic SIRS epidemic models with nonlinear incidence. Phys. A, Stat. Mech. Appl. 428, 140–153 (2015)
Meng, X., Zhao, S., Feng, T., Zhang, T.: Dynamics of a novel nonlinear stochastic SIS epidemic model with double epidemic hypothesis. J. Math. Anal. Appl. 433(1), 227–242 (2016)
Miao, A., Wang, X., Zhang, T., Wang, W., Pradeep, B.G.S.A.: Dynamical analysis of a stochastic SIS epidemic model with nonlinear incidence rate and double epidemic hypothesis. Adv. Differ. Equ. 2017(1), 226 (2017)
Wang, L., Jiang, D., O’Regan, D.: The periodic solutions of a stochastic chemostat model with periodic washout rate. Commun. Nonlinear Sci. Numer. Simul. 37, 1–13 (2016)
Liu, L., Meng, X.: Optimal harvesting control and dynamics of two-species stochastic model with delays. Adv. Differ. Equ. 2017(1), 18 (2017)
Lv, X., Wang, L., Meng, X.: Global analysis of a new nonlinear stochastic differential competition system with impulsive effect. Adv. Differ. Equ. 2017(1), 296 (2017)
Zhang, S., Meng, X., Wang, X.: Application of stochastic inequalities to global analysis of a nonlinear stochastic SIRS epidemic model with saturated treatment function. Adv. Differ. Equ. 2018(1), 50 (2018)
Li, F., Meng, X., Wang, X.: Analysis and numerical simulations of a stochastic SEIQR epidemic system with quarantine-adjusted incidence and imperfect vaccination. Comput. Math. Methods Med. 2018, Article ID 7873902 (2018)
Qi, H., Liu, L., Meng, X.: Dynamics of a nonautonomous stochastic SIS epidemic model with double epidemic hypothesis. Complexity 2017, Article ID 4861391 (2017)
Feng, T., Meng, X., Liu, L., Gao, S.: Application of inequalities technique to dynamics analysis of a stochastic eco-epidemiology model. J. Inequal. Appl. 2016(1), 327 (2016)
Zhuo, X.-L., Zhang, F.-X.: Stability for a new discrete ratio-dependent predator–prey system. Qual. Theory Dyn. Syst. 17(1), 189–202 (2018)
Miao, A., Zhang, J., Zhang, T., Pradeep, B.G.S.A.: Threshold dynamics of a stochastic SIR model with vertical transmission and vaccination. Comput. Math. Methods Med. 2017, Article ID 4820183 (2017)
Zhao, D., Yuan, S.: Critical result on the break-even concentration in a single-species stochastic chemostat model. J. Math. Anal. Appl. 434(2), 1336–1345 (2016)
Xu, C., Yuan, S.: An analogue of break-even concentration in a simple stochastic chemostat model. Appl. Math. Lett. 48, 62–68 (2015)
Sun, S., Sun, Y., Zhang, G., Liu, X.: Dynamical behavior of a stochastic two-species Monod competition chemostat model. Appl. Math. Comput. 298, 153–170 (2017)
Wang, L., Jiang, D.: A note on the stationary distribution of the stochastic chemostat model with general response functions. Appl. Math. Lett. 73, 22–28 (2017)
Xu, C., Yuan, S., Zhang, T.: Stochastic sensitivity analysis for a competitive turbidostat model with inhibitory nutrients. Int. J. Bifurc. Chaos 26(10), 1650173 (2016)
Zhang, T., Chen, Z., Han, M.: Dynamical analysis of a stochastic model for cascaded continuous flow bioreactors. J. Math. Chem. 52, 1441–1459 (2014)
Chen, Z., Zhang, T.: Dynamics of a stochastic model for continuous flow bioreactor with Contois growth rate. J. Math. Chem. 51, 1076–1091 (2013)
Chen, Z., Zhang, T.: Long time behaviour of a stochastic model for continuous flow bioreactor. J. Math. Chem. 51, 451–464 (2013)
Yu, X., Yuan, S., Zhang, T.: The effects of toxin-producing phytoplankton and environmental fluctuations on the planktonic blooms. Nonlinear Dyn. 91(3), 1653–1668 (2018)
Xu, C., Yuan, S., Zhang, T.: Asymptotic behavior of a chemostat model with stochastic perturbation on the dilution rate. Abstr. Appl. Anal. 2013, Article ID 423154 (2013)
Liu, M., Wang, K.: Asymptotic properties and simulations of a stochastic logistic model under regime switching II. Math. Comput. Model. 55(3), 405–418 (2012)
Mao, X.: Stochastic differential equations and applications. Adv. Math. 23, 213–214 (1977)
Kloeden, P.E., Platen, E.: Higher-order implicit strong numerical schemes for stochastic differential equations. J. Stat. Phys. 66(1–2), 283–314 (1992)
Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 11371230), Research Funds for Joint Innovative Center for Safe and Effective Mining Technology and Equipment of Coal Resources by Shandong Province and SDUST Research Fund (2014TDJH102).
Author information
Authors and Affiliations
Contributions
All authors worked together to produce the results and read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chi, M., Zhao, W. Dynamical analysis of multi-nutrient and single microorganism chemostat model in a polluted environment. Adv Differ Equ 2018, 120 (2018). https://doi.org/10.1186/s13662-018-1573-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1573-3