1 Introduction

Recently, kinetic equations with fractional derivatives were recognized as a useful tool for description of anomalous diffusion phenomena. Examples include systems exhibiting underground water pollution, Hamiltonian chaos, disordered medium, dynamics of protein molecules, reactions in complex systems, motions under the influence of optical tweezers, and more; see reviews on fractional kinetics [1–4]. The kinetic equations with time-fractional derivative are used for description of subdiffusion processes, that is, those for which the mean-squared displacement grows in time slower than linearly [5]. Also, it describes slow relaxation processes that are characterized by stretched exponential or power-law response function [6]. It became clear that further theoretical investigations are required to incorporate adequate tools for description of more realistic random processes, which are described by a set of characteristic exponents and are therefore of multifractional type. An adequate kinetic description of these processes requires the use of generalized fractional kinetics based on the concept of variable-order fractional (V-OF) operators. This calculus was proposed in [7, 8] and very recently was introduced in physics [9, 10].

The V-OF operators are nonlocal with singular kernels, which makes the V-OF models complicated. Hence, solving V-OF models is also more complicated. Numerical computation of the V-OF operators is the key to understand the behavior and physical meaning of the V-OF models. Lin et al. [11] investigated the stability and convergence of an explicit finite-difference approximation for a nonlinear V-OF diffusion equation. Chen et al. [12] proposed two numerical schemes for a V-OF anomalous subdiffusion equation, one with first-order temporal accuracy and fourth-order spatial accuracy and the other with second-order temporal accuracy and fourth-order spacial accuracy. Yang et al. [13] proposed a finite difference scheme for solving V-OF reaction–diffusion equation. Abdelkawy et al. [14] proposed a new spectral method to achieve high accurate solution for the V-OF mobile–immobile advection–dispersion model. Chen et al. [15] proposed a numerical method to estimate the V-OF derivatives of an unknown signal in noisy environment. Tavares et al. [16] presented a numerical tool to solve partial differential equations involving V-OF Caputo derivatives. Bhrawy and Zaky [17] proposed a numerical method for solving the V-OF nonlinear cable equation based on shifted Jacobi collocation procedure together with the shifted Jacobi operational matrix for V-OF derivatives. They also proposed an accurate and robust approach to approximate solutions of V-OF functional boundary value problems[18]. Zaky et al. [19] proposed the Jacobi wavelets collocation approach based on the Jacobi wavelets operational matrix of V-OF derivative for solving a general class of V-OF differential equations arising in turbulent fluid dynamics. Doha et al. [20, 21] used polynomial collocation techniques to solve V-OF integro–differential equations. Moghaddam and Tenreiro Machado [22–24] proposed algorithms based on finite difference approximations and B-spline interpolation for different definitions of V-OF derivatives.

Spectral methods are of fundamental importance in computational physics because of their ability in achieving desired solution with a small number of degrees of freedom, which often allows gains in accuracy with considerable reduction in computational cost [25]. Collocation method is one of more applicable types of the spectral methods and is frequently used to solve various types of differential equations, such as the Schrödinger equation [26, 27], Rayleigh–Stokes equation [28], diffusion equation [29], mobile–immobile advection–dispersion equation [14], and cable equation [17]. It is well known that the majority of the fractional differential equations have no exact solutions. Therefore, numerical methods to obtain an approximate solution have become the preferred approach for such equations [30–37]. Approaches for numerically approximating the solution of fractional differential equations have been extensively studied; see, e.g., [38–42].

In this paper, we consider the following V-OF Galilei invariant advection–diffusion equation [43]:

$$\begin{aligned}& \frac{{\partial v(x,t)}}{{\partial t}}+\kappa \frac{{\partial v(x,t)}}{ {\partial x}} = {}_{0} \mathscr{D}_{t}^{1 - \gamma (x,t) } \biggl( \kappa_{\gamma } \frac{{\partial^{2} v(x,t)}}{{\partial x^{2} }} \biggr)+ f(x,t,v), \end{aligned}$$
(1.1)
$$\begin{aligned}& v(x,0) = g_{0}(x),\quad 0 < x < L, \end{aligned}$$
(1.2)
$$\begin{aligned}& v(0,t) = g_{1}(t),\qquad v(L,t) = g_{2}(t),\quad 0 < t \le \tau, \end{aligned}$$
(1.3)

where \(0<\gamma_{\min }\leq \gamma (x,t)\leq \gamma_{\max }<1\), \(\kappa_{\gamma }, \kappa >0\), and \({}_{0}\mathscr{D}_{t}^{1 - \gamma (x,t) }v(x,t)\) is the V-OF Riemann–Liouville derivative. The proposed method is based on the shifted Legendre collocation procedure and a matrix form representation of variable-order Caputo fractional derivative.

This paper is organized as follows. In Sect. 2, we first present some preliminaries from fractional calculus and introduce some properties of the shifted Legendre polynomials. In Sect. 3, we derive the operational matrix of the V-OF derivative for the shifted Legendre polynomials. In Sect. 4, the V-OF Galilei invariant advection–diffusion equation with a nonlinear source term is numerically investigated. In Sect. 5, numerical results are discussed. Finally, In Sect. 6, we outline the main conclusions.

2 Preliminaries

In this section, we recall some mathematical preliminaries of the V-OF operators (see [44]) and relevant properties of Legendre polynomials (see [25, 45–48]).

Definition 2.1

The Caputo and Riemann–Liouville derivatives of a function \(v(t)\) of order γ, when \(n-1<\gamma \leq n \in \mathbb{N}\), are defined, respectively, as

$$ \begin{aligned} &{}_{0}^{C} \mathscr{D}_{t}^{\gamma }v(t) = \frac{1}{{\Gamma (n - \gamma)}} \int _{0}^{t} {\frac{{v^{(n)} (s)}}{{(t - s)^{ \gamma - n + 1} }}}\,ds, \\ &_{0} \mathscr{D}_{t}^{\gamma } v(t) = \frac{1}{{\Gamma (n - \gamma)}}\frac{{d^{n} }}{{dt^{n} }} \int _{0}^{t} {\frac{{v(s)}}{ {(t - s)^{\gamma - n + 1} }}}\,ds, \end{aligned} $$
(2.1)

where Γ represents the Euler gamma function.

Definition 2.2

The V-OF Riemann–Liouville derivative \(\gamma (t)\) is given by

$$ \begin{aligned} &{}_{0}\mathscr{D}_{t}^{ \gamma (t)} v(t) =\frac{1}{{\Gamma (n - {\gamma (t)} )}} \biggl[ {\frac{{d^{n} }}{{d\xi^{n} }} \int _{0} ^{\xi }{\frac{{v(\eta)}}{{(\xi - \eta)^{\gamma (t) - n + 1} }}\,d\eta}} \biggr] _{\xi =t}, \end{aligned} $$
(2.2)

where \(n-1 < \gamma_{\min } < \gamma (t) < \gamma_{\max } < n\), \(n \in \mathbb{N}\).

Definition 2.3

The V-OF Caputo derivative is given by

$$ {}_{0}^{C} \mathscr{D}_{t}^{\gamma (t)}v(t) = \frac{1}{{\Gamma (1 - \gamma (t))}} \int _{0 }^{t} {\frac{{\frac{d^{n}v(s)}{ds^{n}}}}{ {(t - s)^{\gamma (t)} }}\,ds }, $$
(2.3)

where \(n-1 < \gamma_{\min } < \gamma (t) < \gamma_{\max } < n\), \(n \in \mathbb{N}\).

The two previous V-OF operators are related by

$$ _{0} \mathscr{D}_{t}^{\gamma (t)} v(t) = \sum_{r = 0}^{n - 1} {\frac{{v^{(r)} (0)t^{r - \gamma (t)} }}{{\Gamma (r + 1 - \gamma (t))}}} + {}_{0}^{C} \mathscr{D}_{t}^{\gamma (t)} v(t). $$
(2.4)

We introduce the following important relations for the V-OF Caputo derivative \((0< \gamma (t)\leq 1)\):

$$\begin{aligned}& _{0}^{C} \mathscr{D}_{t}^{\gamma (t)} {\bigl(\lambda v(t)+\mu g(t)\bigr)}= \lambda _{0}^{C} \mathscr{D}_{t}^{\gamma (t)}{v(t)}+\mu _{0}^{C} \mathscr{D}_{t}^{\gamma (t)}{g(t)} , \end{aligned}$$
(2.5)
$$\begin{aligned}& \begin{aligned} &_{0}^{C} \mathscr{D}_{t}^{\gamma (t)} t^{\beta }= \textstyle\begin{cases} 0, & \beta =0, \\ \frac{\Gamma {(\beta +1)}}{\Gamma {(\beta +1-\gamma (t))}} t^{ \beta -\gamma (t)}, & \beta =1,2,\dots. \end{cases}\displaystyle \end{aligned} \end{aligned}$$
(2.6)

Now, we present some useful mathematical relations for the shifted Legendre polynomials. The classical Legendre polynomials are defined on \([-1, 1]\) and may be generated from the three-term recurrence relation:

$$\begin{aligned}& P_{k+1}(t)=\frac{2k+1}{k+1} t P_{k}(t)- \frac{k}{k+1}P_{k-1}(t),\quad k\geq 1, \\& P_{0}(t)=1,\qquad P_{1}(t)=t. \end{aligned}$$

Let us consider the transform \(t=\frac{2x}{L}-1\) to define the orthogonal shifted Legendre polynomials \(P_{L,i}{(x)}\) in \(x \in [0,L]\). They satisfy the recurrence relation

$$ P_{L,i+1}{(x)}=\frac{2i+1}{i+1} \biggl( \frac{2x}{L}-1 \biggr) P_{L,i} {(x)}-\frac{i}{i+1}P_{L,i-1}{(x)},\quad i=1,2,\ldots, $$
(2.7)

where \(P_{L,0}{(x)}=1\) and \(P_{L,1}{(x)}=\frac{2x}{L}-1\). The orthogonality property of the shifted Legendre polynomials is

$$ \int_{0}^{L} P_{L,j} (x)P_{L,k}(x)w_{L}(x)\,dx =\hbar^{L}_{k} \delta _{jk}, $$
(2.8)

where \(w_{L}(x)=1\), \(\hbar^{L}_{k} =\frac{L}{2k+1}\), and \(\delta_{jk}\) is the Kronecker symbol.

An explicit analytic form of \(P_{L,i}{(x)}\) is given by

$$ P_{L,i}{(x)}=\sum_{k=0}^{i }{ z_{L,i,k}} x^{k} , $$
(2.9)

where

$$ z_{L,i,k} ={(-1)}^{i+k}\frac{ {(i+k)}!}{ {(i-k)}! ({k}!)^{2} L ^{k}}, $$
(2.10)

which alternatively may be written in the following matrix form:

$$ \Psi_{L,M} (x) = Z_{L} X_{M} (x), $$
(2.11)

where \(z_{L,i,k}\), \(i,k =0,1,\dots,M\), are the matrix entries of \(Z_{L}\),

$$ \begin{aligned} &\Psi_{L,M}(x)=\bigl[P_{L,0}(x), P_{L,1}(x),\ldots,P_{L,M}(x)\bigr]^{T}, \\ &X_{M} (x) =\bigl[1,x,x^{2},\ldots,x^{M} \bigr]^{T}. \end{aligned} $$
(2.12)

Due to property (2.8), the vector \(X_{M} (x)\) may be expressed by means of \(\Psi_{L,M} (x)\) as

$$ X_{M} (x) = Z_{L} ^{ - 1} \Psi_{L,M} (x). $$
(2.13)

Two relations at the endpoints

$$ \begin{aligned} P_{L,i} (0)= ( - 1)^{i} ,\qquad P_{L,i} (L) = 1, \end{aligned} $$
(2.14)

will be further useful.

Assume that \(v(x)\) is a square-integrable function with respect to the shifted Legendre weight function. Then, it can be expressed by means of \(P_{L,j} (L)\) as

$$ v{(x)}=\sum_{j=0}^{\infty }c_{j} P_{L,j}{(x)}, $$
(2.15)

where the coefficients \(c_{j}\) are defined by

$$ c_{j}= \frac{1}{\hbar^{L}_{j}} \int_{0}^{L}v (x)P_{L,j}(x)\,dx,\quad j=0,1,2, \ldots. $$
(2.16)

The function \(v(x)\) can be approximated by the first \((M+1)\) terms as

$$ v_{M}{(x)}\simeq \sum_{j=0}^{M}c_{j} P_{L,j}{(x)}= \mathbf{C} ^{T} \Psi_{L,M}(x), $$
(2.17)

where the shifted Legendre coefficient vector C is given by \(\mathbf{C}^{T}=[c_{0},c_{1},\ldots,c_{M}]\). Accordingly, a function \(v(x,t)\) of two variables \(x \in [0,L]\) and \(t \in [0,\tau ]\) can be approximated by means of the double-shifted Legendre polynomials as

$$ v_{N,M}(x,t) = \sum_{i = 0}^{M} {\sum_{j = 0}^{N} {a _{i,j} P_{L,i}} (x)P_{\tau,j}(t) = \Psi_{\tau,N}^{T} (t) \mathbf{A} \Psi_{L,M}(x)}, $$
(2.18)

where the shifted Legendre vectors \(\Psi_{\tau,N} (t)\) and \(\Psi_{L,M}(x)\) are defined similarly to (2.12), and A is an \((N +1)\times (M +1)\) matrix of the form

$$ \mathbf{A} = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} a_{00} & a_{01} & \cdots & a_{0M} \\ a_{10} & a_{11} & \cdots & a_{1M} \\ \vdots & \vdots & \ddots & \vdots \\ a_{N0} & a_{N1} & \cdots & a_{NM} \end{array}\displaystyle \right ), $$
(2.19)

where

$$a_{ij}=\frac{1}{{\hbar^{L}_{i}}{\hbar^{\tau }_{j}}} \int_{0}^{L}{ \int _{0}^{\tau }}v(x,t)P_{L,i}(x)P_{\tau,j}(t)\,dt\,dx,\quad i=0,1,\ldots,M, j=0,1,\ldots,N. $$

3 Operational matrices based on Legendre polynomials

The first-order derivative of the shifted Legendre vector \(\Psi_{L,M}(x)\) may be written as

$$ \frac{d}{dx}\Psi_{L,M}(x)=\mathbf{D}_{L}^{(1)} \Psi_{L,M}(x), $$
(3.1)

where \(\mathbf{D}^{(1)}_{L}\) is the \((M+1)\times (M+1)\) operational matrix of derivatives. Accordingly,

$$ \begin{aligned} \frac{d}{{dx}}\Psi_{L,M} (x) = Z_{L} \frac{d}{{dx}} X_{M} (x)= Z_{L} \Lambda_{M} X_{M} (x), \end{aligned} $$
(3.2)

where the dimension of the square matrix \(\Lambda _{M}\) is \((M+1)\times (M+1)\); this matrix is the operational matrix of derivatives of \(X_{M} (x)\), and

$$ \Lambda _{M} =(\lambda _{ij}) \quad \text{with } \lambda _{ij}=\textstyle\begin{cases} j+1 & \text{for } i=j+1, j=0,1,\ldots,M-1, \\ 0 & \text{otherwise}. \end{cases} $$
(3.3)

Employing expressions (3.2) and (2.13), we have

$$\begin{aligned} \frac{d}{{dx}}\Psi_{L,M} (x) = &Z_{L} \Lambda_{M} Z_{L} ^{ - 1} \Psi _{L,M} (x)=\mathbf{D}^{(1)}_{L} \Psi_{L,M} (x). \end{aligned}$$
(3.4)

Accordingly, we provide

$$ \mathbf{D}^{(1)}_{L}=Z_{L} \Lambda_{M} Z_{L} ^{ - 1}. $$
(3.5)

Repeated use of (3.4) enables us to write

$$ \frac{d^{p}}{dx^{p}}\Psi_{L,M}(x)=\bigl( \mathbf{D}_{L}^{(1)}\bigr)^{p} \Psi_{L,M}(x)= \mathbf{D}_{L}^{(p)} \Psi_{L,M}(x),\quad p=1,2,\ldots. $$
(3.6)

Theorem 3.1

The V-OF Caputo derivative of the shifted Legendre vector \(\Psi_{ \tau,N}(t)\) is given by

$$ {}_{0}^{C} \mathscr{D}_{t}^{\gamma (t)} \Psi_{\tau,N} (t) = \mathbf{D}_{\tau,\gamma (t)} \Psi_{\tau,N} (t), $$
(3.7)

where \(n-1 < \gamma _{\min } < \gamma (t) < \gamma _{\max } < n\), \(n \in \mathbb{N}\), and \(\mathbf{D}_{\tau,\gamma (t) } \) is an \((N+1)\times (N+1)\) matrix of the form

$$ \mathbf{D}_{\tau,\gamma (t)} = Z_{\tau }\mathbf{B} Z_{\tau }^{ - 1}, $$
(3.8)

where \(Z_{\tau }\) is defined in (2.11), and B is an \((N+1)\times (N+1)\) matrix with elements \(b_{ij}, 0 \leq i,j \leq N \), defined by

$$ b_{ij}= \textstyle\begin{cases} \frac{{\Gamma (i + 1) t^{ - \gamma (t)}}}{{\Gamma (i + 1 - \gamma (t))}} & \textit{for } i=j, j=n,n+1,\ldots,N, \\ 0 & \textit{otherwise}. \end{cases} $$
(3.9)

Proof

Using (2.12) and (2.13) yields

$$ {}_{0}^{C} \mathscr{D}_{t}^{\gamma (t)} \Psi_{\tau,N}(t)={}_{0}^{C} \mathscr{D}_{t}^{\gamma (t)} \bigl[P_{\tau,0}(t),P_{\tau,1}(t),\ldots,P_{\tau,N}(t) \bigr]^{T}= {Z_{\tau }} {}_{0}^{C} \mathscr{D}_{t}^{\gamma (t)} X_{N} (t). $$
(3.10)

This, together with (2.6), leads to

$$\begin{aligned} {}_{0}^{C} \mathscr{D}_{t}^{\gamma (t)} X_{N} (t) = & \biggl[0, \ldots,\frac{ {\Gamma (n+1)}}{{\Gamma (n+1 - \gamma (t))}}t^{n - \gamma (t)}, \frac{ {\Gamma (n+2)}}{{\Gamma (n+2 - \gamma (t))}}t^{n+1 - \gamma (t)}, \ldots, \\ &{} \frac{{\Gamma (N + 1)}}{{\Gamma (N + 1 - \gamma (t))}}t^{N - \gamma (t)} \biggr]^{T} \\ = & \mathbf{B} X_{N} (t), \end{aligned}$$
(3.11)

where B is an \((N +1)\times (N +1)\) matrix with entries \(b_{ij}\), \(0 \leq i,j \leq N\). Equations (3.10) and (3.11) yield

$$ _{0}^{C} \mathcal{D}_{t}^{\gamma (t)} \Psi_{\tau,N}(t)= {Z_{\tau }} \mathbf{B} X_{N} (t). $$
(3.12)

Since \({Z_{\tau }}\) is invertible, we have

$$\begin{aligned} {}_{0}^{C} \mathscr{D}_{t}^{\gamma (t)} \Psi_{\tau,N}(t) = &{Z_{\tau }} \mathbf{B} {Z_{\tau }}^{-1} {Z_{\tau }}X_{N} (t)= {Z_{\tau }} \mathbf{B} {Z_{\tau }}^{-1} \Psi_{\tau,N}(t) \\ = & \mathbf{D}_{\tau,\gamma (t) } \Psi_{\tau,N} (t), \end{aligned}$$
(3.13)

where \(\mathbf{D}_{\tau,\gamma (t) } = {Z_{\tau }} \mathbf{B} {Z_{\tau }} ^{ - 1}\) is an upper triangular matrix. □

This theorem is a generalization of that in [48], where \(0 < \gamma _{\min } < \gamma (t) < \gamma _{\max } < 1\) and \(\tau=1\).

4 The collocation method

After the construction of the V-OF differentiation matrices of Caputo type, we now use the Legendre–Gauss–Lobatto collocation technique in combination with the shifted Legendre operational matrix of V-OF fractional differentiation.

First, \(v(x,t)\) is approximated by means of the double-shifted Legendre polynomials as

$$ v_{N,M}(x,t) = \sum_{i = 0}^{M} {\sum_{j = 0}^{N} {a _{i,j} P_{L,i} } } (x)P_{\tau,j} (t) = \Psi_{\tau,N}^{T} (t) \mathbf{A}\Psi_{L,M} (x), $$
(4.1)

where A is an \((N+1)\times (M+1)\) unknown matrix.

Employing Eqs. (2.4), (2.5), (3.6), (3.7), and (4.1), we obtain

$$\begin{aligned}& \begin{aligned}[b] {} _{0} \mathscr{D}_{t}^{1 - \gamma (x,t)} \biggl(\frac{{\partial^{2} v(x,t)}}{ {\partial x^{2} }} \biggr) ={}& {}_{0}^{C} \mathscr{D}_{t}^{1 - \gamma (x,t)} \biggl( \frac{{\partial^{2} v(x,t)}}{{\partial x^{2} }} \biggr) + \frac{ {\partial^{2} v(x,t)}}{{\partial x^{2} }}\bigg\vert _{t = 0} \frac{{t^{\gamma (x,t) - 1} }}{{\Gamma (\gamma (x,t))}} \\ ={}& \Psi_{\tau,N}^{T} (t)\mathbf{D}_{\tau,1-\gamma (x,t) }^{T} \mathbf{A}\mathbf{D}_{L}^{(2)} \Psi_{L,M} (x) \\ &{} + \Psi_{\tau,N}^{T} (0) \mathbf{A}\mathbf{D}_{L}^{(2)} \Psi_{L,M} (x)\frac{ {t^{\gamma (x,t) - 1} }}{{\Gamma (\gamma (x,t))}}, \end{aligned} \end{aligned}$$
(4.2)
$$\begin{aligned}& \frac{{\partial v(x,t)}}{{\partial t}} = \Psi_{\tau,N}^{T} (t) \bigl( \mathbf{D}_{\tau }^{(1)}\bigr)^{T} \mathbf{A}\Psi_{L,M} (x), \end{aligned}$$
(4.3)
$$\begin{aligned}& \frac{{\partial v(x,t)}}{{\partial x}} = \Psi_{\tau,N}^{T} (t) \mathbf{A} \mathbf{D}_{L}^{(1)} \Psi_{L,M} (x), \end{aligned}$$
(4.4)
$$\begin{aligned}& \begin{aligned} &v(x,0) = \Psi_{\tau,N}^{T} (0) \mathbf{A}\Psi_{L,M} (x), \\ &v(0,t) = \Psi_{\tau,N}^{T} (t) \mathbf{A}\Psi_{L,M} (0), \\ &v(L,t) = \Psi_{\tau,N}^{T} (t) \mathbf{A}\Psi_{L,M} (L). \end{aligned} \end{aligned}$$
(4.5)

By (4.1)–(4.5) we have

$$\begin{aligned}& \Psi_{\tau,N}^{T} (t) \bigl( \mathbf{D}_{\tau }^{(1)}\bigr)^{T} \mathbf{A} \Psi_{L,M} (x) +\kappa \bigl[\Psi_{\tau,N}^{T} (t) \mathbf{A} \mathbf{D}_{L}^{(1)} \Psi_{L,M} (x) \bigr] \\& \quad = \kappa_{\gamma } \biggl[\Psi_{\tau,N}^{T} (t) \mathbf{D}_{\tau,1 - \gamma (x,t) }^{T} \mathbf{A}\mathbf{D}_{L}^{(2)} \Psi_{L,M} (x) \\& \qquad {} + \Psi_{\tau,N}^{T} (0)\mathbf{A}\mathbf{D}_{L}^{(2)} \Psi_{L,M} (x)\frac{ {t^{\gamma (x,t) - 1} }}{{\Gamma (\gamma (x,t))}} \biggr] \\& \qquad {}+ f\bigl(x,t,\Psi_{\tau,N}^{T} (t)\mathbf{A} \Psi_{L,M} (x)\bigr), \end{aligned}$$
(4.6)
$$\begin{aligned}& \begin{aligned} &\Psi_{\tau,N}^{T} (0)\mathbf{A} \Psi_{L,M} (x) = g_{0} (x), \\ &\Psi_{\tau,N}^{T} (t)\mathbf{A}\Psi_{L,M} (0) = g_{1} (t), \\ &\Psi_{\tau,N}^{T} (t)\mathbf{A}\Psi_{L,M} (L) = g_{2} (t). \end{aligned} \end{aligned}$$
(4.7)

Let \(x_{i}\) (\(0\leq i\leq M\)) be the shifted Legendre–Gauss–Lobatto nodes, and let \(t_{j}\) (\(0\leq j\leq N-1\)) be the shifted Legendre roots of \(P_{\tau,N}(t)\), where \(P_{\tau,N}{(t_{j})} =0\) (\(0\leq j\leq N-1\)). Substituting these nodes into (4.6)–(4.7), we can rewrite the collocation scheme as follows:

$$\begin{aligned}& \Psi_{\tau,N}^{T} (t_{j}) \bigl(\mathbf{D}_{\tau }^{(1)} \bigr)^{T} \mathbf{A} \Psi_{L,M} (x_{i}) +\kappa \bigl[\Psi_{\tau,N}^{T} (t_{j}) \mathbf{A} \mathbf{D}_{L}^{(1)} \Psi_{L,M} (x_{i}) \bigr] \\& \quad = \kappa_{\gamma } \biggl[\Psi_{\tau,N}^{T} (t_{j})\mathbf{D}_{ \tau,1 - \gamma (x_{i},t_{j}) }^{T} \mathbf{A} \mathbf{D}_{L}^{(2)} \Psi_{L,M} (x_{i}) \\& \qquad {} + \Psi_{\tau,N}^{T} (0)\mathbf{A}\mathbf{D}_{L}^{(2)} \Psi_{L,M} (x _{i})\frac{{t^{\gamma (x_{i},t_{j}) - 1} }}{{\Gamma (\gamma (x_{i},t _{j}))}} \biggr] \\& \qquad {}+ f\bigl(x_{i},t_{j},\Psi_{\tau,N}^{T} (t_{j})\mathbf{A}\Psi_{L,M} (x _{i})\bigr), \\& \qquad 1\leq i\leq M-1\ (0\leq j\leq N-1), \end{aligned}$$
(4.8)
$$\begin{aligned}& \begin{aligned} &\Psi_{\tau,N}^{T} (0)\mathbf{A} \Psi_{L,M} (x_{i}) = g_{0} (x_{i}), \quad 0 \leq i\leq M, \\ &\Psi_{\tau,N}^{T} (t_{j})\mathbf{A}\Psi_{L,M} (x_{0}) = g_{1} (t_{j}), \quad 0\leq j\leq N-1, \\ & \Psi_{\tau,N}^{T} (t_{j})\mathbf{A}\Psi_{L,M} (x_{M}) = g_{2} (t_{j}),\quad 0\leq j\leq N-1. \end{aligned} \end{aligned}$$
(4.9)

These equations can be combined to produce a nonlinear algebraic system. Therefore, the coefficients \(a_{i,j}\), \(i=0,1,\ldots,M\), \(j=0,1,\ldots,N\), can be achieved. As a result, the approximate solution \(v_{N,M}(x,t)\) can be evaluated.

5 Numerical example

Consider the V-OF Galilei invariant advection–diffusion equation

$$ \frac{{\partial v(x,t)}}{{\partial t}}+ \frac{{\partial v(x,t)}}{{\partial x}} = {}_{0} \mathscr{D}_{t}^{1 - \gamma (x,t) } \biggl( \frac{{\partial^{2} v(x,t)}}{{\partial x^{2} }} \biggr)+ R(x,t,v) $$
(5.1)

with the initial and boundary conditions

$$ \begin{aligned} &v(x,0) = 0,\quad 0< x < 1, \\ & v(0,t) = t^{2} ,\qquad v(1,t) = et^{2}, \quad 0 < t \le 1, \end{aligned} $$
(5.2)

where

$$ R(x,t,v)=v(x,t)-v^{2}(x,t)+e^{x}t \biggl(2+e^{x}t^{3}-2\frac{t^{\gamma (x,t)}}{ \Gamma (2+\gamma (x,t))} \biggr). $$
(5.3)

The exact solution is

$$v(x,t) =e^{x} t^{2}. $$

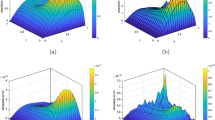
We compare our results with those obtained by Chen et al. [43]. For various choices of \(\gamma (x,t)\), N, and M, the maximum absolute errors are listed in Table 1. Meanwhile, the results of [43] are presented in the first column of this table. Obviously, our method is more accurate than the method proposed in [43]. Moreover, Fig. 1 displays the space-time graph of the absolute error (AE) functions between the approximate and exact solutions for \(\gamma (x,t)=\frac{16+(xt)^{2}- \sin^{3}(xt)+\cos^{4}(xt)}{500}\) with \(N=M=6\) and \(N=M=12\), respectively. To demonstrate the convergence of the proposed method, in Fig. 2, we plot the logarithmic graph of the maximum absolute errors \((\log_{10} Error)\) with \(\gamma (x,t)=\frac{10- \sin (xt)}{310}\). The numerical results of this example show that the numerical errors decay rapidly as N increases. Also, all values of \(\gamma (x,t)\) are accurate and can be simply obtained.

Figure 1
figure 1

The space-time graphs of the AE functions at \(\gamma (x,t)=\frac{16+(xt)^{2}- \sin^{3}(xt)+\cos^{4}(xt)}{500}\)

Full size image
Figure 2
figure 2

Convergence of problem (5.1)

Full size image
Table 1 The maximum absolute errors
Full size table

6 Conclusions

In this paper, we proposed an efficient method for solving the V-OF Galilei invariant advection–diffusion equation with a nonlinear source term. The proposed method based on the Legendre–Gauss–Lobatto collocation technique combined with the associated operational matrices of V-OF derivatives. This algorithm was employed for solving a class of variable-order fractional differential equations. The method has the advantage of transforming the problem into the solution of a system of algebraic equations, which greatly simplifies it. Finally, we presented a numerical example to demonstrate the efficiency of the proposed method.