1 Introduction

Amensalism is one of the basic interactions between the species, where a species inflicts harm on the other species without any costs or benefits received by the other. During the last decade, many scholars [1–15] investigated the dynamic behaviors of the amensalism model. Such topics as the local stability of the equilibrium [1, 5, 12, 14], the existence of the positive periodic solution [2, 11, 13], extinction of the species [3], bifurcation of the system with delay [7] and the influence of the refuge [10, 14] have been studied and many excellent results have been obtained. Recently, Xiong et al. [1] proposed the following amensalism model:

$$ \begin{aligned} \frac{dN_{1}}{dt}&=r_{1}N_{1} \biggl(1- \frac{N_{1}}{P_{1}}-u\frac{N _{2}}{P_{1}} \biggr), \\ \frac{dN_{2}}{dt}&=r_{2}N_{2} \biggl(1-\frac{N_{2}}{P_{2}} \biggr), \end{aligned} $$
(1.1)

where \(r_{i}, P_{i}, u, i=1, 2\), are all positive constants. The system admits four equilibria:

$$ A(0,0), \qquad B(P_{1}, 0), \qquad C(0, P_{2}), \qquad D(P_{1}-uP_{2}, P_{2}). $$

Concerned with the stability property of the above equilibria, the authors obtained the following results.

Theorem A

  1. (1)

    \(A(0,0)\) is unstable;

  2. (2)

    \(B(P_{1}, 0) \) is a saddle point, thus is unstable;

  3. (3)

    if \(u<\frac{P_{1}}{P_{2}}\), \(C(0, P_{2})\) is a saddle point and consequently unstable; if \(u>\frac{P_{1}}{P_{2}}\), \(C(0, P_{2})\) is a stable node;

  4. (4)

    if \(u<\frac{P_{1}}{P_{2}}\), \(D(P_{1}-uP_{2}, P_{2})\) is a stable node.

On the other hand, as was pointed out by Chakraborty et al. [16], the study of resource management, including fisheries, forestry, and wildlife management, has great importance. They argued that it is necessary to harvest the population, but harvesting should be regulated so that both the ecological sustainability and conservation of the species can be implemented in a long run. Already, they proposed a non-selective harvesting predator–prey system incorporating partial closure for the populations, they investigated the local and global stability property of the system, and some interesting results related to the optimal harvesting were obtained.

Though there are many papers concerned with the harvesting of the ecosystem system [15–26], to this day, seldom did scholars consider the influence of harvesting on the amensalism model. Stimulated by the works of Xiong et al. [1] and Chakraborty et al. [16], in this paper, we propose the following non-selective harvesting Lotka–Volterra amensalism model incorporating partial closure for the populations:

$$ \begin{aligned} \frac{dN_{1}}{dt}&=r_{1}N_{1} \biggl(1- \frac{N_{1}}{P_{1}}-u\frac{N _{2}}{P_{1}} \biggr)-q_{1}EmN_{1}, \\ \frac{dN_{2}}{dt}&=r_{2}N_{2} \biggl(1-\frac{N_{2}}{P_{2}} \biggr)-q _{2}EmN_{2}, \end{aligned} $$
(1.2)

where \(r_{i}\), \(P_{i}\), u, \(i=1, 2\), are all positive constants. \(r_{i}(P_{i})\) represents the intrinsic growth rate (environmental carrying capacity) of the ith species, E is the combined fishing effort used to harvest and \(m(0< m<1)\) is the fraction of the stock available for harvesting. One could refer to [1, 16] for more background and the adjustment of system (1.2).

As far as system (1.2) is concerned, one interesting issue is the following:

Find out the influence of the parameter m, which reflects the fraction of the stock available for harvesting.

The paper is arranged as follows. We investigate the existence and locally stability property of the equilibrium solutions of system (1.2) in the next section. In Sect. 3, by constructing some suitable Lyapunov function, we investigate the global stability property of the equilibria. The influence of the parameter m is then discussed in Sect. 4. Some examples together with their numeric simulations are presented in Sect. 5 to show the feasibility of the main results. We end this paper with a brief discussion.

2 Local stability of the equilibria

The system always admits the boundary equilibrium \(A(0,0)\).

If \(r_{1}>Emq_{1}\) holds, the system admits the boundary equilibrium \(B(N_{10}, 0)\), where \(N_{10}= \frac{P_{1}(r_{1}-Emq _{1})}{r_{1}}\).

If \(r_{2}>Emq_{2}\) holds, the system admits the boundary equilibrium \(C(0, N_{20})\), where \(N_{20}= \frac{P_{2}(r_{2}-Emq _{2})}{r_{2}}\).

If \(r_{1}r_{2}P_{1}+r_{1}umEP_{2}q_{2}>r_{1}r_{2}uP_{2}+r_{2}mq _{1}EP_{1}\) and \(r_{2}>Emq_{2}\) hold, then the system admits a unique positive equilibrium

$$ \bigl(N_{1}^{*},N_{2}^{*}\bigr)= \biggl( \frac{r_{1}r_{2}P_{1}+r_{1}umEP_{2}q _{2}-r_{1}r_{2}uP_{2}-r_{2}mq_{1}EP_{1}}{r_{1}r_{2}}, \frac{P_{2}(r_{2}-Emq_{2})}{r_{2}} \biggr). $$

We shall now investigate the local stability property of the above equilibria.

The variational matrix of the system of Eq. (1.2) is

$$ V(N_{1},N_{2})=\left ( \textstyle\begin{array}{@{}c@{\quad }c@{}} L_{1} & - \frac{ur_{1}N_{1}}{P_{1}} \\ 0& L_{2} \end{array}\displaystyle \right ) , $$
(2.1)

where

$$\begin{aligned}& L_{1}= \frac{r_{1}P_{1}-2r_{1}N_{1}-r_{1}uN_{2}-EP_{1}mq_{1}}{P _{1}}, \\& L_{2}= \frac{r_{2}P_{2}-2N_{2}r_{2}-EP_{2}mq_{2}}{P_{2}}. \end{aligned}$$

Theorem 2.1

  1. (1)

    Assume that

    $$ m>\max \biggl\{ \frac{r_{1}}{Eq_{1}}, \frac{r_{2}}{Eq_{2}} \biggr\} $$
    (2.2)

    holds, then \(A(0,0)\) is locally stable, otherwise it is unstable;

  2. (2)

    Assume that

    $$ \frac{r_{2}}{Eq_{2}}< m< \frac{r_{1}}{Eq_{1}} $$
    (2.3)

    holds, then \(B(N_{10}, 0)\) is locally stable, otherwise it is unstable;

  3. (3)

    Assume that

    $$ \frac{r_{1}r_{2}(P_{1}-uP_{2})}{r_{2}q_{1}EP_{1}- r_{1}uEP_{2}q _{2}} < m< \frac{r_{2}}{Eq_{2}} $$
    (2.4)

    holds, then \(C(0, N_{20})\) is locally stable, otherwise it is unstable;

  4. (4)

    Assume that

    $$ m< \min \biggl\{ \frac{r_{2}}{Eq_{2}}, \frac{r_{1}r_{2}(P_{1}-uP_{2})}{r _{2}q_{1}EP_{1}- r_{1}uEP_{2}q_{2}} \biggr\} $$
    (2.5)

    holds, then \(D(N_{1}^{*}, N_{2}^{*})\) is locally stable.

Proof

(1) From (2.1) we could see that the Jacobian of the system about the equilibrium point \(A(0,0)\) is given by

$$ \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} r_{1}-Emq_{1}& 0 \\ 0& r_{2}-Emq_{2} \end{array}\displaystyle \right ) . $$
(2.6)

The eigenvalues of the matrix are \(\lambda_{1}=r_{1}-Emq_{1}, \lambda _{2}=r_{2}-Emq_{2}\). Hence, under assumption (2.2), \(\lambda_{1}<0, \lambda_{2}<0\), and \(A(0,0)\) is locally stable, otherwise it is unstable;

(2) The Jacobian of the system about the equilibrium point \(B(N_{10},0)\) is given by

$$ \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} Emq_{1}-r_{1}& (Emq_{1}-r_{1})u \\ 0&r_{2}-Emq_{2} \end{array}\displaystyle \right ) . $$
(2.7)

The eigenvalues of the matrix are \(\lambda_{1}=Emq_{1}-r_{1}, \lambda _{2}= r_{2}-Emq_{2}\). Under assumption (2.3), \(\lambda_{1}<0, \lambda _{2}<0\), and \(B(N_{10}, 0)\) is locally stable, otherwise it is unstable;

(3) The Jacobian of the system about the equilibrium point \(C(0,N_{20})\) is given by

$$ \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} \frac{r_{1}r_{2}P_{1}+r_{1}umEP_{2}q_{2}-r_{1}r_{2}uP_{2}-r_{2}mq _{1}EP_{1}}{r_{2}P_{1}}&0 \\ 0&Emq_{2}-r_{2} \end{array}\displaystyle \right ) . $$
(2.8)

Under assumption (2.4), the two eigenvalues of the matrix satisfy

$$\begin{aligned} \lambda_{1}= \frac{r_{1}r_{2}P_{1}+r_{1}umEP_{2}q_{2}-r_{1}r_{2}uP _{2}-r_{2}mq_{1}EP_{1}}{r_{2}P_{1}}< 0, \qquad \lambda_{2}=Emq_{2}-r_{2}< 0. \end{aligned}$$

Consequently, \(C(0, N_{20})\) is locally stable, otherwise it is unstable;

(4) Noting that the positive equilibrium \(D(N_{1}^{*}, N_{2}^{*})\) satisfies

$$ \begin{aligned} &r_{1} \biggl(1- \frac{N_{1}^{*}}{P_{1}}-u \frac{N_{2}^{*}}{P_{1}} \biggr)-q_{1}Em=0, \\ &r_{2} \biggl(1- \frac{N_{2}^{*}}{P_{2}} \biggr)-q_{2}Em=0, \end{aligned} $$
(2.9)

combining with (2.1) and (2.9), we could see that the Jacobian of the system about the equilibrium point \(D(N_{1}^{*},N_{2}^{*})\) is given by

$$ \left ( \textstyle\begin{array}{@{}c@{\quad }c@{}} - \frac{r_{1}N_{1}^{*}}{P_{1}}&- \frac{r_{1}N_{1}^{*}u}{P_{1}} \\ 0&- \frac{r_{2}N_{2}^{*}}{P_{2}} \end{array}\displaystyle \right ) . $$
(2.10)

The eigenvalues of the variational matrix (2.10) are the roots \(\lambda_{1}=- \frac{r_{1}N_{1}^{*}}{P_{1}}<0, \lambda_{2}=- \frac{r _{2}N_{2}^{*}}{P_{2}}<0\). Thus, \(D(N_{1}^{*}, N_{2}^{*})\) is locally stable.

The proof of Theorem 2.1 is finished. □

3 Global stability

One interesting problem is to further investigate the global stability property of the equilibria of system (1.2), since the global one means that despite the random initial condition, the finial dynamic behaviors of the system could be forecasted. In this aspect, we could obtain the following result.

Theorem 3.1

  1. (1)

    Assume that

    $$ m>\max \biggl\{ \frac{r_{1}}{Eq_{1}}, \frac{r_{2}}{Eq_{2}} \biggr\} $$
    (3.1)

    holds, then \(A(0,0)\) is globally asymptotically stable;

  2. (2)

    Assume that

    $$ \frac{r_{2}}{Eq_{2}}< m< \frac{r_{1}}{Eq_{1}} $$
    (3.2)

    holds, then \(B(N_{10}, 0)\) is globally asymptotically stable;

  3. (3)

    Assume that

    $$ \frac{r_{2}}{Eq_{2}}>m> \frac{r_{1}}{Eq_{1}} $$
    (3.3)

    holds, then \(C(0, N_{20})\) is globally asymptotically stable;

  4. (4)

    Assume that

    $$ m< \min \biggl\{ \frac{r_{2}}{Eq_{2}}, \frac{r_{1}r_{2}(P_{1}-uP_{2})}{r _{2}q_{1}EP_{1}- r_{1}uEP_{2}q_{2}} \biggr\} $$
    (3.4)

    holds, then \(D(N_{1}^{*}, N_{2}^{*})\) is globally asymptotically stable.

Proof

We will prove Theorem 3.1 by constructing some suitable Lyapunov functions.

(1) We define a Lyapunov function

$$ V_{1}(N_{1},N_{2})= N_{1}+ N_{2}. $$

One could easily see that the function \(V_{1}\) is zero at the equilibrium \(A(0,0)\) and is positive for all other positive values of \(N_{1}\) and \(N_{2}\). The time derivative of \(V_{1}\) along the trajectories of (1.2) is

$$\begin{aligned} &D^{+}V_{1}(t) \\ &\quad = N_{1} \biggl(r_{1} \biggl(1-\frac{N_{1}}{P_{1}}-u \frac{N_{2}}{P_{1}} \biggr)-q_{1}Em \biggr)+ N_{2} \biggl(r_{2} \biggl(1-\frac{N_{2}}{P_{2}} \biggr)-q _{2}Em \biggr) \\ &\quad = (r_{1}-q_{1}Em)N_{1} - \frac{r_{1}}{P_{1}}N_{1}^{2}- \frac{u }{P_{1}}N_{1}N_{2} \\ &\quad \quad {}+ (r_{2}-Eq_{2}m)N_{2}- \frac{r_{2} }{P_{2}}N_{2}^{2}. \end{aligned}$$
(3.5)

Obviously, under assumption (3.1), \(D^{+}V_{1}(t)<0\) strictly for all \(N_{1}, N_{2}>0\) except the boundary equilibrium \(A(0, 0)\), where \(D^{+}V_{1}(t)=0\). Thus, \(V_{1}(N_{1},N_{2})\) satisfies Lyapunov’s asymptotic stability theorem, and the boundary equilibrium \(A(0, 0)\) of system (1.2) is globally asymptotically stable.

(2) Noting that \((N_{10},0)\) satisfies

$$ r_{1} \biggl(1-\frac{N_{10}}{P_{1}} \biggr)-q_{1}Em =0, $$
(3.6)

we define a Lyapunov function

$$ V_{2}(N_{1},N_{2})=\eta \biggl(N_{1}-N_{10}-N_{10} \ln \frac{N_{1}}{N _{10}} \biggr)+ N_{2}, $$

where η is a suitable constant to be determined in the subsequent steps. One could easily see that the function \(V_{2}\) is zero at the equilibrium \(B(N_{10},0)\) and is positive for all other positive values of \(N_{1}\) and \(N_{2}\). By applying (3.6), the time derivative of \(V_{2}\) along the trajectories of (1.2) is

$$\begin{aligned} &D^{+}V_{2}(t) \\ &\quad =\eta (N_{1}-N_{10}) \biggl(r_{1} \biggl(1- \frac{N_{1}}{P_{1}}-u\frac{N _{2}}{P_{1}} \biggr)-q_{1}Em \biggr) \\ &\quad \quad {}+ N_{2} \biggl(r_{2} \biggl(1- \frac{N_{2}}{P_{2}} \biggr)-q_{2}Em \biggr) \\ &\quad = \eta (N_{1}-N_{10}) \biggl( \frac{r_{1} }{P_{1}}(N_{10}-N_{1})-r _{1}u\frac{N_{2}}{P_{1}} \biggr) \\ &\quad \quad {}+ (r_{2}-Eq_{2}m)N_{2}- \frac{r_{2} }{P_{2}}N_{2}^{2} \\ &\quad = - \frac{r_{1}\eta }{P_{1}}(N_{1}-N_{10})^{2} - \frac{r_{1}u \eta }{P_{1}}N_{1}N_{2} \\ &\quad \quad {}+ \frac{N_{10}r_{1}u\eta }{P_{1}}N_{2} +(r_{2}-Eq_{2}m)N_{2}- \frac{r _{2} }{P_{2}}N_{2}^{2} \\ &\quad = - \frac{r_{1}\eta }{P_{1}}(N_{1}-N_{10})^{2} - \frac{r_{1}u \eta }{P_{1}}N_{1}N_{2} \\ &\quad \quad {}+ \biggl( \frac{N_{10}r_{1}u\eta }{P_{1}}+(r_{2}-Eq_{2}m) \biggr)N_{2} - \frac{r_{2} }{P_{2}}N_{2}^{2}. \end{aligned}$$

Noting that \(r_{2}< Emq_{2}\), we can choose \(\eta = \frac{( Eq_{2}m-r _{2})P_{1}}{N_{10}r_{1}u}>0\), and

$$ D^{+}V_{2}(t) = - \frac{r_{1}\eta }{P_{1}}(N_{1}-N_{10})^{2} - \frac{r_{1}u}{P_{1}}N_{1}N_{2} - \frac{r_{2} }{P_{2}}N_{2}^{2}. $$

Therefore, \(D^{+}V_{2}(t)<0\) strictly for all \(N_{1}, N_{2}>0\) except the boundary equilibrium \(B(N_{10}, 0)\), where \(D^{+}V_{2}(t)=0\). Thus, \(V_{2}(N_{1},N_{2})\) satisfies Lyapunov’s asymptotic stability theorem, and the boundary equilibrium \(B(N_{10}, 0)\) of system (1.2) is globally asymptotically stable.

(3) Noting that \(C(0,N_{20})\) satisfies

$$ r_{2} \biggl(1-\frac{N_{20}}{P_{2}} \biggr)-q_{2}Em =0, $$
(3.7)

we define a Lyapunov function

$$ V_{3}(N_{1},N_{2})= N_{1}+ N_{2}-N_{20}-N_{20}\ln \frac{N_{2}}{N_{20}} . $$

One could easily see that the function \(V_{3}\) is zero at the equilibrium \(C(0,N_{20})\) and is positive for all other positive values of \(N_{1}\) and \(N_{2}\). By using (3.3) and (3.7), the time derivative of \(V_{3}\) along the trajectories of (1.2) is

$$ \begin{aligned}[b] &D^{+}V_{3}(t) \\ &\quad = r_{1}N_{1} \biggl(1-\frac{N_{1}}{P_{1}}-u \frac{N_{2}}{P_{1}} \biggr)-q _{1}EmN_{1} \\ &\quad \quad {}+ (N_{2}-N_{20}) \biggl(r_{2} \biggl(1-\frac{N_{2}}{P_{2}} \biggr)-q_{2}Em \biggr) \\ &\quad = (r_{1}-q_{1}Em)N_{1}- \frac{r_{1}}{P_{1}}N_{1}^{2}- \frac{r _{1}u}{P_{1}}N_{1}N_{2} \\ &\quad \quad {}+ (N_{2}-N_{20}) \frac{r_{2}}{P_{2}}(N_{20}-N_{2}) \\ &\quad = (r_{1}-q_{1}Em)N_{1}- \frac{r_{1}}{P_{1}}N_{1}^{2}- \frac{r _{1}u}{P_{1}}N_{1}N_{2}- \frac{r_{2}}{P_{2}} (N_{2}-N_{20})^{2}. \end{aligned} $$
(3.8)

Therefore, \(D^{+}V_{3}(t)<0\) strictly for all \(N_{1}, N_{2}>0\) except the boundary equilibrium \(C(0, N_{20})\), where \(D^{+}V_{3}(t)=0\). Thus, \(V_{3}(N_{1},N_{2})\) satisfies Lyapunov’s asymptotic stability theorem, and the boundary equilibrium \(C(0, N_{20})\) of system (1.2) is globally asymptotically stable.

(4) Noting that \(D(N_{1}^{*},N_{2}^{*})\) satisfies

$$ \begin{aligned}& r_{1} \biggl(1- \frac{N_{1}^{*}}{P_{1}}-u \frac{N_{2}^{*}}{P_{1}} \biggr)-q_{1}Em=0, \\ &r_{2} \biggl(1- \frac{N_{2}^{*}}{P_{2}} \biggr)-q_{2}Em=0, \end{aligned} $$
(3.9)

we define a Lyapunov function

$$ V_{4}(x,y)=\eta_{1} \biggl(N_{1}-N_{1}^{*}-N_{1}^{*} \ln \frac{N_{1}}{N _{1}^{*}} \biggr)+\eta_{2} \biggl(N_{2}-N_{2}^{*}-N_{2}^{*} \ln \frac{N_{2}}{N _{2}^{*}} \biggr), $$

where \(\eta_{1}\) and \(\eta_{2}\) are suitable constants to be determined in the subsequent steps. One could easily see that the function \(V_{4}\) is zero at the equilibrium \(D(N_{1}^{*},N_{2}^{*})\) and is positive for all other positive values of \(N_{1}\) and \(N_{2}\). By applying (3.9), the time derivative of \(V_{4}\) along the trajectories of (1.2) is

$$ \begin{aligned}[b] &D^{+}V_{4}(t) \\ &=\eta_{1}\bigl(N_{1}-N_{1}^{*}\bigr) \biggl(r_{1} \biggl(1-\frac{N_{1}}{P_{1}}-u\frac{N _{2}}{P_{1}} \biggr)-q_{1}Em \biggr) \\ &\quad {}+\eta_{2}\bigl(N_{2}-N_{2}^{*} \bigr) \biggl(r_{2} \biggl(1-\frac{N_{2}}{P_{2}} \biggr)-q_{2}Em \biggr) \\ &=\eta_{1} \bigl(N_{1}-N_{1}^{*}\bigr) \biggl( \frac{r_{1}N_{1}^{*}}{P_{1}}+ \frac{r _{1}uN_{2}^{*}}{P_{1}}- \frac{r_{1}N_{1} }{P_{1}}- \frac{r_{1}uN _{2} }{P_{1}} \biggr) \\ &\quad {}+\eta_{2}\bigl(N_{2}-N_{2}^{*} \bigr) \biggl( \frac{r_{2}N_{2}^{*}}{P_{2}}- \frac{r _{2}N_{2}}{P_{2}} \biggr) \\ &= - \frac{r_{1}}{P_{1}}\eta_{1}\bigl(N_{1}-N_{1}^{*} \bigr)^{2}- \frac{r _{1}u\eta_{1}}{P_{1}}\bigl(N_{1}-N_{1}^{*} \bigr) \bigl(N_{2}-N_{2}^{*}\bigr) \\ &\quad {}- \frac{r_{2}\eta_{2}}{P_{2}}\bigl(N_{2}-N_{2}^{*} \bigr)^{2}. \end{aligned} $$
(3.10)

Now let us take \(\eta_{1}=1, \eta_{2}= \frac{2r_{1}u^{2}P_{2}}{r _{2}P_{1}}\), then

$$ \begin{aligned}[b] &D^{+}V_{4}(t) \\ &\quad = - \frac{r_{1}}{P_{1}} \bigl(N_{1}-N_{1}^{*} \bigr)^{2}- \frac{r_{1}u }{P _{1}}\bigl(N_{1}-N_{1}^{*} \bigr) \bigl(N_{2}-N_{2}^{*}\bigr)- \frac{2r_{1}u^{2}}{P_{1}}\bigl(N _{2}-N_{2}^{*} \bigr)^{2} \\ &\quad = \frac{r_{1}}{P_{1}} \bigl[ \bigl(N_{1}-N_{1}^{*} \bigr)^{2}+u\bigl(N_{1}-N_{1} ^{*}\bigr) \bigl(N_{2}-N_{2}^{*}\bigr)+ u^{2} \bigl(N_{2}-N_{2}^{*}\bigr)^{2} \bigr] \\ &\quad =- \frac{r_{1}}{P_{1}} \bigl(N_{1}-N_{1}^{*}, N_{2}-N_{2}^{*}\bigr)\left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} 1&\frac{u}{2} \\ \frac{u}{2}&u^{2} \end{array}\displaystyle \right ) \left ( \textstyle\begin{array}{@{}c@{}} N_{1}-N_{1}^{*} \\ N_{2}-N_{2}^{*} \end{array}\displaystyle \right ) . \end{aligned} $$
(3.11)

Since

$$ \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} 1&\frac{u}{2} \\ \frac{u}{2}&u^{2} \end{array}\displaystyle \right ) $$

is positive definite, it follows that \(D^{+}V_{4}(t)<0\) strictly for all \(N_{1}, N_{2}>0\) except the positive equilibrium \(C(N_{1}^{*}, N_{2} ^{*})\), where \(D^{+}V_{4}(t)=0\). Thus, \(V_{4}(N_{1},N_{2})\) satisfies Lyapunov’s asymptotic stability theorem, and the positive equilibrium \(D(N_{1}^{*}, N_{2}^{*})\) of system (1.2) is globally asymptotically stable. This ends the proof of Theorem 3.1. □

Remark 3.1

Theorems 2.1 and 3.1 show that if system (1.2) admits the unique positive equilibrium, then the positive equilibrium is globally asymptotically stable.

Remark 3.2

Compared with Theorems 2.1 and 3.1, one could see that in three cases, the local stability of the equilibrium also implies the global one. However, to ensure \(C(0,N_{20})\) is globally stable, we need assumption (3.3) since our condition is a set of sufficient conditions, maybe it is not the necessary one. Whether (2.4) is enough to ensure the globally attractivity of \(C(0,N_{20})\) or not is still unknown. Obviously, we could not deal with this problem by constructing a suitable Lyapunov function.

Remark 3.3

From Theorem 3.1(4) and the biological meaning of the parameter m, we can draw the conclusion: if the fraction of the stock available for harvesting is limited, then two species could coexist in the long run, despite the initial state.

4 The influence of the parameter m

Now let us consider the influence of the parameter on the finial density of the two species.

$$ \frac{dN_{1}^{*}}{dm}= \frac{EP_{2}q_{2}r_{1}u-EP_{1}q_{1}r _{2}}{r_{1}r_{2}}, $$

thus

  1. (1)

    If \(P_{2}q_{2}r_{1}u>P_{1}q_{1}r_{2}\), then \(\frac{dN_{1}^{*}}{dt}>0\), and \(N_{1}^{*}\) is the strictly increasing function of m;

  2. (2)

    If \(P_{2}q_{2}r_{1}u< P_{1}q_{1}r_{2}\), then \(\frac{dN_{1}^{*}}{dt}<0\), and \(N_{1}^{*}\) is the strictly decreasing function of m.

Since

$$ \frac{dN_{2}^{*}}{dm}= \frac{EP_{2}q_{2} }{ r_{2}}< 0, $$

then \(N_{2}^{*}\) is the strictly decreasing function of m.

5 Numerical simulations

Example 5.1

Consider the following amensalism system:

$$ \begin{aligned} \frac{dN_{1}}{dt}&= N_{1} \biggl(1-N_{1}- \frac{1}{2} N_{2} \biggr)-4mN_{1}, \\ \frac{dN_{2}}{dt}&= N_{2} (1-N_{2} )-2mN_{2}. \end{aligned} $$
(5.1)

Here, corresponding to system (1.2), we take \(r_{1}=r_{2}=P_{1}=P_{2}=E=1, q_{1}=4, q_{2}=2, u=\frac{1}{2}\).

  1. (1)

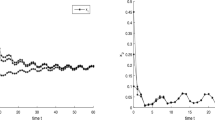
    For the system without harvesting, i.e., for \(m=0\), the system admits a unique positive equilibrium \((\frac{1}{2},1)\) (see Fig. 1, Fig. 2);

    Figure 1
    figure 1

    Numeric simulations of the first components of system (5.1) with \(m=0\), the initial conditions \((x(0), y(0))=(0.5,0.1), (0.8,1), (0.3, 3)\), and \((0.7,2)\), respectively

    Full size image
    Figure 2
    figure 2

    Numeric simulations of the second components of system (5.1) with \(m=0\), the initial conditions \((x(0), y(0))=(0.5,0.1), (0.8,1), (0.3, 3)\), and \((0.7,2)\), respectively

    Full size image
  2. (2)

    Take \(m=0.6\), then \(m>\max \{ \frac{r_{1}}{Eq_{1}}, \frac{r _{2}}{Eq_{2}}\}\), and both species will be driven to extinction (see Fig. 3, Fig. 4);

    Figure 3
    figure 3

    Numeric simulations of the first components of system (5.1) with \(m=0.6\), the initial conditions \((x(0), y(0))=(0.5,0.1), (0.8,1), (0.3, 3)\), and \((0.7,2)\), respectively

    Full size image
    Figure 4
    figure 4

    Numeric simulations of the second components of system (5.1) with \(m=0.6\), the initial conditions \((x(0), y(0))=(0.5,0.1), (0.8,1), (0.3, 3)\), and \((0.7,2)\), respectively

    Full size image
  3. (3)

    Take \(m=0.3\), then \(\frac{r_{1}}{Eq_{1}}< m< \frac{r_{2}}{Eq _{2}}\), and \(C(0, 0.4)\) is globally attractive, that is, \(N_{2}\) will be driven to extinction, and \(N_{1}\) is globally attractive (see Fig. 5, Fig. 6);

    Figure 5
    figure 5

    Numeric simulations of the first components of system (5.1) with \(m=0.3\), the initial conditions \((x(0), y(0))=(0.5,0.1), (0.8,1), (0.3, 3)\), and \((0.7,2)\), respectively

    Full size image
    Figure 6
    figure 6

    Numeric simulations of the second components of system (5.1) with \(m=0.3\), the initial conditions \((x(0), y(0))=(0.5,0.1), (0.8,1), (0.3, 3)\), and \((0.7,2)\), respectively

    Full size image
  4. (4)

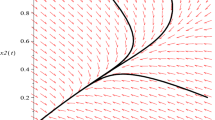
    Take \(m=0.1\), then \(m<\min \{\frac{r_{2}}{Eq_{2}}, \frac{r _{1}r_{2}(P_{1}-uP_{2})}{r_{2}q_{1}EP_{1}- r_{1}uEP_{2}q_{2}} \}= \frac{1}{6}\) and \(D(0.2,0.8)\) is globally attractive, that is, both species could coexist in a stable state (see Fig. 7, Fig. 8).

    Figure 7
    figure 7

    Numeric simulations of the first components of system (5.1) with \(m=0.1\), the initial conditions \((x(0), y(0))=(0.5,0.1), (0.8,1), (0.3, 3)\), and \((0.7,2)\), respectively

    Full size image
    Figure 8
    figure 8

    Numeric simulations of the second components of system (5.1) with \(m=0.1\), the initial conditions \((x(0), y(0))=(0.5,0.1), (0.8,1), (0.3, 3)\), and \((0.7,2)\), respectively

    Full size image

6 Discussion

With the aim of the ecological sustainability and conservation of the species to be implemented in a long run, in this paper, we propose a non-selective harvesting Lotka–Volterra amensalism model incorporating partial closure for the populations, i.e., system (1.2), which can be seen as the generalization of system (1.1), and the model is more suitable for the real situation.

With the introducing of harvesting, the dynamic behaviors of the system become very complicated. Depending on the fraction of the stock that could be harvested, the system may have positive equilibrium, which is globally asymptotically stable, which means that two species could coexist in a stable state; or one of the species will be driven to extinction, or both of the species could be driven to extinction.

To sum up, to ensure the conservation of the species, we need to restrict the harvesting to a limited area. Otherwise, although we can afford the area which could not be harvested, the species may still be driven to extinction. Theorem 2.1 and 3.1 give some threshold on m, which ensures the coexistence of the two species. The results obtained in this paper maybe useful in designing the natural protection area.