Abstract
By means of a variational analysis and the theory of variable exponent Sobolev spaces, the existence of weak solutions for two point boundary value problems of Schrödingerean predator-prey system with latent period is investigated either analytically or numerically. More precisely, the local stability of the Schrödingerean equilibrium and endemic equilibrium of the model are discussed in detail. And we specially analyzed the existence and stability of the Schrödingerean Hopf bifurcation by using the center manifold theorem and the bifurcation theory. As applications, theoretic analysis and numerical simulation show that the Schrödingerean predator-prey system with latent period has very rich dynamic characteristics.
Similar content being viewed by others
1 Introduction
The role of mathematical modeling has been intensively growing in the study of epidemiology. Various epidemic models have been proposed and explored extensively and great progress has been achieved in the studies of disease control and prevention. Many authors have investigated the autonomous epidemic models. May and Odter [1] proposed a time-periodic reaction-diffusion epidemic model which incorporates a simple demographic structure and the latent period of an infectious disease. Guckenheimer and Holmes [2] examined an SIR epidemic model with a non-monotonic incidence rate, and they also analyzed the dynamical behavior of the model and derived the stability conditions for the disease-free and the endemic equilibrium. Berryman and Millstein [3] investigated an SVEIS epidemic model for an infectious disease that spreads in the host population through horizontal transmission, and they have shown that the model exhibits two equilibria, namely, the disease-free equilibrium and the endemic equilibrium. Hassell et al. [4] presented four discrete epidemic models with the nonlinear incidence rate by using the forward Euler and backward Euler methods, and they discussed the effect of two discretizations on the stability of the endemic equilibrium for these models. Shilnikov et al. [5] proposed an VEISV network worm attack model and derived global stability of a worm-free state and local stability of a unique worm-epidemic state by using the reproduction rate. Robinson and Holmes [6] discussed the dynamical behaviors of a Schrödingerean predator-prey system, and they showed that the model undergoes a flip bifurcation and Hopf bifurcation by using the center manifold theorem and bifurcation theory. Bacaër and Dads [7] investigated an SVEIS epidemic model for an infectious disease that spreads in the host population through horizontal transmission.
Recently, Yan et al. [8, 9] and Xue [10] discussed the threshold dynamics of a time-periodic reaction-diffusion epidemic model with latent period. In this paper, we will study the existence of the disease-free equilibrium and endemic equilibrium, and the stability of the disease-free equilibrium and the endemic equilibrium for this system. Conditions will be derived for the existence of a flip bifurcation and a Hopf bifurcation by using the center manifold theorem [11] and bifurcation theory [12–14].
The rest of this paper is organized as follows. A discrete SIR epidemic model with latent period is established in Section 2. In Section 3 we obtain the main results: the existence and local stability of fixed points for this system. We show that this system undergoes the flip bifurcation and the Hopf bifurcation by choosing a bifurcation parameter in Section 4. A brief discussion is given in Section 5.
2 Model formulation
In 2015, Yan et al. [10] discussed the threshold dynamics of a time-periodic reaction-diffusion epidemic model with latent period. We consider the continuous-time SIR epidemic model described by the differential equations
where \(S(t)\), \(I(t)\) and \(R(t)\) denote the sizes of the susceptible, infected and removed individuals, respectively, the constant β is the transmission coefficient, and γ is the recovery rate. Let \(S_{0}=S(0)\) be the density of the population at the beginning of the epidemic with everyone susceptible. It is well known that the basic reproduction number \(R_{0}=\beta S_{0}/\gamma\) completely determines the transmission dynamics (an epidemic occurs if and only if \(R_{0}>1\)); see also [8]. It should be emphasized that system (1) has no vital dynamics (births and deaths) because it was usually used to describe the transmission dynamics of disease within a short outbreak period. However, for an endemic disease, we should incorporate the demographic structure into the epidemic model. The classical endemic model is the following SIR model with vital dynamics:
which is almost the same as the SIR epidemic model (1) above, except that it has an inflow of newborns into the susceptible class at rate μN and deaths in the classes at rates μN, μI and μR, where N is a positive constant denoting the total population size. For this model, the basic reproduction number is given by
which is the contact rate times the average death-adjusted infectious period \(\frac{1}{\gamma+\mu}\). The disease-free equilibrium \(E_{0}(N,0,0)\) of model (2) is as follows:
where h, N, μ, β and γ are all defined in (2).
Remark 1
If the basic reproductive rate \(R_{0}<1\), then model (2) has only a disease-free equilibrium \(E_{1}(N,0)\). If the basic reproductive rate \(R_{0}>1\), then model (2) has two equilibria: a disease-free equilibrium \(E_{1}(N,0)\) and an endemic equilibrium \(E_{2}(S^{*},I^{*})\), where
3 Main results
We firstly discuss the existence of the equilibria of model (2) by using a linearization method and the Jacobian matrix. The Jacobian matrix of it is defined by
If we take the two eigenvalues of \(J(E_{1})\)
then we have the following results from Remark 1 and a simple calculation.
Theorem 1
Let \(R_{0}\)be the basic reproductive rate such that \(R_{0}<1\). Then:
- (1)
If
$$0< h< \min\biggl\{ \frac{2}{\mu},\frac{2}{(\gamma+\mu)-\beta}\biggr\} , $$then \(E_{1}(N,0)\)is asymptotically stable.
- (2)
If
$$h>\max\biggl\{ \frac{2}{\mu},\frac{2}{(\gamma+\mu)-\beta}\biggr\} \quad \textit{or} \quad \frac {2}{\mu}< h< \frac{2}{(\gamma+\mu)-\beta} $$or
$$\frac{2}{(\gamma+\mu)-\beta}< h< \frac{2}{\mu}, $$then \(E_{1}(N,0)\)is unstable.
- (3)
If
$$h=\frac{2}{\mu} \quad \textit{or}\quad h=\frac{2}{(\gamma+\mu)-\beta}, $$then \(E_{1}(N,0)\)is non-hyperbolic.
The Jacobian matrix of model (2) at \(E_{2}(S^{*},I^{*})\) is
which gives
where
and
The two eigenvalues of \(J(E_{2})\) are
Next we obtain the following result for \(E_{2}(S^{*},I^{*})\) by Remark 1 and a simple calculation.
Theorem 2
Let \(R_{0}\)be the basic reproductive rate such that \(R_{0}<1\). Then:
- (1)
Put
- (A)
\(0< h< h_{*}\)and \((\mu R_{0})^{2}-4[\mu\beta-\mu(\gamma +\mu)]\ge0\),
- (B)
\(0< h< h_{**}\)and \((\mu R_{0})^{2}-4[\mu\beta-\mu(\gamma+\mu)]<0\).
If one of the above conditions holds, then we see that \(E_{2}(S^{*},I^{*})\)is asymptotically stable.
- (A)
- (2)
Put
- (A)
\(h>h_{***}\)and \((\mu R_{0})^{2}-4[\mu\beta-\mu(\gamma+\mu )]\ge0\),
- (B)
\(0< h< h_{**}\)and \((\mu R_{0})^{2}-4[\mu\beta-\mu(\gamma+\mu)]<0\),
- (C)
\(h_{*}< h< h_{***}\)and \((\mu R_{0})^{2}-4[\mu\beta-\mu(\gamma +\mu)]\ge0\).
If one of the above conditions holds, then \(E_{2}(S^{*},I^{*})\)is unstable.
- (A)
- (3)
Put
- (A)
\(h=h_{*}\)or \(h=h_{***}\)and \((\mu R_{0})^{2}-4[\mu\beta -\mu(\gamma+\mu)]\ge0\),
- (B)
\(h=h_{**}\)and \((\mu R_{0})^{2}-4[\mu\beta-\mu(\gamma+\mu)]<0\),
where
$$\begin{aligned}& h_{*}=\frac{\mu\beta-\mu(\gamma+\mu)\sqrt{(\mu R_{0})^{2}-4[\mu \beta -\mu(\gamma+\mu)]}}{(\gamma+\mu)[\mu\beta-\mu(\gamma+\mu)]}, \\& h_{**}=\frac{\mu\beta}{(\gamma+\mu)[\mu\beta-\mu(\gamma+\mu)]}, \end{aligned}$$and
$$h_{***}=\frac{\mu\beta+\mu(\gamma+\mu)\sqrt{(\mu R_{0})^{2}-4[\mu \beta -\mu(\gamma+\mu)]}}{(\gamma+\mu)[\mu\beta-\mu(\gamma+\mu)]}. $$If one of the above conditions holds, then \(E_{2}(S^{*},I^{*})\)is non-hyperbolic.
- (A)
By a simple calculation, Conditions (A) in Theorem 2 can be written in the following form:
where
and
It is well known that if h varies in a small neighborhood of \(h_{*}\) or \(h_{***}\) and \((\mu,N,\beta,h_{*},\gamma)\in M_{1}\) or \((\mu ,N,\beta ,h_{***},\gamma)\in M_{2}\), then there may be a flip bifurcation of equilibrium \(E_{2}(S^{*},I^{*})\).
4 Bifurcation analysis
If h varies in a neighborhood of \(h_{*}\) and \((\mu,N,\beta ,h_{*},\gamma)\in M_{1}\), then we derive the flip bifurcation of model (2) at \(E_{2}(S^{*},I^{*})\). In particular, in the case that h changes in the neighborhood of \(h_{***}\) and \((\mu,N,\beta,h_{***},\gamma)\in M_{2}\) we need to make a similar calculation.
Set
If we give the parameter \(h_{1}\) a perturbation \(h^{*}\), model (2) is considered as follows:
where \(| h^{*}|\ll1\).
Put \(U_{n}=S_{n}-S^{*}\) and \(V_{n}=I_{n}-I^{*}\). We have
where
If we define matrix T as follows:
then we know that T is invertible. If we use the transformation
then model (2) becomes
Thus
where \(o((|X_{n}|+|h^{*}|)^{2})\) is a transform function, and
and
Further we find that the manifold \(W^{c}(0,0)\) has the following form:
and
Therefore the map \(G^{*}\) with respect to \(W^{c}(0,0)\) can be defined by
In order to calculate map (11), we need two quantities \(\alpha_{1}\) and \(\alpha_{2}\) which are not zero,
and
By a simply calculation, we obtain
where
Therefore we have the following result.
Theorem 3
Let \(h^{*}\)change in the a neighborhood of the origin. If \(\alpha_{2} \neq0\), then the model (9) has a flip bifurcation at \(E_{2}(S^{*},I^{*})\). If \(\alpha_{2}>0\), then the period-2 points that bifurcation from \(E_{2}(S^{*},I^{*})\)are stable. If \(\alpha_{2}<0\), then it is unstable.
We further consider the bifurcation of \(E_{2}(S^{*},I^{*})\) if h varies in a neighborhood of \(h_{***}\). Taking the parameters \((\mu,N,\beta ,h,\gamma)=(\mu_{2},N_{2},\beta_{2},h_{2},\gamma_{2})\in N^{*}\) arbitrarily, and also giving h a perturbation \(h^{*}\) at \(h_{2}\), then model (2) gets the following form:
Put \(U_{n}=S_{n}-S^{*}\) and \(V_{n}=I_{n}-I^{*}\). We change the equilibrium \(E_{2}(S^{*},I^{*})\) of model (9) and have the following result:
which gives
where
and
It is easy to see that
which yields
We remark that \((\mu_{2},N_{2},\beta_{2},h_{2},\gamma_{2})\in N^{+}\) and \(\bigtriangleup<0\), and then we have
Thus
which means that
Hence, the eigenvalues \(\omega_{1,2}\) of equilibrium (0,0) of model (14) do not lay in the intersection when \(h^{*}=0\) and (14) holds.
When \(h^{*}=0\) we may begin to study the model (14). Put
and
where T is invertible.
If we use the transformation
then the model (14) gets the following form:
where
and
Moreover,
Thus we have
where
and
Therefore we have the following result.
Theorem 4
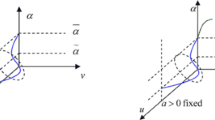
Let \(a \neq0\)and \(h^{*}\)change in a neighborhood of \(h_{***}\). If the condition (15) holds, then model (13) undergoes a Hopf bifurcation at \(E_{2}(S^{*},I^{*})\). If \(a>0\), then the repelling invariant closed curve bifurcates from \(E_{2}\)for \(h^{*}<0\). If \(a<0\), then an attracting invariant closed curve bifurcates from \(E_{2}\)for \(h^{*}>0\).
5 Conclusions
The paper investigated the basic dynamic characteristics of a Schrödingerean predator-prey system with latent period. First, we applied the forward Euler scheme to a continuous-time SIR epidemic model and obtained the Schrödingerean predator-prey system. Then the existence and local stability of the disease-free equilibrium and endemic equilibrium of the model were discussed. In addition, we chose h as the bifurcation parameter and studied the existence and stability of flip bifurcation and Hopf bifurcation of this model by using the center manifold theorem and the bifurcation theory. Numerical simulation results show that the model (2) shows a flip bifurcation and Hopf bifurcation when the bifurcation parameter h passes through the respective critical value, and the direction and stability of flip bifurcation and Hopf bifurcation can be determined by the sign of \(\alpha_{2}\) and a, respectively. Apparently there are more interesting problems as regards this Schrödingerean predator-prey system with latent period which deserve further investigation.
Change history
20 March 2020
The Editors-in-Chief have retracted this article [1] because it significantly overlaps with an article by different authors that was simultaneously under consideration with another journal [2]. In addition, the identity of the corresponding author could not be verified: Universidad Austral confirmed that Tanriver ��lker was never affiliated to this institution. The authors have not responded to any correspondence regarding this retraction.
References
May, RM, Odter, GF: Bifurcations and dynamic complexity in simple ecological models. Am. Nat. 110, 573-599 (1976)
Guckenheimer, J, Holmes, P: Nonlinear Oscillations, Dynamical Model and Bifurcation of Vector Field. Springer, New York (1983)
Berryman, AA, Millstein, JA: Are ecological systems chaotic - and if not, why not? Trends Ecol. Evol. 4, 26-28 (1989)
Hassell, MP, Comins, HN, May, RM: Spatial structure and chaos in insect population dynamics. Nature 353, 255-258 (1991)
Shilnikov, LP, Shilnikov, A, Turaev, D, Chua, L: Methods of Qualitative Theory in Nonlinear Dynamics. World. Sci. Ser. Nonlinear Sci. Ser. A. World Scientific, River Edge (1998)
Robinson, C, Holmes, P: Dynamical Models: Stability, Symbolic Dynamics and Chaos, 2nd edn. CRC Press, Boca Raton (1999)
Bacaër, N, Dads, E: Genealogy with seasonality, the basic reproduction number, and the influenza pandemic. J. Math. Biol. 62, 741-762 (2011)
Xue, G, Yuzbasi, E: Fixed point theorems for solutions of the stationary Schrödinger equation on cones. Fixed Point Theory Appl. 2015, 34 (2015)
Yan, Z: Sufficient conditions for non-stability of stochastic differential systems. J. Inequal. Appl. 2015, 377 (2015)
Yan, Z, Yan, G, Miyamoto, I: Fixed point theorems and explicit estimates for convergence rates of continuous time Markov chains. Fixed Point Theory Appl. 2015, 197 (2015)
Wang, J, Pu, J, Zama, A: Solutions of the Dirichlet-Schrödinger problems with continuous data admitting arbitrary growth property in the boundary. Adv. Differ. Equ. 2016, 33 (2016)
Huang, J: A new type of minimal thinness with respect to the stationary Schrödinger operator and its applications. Monatshefte Math. (2017). doi:10.1007/s00605-016-0998-6
Jiang, Z: Some Schrödinger type inequalities for stabilization of discrete linear systems associated with the stationary Schrödinger operator. J. Inequal. Appl. 2016, 247 (2016)
Jiang, Z, Uso, FM: Boundary behaviors for linear systems of subsolutions of the stationary Schrödinger equation. J. Inequal. Appl. 2016, 233 (2016)
Acknowledgements
The authors would like to express their deep-felt gratitude for the reviewer’s detailed reviewing and useful comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The first draft was prepared by TÜ. The final version was prepared by FL, which was verified and improved by TÜ. Both authors read and approved the final manuscript.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The Editors-in-Chief have retracted this article because it significantly overlaps with an article by different authors that was simultaneously under consideration with another journal (Chen & Zhang 2017 https://doi.org/10.1186/s13660-017-1417-9). In addition, the identity of the corresponding author could not be verified: Universidad Austral confirmed that Tanriver Ülker was never affiliated to this institution. The authors have not responded to any correspondence regarding this retraction.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lü, F., Ülker, T. RETRACTED ARTICLE: Existence of weak solutions for two point boundary value problems of Schrödingerean predator-prey system and their applications. Adv Differ Equ 2017, 159 (2017). https://doi.org/10.1186/s13662-017-1213-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-017-1213-3