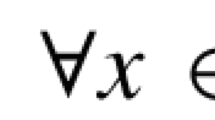1 Introduction

A switched system is composed of several subsystems and a decision rule that orchestrates switching between these subsystems. Due to their wide existence in engineering applications, this kind of dynamical systems has attracted considerable attention during the past decades. In the real word, many quantities are nonnegative [2–4]. As a special case of switched systems, a switched positive system with all subsystems associated with the Schrödinger operator being positive systems is very common in communication systems associated with the Schrödinger operator, formation flying, and rival mutation treatment system [5].

As we all know, it is necessary to address the stability and stabilization issues for switched positive systems associated with the Schrödinger operator. Generally, the synthesis problem of switched systems associated with the Schrödinger operator primarily concerns on two topics: stabilization by feedback controllers and stabilization by feedback switching law. The former topic is studied mainly based on state feedback or output feedback controller designation [6, 7], whereas the latter topic is proved by feedback switching law [8, 9]. Furthermore, there are many switched systems associated with the Schrödinger operator whose subsystems associated with the Schrödinger operator are not stable in real control systems associated with the Schrödinger operator [1, 10]. To the best of our knowledge, existing stabilization results on switched positive linear systems associated with the Schrödinger operator have little results referring to the state-dependent switching law, which motivates the research of this paper.

This paper investigates the boundary value problems of discrete linear systems associated with the Schrödinger operator in discrete time context, which contain unstable subsystems associated with the Schrödinger operator. The state feedback switching law is designed to guarantee the stabilization of the switched positive linear systems associated with the Schrödinger operator. The result is then applied to systems associated with the Schrödinger operator with two subsystems associated with the Schrödinger operator, and sufficient and necessary condition is also derived. The rest of paper is organized as follows. Section 2 gives introduces some preliminaries. In Section 3, we give the main results. Section 4 concludes this paper.

Throughout the paper, \(\Re^{n}\) and \(\Re^{n\times n}\) represent the vectors of n-tuples of real numbers and the space of \(n\times n\) matrices with real entries, respectively, and \(\mathbb{N}\) is the set of nonnegative integers. For v in \(\Re^{n}\), \(v_{i}\) is the ith component of v. The notation \(v\succ0 \) (⪰0) means that all components of v are positive (nonnegative), that is, \(v_{i}>0 \) (≥0), and \(\overline{\lambda}_{v}\) and \(\underline{\lambda}_{v}\) stand for the maximal and minimal components of v, respectively. For a matrix A in \(\Re^{n\times m}\), \(a_{ij}\) is the element in the ith row of the jth column of A, and \(A\succ0 \) (⪰0) means that all elements of A are positive (nonnegative), that is, \(a_{ij}>0\) (≥0).

2 Preliminaries

Consider the following discrete-time switched linear system:

$$ x(k+1)=A_{\sigma(k)}x(k),\quad k\in\mathbb{N}, $$
(2.1)

where \(\sigma(k)\) is a piecewise constant switching signal taking values in the finite set \(S=\{1,2,\ldots,N \}\), and \(A_{i}\in\Re ^{n\times n} \) (\(i\in S\)) are system matrices.

Assumption 1

For system (2.1), \(A_{i}\succeq0\) for each \(i\in S\).

Definition 1

A switching signal σ is said to be a state-feedback switching law if it depends on system states and its past value, that is, \(\sigma(t^{+})=\sigma(x(t),\sigma(t^{-}))\) for system (2.1), where \(\sigma(k+1)=\sigma(x(k),\sigma(k-1))\).

Lemma 1

([2])

A discrete-time system

$$ x(k+1)=Ax(k), \quad k\in\mathbb{N}, $$
(2.2)

is positive if and only if \(A\succeq0\).

Lemma 2

Let \(A\succeq0\). Then the following conditions are equivalent:

  1. (i)

    A is a Schur matrix;

  2. (ii)

    There exists vector \(v\succ0\) in \(\Re^{n}\) with \((A-I)v\prec0\).

Proof

(i) For any \(i\in E,i\geq3\),

$$E^{i} \bigl\{ e^{\lambda\sigma_{2}} \bigr\} =E^{i} \bigl\{ e^{\lambda(T_{1}+\sigma_{2}\circ\theta _{T_{1}})} \bigr\} =\frac{1}{q_{i}-\lambda}E^{1} \bigl\{ e^{\lambda\sigma_{2}} \bigr\} . $$

In the following, we compute \(E^{1}\{e^{\lambda\sigma_{1}}\}\). Consider the coordinate process \(W(s)\) on excursion space \((U,\mathcal {U})\). For any \(i\in E\), we define

$$\eta_{i}=\inf \bigl\{ s|W(s)=i \bigr\} $$

and

$$C_{0}=\{W|W_{0}\neq2\},\qquad C_{1}= \{W|W_{0}=2\}. $$

Obviously, \(C_{0}, C_{1}\in\mathcal{U}\) and \(C_{0}\cup C_{1}=U\). Let \(\tau=\inf\{t|\beta_{t}>\sigma_{2}\}\) for any \(t>0\), and

$$Z_{t}^{1}=\sharp\{s|s\in D_{p},s\leq t,Y_{s}\in C_{1}\}. $$

Then we have

$$\begin{aligned} P^{1} \{\tau>t\} =&\hat{P} \bigl\{ Z_{t}^{1}=0 \bigr\} \\ =& e^{-\hat{P}(W_{0}=2)t}=e^{-t}. \end{aligned}$$

So we know that τ is an exponential random variable with mean 1. Hence, we have

$$\begin{aligned} E^{1} \bigl\{ e^{\lambda\sigma_{2}} \bigr\} =& E^{1} \biggl[\exp \biggl\{ \lambda \biggl(\sum_{s\in G} \bigl(I_{(0,\sigma_{2}]}(s) \sigma_{\infty}I_{\{C_{0}\}}(Y_{s}) \bigr)\circ \theta_{s} \biggr) \biggr\} \biggr] \\ =&E^{1} \bigl\{ \exp[\lambda\beta_{\tau}] \bigr\} \\ =& \int_{0}^{\infty} E^{1} \bigl\{ e^{\lambda\beta_{t}} \bigr\} e^{-t}\,dt. \end{aligned}$$

From the computation of a Poisson point process we know that

$$\begin{aligned} E^{1} \bigl\{ e^{\lambda\beta_{t}} \bigr\} =& E^{1} \bigl\{ e^{\lambda z^{1}_{t}} \bigr\} \\ =&\exp \bigl\{ t\hat{P} \bigl( \bigl(e^{\lambda\sigma_{1}}-1 \bigr) I_{\{C_{1}\}}(Y_{s}) \bigr) \bigr\} , \end{aligned}$$

which yields that

$$\hat{P} \bigl( \bigl(e^{\lambda\sigma_{1}}-1 \bigr)I_{\{C_{1}\}}(Y_{s}) \bigr) =\sum_{k=3}^{\infty} E^{k} \bigl[e^{\lambda\sigma_{1}}-1 \bigr] =\sum_{k=3}^{\infty} \frac{ \lambda}{q_{k}-\lambda}. $$

Hence, we have

$$\begin{aligned} E^{1} \bigl\{ e^{\lambda\sigma_{1}} \bigr\} =& \int_{0}^{\infty} \exp t \Biggl\{ \sum _{k=3}^{\infty}\frac{ \lambda}{q_{k}-\lambda}-1 \Biggr\} \,dt =\frac{1}{1-\sum_{k=3}^{\infty}\frac{ \lambda}{q_{k}-\lambda}}. \end{aligned}$$

Therefore, if \(0<\lambda< \frac{1}{\sum_{n=3}^{\infty} (q_{n}-q_{2})^{-}1}\wedge q_{2}\), then we have \(E^{1}[e^{\lambda \sigma_{2}}]<\infty\). So \(E^{i}\{e^{\lambda \sigma_{1}}\}<\infty\). It is easy to see that \(p_{ij}(t)\) is exponentially ergodic.

(ii) By Lemma 1 and the previous results we have that if \(i\geq3\), then \(\tau_{2}^{+}=\sigma_{2} \). Let λ satisfy \(0<\lambda<\frac{1}{\sum_{n=3}^{\infty} (q_{n}-q_{1})^{-}1}\wedge q_{2}\). Then, for any \(i\in E \), we have

$$E^{i} \bigl\{ e^{\lambda\tau_{1}^{+}} \bigr\} =E^{i} \bigl\{ e^{\lambda \sigma_{2}} \bigr\} < \infty. $$

Put \(m=2\) in Theorem 1. By using a computable method of (2.1) we know that

$$\begin{aligned} E^{2} \bigl\{ e^{\lambda\tau_{1}^{+}} \bigr\} =&E^{2} \bigl\{ e^{\lambda(T_{1}+\sigma_{2}\circ T_{1})} \bigr\} \\ =&E^{2} \bigl[e^{\lambda T_{1}} \bigr]E^{1} \bigl[e^{\lambda\sigma_{2}} \bigr] \\ =&\frac{1}{q_{1}-\lambda}\frac{1}{1-\sum_{k=3}^{\infty}\frac{ \lambda}{q_{k}-\lambda}}. \end{aligned}$$

So Lemma 2 is proved. □

For system (2.2), if there exists a vector \(v\succ0\) with \(v\in \Re^{n}\) such that \((A-I_{n})v\prec0\), then \(V=v^{T}x\) is said to be a linear copositive Lyapunov function of system (2.2).

Next, we give an example to introduce our results.

Example 1

Consider system (2.1) with two subsystems associated with the Schrödinger operator described by

$$A_{1}= \begin{pmatrix} 0.5 & 1.4\\ 1.5& 1.2 \end{pmatrix}, \qquad A_{2}= \begin{pmatrix} 1.3 & 1.5\\ 1.4& 0.6 \end{pmatrix}. $$

For the first subsystem matrix \(A_{1}\), there does not exist a vector \(v_{1}\succ0\) such that \((A_{1}-I)v_{1}\prec0\). Similarly, there does not exist a vector \(v_{2}\succ0\) such that \((A_{2}-I)v_{2}\prec0\).

It is easy to verify that these two subsystem matrices are not Schur matrices. Despite this disadvantage, we find that there exist some combinations \(A_{0}\) of \(A_{1}\) and \(A_{2}\) that are positive and Schur matrices, that is, \(A_{0}=\lambda_{1}A_{1}+\lambda _{2}A_{2}\) is a positive Schur matrix, where \(\lambda_{1},\lambda _{2}\in(0,1)\) and \(\lambda_{1}+\lambda_{2}=1\).

For example, choose \(\lambda_{1}=0.5\) and \(\lambda_{2}=0.5\). We obtain

$$A_{0}= \begin{pmatrix} 0.9 & 1.45\\ 1.45& 0.9 \end{pmatrix}. $$

Note that there exists a vector \(v\succ0\) in \(\Re^{n}\) with \((A_{0}-I)v\prec0\). Thus, \(A_{0}\) is a positive and stable matrix.

This example contains an instantaneous state.

Suppose that \(q_{2},q_{3},\ldots \) are sequences of positive real numbers and consider the following Q-matrix:

$$Q= \begin{pmatrix} -\infty& 1 & 1&1 & \cdots\\ q_{2}&-q_{2} & 0 &0 & \cdots\\ q_{3}&0 &-q_{3} & 0&\cdots\\ q_{4}& 0&0& -q_{4}&\cdots\\ \vdots& \vdots& \vdots& \vdots& \cdots \end{pmatrix}, $$

where \(\sum_{i=2}^{\infty}{q_{i}}^{-1}<\infty\). This matrix is called the Kolmogorov matrix. There exist infinitely many dishonest processes with this Q-matrix. In [9, 10], it is shown that the process with following resolvent is the only honest one:

$$\begin{aligned}& R_{11}(\lambda) =\frac{1}{\lambda} \Biggl(1+\sum _{k=2}^{\infty}\frac {1}{\lambda+q_{k}} \Biggr)^{-1}, \\& R_{1j}(\lambda) = R_{11}(\lambda)\cdot\frac{1}{\lambda+q_{j}}, \quad j\geq 2, \\& R_{i1}(\lambda) = \frac{q_{i}}{\lambda+q_{i}} \cdot R_{11}(\lambda ), \quad i\geq2 , \\& R_{ij}(\lambda) = \frac{q_{i}}{\lambda+q_{i}}\cdot R_{11}(\lambda) \cdot\frac{1}{\lambda+q_{j}}+\frac{\delta_{ij}}{\lambda+q_{j}}, \quad i,j\geq2, \end{aligned}$$

where \(\lambda>0\). Let the state space be \(E=\{1,2,3,\ldots\}\). Obviously, the transition function \(p_{ij}(t)\) that corresponds to the resolvent is the only honest one. Though this chain is weakly symmetric, so far its convergence rate is still unknown because of its instantaneous state.

Next, we discusses the stability for system (2.1). Define the following stable convex combination of the system matrices:

$$ \overline{A}_{0}=\sum_{i\in S} \overline{w}_{i}A_{i}, $$
(2.3)

where

$$ \sum_{i\in S}\overline{w}_{i}=1, \quad\overline{w}_{i}\in(0,1). $$
(2.4)

Assumption 2

There exists a vector \(\overline{v}\in\Re^{n}\) with \(\overline{v}\succ0\) such that

$$ (\overline{A}_{0}-I_{n})^{T} \overline{v}\prec0. $$
(2.5)

Without loss of generality, let

$$ (\overline{A}_{0}-I_{n})^{T} \overline{v}=-\overline{\mathbf{e}}, $$
(2.6)

where \(\overline{\mathbf{e}}\in\Re^{n}\) with \(\overline{\mathbf{e}}\succ0\), and \(\frac{\underline{\lambda}_{\overline{\mathbf{e}}}}{\overline{\lambda }_{\overline{v}}}\leq1\).

Denote

$$ \overline{\mathbf{\ell}}_{i}=(A_{i}-I_{n})^{T} \overline{v},\quad i\in S. $$
(2.7)

Combing (2.3), (2.4), (2.5), (2.6), and (2.7), we get

$$ \bigl[(\overline{w}_{1}A_{1}+\cdots+\overline{w}_{N}A_{N})-( \overline {w}_{1}+\cdots+\overline{w}_{N})I_{n} \bigr]^{T}\overline{v} =\overline{w}_{1}\overline{\mathbf{ \ell}}_{1}+\cdots+\overline {w}_{N}\overline{\mathbf{ \ell}}_{N}=-\overline{\mathbf{e}}. $$

Switching rule 1

  1. (i)

    For any initial state \(x(k_{0})=x_{0}\), we select

    $$\sigma(k_{0})=\operatorname*{\arg\min}_{i\in S} \bigl\{ x_{0}^{T}\overline{\mathbf{\ell}}_{i} \bigr\} . $$
  2. (ii)

    The first switching time instant is selected as

    $$k_{1}=\inf \bigl\{ k\geq k_{0}| x(k)^{T} \overline{\mathbf{\ell}}_{\sigma (k_{0})}>-r_{\sigma(k_{0})}x(k)^{T} \overline{\mathbf{e}} \bigr\} . $$

    Thus, the switching index can be determined by

    $$\sigma(k_{1})=\operatorname*{\arg\min}_{i\in S} \bigl\{ x(k_{1})^{T}\overline {\mathbf{\ell}}_{i} \bigr\} . $$
  3. (iii)

    The switching index sequences are defined by

    $$\begin{aligned}& k_{j+1}=\inf \bigl\{ k\geq k_{j}| x(k)^{T} \overline{\mathbf{\ell}}_{\sigma (k_{j})}>-r_{\sigma(k_{j})}x(k)^{T} \overline{\mathbf{e}} \bigr\} , \\& \sigma(k_{j+1})=\operatorname*{\arg\min}_{i\in S} \bigl\{ x(k_{j+1})^{T}\overline{\mathbf{\ell}}_{i} \bigr\} , \end{aligned}$$

    where \(r_{\sigma(k_{j})}\in(0, 1)\) and \(j\in\mathbb{N}\).

3 Main results

Theorem 1

Under Assumption  2 and Switching rule 1, system (2.1) is uniformly exponentially stable.

Proof

Choose \(V(k, x(k))=x(k)^{T}\overline{v}\). For any \(k\in[k_{m}, k_{m+1})\), by system (2.1) it follows that

$$ x(k)^{T} \overline{v}=x(k-1)^{T}A^{T}_{\sigma(k_{m})} \overline{v}, $$
(3.1)

which, together with (2.1) and (3.1), gives that

$$ x(k)^{T}\overline{v}=x(k-1)^{T}\overline{ \mathbf{\ell}}_{\sigma (k_{m})}+x(k-1)^{T}\overline{v}. $$
(3.2)

By (3.2) and (iii) of Switching rule 1 we know that

$$ x(k)^{T} \overline{v}\leq -r_{\sigma(k_{m})}x(k-1)^{T} \overline{\mathbf{e}}+x(k-1)^{T}\overline{v}. $$
(3.3)

Using (3.3) and (iii) of Switching rule 1, we can obtain the following inequality

$$ V \bigl(k, x(k) \bigr)-V \bigl(k-1,x(k-1) \bigr)\leq - \frac{r_{\sigma(k_{m})}\underline{\lambda}_{\overline{\mathbf {e}}}}{\overline{\lambda}_{\overline{v}}}V \bigl(k-1,x(k-1) \bigr). $$
(3.4)

So (3.3) and (3.4) give that

$$ V \bigl(k, x(k) \bigr)\leq \biggl(1-\frac{r_{\sigma(k_{m})}\underline{\lambda}_{\overline {\mathbf{e}}}}{\overline{\lambda}_{\overline{v}}} \biggr)V \bigl(k-1,x(k-1) \bigr). $$
(3.5)

Since \(\frac{\underline{\lambda}_{\overline{M}}}{\overline{\lambda }_{\overline{v}}}\leq1\) and \(r_{\sigma(k_{m})}\in(0, 1)\), we have that

$$ 1-\frac{r_{\sigma(k_{m})}\underline{\lambda}_{\overline{\mathbf {e}}}}{\overline{\lambda}_{\overline{v}}}\in (0, 1). $$
(3.6)

With (3.5) in mind, using (3.6), we get that

$$ V \bigl(k, x(k) \bigr)\leq \biggl(1-\frac{r_{\sigma(k_{m})}\underline{\lambda}_{\overline {\mathbf{e}}}}{\overline{\lambda}_{\overline{v}}} \biggr)^{k-k_{m}}V \bigl(k_{m},x(k_{m}) \bigr). $$
(3.7)

Repeating the above steps in (3.4)-(3.7), it straightforwardly follows that

$$ V \bigl(k, x(k) \bigr)\leq \biggl(1-\frac{r_{\sigma(k_{m})}\underline{\lambda}_{\overline {\mathbf{e}}}}{\overline{\lambda}_{\overline{v}}} \biggr)^{k-k_{m}} \biggl(1-\frac {r_{\sigma(k_{m-1})}\underline{\lambda} _{\overline{\mathbf{e}}}}{\overline{\lambda}_{\overline{v}}} \biggr)^{k_{m}-k_{m-1}}. $$
(3.8)

From (3.8) and (3.7) it follows that

$$ 1-\frac{r_{\sigma(k_{i})}\underline{\lambda}_{\overline{\mathbf {e}}}}{\overline{\lambda}_{\overline{v}}}\in(0, 1), \quad i=0,1,\ldots,m. $$

Choose \(\eta=\max_{i=0, 1, \ldots, m}\{1-\frac{r_{\sigma (k_{i})}\underline{\lambda}_{\overline{\mathbf{e}}}}{\overline{\lambda }_{\overline{v}}} \}\). So

$$ V \bigl(k, x(k) \bigr)\leq\eta^{k-k_{0}} V \bigl(k_{0}, x(k_{0}) \bigr), $$

which immediately gives that

$$ x(k)^{T}\overline{v}\leq\eta^{k-k_{0}} x(k_{0})^{T} \overline{v}. $$

So

$$ \bigl\| x(k)\bigr\| \leq\alpha\eta^{k-k_{0}}\bigl\| x(k_{0})\bigr\| , $$

where \(\alpha=\frac{\overline{\lambda}_{\overline{v}}}{\underline{\lambda }_{\overline{v}}}\).

Thus, system (2.1) is uniformly exponentially stable. □

Remark 1

By the properties of discrete-time systems associated with the Schrödinger operator and (ii) and (iii) of Switching rule 1, it is not hard to find that the dwell time in each time interval is at least greater than 1. So there exist finite switchings in any finite time interval. Thus, Switching rule 1 is well defined.

Corollary 1

Suppose \(N=2\). Consider the stability of system (2.1) in the sense of Lyapunov function. Then system (2.1) is stable if and only if Assumption  2 holds.

Proof

Here we only give the proof of “only if”. The stability of system (2.1) implies that there exists an LCLF \(V(k,x(k))=x^{T}(k)\overline{v}\) such that

$$V \bigl(k+1,x(k+1) \bigr)-V \bigl(k,x(k) \bigr)< -\overline{\varsigma}x^{T}(k) \overline{\mathbf{e}'} $$

or

$$V \bigl(k+1,x(k+1) \bigr)-V \bigl(k,x(k) \bigr)< -\overline{\varsigma}x^{T}(k) \overline{\mathbf{e}'}, $$

where \(\overline{v}\succ0, \overline{\mathbf{e}'}\succ0\), and ς̅ is a positive real number.

That is to say, \(x^{T}(k)(A^{T}_{1}-I_{2})\overline{v}<-\overline {\varsigma}x^{T}(k)\overline{\mathbf{e}'}\) whenever \(x^{T}(k)(A^{T}_{2}-I_{2})\overline{v}\geq-\overline{\varsigma }x^{T}(k)\overline{\mathbf{e}'}\), and \(x^{T}(k)(A^{T}_{2}-I_{2})\overline{v}<-\overline{\varsigma }x^{T}(k)\overline{\mathbf{e}'}\) whenever \(x^{T}(k)(A^{T}_{1} -I_{2})\overline{v}\geq-\overline{\varsigma}x^{T}(k)\overline{\mathbf {e}'}\). We only prove the first case since the second case can be derived as the first one. By the compactness theorem there exists a positive real number μ̅ such that \(-x^{T}(k)(A^{T}_{1}-I_{2})\overline{v}-\overline{\varsigma }x^{T}(k)\overline{\mathbf{e}'}>\overline{\mu}\). Between any two consecutive switching instants, \(x(k)\) is bound. Thus, there exists a positive real number κ̅ such that

$$\overline{\kappa}\geq x^{T}(k) \bigl(A^{T}_{2}-I_{2} \bigr)\overline{v}+ \overline {\varsigma}x^{T}(k)\overline{ \mathbf{e}'}>0. $$

Choose \(\overline{\varepsilon}=\frac{\overline{\mu}}{\overline{\kappa}}\). We obtain that \(-x^{T}(k)(A^{T}_{1}-I_{2})\overline{v}-\overline{\varsigma }x^{T}(k)\overline{\mathbf{e}'}-\overline{\varepsilon }(x^{T}(k)(A^{T}_{2}-I_{2})\overline{v}+\overline{\varsigma }x^{T}(k)\overline{\mathbf{e}'})>-x^{T}A^{T}_{1}v-\overline{\varsigma}x^{T} \mathbf{e}'-\overline{\mu}>0\), which yields that

$$x^{T} \bigl[ \bigl(A^{T}_{1}-I_{2} \bigr)+\overline{\varepsilon } \bigl(A^{T}_{2}-I_{2} \bigr) \bigr]\overline{v}< -(1+\overline{\varepsilon})\overline {\varsigma} x^{T}\overline{\mathbf{e}'}. $$

Define \(\overline{w}_{1}=\frac{1}{1+\overline{\varepsilon}}\) and \(\overline{w}_{2}=\frac{\overline{\varepsilon}}{1+\overline{\varepsilon }}\). We have \(x^{T}[A_{0}-I_{2}]\overline{v}\) \(<-\overline{\varsigma }x^{T}\overline{\mathbf{e}'}\), where \(A_{0}=\overline {w}_{1}A^{T}_{1}+\overline{w}_{2}A^{T}_{2}\). This inequality implies that Assumption 2 holds. □

4 Conclusions

In this paper, we consider the stabilization problem of discrete-time switched positive linear systems associated with the Schrödinger operator that contain unstable subsystems associated with the Schrödinger operator. We present a state-dependent switching law guaranteeing that the systems associated with the Schrödinger operator are uniformly exponentially stable. Furthermore, we establish a necessary and sufficient condition for the stabilization of the system with two subsystems associated with the Schrödinger operator.