Abstract
We propose a new method called the fractional reduced differential transform method (FRDTM) to solve nonlinear fractional partial differential equations such as the space-time fractional Burgers equations and the time-fractional Cahn-Allen equation. The solutions are given in the form of series with easily computable terms. Numerical solutions are calculated for the fractional Burgers and Cahn-Allen equations to show the nature of solutions as the fractional derivative parameter is changed. The results prove that the proposed method is very effective and simple for obtaining approximate solutions of nonlinear fractional partial differential equations.
Similar content being viewed by others
1 Introduction
The space-fractional Burgers equation describes the physical processes of unidirectional propagation of weakly nonlinear acoustic waves through a gas-filled pipe. They are also connected with applications in acoustic phenomena and have been used to model turbulence and certain steady-state viscous flows. Moreover, Burgers equations are used to model the formation and decay of nonplanar shock waves, where the variable x is a coordinate moving with the wave at the speed of sound and the dependent variable u represents the velocity fluctuations. The Burgers equations occur in various areas of applied sciences and physical applications, such as modeling of fluid mechanics and financial mathematics, and the equation has still interesting applications in physics and astrophysics.
The fractional differential equations (FDE) appear more and more frequently in different research areas and engineering applications. There are many physical applications in science and engineering that can be represented by models using fractional differential equations [1–10], which are quite useful for many physical problems. These equations are represented by fractional linear and nonlinear PDEs, and solving such fractional differential equations is very important [11–21].
Many approximation and numerical techniques have been used to solve fractional differential equations [12, 16, 22–25]. Lately, many new approaches to fractional differential equations have been proposed, a few of these methods are as follows: the fractional differential transform method (FDTM) [25–28], the fractional Adomian decomposition method (FADM) [2], the fractional variational iteration method (FVIM) [4], the fractional sub-equation method [23], the fractional natural decomposition method [17, 29] and the fractional homotopy perturbation method (FHPM) [22, 30]. Kurulay [26] found approximate and exact solutions of the space- and time-fractional Burgers equations. Bekir et al. [23] found exact solutions of the time-fractional Cahn-Allen equation. Khan et al. [22] used the generalized differential transform method (GDTM) and the homotopy perturbation method (HPM) to solve the time-fractional Burgers and coupled Burgers equations. Recently, Rawashdeh [16, 31] used the FRDTM to solve nonlinear fractional partial differential equations.
The general response expression contains a parameter describing the order of the fractional derivative that can be varied to obtain various responses. Note that we call Eq. (1.1) the time-fractional Burgers and the space-fractional Burgers equation in the case \(0<\alpha\le1, \eta=0\) and \(0<\beta\le1, \alpha=1\), respectively.
In this work, we first consider the nonlinear fractional generalized Burgers equation with time- and space-fractional derivatives of the form [30]
where \(\varepsilon, \nu\) and η are parameters and α and β are parameters describing the order of the fractional time- and space-derivatives, respectively. The function \(u(x,t)\) is a function of x and t and \(u(x,t)\) will vanish when \(t<0\) and \(x<0\).
Second, we consider the time-fractional Cahn-Allen equation [23, 32]
The rest of this paper is divided into six sections. In Section 2, we give a background of fractional calculus. In Section 3, the RDTM is introduced. Section 4 is devoted to application of the FRDTM to three test problems and presentation of graphs to show the effectiveness of the FRDTM for some values of x and t. In Section 5, we present tables for Examples 4.1, 4.2 and 4.3. Section 6 is for discussion and conclusion of this paper.
2 Background of fractional calculus
Here are some definitions and facts that we shall use in our work. Some of these basic definitions are due to Liouville [3, 4, 33, 34].
Definition 2.1
A real function \(f(x)\), \(x>0\), is said to be in the space \(C_{\mu }\), \(\mu\in{\mathbb {R}}\), if there exists a real number \(q(>\mu )\) such that \(f(x)=x^{q} g(x)\), where \(g(x)\in C [0,\infty )\), and it is said to be in the space \(C_{\mu}^{m} \) if \(f^{(m)} \in C_{\mu}, m\in{\mathbb {N}}\).
Definition 2.2
For an integrable function \(f\in C_{\mu}\), the Riemann-Liouville fractional integral operator of order \(\alpha\ge0\) is defined as
Definition 2.3
The fractional derivative of \(f\in C_{-1}^{m}\) in the Caputo sense can be defined as
Lemma 2.4
[6]
If \(m-1<\alpha\le m, m\in{\mathbb {N}}\) and \(f\in C_{\mu }^{m}, \mu\ge-1\), then
We use the Caputo fractional derivative because it allows traditional initial and boundary conditions to be included in the formulation of our work.
3 Analysis of the FRDTM
We present the methodology of the FRDTM as follows. Consider a function \(u (x,t )\) which is analytic and k-times continuously differentiable with respect to time t and space x in the domain of the interest. Now one can represent \(u (x,t )\) as a product of two single-variable functions such as \(u (x,t )=f(x). g(t)\). Thus the function can be represented as
Definition 3.1
If \(u (x,t )\) is analytic and continuously differentiable with respect to space variable x and time t in the domain of interest, then the t-dimensional spectrum function
is the reduced transformed function of \(u (x,t )\), where α is a parameter which describes the order of time-fractional derivative.
Throughout this paper, \(u(x,t)\) represents the original function and \(U_{k} (x)\) represents the reduced transformed function. The differential inverse transform of \(U_{k} (x)\) is given by
From Eqs. (3.3) and (3.2) one can deduce
Note that when \(t_{0}=0\), Eq. (3.4) becomes
Some basic operations of the reduced differential transformation [35–38] obtained from Eqs. (3.2) and (3.4) are given in Table 1, and the proofs of some of the properties can be found in [39].
Remark 3.2
In Table 1, Γ represents the gamma function, where \(\Gamma (z+1)=z\Gamma(z), z>0\).
3.1 Methodology
To explain how the FRDTM works, we consider the general fractional nonlinear nonhomogeneous partial differential equation
subject to the initial conditions
Here the \(L=D_{t}^{\alpha}\), R is the linear differential operator, N represents the general nonlinear operator and \(h(x,t)\) is the nonhomogeneous source term.
From Table 1 and Eq. (3.6), we can get the following:
where \(U_{k}(x)\), \(R(U_{k}(x))\), \(N(U_{k}(x))\) and \(H_{k}(x)\) are the transformations of the functions \(L (u(x,t) )\), \(R (u(x,t) )\), \(N (u(x,t) )\) and \(L (h(x,t) )\), respectively.
Now from Eq. (3.7) we can get
To find all other iterations, we first substitute Eq. (3.10) into Eq. (3.9) to find the remaining values of \(U_{k}(x)\). Finally, we apply the inverse transformation to all the values of \(\{U_{k} (x) \}_{k=0}^{n}\) to obtain
Finally, the exact solution of the problem is given by \(u(x,t)=\lim_{n\to\infty} \stackrel{\frown}{u}(x,t)\).
4 Worked examples
We shall employ the FRDTM to three different applications to illustrate the accuracy and efficiency of the method.
4.1 The time-fractional Burgers equation
We consider the following time-fractional Burgers equation [30]:
subject to the initial condition
where \(\gamma=\frac{\mu}{\nu} (x-\lambda)\), and the parameters \(\mu , \sigma, \lambda\) and ν are arbitrary constants.
Using Table 1, Eq. (4.1) and Eq. (4.2) become
where
Substitute Eq. (4.4) into Eq. (4.3) to get
We proceed in this way to get
Thus, we have the solution of Eq. (4.1) in a series form for \(\alpha =1\) and \(\varepsilon=1\)
Hence
This is the exact solution given by the ADM in [2] and the VIM in [4], where \(\gamma=\frac{\mu}{\nu} (x-\lambda)\) and the parameters \(\mu , \sigma, \lambda\) and ν are arbitrary constants.
For a special case, we consider the case when \(\nu=0.1,\mu=0.4\), \(\sigma=0.6, \lambda=0.125,\epsilon=1\) to obtain
If we proceed in this direction, the differential inverse transform of \(\{U_{k} (x) \}_{k=0}^{\infty}\) is given by
Thus, the exact solution of the problem is given by \(u(x,t)=\lim_{n\to\infty} \stackrel{\frown}{u}_{n} (x,t)\).
Remark 4.1
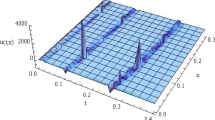
The sketches of the approximate solutions and the exact solution \(u(x,t)\) of Eq. (4.1) given by Momani [40] for the values of \(\alpha=0.25, \alpha=0.5, \alpha=0.75, \alpha=1\) and different values of x and t are shown in Figure 1. Also from Figure 2 one can observe that the exact and approximate solutions for Example 4.1 are very close when \(\nu =0.1,\mu=0.4,\sigma=0.6,\lambda=0.125,\eta=1\).
4.2 The space-fractional Burgers equation
Consider the space-fractional Burgers equation [30]
where \(\epsilon, \nu, \eta\) are parameters, and the boundary conditions are as follows:
Apply the FRDTM operator to Eq. (4.10) and Eq. (4.11) to get
and
Substitute Eq. (4.13) into Eq. (4.12) to obtain
We proceed, and after the 7th iteration we get the following approximate solution:
Thus, when \(\beta=1\) and \(\varepsilon=1\), the approximate solution becomes
This is the approximate solution of Eq. (4.10) in a series form. Thus the exact solution in the special case when \(\eta=0\) is given by
This is the exact solution of Eq. (4.10) which was given in [30].
Remark 4.2
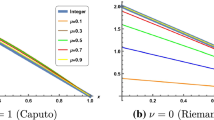
The sketches of the approximate solutions and the exact solution \(u(x,t)\) of Eq. (4.10) given by Momani [12] for the values of \(\beta =0.25, \beta=0.5, \beta=0.75, \beta=0.90\) and different values of x and t when \(\eta=1, \nu=1, \varepsilon=1\) are shown in Figure 3 and 4.
4.3 The time-fractional Cahn-Allen equation
Consider the following nonlinear time-fractional Cahn-Allen equation [23, 32]:
subject to
Apply the FRDTM to Eq. (4.14) to get
Using Table 1 and Eq. (4.15), we conclude
Substitute Eq. (4.17) into Eq. (4.16) to obtain
We proceed in this way, and after the 4th iteration the approximate solution is given by
Thus
Hence the exact solution when \(\alpha=1\) is given by
This is the exact solution of Eq. (4.14) which was given in [23, 32].
Remark 4.3
The sketches of the approximate solutions and the exact solution \(u(x,t)\) of Eq. (4.19) are given in Figures 5 and 6 for a constant value of \(a=4\) and for the values of \(\alpha =0.25, \alpha=0.5, \alpha=0.75, \alpha=0.90\) and for different values of x and t. Note that the accuracy increases as the order of approximation increases.
5 Tables of numerical calculations
In this section, we present tables to show the comparison of results of the FRDTM approximate solutions and the exact solution for different values of α and β. In Table 2 we use different values of x and t and \(\nu=0.1, \mu=0.4, \sigma =0.6, \lambda=0.125, \eta=1\), and in Table 3 we use different values of x and t and \(\eta=1, \nu=1, \varepsilon =1\). Finally, we present Table 4 for different values of x and t and different values for α with only four iterations. It is important to mention that for Example 4.3 we only used \(n=4\), i.e., four iterations, and we obtained better approximate values, while in [32] the authors used five iterations. This shows that the FRDTM converges faster than the existing methods in the literature.
6 Conclusion
In this paper, we successfully implemented the FRDTM to find approximate solutions of the space-time fractional Burgers equations and the time-fractional Cahn-Allen equation for different values of α and β and the results we obtained in Examples 4.1, 4.2 and 4.3 were in excellent agreement with the exact solutions. The FRDTM introduces a significant improvement in the field over the existing methods.
References
Garg, M, Manohar, P: Numerical solution of fractional diffusion-wave equation with two space variables by matrix method. Fract. Calc. Appl. Anal. 13(2), 191-207 (2010)
Garg, M, Sharma, A: Solution of space-time fractional telegraph equation by Adomian decomposition method. J. Inequal. Spec. Funct. 2(1), 1-7 (2011)
Hilfer, R: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)
Inc, M: The approximate and exact solutions of the space- and time-fractional Burgers equations with initial conditions by variational iteration method. J. Math. Anal. Appl. 345, 476-484 (2008)
Jafari, H, et al.: A new algorithm for solving dynamic equations on a time scale. J. Comput. Appl. Math. 312, 167-173 (2017)
Kilbas, AA, Srivastava, HH, Trujillo, JJ: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Sakar, GM, et al.: On solutions of fractional Riccati differential equations. Adv. Differ. Equ. 2017, 39 (2017). doi:10.1186/s13662-017-1091-8
Yang, X-J, Gao, F, Srivastava, HM: Exact travelling wave solutions for the local fractional two-dimensional Burgers-type equations. Computers & Mathematics with Applications (2016). doi:10.1016/j.camwa.2016.11.012
Yang, X-J, Tenreiro Machado, JA, Srivastava, HM: A new numerical technique for solving the local fractional diffusion equation: two-dimensional extended differential transform approach. Appl. Comput. Math. 274, 143-151 (2016)
Yang, X-J: Fractional derivatives of constant and variable orders applied to anomalous relaxation models in heat-transfer problems. arXiv:1612.03202 (2016)
Caputo, M: Linear models of dissipation whose Q is almost frequency independent. Part II. Ann. Geophys. 19(4), 383-393 (1966)
Marin, M, Marinescu, C: Thermoelasticity of initially stressed bodies, asymptotic equipartition of energies. Int. J. Eng. Sci. 36(1), 73-86 (1998)
Marin, M: A domain of influence theorem for microstretch elastic materials. Nonlinear Anal., Real World Appl. 11(5), 3446-3452 (2010)
Miller, KS, Ross, B: An Introduction to the Fractional Calculus and Differential Equations. John Wiley, New York (1993)
Podlubny, I: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Academic Press, San Diego (1998)
Rawashdeh, SM: An efficient approach for time-fractional damped Burger and time-sharma-tasso-Olver equations using the FRDTM. Appl. Math. Inf. Sci. 9(3), 1239-1246 (2015)
Rawashdeh, MS, Al-Jammal, H: Numerical solutions for systems of nonlinear fractional ordinary differential equations using the FNDM. Mediterr. J. Math. 13(6), 4661-4677 (2016)
He, JH: Approximate analytical solution for seepage flow with fractional derivatives in porous media. Comput. Methods Appl. Mech. Eng. 167, 57-68 (1998)
Ray, SS, Bera, RK: Solution of an extraordinary differential equation by Adomian decomposition method. J. Appl. Math. 4, 331-338 (2004)
Ray, SS, Bera, RK: An approximate solution of a nonlinear fractional differential equation by Adomian decomposition method. Appl. Math. Comput. 167, 561-571 (2005)
Cascaval, RC, Eckstein, EC, Frota, CL, Goldstein, JA: Fractional telegraph equations. J. Math. Anal. Appl. 276(1), 145-159 (2002)
Alam Khan, N, Ara, A, Mahmood, A: Numerical solutions of time-fractional Burgers equations: a comparison between generalized differential transformation technique and homotopy perturbation method. Int. J. Numer. Methods Heat Fluid Flow 22(2), 175-193 (2015)
Bekir, A, Aksoy, E, Cevikel, AC: Exact solutions of nonlinear time fractional partial differential equations by sub-equation method. Math. Methods Appl. Sci. 38(13), 2779-2784 (2015)
Kumar, D, Singh, J, Kiliman, A: Efficient approach for fractional Harry Dym equation by using Sumudu transform. Abstr. Appl. Anal. 2013, Article ID 608943 (2013)
Momani, S, Odibat, Z, Erturk, VS: Generalized differential transform method for solving a space and time fractional diffusion-wave equation. Phys. Lett. A 370, 379-387 (2007)
Kurulay, M: The approximate and exact solutions of the space-and time-fractional Burgers equations. Int. J. Res. Rev. Appl. Sci. 3(3), 257-263 (2010)
Momani, S, Odibat, Z: A generalized differential transform method for linear partial differential equations of fractional order. Appl. Math. Lett. 21, 194-199 (2008)
Odibat, Z, Momani, S, Erturk, VS: Generalized differential transform method: application to differential equations of fractional order. Appl. Math. Comput. 197, 467-477 (2008)
Rawashdeh, MS, Al-Jammal, H: New approximate solutions to fractional nonlinear systems of partial differential equations using the FNDM. Adv. Differ. Equ. 2016(1), 235 (2016)
Momani, S: Non-perturbative analytical solutions of the space- and time-fractional Burgers equations. Chaos Solitons Fractals 28, 930-937 (2006)
Rawashdeh, M: A new approach to solve the fractional Harry Dym equation using the FRDTM. Int. J. Pure Appl. Math. 95(4), 553-566 (2014)
Esen, A, Yagmurlu, NM, Tasbozan, O: Approximate analytical solution to time-fractional damped Burger and Cahn-Allen equations. Appl. Math. Inf. Sci. 7(5), 1951-1956 (2013)
Caputo, M: Elasticitá e Dissipazione (Elasticity and Anelastic Dissipation). Zanichelli, Bologna (1969)
Caputo, M, Mainardi, F: Linear models of dissipation in anelastic solids. Riv. Nuovo Cimento 1(2), 161-198 (1971)
Rawashdeh, M: Improved approximate solutions for nonlinear evolutions equations in mathematical physics using the reduced differential transform method. Journal of Applied Mathematics and Bioinformatics 3(2), 1-14 (2013)
Rawashdeh, M: Using the reduced differential transform method to solve nonlinear PDEs arises in biology and physics. World Appl. Sci. J. 23(8), 1037-1043 (2013)
Rawashdeh, M, Obeidat, NA: On finding exact and approximate solutions to some PDEs using the reduced differential transform method. Appl. Math. Inf. Sci. 8(5), 2171-2176 (2014)
Rawashdeh, M: Approximate solutions for coupled systems of nonlinear PDES using the reduced differential transform method. Math. Comput. Appl. 19(2), 161-171 (2014)
Keskin, KY: Ph.D. Thesis. Selcuk University (2010) (in Turkish)
Momani, S: Analytic and approximate solutions of the space-and time-fractional telegraph equations. Appl. Math. Comput. 170(2), 1126-1134 (2005)
Acknowledgements
The author would like to thank the editor and the anonymous referees for their comments and suggestions on this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that he has no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rawashdeh, M.S. A reliable method for the space-time fractional Burgers and time-fractional Cahn-Allen equations via the FRDTM. Adv Differ Equ 2017, 99 (2017). https://doi.org/10.1186/s13662-017-1148-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-017-1148-8