Skip to main content
SpringerLink
Log in

The generalized Kudryashov method for nonlinear space–time fractional partial differential equations of Burgers type

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

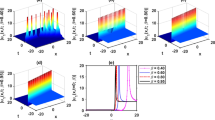
The nonlinear space–time fractional differential equations (FDE) of Burgers’ type play an important role for describing many phenomena in applied sciences. This paper develops a generalized version of the modified Kudryashov method to obtain the exact solutions for FDE of Burgers’ type. The FDE are firstly reduced to a set of ordinary differential equations by means of a fractional complex transformation and, afterward, they are solved by applying the generalized Kudryashov method (GKM). Several kinds of traveling wave solutions such as kink and singular kink waves are illustrated with various figures and discussed. The results demonstrate the efficiency of the GKM in tackling space–time partial FDE.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Zheng, B.: Exp-function method for solving fractional partial differential equations. Sci. World J. 2013, Article ID 465723 (2013)

  2. Guner, O., Bekir, A., Bilgil, H.: A note on exp-function method combined with complex transform method applied to fractional differential equations. Adv. Nonlinear Anal. 4(3), 201–208 (2015)

    MathSciNet  MATH  Google Scholar 

  3. Bekir, A., Guner, O.: Exact solutions of nonlinear fractional differential equations by \((G^{\prime }/G)\)-expansion method. Chin. Phys. B. 22(11), 110202 (2013)

    Article  Google Scholar 

  4. Bin, Z.: \((G^{\prime }/G)\)-expansion method for solving fractional partial differential equations in the theory of mathematical physics. Commun. Theor. Phys. 58, 623–630 (2012)

    Article  MathSciNet  Google Scholar 

  5. Alzaidy, J.F.: Fractional sub-equation method and its applications to the space–time fractional differential equations in mathematical physics. Br. J. Math. Comput. Sci. 3, 153–163 (2013)

    Article  Google Scholar 

  6. Zheng, B., Wen, C.: Exact solutions for fractional partial differential equations by a new fractional sub-equation method. Adv. Differ. Equ. 2013(1), 199 (2013)

    Article  MathSciNet  Google Scholar 

  7. Bekir, A., Guner, O., Unsal, O.: The first integral method for exact solutions of nonlinear fractional differential equations. J. Comput. Nonlinear Dyn. 10, 463–470 (2015)

    Google Scholar 

  8. Eslami, O., Vajargah, B.F., Mirzazadeh, M., Biswas, A.: Application of first integral method to fractional partial differential equations. Indian J. Phys. 8(2), 177–184 (2014)

    Article  Google Scholar 

  9. Singla, K., Gupta, R.K.: Space-time fractional nonlinear partial differential equations: symmetry analysis and conservation laws. Nonlinear Dyn. 89, 321 (2017)

    Article  MathSciNet  Google Scholar 

  10. Lukashchuk, S.Y., Saburova, R.D.: Approximate symmetry group classification for a nonlinear fractional filtration equation of diffusion-wave type. Nonlinear Dyn. (2018). https://doi.org/10.1007/s11071-018-4192-3

    Article  MATH  Google Scholar 

  11. Kabira, M.M., Khajeh, A., Aghdam, E.A., Koma, A.Y.: Modified Kudryashov method for finding exact solitary wave solutions of higher-order nonlinear equations. Math. Methods Appl. Sci. 34, 213–219 (2011)

    Article  MathSciNet  Google Scholar 

  12. Guner, O., Aksoy, E., Bekir, A., Cevikel, A.C.: Different methods for (3 + 1)-dimensional space-time fractional modified KdV-Zakharov-Kuznetsov equation. Comput. Math. Appl. 71, 1259–1269 (2016)

    Article  MathSciNet  Google Scholar 

  13. Hosseini, K., Mayeli, P., Kumar, D.: New exact solutions of the coupled sine-Gordon equations in nonlinear optics using the modified Kudryashov method. J. Mod. Opt. 65(3), 361–364 (2018)

    Article  MathSciNet  Google Scholar 

  14. Hosseini, K., Mayeli, P., Bejarbaneh, E.Y., Zhou, Q.: New optical solitons of the longitudinal wave equation in a magnetoelectro-elastic circular rod. Acta Phys. Pol. A. 133, 20–22 (2018)

    Article  Google Scholar 

  15. Ali, M.N., Husnine, S.M., Saha, A., Bhowmik, S.K., Dhawan, S., Ak, T.: Exact solutions, conservation laws, bifurcation of nonlinear and supernonlinear traveling waves for Sharma–Tasso–Olver equation. Nonlinear Dyn. (2018)

  16. Wazwaz, A.M., El-Tantawy, S.A.: New (3 + 1)-dimensional equations of Burgers type and Sharma–Tasso–Olver type: multiple-soliton solutions. Nonlinear Dyn. 87(4), 2457–2461 (2017)

    Article  MathSciNet  Google Scholar 

  17. Ebaid, A.: Generalization of He’s exp-function method and new exact solutions for Burgers equation. Z. Nat. A 64, 604–608 (2009)

    Google Scholar 

  18. Demetriou, E., Ivanova, N.M., Sophocleousa, C.: Group analysis of and dimensional diffusion–convection equations. J. Math. Anal. Appl. 348, 55–65 (2008)

    Article  MathSciNet  Google Scholar 

  19. Lighthill, M.J., Batchelor, G.K., Davis, R.M. (eds.): Surveys in Mechanics. Cambridge University Press. Cambridge, pp. 250–351 (1956)

  20. Demetriou, E., Christou, M.A., Sophocleous, C.: On the classification of similarity solutions of a two-dimensional diffusion–advection equation. Appl. Math. Comput. 187, 1333–1350 (2007)

    MathSciNet  MATH  Google Scholar 

  21. Hızel, E., Kucukarslan, S.: Homotopy perturbation method for (2+1)-dimensional coupled Burgers system. Nonlinear Anal: Real World Appl. 10, 1932–1938 (2009)

    Article  MathSciNet  Google Scholar 

  22. Bateman, H.: Some recent researches on the motion of fluids. Mon. Weather Rev. 43, 163–170 (1915)

    Article  Google Scholar 

  23. Burgers, J.M.: Mathematical examples illustrating relations occurring in the theory of turbulent fluid motion. Trans. R. Neth. Acad. Sci. 17, 1–53 (1939)

    MathSciNet  MATH  Google Scholar 

  24. Burgers, J.M.: A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1, 171–199 (1948)

    Article  MathSciNet  Google Scholar 

  25. Kofman, L., Raga, A.C.: Modeling structures of knots in jet flows with the Burgers equation. Astrophys. J. 390, 359–364 (1992)

    Article  Google Scholar 

  26. Gao, Q., Zou, M.Y.: An analytical solution for two and three dimensional nonlinear Burgers’ equation. App. Math. Model. 45, 255–270 (2017)

    Article  MathSciNet  Google Scholar 

  27. Kardar, M., Parisi, G., Zhang, Y.C.: Dynamical scaling of growing interfaces. Phys. Rev. Lett. 56, 889–892 (1986)

    Article  Google Scholar 

  28. Velasco, R.M., Saavedra, P.: A first order model in traffic flow. Phys. D 228, 153–158 (2007)

    Article  MathSciNet  Google Scholar 

  29. Watanabe, S., Ishiwata, S., Kawamura, K., Oh, H.G.: Higher order solution of nonlinear waves. II. Shock wave described by Burgers equation. J. Phys. Soc. Jpn. 66, 984–987 (1997)

    Article  MathSciNet  Google Scholar 

  30. Albeverio, S., Korshunova, A., Rozanova, O.: A probabilistic model associated with the pressureless gas dynamics. Bull. Sci. Math. 137, 902–922 (2013)

    Article  MathSciNet  Google Scholar 

  31. Pospelov, L.A.: Propagation of finite-amplitude elastic waves. Sov. Phys. Acoust. 11, 302–304 (1966)

    Google Scholar 

Download references

Acknowledgements

The authors would like to thank the deanship of scientific research of Majmaah University for the financial grant received for conducting this research (Project Number 68/38).

Author information

Authors and Affiliations

  1. Department of Mathematics, College of Science and Humanities at Howtat Sudair, Majmaah University, Majmaah, 11952, Saudi Arabia

    A. A. Gaber

  2. Kingdom of Saudi Arabia Department of Mathematics, Faculty of Science, University of Tabuk, P.O. Box 741, Tabuk, 71491, Saudi Arabia

    A. F. Aljohani & A. Ebaid

  3. Institute of Engineering, Polytechnic of Porto, Rua Dr. António Bernardino de Almeida, 431, 4249-015, Porto, Portugal

    J. Tenreiro Machado

Authors
  1. A. A. Gaber
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. F. Aljohani
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Ebaid
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. J. Tenreiro Machado
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Ebaid.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest with regard to the publication of this manuscript. All authors contributed equally to this work.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gaber, A.A., Aljohani, A.F., Ebaid, A. et al. The generalized Kudryashov method for nonlinear space–time fractional partial differential equations of Burgers type. Nonlinear Dyn 95, 361–368 (2019). https://doi.org/10.1007/s11071-018-4568-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4568-4

Keywords

Search

Navigation