1 Introduction

In recent years, considerable attention has been paid to bidirectional associative memory (BAM) Cohen-Grossberg neural networks [1] due to their potential applications in various fields such as neural biology, pattern recognition, classification of patterns, parallel computation and so on [2–4]. In real life, numerous application examples appear, for example, emerging parallel/distributed architectures were explored for the digital VLSI implementation of adaptive bidirectional associative memory (BAM) [5], Teddy and Ng [6] applied a novel local learning model of the pseudo self-evolving cerebellar model articulation controller (PSECMAC) associative memory network to produce accurate forecasts of ATM cash demands. Chang et al. [7] proposed a maximum-likelihood-criterion based on BAM networks to evaluate the similarity between a template and a matching region. Sudo et al. [8] proposed a novel associative memory that operated in noisy environments and performed well in online incremental learning applying self-organizing incremental neural networks. On the one hand, the existence and stability of the equilibrium point of BAM Cohen-Grossberg neural networks plays an important role in practical application. On the other hand, time delay is inevitable due to the finite switching speed of amplifiers in the electronic implementation of analog neural networks, moreover, time delays may have important effect on the stability of neural networks and lead to periodic oscillation, bifurcation, chaos and so on [3, 9, 10]. Thus many interesting stability results on BAM Cohen-Grossberg neural networks with delays have been available [11–30].

As is well known, numerous dynamical systems of electronic networks, biological neural networks, and engineering fields often undergo abrupt change at certain moments due to instantaneous perturbations which leads to impulsive effects [4, 19, 20, 31–36]. Many scholars [37, 38] think that uncertainty or vagueness often appear in mathematical modeling of real world problems, thus it is necessary to take vagueness into consideration. Fuzzy neural networks (FNNs) pay an important role in image processing and pattern recognition [37] and some results have been reported on stability and periodicity of FNNs [11, 39–41]. Here we would like to point out that most neural networks involve negative feedback terms and do not possess amplification functions or behaved functions. The model (1.1) of this paper has amplifications function and behaved functions which differ from most neural networks with negative feedback term. Up to now, there are rare papers that consider exponential stability of this kind of fuzzy bidirectional associative memory Cohen-Grossberg neural networks with mixed delays and impulses.

Inspired by the discussion above, in this paper, we are to consider the following fuzzy bidirectional associative memory Cohen-Grossberg neural networks with mixed delays and impulses,

$$ \left \{ \textstyle\begin{array}{l} \dot{x}_{i}(t)=\iota_{i}(x_{i}(t)) [-a_{i}(t,x_{i}(t))+\sum_{j=1}^{m}c_{ji}(t)f_{j}(y_{j}(t-\tau(t)))\\ \hphantom{\dot{x}_{i}(t)=}+\bigwedge_{j=1}^{m}\alpha_{ji}(t)\int_{-\infty }^{t}K_{ji}(t-s)f_{j}(y_{j}(s))\,ds+\bigwedge_{j=1}^{m}T_{ji}u_{j}+\bigvee_{j=1}^{m}H_{ji}u_{j}\\ \hphantom{\dot{x}_{i}(t)=}+\bigvee_{j=1}^{m} \beta_{ji}(t)\int_{-\infty}^{t}K_{ji}(t-s)f_{j}(y_{j}(s))\,ds+I_{i}(t) ], \quad t\neq t_{k}, i\in\ell,\\ \triangle x_{i}(t_{k})=x_{i}(t_{k})-x_{i}(t_{k}^{-})=-\gamma_{ik}x_{i}(t_{k}^{-})+\sum_{j=1}^{m}e_{ij}(t_{k}^{-})E_{j}(y_{j}(t_{k}^{-}-\tau)), \quad k\in{\mathbb{Z_{+}}},\\ \dot{y}_{j}(t)=\vartheta_{j}(y_{j}(t)) [-b_{j}(t,y_{j}(t))+\sum_{i=1}^{n}d_{ij}(t)g_{i}(x_{i}(t-\tau(t)))\\ \hphantom{\dot{y}_{j}(t)=}+\bigwedge_{i=1}^{n}p_{ij}(t)\int_{-\infty }^{t}N_{ij}(t-s)g_{i}(x_{i}(s))\,ds+\bigwedge_{i=1}^{n}S_{ij}u_{i}+\bigvee_{i=1}^{n}L_{ij}u_{i}\\ \hphantom{\dot{y}_{j}(t)=}+\bigvee_{i=1}^{n} q_{ij}(t)\int_{-\infty}^{t}N_{ij}(t-s)g_{i}(x_{i}(s))\,ds+J_{j}(t) ], \quad t\neq t_{k}, j\in\hbar,\\ \triangle y_{j}(t_{k})=y_{j}(t_{k})-y_{j}(t_{k}^{-})=-\delta_{jk}y_{i}(t_{k}^{-})+\sum_{i=1}^{n}h_{ji}(t_{k}^{-})H_{i}(x_{i}(t_{k}^{-}-\tau)), \quad k\in{\mathbb{Z_{+}}}, \end{array}\displaystyle \right . $$
(1.1)

with initial conditions

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} x_{i}(s)=\phi_{1i}(s), &s\in(-\infty,0], i\in\ell,\\ y_{j}(s)=\phi_{2i}(s),& s\in(-\infty,0], j\in\hbar, \end{array}\displaystyle \right . $$
(1.2)

where n and m correspond to the number of neurons in X-layer and Y-layer, respectively. \(x_{i}(t)\) and \(y_{j}(t)\) are the activations of the ith neuron and the jth neurons, respectively. \(\iota_{i}(\cdot)\) and \(\vartheta_{j}(\cdot)\) are the abstract amplification functions, \(a_{i}(t,\cdot)\) and \(b_{j}(t,\cdot)\) stand for the rate functions with which the ith neuron and jth neuron will reset its potential to the resting state in isolation when disconnected from the network and external inputs; \(\alpha_{ji}(t)\), \(\beta_{ji}(t)\), \(T_{ji}\) and \(H_{ji}\) are elements of fuzzy feedback MIN template and fuzzy feedback MAX template, fuzzy feed-forward MIN template and fuzzy feed-forward MAX template in X-layer, respectively; \(p_{ij}(t)\), \(q_{ij}(t)\), \(S_{ij}\) and \(L_{ij}\) are elements of fuzzy feedback MIN template and fuzzy feedback MAX template, fuzzy feed-forward MIN template and fuzzy feed-forward MAX template in Y-layer, respectively; ⋀ and ⋁ denote the fuzzy AND and fuzzy OR operation, respectively; \(u_{j}\), \(u_{i}\) denote external input of the ith neurons in X-layer and external input of the jth neurons in Y-layer, respectively; \(I_{i}(t)\) and \(J_{j}(t)\) are external bias of X-layer and Y-layer, respectively, \(f_{j}(\cdot)\) and \(g_{i}(\cdot)\) are signal transmission functions, \(K_{ji}(t)\) and \(N_{ij}(t)\) are delay kernels, \(\ell=\{1,2,\ldots,n\}\), \(\hbar=\{1,2,\ldots,m\}\), \(\mathbb{Z_{+}} \) denotes the set of positive integral numbers, the impulse times \(t_{k}\) satisfy \(0=t_{0}< t_{1}< t_{2}<\cdots<t_{k}<\cdots\), \(\lim_{k\rightarrow\infty}t_{k}=\infty\), \(\phi_{1i}(\cdot), \phi_{2j}(\cdot) \in{\mathbb{C}}\), where \({\mathbb{C}}\) denotes real-valued continuous functions defined on \((-\infty,0]\), \(\tau(t)\) is the transmission delay such that \(0\leq\tau(t)\leq\tau\), τ is a positive constant, \(e_{ij}(t_{k}^{-})\) represents impulsive perturbations of the ith unit at time \(t_{k}\), \(h_{ji}(t_{k}^{-})\) represents impulsive perturbations of the jth unit at time \(t_{k}\), \(E_{j}(y_{j}(t_{k}^{-}))\) represents impulsive perturbations of the jth unit at time \(t_{k}\) and \(y_{j}(t_{k}^{-})\) denotes impulsive perturbations of the jth unit at time \(t_{k}\) caused by the transmission delays, \(H_{i}(x_{i}(t_{k}^{-}))\) represents impulsive perturbations of the ith unit at time \(t_{k}\) and \(x_{i}(t_{k}^{-})\) denotes impulsive perturbations of the ith unit at time \(t_{k}\) which caused by the transmission delays. For details, see [42–44].

The main purpose of this paper is to investigate the existence and global exponential stability of a periodic solution of fuzzy BAM Cohen-Grossberg neural networks with mixed delays and impulses. By constructing a suitable Lyapunov function and a new differential inequality, we establish some sufficient conditions to ensure the existence and global exponential stability of a periodic solution of the model (1.1). The results obtained in this paper extend and complement the previous studies in [4, 10]. Two examples are given to illustrate the effectiveness of our theoretical findings. To the best of our knowledge, there are very few papers that deal with this aspect. Therefore we think that the study of the fuzzy BAM Cohen-Grossberg neural networks with mixed delays and impulses has important theoretical and practical value. Here we shall mention that since the existence of amplifications function and behaved functions in model (1.1), thus there are some difficulties in dealing with the exponential stability. We will apply some inequality techniques, meanwhile, the construction of Lyapunov function is a key issue.

The remaining part of this paper is organized as follows. In Section 2, the necessary definitions and lemmas are introduced. In Section 3, we present some new sufficient conditions to ensure the existence and global exponential stability of a periodic solution of model (1.1). In Section 4, an illustrative example is given to show the effectiveness of the proposed method. A brief conclusion is drawn in Section 5.

2 Preliminaries

Let \({\mathbb{R}}\) denote the set of real number, \({\mathbb{R}}^{n}\) the n-dimensional real space equipped with the Euclidean norm \(|\cdot|\), \({\mathbb{R}}_{+}\) the set of positive numbers. Denote \(PC({\mathbb{R}},{\mathbb{R}}_{+})=\{\phi:{\mathbb{R}}\rightarrow {\mathbb{R}}^{n}: \phi(t)\text{ is continuous for }t\neq t_{k}, \phi(t_{k}^{+}), \phi(t_{k}^{-})\in{\mathbb{R}}^{n}\text{ and } \phi(t_{k}^{-})=\phi(t_{k})\}\).

Throughout this paper, we make the following assumptions:

  1. (H1)

    For \(i\in\ell\), \(j\in\hbar\), \(c_{ji}(t)\), \(\alpha_{ji}(t)\), \(\beta _{ji}(t)\), \(e_{ij}(t)\), \(d_{ij}(t)\), \(p_{ij}(t)\), \(q_{ij}(t)\), \(h_{ji}(t)\), \(\tau(t)\), \(I_{i}(t)\) and \(J_{j}(t)\) are all continuously periodic functions defined on \(t\in[0,\infty)\) with common period \(\omega>0\).

  2. (H2)

    For \(i\in\ell\), \(j\in\hbar\), there exist positive constants \(L_{j}^{f}\), \(L_{j}^{E}\), \(L_{i}^{g}\) and \(L_{j}^{H}\) such that

    $$\begin{aligned} &\bigl|f_{j}(u)-f_{j}(v)\bigr|\leq L_{j}^{f}|u-v|,\qquad \bigl|E_{j}(u)-E_{j}(v)\bigr|\leq L_{j}^{E}|u-v|,\\ &\bigl|g_{i}(u)-g_{i}(v)\bigr|\leq L_{i}^{g}|u-v|,\qquad \bigl|H_{i}(u)-H_{i}(v)\bigr| \leq L_{j}^{H}|u-v| \end{aligned} $$

    for all \(u,v\in{\mathbb{R}}\).

  3. (H3)

    For \(i\in\ell\), \(j\in\hbar\), \(\iota_{i}(\cdot)\) and \(\vartheta_{j}(\cdot)\) are continuous and satisfy \(0\leq\underline{\iota}_{i}\leq \iota_{i}(\cdot)\leq\overline{\iota}_{i}\), \(0\leq\underline{\vartheta}_{j}\leq \vartheta_{j}(\cdot)\leq\overline{\vartheta}_{j}\), where \(\underline{\iota}_{i}\), \(\overline{\iota}_{i}\), \(\underline{\vartheta}_{j}\), \(\overline{\vartheta}_{j}\) are some positive constants.

  4. (H4)

    For \(i\in\ell\), \(j\in\hbar\), there exist continuous positive ω-periodic functions \(\varrho_{i}(t)\) and \(\sigma_{j}(t)\) such that

    $$\frac{a_{i}(t,u)-a_{i}(t,v)}{u-v}\geq\varrho_{i}(t),\quad\quad\frac {b_{j}(t,u)-b_{j}(t,v)}{u-v}\geq \sigma_{j}(t) $$

    for all \(u,v\in{\mathbb{R}}\).

  5. (H5)

    For \(i\in\ell\), \(j\in\hbar\), the delay kernels \(K_{ij}(\cdot), N_{ji}(\cdot) \in C ({\mathbb{R}}^{+},{\mathbb{R}}^{+})\) are piecewise continuous and satisfy \(K_{ij}(s)\leq\tilde{K}(s)\) and \(N_{ji}(s)\leq\tilde{K}(s)\) for all \(s\in{\mathbb{R}}^{+}\), where \(\tilde{K}(s)\in C ({\mathbb{R}}^{+},{\mathbb{R}}^{+})\) and integrable, satisfying \(\int_{0}^{\infty}\tilde{K}(s) e^{\mu s}\,ds<\infty\), in which the constant μ denotes some positive number.

  6. (H6)

    For \(i\in\ell\), \(j\in\hbar\omega>0\), there exists \(q\in {\mathbb{Z}}^{+}\) such that \(t_{k}+\omega=t_{k+q}\) and \(\gamma_{ik}=\gamma_{i(k+q)}\), \(\delta_{jk}=\delta_{j(k+q)}\), \(k \in {\mathbb{Z}}^{+}\).

  7. (H7)

    For \(i\in\ell\), \(j\in\hbar\), \(c_{ji}^{*}=\max_{t\in[0,\omega]}|c_{ji}(t)|\), \(\alpha_{ji}^{*}=\max_{t\in[0,\omega]}|\alpha_{ji}(t)|\), \(\beta_{ji}^{*}=\max_{t\in[0,\omega]}|\beta_{ji}(t)|\), \(e_{ij}^{*}=\max_{t\in[0,\omega]}|e_{ij}(t)|\), \(d_{ij}^{*}=\max_{t\in[0,\omega]}|d_{ij}(t)|\), \(p_{ij}^{*}=\max_{t\in[0,\omega]}|p_{ij}(t)|\), \(q_{ij}^{*}=\max_{t\in[0,\omega]}|q_{ij}(t)|\), \(h_{ji}^{*}=\max_{t\in[0,\omega]}|h_{ji}(t)|\), \(\varrho_{i}^{\star}=\min_{t\in[0,\omega]}|\varrho_{i}(t)|\), \(\sigma_{i}^{\star}=\min_{t\in[0,\omega]}|\sigma_{j}(t)|\).

In this paper, we use the following norm of \({\mathbb{R}}^{n+m}\):

$$\|u\|=\sum_{i=1}^{n}|x_{i}|+\sum _{j=1}^{m}|y_{j}|,\qquad \|\phi\|=\sup _{s\in(-\infty,0]} \Biggl[\sum_{i=1}^{n}\bigl| \phi _{1i}(s)\bigr|+\sum_{j=1}^{m}\bigl|\phi_{2j}(s)\bigr| \Biggr] $$

for \(u=(x_{1},x_{2},\ldots,x_{n},y_{1},y_{2},\ldots,y_{m})^{T}\in{\mathbb{R}}^{n+m}\), \(\phi=(\phi_{11},\phi_{12},\ldots,\phi_{1n},\phi_{21},\phi _{22},\ldots,\phi_{2m})^{T}\in{\mathbb{C}}^{n+m}\).

Lemma 2.1

[37]

Let x and y be two states of system (1.1). Then

$$\Biggl\vert \bigwedge_{j=1}^{n} \alpha_{ij}(t)g_{j}(x)-\bigwedge _{j=1}^{n}\alpha _{ij}(t)g_{j}(y) \Biggr\vert \leq\sum_{j=1}^{n}\bigl| \alpha_{ij}(t)\bigr|\bigl|g_{j}(x)-g_{j}(y)\bigr| $$

and

$$\Biggl\vert \bigvee_{j=1}^{n} \beta_{ij}(t)g_{j}(x)-\bigvee_{j=1}^{n} \beta _{ij}(t)g_{j}(y)\Biggr\vert \leq\sum _{j=1}^{n}\bigl|\beta_{ij}(t)\bigr|\bigl|g_{j}(x)-g_{j}(y)\bigr|. $$

Lemma 2.2

[4]

Let p, q, r and τ denote nonnegative constants and \(f\in PC ({\mathbb{R}},{\mathbb{R}}_{+})\) satisfies the scalar impulsive differential inequality

$$ \left \{ \textstyle\begin{array}{l} D^{+}f(t)\leq-pf(t)+q\sup_{t-\tau\leq s\leq t}f(s)+r\int_{0}^{\sigma}k(s)f(t-s)\,ds,\quad t\neq t_{k}, t\geq t_{0},\\ f(t_{k})\leq a_{k}f(t_{k}^{-})+b_{k}f(t_{k}^{-}-\tau),\quad k\in {\mathbb{Z}}^{+}, \end{array}\displaystyle \right . $$
(2.1)

where \(0<\sigma\leq+\infty\), \(a_{k},b_{k}\in{\mathbb{R}}\), \(k(\cdot)\in PC([0,\sigma],{\mathbb{R}}^{+})\) satisfies \(\int_{0}^{\sigma}k(s)e^{\eta_{0} s}\,ds<\infty\) for some positive constant \(\eta_{0}>0\) in this case when \(\sigma=+\infty\). Moreover, when \(\sigma=+\infty\), the interval \({[t-\sigma,t]}\) is understood to be replaced by \((-\infty,t]\). Assume that (i) \(p>q+r\int_{0}^{\sigma}k(s)\,ds\). (ii) There exist constant \(M>0\), \(\eta>0\) such that

$$\prod_{k=1}^{n} \max\bigl\{ 1,a_{k}+b_{k}e^{\lambda\tau} \bigr\} \leq Me^{\eta(t_{n}-t_{0})}, \quad n\in {\mathbb{Z}}_{+}, $$

where \(\lambda\in(0,\eta_{0})\) satisfies

$$\lambda< p-qe^{\lambda\tau}-r \int_{0}^{\sigma}k(s)e^{\lambda s}\,ds. $$

Then

$$f(t)\leq M\overline{f}(t_{0})e^{-(\lambda-\eta)(t-t_{0})}, \quad t\geq t_{0}, $$

where \(\overline{f}(t_{0})=\sup_{t_{0}-\max\{\sigma,\tau\}}f(s)\).

3 Global exponential stability of the periodic solution

In this section, we will discuss the global exponential stability of the periodic solution for (1.1).

Theorem 3.1

Assume that (H1)-(H7) hold, then there exists a unique ω-periodic solution of system (1.1) which is globally exponentially stable if the following conditions are fulfilled.

  1. (H8)
    $$ \begin{aligned} & \frac{\min\{\varrho_{i}^{\star}, \sigma_{j}^{\star}\}\min_{i\in\ell, j\in\hbar}\{\underline{\iota}_{i}, \underline{\vartheta}_{j}\}}{\max_{i\in\ell, j\in\hbar}\{\overline{\iota}_{i}, \overline{\vartheta}_{j}\}}\\ &\quad >\max \Biggl\{ \sum_{i=1}^{n} \max_{j\in\hbar} c_{ji}^{*}L_{j}^{f}, \sum_{j=1}^{m} \max_{i\in\ell}d_{ij}^{*}L_{i}^{g} \Biggr\} \\ &\qquad{}+\max \Biggl\{ \sum_{i=1}^{n}\max _{j\in\hbar} \alpha_{ji}^{*}L_{j}^{f}, \sum_{i=1}^{n}\max_{j\in\hbar} \beta_{ji}^{*}L_{j}^{f}, \sum _{j=1}^{m}\max_{i\in\ell} p_{ij}^{*}L_{i}^{g}, \sum _{j=1}^{m}\max_{i\in\ell} q_{ij}^{*}L_{i}^{g} \Biggr\} \\ &{}\qquad\times \int_{0}^{\infty}\tilde{K}(s)\,ds. \end{aligned} $$
  2. (H9)

    There exist constants \(M\geq1\), \(\lambda\in(0, \lambda_{0})\) and \(\eta\in(0,\lambda)\) such that \(\prod_{l=1}^{n} \max\{1, \chi_{l}\}\leq Me^{\eta t_{n}}\) for all \(n\in{\mathbb{Z}_{+}}\) holds and

    $$\begin{aligned} \lambda < &\frac{\min\{\varrho_{i}^{\star}, \sigma_{j}^{\star}\}\min_{i\in\ell, j\in\hbar}\{\underline{\iota}_{i}, \underline{\vartheta}_{j}\}}{\max_{i\in\ell, j\in\hbar}\{\overline{\iota}_{i}, \overline{\vartheta}_{j}\}} -\max \Biggl\{ \sum_{i=1}^{n} \max_{j\in\hbar} c_{ji}^{*}L_{j}^{f}, \sum_{j=1}^{m} \max_{i\in\ell}d_{ij}^{*}L_{i}^{g} \Biggr\} e^{\lambda\tau} \\ &{}-\max \Biggl\{ \sum_{i=1}^{n}\max _{j\in\hbar} \alpha_{ji}^{*}L_{j}^{f}, \sum_{i=1}^{n}\max_{j\in\hbar} \beta_{ji}^{*}L_{j}^{f}, \sum _{j=1}^{m}\max_{i\in\ell} p_{ij}^{*}L_{i}^{g}, \sum _{j=1}^{m}\max_{i\in\ell} q_{ij}^{*}L_{i}^{g} \Biggr\} \\ &{}\times \int_{0}^{\infty}\tilde{K}(s)\,ds, \end{aligned}$$

    where

    $$\chi_{l}=\frac{\max_{i\in\ell, j\in\hbar}\{\overline{\iota}_{i}, \overline{\vartheta}_{j}\}}{\min_{i\in\ell, j\in\hbar}\{\underline{\iota}_{i}, \underline{\vartheta}_{j}\}}\max_{i\in\ell, j\in\hbar} \Biggl\{ |1- \gamma_{il}|, |1-\delta_{jl}|+\max \Biggl\{ \sum _{i=1}^{n} \max_{j\in\hbar}e_{ij}^{*}L_{j}^{E}, \sum_{j=1}^{m} \max_{i\in\ell}h_{ji}^{*}L_{i}^{H} \Biggr\} e^{\lambda\tau} \Biggr\} . $$

Proof

Assume that \(u(t)=(x_{1}(t,\phi_{1}),x_{2}(t,\phi_{1}),\ldots ,x_{n}(t,\phi_{1}), y_{1}(t,\phi_{2}),y_{2}(t,\phi_{2}),\ldots,y_{m}(t,\phi _{2}))^{T}\) is an arbitrary solution of system (1.1) through \((t,\phi_{1},\phi_{2})\), where \(\phi_{1}=(\phi_{11},\phi_{12}, \ldots,\phi_{1n})^{T}\), \({\phi _{2}=(\phi_{21},\phi_{22}, \ldots,\phi_{2m})^{T}}\). Define

$$x_{i}(t+\omega,\phi_{1})=\varphi_{1i},\quad t\leq0, i \in\ell, \qquad y_{j}(t+\omega,\phi_{2})=\varphi_{2j},\quad t \leq0, j\in\hbar, $$

then \(\varphi_{1}=(\varphi_{11},\varphi_{12},\ldots,\varphi _{1n})^{T}\in {\mathbb{C}}^{n}\), \(\varphi_{2}=(\varphi_{21},\varphi_{22},\ldots,\varphi_{2m})^{T}\in {\mathbb{C}}^{m}\).

Now we construct the following Lyapunov function:

$$\begin{aligned} V(t) =&\sum_{i=1}^{n} \int_{x_{i}(t)}^{x_{i}(t+\omega)}\frac{1}{\iota_{i}(s)}\,ds \operatorname{sgn} \bigl[x_{i}(t+\omega)-x_{i}(t)\bigr] \\ &{} +\sum_{j=1}^{m} \int_{y_{j}(t)}^{y_{j}(t+\omega)}\frac{1}{\vartheta_{j}(s)}\,ds \operatorname{sgn} \bigl[y_{j}(t+\omega)-y_{j}(t)\bigr]. \end{aligned}$$
(3.1)

It is easy to see that

$$ \begin{aligned}[b] &\min_{i\in\ell,j\in \hbar} \biggl\{ \frac{1}{\overline{\iota}_{i}},\frac{1}{\overline{\vartheta }_{j}} \biggr\} \Biggl(\sum_{i=1}^{n}\bigl|x_{i}(t+ \omega)-x_{i}(t)\bigr|+\sum_{j=1}^{m}\bigl|y_{j}(t+ \omega)-y_{j}(t)\bigr| \Biggr) \\ &\quad\leq V(t) \leq\max_{i\in\ell,j\in \hbar} \biggl\{ \frac{1}{\underline{\iota}_{i}}, \frac{1}{\underline {\vartheta}_{j}} \biggr\} \Biggl(\sum_{i=1}^{n}\bigl|x_{i}(t+ \omega )-x_{i}(t)\bigr|+\sum_{j=1}^{m}\bigl|y_{j}(t+ \omega)-y_{j}(t)\bigr| \Biggr). \end{aligned} $$
(3.2)

When \(t\neq t_{k}\), calculating the derivative of \(D^{+}V(t)\) along the solution of (1.1), we have

$$\begin{aligned} D^{+}V(t) \leq&\sum_{i=1}^{n} \biggl[\frac{D^{+}x_{i}(t+\omega)}{\iota _{i}(x_{i}(t+\omega))}-\frac{D^{+}x_{i}(t)}{\iota_{i}(x_{i}(t))} \biggr]\operatorname{sgn} \bigl[x_{i}(t+\omega)-x_{i}(t)\bigr] \\ &{}+\sum_{j=1}^{m} \biggl[ \frac{D^{+}y_{j}(t+\omega)}{\vartheta _{j}(y_{j}(t+\omega))}-\frac{D^{+}y_{j}(t)}{\vartheta_{j}(y_{j}(t))} \biggr]\operatorname{sgn}\bigl[y_{j}(t+ \omega)-y_{j}(t)\bigr] \\ =&\sum_{i=1}^{n} \Biggl[-a_{i} \bigl(t,x_{i}(t+\omega)\bigr)+a_{i}\bigl(t,x_{i}(t) \bigr)+\sum_{j=1}^{m}c_{ji}(t)f_{j} \bigl(y_{j}\bigl(t+\omega-\tau(t+\omega)\bigr)\bigr) \\ &{}-\sum_{j=1}^{m}c_{ji}(t)f_{j} \bigl(y_{j}\bigl(t-\tau(t)\bigr)\bigr)+\bigwedge _{j=1}^{m}\alpha _{ji}(t) \int_{-\infty}^{t+\omega}K_{ji}(t+ \omega-s)f_{j}\bigl(y_{j}(s)\bigr)\,ds \\ &{}-\bigwedge_{j=1}^{m} \alpha_{ji}(t) \int_{-\infty }^{t}K_{ji}(t-s)f_{j} \bigl(y_{j}(s)\bigr)\,ds+ \bigvee_{j=1}^{m} \beta_{ji}(t) \int_{-\infty}^{t+\omega}K_{ji}(t+\omega -s)f_{j}\bigl(y_{j}(s)\bigr)\,ds \\ &{}-\bigvee_{j=1}^{m} \beta_{ji}(t) \int_{-\infty}^{t}K_{ji}(t-s)f_{j} \bigl(y_{j}(s)\bigr)\,ds \Biggr]\operatorname{sgn} \bigl[x_{i}(t+ \omega)-x_{i}(t)\bigr] \\ &{}+\sum_{j=1}^{m} \Biggl[-b_{j} \bigl(t,y_{j}(t+\omega)\bigr)+b_{j}\bigl(t,y_{j}(t) \bigr)+\sum_{i=1}^{n}d_{ij}(t)g_{i} \bigl(x_{i}\bigl(t+\omega-\tau(t+\omega)\bigr)\bigr) \\ &{}-\sum_{i=1}^{n}d_{ij}(t)g_{i} \bigl(x_{i}\bigl(t-\tau(t)\bigr)\bigr)+\bigwedge _{i=1}^{n}p_{ij}(t) \int_{-\infty}^{t+\omega}N_{ij}(t+\omega -s)g_{i}\bigl(x_{i}(s)\bigr)\,ds \\ &{}-\bigwedge_{i=1}^{n}p_{ij}(t) \int_{-\infty}^{t}N_{ij}(t-s)g_{i} \bigl(x_{i}(s)\bigr)\,ds+ \bigvee_{i=1}^{n} q_{ij}(t) \int_{-\infty}^{t+\omega}N_{ij}(t+\omega -s)g_{i}\bigl(x_{i}(s)\bigr)\,ds \\ &{}-\bigvee_{i=1}^{n} q_{ij}(t) \int_{-\infty}^{t+\omega}N_{ij}(t+\omega -s)g_{i}\bigl(x_{i}(s)\bigr)\,ds \Biggr]\operatorname{sgn} \bigl[y_{j}(t+\omega)-y_{j}(t)\bigr] \\ \leq&-\min_{i\in\ell}\varrho_{i}^{\star}\sum _{i=1}^{n}\bigl|x_{i}(t+\omega )-x_{i}(t)\bigr|+\sum_{i=1}^{n}\sum _{j=1}^{m} c_{ji}^{*}L_{j}^{f}\bigl|y_{j} \bigl(t+\omega-\tau (t)\bigr)-y_{j}\bigl(t-\tau(t)\bigr)\bigr| \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{m} \alpha_{ji}^{*}L_{j}^{f} \int_{0}^{\infty}\tilde {K}(s)\bigl|y_{j}(t+ \omega-s)-y_{j}(t-s)\bigr|\,ds \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{m} \beta_{ji}^{*}L_{j}^{f} \int_{0}^{\infty}\tilde {K}(s)\bigl|y_{j}(t+ \omega-s)-y_{j}(t-s)\bigr|\,ds \\ &{}-\min_{j\in\hbar}\sigma_{j}^{\star}\sum _{j=1}^{m}\bigl|y_{j}(t+\omega )-y_{j}(t)\bigr|+\sum_{j=1}^{m}\sum _{i=1}^{n} d_{ij}^{*}L_{i}^{g}\bigl|x_{i} \bigl(t+\omega-\tau (t)\bigr)-x_{i}\bigl(t-\tau(t)\bigr)\bigr| \\ &{}+\sum_{j=1}^{m}\sum _{i=1}^{n} p_{ij}^{*}L_{i}^{g} \int_{0}^{\infty}\tilde {K}(s)\bigl|x_{i}(t+ \omega-s)-x_{i}(t-s)\bigr|\,ds \\ &{}+\sum_{j=1}^{m}\sum _{i=1}^{n} q_{ij}^{*}L_{i}^{g} \int_{0}^{\infty}\tilde{K}(s)\bigl|x_{i}(t+ \omega-s)-x_{i}(t-s)\bigr|\,ds \\ \leq& -\min\bigl\{ \varrho_{i}^{\star}, \sigma_{j}^{\star}\bigr\} \Biggl[\sum_{i=1}^{n} \bigl(x_{i}(t+\omega)-x_{i}(t)\bigr)+\sum _{j=1}^{m}\bigl(y_{j}(t+ \omega)-y_{j}(t)\bigr) \Biggr] \\ &{}+\sum_{i=1}^{n}\max_{j\in\hbar} c_{ji}^{*}L_{j}^{f}\sum _{j=1}^{m}\bigl|y_{j}\bigl(t+\omega-\tau(t) \bigr)-y_{j}\bigl(t-\tau(t)\bigr)\bigr| \\ &{}+\sum_{i=1}^{n}\max_{j\in\hbar} \alpha_{ji}^{*}L_{j}^{f} \int_{0}^{\infty}\tilde{K}(s)\bigl|y_{j}(t+ \omega-s)-y_{j}(t-s)\bigr|\,ds \\ &{}+\sum_{i=1}^{n}\max_{j\in\hbar} \beta_{ji}^{*}L_{j}^{f} \int_{0}^{\infty}\tilde{K}(s)\sum _{j=1}^{m}\bigl|y_{j}(t+\omega-s)-y_{j}(t-s)\bigr|\,ds \\ &{}+\sum_{j=1}^{m} \max _{i\in\ell}d_{ij}^{*}L_{i}^{g}\sum _{i=1}^{n}\bigl|x_{i}\bigl(t+\omega- \tau(t)\bigr)-x_{i}\bigl(t-\tau(t)\bigr)\bigr| \\ &{}+\sum_{j=1}^{m}\max_{i\in\ell} p_{ij}^{*}L_{i}^{g} \int_{0}^{\infty}\tilde {K}(s)\sum _{i=1}^{n}\bigl|x_{i}(t+\omega-s)-x_{i}(t-s)\bigr|\,ds \\ &{}+\sum_{j=1}^{m}\max_{i\in\ell} q_{ij}^{*}L_{i}^{g} \int_{0}^{\infty}\tilde {K}(s)\sum _{i=1}^{n}\bigl|x_{i}(t+\omega-s)-x_{i}(t-s)\bigr|\,ds \\ \leq& -\min\bigl\{ \varrho_{i}^{\star}, \sigma_{j}^{\star}\bigr\} \Biggl[\sum_{i=1}^{n} \bigl(x_{i}(t+\omega)-x_{i}(t)\bigr)+\sum _{j=1}^{m}\bigl(y_{j}(t+ \omega)-y_{j}(t)\bigr) \Biggr] \\ &{}+\max \Biggl\{ \sum_{i=1}^{n}\max _{j\in\hbar} c_{ji}^{*}L_{j}^{f}, \sum _{j=1}^{m} \max_{i\in\ell}d_{ij}^{*}L_{i}^{g} \Biggr\} \\ &{}\times \Biggl[\sum_{i=1}^{n}\bigl|x_{i} \bigl(t+\omega-\tau(t)\bigr)-x_{i}\bigl(t-\tau (t)\bigr)\bigr|+\sum _{j=1}^{m}\bigl|y_{j}\bigl(t+\omega-\tau(t) \bigr)-y_{j}\bigl(t-\tau(t)\bigr)\bigr| \Biggr] \\ &{}+\max \Biggl\{ \sum_{i=1}^{n}\max _{j\in\hbar} \alpha_{ji}^{*}L_{j}^{f}, \sum_{i=1}^{n}\max_{j\in\hbar} \beta_{ji}^{*}L_{j}^{f}, \sum _{j=1}^{m}\max_{i\in\ell} p_{ij}^{*}L_{i}^{g}, \sum _{j=1}^{m}\max_{i\in\ell} q_{ij}^{*}L_{i}^{g} \Biggr\} \\ &{}\times \int_{0}^{\infty}\tilde{K}(s) \Biggl[\sum _{i=1}^{n}\bigl|x_{i}(t+\omega-s)-x_{i}(t-s)\bigr|+ \sum_{j=1}^{m}\bigl|y_{j}(t+ \omega-s)-y_{j}(t-s)\bigr| \Biggr]\,ds. \end{aligned}$$
(3.3)

In view of (3.2), it follows from (3.3) that

$$\begin{aligned} D^{+}V(t) \leq& -\min\bigl\{ \varrho_{i}^{\star}, \sigma_{j}^{\star}\bigr\} \min_{i\in\ell, j\in\hbar}\{ \underline{\iota}_{i}, \underline{\vartheta}_{j}\}V(t) \\ &{}+\max \Biggl\{ \sum_{i=1}^{n}\max _{j\in\hbar} c_{ji}^{*}L_{j}^{f}, \sum _{j=1}^{m} \max_{i\in\ell}d_{ij}^{*}L_{i}^{g} \Biggr\} \max_{i\in\ell, j\in\hbar}\{\overline{\iota}_{i}, \overline{ \vartheta}_{j}\}V\bigl(t-\tau (t)\bigr) \\ &{}+\max \Biggl\{ \sum_{i=1}^{n}\max _{j\in\hbar} \alpha_{ji}^{*}L_{j}^{f}, \sum_{i=1}^{n}\max_{j\in\hbar} \beta_{ji}^{*}L_{j}^{f}, \sum _{j=1}^{m}\max_{i\in\ell} p_{ij}^{*}L_{i}^{g}, \sum _{j=1}^{m}\max_{i\in \ell} q_{ij}^{*}L_{i}^{g} \Biggr\} \\ &{}\times \int_{0}^{\infty}\tilde{K}(s)V(t-s)\,ds. \end{aligned}$$
(3.4)

When \(t= t_{k}\), in view of (H6), (H7), and (3.2), we get

$$\begin{aligned} V(t_{k}) \leq& \max_{i\in\ell,j\in \hbar} \biggl\{ \frac{1}{\underline{\iota}_{i}}, \frac{1}{\underline {\vartheta}_{j}} \biggr\} \Biggl(\sum_{i=1}^{n}\bigl|x_{i}(t_{k}+ \omega )-x_{i}(t_{k})\bigr|+\sum_{j=1}^{m}\bigl|y_{j}(t_{k}+ \omega)-y_{j}(t_{k})\bigr| \Biggr) \\ =& \max_{i\in\ell,j\in \hbar} \biggl\{ \frac{1}{\underline{\iota}_{i}},\frac{1}{\underline {\vartheta}_{j}} \biggr\} \Biggl(\sum_{i=1}^{n}\bigl|x_{i}(t_{k+q})-x_{i}(t_{k})\bigr|+ \sum_{j=1}^{m}\bigl|y_{j}(t_{k+q})-y_{j}(t_{k})\bigr| \Biggr) \\ \leq&\max_{i\in\ell,j\in \hbar} \biggl\{ \frac{1}{\underline{\iota}_{i}},\frac{1}{\underline {\vartheta}_{j}} \biggr\} \Biggl\{ \sum_{i=1}^{n}|1-\gamma _{ik}|\bigl|x_{i}\bigl(t_{k+q}^{-} \bigr)-x_{i}\bigl(t_{k}^{-}\bigr)\bigr| \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{m}e_{ij}^{*}L_{j}^{E}\bigl|y_{j} \bigl(t_{k+q}^{-}-\tau \bigr)-y_{j} \bigl(t_{k}^{-}-\tau\bigr)\bigr| \\ &{}+\sum_{j=1}^{m}|1-\delta_{jk}|\bigl|y_{j} \bigl(t_{k+q}^{-}\bigr)-y_{j}\bigl(t_{k}^{-} \bigr)\bigr| +\sum_{j=1}^{m}\sum _{i=1}^{n}h_{ji}^{*}L_{i}^{H}\bigl|x_{i} \bigl(t_{k+q}^{-}-\tau \bigr)-x_{i} \bigl(t_{k}^{-}-\tau\bigr)\bigr| \Biggr\} \\ \leq&\max_{i\in\ell,j\in \hbar} \biggl\{ \frac{1}{\underline{\iota}_{i}},\frac{1}{\underline {\vartheta}_{j}} \biggr\} \Biggl\{ \max_{i\in\ell}|1-\gamma_{ik}|\sum _{i=1}^{n}\bigl|x_{i} \bigl(t_{k}^{-}+\omega\bigr)-x_{i} \bigl(t_{k}^{-}\bigr)\bigr| \\ &{}+\sum_{i=1}^{n}\max_{j\in\hbar}e_{ij}^{*}L_{j}^{E} \sum_{j=1}^{m}\bigl|y_{j} \bigl(t_{k}^{-}+\omega-\tau\bigr)-y_{j} \bigl(t_{k}^{-}-\tau\bigr)\bigr| \\ &{}+\max_{j\in\hbar}|1-\delta_{jk}|\sum _{j=1}^{m}\bigl|y_{j}\bigl(t_{k}^{-}+ \omega\bigr)-y_{j}\bigl(t_{k}^{-}\bigr)\bigr| \\ &{}+\sum_{i=1}^{n}\max_{i\in\ell}h_{ji}^{*}L_{i}^{H} \sum_{j=1}^{m}\bigl|x_{i} \bigl(t_{k}^{-}+\omega-\tau\bigr)-x_{i} \bigl(t_{k}^{-}-\tau\bigr)\bigr| \Biggr\} \\ \leq&\max_{i\in\ell,j\in \hbar} \biggl\{ \frac{1}{\underline{\iota}_{i}},\frac{1}{\underline {\vartheta}_{j}} \biggr\} \max_{i\in\ell,j\in\hbar}\bigl\{ |1-\gamma_{ik}|, |1- \delta_{jk}|\bigr\} \\ &{}\times \Biggl(\sum_{i=1}^{n}\bigl|x_{i} \bigl(t_{k}^{-}+\omega \bigr)-x_{i} \bigl(t_{k}^{-}\bigr)\bigr|+\sum_{j=1}^{m}\bigl|y_{j} \bigl(t_{k}^{-}+\omega \bigr)-y_{j} \bigl(t_{k}^{-}\bigr)\bigr| \Biggr) \\ &{}+\max \Biggl\{ \sum_{i=1}^{n}\max _{j\in\hbar}e_{ij}^{*}L_{j}^{E},\sum _{i=1}^{n}\max_{i\in\ell}h_{ji}^{*}L_{i}^{H} \Biggr\} \\ &{}\times \Biggl(\sum_{i=1}^{n}\bigl|x_{i} \bigl(t_{k}^{-}+\omega \bigr)-x_{i} \bigl(t_{k}^{-}\bigr)\bigr|+\sum_{j=1}^{m}\bigl|y_{j} \bigl(t_{k}^{-}+\omega \bigr)-y_{j} \bigl(t_{k}^{-}\bigr)\bigr| \Biggr) \\ \leq&\frac{\max_{i\in\ell, j\in\hbar}\{\overline{\iota}_{i}, \overline{\vartheta}_{j}\}}{\min_{i\in\ell, j\in\hbar}\{\underline{\iota}_{i}, \underline{\vartheta}_{j}\}}\max_{i\in\ell,j\in\hbar}\bigl\{ |1-\gamma_{ik}|, |1-\delta_{jk}|\bigr\} V\bigl(t_{k}^{-}\bigr) \\ &{}+\frac{\max_{i\in\ell, j\in\hbar}\{\overline{\iota}_{i}, \overline{\vartheta}_{j}\}}{\min_{i\in\ell, j\in\hbar}\{\underline{\iota}_{i}, \underline{\vartheta}_{j}\}}\max \Biggl\{ \sum_{i=1}^{n} \max_{j\in\hbar }e_{ij}^{*}L_{j}^{E},\sum _{i=1}^{n}\max_{i\in\ell}h_{ji}^{*}L_{i}^{H} \Biggr\} V\bigl(t_{k}^{-}-\tau\bigr). \end{aligned}$$
(3.5)

In view of (3.4)-(3.5) and (H8)-(H9), using Lemma 2.2, we have

$$ V(t)\leq M \overline{V}(0)e^{-(\lambda-\eta)t},\quad t\geq0, $$
(3.6)

where \(\overline{V}(0)=\sup_{-\infty\leq s\leq0}V(s)\). It follows from (3.6) that

$$ \sum_{i=1}^{n}\bigl|x_{i}(t+ \omega)-x_{i}(t)\bigr|+\sum_{j=1}^{m}\bigl|y_{j}(t+ \omega )-y_{j}(t)\bigr|\leq \nu\|\phi-\varphi\|e^{-(\lambda-\eta)t},\quad t\geq0, $$
(3.7)

where

$$\nu=M\frac{\max_{i\in\ell, j\in\hbar}\{\overline{\iota}_{i}, \overline{\vartheta}_{j}\}}{\min_{i\in\ell, j\in\hbar}\{\underline{\iota}_{i}, \underline{\vartheta}_{j}\}}\geq1, $$

λ satisfies the condition (H9). Notice that

$$\begin{aligned}& x_{i}(t+k\omega)=x_{i}(t)+\sum _{l=1}^{k}\bigl[x_{i}(t+l\omega )-x_{i}\bigl(t+(l-1)\omega\bigr)\bigr], \quad i\in\ell, \\& y_{j}(t+k\omega)=y_{j}(t)+\sum _{l=1}^{k}\bigl[y_{j}(t+l\omega )-y_{j}\bigl(t+(l-1)\omega\bigr)\bigr], \quad j\in\hbar. \end{aligned}$$

In view of (3.7), we have

$$ \begin{aligned}[b] &\sum_{l=1}^{\infty}\bigl[x_{i}(t+l \omega)-x_{i}\bigl(t+(l-1)\omega\bigr)\bigr]\\ &\quad=\lim _{k\rightarrow \infty}\sum_{l=1}^{k} \bigl[x_{i}(t+l\omega)-x_{i}\bigl(t+(l-1)\omega\bigr)\bigr] \\ &\quad\leq \nu\|\phi-\varphi\|\lim_{k\rightarrow\infty}\sum _{l=1}^{k} e^{-(\lambda-\eta)(t+(l-1)\omega)} \\ &\quad\leq \nu\|\phi-\varphi\|e^{-(\lambda-\eta)t}\sum_{l=1}^{\infty}e^{-(\lambda-\eta)(l-1)\omega}< \infty, \quad\mbox{as } k\rightarrow\infty, \end{aligned} $$
(3.8)

for any given \(t\geq0\). By (3.8), we know that \(\lim_{k\rightarrow\infty}x_{i}(t+k\omega)\) exists. Similarly, we know that \(\lim_{k\rightarrow\infty}y_{j}(t+k\omega)\) also exists.

Set \((x^{*}(t),y^{*}(t))^{T}=(x_{1}^{*}(t),x_{2}^{*}(t),\ldots, x_{n}^{*}(t),y_{1}^{*}(t),y_{2}^{*}(t),\ldots,y_{m}^{*}(t))^{T}\), where \(x_{i}^{*}=\lim_{k\rightarrow\infty}x_{i}(t+k\omega)\), \(y_{j}^{*}=\lim_{k\rightarrow\infty}y_{j}(t+k\omega)\), then \((x^{*}(t),y^{*}(t))^{T}\) is a periodic function with period ω for system (1.1).

Assume that system (1.1) has another ω-periodic solution \((x^{**}(t),y^{**}(t))^{T}\) as follows:

$$\begin{aligned} \bigl(x^{**}(t,\psi_{1}),y^{**}(t, \psi_{2})\bigr)^{T}={}&\bigl(x_{1}^{**}(t,\psi_{1}),x_{2}^{**}(t,\psi_{1}),\ldots, x_{n}^{**}(t,\psi_{1}),\\ &y_{1}^{**}(t,\psi_{2}),y_{2}^{**}(t,\psi_{2}),\ldots , y_{m}^{**}(t,\psi_{2})\bigr)^{T}, \end{aligned} $$

where \(\psi_{1}\in{\mathbb{C}}^{n}\), \(\psi_{2}\in{\mathbb{C}}^{m}\). It follows from (3.7) that

$$ \begin{aligned}[b] &\sum_{i=1}^{n}\bigl|x_{i}^{*}(t)-x_{i}^{**}(t)\bigr|+ \sum_{j=1}^{m}\bigl|y_{j}^{*}(t)-y_{j}^{**}(t)\bigr| \\ &\quad=\sum_{i=1}^{n}\bigl|x_{i}^{*}(t+k \omega)-x_{i}^{**}(t+k\omega)\bigr|+\sum _{j=1}^{m}\bigl|y_{j}^{*}(t+k\omega)-y_{j}^{**}(t+k \omega)\bigr| \\ &\quad \leq\nu\|\phi-\psi\|e^{(\lambda-\eta)(t+k\omega)},\quad t\geq0. \end{aligned} $$
(3.9)

Let \(k\rightarrow\infty\), then \(x_{i}^{*}(t)=x_{i}^{**}(t)\), \(y_{j}^{*}(t)=y_{j}^{**}(t)\), \(t\geq0\). Thus we can conclude that system (1.1) has a unique ω-periodic solution which is globally exponentially stable. The proof of Theorem 3.1 is complete. □

Remark 3.1

Li [4] investigated the existence and global exponential stability of a periodic solution for impulsive Cohen-Grossberg-type BAM neural networks with continuously distributed delays, the model in [4] is not concerned with fuzzy terms. Bao [10] discussed the existence and exponential stability of a periodic solution for BAM fuzzy Cohen-Grossberg neural networks with mixed delays, the model in [10] is not concerned with impulsive effects. Yang [16] considered the periodic solution for fuzzy Cohen-Grossberg BAM neural networks with both time-varying and distributed delays and variable coefficients, the model in [16] is not concerned with impulsive effect and distributed delays. Balasubramaniam et al. [38] analyzed the global asymptotic stability of stochastic fuzzy cellular neural networks with multiple time-varying delays, the model in [38] is not concerned with impulsive effect and distributed delays, Balasubramaniam and Vembarasan [41] studied the robust stability of uncertain fuzzy BAM neural networks of neutral-type with Markovian jumping parameters and impulses, the authors did not discuss the existence and global exponential stability of a periodic solution of neural networks and the model in [41] is also not concerned with distributed delays. In this paper, we study the exponential stability for fuzzy bidirectional associative memory Cohen-Grossberg neural networks with mixed delays and impulses. All the obtained results in [4, 10, 16, 38, 41] cannot be applicable to model (1.1) to obtain the exponential stability of model (1.1). From this viewpoint, our results on the exponential stability for fuzzy bidirectional associative memory Cohen-Grossberg neural networks with mixed delays and impulses are essentially new and complement earlier works to some extent.

4 Examples

In this section, we consider the following neural networks with mixed delays and impulses

$$ \left \{ \textstyle\begin{array}{l} \dot{x}_{1}(t)=\iota_{1}(x_{1}(t)) [-a_{1}(t,x_{1}(t))+\sum_{j=1}^{2}c_{j1}(t)f_{j}(y_{j}(t-\tau(t)))\\ \hphantom{\dot{x}_{1}(t)=}+\bigwedge_{j=1}^{2}\alpha_{j1}(t)\int_{-\infty }^{t}K_{j1}(t-s)f_{j}(y_{j}(s))\,ds+\bigwedge_{j=1}^{2}T_{j1}u_{j}+\bigvee_{j=1}^{2}H_{j1}u_{j}\\ \hphantom{\dot{x}_{1}(t)=}+\bigvee_{j=1}^{2} \beta_{j1}(t)\int_{-\infty}^{t}K_{j1}(t-s)f_{j}(y_{j}(s))\,ds+I_{1}(t) ], \quad t\neq t_{k},\\ \dot{x}_{2}(t)=\iota_{2}(x_{2}(t)) [-a_{2}(t,x_{2}(t))+\sum_{j=1}^{2}c_{j2}(t)f_{j}(y_{j}(t-\tau(t)))\\ \hphantom{\dot{x}_{2}(t)=}+\bigwedge_{j=1}^{2}\alpha_{j2}(t)\int_{-\infty }^{t}K_{j2}(t-s)f_{j}(y_{j}(s))\,ds+\bigwedge_{j=1}^{2}T_{j2}u_{j}+\bigvee_{j=1}^{2}H_{j2}u_{j}\\ \hphantom{\dot{x}_{2}(t)=}+\bigvee_{j=1}^{2} \beta_{j2}(t)\int_{-\infty}^{t}K_{j2}(t-s)f_{j}(y_{j}(s))\,ds+I_{2}(t) ], \quad t\neq t_{k},\\ \triangle x_{1}(t_{k})=x_{1}(t_{k})-x_{1}(t_{k}^{-})=-\gamma_{1k}x_{i}(t_{k}^{-})+\sum_{j=1}^{2}e_{1j}(t_{k}^{-})E_{j}(y_{j}(t_{k}^{-}-\tau)), \quad k\in{\mathbb{Z_{+}}},\\ \triangle x_{2}(t_{k})=x_{2}(t_{k})-x_{2}(t_{k}^{-})=-\gamma_{2k}x_{2}(t_{k}^{-})+\sum_{j=1}^{2}e_{2j}(t_{k}^{-})E_{j}(y_{j}(t_{k}^{-}-\tau)), \quad k\in{\mathbb{Z_{+}}},\\ \dot{y}_{1}(t)=\vartheta_{1}(y_{1}(t)) [-b_{1}(t,y_{j}(t))+\sum_{i=1}^{2}d_{i1}(t)g_{i}(x_{i}(t-\tau(t)))\\ \hphantom{\dot{y}_{1}(t)=}+\bigwedge_{i=1}^{2}p_{i1}(t)\int_{-\infty }^{t}N_{i1}(t-s)g_{i}(x_{i}(s))\,ds+\bigwedge_{i=1}^{2}S_{i1}u_{i}+\bigvee_{i=1}^{2}L_{i1}u_{i}\\ \hphantom{\dot{y}_{1}(t)=}+\bigvee_{i=1}^{2} q_{i1}(t)\int_{-\infty}^{t}N_{i1}(t-s)g_{i}(x_{i}(s))\,ds+J_{1}(t) ], \quad t\neq t_{k},\\ \dot{y}_{2}(t)=\vartheta_{2}(y_{2}(t)) [-b_{2}(t,y_{j}(t))+\sum_{i=1}^{2}d_{i2}(t)g_{i}(x_{i}(t-\tau(t)))\\ \hphantom{\dot{y}_{2}(t)=}+\bigwedge_{i=1}^{2}p_{i2}(t)\int_{-\infty }^{t}N_{i2}(t-s)g_{i}(x_{i}(s))\,ds+\bigwedge_{i=1}^{2}S_{i2}u_{i}+\bigvee_{i=1}^{2}L_{i2}u_{i}\\ \hphantom{\dot{y}_{2}(t)=} +\bigvee_{i=1}^{2} q_{i2}(t)\int_{-\infty}^{t}N_{i2}(t-s)g_{i}(x_{i}(s))\,ds+J_{2}(t) ], \quad t\neq t_{k}, \\ \triangle y_{1}(t_{k})=y_{1}(t_{k})-y_{1}(t_{k}^{-})=-\delta_{1k}y_{1}(t_{k}^{-})+\sum_{i=1}^{2}h_{1i}(t_{k}^{-})H_{i}(x_{i}(t_{k}^{-}-\tau)), \quad k\in{\mathbb{Z_{+}}},\\ \triangle y_{2}(t_{k})=y_{2}(t_{k})-y_{2}(t_{k}^{-})=-\delta_{2k}y_{2}(t_{k}^{-})+\sum_{i=1}^{2}h_{2i}(t_{k}^{-})H_{i}(x_{i}(t_{k}^{-}-\tau)), \quad k\in{\mathbb{Z_{+}}}, \end{array}\displaystyle \right . $$
(4.1)

where

$$\begin{aligned}& \left [ \textstyle\begin{array}{c@{\quad}c} c_{11}(t) & c_{21}(t) \\ c_{21}(t) & c_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 0.9+0.2\sin t & 0.5+0.4\cos t \\ 0.4+0.2\sin t & 0.5+0.1\cos t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} d_{11}(t) & d_{21}(t) \\ d_{12}(t) & d_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 0.5+0.2\sin t & 0.4+0.2\cos t \\ 0.3+0.1\sin t & 0.5+0.2\cos t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} \alpha_{11}(t) & \alpha_{21}(t) \\ \alpha_{12}(t) & \alpha_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 0.5+0.2\cos t & 0.5+0.2\sin t \\ 0.4+0.2\cos t & 0.4+0.2\sin t \end{array}\displaystyle \right ],\\& \left [ \textstyle\begin{array}{c@{\quad}c} p_{11}(t) & p_{21}(t) \\ p_{12}(t) & p_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 0.5+0.2\cos t & 0.4+0.2\sin t \\ 0.3+0.1\cos t & 0.3+0.2\sin t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} \beta_{11}(t) & \beta_{21}(t) \\ \beta_{12}(t) & \beta_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 0.4+0.1\sin t & 0.6+0.3\cos t \\ 0.3+0.2\sin t & 0.5+0.3\cos t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} q_{11}(t) & q_{21}(t) \\ q_{12}(t) & q_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 0.5+0.3\cos t & 0.4+0.1\sin t \\ 0.3+0.2\cos t & 0.5+0.2\sin t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} T_{11} & T_{21} \\ T_{12} & t_{22} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 1 & 1 \\ 1 & 1 \end{array}\displaystyle \right ],\qquad \left [ \textstyle\begin{array}{c@{\quad}c} S_{11} & S_{21} \\ S_{12} & S_{22} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 1 & 1 \\ 1 & 1 \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} H_{11} & H_{21} \\ H_{12} & H_{22} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 1 & 1 \\ 1 & 1 \end{array}\displaystyle \right ],\qquad \left [ \textstyle\begin{array}{c@{\quad}c} L_{11} & L_{21} \\ L_{12} & L_{22} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 1 & 1 \\ 1 & 1 \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} u_{1} & u_{2} \\ I_{1} & J_{1} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 1+\sin t & 1+\cos t \\ 1+\sin t & 1+\cos t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} e_{11}(t) & e_{12}(t) \\ e_{21}(t) & e_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} \tanh(0.2t) & \tanh(0.2t) \\ \tanh(0.2t) & \tanh(0.2t) \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} h_{11}(t) & h_{12}(t) \\ h_{21}(t) & h_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} \tanh(0.3t) & \tanh(0.3t) \\ \tanh(0.3t) & \tanh(0.3t) \end{array}\displaystyle \right ],\qquad \left [ \textstyle\begin{array}{c@{\quad}c} \gamma_{1k}(s) & \gamma_{2k}(s) \\ \delta_{1k}(s) & \delta_{1k}(s) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} -1 & -1 \\ -1 & -1 \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} \iota_{1}(x_{1}(t)) & \vartheta_{1}(y_{1}(t))\\ a_{1}(t,x_{1}(t)) & b_{1}(t,y_{1}(t)) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 0.55+0.05\cos(x_{1}(t)) & 4x_{1}(t)\\ 0.55+0.05\sin(y_{1}(t)) & 3y_{1}(t) \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} \iota_{2}(x_{2}(t)) & \vartheta_{2}(y_{2}(t))\\ a_{2}(t,x_{2}(t)) & b_{2}(t,y_{2}(t)) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} 0.55+0.05\sin(x_{2}(t)) & 4x_{2}(t)\\ 0.55+0.05\cos(y_{2}(t)) & 3y_{2}(t) \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} K_{11}(s) & K_{21}(s) \\ K_{12}(s) & K_{22}(s) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} e^{-3s} & e^{-3s} \\ e^{-3s} & e^{-3s} \end{array}\displaystyle \right ],\qquad \left [ \textstyle\begin{array}{c@{\quad}c} N_{11}(s) & N_{21}(s) \\ N_{12}(s) & N_{22}(s) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} e^{-3s} & e^{-3s} \\ e^{-3s} & e^{-3s} \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{c@{\quad}c} E_{1}(y_{1}(t_{k}^{-}-\tau)) & E_{2}(y_{2}(t_{k}^{-}-\tau)) \\ H_{1}(x_{1}(t_{k}^{-}-\tau)) & H_{2}(x_{2}(t_{k}^{-}-\tau)) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{c@{\quad}c} \tanh(0.2y_{1}(t_{k}^{-}-0.2)) & \tanh(0.2y_{2}(t_{k}^{-}-0.2)) \\ \tanh(0.2x_{1}(t_{k}^{-}-0.2)) & \tanh(0.2x_{2}(t_{k}^{-}-0.2)) \end{array}\displaystyle \right ]. \end{aligned}$$

Let \(t_{k}=0.5\pi k\), \(\tau(t)=0.2|\sin2t|\), \(f_{1}(u)=|u+1|\), \(g_{1}(u)=|u-1|\), then we get \(\overline{\iota}_{1}=0.6\), \(\underline{\iota}_{1}=0.5\), \(\overline{\vartheta}_{1}=0.6\), \(\underline{\vartheta}_{1}=0.5\), \(\overline{\iota}_{2}=0.6\), \(\underline{\iota}_{2}=0.5\), \(\overline{\vartheta}_{2}=0.6\), \(\underline{\vartheta}_{2}=0.5\), \(c_{11}^{*}=1.1\), \(c_{21}^{*}=0.9\), \(c_{12}^{*}=0.6\), \(c_{22}^{*}=0.6\), \(d_{11}^{*}=0.6\), \(d_{21}^{*}=0.6\), \(d_{12}^{*}=0.4\), \(d_{22}^{*}=0.6\), \(\alpha _{11}^{*}=0.7\), \(\alpha_{21}^{*}=0.7\), \(\alpha_{12}^{*}=0.6\), \(\alpha_{22}^{*}=0.6\), \(p_{11}^{*}=0.6\), \(p_{21}^{*}=0.6\), \(p_{12}^{*}=0.4\), \(p_{22}^{*}=0.5\), \(\beta_{11}^{*}=0.6\), \(\beta_{21}^{*}=0.7\), \(\beta_{12}^{*}=0.5\), \(\beta_{22}^{*}=0.8\), \(q_{11}^{*}=0.4\), \(q_{21}^{*}=0.9\), \(q_{12}^{*}=0.5\), \(q_{22}^{*}=0.7\), \(h_{11}^{*}=1\), \(h_{21}^{*}=1\), \(h_{12}^{*}=1\), \(h_{22}^{*}=1\), \(\tau=0.2\), \(\overline{K}(s)=e^{-3s}\), \(\lambda_{0}=1.5\), \(\omega=2\pi\), \(L_{1}^{f}=L_{1}^{g}=1\), \(L_{1}^{E}=0.2\), \(L_{2}^{E}=0.2\), \(L_{1}^{H}=0.2\), \(L_{2}^{H}=0.2\). It is easy to check that

$$\begin{aligned} \begin{aligned} & \frac{\min_{i\in\ell, j\in\hbar}\{\varrho_{i}^{\star}, \sigma_{j}^{\star}\}\min_{i\in\ell, j\in\hbar}\{\underline{\iota}_{i}, \underline{\vartheta}_{j}\}}{\max_{i\in\ell, j\in\hbar}\{\overline{\iota}_{i}, \overline{\vartheta}_{j}\}}=7.5, \\ &\max \Biggl\{ \sum_{i=1}^{n}\max _{j\in\hbar} c_{ji}^{*}L_{j}^{f}, \sum _{j=1}^{m} \max_{i\in\ell}d_{ij}^{*}L_{i}^{g} \Biggr\} \\ &\qquad+\max \Biggl\{ \sum_{i=1}^{n}\max _{j\in\hbar} \alpha_{ji}^{*}L_{j}^{f}, \sum_{i=1}^{n}\max_{j\in\hbar} \beta_{ji}^{*}L_{j}^{f}, \sum_{j=1}^{m}\max_{i\in\ell} p_{ij}^{*}L_{i}^{g}, \sum _{j=1}^{m}\max_{i\in\ell} q_{ij}^{*}L_{i}^{g} \Biggr\} \int_{0}^{\infty}\tilde{K}(s)\,ds\\ &\quad\approx6.4237. \end{aligned} \end{aligned}$$

Choose \(\lambda=0.9<\lambda_{0}\) such that

$$\lambda< 7.5-2e^{0.2\lambda}-1.4 \int_{0}^{\infty}e^{(\lambda-3)s}\,ds. $$

Then we obtain

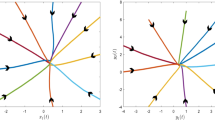
$$\begin{aligned} \chi_{l}={}&\frac{\max_{i\in\ell, j\in\hbar}\{\overline{\iota}_{i}, \overline{\vartheta}_{j}\}}{\min_{i\in\ell, j\in\hbar}\{\underline{\iota}_{i}, \underline{\vartheta}_{j}\}}\\ &\times\max_{i\in\ell, j\in\hbar} \Biggl\{ |1- \gamma_{il}|, |1-\delta_{jl}|+\max \Biggl\{ \sum _{i=1}^{n} \max_{j\in\hbar}e_{ij}^{*}L_{j}^{E}, \sum_{j=1}^{m} \max_{i\in\ell}h_{ji}^{*}L_{i}^{H} \Biggr\} e^{\lambda\tau} \Biggr\} \\ \approx{}& 1.9503. \end{aligned} $$

Thus we can choose \(\eta=0.95<\lambda\) such that \(\prod_{l=1}^{n} \max\{1, \chi_{l}\}=1.9503^{n}<2.5857^{n}\approx e^{\eta t_{n}}\) for all \(n\in{\mathbb{Z}_{+}}\). Then all the conditions of Theorem 3.1 hold. Thus (4.1) has exactly one 2π-periodic solution which is globally exponentially stable. These results are illustrated in Figures 1, 2, 3, 4.

Figure 1
figure 1

Numerical solutions of system ( 3.1 ): times series of \(\pmb{x_{1}}\) .

Full size image
Figure 2
figure 2

Numerical solutions of system ( 3.1 ): times series of \(\pmb{x_{2}}\) .

Full size image
Figure 3
figure 3

Numerical solutions of system ( 3.1 ): times series of \(\pmb{y_{1}}\) .

Full size image
Figure 4
figure 4

Numerical solutions of system ( 3.1 ): times series of \(\pmb{y_{2}}\) .

Full size image

5 Conclusions

In this article, we have analyzed the global exponential stability of fuzzy bidirectional associative memory Cohen-Grossberg neural networks with mixed delays and impulses. By constructing a suitable Lyapunov function and a new differential inequality, some sufficient criteria which ensure the existence and global exponential stability of a periodic solution of the model have been established. The obtained conditions are easy to check in practice. The results in this paper extend and complement some previous studies. Finally, an example with their numerical simulations is carried out to illustrate the correctness. To the best of our knowledge, there are only rare results on the exponential stability for fuzzy bidirectional associative memory Cohen-Grossberg neural networks with proportional delays, which will be our future research direction.