1 Introduction

In recent years, a lot of authors pay much attention to dynamics of bidirectional associative memory (BAM) neural networks due to their potential application prospect in many disciplines such as pattern recognition, automatic control engineering, optimization problems, image processing, speed detection of moving objects and so on [1–4]. Since time delays usually occur in neural networks due to the finite switching of amplifiers in practical implementation, and the time delay may result in oscillation and instability of system, many researchers investigate the dynamical nature of delayed BAM neural networks. For example, Xiong et al. [5] discussed the stability of two-dimensional neutral-type Cohen-Grossberg BAM neural networks, Zhang et al. [6] investigated the global stability and synchronization of Markovian switching neural networks with stochastic perturbation and impulsive delay. Some novel generic criteria for Markovian switching neural networks with stochastic perturbation and impulsive delay are derived by establishing an extended Halanay differential inequality on impulsive dynamical systems, in addition, some sufficient conditions ensuring synchronization are established, Wang et al. [7] made a detailed analysis on the exponential stability of delayed memristor-based recurrent neural networks with impulse effects. By using an impulsive delayed differential inequality and Lyapunov function, several exponential and uniform stability criteria of the impulsive delayed memristor-based recurrent neural networks are obtained. Li et al. [8] studied the existence and stability of pseudo almost periodic solution for neutral type high-order Hopfield neural networks with delays in leakage terms on time scales. Applying the exponential dichotomy of linear dynamic equations on time scales, a fixed point theorem, and the theory of calculus on time scales, the authors established some sufficient conditions for the existence and global exponential stability of pseudo almost periodic solutions for the model. For more related work, we refer the reader to [9–20].

Some authors argue that a typical time delay called leakage (or ‘forgetting’) delay may occur in the negative feedback term of the neural networks model (these terms are variously known as forgetting or leakage terms) and have a great impact on the dynamics of neural networks [21–30]. For example, time delay in the stabilizing negative feedback term has a tendency to destabilize a system [31], Balasubramanianm et al. [32] pointed out that the existence and uniqueness of the equilibrium point are independent of time delays and initial conditions. In real world, uncertainty or vagueness is unavoidable. Thus it is necessary to introduce the fuzzy operator into the neural networks. In 2011, Balasubramaniam et al. [33] considered the global asymptotic stability of the following BAM fuzzy cellular neural networks with time delay in the leakage term, discrete and unbounded distributed delays:

$$ \left \{ \textstyle\begin{array}{l} x_{i}'(t)=-a_{i}x_{i}(t-\sigma_{1})+\sum_{j=1}^{m}a_{ij}(t)f_{j}(y_{j}(t)) \\ \hphantom{x_{i}'(t)={}}{}+\sum_{j=1}^{m} b_{ij}(t)f_{j}(y_{j}(t-\tau(t)))+\sum_{j=1}^{m} c_{ij}(t)\omega_{j} \\ \hphantom{x_{i}'(t)={}}{}+\bigwedge_{j=1}^{m}\alpha_{ij}\int _{-\infty}^{t}k_{j}(t-s)f_{j}(y_{j}(s))\,ds+\bigvee_{j=1}^{m}\beta_{ij}\int _{-\infty}^{t}k_{j}(t-s)f_{j}(y_{j}(s))\,ds \\ \hphantom{x_{i}'(t)={}}{}+\bigwedge_{j=1}^{m}T_{ij}\omega_{j}+\bigvee_{j=1}^{m}H_{ij}\omega_{j}+I_{i},\quad t>0, i=1,2,\ldots,n, \\ y_{j}'(t)=-b_{j}y_{j}(t-\sigma_{2})+\sum_{i=1}^{n}\bar {a}_{ji}(t)g_{i}(x_{i}(t))+\sum_{i=1}^{n} \bar{b}_{ji}(t)g_{i}(x_{i}(t-\rho(t))) \\ \hphantom{y_{j}'(t)={}}{}+\sum_{i=1}^{n} \bar{c}_{ji}(t)\bar{\omega}_{i}+\bigwedge_{i=1}^{n}\bar{\alpha}_{ji}\int _{-\infty}^{t}k_{i}(t-s)g_{i}(x_{i}(s))\,ds \\ \hphantom{y_{j}'(t)={}}{}+\bigvee_{i=1}^{n}\bar{\beta }_{ji}\int_{-\infty}^{t}k_{i}(t-s)g_{i}(x_{i}(s))\,ds \\ \hphantom{y_{j}'(t)={}}{}+\bigwedge_{i=1}^{n}\bar{T}_{ji}\bar{\omega}_{i}+\bigvee_{i=1}^{n}\bar{H}_{ji}\bar{\omega}_{i}+J_{j},\quad t>0, j=1,2,\ldots,m. \end{array}\displaystyle \right . $$
(1.1)

The meaning of all the parameters of system (1.1) can be found in [33]. By applying the quadratic convex combination method, reciprocal convex approach, Jensen integral inequality, and linear convex combination technique, Balasubramaniam et al. [33] obtained several sufficient conditions to ensure the global asymptotic stability of the equilibrium point of system (1.1).

Considering that time-varying delays in the leakage terms inevitably occur in electronic neural networks due to the unavoidable finite switching speed of amplifiers [34], Li et al. [34] considered the existence and exponential stability of an equilibrium point for the following fuzzy BAM neural networks with time-varying delays in leakage terms on time scales:

$$ \left \{ \textstyle\begin{array}{l} x_{i}'(t)=-a_{i}x_{i}(t-\sigma_{i}(t))+\sum_{j=1}^{m}c_{ji}(t)f_{j}(y_{j}(t-\tau _{ji}(t))) \\ \hphantom{x_{i}'(t)={}}{}+\bigwedge_{j=1}^{m}\alpha_{ji}f_{j}(y_{j}(t-\tau_{ji}(t)))+\bigwedge_{j=1}^{m}T_{ji}\mu_{j}+\bigvee_{j=1}^{m}\beta _{ji}f_{j}(y_{j}(t-\tau_{ji}(t))) \\ \hphantom{x_{i}'(t)={}}{}+\bigvee_{j=1}^{m}H_{ji}\mu_{j}+I_{i}, \quad t\in{\mathbb{T}}, i=1,2,\ldots ,n, \\ y_{j}'(t)=-b_{j}y_{j}(t-\eta_{j}(t))+\sum_{i=1}^{n}d_{ij}(t)g_{i}(x_{i}(t-\sigma _{ij}(t))) \\ \hphantom{y_{j}'(t)={}}{}+\bigwedge_{j=1}^{m}p_{ij}g_{i}(x_{i}(t-\sigma_{ij}(t)))+\bigwedge_{i=1}^{n}F_{ij}\nu_{i}+\bigvee_{i=1}^{n}q_{ij}g_{i}(x_{i}(t-\sigma_{ij}(t))) \\ \hphantom{y_{j}'(t)={}}{}+\bigvee_{i=1}^{n}G_{ij}\nu_{i}+J_{j},\quad t\in{\mathbb{T}}, j=1,2,\ldots,m, \end{array}\displaystyle \right .$$
(1.2)

where \({\mathbb{T}}\) is a time scale. Applying fixed point theorem and differential inequality techniques, Li et al. [34] obtained the sufficient condition which ensures the existence and global exponential stability of an equilibrium point for system (1.2). Noticing that the impulsive perturbations usually occur in neural networks, Li and Li [35] investigated the exponential stability of the following BAM fuzzy cellular neural networks with time-varying delays in leakage terms and impulses:

$$ \left \{ \textstyle\begin{array}{l} x_{i}'(t)=-a_{i}(t)x_{i}(t-\alpha_{i}(t))+\sum_{j=1}^{m}a_{ij}(t)f_{j}(y_{j}(t))+\sum_{j=1}^{m} b_{ij}(t)f_{j}(y_{j}(t-\tau(t))) \\ \hphantom{x_{i}'(t)={}}{}+\sum_{j=1}^{m} c_{ij}(t)\omega_{j}+\bigwedge_{j=1}^{m}\alpha_{ij}(t)\int _{-\infty}^{t}k_{j}(t-s)f_{j}(y_{j}(s))\,ds \\ \hphantom{x_{i}'(t)={}}{}+\bigvee_{j=1}^{m}\beta_{ij}(t)\int _{-\infty}^{t}k_{j}(t-s)f_{j}(y_{j}(s))\,ds \\ \hphantom{x_{i}'(t)={}}{}+\bigwedge_{j=1}^{m}T_{ij}\omega_{j}+\bigvee_{j=1}^{m}H_{ij}\omega_{j}+A_{i}(t),\quad t\geq0,t\neq t_{k}, i=1,2,\ldots,n, \\ \triangle x_{i}(t_{k})=I_{k}(x_{i}(t_{k})),\quad i=1,2,\ldots,n, k=1,2,\ldots, \\ y_{j}'(t)=-b_{j}(t)y_{j}(t-\beta_{j}(t))+\sum_{i=1}^{n}d_{ji}(t)g_{i}(x_{i}(t))+\sum_{i=1}^{n} p_{ji}(t)g_{i}(x_{i}(t-\rho(t))) \\ \hphantom{y_{j}'(t)={}}{}+\sum_{i=1}^{n} q_{ji}(t)\mu_{i}+\bigwedge_{i=1}^{n}\gamma_{ji}(t)\int _{-\infty}^{t}k_{i}(t-s)g_{i}(x_{i}(s))\,ds \\ \hphantom{y_{j}'(t)={}}{}+\bigvee_{i=1}^{n}\eta_{ji}(t)\int _{-\infty}^{t}k_{i}(t-s)g_{i}(x_{i}(s))\,ds \\ \hphantom{y_{j}'(t)={}}{}+\bigwedge_{i=1}^{n}R_{ji}\mu_{i}+\bigvee_{i=1}^{n}S_{ji}\mu _{i}+B_{j}(t),\quad t\geq0,t\neq t_{k}, j=1,2,\ldots,m, \\ \triangle y_{j}(t_{k})=J_{k}(y_{j}(t_{k})),\quad j=1,2,\ldots,m, k=1,2,\ldots. \end{array}\displaystyle \right .$$
(1.3)

By applying differential inequality techniques, Li and Li [35] established some sufficient conditions which guarantee the exponential stability of model (1.3).

Here we would like to point out that neural networks usually have spatial natures due to the presence of an amount of parallel pathways of a variety of axon sizes and lengths. It is reasonable to introduce continuously distributed delays over a certain duration of time such that the distant past has less influence compared with the recent behavior of the state [1, 36]. Inspired by the analysis above, in this paper we consider the following fuzzy BAM neural networks with distributed leakage delays and impulses:

$$ \left \{ \textstyle\begin{array}{l} x_{i}'(t)=-a_{i}(t)\int_{0}^{\infty}h_{i}(s)x_{i}(t-s)\,ds+\sum_{j=1}^{m}a_{ij}(t)f_{j}(y_{j}(t))+\sum_{j=1}^{m} b_{ij}(t)f_{j}(y_{j}(t-\tau(t))) \\ \hphantom{x_{i}'(t)={}}{}+\bigwedge_{j=1}^{m}\alpha_{ij}(t)\int _{-\infty}^{t}k_{j}(t-s)f_{j}(y_{j}(s))\,ds+\bigvee_{j=1}^{m}\beta_{ij}(t)\int _{-\infty}^{t}k_{j}(t-s)f_{j}(y_{j}(s))\,ds \\ \hphantom{x_{i}'(t)={}}{}+\bigwedge_{j=1}^{m}T_{ij}\omega_{j}+\bigvee_{j=1}^{m}H_{ij}\omega_{j}+\sum_{j=1}^{m} c_{ij}(t)\omega_{j} \\ \hphantom{x_{i}'(t)={}}{}+A_{i}(t),\quad t\geq0,t\neq t_{k}, i=1,2,\ldots,n, \\ \triangle x_{i}(t_{k})=I_{k}(x_{i}(t_{k})),\quad i=1,2,\ldots,n, k=1,2,\ldots, \\ y_{j}'(t)=-b_{j}(t)\int_{0}^{\infty}l_{j}(s)y_{j}(t-s)\,ds+\sum_{i=1}^{n}d_{ji}(t)g_{i}(x_{i}(t))+\sum_{i=1}^{n} p_{ji}(t)g_{i}(x_{i}(t-\rho(t))) \\ \hphantom{y_{j}'(t)={}}{}+\bigwedge_{i=1}^{n}\gamma_{ji}(t)\int _{-\infty}^{t}k_{i}(t-s)g_{i}(x_{i}(s))\,ds+\bigvee_{i=1}^{n}\eta_{ji}(t)\int _{-\infty}^{t}k_{i}(t-s)g_{i}(x_{i}(s))\,ds \\ \hphantom{y_{j}'(t)={}}{}+\bigwedge_{i=1}^{n}R_{ji}\mu_{i}+\bigvee_{i=1}^{n}S_{ji}\mu _{i}+\sum_{i=1}^{n} q_{ji}(t)\mu_{i} \\ \hphantom{y_{j}'(t)={}}{}+B_{j}(t),\quad t\geq0,t\neq t_{k}, j=1,2,\ldots,m, \\ \triangle y_{j}(t_{k})=J_{k}(y_{j}(t_{k})),\quad j=1,2,\ldots,m, k=1,2,\ldots, \end{array}\displaystyle \right .$$
(1.4)

which is a revised version of model (1.3). Here \(x_{i}(t)\) and \(y_{j}(t)\) are the states of the ith neuron and the jth neuron at time t, \(g_{i}(t)\) and \(f_{j}(t)\) denote the activation functions of the ith neuron and the jth neuron at time t, \(\mu_{i}\) and \(\omega_{j}\) denote the inputs of the ith neuron and the jth neuron, \(A_{i}(t)\) and \(B_{j}(t)\) denote the bias of the ith neuron and the jth neuron at time t, \(a_{i}(t)\) and \(b_{j}(t)\) represent the rates with which the ith neuron and the jth neuron at time t will reset their potential to the resting state in isolation when disconnected from the networks and external inputs, \(a_{ij}(t)\), \(b_{ij}(t)\), \(d_{ji}(t)\), and \(p_{ji}(t)\) denote the connection weights of the feedback template at time t and \(c_{ij}(t)\), \(q_{ji}(t)\) denote the connection weights of the feedforward template at time t, \(\gamma_{ji}(t)\) and \(\eta_{ji}(t)\) denote the connection weights of the delays fuzzy feedback MIN template at time t and the delays fuzzy feedback MAX template at time t, \(T_{ij}\), \(R_{ij}\), and \(H_{ji}\), \(S_{ij}\) are the elements of the fuzzy feedforward MIN template and fuzzy feedforward MAX template, ⋀ and ⋁ denote the fuzzy AND and fuzzy OR operators, \(0\leq\tau(t)\leq\tau\) and \(0\leq\rho(t)\leq \rho\) denote the transmission delays at time t, \(\triangle x_{i}(t_{k})=x_{i}(t_{k}^{+})-x_{i}(t_{k}^{-})\), \(\triangle y_{j}(t_{k})=y_{j}(t_{k}^{+})-y_{j}(t_{k}^{-})\) are the impulses at moments \(t_{k}\) and \(t_{1}< t_{2}<\cdots\) is a strictly increasing sequence such that \(\lim_{k\rightarrow\infty}t_{k}=+\infty\), \(k_{j}(s)\geq0\), and \(k_{i}(s)\geq0 \) are the feedback kernels and satisfy \(\int_{0}^{+\infty}k_{j}(s)\,ds=1\), \(\int_{0}^{+\infty}k_{i}(s)\,ds=1\), \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\).

Our main object of this article is by applying differential inequality techniques to analyze the exponential stability of model (1.4). We expect that this study of the exponential stability of model (1.4) has important theoretical value and tremendous potential for application in designing the BAM cellular neural networks with distributed leakage delays.

Let R and \(R^{+}\) denote the set of all real numbers and nonnegative real numbers, respectively. For the sake of simplification, we introduce the notations as follows: \(f^{+}=\sup_{t\in R}|f(t)|\), \(f^{-}=\inf_{t\in R}|f(t)|\), where \(f: R\rightarrow R\) is a continuous function.

The initial value of system (1.4) is given by

$$ x_{i}(s)=\varphi_{i}(s),\qquad y_{j}(s)=\psi_{j}(s),\quad s\in(-\infty,0], $$
(1.5)

where \(\varphi_{i}(s),\psi_{j}(s)\in C((-\infty,0],R)\), \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\).

Throughout this paper, we assume that the following conditions are satisfied.

  1. (H1)

    For \(i = 1, 2, \ldots, n\), \(j = 1, 2, \ldots,m\), \(f_{j},g_{i}\in C(R,R)\) and there exist positive constants \(L_{j}^{f}\) and \(L_{i}^{g} \) such that

    $$\bigl\vert f_{j}(u)-f_{j}(v)\bigr\vert \leq L_{j}^{f}\vert u-v\vert ,\qquad \bigl\vert g_{i}(u)-g_{i}(v)\bigr\vert \leq L_{i}^{g} \vert u-v\vert $$

    for \(u,n\in R\).

  2. (H2)

    For \(i = 1, 2, \ldots, n\), \(j = 1, 2, \ldots,m\), \(a_{i}(t)>0\) and \(b_{j}(t)>0\) for \(t\in R\).

The remainder of the paper is organized as follows: in Section 2, we introduce a useful definition and a lemma. In Section 3, some sufficient conditions which ensure the exponential stability of model (1.4) are established. In Section 3, an example which illustrates the theoretical findings is given. A brief conclusion is drawn in Section 4.

2 Preliminaries

In order to obtain the main result of this paper, we shall first state a definition and a lemma which will be useful in proving the main result.

Definition 2.1

Let \(u^{*}=(x_{1}^{*},x_{2}^{*},\ldots,x_{n}^{*},y_{1}^{*},y_{2}^{*},\ldots,y_{m}^{*})^{T}\) be a solution of system (1.4) with initial value \(\phi^{*}=(\varphi_{1}^{*},\varphi_{2}^{*},\ldots,\varphi_{n}^{*},\psi_{1}^{*},\psi _{2}^{*},\ldots,\psi_{m}^{*})^{T}\), there exists a constant \(\lambda>0\) that, for every solution \(u(t)=(x_{1}(t), x_{2}(t),\ldots, x_{n}(t),y_{1}(t),y_{2}(t),\ldots,y_{m}(t))^{T}\) of equation (1.4) with initial value \(\phi(s)=(\varphi_{1}(s),\varphi_{2}(s),\ldots,\varphi_{n}(s), \psi_{1}(s),\psi_{2}(s), \ldots,\psi_{m}(s))^{T}\), satisfies

$$x_{i}(t)-x_{i}^{*}(t)=O\bigl(e^{-\lambda t}\bigr),\qquad y_{j}(t)-y_{j}^{*}(t)=O\bigl(e^{-\lambda t}\bigr), $$

where \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\).

Lemma 2.1

[37]

Let x and y be two states of system (1.4). Then

$$\Biggl\vert \bigwedge_{j=1}^{n} \alpha_{ij}(t)g_{j}(x)-\bigwedge _{j=1}^{n}\alpha _{ij}(t)g_{j}(y) \Biggr\vert \leq\sum_{j=1}^{n}\bigl\vert \alpha_{ij}(t)\bigr\vert \bigl\vert g_{j}(x)-g_{j}(y) \bigr\vert $$

and

$$\Biggl\vert \bigvee_{j=1}^{n} \beta_{ij}(t)g_{j}(x)-\bigvee_{j=1}^{n} \beta _{ij}(t)g_{j}(y)\Biggr\vert \leq\sum _{j=1}^{n}\bigl\vert \beta_{ij}(t)\bigr\vert \bigl\vert g_{j}(x)-g_{j}(y)\bigr\vert . $$

3 Exponential stability

In this section, we will consider the exponential stability of system (1.4).

Theorem 3.1

Let \(u^{*}=(x_{1}^{*},x_{2}^{*},\ldots,x_{n}^{*},y_{1}^{*},y_{2}^{*},\ldots,y_{m}^{*})^{T}\) be a solution of system (1.4) with initial value \(\phi^{*}=(\varphi_{1}^{*},\varphi_{2}^{*},\ldots,\varphi_{n}^{*},\psi_{1}^{*},\psi _{2}^{*},\ldots,\psi_{m}^{*})^{T}\) In addition to (H1) and (H2), assume that:

  1. (H3)

    For \(i=1,2,\ldots, n\), \(j=1,2,\ldots,m\), \(t\in R\),

    $$\left \{ \textstyle\begin{array}{l} -a_{i}(t)\int_{0}^{\infty}h_{i}(s)\,ds +a_{i}^{+}\int_{0}^{\infty}h_{i}(s)s \,ds \\ \quad {}+\sum_{j=1}^{m} [(a_{ij}^{+}+b_{ij}^{+})+(\alpha_{ij}^{+}+\beta _{ij}^{+})\int_{0}^{+\infty}k_{j}(t-s) \,ds ]L_{j}^{f}< 0, \\ -b_{j}(t)\int_{0}^{\infty}l_{j}(s)\,ds +b_{j}^{+}\int_{0}^{\infty}l_{j}(s)s \,ds \\ \quad {}+\sum_{i=1}^{n} [(d_{ji}^{+}+p_{ji}^{+})+(\gamma_{ji}^{+}+\eta _{ji}^{+})\int_{0}^{+\infty}k_{i}(t-s) \,ds ]L_{i}^{g}< 0. \end{array}\displaystyle \right . $$
  2. (H4)

    For \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\), \(k=1,2,\ldots\) ,

    $$\begin{aligned}& I_{k}\bigl(x_{i}(t_{k})\bigr)=- \theta_{ik}x_{i}(t_{k}),\quad 0\leq \theta_{ik}\leq 2, \\& J_{k}\bigl(y_{j}(t_{k})\bigr)=- \vartheta_{jk}y_{j}(t_{k}), \quad 0\leq \vartheta_{jk}\leq2. \end{aligned}$$

Then system (1.4) is exponentially stable.

Proof

Let \(u(t)=(x_{1}(t), x_{2}(t),\ldots, x_{n}(t),y_{1}(t),y_{2}(t),\ldots,y_{m}(t))^{T}\) of equation (1.4) with initial value \(\phi(s)=(\varphi_{1}(s),\varphi_{2}(s),\ldots,\varphi_{n}(s), \psi_{1}(s),\psi_{2}(s), \ldots,\psi_{m}(s))^{T}\). Set

$$ \left \{ \textstyle\begin{array}{l} \bar{x}_{i}= x_{i}(t)-x_{i}^{*}(t),\quad i=1,2,\ldots,n, \\ \bar{y}_{j}=y_{j}(t)-y_{j}^{*}(t),\quad j=1,2,\ldots,m, \end{array}\displaystyle \right .$$
(3.1)

and

$$ \left \{ \textstyle\begin{array}{l} \bar{f}_{j}(\bar{y}_{j}(t))= f_{j}(\bar {y}_{j}(t)+y_{j}^{*}(t))-f_{j}(y_{j}^{*}(t)), \quad j=1,2,\ldots,m, \\ \bar{g}_{i}(\bar{x}_{i}(t))= g_{i}(\bar{x}_{i}(t)+x_{x}^{*}(t))-g_{i}(x_{i}^{*}(t)),\quad i=1,2,\ldots,n. \end{array}\displaystyle \right .$$
(3.2)

For \(t>0\), \(t\neq t_{k}\), \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\), \(k=1,2,\ldots\) , it follows from (H4), (1.4), (3.1), and (3.2) that

$$ \left \{ \textstyle\begin{array}{l} \bar{x}_{i}'(t)=-a_{i}(t)\int_{0}^{\infty}h_{i}(s)\bar{x}_{i}(t-s)\,ds+\sum_{j=1}^{m}a_{ij}(t)\bar{f}_{j}(\bar {y}_{j}(t)) \\ \hphantom{\bar{x}_{i}'(t)={}}{}+\sum_{j=1}^{m} b_{ij}(t)\bar{f}_{j}(\bar{y}_{j}(t-\tau(t)))+\bigwedge_{j=1}^{m}\alpha_{ij}(t)\int _{-\infty}^{t}k_{j}(t-s)\bar{f}_{j}(\bar{y}_{j}(s))\,ds \\ \hphantom{\bar{x}_{i}'(t)={}}{}+\bigvee_{j=1}^{m}\beta _{ij}(t)\int_{-\infty}^{t}k_{j}(t-s)\bar{f}_{j}(\bar{y}_{j}(s))\,ds, \\ \bar{y}_{j}'(t)=-b_{j}(t)\int_{0}^{\infty}l_{j}(s)\bar{y}_{j}(t-s)\,ds+\sum_{i=1}^{n}d_{ji}(t)\bar{g}_{i}(\bar {x}_{i}(t)) \\ \hphantom{\bar{y}_{j}'(t)={}}{}+\sum_{i=1}^{n} p_{ji}(t)\bar{g}_{i}(\bar{x}_{i}(t-\rho(t)))+\bigwedge_{i=1}^{n}\gamma_{ji}(t)\int_{-\infty }^{t}k_{i}(t-s)\bar{g}_{i}(\bar{x}_{i}(s))\,ds \\ \hphantom{\bar{y}_{j}'(t)={}}{}+\bigvee_{i=1}^{n}\eta _{ji}(t)\int_{-\infty}^{t}k_{i}(t-s)\bar{g}_{i}(\bar{x}_{i}(s))\,ds \end{array}\displaystyle \right .$$
(3.3)

and

$$ \left \{ \textstyle\begin{array}{l} |x_{i}(t_{k}^{+})-x_{i}^{*}(t_{k}^{+})|= |x_{i}(t_{k})+I_{k}(x_{i}(t_{k}))-x_{i}^{*}(t_{k})-I_{k}(x_{i}^{*}(t_{k}))| \\ \hphantom{|x_{i}(t_{k}^{+})-x_{i}^{*}(t_{k}^{+})|}=|(1-\theta _{ik})(x_{i}(t_{k})-x_{i}^{*}(t_{k}))| \\ \hphantom{|x_{i}(t_{k}^{+})-x_{i}^{*}(t_{k}^{+})|}\leq|x_{i}(t_{k})-x_{i}^{*}(t_{k})|, \\ |y_{j}(t_{k}^{+})-y_{j}^{*}(t_{k}^{+})|= |y_{j}(t_{k})+J_{k}(y_{j}(t_{k}))-y_{j}^{*}(t_{k})-J_{k}(y_{j}^{*}(t_{k}))| \\ \hphantom{|y_{j}(t_{k}^{+})-y_{j}^{*}(t_{k}^{+})|}=|(1-\vartheta _{jk})(y_{j}(t_{k})-y_{j}^{*}(t_{k}))| \\ \hphantom{|y_{j}(t_{k}^{+})-y_{j}^{*}(t_{k}^{+})|}\leq|y_{j}(t_{k})-y_{j}^{*}(t_{k})|. \end{array}\displaystyle \right .$$
(3.4)

By (3.4), we have

$$ \left \{ \textstyle\begin{array}{l} |\bar{x}_{i}(t_{k}^{+})|= |x_{i}(t_{k}^{+})-x_{i}^{*}(t_{k}^{+})| \\ \hphantom{|\bar{x}_{i}(t_{k}^{+})|}\leq|x_{i}(t_{k})-x_{i}^{*}(t_{k})| \\ \hphantom{|\bar{x}_{i}(t_{k}^{+})|}=|\bar {x}_{i}(t_{k}^{-})|,\quad i=1,2,\ldots,n, k=1,2,\ldots, \\ |\bar{y}_{j}(t_{k}^{+})|= |y_{j}(t_{k}^{+})-y_{j}^{*}(t_{k}^{+})| \\ \hphantom{|\bar{y}_{j}(t_{k}^{+})|}\leq|y_{i}(t_{k})-y_{i}^{*}(t_{k})| \\ \hphantom{|\bar{y}_{j}(t_{k}^{+})|}=|\bar{y}_{j}(t_{k}^{-})|,\quad j=1,2,\ldots,m, k=1,2,\ldots. \end{array}\displaystyle \right .$$
(3.5)

Now we define continuous functions \(\Psi_{i}(\varsigma)\) (\(i=1,2,\ldots,n\)) and \(\Lambda_{j}(\varsigma)\) (\(j=1,2,\ldots,m\)) as follows:

$$ \left \{ \textstyle\begin{array}{l} \Psi_{i}(\varsigma)=- (a_{i}(t)\int_{0}^{\infty}h_{i}(s)\,ds -\varsigma ) +a_{i}^{+}\int_{0}^{\infty}h_{i}(s)s \,ds \\ \hphantom{\Psi_{i}(\varsigma)={}}{}+\sum_{j=1}^{m} [(a_{ij}^{+}+b_{ij}^{+}e^{\varsigma \tau^{+}})+(\alpha_{ij}^{+}+\beta_{ij}^{+})\int_{0}^{+\infty }k_{j}(t-s)e^{\varsigma (s-t)} \,ds ]L_{j}^{f}, \\ \Lambda_{j}(\varsigma)=- (b_{j}(t)\int_{0}^{\infty}l_{j}(s)\,ds -\varsigma ) +b_{j}^{+}\int_{0}^{\infty}l_{j}(s)s \,ds \\ \hphantom{\Lambda_{j}(\varsigma)={}}{}+\sum_{i=1}^{n} [(d_{ji}^{+}+p_{ji}^{+}e^{\varsigma \rho^{+}})+(\gamma_{ji}^{+}+\eta_{ji}^{+})\int_{0}^{+\infty }k_{i}(t-s)e^{\varsigma (s-t)} \,ds ]L_{i}^{g}. \end{array}\displaystyle \right .$$
(3.6)

Then we have

$$ \left \{ \textstyle\begin{array}{l} \Psi_{i}(0)=-a_{i}(t)\int_{0}^{\infty}h_{i}(s)\,ds +a_{i}^{+}\int_{0}^{\infty}h_{i}(s)s \,ds \\ \hphantom{\Psi_{i}(0)={}}{}+\sum_{j=1}^{m} [(a_{ij}^{+}+b_{ij}^{+})+(\alpha _{ij}^{+}+\beta_{ij}^{+})\int_{0}^{+\infty}k_{j}(t-s) \,ds ]L_{j}^{f}< 0, \\ \Lambda_{j}(0)=-b_{j}(t)\int_{0}^{\infty}l_{j}(s)\,ds +b_{j}^{+}\int_{0}^{\infty}l_{j}(s)s \,ds \\ \hphantom{\Lambda_{j}(0)={}}{}+\sum_{i=1}^{n} [(d_{ji}^{+}+p_{ji}^{+})+(\gamma _{ji}^{+}+\eta_{ji}^{+})\int_{0}^{+\infty}k_{i}(t-s) \,ds ]L_{i}^{g}< 0. \end{array}\displaystyle \right .$$
(3.7)

In view of the continuity of \(\Psi_{i}(\varsigma)\) (\(i=1,2,\ldots,n\)) and \(\Lambda_{j}(\varsigma)\) (\(j=1,2,\ldots,m\)), then there exists a positive constant λ such that

$$ \left \{ \textstyle\begin{array}{l} \Psi_{i}(\lambda)=- (a_{i}(t)\int_{0}^{\infty}h_{i}(s)\,ds -\lambda ) +a_{i}^{+}\int_{0}^{\infty}h_{i}(s)s \,ds \\ \hphantom{\Psi_{i}(\lambda)={}}{}+\sum_{j=1}^{m} [(a_{ij}^{+}+b_{ij}^{+}e^{\lambda \tau^{+}})+(\alpha_{ij}^{+}+\beta_{ij}^{+})\int_{0}^{+\infty }k_{j}(t-s)e^{\lambda (s-t)} \,ds ]L_{j}^{f}< 0, \\ \Lambda_{j}(\lambda)=- (b_{j}(t)\int_{0}^{\infty}l_{j}(s)\,ds -\lambda ) +b_{j}^{+}\int_{0}^{\infty}l_{j}(s)s \,ds \\ \hphantom{\Lambda_{j}(\lambda)={}}+\sum_{i=1}^{n} [(d_{ji}^{+}+p_{ji}^{+}e^{\lambda \rho^{+}})+(\gamma_{ji}^{+}+\eta_{ji}^{+})\int_{0}^{+\infty }k_{i}(t-s)e^{\lambda (s-t)} \,ds ]L_{i}^{g}< 0, \end{array}\displaystyle \right .$$
(3.8)

where \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\). Let

$$ \left \{ \textstyle\begin{array}{l} U_{i}(t)=e^{\lambda t}\bar{x}_{i}(t),\quad i=1,2,\ldots,n, \\ V_{j}(t)=e^{\lambda t}\bar{y}_{j}(t),\quad j=1,2,\ldots,m. \end{array}\displaystyle \right .$$
(3.9)

It follows from (3.9) that

$$\begin{aligned}& \frac{dU_{i}(t)}{dt} = \lambda e^{\lambda t}\bar{x}_{i}(t)+e^{\lambda t} \frac{d\bar{x}_{i}(t)}{dt} \\& \hphantom{\frac{dU_{i}(t)}{dt}}= \lambda U_{i}(t)+e^{\lambda t} \Biggl[-a_{i}(t) \int_{0}^{\infty}h_{i}(s) \bar{x}_{i}(t-s)\,ds \\& \hphantom{\frac{dU_{i}(t)}{dt} ={}}{}+\sum_{j=1}^{m}a_{ij}(t) \bar{f}_{j}\bigl(\bar{y}_{j}(t)\bigr)+\sum _{j=1}^{m} b_{ij}(t)e^{\lambda t} \bar{f}_{j}\bigl(\bar{y}_{j}\bigl(t-\tau(t)\bigr)\bigr) \\& \hphantom{\frac{dU_{i}(t)}{dt} ={}}{}+\bigwedge_{j=1}^{m} \alpha_{ij}(t) \int_{-\infty}^{t}k_{j}(t-s)\bar {f}_{j}\bigl(\bar{y}_{j}(s)\bigr)\,ds \\& \hphantom{\frac{dU_{i}(t)}{dt} ={}}{}+\bigvee_{j=1}^{m} \beta_{ij}(t) \int_{-\infty}^{t}k_{j}(t-s)\bar {f}_{j}\bigl(\bar{y}_{j}(s)\bigr)\,ds \Biggr] \\& \hphantom{\frac{dU_{i}(t)}{dt}}= \lambda U_{i}(t)-a_{i}(t) \int_{0}^{\infty}h_{i}(s)\,ds U_{i}(t) +a_{i}(t) \int_{0}^{\infty}h_{i}(s) \int_{t-s}^{t}\dot{U}_{i}(\kappa)\,d\kappa \,ds \\& \hphantom{\frac{dU_{i}(t)}{dt} ={}}{}+\sum_{j=1}^{m}a_{ij}(t)e^{\lambda t} \bar{f}_{j}\bigl(\bar{y}_{j}(t)\bigr)+\sum _{j=1}^{m} b_{ij}(t)e^{\lambda t} \bar{f}_{j}\bigl(\bar{y}_{j}\bigl(t-\tau(t)\bigr)\bigr) \\& \hphantom{\frac{dU_{i}(t)}{dt} ={}}{}+\bigwedge_{j=1}^{m} \alpha_{ij}(t)e^{\lambda t} \int_{-\infty }^{t}k_{j}(t-s) \bar{f}_{j}\bigl(\bar{y}_{j}(s)\bigr)\,ds \\& \hphantom{\frac{dU_{i}(t)}{dt} ={}}{}+\bigvee_{j=1}^{m} \beta_{ij}(t)e^{\lambda t} \int_{-\infty }^{t}k_{j}(t-s) \bar{f}_{j}\bigl(\bar{y}_{j}(s)\bigr)\,ds, \end{aligned}$$
(3.10)
$$\begin{aligned}& \frac{dV_{j}(t)}{dt} = \lambda e^{\lambda t}\bar{y}_{j}(t)+e^{\lambda t} \frac{d\bar{y}_{j}(t)}{dt} \\& \hphantom{\frac{dV_{j}(t)}{dt}}= \lambda V_{j}(t)+e^{\lambda t} \Biggl[-b_{j}(t) \int_{0}^{\infty}l_{j}(s) \bar{y}_{j}(t-s)\,ds \\& \hphantom{\frac{dV_{j}(t)}{dt} ={}}{}+\sum_{i=1}^{n}d_{ji}(t) \bar{g}_{i}\bigl(\bar{x}_{i}(t)\bigr)+\sum _{i=1}^{n} p_{ji}(t)e^{\lambda t} \bar{g}_{i}\bigl(\bar{x}_{i}\bigl(t-\rho(t)\bigr)\bigr) \\& \hphantom{\frac{dV_{j}(t)}{dt} ={}}{}+\bigwedge_{i=1}^{n} \gamma_{ji}(t) \int_{-\infty}^{t}l_{i}(t-s)\bar {g}_{i}\bigl(\bar{x}_{i}(s)\bigr)\,ds \\& \hphantom{\frac{dV_{j}(t)}{dt} ={}}{}+\bigvee_{i=1}^{n} \eta_{ji}(t) \int_{-\infty}^{t}l_{i}(t-s)\bar {g}_{i}\bigl(\bar{x}_{i}(s)\bigr)\,ds \Biggr] \\& \hphantom{\frac{dV_{j}(t)}{dt}}= \lambda V_{j}(t)-b_{j}(t) \int_{0}^{\infty}l_{j}(s)\,ds V_{j}(t) +b_{j}(t) \int_{0}^{\infty}l_{j}(s) \int_{t-s}^{t}\dot{V}_{j}(\kappa)\,d\kappa \,ds \\& \hphantom{\frac{dV_{j}(t)}{dt} ={}}{}+\sum_{i=1}^{n}d_{ji}(t)e^{\lambda t} \bar{g}_{i}\bigl(\bar{x}_{i}(t)\bigr)+\sum _{i=1}^{n} p_{ji}(t)e^{\lambda t} \bar{g}_{i}\bigl(\bar{x}_{i}\bigl(t-\rho(t)\bigr)\bigr) \\& \hphantom{\frac{dV_{j}(t)}{dt} ={}}{}+\bigwedge_{i=1}^{n} \gamma_{ji}(t)e^{\lambda t} \int_{-\infty }^{t}l_{i}(t-s) \bar{g}_{i}\bigl(\bar{x}_{i}(s)\bigr)\,ds \\& \hphantom{\frac{dV_{j}(t)}{dt} ={}}{}+\bigvee_{i=1}^{n} \eta_{ji}(t)e^{\lambda t} \int_{-\infty }^{t}l_{i}(t-s) \bar{g}_{i}\bigl(\bar{x}_{i}(s)\bigr)\,ds, \end{aligned}$$
(3.11)

where \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\). Let

$$\Upsilon=\max\Bigl\{ \max_{1\leq i\leq n}\bigl\{ \bigl\vert U_{i}(s)\bigr\vert , \bigl\vert \dot{U}_{i}(s)\bigr\vert \bigr\} , \max_{1\leq j\leq m}\bigl\{ \bigl\vert V_{j}(s)\bigr\vert , \bigl\vert \dot{V}_{j}(s)\bigr\vert \bigr\} , s\in(-\infty,0]\Bigr\} . $$

It follows, for \(t\in(-\infty,0]\), \(t\neq t_{k}\), and \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\), that

$$ \bigl\vert U_{i}(t)\bigr\vert \leq\Upsilon,\qquad \bigl\vert \dot{U}_{i}(t)\bigr\vert \leq\Upsilon,\qquad \bigl\vert V_{j}(t)\bigr\vert \leq \Upsilon, \qquad \bigl\vert \dot{V}_{j}(t)\bigr\vert \leq\Upsilon. $$
(3.12)

Next we prove, for \(t>0\) and \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\), that

$$ \bigl\vert U_{i}(t)\bigr\vert \leq\Upsilon,\qquad \bigl\vert \dot{U}_{i}(t)\bigr\vert \leq\Upsilon,\qquad \bigl\vert V_{j}(t)\bigr\vert \leq \Upsilon,\qquad \bigl\vert \dot{V}_{j}(t)\bigr\vert \leq\Upsilon. $$
(3.13)

If (3.13) does not hold true, then there exist \(i\in\{1,2,\ldots,n\}\), \(j\in\{1,2,\ldots,m\}\), and a first time \(t^{*}>0\) such that one of the following cases (3.14)-(3.21) is satisfied:

$$\begin{aligned}& \begin{aligned} &U_{i}\bigl(t^{*}\bigr)=\Upsilon,\qquad \dot{U}_{i}\bigl(t^{*} \bigr)\geq0, \qquad \bigl\vert U_{i}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{U}_{i}(t)\bigr\vert < \Upsilon, \\ &\bigl\vert V_{j}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{V}_{j}(t)\bigr\vert < \Upsilon \quad \mbox{for } t< t^{*}; \end{aligned} \end{aligned}$$
(3.14)
$$\begin{aligned}& \begin{aligned} &U_{i}\bigl(t^{*}\bigr)=-\Upsilon,\qquad \dot{U}_{i}\bigl(t^{*} \bigr)\leq0,\qquad \bigl\vert U_{i}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{U}_{i}(t)\bigr\vert < \Upsilon, \\ &\bigl\vert V_{j}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{V}_{j}(t)\bigr\vert < \Upsilon \quad \mbox{for } t< t^{*}; \end{aligned} \end{aligned}$$
(3.15)
$$\begin{aligned}& \begin{aligned} &V_{j}\bigl(t^{*}\bigr)=\Upsilon,\qquad \dot{V}_{j}\bigl(t^{*} \bigr)\geq0,\qquad \bigl\vert U_{i}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{U}_{i}(t)\bigr\vert < \Upsilon, \\ &\bigl\vert V_{j}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{V}_{j}(t)\bigr\vert < \Upsilon \quad \mbox{for } t< t^{*}; \end{aligned} \end{aligned}$$
(3.16)
$$\begin{aligned}& \begin{aligned} &V_{j}\bigl(t^{*}\bigr)=-\Upsilon, \qquad \dot{V}_{j} \bigl(t^{*}\bigr)\leq0,\qquad \bigl\vert U_{i}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{U}_{i}(t)\bigr\vert < \Upsilon, \\ &\bigl\vert V_{j}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{V}_{j}(t)\bigr\vert < \Upsilon \quad \mbox{for } t< t^{*}; \end{aligned} \end{aligned}$$
(3.17)
$$\begin{aligned}& \begin{aligned} &U_{i}\bigl(t^{*}\bigr)=\Upsilon,\qquad \dot{U}_{i}\bigl(t^{*} \bigr)>0,\qquad \bigl\vert u_{i}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{U}_{i}(t)\bigr\vert < \Upsilon, \\ &\bigl\vert V_{j}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{V}_{j}(t)\bigr\vert < \Upsilon \quad \mbox{for } t< t^{*}; \end{aligned} \end{aligned}$$
(3.18)
$$\begin{aligned}& \begin{aligned} &U_{i}\bigl(t^{*}\bigr)=-\Upsilon, \qquad \dot{U}_{i} \bigl(t^{*}\bigr)< 0, \qquad \bigl\vert U_{i}(t)\bigr\vert < \Upsilon, \qquad \bigl\vert \dot{U}_{i}(t)\bigr\vert < \Upsilon, \\ &\bigl\vert V_{j}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{V}_{j}(t)\bigr\vert < \Upsilon \quad \mbox{for } t< t^{*}; \end{aligned} \end{aligned}$$
(3.19)
$$\begin{aligned}& \begin{aligned} &V_{j}\bigl(t^{*}\bigr)=\Upsilon,\qquad \dot{V}_{j}\bigl(t^{*} \bigr)>0,\qquad \bigl\vert U_{i}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{U}_{i}(t)\bigr\vert < \Upsilon, \\ &\bigl\vert V_{j}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{V}_{j}(t)\bigr\vert < \Upsilon \quad \mbox{for } t< t^{*}; \end{aligned} \end{aligned}$$
(3.20)
$$\begin{aligned}& \begin{aligned} &V_{j}\bigl(t^{*}\bigr)=-\Upsilon,\qquad \dot{V}_{j}\bigl(t^{*} \bigr)< 0,\qquad \bigl\vert U_{i}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{U}_{i}(t)\bigr\vert < \Upsilon, \\ &\bigl\vert V_{j}(t)\bigr\vert < \Upsilon,\qquad \bigl\vert \dot{V}_{j}(t)\bigr\vert < \Upsilon \quad \mbox{for } t< t^{*}. \end{aligned} \end{aligned}$$
(3.21)

If (3.14) holds, then according to (H3), (3.8), and (3.10), we have

$$\begin{aligned} \frac{dU_{i}(t)}{dt}\bigg|_{t=t^{*}} =&\lambda U_{i} \bigl(t^{*}\bigr)-a_{i}\bigl(t^{*}\bigr) \int_{0}^{\infty}h_{i}(s)\,ds U_{i}\bigl(t^{*}\bigr) \\ &{}+a_{i}\bigl(t^{*}\bigr) \int_{0}^{\infty}h_{i}(s) \int_{t^{*}-s}^{t^{*}}\dot{U}_{i}(\kappa )\,d \kappa \,ds \\ &{}+\sum_{j=1}^{m}a_{ij} \bigl(t^{*}\bigr)e^{\lambda t^{*}}\bar{f}_{j}\bigl(\bar{y}_{j} \bigl(t^{*}\bigr)\bigr)+\sum_{j=1}^{m} b_{ij}\bigl(t^{*}\bigr)e^{\lambda t^{*}}\bar{f}_{j}\bigl( \bar{y}_{j}\bigl(t^{*}-\tau \bigl(t^{*}\bigr)\bigr)\bigr) \\ &{}+\bigwedge_{j=1}^{m} \alpha_{ij}\bigl(t^{*}\bigr)e^{\lambda t^{*}} \int_{-\infty}^{t^{*}}k_{j}\bigl(t^{*}-s\bigr) \bar{f}_{j}\bigl(\bar {y}_{j}(s)\bigr)\,ds \\ &{}+\bigvee_{j=1}^{m}\beta_{ij} \bigl(t^{*}\bigr)e^{\lambda t^{*}} \int_{-\infty }^{t^{*}}k_{j}(t-s) \bar{f}_{j}\bigl(\bar{y}_{j}(s)\bigr)\,ds \\ \leq& \biggl(\lambda-a_{i}\bigl(t^{*}\bigr) \int_{0}^{\infty}h_{i}(s)\,ds \biggr)U_{i}\bigl(t^{*}\bigr) +a_{i}^{+} \int_{0}^{\infty}h_{i}(s)s \,ds \Upsilon \\ &{}+\sum_{j=1}^{m}a_{ij}^{+}L_{j}^{f} \bigl\vert {V}_{j}\bigl(t^{*}\bigr)\bigr\vert +\sum _{j=1}^{m} b_{ij}^{+}e^{\lambda\tau^{+}}L_{j}^{f} \bigl\vert {V}_{j}\bigl(t^{*}-\tau\bigl(t^{*}\bigr)\bigr)\bigr\vert \\ &{}+\sum_{j=1}^{m}\alpha_{ij}^{+} \int_{-\infty }^{t^{*}}k_{j}\bigl(t^{*}-s \bigr)e^{\lambda(s-t^{*})}L_{j}^{f}\bigl\vert {y}_{j}(s)\bigr\vert \,ds \\ &{}+\sum_{j=1}^{m}\beta_{ij}^{+} \int_{-\infty }^{t^{*}}k_{j}(t-s)e^{\lambda(s-t^{*})}L_{j}^{f} \bigl\vert {y}_{j}(s)\bigr\vert \,ds \\ \leq& \biggl(\lambda-a_{i}\bigl(t^{*}\bigr) \int_{0}^{\infty}h_{i}(s)\,ds \biggr) \Upsilon +a_{i}^{+} \int_{0}^{\infty}h_{i}(s)s \,ds \Upsilon \\ &{}+\sum_{j=1}^{m}a_{ij}^{+}L_{j}^{f} \Upsilon+\sum_{j=1}^{m} b_{ij}^{+}e^{\lambda\tau^{+}}L_{j}^{f} \Upsilon +\sum_{j=1}^{m}\alpha_{ij}^{+} \int_{0}^{+\infty}k_{j}(s)e^{\lambda s}L_{j}^{f} \Upsilon \,ds \\ &{}+\sum_{j=1}^{m}\beta_{ij}^{+} \int_{0}^{+\infty}k_{j}(s)e^{\lambda s}L_{j}^{f} \Upsilon \,ds \\ \leq& \Biggl\{ - \biggl(a_{i}\bigl(t^{*}\bigr) \int_{0}^{\infty}h_{i}(s)\,ds -\lambda \biggr) +a_{i}^{+} \int_{0}^{\infty}h_{i}(s)s \,ds \\ &{}+\sum_{j=1}^{m} \biggl[ \bigl(a_{ij}^{+}+b_{ij}^{+}e^{\lambda \tau^{+}} \bigr)+\bigl(\alpha_{ij}^{+}+\beta_{ij}^{+} \bigr) \int_{0}^{+\infty }k_{j}(t-s)e^{\lambda (s-t^{*})} \,ds \biggr]L_{j}^{f} \Biggr\} \Upsilon \\ < &0, \end{aligned}$$
(3.22)

which is a contradiction. Thus (3.14) is not hold true. If (3.15) holds, then according to (H3), (3.8), and (3.11), we have

$$\begin{aligned} \frac{dU_{i}(t)}{dt}\bigg|_{t=t^{*}} =&\lambda U_{i}\bigl(t^{*} \bigr)-a_{i}\bigl(t^{*}\bigr) \int_{0}^{\infty}h_{i}(s)\,ds U_{i}\bigl(t^{*}\bigr) \\ &{}+a_{i}\bigl(t^{*}\bigr) \int_{0}^{\infty}h_{i}(s) \int_{t^{*}-s}^{t^{*}}\dot{U}_{i}(\kappa )\,d \kappa \,ds \\ &{}+\sum_{j=1}^{m}a_{ij} \bigl(t^{*}\bigr)e^{\lambda t^{*}}\bar{f}_{j}\bigl(\bar{y}_{j} \bigl(t^{*}\bigr)\bigr)+\sum_{j=1}^{m} b_{ij}\bigl(t^{*}\bigr)e^{\lambda t^{*}}\bar{f}_{j}\bigl( \bar{y}_{j}\bigl(t^{*}-\tau \bigl(t^{*}\bigr)\bigr)\bigr) \\ &{}+\bigwedge_{j=1}^{m} \alpha_{ij}\bigl(t^{*}\bigr)e^{\lambda t^{*}} \int_{-\infty }^{t^{*}}k_{j}\bigl(t^{*}-s\bigr) \bar{f}_{j}\bigl(\bar{y}_{j}(s)\bigr)\,ds \\ &{}+\bigvee_{j=1}^{m}\beta_{ij} \bigl(t^{*}\bigr)e^{\lambda t^{*}} \int_{-\infty}^{t^{*}}k_{j}(t-s) \bar{f}_{j}\bigl(\bar{y}_{j}(s)\bigr)\,ds \\ \geq& \biggl(\lambda-a_{i}\bigl(t^{*}\bigr) \int_{0}^{\infty}h_{i}(s)\,ds \biggr)U_{i}\bigl(t^{*}\bigr) -a_{i}^{+} \int_{0}^{\infty}h_{i}(s)s \,ds \Upsilon \\ &{}-\sum_{j=1}^{m}a_{ij}^{+}L_{j}^{f} \bigl\vert {V}_{j}\bigl(t^{*}\bigr)\bigr\vert -\sum _{j=1}^{m} b_{ij}^{+}e^{\lambda\tau^{+}}L_{j}^{f} \bigl\vert {V}_{j}\bigl(t^{*}-\tau\bigl(t^{*}\bigr)\bigr)\bigr\vert \\ &{}-\sum_{j=1}^{m}\alpha_{ij}^{+} \int_{-\infty }^{t^{*}}k_{j}\bigl(t^{*}-s \bigr)e^{\lambda(s-t^{*})}L_{j}^{f}\bigl\vert {y}_{j}(s)\bigr\vert \,ds \\ &{}-\sum_{j=1}^{m}\beta_{ij}^{+} \int_{-\infty }^{t^{*}}k_{j}(t-s)e^{\lambda (s-t^{*})}L_{j}^{f} \bigl\vert {y}_{j}(s)\bigr\vert \,ds \\ \geq& \biggl(\lambda-a_{i}\bigl(t^{*}\bigr) \int_{0}^{\infty}h_{i}(s)\,ds \biggr) \Upsilon -a_{i}^{+} \int_{0}^{\infty}h_{i}(s)s \,ds \Upsilon \\ &{}-\sum_{j=1}^{m}a_{ij}^{+}L_{j}^{f} \Upsilon-\sum_{j=1}^{m} b_{ij}^{+}e^{\lambda\tau^{+}}L_{j}^{f} \Upsilon -\sum_{j=1}^{m}\alpha_{ij}^{+} \int_{0}^{+\infty}k_{j}(s)e^{\lambda s}L_{j}^{f} \Upsilon \,ds \\ &{}-\sum_{j=1}^{m}\beta_{ij}^{+} \int_{0}^{+\infty}k_{j}(s)e^{\lambda s}L_{j}^{f} \Upsilon \,ds \\ \geq& \Biggl\{ - \biggl(a_{i}\bigl(t^{*}\bigr) \int_{0}^{\infty}h_{i}(s)\,ds -\lambda \biggr) +a_{i}^{+} \int_{0}^{\infty}h_{i}(s)s \,ds \\ &{}+\sum_{j=1}^{m} \biggl[ \bigl(a_{ij}^{+}+b_{ij}^{+}e^{\lambda \tau^{+}} \bigr)+\bigl(\alpha_{ij}^{+}+\beta_{ij}^{+} \bigr) \int_{0}^{+\infty }k_{j}(t-s)e^{\lambda (s-t^{*})} \,ds \biggr]L_{j}^{f} \Biggr\} (-\Upsilon) \\ >&0, \end{aligned}$$
(3.23)

which is also a contradiction, thus (3.15) does not hold true. In a similar way, we can also prove that (3.16)-(3.21) do not hold true. On the other hand, by (3.5) and (3.6), we get

$$ \left \{ \textstyle\begin{array}{l} |\bar{x}_{i}(t_{k}^{+})|= |x_{i}(t_{k}^{+})-x_{i}^{*}(t_{k}^{+})| \\ \hphantom{|\bar{x}_{i}(t_{k}^{+})|}\leq|x_{i}(t_{k})-x_{i}^{*}(t_{k})|=|\bar {x}_{i}(t_{k}^{-})| \\ \hphantom{|\bar{x}_{i}(t_{k}^{+})|}=|U_{i}(t_{k}^{-})|e^{-\lambda t_{k}}\leq|\Upsilon e^{-\lambda t_{k}}, \\ |\bar{y}_{j}(t_{k}^{+})|= |y_{j}(t_{k}^{+})-y_{j}^{*}(t_{k}^{+})| \\ \hphantom{|\bar{y}_{j}(t_{k}^{+})|}\leq|y_{i}(t_{k})-y_{i}^{*}(t_{k})|=|\bar{y}_{j}(t_{k}^{-})| \\ \hphantom{|\bar{y}_{j}(t_{k}^{+})|}=|V_{j}(t_{k}^{-})|e^{-\lambda t_{k}}\leq |\Upsilon e^{-\lambda t_{k}}, \end{array}\displaystyle \right . $$
(3.24)

where \(i=1,2,\ldots,n\), \(j=1,2,\ldots,m\), \(k=1,2,\ldots\) . It follows from (3.13) and (3.24) that we have

$$ \left \{ \textstyle\begin{array}{l} |x_{i}(t)-x_{i}^{*}(t)|= O(e^{-\lambda t}),\quad t>0, i=1,2,\ldots ,n, \\ |y_{j}(t)-y_{j}^{*}(t)|= O(e^{-\lambda t}),\quad t>0, j=1,2,\ldots,m. \end{array}\displaystyle \right .$$
(3.25)

Therefore system (1.4) is exponentially stable. The proof of Theorem 3.1 is completed. □

Remark 3.1

Duan and Huang [1] investigated the global exponential stability of fuzzy BAM neural networks with distributed delays and time-varying delays in the leakage terms, the model (1.1) in [1] does not involves distributed leakage delays and impulses. In this paper, we studied the exponential stability of system (1.4) with distributed leakage delays and impulses. System (1.4) is more general than those of numerous previous works. All the results obtained in [1] cannot be applicable to model (1.4) to obtain the exponential stability of system (1.4). From this viewpoint, our results on the exponential stability for fuzzy BAM neural networks are essentially new and complement previously known results to some extent.

4 Examples

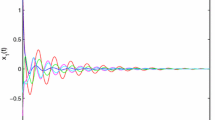
In this section, we present an example to verify the analytical predictions obtained in the previous section. Consider the following fuzzy BAM cellular neural networks with distributed leakage delays and impulses:

$$ \left \{ \textstyle\begin{array}{l} x_{i}'(t)=-a_{i}(t)\int_{0}^{\infty}h_{i}(s)x_{i}(t-s)\,ds+\sum_{j=1}^{2}a_{ij}(t)f_{j}(y_{j}(t)) \\ \hphantom{x_{i}'(t)={}}{}+\sum_{j=1}^{2} b_{ij}(t)f_{j}(y_{j}(t-\tau(t)))+\bigwedge_{j=1}^{2}\alpha_{ij}(t)\int _{-\infty}^{t}k_{j}(t-s)f_{j}(y_{j}(s))\,ds \\ \hphantom{x_{i}'(t)={}}{}+\bigvee_{j=1}^{2}\beta_{ij}(t)\int _{-\infty}^{t}k_{j}(t-s)f_{j}(y_{j}(s))\,ds \\ \hphantom{x_{i}'(t)={}}{}+\bigwedge_{j=1}^{2}T_{ij}\omega_{j}+\bigvee_{j=1}^{2}H_{ij}\omega_{j}+\sum_{j=1}^{2} c_{ij}(t)\omega_{j} \\ \hphantom{x_{i}'(t)={}}{}+A_{i}(t),\quad t\geq0,t\neq t_{k}, i=1,2,\ldots,n, \\ \triangle x_{i}(t_{k})=I_{k}(x_{i}(t_{k})),\quad i=1,2,\ldots,n, k=1,2,\ldots, \\ y_{j}'(t)=-b_{j}(t)\int_{0}^{\infty}l_{j}(s)y_{j}(t-s)\,ds+\sum_{i=1}^{2}d_{ji}(t)g_{i}(x_{i}(t)) \\ \hphantom{y_{j}'(t)={}}{}+\sum_{i=1}^{2} p_{ji}(t)g_{i}(x_{i}(t-\rho(t)))+\bigwedge_{i=1}^{2}\gamma_{ji}(t)\int _{-\infty}^{t}k_{i}(t-s)g_{i}(x_{i}(s))\,ds \\ \hphantom{y_{j}'(t)={}}{}+\bigvee_{i=1}^{2}\eta_{ji}(t)\int _{-\infty}^{t}k_{i}(t-s)g_{i}(x_{i}(s))\,ds \\ \hphantom{y_{j}'(t)={}}{}+\bigwedge_{i=1}^{2}R_{ji}\mu_{i}+\bigvee_{i=1}^{2}S_{ji}\mu _{i}+\sum_{i=1}^{2} q_{ji}(t)\mu_{i} \\ \hphantom{y_{j}'(t)={}}{}+B_{j}(t),\quad t\geq0,t\neq t_{k}, j=1,2,\ldots,m, \\ \triangle y_{j}(t_{k})=J_{k}(y_{j}(t_{k})),\quad j=1,2,\ldots,m, k=1,2,\ldots, \end{array}\displaystyle \right .$$
(4.1)

where

$$\begin{aligned}& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} a_{1}(t) & a_{2}(t)\\ b_{1}(t) & b_{2}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.55+0.2|\cos t| & 0.62+0.2|\sin t|\\ 0.45+0.1|\sin t| & 0.52+0.4|\sin t| \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} a_{11}(t) & a_{12}(t)\\ a_{21}(t) & a_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.35+0.2|\sin t| & 0.73+0.2|\cos t|\\ 0.45+0.2|\sin t| & 0.57+0.4|\cos t| \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} d_{11}(t) & d_{12}(t)\\ d_{21}(t) & d_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.06+0.01\sin t & 0.06+0.02\sin t\\ 0.07+0.04\cos t & 0.07+0.04\sin t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} b_{11}(t) & b_{12}(t)\\ b_{21}(t) & b_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.07+0.03\cos t & 0.07+0.04\sin t\\ 0.08+0.03\cos t & 0.09+0.05\cos t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} p_{11}(t) & p_{12}(t)\\ p_{21}(t) & p_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.06+0.03\sin t & 0.08+0.04\sin t\\ 0.05+0.03\cos t & 0.08+0.05\sin t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \alpha_{11}(t) & \alpha_{12}(t)\\ \alpha_{21}(t) & \alpha_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.05+0.03\cos t & 0.09+0.05\sin t\\ 0.06+0.02\cos t & 0.06+0.01\cos t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \gamma_{11}(t) & \gamma_{12}(t)\\ \gamma_{21}(t) & \gamma_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.06+0.02\cos t & 0.06+0.01\sin t\\ 0.08+0.04\cos t & 0.07+0.03\cos t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \beta_{11}(t) & \beta_{12}(t)\\ \beta_{21}(t) & \beta_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.05+0.02\cos t & 0.05+0.01\sin t\\ 0.05+0.04\cos t & 0.05+0.03\cos t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \eta_{11}(t) & \eta_{12}(t)\\ \eta_{21}(t) & \eta_{22}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.04+0.01\cos t & 0.07+0.01\sin t\\ 0.07+0.02\cos t & 0.07+0.03\cos t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} T_{11} & T_{12}\\ T_{21} & T_{22} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} H_{11} & H_{12}\\ H_{21} & H_{22} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} R_{11} & R_{12}\\ R_{21} & R_{22} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 1 & 1\\ 1 & 1 \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} T_{11} & T_{12}\\ T_{21} & T_{22} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 1 & 1\\ 1 & 1 \end{array}\displaystyle \right ],\qquad \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} A_{1}(t) & A_{2}(t)\\ B_{1}(t) & B_{2}(t) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.5\cos t & 0.4\sin t\\ 0.4\sin t & 0.5\sin t \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} h_{1}(s) & h_{2}(s)\\ l_{1}(s) & l_{2}(s) \\ k_{1}(s) & k_{2}(s) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} e^{-4s^{2}} & e^{-4s^{2}} \\ e^{-4s^{2}} & e^{-4s^{2}} \\ e^{-s} & e^{-s} \end{array}\displaystyle \right ],\qquad \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} f_{1}(x) & f_{2}(x)\\ g_{1}(x) & g_{2}(x) \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} |x| & |x|\\ |x| & |x| \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \tau(t) & \mu_{1}\\ \rho(t) & \mu_{2} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.5+ 0.2|\cos t| & 1\\ 0.4+0.2|\sin t| & 1 \end{array}\displaystyle \right ],\qquad \left [ \textstyle\begin{array}{@{}c@{}} \theta_{ik} \\ \vartheta_{jk} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{}} 1-0.2\sin(1+k) \\ 1+0.2\cos(2+k) \end{array}\displaystyle \right ], \end{aligned}$$

where \(i,j=1,2\). Then

$$\begin{aligned}& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} a_{1}^{+} & a_{2}^{+}\\ b_{1}^{+} & b_{2}^{+} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.75 & 0.82\\ 0.55 & 0.92 \end{array}\displaystyle \right ],\qquad \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} a_{1}^{-} & a_{2}^{-}\\ b_{1}^{-} & b_{2}^{-} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.55 & 0.62\\ 0.45 & 0.52 \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} d_{11}^{+} & d_{12}^{+}\\ d_{21}^{+} & d_{22}^{+} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.07 & 0.08\\ 0.11 & 0.11 \end{array}\displaystyle \right ],\qquad \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} b_{11}^{+} & b_{12}^{+}\\ b_{21}^{+} & b_{22}^{+} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.10 & 0.11\\ 0.11 & 0.14 \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} p_{11}^{+} & p_{12}^{+}\\ p_{21}^{+} & p_{22}^{+} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.09 & 0.12\\ 0.08 & 0.13 \end{array}\displaystyle \right ],\qquad \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \alpha_{11}^{+} & \alpha_{12}^{+}\\ \alpha_{21}^{+}& \alpha_{22}^{+} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.08 & 0.14\\ 0.08 & 0.07 \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \gamma_{11}^{+} & \gamma_{12}^{+}\\ \gamma_{21}^{+} & \gamma_{22}^{+} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.08 & 0.08\\ 0.12 & 0.10 \end{array}\displaystyle \right ],\qquad \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \beta_{11}^{+} & \beta_{12}^{+}\\ \beta_{21}^{+} & \beta_{22}^{+} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.07 & 0.06\\ 0.09 & 0.08 \end{array}\displaystyle \right ], \\& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \eta_{11}^{+} & \eta_{12}^{+}\\ \eta_{21}^{+} & \eta_{22}^{+} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.05 & 0.08\\ 0.09 & 0.10 \end{array}\displaystyle \right ],\qquad \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} L_{1}^{g} & L_{2}^{g}\\ L_{1}^{f} & L_{2}^{f} \end{array}\displaystyle \right ]=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 1 & 1\\ 1 & 1 \end{array}\displaystyle \right ]. \end{aligned}$$

It is easy to check that (H1) and (H2) hold. In addition, we have

$$\begin{aligned}& -a_{1}^{-} \int_{0}^{\infty}h_{1}(s)\,ds +a_{1}^{+} \int_{0}^{\infty}h_{1}(s)s \,ds \\& \quad {}+\sum_{j=1}^{2} \biggl[ \bigl(a_{1j}^{+}+b_{1j}^{+}\bigr)+\bigl( \alpha_{1j}^{+}+\beta _{1j}^{+}\bigr) \int_{0}^{+\infty}k_{j}(t-s) \,ds \biggr]L_{j}^{f}\approx -0.3045< 0, \\& -a_{2}^{-} \int_{0}^{\infty}h_{2}(s)\,ds +a_{2}^{+} \int_{0}^{\infty}h_{2}(s)s \,ds \\& \quad {}+\sum_{j=1}^{2} \biggl[ \bigl(a_{2j}^{+}+b_{2j}^{+}\bigr)+\bigl( \alpha_{2j}^{+}+\beta _{2j}^{+}\bigr) \int_{0}^{+\infty}k_{j}(t-s) \,ds \biggr]L_{j}^{f}\approx -0.6822< 0, \\& -b_{1}^{-} \int_{0}^{\infty}l_{1}(s)\,ds +b_{1}^{+} \int_{0}^{\infty}l_{1}(s)s \,ds \\& \quad {}+\sum_{i=1}^{2} \biggl[ \bigl(d_{1i}^{+}+p_{1i}^{+}\bigr)+\bigl( \gamma_{1i}^{+}+\eta _{1i}^{+}\bigr) \int_{0}^{+\infty}k_{i}(t-s) \,ds \biggr]L_{i}^{g}\approx-0.5743< 0, \\& -b_{2}^{-} \int_{0}^{\infty}l_{2}(s)\,ds +b_{2}^{+} \int_{0}^{\infty}l_{2}(s)s \,ds \\& \quad {}+\sum_{i=1}^{2} \biggl[ \bigl(d_{2i}^{+}+p_{2i}^{+}\bigr)+\bigl( \gamma_{2i}^{+}+\eta _{2i}^{+}\bigr) \int_{0}^{+\infty}k_{i}(t-s) \,ds \biggr]L_{i}^{g}\approx-0.9208< 0, \end{aligned}$$

which implies that (H3) holds. Thus all the conditions in Theorem 3.1 are satisfied. Then we can conclude that system (4.1) is exponentially stable.

5 Conclusions

In the present paper, we are concerned with a class of fuzzy BAM cellular neural networks with distributed leakage delays and impulses. A set of sufficient conditions to ensure the exponential stability of such fuzzy BAM cellular neural networks with distributed leakage delays and impulses are established by applying differential inequality techniques. It is shown that distributed leakage delays and impulses play an important role in exponential stability of the neural networks. The results obtained in this paper are completely new and complement the previously known work of [34, 35].