1 Introduction

The aim of this paper is to investigate the stability property of the following two-species discrete competition model of plankton allelopathy with infinite deviating arguments:

$$\begin{aligned}& \begin{aligned}[b] x_{1}(k+1)={}& x_{1}(k)\exp \Biggl\{ K_{1}-\alpha_{1} x_{1}(k)- \beta_{12} \sum_{s=-\infty}^{n}K_{12}(n-s)x_{2}(s) \\ &{}-\gamma_{1} x_{1}(k) \sum_{s=-\infty }^{n}f_{12}(n-s)x_{2}(s) \Biggr\} , \end{aligned}\\& \begin{aligned}[b] x_{2}(k+1)={}& x_{2}(k)\exp \Biggl\{ K_{2}- \beta_{21} \sum_{s=-\infty }^{n}K_{21}(n-s)x_{1}(s) -\alpha_{2}x_{2}(k) \\ &{}-\gamma_{2} x_{2}(k)\sum_{s=-\infty }^{n}f_{21}(n-s)x_{1}(s) \Biggr\} , \end{aligned} \end{aligned}$$
(1.1)

together with the initial conditions

$$\begin{aligned} x_{i}(s)=\phi_{i}(s)\geq0,\qquad x_{i}(0)>0, \qquad s= \ldots, -k, -k+1,\ldots, -2, -1,\qquad i=1,2, \end{aligned}$$
(1.2)

where the coefficients \(K_{i}, \alpha_{i}\), \(\beta_{ij}\), and \(\gamma_{i}, i,j=1,2 \), are all positive constants, \(\sum_{j=1}^{+\infty }K_{ij}(n)=1\), and \(\sum_{j=1}^{+\infty}f_{ij}(n)=1\).

During the last decades, many scholars proposed and studied the competitive system with the effect of toxic substances, and numerous excellent results have been obtained; see [1–34] and the references therein.

The main motivation for this work comes from a paper by Chen, Xie, and Wang [6], where they studied the stability property of the following competition model of plankton allelopathy with infinite delay:

$$\begin{aligned} \begin{aligned} \dot{x}_{1}(t)={}& x_{1}(t) \biggl[K_{1}-\alpha_{1} x_{1}(t)- \beta_{12} \int_{-\infty }^{t}K_{12}(s)x_{2}(t-s) \,ds \\ &{}-\gamma_{1} x_{1}(t) \int_{-\infty }^{t}f_{12}(s)x_{2}(t-s) \,ds \biggr], \\ \dot{x}_{2}(t)={}& x_{2}(t) \biggl[K_{2}- \beta_{21} \int_{-\infty }^{t}K_{21}(s)x_{1}(t-s) \,ds-\alpha_{2}x_{2}(t) \\ &{}-\gamma_{2} x_{2}(t) \int_{-\infty }^{t}f_{21}(s)x_{1}(t-s) \,ds \biggr]. \end{aligned} \end{aligned}$$
(1.3)

In [6], it was shown that if the coefficients satisfy the inequality

$$\begin{aligned} \frac{\alpha_{1}}{\beta_{21}}>\frac{K_{1}}{K_{2}}>\frac{\beta _{12}}{\alpha_{2}}, \end{aligned}$$
(1.4)

then \(x_{1}(t)\rightarrow x_{1}^{*}\) and \(x_{2}(t)\rightarrow x_{2}^{*}\) as \(t \rightarrow+\infty\).

Its well known that discrete-time models governed by difference equations are more appropriate than the continuous ones when the populations have nonoverlapping generations. By applying the idea of Chen [14] we could establish the corresponding discrete-type competition system (1.1). For system (1.1), we may conjecture that under assumption (1.4), the system can admit a unique globally attractive positive equilibrium. Unfortunately, this may not be true. Indeed, for the most simple single-species model, that is, the continuous logistic model

$$\dot{x}=x(a-bx), $$

the system admits a unique positive equilibrium, which is globally attractive, whereas for the discrete model

$$x(k+1)=x(k)\exp \bigl\{ a-bx(k) \bigr\} , $$

to ensure that the model admits a unique positive equilibrium, some additional restriction on the coefficients is needed; otherwise, the system may admit chaotic behavior, which could not be observed in the continuous-time case. Also, in the study of the stability property of the mutualism model, Yang, Xie, and Chen [35] showed that some additional condition should be added to ensure the global stability of the system. Hence, it becomes an interesting and challenging task to investigate the stability property of system (1.1).

The aim of this paper is to obtain a set of sufficient conditions that ensure the global attractivity of system (1.1). More precisely, we prove the following result.

Theorem 1.1

Assume that (1.4) holds and that \(K_{i}\leq1, i=1, 2\). Then the unique interior equilibrium \(E^{*}(x_{1}^{*},x_{2}^{*})\) of system (1.1) is globally attractive, that is,

$$\lim_{k\rightarrow+\infty}x_{i}(k)=x_{i}^{*},\quad i=1,2. $$

We will prove this theorem in the next section.

2 Proof of the main result

The interior positive equilibrium \(E^{*}(x_{1}^{*},x_{2}^{*})\) of system (1.1) satisfies the following equations:

$$ \textstyle\begin{cases} K_{1}-\alpha_{1}x_{1}-\beta_{12}x_{2}-\gamma_{1}x_{1}x_{2}=0,\\ K_{2}-\alpha_{2}x_{2}-\beta_{21}x_{1}-\gamma_{2}x_{1}x_{2}=0. \end{cases} $$
(2.1)

Concerning with the positive solution of system (2.1), similarly to the analysis of Lemma 2.1 in [1], we have the following:

Lemma 2.1

If (1.4) holds, then system (1.1) has a unique interior positive equilibrium \(E^{*}(x_{1}^{*},x_{2}^{*})\).

Lemma 2.2

[36]

Let \(f(u)=u\exp(\alpha-\beta u)\), where α and β are positive constants. Then \(f(u)\) is nondecreasing for \(u\in(0,\frac{1}{\beta}]\).

Lemma 2.3

[36]

Assume that a sequence \(\{u(k) \}\) satisfies

$$u(k+1)=u(k)\exp \bigl(\alpha-\beta u(k) \bigr),\quad k=1, 2,\ldots, $$

where α and β are positive constants, and \(u(0)>0\). Then:

  1. (i)

    if \(\alpha<2\), then \(\lim_{k\rightarrow+\infty}{u(k)}=\frac{\alpha}{\beta}\);

  2. (ii)

    if \(\alpha\leq1\), then \(u(k)\leq\frac{1}{\beta},k=2,3,\ldots\) .

Lemma 2.4

[37]

Suppose that functions \(f,g:Z_{+}\times[0,\infty)\rightarrow[0,\infty)\) satisfy \(f(k,x)\leq g(k,x)\ (f(k,x)\geq g(k,x))\) for \(k\in Z_{+}\) and \(x\in[0,\infty)\) and that \(g(k,x)\) is nondecreasing with respect to x. Suppose that \(\{x(k) \}\) and \(\{ u(k) \}\) are nonnegative solutions of the difference equations

$$x(k+1)=f \bigl(k,x(k) \bigr),\qquad u(k+1)=g \bigl(k,u(k) \bigr), $$

respectively, and \(x(0)\leq u(0)\ (x(0)\geq u(0))\). Then

$$x(k)\leq u(k)\qquad (x(k)\geq u(k))\quad \textit{for all } k\geq0. $$

Lemma 2.5

[14]

Let \(x:Z\rightarrow R\) be a nonnegative bounded sequence, and let \(H: N\rightarrow R\) be a nonnegative sequence such that \(\sum_{n=0}^{\infty}H(n)=1\). Then

$$\begin{aligned} \liminf_{n\rightarrow+\infty}x(n) \leq& \liminf_{n\rightarrow+\infty}\sum _{s=-\infty }^{n}H(n-s)x(s) \\ \leq&\limsup_{n\rightarrow+\infty}\sum_{s=-\infty }^{n}H(n-s)x(s) \leq\limsup_{n\rightarrow+\infty}x(n). \end{aligned}$$

Lemma 2.6

Let \(f(x)=\frac{a-bx}{c+dx}\), \(x>0\), be the strictly decreasing function of x, where \(a, b, c, d\) are positive constants.

Proof

Since

$$f^{'}(x)=-\frac{ad+bc}{(c+dx)^{2}}>0, $$

the conclusion of Lemma 2.6 immediately follows. □

Now we are in the position to prove the main result of this paper.

Proof of Theorem 1.1

Let \((x_{1}(k),x_{2}(k) )\) be an arbitrary solution of system (1.1) with initial condition (1.2). Denote

$$U_{i}=\limsup_{k\rightarrow+\infty}{x_{i}(k)},\qquad V_{i}=\liminf_{k\rightarrow+\infty}{x_{i}(k)},\quad i=1, 2. $$

We claim that \(U_{1}=V_{1}=x_{1}^{*}\) and \(U_{2}=V_{2}=x_{2}^{*}\).

Condition (1.4) implies that there exists a small enough positive constant \(\varepsilon>0\) such that

$$\begin{aligned} \frac{K_{1}-\beta_{12}(\frac{K_{2}}{\alpha_{2}}+\varepsilon)}{\alpha _{1}+\gamma_{1}(\frac{K_{2}}{\alpha_{2}}+\varepsilon)}-\varepsilon &>0, \end{aligned}$$
(2.2)
$$\begin{aligned} \frac{K_{2}-\beta_{21}(\frac{K_{1}}{\alpha_{1}}+\varepsilon)}{\alpha _{2}+\gamma_{2}(\frac{K_{1}}{\alpha_{1}}+\varepsilon)}-\varepsilon &>0. \end{aligned}$$
(2.3)

By the first equation of system (1.1) we have

$$\begin{aligned} x_{1}(k+1)\leq x_{1}(k)\exp \bigl\{ K_{1}- \alpha_{1} x_{1}(k) \bigr\} . \end{aligned}$$
(2.4)

Consider the following auxiliary equation:

$$\begin{aligned} u(k+1)=u(k)\exp \bigl\{ K_{1}-\alpha_{1}u(k) \bigr\} ,\quad k=0, 1, 2,\ldots. \end{aligned}$$
(2.5)

Because of \(K_{1}\leq1\), according to (ii) of Lemma 2.3, we obtain \(u(k)\leq\frac{1}{\alpha_{1}}\) for all \(k\geq2\), where \(u(k)\) is an arbitrary positive solution of (2.5) with initial value \(u(0)>0\). By Lemma 2.2, \(f(u)=u\exp(K_{1}-\alpha_{1}u)\) is nondecreasing for \(u\in(0,\frac{1}{\alpha_{1}}]\). According to Lemma 2.4, we obtain \(x_{1}(k)\leq u(k)\) for all \(k\geq2\), where \(u(k)\) is the solution of (2.5) with initial value \(u(2)= x(2)\). According to (i) of Lemma 2.3, we obtain

$$\begin{aligned} U_{1}=\limsup_{k\rightarrow+\infty}{x_{1}(k)}\leq\lim _{k\rightarrow+\infty}{u(k)}=\frac{K_{1}}{\alpha_{1}}. \end{aligned}$$
(2.6)

From (2.6) and Lemma 2.5 we have

$$\begin{aligned} &\limsup_{k\rightarrow+\infty} \sum_{s=-\infty }^{k}K_{21}(k-s)x_{1}(s) \leq\limsup_{k\rightarrow+\infty }{x_{1}(k)}\leq\frac{K_{1}}{\alpha_{1}}, \end{aligned}$$
(2.7)
$$\begin{aligned} &\limsup_{k\rightarrow+\infty}\sum_{s=-\infty }^{k}f_{21}(k-s)x_{1}(s) \leq\limsup_{k\rightarrow+\infty }{x_{1}(k)}\leq\frac{K_{1}}{\alpha_{1}}. \end{aligned}$$
(2.8)

Hence, for \(\varepsilon>0\) defined by (2.2)-(2.3), it follows from (2.6)-(2.8) that there exists \(k_{1}>2\) such that

$$\begin{aligned} & x_{1}(k)< \frac{K_{1}}{\alpha_{1}}+\varepsilon\stackrel{ \mathrm {def}}{=}M_{1}^{(1)} \quad\text{for } k>k_{1}, \\ &\sum_{s=-\infty}^{k}K_{21}(k-s)x_{1}(s) < \frac{K_{1}}{\alpha _{1}}+\varepsilon\stackrel{\mathrm{def}}{=}M_{1}^{(1)}\quad \text{for } k>k_{1}, \\ &\sum_{s=-\infty}^{k}f_{21}(k-s)x_{1}(s) < \frac{K_{1}}{\alpha _{1}}+\varepsilon\stackrel{\mathrm{def}}{=}M_{1}^{(1)} \quad\text{for } k>k_{1}. \end{aligned}$$
(2.9)

From the second equation of system (1.1) we have

$$\begin{aligned} x_{2}(k+1)\leq x_{2}(k)\exp \bigl\{ K_{2}- \alpha_{2}x_{2}(k) \bigr\} . \end{aligned}$$
(2.10)

Similarly to the analysis of (2.4)-(2.9), for the same \(\varepsilon >0\), it follows from the second equation of system (1.1) that there exists \(k_{2}>k_{1}\) such that

$$\begin{aligned} & x_{2}(k)< \frac{K_{2}}{\alpha_{2}}+\varepsilon\stackrel{\mathrm {def}}{=}M_{2}^{(1)} \quad\text{for } k>k_{2}, \\ &\sum_{s=-\infty}^{k}K_{12}(k-s)x_{2}(s) < \frac{K_{2}}{\alpha _{2}}+\varepsilon\stackrel{\mathrm{def}}{=}M_{2}^{(1)}\quad \text{for } k>k_{2}, \\ &\sum_{s=-\infty}^{k}f_{12}(k-s)x_{2}(s) < \frac{K_{2}}{\alpha _{2}}+\varepsilon\stackrel{\mathrm{def}}{=}M_{2}^{(1)} \quad\text{for } k>k_{2}. \end{aligned}$$
(2.11)

Inequalities (2.11), together with the first equation of system (1.1), show that, for \(k>k_{2}\),

$$\begin{aligned} x_{1}(k+1)={}& x_{1}(k)\exp \Biggl\{ K_{1}-\alpha_{1} x_{1}(k)-\beta_{12} \sum_{s=-\infty}^{n}K_{12}(n-s)x_{2}(s) \\ &{}-\gamma_{1} x_{1}(k) \sum_{s=-\infty }^{n}f_{12}(n-s)x_{2}(s) \Biggr\} \\ \geq{}&x_{1}(k) \exp \bigl\{ K_{1}-\alpha_{1} x_{1}(k)-\beta_{12}M_{2}^{(1)} - \gamma_{1} x_{1}(k)M_{2}^{(1)} \bigr\} . \end{aligned}$$
(2.12)

Inequality (2.2) shows that, under assumption (1.4), for the same \(\varepsilon>0\), we have \(0< K_{1}-\beta_{12}M_{2}^{(1)} <K_{1}\leq1\). Thus, similarly to the analysis of (2.4)-(2.6), we obtain

$$\begin{aligned} \liminf_{k\rightarrow+\infty}x_{1}(k)\geq \frac{K_{1}-\beta _{12}M_{2}^{(1)}}{\alpha_{1}+\gamma_{1}M_{2}^{(1)}}. \end{aligned}$$
(2.13)

From (2.13) and Lemma 2.5 we have

$$\begin{aligned} &\liminf_{k\rightarrow+\infty} \sum_{s=-\infty }^{k}K_{21}(k-s)x_{1}(s) \geq\liminf_{k\rightarrow+\infty }{x_{1}(k)}\geq\frac{K_{1}-\beta_{12}M_{2}^{(1)}}{\alpha_{1}+\gamma _{1}M_{2}^{(1)}}, \end{aligned}$$
(2.14)
$$\begin{aligned} &\liminf_{k\rightarrow+\infty}\sum_{s=-\infty }^{k}f_{21}(k-s)x_{1}(s) \geq\liminf_{k\rightarrow+\infty }{x_{1}(k)}\geq\frac{K_{1}-\beta_{12}M_{2}^{(1)}}{\alpha_{1}+\gamma _{1}M_{2}^{(1)}}, \end{aligned}$$
(2.15)

that is, for \(\varepsilon>0\) defined by (2.2), there exists \(k_{3}>k_{2}\) such that

$$\begin{aligned} &x_{1}(k)>\frac{K_{1}-\beta_{12}M_{2}^{(1)}}{\alpha_{1}+\gamma _{1}M_{2}^{(1)}}-\varepsilon\stackrel{ \mathrm{def}}{=}m_{1}^{(1)}>0 \quad\text{for } k>k_{3}, \\ &\sum_{s=-\infty}^{k}K_{21}(k-s)x_{1}(s)> \frac{K_{1}-\beta _{12}M_{2}^{(1)}}{\alpha_{1}+\gamma_{1}M_{2}^{(1)}}-\varepsilon\stackrel {\mathrm{def}}{=}m_{1}^{(1)}>0 \quad\text{for } k>k_{3}, \\ &\sum_{s=-\infty}^{k}f_{21}(k-s)x_{1}(s) >\frac{K_{1}-\beta _{12}M_{2}^{(1)}}{\alpha_{1}+\gamma_{1}M_{2}^{(1)}}-\varepsilon\stackrel {\mathrm{def}}{=}m_{1}^{(1)}>0 \quad\text{for } k>k_{3}. \end{aligned}$$
(2.16)

It follows from (2.9) and the second equation of system (1.1) that

$$\begin{aligned} x_{2}(k+1)={}& x_{2}(k)\exp \Biggl\{ K_{2}-\beta_{21} \sum_{s=-\infty }^{n}K_{21}(n-s)x_{1}(s) -\alpha_{2}x_{2}(k) \\ &{}-\gamma_{2} x_{2}(k)\sum_{s=-\infty }^{n}f_{21}(n-s)x_{1}(s) \Biggr\} \\ \geq{}& x_{2}(k)\exp \bigl\{ K_{2}-\beta_{21}M_{1}^{(1)} -\alpha_{2}x_{2}(k) -\gamma_{2} x_{2}(k)M_{1}^{(1)} \bigr\} . \end{aligned}$$
(2.17)

From (2.17), similarly to the analysis of (2.12)-(2.16), for \(\varepsilon>0\) defined by (2.2), there exists \(k_{4}>k_{3}\) such that

$$\begin{aligned} & x_{2}(k)>\frac{K_{2}-\beta_{21}M_{1}^{(1)}}{\alpha_{2}+\gamma _{2}M_{1}^{(1)}}-\varepsilon\stackrel{ \mathrm{def}}{=}m_{2}^{(1)}>0 \quad\text{for } k>k_{4}, \\ &\sum_{s=-\infty}^{k}K_{12}(k-s)x_{2}(s)> \frac{K_{2}-\beta _{21}M_{1}^{(1)}}{\alpha_{2}+\gamma_{2}M_{1}^{(1)}}-\varepsilon\stackrel {\mathrm{def}}{=}m_{2}^{(1)}>0 \quad\text{for } k>k_{4}, \\ &\sum_{s=-\infty}^{k}f_{12}(k-s)x_{2}(s) >\frac{K_{2}-\beta _{21}M_{1}^{(1)}}{\alpha_{2}+\gamma_{2}M_{1}^{(1)}}-\varepsilon\stackrel {\mathrm{def}}{=}m_{2}^{(1)}>0 \quad\text{for } k>k_{4}. \end{aligned}$$
(2.18)

From (2.18) and the first equation of system (1.1) we have

$$\begin{aligned} x_{1}(k+1)={}& x_{1}(k)\exp \Biggl\{ K_{1}-\alpha_{1} x_{1}(k)-\beta_{12} \sum_{s=-\infty}^{n}K_{12}(n-s)x_{2}(s) \\ &{}-\gamma_{1} x_{1}(k) \sum_{s=-\infty }^{n}f_{12}(n-s)x_{2}(s) \Biggr\} \\ \leq{}& x_{1}(k) \exp \bigl\{ K_{1}-\alpha_{1} x_{1}(k)-\beta_{12} m_{2}^{(1)}- \gamma_{1} x_{1}(k) m_{2}^{(1)} \bigr\} . \end{aligned}$$
(2.19)

It follows from (2.2) and (2.18) that

$$\begin{aligned} 1\geq K_{1}\geq K_{1}-\beta_{12}m_{2}^{(1)}>K_{1}- \beta_{12}M_{2}^{(1)}>0. \end{aligned}$$
(2.20)

Therefore, similarly to the analysis of (2.4)-(2.6), we have

$$\begin{aligned} \limsup_{k\rightarrow+\infty}x_{1}(k)\leq \frac{K_{1}-\beta _{12}m_{2}^{(1)}}{\alpha_{1}+\gamma_{1}m_{2}^{(1)}}. \end{aligned}$$
(2.21)

From (2.21) and Lemma 2.5 we have

$$\begin{aligned} &\limsup_{k\rightarrow+\infty} \sum_{s=-\infty }^{k}K_{21}(k-s)x_{1}(s) \leq\limsup_{k\rightarrow+\infty }{x_{1}(k)}\leq\frac{K_{1}-\beta_{12}m_{2}^{(1)}}{\alpha_{1}+\gamma _{1}m_{2}^{(1)}}, \end{aligned}$$
(2.22)
$$\begin{aligned} &\limsup_{k\rightarrow+\infty}\sum_{s=-\infty }^{k}f_{21}(k-s)x_{1}(s) \leq\limsup_{k\rightarrow+\infty }{x_{1}(k)}\leq\frac{K_{1}-\beta_{12}m_{2}^{(1)}}{\alpha_{1}+\gamma _{1}m_{2}^{(1)}}. \end{aligned}$$
(2.23)

Hence, for \(\varepsilon>0\) defined by (2.2)-(2.3), it follows from (2.21)-(2.23) that there exists \(k_{5}>k_{4}\) such that

$$\begin{aligned} &x_{1}(k)< \frac{K_{1}-\beta_{12}m_{2}^{(1)}}{\alpha_{1}+\gamma _{1}m_{2}^{(1)}}+\frac{\varepsilon}{2} \stackrel{\mathrm {def}}{=}M_{1}^{(2)} \quad\text{for } k>k_{5}, \\ &\sum_{s=-\infty}^{k}K_{21}(k-s)x_{1}(s) < \frac{K_{1}-\beta _{12}m_{2}^{(1)}}{\alpha_{1}+\gamma_{1}m_{2}^{(1)}}+\frac{\varepsilon }{2}\stackrel{\mathrm{def}}{=}M_{1}^{(2)}\quad \text{for } k>k_{5}, \\ &\sum_{s=-\infty}^{k}f_{21}(k-s)x_{1}(s) < \frac{K_{1}-\beta _{12}m_{2}^{(1)}}{\alpha_{1}+\gamma_{1}m_{2}^{(1)}}+\frac{\varepsilon }{2}\stackrel{\mathrm{def}}{=}M_{1}^{(2)} \quad\text{for } k>k_{5}. \end{aligned}$$
(2.24)

It follows from the second equation of system (1.1) that

$$\begin{aligned} x_{2}(k+1)={}& x_{2}(k)\exp \Biggl\{ K_{2}-\alpha_{2} x_{2}(k)-\beta_{21} \sum _{s=-\infty}^{n}K_{21}(n-s)x_{1}(s) \\ &{}-\gamma_{2} x_{2}(k) \sum_{s=-\infty }^{n}f_{21}(n-s)x_{1}(s) \Biggr\} \\ \leq{}& x_{2}(k) \exp \bigl\{ K_{2}-\alpha_{2} x_{2}(k)-\beta_{21} m_{1}^{(1)}- \gamma_{1} x_{2}(k) m_{1}^{(1)} \bigr\} . \end{aligned}$$
(2.25)

Similarly to the analysis of (2.19)-(2.24), there exists \(k_{6}>k_{5}\) such that

$$\begin{aligned} & x_{2}(k)< \frac{K_{2}-\beta_{21}m_{1}^{(1)}}{\alpha_{2}+\gamma _{2}m_{1}^{(1)}}+\frac{\varepsilon}{2}\stackrel{ \mathrm {def}}{=}M_{2}^{(2)} \quad\text{for } k>k_{6}, \\ &\sum_{s=-\infty}^{k}K_{12}(k-s)x_{2}(s) < \frac{K_{2}-\beta _{21}m_{1}^{(1)}}{\alpha_{2}+\gamma_{2}m_{1}^{(1)}}+\frac{\varepsilon }{2}\stackrel{\mathrm{def}}{=}M_{2}^{(2)} \quad\text{for } k>k_{6}, \\ &\sum_{s=-\infty}^{k}f_{12}(k-s)x_{2}(s) < \frac{K_{2}-\beta _{21}m_{1}^{(1)}}{\alpha_{2}+\gamma_{2}m_{1}^{(1)}}+\frac{\varepsilon }{2}\stackrel{\mathrm{def}}{=}M_{2}^{(2)} \quad\text{for } k>k_{6}. \end{aligned}$$
(2.26)

Inequalities (2.26), together with the first equation of system (1.1), imply

$$\begin{aligned} x_{1}(k+1)={}& x_{1}(k)\exp \Biggl\{ K_{1}-\alpha_{1} x_{1}(k)-\beta_{12} \sum_{s=-\infty}^{n}K_{12}(n-s)x_{2}(s) \\ &{}-\gamma_{1} x_{1}(k) \sum_{s=-\infty }^{n}f_{12}(n-s)x_{2}(s) \Biggr\} \\ \geq{}&x_{1}(k) \exp \bigl\{ K_{1}-\alpha_{1} x_{1}(k)-\beta_{12}M_{2}^{(2)} - \gamma_{1} x_{1}(k)M_{2}^{(2)} \bigr\} . \end{aligned}$$
(2.27)

Inequality (2.2) shows that, under assumption (1.4), for the same \(\varepsilon>0\), we have \(0< K_{1}-\beta_{12}M_{2}^{(2)} <K_{1}-\beta_{12}M_{2}^{(1)} <K_{1}\leq 1\). Thus, similarly to the analysis of (2.4)-(2.6), we obtain

$$\begin{aligned} \liminf_{k\rightarrow+\infty}x_{1}(k)\geq \frac{K_{1}-\beta _{12}M_{2}^{(2)}}{\alpha_{1}+\gamma_{1}M_{2}^{(2)}}. \end{aligned}$$
(2.28)

From (2.28) and Lemma 2.5 we have

$$\begin{aligned} &\liminf_{k\rightarrow+\infty} \sum_{s=-\infty }^{k}K_{21}(k-s)x_{1}(s) \geq\liminf_{k\rightarrow+\infty }{x_{1}(k)}\geq\frac{K_{1}-\beta_{12}M_{2}^{(2)}}{\alpha_{1}+\gamma _{1}M_{2}^{(2)}}, \end{aligned}$$
(2.29)
$$\begin{aligned} &\liminf_{k\rightarrow+\infty}\sum_{s=-\infty }^{k}f_{21}(k-s)x_{1}(s) \geq\liminf_{k\rightarrow+\infty }{x_{1}(k)}\geq\frac{K_{1}-\beta_{12}M_{2}^{(2)}}{\alpha_{1}+\gamma _{1}M_{2}^{(2)}}, \end{aligned}$$
(2.30)

that is, for \(\varepsilon>0\) defined by (2.2), there exists \(k_{7}>k_{6}\) such that

$$\begin{aligned} & x_{1}(k)>\frac{K_{1}-\beta_{12}M_{2}^{(2)}}{\alpha_{1}+\gamma _{1}M_{2}^{(2)}}-\frac{\varepsilon}{2} \stackrel{\mathrm {def}}{=}m_{1}^{(2)}>0 \quad\text{for } k>k_{7}, \\ &\sum_{s=-\infty}^{k}K_{21}(k-s)x_{1}(s)> \frac{K_{1}-\beta _{12}M_{2}^{(2)}}{\alpha_{1}+\gamma_{1}M_{2}^{(2)}}-\frac{\varepsilon}{2} \stackrel{\mathrm{def}}{=}m_{1}^{(2)}>0 \quad\text{for } k>k_{7}, \\ &\sum_{s=-\infty}^{k}f_{21}(k-s)x_{1}(s) >\frac{K_{1}-\beta _{12}M_{2}^{(2)}}{\alpha_{1}+\gamma_{1}M_{2}^{(2)}}-\frac{\varepsilon }{2}\stackrel{\mathrm{def}}{=}m_{1}^{(2)}>0 \quad\text{for } k>k_{7}. \end{aligned}$$
(2.31)

It follows from (2.24) and the second equation of system (1.1) that

$$\begin{aligned} x_{2}(k+1) \geq x_{2}(k)\exp \bigl\{ K_{2}-\beta_{21}M_{1}^{(2)} - \alpha_{2}x_{2}(k) -\gamma_{2} x_{2}(k)M_{1}^{(2)} \bigr\} . \end{aligned}$$
(2.32)

From (2.32), similarly to the analysis of (2.25)-(2.31), for \(\varepsilon>0\) defined by (2.2), there exists \(k_{8}>k_{7}\) such that

$$\begin{aligned} & x_{2}(k)>\frac{K_{2}-\beta_{21}M_{1}^{(2)}}{\alpha_{2}+\gamma _{2}M_{1}^{(2)}}-\frac{\varepsilon}{2} \stackrel{\mathrm{def}}{=}m_{2}^{(2)}>0\quad \text{for } k>k_{8}, \\ &\sum_{s=-\infty}^{k}K_{12}(k-s)x_{2}(s)> \frac{K_{2}-\beta _{21}M_{1}^{(2)}}{\alpha_{2}+\gamma_{2}M_{1}^{(2)}} -\frac{\varepsilon}{2}\stackrel{\mathrm{def}}{=}m_{2}^{(2)}>0 \quad\text{for } k>k_{8}, \\ &\sum_{s=-\infty}^{k}f_{12}(k-s)x_{2}(s) >\frac{K_{2}-\beta _{21}M_{1}^{(2)}}{\alpha_{2}+\gamma_{2}M_{1}^{(2)}}-\frac{\varepsilon }{2}\stackrel{\mathrm{def}}{=}m_{2}^{(2)}>0 \quad\text{for } k>k_{8}. \end{aligned}$$
(2.33)

Repeating the previous procedure, we get four sequences \(M_{i}^{(n)}, m_{i}^{(n)}, i=1,2, n=1,2,\ldots\) , such that, for \(n\geq2\),

$$\begin{aligned} \begin{aligned}&M_{1}^{(n)}=\frac{K_{1}-\beta_{12}m_{2}^{(n-1)}}{\alpha_{1}+\gamma _{1}m_{2}^{(n-1)}}+ \frac{\varepsilon}{n}, \\ &M_{2}^{(n)}=\frac{K_{2}-\beta_{21}m_{1}^{(n-1)}}{\alpha_{2}+\gamma _{2}m_{1}^{(n-1)}}+\frac{\varepsilon}{n}, \\ &m_{1}^{(n)}=\frac{K_{1}-\beta_{12}M_{2}^{(n)}}{\alpha_{1}+\gamma _{1}M_{2}^{(n)}}-\frac{\varepsilon}{n}, \\ &m_{2}^{(n)}=\frac{K_{2}-\beta_{21}M_{1}^{(n)}}{\alpha_{2}+\gamma _{2}M_{1}^{(n)}}-\frac{\varepsilon}{n}. \end{aligned} \end{aligned}$$
(2.34)

Using Lemma 2.6 and induction, similarly to the analysis on p. 7160 of [1], we can show that the sequences \(M_{i}^{(n)}, i=1,2\), are strictly decreasing and the sequences \(m_{i}^{(n)}, i=1,2\), are strictly increasing. Also,

$$m_{i}^{(n)}< x_{i}(t)< M_{i}^{(n)}\quad \text{for } t\geq T_{2n}, i=1,2. $$

Therefore,

$$\begin{aligned} \lim_{t\rightarrow+\infty}M_{i}^{(n)}= \overline{x}_{i},\qquad \lim_{t\rightarrow+\infty}m_{i}^{(n)}= \underline{x}_{i}, \quad i=1,2. \end{aligned}$$
(2.35)

Letting \(n\rightarrow+\infty\) in (2.34), we obtain

$$\begin{aligned} \begin{aligned}&\overline{x}_{1}=\frac{K_{1}-\beta_{12}\underline{x}_{2}}{\alpha _{1}+\gamma_{1}\underline{x}_{2}},\qquad \overline{x}_{2}=\frac{K_{2}-\beta_{21}\underline{x}_{1}}{\alpha _{2}+\gamma_{2}\underline{x}_{1}}, \\ &\underline{x}_{1}=\frac{K_{1}-\beta_{12}\overline{x}_{2}}{\alpha _{1}+\gamma_{1}\overline{x}_{2}}, \qquad\underline{x}_{2}= \frac{K_{2}-\beta_{21}\overline{x}_{1}}{\alpha _{2}+\gamma_{2}\overline{x}_{1}}. \end{aligned} \end{aligned}$$
(2.36)

Equalities (2.36) are equivalent to

$$\begin{aligned} \begin{aligned} & K_{1}-\alpha_{1}\overline{x}_{1}- \beta_{12}\underline{x}_{2}-\gamma _{1} \overline{x}_{1}\underline{x}_{2}=0 =K_{2}- \alpha_{2}\underline{x}_{2}-\beta_{21} \overline{x}_{1}-\gamma _{2}\overline{x}_{1} \underline{x}_{2}, \\ &K_{1}-\alpha_{1}\underline{x}_{1}- \beta_{12}\overline{x}_{2}-\gamma _{1} \underline{x}_{1}\overline{x}_{2}=0 =K_{2}- \alpha_{2}\overline{x}_{2}-\beta_{21} \underline{x}_{1}-\gamma _{2}\underline{x}_{1} \overline{x}_{2}. \end{aligned} \end{aligned}$$
(2.37)

Note that \((\overline{x}_{1},\underline{x}_{2})\) and \((\underline{x}_{1},\overline{x}_{2})\) are positive solutions of (2.1). By Lemma 2.1, system (2.1) has a unique positive solution \(E^{*}(x_{1}^{*},x_{2}^{*})\). Hence, we conclude that

$$\overline{x}_{i}=\underline{x}_{i}=x_{i}^{*},\quad i=1,2, $$

that is,

$$\lim_{t\rightarrow+\infty}x_{i}(k)=x_{i}^{*},\quad i=1,2. $$

Thus, the unique interior equilibrium \(E^{*}(x_{1}^{*},x_{2}^{*})\) is globally attractive. This completes the proof of Theorem 1.1. □

3 Example

In this section, we give an example to illustrate the feasibility of main result.

Example 3.1

Consider the system

$$\begin{aligned} \begin{aligned}{x}_{1}(n+1)={}&x_{1}(n)\exp \Biggl\{ 0.9 -0.6x_{1}(n)-0.4\sum^{\infty }_{s=0} \frac{e-1}{e}e^{-s}x_{2}(n-s) \\ &{}-0.1x_{1}(n)\sum^{\infty}_{s=0} \frac {e-1}{e}e^{-s}x_{2}(n-s) \Biggr\} , \\ {x}_{2}(n+1)={}&x_{2}(n)\exp \Biggl\{ 0.8 -0.8x_{2}(n)-0.3 \sum^{\infty }_{s=0}\frac{e-1}{e}e^{-s}x_{1}(n-s) \\ &{}-0.1x_{2}(n)\sum^{\infty}_{s=0} \frac {e-1}{e}e^{-s}x_{1}(n-s) \Biggr\} . \end{aligned} \end{aligned}$$
(3.1)

Corresponding to system (1.1), we have \(K_{1}=0.9, \alpha_{1}=0.6, \beta_{12}=0.4, \gamma_{1}=0.1, K_{2}=0.8, \alpha_{2}=0.8, \beta_{21}=0.3, \gamma_{2}=0.1\). Hence,

$$\frac{\alpha_{1}}{\beta_{21}}=\frac{0.6}{0.3}=2>\frac {K_{1}}{K_{2}}=\frac{9}{8}> \frac{\beta_{12}}{\alpha_{2}}=\frac{1}{2}. $$

Also,

$$K_{1}=0.9< 1,\qquad K_{2}=0.8< 1. $$

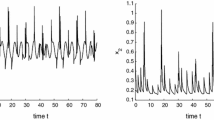
Hence, all the conditions of Theorem 1.1 are satisfied, and it follows from Theorem 1.1 that system (3.1) admits a unique globally attractive positive equilibrium. Figure 1 supports this assertion.

Figure 1
figure 1

Dynamic behaviors of the solution \(\pmb{{(x_{1}(n),x_{2}(n))}}\) of system ( 3.1 ), with the initial conditions \(\pmb{(x_{1}(s), x_{2}(s))= {(0.8,0.4)}, {(0.5,0.5)}, {(1.5,1.5)}}\) , \(\pmb{s=\ldots,-n,-n+1,\ldots,-1,0}\) .

Full size image

4 Conclusions

Stimulated by the work of Chen, Xie, and Wang [6], we propose a discrete competition model of plankton allelopathy with infinite deviating arguments. We focus our attention on the stability property of the positive equilibrium of the system since it represents the stable coexistence of the two species. With the additional restriction on the coefficients of the system \(K_{i}\leq1\), \(i=1, 2\), using the iterative method again, we finally proved that the positive equilibrium is globally attractive. Also, since the conditions of Theorem 1.1 are independent of delay and the coefficients of the toxic substance term, we can draw the conclusion that, under the assumptions of Theorem 1.1, the delay and toxic substance are harmless for the stability of the interior equilibrium of system (1.1).