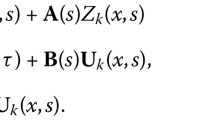1 Introduction

ILC is an intelligent control methodology for repetitive processes and tasks over a finite interval. ILC was first formulated mathematically by Arimoto et al. [1]. In the last three decades, it has been constantly studied and widely applied in various engineering practice, such as robotics, freeway traffic control, biomedical engineering, industrial process control, et cetera [2–9]. The major benefit of ILC are completely tracking feasible reference trajectories (or evolutional profiles) for that complex systems include uncertainty or nonlinear. It can be achieved only based on the input and output signals [10–14]. It is a truly model-free method motivated by the human trial-and-error experience in practice.

Despite ILC has been widely investigated for finite-dimensional systems, research work of related to spatial temporal processes are quiet few and even less using infinite-dimensional framework. Qu [15] proposed an iterative learning algorithm for boundary control of a stretched moving string, which is a pioneer work of extending the ILC framework to distributed parameter systems. Tension control system is studied in [16] by using the PD-type learning algorithm. Both P-type and D-type iterative learning algorithms based on the operator semigroup theory are designed for one-dimensional distributed parameter systems governed by parabolic PDEs in [17] and have been extended to a class of impulsive first-order distributed parameter systems in [18]. In [19], a steady state ILC scheme is proposed for single-input-single-output nonlinear PDEs. A D-type anticipatory ILC scheme is applied to the boundary control of a class of inhomogeneous heat equations in [20], where the heat flux at one side is the control input, whereas the temperature measurement at the other side is the control output. The learning convergence of ILC is guaranteed by transforming the inhomogeneous heat equation into its integral form and exploiting the properties of the embedded Jacobi theta functions. In [21], for applied convenience, using Crank-Nicholson discretization, ILC for a heat equation is designed, where the control allows the selection of a finite number of points for sensing and actuation. Recently, a frequency domain design and analysis framework of ILC for inhomogeneous distributed parameter systems are proposed in [22]. However, these works did not involve MIMO second-order hyperbolic distributed parameter systems.

The control problem of hyperbolic distributed parameter systems has been frequently encountered in many dynamic processes, for example, wave transportation, fluid dynamics, elastic vibration. In [23], a P-type ILC algorithm is proposed for a first-order hyperbolic distributed parameter system arising in a nonisothermal tubular reactor using a set of ordinary differential equations (ODEs) for model approximation. In addition, ILC problem is considered in [24] for a first-order strict hyperbolic distributed parameter system in a Hilbert space, where convergence conditions are given based on P-type algorithms and require the initial state value to be identical.

In this paper, an ILC problem is considered for a class of MIMO second-order hyperbolic distributed parameter systems with uncertainties. A P-type ILC scheme is introduced, and a sufficient condition for tracking error convergence in the sense of \(\mathbf{L}^{2}\) norm is given. The conditions do not require analytical solutions but only bounds and an appropriate norm space assumption for uncertainties of the system coefficients matrix. The proposed control scheme is the first work on extension to MIMO second-order hyperbolic distributed parameter systems with admissible initial state error. On the other hand, the convergence analysis is more complex than for finite-dimensional systems because it involves time, space, and the iterative domain. We do not simplify the infinite-dimensional systems to finite-dimensional systems or replace them with discrete-time equivalences (see [23]). Only in simulation, in order to illustrate the effectiveness of the presented ILC approach, we used the forward difference method to discretize the infinite-dimensional systems.

Notation

The superscript ‘T’ denotes the matrix transposition; I and 0 denote the identity matrix and zero matrix of appropriate dimensions, respectively. For an n-dimensional constant vector \({\mathbf{q}}=(q_{1},q_{2},\ldots ,q_{n})^{\mathrm{T}}\), its Euclid norm is defined as \(\|{\mathbf{q}}\|=\sqrt{\sum_{i=1}^{n}q_{i}^{2}}\). The spectrum norm of an \(n \times n\)-order square matrix A is defined as \(\|A\|=\sqrt{\lambda_{\mathrm{max}}(A^{\mathrm{T}}A)}\), where \(\lambda_{\mathrm{max}}(\cdot)\) (\(\lambda_{\mathrm{min}}(\cdot)\)) represents the maximum (minimum) eigenvalue. Let \({\mathbf{L}}^{2}(\Omega)\) be the set of measurable functions q defined on a bounded domain \(\Omega\in\mathbf{R}^{m} \) such that \(\|q\|_{{\mathbf{L}}^{2}}^{2}=\int_{\Omega}|q(x)|^{2}\, \mathrm{d}x<\infty\). If \(q_{i}(x)\in {\mathbf{L}}^{2}(\Omega)\) (\(i=1,2,\ldots,k\)) (for convenience, we denote \({\mathbf{L}}^{2}(\Omega)\) as \(\mathrm{L}^{2}(\Omega;\mathbf{R})\)), then we write \({\mathbf{q}}(x)=(q_{1}(x),\ldots,q_{n}(x))\in \mathbf{R}^{n}\cap{\mathbf{L}}^{2}(\Omega)\), and \(\|{\mathbf{q}}\|_{{\mathbf{L}}^{2}}^{2}=\int_{\Omega}{\mathbf{q}}^{\mathrm{T}}(x){\mathbf{q}}(x)\, \mathrm{d}x\). For \({\mathbf{w}}(x,t):\Omega \times[0,T]\rightarrow\mathbf{R}^{m}\) such that \({\mathbf{w}}(\cdot,t)\in \mathbf{R}^{m}\cap{\mathbf{L}}^{2}(\Omega)\), \(t\in[0,T]\), given \(\lambda >0\), its \(({\mathbf{L}}^{2};\lambda)\) norm is defined as

$$\Vert {\mathbf{w}}\Vert _{({\mathbf{L}}^{2};\lambda)} =\sup_{0\leqslant t\leqslant T}\bigl\{ \bigl\Vert {\mathbf{w}}(\cdot,t)\bigr\Vert ^{2}_{{\mathbf{L}}^{2}(\Omega)}e^{-\lambda t} \bigr\} . $$

2 ILC system description

We consider the following MIMO second-order hyperbolic distributed parameter system governed by partial differential equations:

$$ \left \{ \textstyle\begin{array}{l} \frac{\partial^{2}{\mathbf{q}}(x,t)}{\partial{t^{2}}} =D\triangle{\mathbf{q}}(x,t)-A(t)\frac{\partial{\mathbf{q}}(x,t)}{\partial{t}}+B(t){\mathbf{u}}(x,t), \\ {\mathbf{y}}(x,t) =C(t){\mathbf{q}}(x,t)+G(t){\mathbf{u}}(x,t), \end{array}\displaystyle \right . $$
(1)

where \((x,t)\in \Omega\times[0,T]\), that is, x, t denote the space and time variables, respectively, T is given, Ω is a bounded open subset of \(\mathbf{R}^{m}\) with smooth boundary ∂Ω, \({\mathbf{q}}(\cdot,\cdot)\in\mathbf{R}^{n}\), \({\mathbf{u}}(\cdot,\cdot)\in \mathbf{R}^{u}\), and \({\mathbf{y}}(\cdot,\cdot)\in\mathbf{R}^{y}\) are the state vector, input vector, and output vector of the systems, respectively, D is a bounded positive constant diagonal matrix, that is, \(D=\operatorname{diag}\{d_{1},d_{2},\ldots,d_{n}\}\), \(0< p_{i}\leqslant d_{i}<\infty\) (\(i=1,2,\ldots,n\)), and \(p_{i}\) are known, \(\triangle=\sum_{i=1}^{m}{\frac{\partial^{2}}{\partial x_{i}^{2}}}\) is the Laplacian operator defined over Ω, \(A(t)\) is a bounded and positive definite matrix for all \(t\in[0, T]\), and \(B(t)\), \(C(t)\), and \(G(t)\) are the bounded time-varying uncertain matrices of appropriate dimensions.

The initial and boundary conditions of (1) are given as

$$\begin{aligned}& {\mathbf{q}}(x,t)=0 ,\quad (x,t) \in\partial\Omega\times[0,T], \end{aligned}$$
(2)
$$\begin{aligned}& {\mathbf{q}}(x,0)=\varphi(x),\qquad \frac{\partial{\mathbf{q}}(x,t)}{\partial t} \bigg|_{t=0}= \psi(x). \end{aligned}$$
(3)

The control target is to determine an input vector \({\mathbf{u}}_{d}(x,t)\) such that the output vector \({\mathbf{y}}(x,t)\) is capable tracking a desired feasible trajectory \({\mathbf{y}}_{d}(x,t)\), namely seeking a corresponding desired input \({\mathbf{u}}_{d}(x,t)\) such that the actual output of the system (1),

$$ {\mathbf{y}}^{*}(x,t)=C(t){\mathbf{q}}_{d}(x,t)+G(t){ \mathbf{u}}_{d}(x,t), $$

approximates the desired output \({\mathbf{y}}_{d}(x,t)\). Because in the system there exists uncertainty, it is difficult to obtain a complete tracking, so we will gradually gain the control sequence \({{\mathbf{u}}_{k}(x,t)}\), using the ILC method, such that

$$\lim_{k \to\infty}{\mathbf{u}}_{k}(x,t)={ \mathbf{u}}_{d}(x,t), $$

where the kth iteration control input satisfies

$$ \left \{ \textstyle\begin{array}{l} \frac{\partial^{2}{\mathbf{q}}_{k}(x,t)}{\partial{t^{2}}} =D\triangle{\mathbf{q}}_{k}(x,t)-A(t)\frac{\partial{\mathbf{q}}_{k}(x,t)}{\partial{t}}+B(t){\mathbf{u}}_{k}(x,t), \\ {\mathbf{y}}_{k}(x,t) =C(t){\mathbf{q}}_{k}(x,t)+G(t){\mathbf{u}}_{k}(x,t). \end{array}\displaystyle \right . $$
(4)

Assumption 2.1

We assume that there exists a unique bounded classic solution \({\mathbf{q}}(x,t)\) for system (1). Thus, for a desired output \({\mathbf{y}}_{d}(x,t)\), there exists a unique \({\mathbf{u}}_{d}(x,t)\) such that

$$ \left \{ \textstyle\begin{array}{l} \frac{\partial^{2}{\mathbf{q}}_{d}(x,t)}{\partial{t}^{2}} =D\triangle{\mathbf{q}}_{d}(x,t)-A(t)\frac{\partial{\mathbf{q}}_{d}(x,t)}{\partial{t}}+B(t){\mathbf{u}}_{d}(x,t), \\ {\mathbf{y}}_{d}(x,t) =C(t){\mathbf{q}}_{d}(x,t)+G(t){\mathbf{u}}_{d}(x,t), \end{array}\displaystyle \right . $$
(5)

satisfying the initial and boundary conditions

$$\begin{aligned}& {\mathbf{q}}_{d}(x,t) =0,\quad (x,t) \in\partial\Omega \times[0,T], \end{aligned}$$
(6)
$$\begin{aligned}& {\mathbf{q}}_{d}(x,0)={\mathbf{q}}_{d0}(x),\qquad \frac{\partial{\mathbf{q}}_{d}(x,t)}{\partial t}\bigg|_{t=0}={\dot{\mathbf{q}}}_{d0}(x),\quad x\in \Omega, \end{aligned}$$
(7)

where \({\mathbf {q}}_{d}(x,t)\) is the desired state, and \(({\mathbf{q}}_{d0}(x),{\dot{\mathbf{q}}}_{d0}(x))\) is the initial value of the desired state.

Assumption 2.2

In a learning process, we assume the following boundary and initial conditions:

$$\begin{aligned}& {\mathbf{q}}_{k}(x,t)=0, \quad (x,t) \in \partial\Omega \times[0,T], \end{aligned}$$
(8)
$$\begin{aligned}& {\mathbf{q}}_{k}(x,0)=\varphi_{k}(x),\qquad \frac{\partial{\mathbf{q}}_{k}(x,0)}{\partial t}=\psi_{k}(x),\quad x\in\Omega. \end{aligned}$$
(9)

The functions \(\varphi_{k}(x)\), \(\psi_{k}(x)\) satisfy

$$ \biggl\Vert \frac{\partial\varphi_{k+1}}{\partial x}-\frac{\partial\varphi _{k}(x)}{\partial x}\biggr\Vert _{{\mathbf{L}^{2}(\Omega)}}^{2}\leqslant l_{1}\alpha^{k},\qquad \Vert \psi_{k+1}-\psi_{k}\Vert _{{\mathbf{L}^{2}(\Omega)}}^{2}\leqslant l_{2}\beta^{k}, $$
(10)

where \(l_{1}\), \(l_{2}\) are constants, and \(\alpha,\beta\in[0,1)\).

Remark 2.1

Assumption 2.1 is a necessary condition for ILC method. Assumption 2.2 means that, in the initial state, there may exist an error and the identical initial condition in ILC systems (4) is not required. On the other hand, from practical point of view, in iterations, the initial condition reset should be closer and closer to the initial value of the desired state, so condition (10) is reasonable.

3 ILC design and convergence analysis

In this paper, we employ the following P-type ILC law:

$$ {\mathbf{u}}_{k+1}(x,t)={\mathbf{u}}_{k}(x,t)+ \Gamma(t){\mathbf{e}}_{k}(x,t), $$
(11)

where \(\Gamma(t)\) is the learning gain.

For a brief presentation, let

$$\begin{aligned}& {\mathbf{e}}_{k+1}(x,t)={\mathbf{y}}_{d}(x,t)-{ \mathbf{y}}_{k+1}(x,t), \\& {\bar{\mathbf{q}}}_{k}(x,t)={\mathbf{q}}_{k+1}(x,t)-{ \mathbf{q}}_{k}(x,t), \\& {\bar{\mathbf{u}}}_{k}(x,t)={\mathbf{u}}_{k+1}(x,t)-{ \mathbf{u}}_{k}(x,t), \end{aligned}$$

where \({\mathbf{e}}_{k+1}(x,t)\) is the tracking error of the \((k+1)\)th iteration. Then the control target can be rewritten as

$$ \lim_{k \to\infty}\bigl\Vert {\mathbf{e}}_{k}( \cdot,t)\bigr\Vert _{\mathbf{L}^{2}(\Omega)}=0,\quad \forall t \in[0,T]. $$
(12)

Remark 3.1

The ILC law (11) is distributed, that is, it depends on both time and space. although many distributed systems require that only boundary control can be used as physical constraint, but distributed sensors/actuators can be effectively applied in recent developments in supporting material science and technologies [21], such as piezoelectric ceramics.

We need the following technical lemmas, which are widely used in the proof of the main theorem.

Lemma 3.1

([25])

Let \(A\in\mathbf{R}^{n\times m}\), \(B\in\mathbf{R}^{n\times l}\), \(\zeta\in\mathbf{R}^{ m}\), \(\eta\in \mathbf{R}^{l}\). Then we have

$$ \zeta^{\mathrm{T}}A^{\mathrm{T}}B\eta\leqslant \frac{1}{2}\bigl(\zeta^{\mathrm{T}}A^{\mathrm{T}}A\zeta+ \eta^{\mathrm{T}}B^{\mathrm{T}}B\eta\bigr). $$
(13)

Lemma 3.2

([13])

Let a nonnegative real series \(\{ a_{k}\}_{k=0}^{\infty}\) satisfy

$$ a_{k+1}\leqslant r a_{k}+z_{k}, $$
(14)

where \(0\leqslant r<1\) and \(\lim_{k\rightarrow\infty}z_{k}=0\). Then we have

$$ \lim_{k\rightarrow\infty}a_{k}=0. $$
(15)

Theorem 3.1

Consider the ILC updating law (11) applied to the repetitive system (1) under (2), (3) and satisfying Assumptions 2.1 and 2.2. If the gain matrix \(\Gamma(t)\) satisfies

$$ \bigl\Vert I-G(t)\Gamma(t)\bigr\Vert ^{2}\leqslant \rho\in[0,1),\quad 2\rho< 1, $$
(16)

then the tracking error converges to zero in the sense of \(\mathbf{L}_{2}\) norm for all \(t\in[0,T]\) as \(k\rightarrow\infty\), that is,

$$\begin{aligned} \lim_{k \to\infty}\bigl\Vert {\mathbf{e}}_{k}( \cdot,t)\bigr\Vert _{\mathbf{L}^{2}(\Omega)}=0,\quad \forall t \in[0,T]. \end{aligned}$$
(17)

Proof

According to the learning law (11), we have

$$\begin{aligned} {\mathbf{e}}_{k+1}(x,t) =&{\mathbf{e}}_{k}(x,t)-{ \mathbf{y}}_{k+1}(x,t)+{\mathbf{y}}_{k}(x,t) \\ =&{\mathbf{e}}_{k}(x,t)-G(t) \bigl({\mathbf{u}}_{k+1}(x,t)-{ \mathbf{u}}_{k}(x,t) \bigr)-C(t) \bigl({\mathbf{q}}_{k+1}(x,t)-{ \mathbf{q}}_{k}(x,t)\bigr) \\ =&\bigl(I-G(t)\Gamma(t)\bigr){\mathbf{e}}_{k}(x,t)+C(t) \bigl({ \mathbf{q}}_{k+1}(x,t)-{\mathbf{q}}_{k}(x,t)\bigr) \\ \triangleq&\hat{{\mathbf{e}}}_{k}(x,t)+\hat{{\mathbf{q}}}_{k}(x,t), \end{aligned}$$
(18)

where

$$\hat{{\mathbf{e}}}_{k}(x,t)\triangleq\bigl(I-G(t)\Gamma(t)\bigr){ \mathbf{e}}_{k}(x,t),\qquad \hat{{\mathbf{q}}}_{k}(x,t) \triangleq C(t) \bigl({\mathbf{q}}_{k+1}(x,t)-{\mathbf{q}}_{k}(x,t) \bigr). $$

Then, by Lemma 3.1 we have

$$\begin{aligned} {\mathbf{e}}_{k+1}^{\mathrm{T}}(x,t){\mathbf{e}}_{k+1}(x,t) =& \bigl(\hat{{\mathbf{e}}}^{T}_{k}(x,t)+\hat{{ \mathbf{q}}}^{T}_{k}(x,t)\bigr) \bigl(\hat{{ \mathbf{e}}}_{k}(x,t)+\hat{{\mathbf{q}}}_{k}(x,t)\bigr) \\ \leqslant&2\bigl[\hat{{\mathbf{e}}}^{T}_{k}(x,t)\hat{{ \mathbf{e}}}_{k}(x,t)+\hat{{\mathbf{q}}}^{T}_{k}(x,t) \hat{{\mathbf{q}}}_{k}(x,t)\bigr] \\ \leqslant&2\lambda_{G\Gamma}{\mathbf{e}}^{T}_{k}(x,t){ \mathbf{e}}_{k}(x,t)+2\lambda_{C}\bar{{\mathbf{q}}}^{T}_{k}(x,t) \bar{{\mathbf{q}}}_{k}(x,t), \end{aligned}$$
(19)

where

$$\lambda_{G\Gamma}=\max_{0\leqslant t\leqslant T}\bigl\{ \bigl\Vert I-G(t) \Gamma(t)\bigr\Vert ^{2}\bigr\} ,\qquad \lambda_{C}=\max _{0\leqslant t\leqslant T}\bigl\{ \bigl\Vert C(t)\bigr\Vert ^{2}\bigr\} . $$

From (4) and from

$$ \frac{\partial^{2}{\mathbf{q}}_{k+1}(x,t)}{\partial{t^{2}}} =D\triangle {\mathbf{q}}_{k+1}(x,t) -A(t)\frac{\partial{\mathbf{q}}_{k+1}(x,t)}{\partial t}+B(t){\mathbf{u}}_{k+1}(x,t) $$
(20)

we have

$$ \frac{\partial^{2}{\bar{\mathbf{q}}}_{k}(x,t)}{\partial{t^{2}}} =D\triangle {\bar{\mathbf{q}}}_{k}(x,t)-A(t) \frac{\partial{\bar{\mathbf{q}}}_{k}(x,t)}{\partial{t}}+B(t){\bar{\mathbf{u}}}_{k}(x,t). $$
(21)

We define

$$\frac{\partial^{2}{\bar{\mathbf{q}}}_{k}(x,t)}{\partial{t^{2}}}\triangleq \ddot{{\bar{\mathbf{q}}}}_{k}(x,t), \qquad \frac{\partial{\bar{\mathbf{q}}}_{k}(x,t)}{\partial{t}}\triangleq\dot{{\bar{\mathbf{q}}}}_{k}(x,t). $$

Then by (21) we obtain

$$\begin{aligned} 2 \int_{\Omega}\dot{{\bar{\mathbf{q}}}}_{k}^{\mathrm{T}}(x,t) \ddot{{\bar{\mathbf{q}}}}_{k}^{\mathrm{T}}(x,t)\,{\mathrm{d}}x =&2 \int_{\Omega}\dot{{\bar{\mathbf{q}}}}_{k}^{\mathrm{T}}(x,t) \bigl[D\triangle \bar{\mathbf{q}}_{k}(x,t)-A(t)\dot{\bar{\mathbf{q}}}_{k}(x,t) \\ &{}+B(t)\bar{\mathbf{u}}_{k}(x,t)\bigr]\,{\mathrm{d}}x \\ =&2 \int_{\Omega}\dot{{\bar{\mathbf{q}}}}_{k}^{\mathrm{T}}(x,t) D\triangle \bar{\mathbf{q}}_{k}(x,t)\,{\mathrm{d}}x \\ &{}-2 \int_{\Omega}\dot{{\bar{\mathbf{q}}}}_{k}^{\mathrm{T}}(x,t)A(t) \dot {{\bar{\mathbf{q}}}}_{k}(x,t)\,{\mathrm{d}}x \\ &{} +2 \int_{\Omega}\dot{{\bar{\mathbf{q}}}}_{k}^{\mathrm{T}}(x,t)B(t) \bar {\mathbf{u}}_{k}(x,t)\,{\mathrm{d}}x \\ \triangleq&\sum_{i=1}^{3} I_{i}, \end{aligned}$$
(22)

where

$$\begin{aligned}& I_{1}=2 \int_{\Omega}\dot{{\bar{\mathbf{q}}}}_{k}^{\mathrm{T}}(x,t)D \triangle \bar{\mathbf{q}}_{k}(x,t)\,{\mathrm{d}}x,\qquad I_{2}=-2 \int_{\Omega}\dot{{\bar{\mathbf{q}}}}_{k}^{\mathrm{T}}(x,t)A(t) \dot{{\bar{\mathbf{q}}}}_{k}(x,t)\,{\mathrm{d}}x, \\& I_{3}=2 \int_{\Omega}\dot{{\bar{\mathbf{q}}}}_{k}^{\mathrm{T}}(x,t)B(t) \bar{\mathbf{u}}_{k}(x,t)\,{\mathrm{d}}x. \end{aligned}$$

Note that

$$ 2 \int_{\Omega}\dot{{\bar{\mathbf{q}}}}_{k}^{\mathrm{T}}(x,t) \ddot{{\bar{\mathbf{q}}}}_{k}^{\mathrm{T}}(x,t)\,{\mathrm{d}}x= \frac{\mathrm{d}(\| \dot{{\bar{\mathbf{q}}}}_{k}(\cdot,t)\|^{2}_{\mathbf{L}^{2}(\Omega )})}{{\mathrm{d}}t}. $$
(23)

Using the boundary condition and noting that \(D=\operatorname{diag}\{ d_{1},d_{2},\ldots,d_{n}\}\), \(0< p_{i}\leqslant d_{i}<\infty\) (\(i=1,2,\ldots,n\)), and \(p_{i}\) are known, we have

$$\begin{aligned} I_{1} =&-2\sum_{i=1}^{n} \int_{\Omega}\nabla\dot{{\bar{\mathbf{q}}}}_{ki}^{\mathrm{T}}(x,t)d_{i} \nabla{{\bar{\mathbf{q}}}}_{ki}(x,t)\,{\mathrm{d}}x \\ \leqslant&-\lambda_{\mathrm{min}}(D)\frac{\mathrm{d}(\|\nabla\bar{\mathbf{q}}_{k}(\cdot,t)\|^{2}_{{\mathbf{L}^{2}(\Omega)}})}{\mathrm{d} t}. \end{aligned}$$
(24)

Meanwhile, because

$$ I_{2} \leqslant-2\lambda_{\mathrm{min}}(A)\bigl\Vert \dot{{\bar{\mathbf{q}}}}_{k}(\cdot ,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)}, $$
(25)

using Lemma 3.1 again for \(I_{3}\), we get

$$ I_{3} \leqslant\bigl\Vert \dot{{\bar{ \mathbf{q}}}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf {L}^{2}(\Omega)}+ \lambda_{B}\bigl\Vert {{\bar{\mathbf{u}}}}_{k}(\cdot,t) \bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)}. $$
(26)

So from (22) and (24)-(26) we obtain

$$\begin{aligned} \frac{\mathrm{d}(\Vert \dot{{\bar{\mathbf{q}}}}_{k}(\cdot,t)\Vert ^{2}_{\mathbf {L}^{2}(\Omega)})}{{\mathrm{d}}t} \leqslant&-\lambda_{\mathrm{min}}(D) \frac{\mathrm{d}\Vert \nabla\bar{\mathbf{q}}_{k}(\cdot,t)\Vert ^{2}_{{\mathbf{L}^{2}(\Omega)}}}{\mathrm{d} t}-2\lambda _{\mathrm{min}}(A)\bigl\Vert \dot{{\bar{ \mathbf{q}}}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf {L}^{2}(\Omega)} \\ &{}+\bigl\Vert \dot{{\bar{\mathbf{q}}}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega )}+\lambda_{B}\bigl\Vert {\bar{ \mathbf{u}}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)}, \end{aligned}$$
(27)

that is,

$$\begin{aligned}& \frac{\mathrm{d}(\Vert \dot{\bar{\mathbf{q}}}_{k}(\cdot,t)\Vert ^{2}_{\mathbf {L}^{2}(\Omega)}+\lambda_{\mathrm{min}}(D)\Vert \nabla\bar{\mathbf{q}}_{k}(\cdot ,t)\Vert ^{2}_{\mathbf{L}^{2}(\Omega)})}{{\mathrm{d}}t} \\& \quad \leqslant-2\lambda_{\mathrm{min}}(A)\bigl\Vert \dot{{\bar{ \mathbf{q}}}}_{k}(\cdot ,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)} + \bigl\Vert \dot{{\bar{\mathbf{q}}}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega )}+\lambda_{B}\bigl\Vert {\bar{ \mathbf{u}}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega )}. \end{aligned}$$

Because \(A(t)\) is positive definite matrix for all \(t\in[0,T]\), we get

$$\begin{aligned}& \frac{\mathrm{d}(\Vert \dot{\bar{\mathbf{q}}}_{k}(\cdot,t)\Vert ^{2}_{\mathbf {L}^{2}(\Omega)}+\lambda_{\mathrm{min}}(D)\Vert \nabla\bar{\mathbf{q}}_{k}(\cdot ,t)\Vert ^{2}_{\mathbf{L}^{2}(\Omega)})}{{\mathrm{d}}t} \\& \quad \leqslant\bigl\Vert \dot{{\bar{\mathbf{q}}}}_{k}(\cdot,t) \bigr\Vert ^{2}_{\mathbf {L}^{2}(\Omega)}+\lambda_{B}\bigl\Vert { \bar{\mathbf{u}}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf {L}^{2}(\Omega)} \\& \quad \leqslant\bigl(\bigl\Vert \dot{{\bar{\mathbf{q}}}}_{k}( \cdot,t)\bigr\Vert ^{2}_{\mathbf {L}^{2}(\Omega)}+\lambda_{\mathrm{min}}(D)\bigl\Vert \nabla\bar{\mathbf{q}}_{k}(\cdot ,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)}\bigr)+\lambda_{B}\bigl\Vert {\bar{ \mathbf{u}}}_{k}(\cdot ,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)}. \end{aligned}$$
(28)

By the Bellman-Gronwall inequality we have

$$\begin{aligned}& \bigl\Vert \dot{\bar{\mathbf{q}}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega )}+\lambda_{\mathrm{min}}(D)\bigl\Vert \nabla \bar{\mathbf{q}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf {L}^{2}(\Omega)} \\& \quad \leqslant\bigl(\bigl\Vert \dot{\bar{\mathbf{q}}}_{k}(\cdot,0) \bigr\Vert ^{2}_{\mathbf {L}^{2}(\Omega)} +\lambda_{\mathrm{min}}(D)\bigl\Vert \nabla\bar{\mathbf{q}}_{k}(\cdot,0)\bigr\Vert ^{2}_{\mathbf {L}^{2}(\Omega)} \bigr)e^{t}+\lambda_{B} \int_{0}^{t}e^{(t-s)}\bigl\Vert {\bar{ \mathbf{u}}}_{k}(\cdot,s)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)}\, \mathrm{d}s \\& \quad \leqslant\bigl(\lambda_{\mathrm{min}}(D)l_{1} \alpha^{k}+l_{2}\beta^{k}\bigr)e^{t}+ \lambda _{B} \int_{0}^{t}e^{(t-s)}\bigl\Vert {\bar{ \mathbf{u}}}_{k}(\cdot,s)\bigr\Vert ^{2}_{\mathbf {L}^{2}(\Omega)}\, \mathrm{d}s. \end{aligned}$$
(29)

Due to the Poincaré inequality, there exists a constant \(c_{0}=c_{0}(\Omega)\) such that

$$ \bigl\Vert \bar{\mathbf{q}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega )}\leqslant c_{0}\bigl\Vert \nabla\bar{ \mathbf{q}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)}. $$
(30)

Therefore, by (29) and (30) we have

$$\begin{aligned} \bigl\Vert \bar{\mathbf{q}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)} \leqslant& \frac{c_{0}}{\lambda_{\mathrm{min}}(D)}\bigl( \lambda_{\mathrm{min}}(D)l_{1}\alpha ^{k}+l_{2} \beta^{k}\bigr)e^{t} \\ &{}+\frac{c_{0}\lambda_{B}}{\lambda_{\mathrm{min}}(D)} \int_{0}^{t}e^{(t-s)}\bigl\Vert {\bar{ \mathbf{u}}}_{k}(\cdot,s)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)}\, \mathrm{d}s. \end{aligned}$$
(31)

Choosing a sufficiently large constant \(\lambda>1\) and multiplying both sides of (31) by \(e^{-\lambda t}\), we have

$$\begin{aligned} \bigl\Vert \bar{\mathbf{q}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)}e^{-\lambda t} \leqslant& \frac{c_{0}}{\lambda_{\mathrm{min}}(D)}\bigl( \lambda_{\mathrm{min}}(D)l_{1}\alpha ^{k}+l_{2} \beta^{k}\bigr)e^{-(\lambda-1)t} \\ &{}+\frac{c_{0}\lambda_{B}}{\lambda_{\mathrm{min}}(D)} \int_{0}^{t}e^{-(\lambda -1)(t-s)}\bigl\Vert {\bar{ \mathbf{u}}}_{k}(\cdot,s)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega )}e^{-\lambda s} \,\mathrm{d}s \\ \leqslant&\frac{c_{0}}{\lambda_{\mathrm{min}}(D)}\bigl(\lambda_{\mathrm{min} }(D)l_{1} \alpha^{k}+l_{2}\beta^{k}\bigr) \\ &{}+\frac{c_{0}\lambda_{B}}{\lambda_{\mathrm{min}}(D)}\Vert {\bar{\mathbf{u}}}_{k}\Vert _{(\mathbf{L}^{2};\lambda)} \int_{0}^{t}e^{-(\lambda-1)(t-s)}\,\mathrm{d}s \\ \leqslant&\frac{c_{0}}{\lambda_{\mathrm{min}}(D)}\bigl(\lambda_{\mathrm{min} }(D)l_{1} \alpha^{k}+l_{2}\beta^{k}\bigr) \\ &{}+\frac{c_{0}\lambda_{B}}{\lambda_{\mathrm{min}}(D)(\lambda-1)}\Vert {\bar {\mathbf{u}}}_{k}\Vert _{(\mathbf{L}^{2};\lambda)}. \end{aligned}$$
(32)

On the other hand, according to the P-type ILC law (11), we have

$$ \bigl\Vert u_{k+1}(\cdot,t)-u_{k}(\cdot,t) \bigr\Vert _{\mathbf{L}^{2}(\Omega)}^{2} \leqslant\lambda_{\mathrm{max}}\bigl( \Gamma^{T}(t)\Gamma(t)\bigr)\bigl\Vert e_{k}(\cdot,t)\bigr\Vert _{\mathbf{L}^{2}(\Omega)}^{2}. $$
(33)

Letting \(\lambda_{\Gamma}=\max_{0\leqslant t\leqslant T}\{\lambda_{\mathrm{max}}(\Gamma^{T}(t)\Gamma(t))\}\), we have

$$ \|u_{k+1}-u_{k}\|_{(\mathbf{L}^{2};\lambda)}\leqslant \lambda_{\Gamma}\|e_{k}\| _{(\mathbf{L}^{2};\lambda)} $$
(34)

and also

$$\begin{aligned} \bigl\Vert \bar{\mathbf{q}}_{k}(\cdot,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)}e^{-\lambda t} \leqslant&\frac{c_{0}}{\lambda_{\mathrm{min}}(D)}\bigl( \lambda_{\mathrm{min} }(D)l_{1}\alpha^{k}+l_{2} \beta^{k}\bigr) \\ &{}+\frac{c_{0}\lambda_{B}\lambda_{\Gamma}}{\lambda_{\mathrm{min} }(D)(\lambda-1)}\Vert {\bar{\mathbf{u}}}_{k}\Vert ^{2}_{(\mathbf{L}^{2};\lambda)}. \end{aligned}$$
(35)

From (18), (23), and (24) we have

$$\begin{aligned} \Vert {\mathbf{e}}_{k+1}\Vert _{(\mathbf{L}^{2};\lambda)} \leqslant& \biggl(2\lambda_{G\Gamma} +\frac{2c_{0}\lambda_{C}\lambda_{\Gamma}\lambda_{B}}{\lambda_{\mathrm{min} }(D)(\lambda-1)}\biggr)\Vert { \mathbf{e}}_{k}\Vert _{(\mathbf{L}^{2};\lambda)} \\ &{}+\frac{2 c_{0}\lambda_{C}}{\lambda_{\mathrm{min}}(D)}\bigl(\lambda_{\mathrm{min} }(D)l_{1} \alpha^{k}+l_{2}\beta^{k}\bigr). \end{aligned}$$
(36)

Then, by (16), we can select a suitable large λ such that

$$ \lambda>1\quad \text{and }\quad 2\lambda_{G\Gamma} + \frac{2c_{0}\lambda_{C}\lambda_{\Gamma}\lambda_{B}}{\lambda_{\mathrm{min} }(D)(\lambda-1)}< 1. $$
(37)

Let \(z_{k}=\frac{2 c_{0}\lambda_{C}}{\lambda_{\mathrm{min}}(D)}(\lambda_{\mathrm{min} }(D)l_{1}\alpha^{k}+l_{2}\beta^{k})\). Then by Lemma 3.2 and (36)-(37) we have

$$ \lim_{k\rightarrow\infty}\|{\mathbf{e}}_{k+1} \|_{(\mathbf{L}^{2};\lambda)}=0. $$
(38)

Finally, by the inequality

$$ \Vert {\mathbf{e}}_{k}\Vert _{(\mathbf{L}^{2};\lambda)} \leqslant\sup_{0\leqslant t\leqslant T}\bigl\Vert {\mathbf{e}}_{k}( \cdot,t)\bigr\Vert ^{2}_{\mathbf{L}^{2}(\Omega)} \leqslant\lambda^{T}\Vert { \mathbf{e}}_{k}\Vert _{(\mathbf{L}^{2};\lambda)} $$
(39)

we have the convergence

$$ \lim_{k\rightarrow\infty}\bigl\Vert {\mathbf{e}}_{k}( \cdot,t)\bigr\Vert _{\mathbf{L}^{2}(\Omega)}=0,\quad t\in[0,T]. $$
(40)

This completes the proof of Theorem 3.1. □

Remark 3.2

In Theorem 3.1, we must point out that (16) requires \(G(t)\) to be a nonsingular matrix (or regular matrix), that is, there exists a direct channel in between the output and input for systems (1). We will consider the case \(G(t)=0\) in the future.

4 Numerical simulations

In order to illustrate the effectiveness of the proposed ILC scheme, we give the following specific numerical example:

$$ \left \{ \textstyle\begin{array}{l} \frac{\partial{\mathbf{q}}(x,t)}{\partial{t}} =D\triangle{\mathbf{q}}(x,t)-A(t)\frac{\partial{\mathbf{q}}(x,t)}{\partial t}+B(t){\mathbf{u}}(x,t), \\ {\mathbf{y}}(x,t) =C(t){\mathbf{q}}(x,t)+G(t){\mathbf{u}}(x,t), \end{array}\displaystyle \right . $$
(41)

where

$$\begin{aligned}& {\mathbf{q}}(x,t)=\left [ \textstyle\begin{array}{@{}c@{}} q_{1}(x,t)\\ q_{2}(x,t) \end{array}\displaystyle \right ],\qquad { \mathbf{u}}(x,t)=\left [ \textstyle\begin{array}{@{}c@{}} u_{1}(x,t)\\ u_{2}(x,t) \end{array}\displaystyle \right ],\qquad { \mathbf{y}}(x,t)=\left [ \textstyle\begin{array}{@{}c@{}} y_{1}(x,t)\\ y_{2}(x,t) \end{array}\displaystyle \right ], \\& D=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 1&0\\ 0&1 \end{array}\displaystyle \right ],\qquad A(t)=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 1.5-e^{-5t}&0\\ 0&0.5 \end{array}\displaystyle \right ],\qquad B=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 1/3&0\\ 0.25&0.2 \end{array}\displaystyle \right ], \\& C=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.25&1\\ 0&0.25 \end{array}\displaystyle \right ],\qquad G=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 1&0.5\\ 0&1 \end{array}\displaystyle \right ],\qquad \Gamma=\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0.85&0\\ 0&0.9 \end{array}\displaystyle \right ], \end{aligned}$$

and \((x,t)\in[0,1]\times[0,1]\). The desired evolutionary profile vector is given as the iterative learning:

$${\mathbf{y}}_{d}(x,t)=\bigl(y_{d1}(x,t),y_{d2}(x,t) \bigr)=\bigl(-2\bigl(e^{-2t}-1\bigr)\sin\pi x, -4\sin\pi t\sin2\pi x \bigr). $$

Both the initial state profiles are \(\varphi_{1}(x)=0.02x\), \(\varphi_{2}(x)=0.01\sin x\), so \(\psi_{1}(x)=\psi_{2}(x)=0\), and the input value of the controlling at the beginning of learning are set to be 0 and \(\alpha=\beta=0\) in (10). Then the condition of Theorem 3.1 is satisfied. that is, \(\|I-G\Gamma\|=0.15<0.5\). We use the following forward difference method:

$$\begin{aligned}& \frac{\partial^{2}{\mathbf{q}}_{k}(x,t)}{\partial{x^{2}}} = \frac{{\mathbf{q}}(x_{i-1},t_{j}) -2{\mathbf{q}}(x_{i},t_{j})+{\mathbf{q}}(x_{i+1},t_{j})}{h^{2}}, \\& \frac{\partial^{2}{\mathbf{q}}_{k}(x,t)}{\partial{t^{2}}} = \frac{{\mathbf{q}}(x_{i},t_{j-1}) -2{\mathbf{q}}(x_{i},t_{j})+{\mathbf{q}}(x_{i},t_{j+1})}{\tau^{2}}, \\& \frac{\partial{\mathbf{q}}_{k}(x,t)}{\partial{t}} = \frac{{\mathbf{q}}(x_{i},t_{j+1})-{\mathbf{q}}(x_{i},t_{j})}{\tau}, \\& {\mathbf{y}}(x_{i},t_{j}) = C(t_{i}){ \mathbf{q}}(x_{i},t_{j})+G(t_{i}){ \mathbf{u}}(x_{i},t_{j}), \end{aligned}$$

where h, τ are space and time sizes, respectively, and \((x_{i},t_{j})\) is discrete point.

The iterative learning process is the following:

  • Step 1. Iterative number \(k=0\) (for convenience, the iterative time begins from 0).

    1. 1.1.

      Let control input \({\mathbf{u}}_{0}(x,t)=0\) with \({\mathbf{q}}_{0}(0,t)=0={\mathbf{q}}_{0}(1,t)\), \({\mathbf{q}}_{0}(x,0)\), \(\frac{\partial{\mathbf{q}}_{0}(x,0)}{\partial t}\), \(A(t)\), \(B(t)\), D. Based on the second-order differential equations and above difference method, we can solve (4) and obtain \({\mathbf{q}}_{0}(x,t)\).

    2. 1.2.

      By the output equation \({\mathbf{y}}_{0}(x,t)=C(t){\mathbf{q}}_{0}(x,t)+G(t){\mathbf{u}}_{0}(x,t)\) we calculate \({\mathbf{y}}_{0}(x,t)\).

    3. 1.3.

      Calculate \({\mathbf{e}}_{0}(x,t)={\mathbf{y}}_{d}(x,t)-{\mathbf{y}}_{0}(x,t)\).

  • Step 2. Iterative number \(k=1\), \({\mathbf{u}}_{1}(x,t)={\mathbf{u}}_{0}(x,t)+\Gamma(t){\mathbf{e}}_{0}(x,t)\).

  • Step 3. Repeating Step 1, but with control input \({\mathbf{u}}_{1}(x,t)\) (≠0), we obtain \({\mathbf{e}}_{1}(x,t)\).

  • Step 4. At the kth iteration, if the tracking error \({\mathbf{e}}_{k}(x,t)\) is less than the given error, then end, else continue.

It should be pointed out that we did not need know (but require to be bounded) the uncertain coefficients \(A(t)\), \(B(t)\), \(C(t)\), \(G(t)\) in practical process control; we only need remember the tracking error and calculate (offline) the next time control input \({\mathbf{u}}_{k+1}(x,t)\).

The simulation results obtained using this iterative learning algorithm and difference method are shown in Figures 1-7.

Figure 1
figure 1

Desired surface \(\pmb{y_{d1}(x,t)}\) .

Full size image

Figures 1 and 2 show the desired profile, Figures 3 and 4 show the relative profile at the twentieth iteration, Figures 5 and 6 show the error curved surface, where \(e_{ki}(x,t)=y_{di}(x,t)-y_{ki}(x,t)\), \(i=1,2\), \(k=20\). Figure 7 is the curve chart describing the variation of the maximum tracking error with iteration numbers. Numerically, in the twentieth iteration, the absolute values of the maximum tracking error are \(1.9185\times10^{-8}\) and \(1.5564\times10^{-9}\). These simulation results demonstrate the efficacy of the ILC law (11).

Figure 2
figure 2

Desired surface \(\pmb{y_{d2}(x,t)}\) .

Full size image
Figure 3
figure 3

Output surface \(\pmb{y_{k1}(x,t)}\) .

Full size image
Figure 4
figure 4

Output surface \(\pmb{y_{k2}(x,t)}\) .

Full size image
Figure 5
figure 5

Error surface \(\pmb{e_{k1}(x,t)}\) .

Full size image
Figure 6
figure 6

Error surface \(\pmb{e_{k2}(x,t)}\) .

Full size image
Figure 7
figure 7

Max error-iterative number curve.

Full size image

5 Conclusions

In this paper, a P-type ILC law is applied to a class of MIMO second-order hyperbolic PDEs with dissipation and bounded coefficient uncertainty. We established sufficient conditions that guarantee the tracking error convergence in the sense of \(\mathbf{L}^{2}\) norm. A simulation example is given to illustrate the effectiveness of the proposed algorithm.