For system (1.1) we have
$$\begin{aligned} &\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0,\ldots,\bar{\Delta}_{n} ( u(\bar{t}_{n}^{ -} ) ) \to 0} \bigl\{ \mbox{system } (1.1) \bigr\} \\ &\quad\to \left \{ \textstyle\begin{array}{@{}l} {}_{H}D_{a^{ +}}^{q}u(t) = f(t,u(t)), \quad q \in (1,2),t \in (a,T] \mbox{ and } t \ne t_{k}\ (k = 1,2,\ldots,m), \\ \Delta ( {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u ) \vert _{t = t_{k}} = {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(t_{k}^{ +} ) - {}_{H}\mathcal {J}_{a^{ +}}^{2 - q}u(t_{k}^{ -} ) = \Delta_{k} ( u(t_{k}^{ -} ) ),\\ \quad k = 1,2,\ldots,m, \\ {}_{H}\mathcal {J}_{a^{ +}}^{2 - q}u(a^{ +} ) = u_{2},\qquad{}_{H}D_{a^{ +}}^{q - 1}u(a^{ +} ) = u_{1}. \end{array}\displaystyle \right . \end{aligned}$$
(3.1)
$$\begin{aligned} &\lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0,\ldots,\Delta_{m} ( u(t_{m}^{ -} ) ) \to 0} \bigl\{ \mbox{system } (1.1) \bigr\} \\ &\quad\to \left \{ \textstyle\begin{array}{@{}l} {}_{H}D_{a^{ +}}^{q}u(t) = f(t,u(t)),\quad q \in (1,2),t \in (a,T] \mbox{ and } t \ne \bar{t}_{l}\ (l = 1,2,\ldots,n), \\ \Delta ( {}_{H}D_{a^{ +}}^{q - 1}u ) \vert _{t = \bar{t}_{l}} = {}_{H}D_{a^{ +}}^{q - 1}u(\bar{t}_{l}^{ +} ) - {}_{H}D_{a^{ +}}^{q - 1}u(\bar{t}_{l}^{ -} ) = \bar{\Delta}_{l} ( u(\bar{t}_{l}^{ -} ) ),\\ \quad l = 1,2,\ldots,n, \\ {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(a^{ +} ) = u_{2},\qquad{}_{H}D_{a^{ +}}^{q - 1}u(a^{ +} ) = u_{1}. \end{array}\displaystyle \right . \end{aligned}$$
(3.2)
$$\begin{aligned} & \mathop{\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0,\ldots,\bar{\Delta}_{n} ( u(\bar{t}_{n}^{ -} ) ) \to 0, }}\limits_{ \Delta_{1} ( u(t_{1}^{ -} ) ) \to 0,\ldots,\Delta_{m} ( u(t_{m}^{ -} ) ) \to 0} \bigl\{ \mbox{system } (1.1) \bigr\} \\ &\quad\to \left \{ \textstyle\begin{array}{@{}l} {}_{H}D_{a^{ +}}^{q}u(t) = f(t,u(t)),\quad q \in (1,2),t \in (a,T], \\ {}_{H}D_{a^{ +}}^{q - 1}u(a^{ +} ) = u_{1},\qquad {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(a^{ +} ) = u_{2}, \end{array}\displaystyle \right . \end{aligned}$$
(3.3)
Therefore, the solution of system (1.1) satisfies the following three conditions:
$$\begin{aligned} (\mathrm{i})&\quad \lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0, \ldots,\bar{\Delta}_{n} ( u(\bar{t}_{n}^{ -} ) ) \to 0} \bigl\{ \mbox{the solution of system } (1.1) \bigr\} \\ &\qquad= \bigl\{ \mbox{the solution of system } (3.1) \bigr\} , \\ (\mathrm{ii})&\quad \lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0, \ldots,\Delta_{m} ( u(t_{m}^{ -} ) ) \to 0} \bigl\{ \mbox{the solution of system } (1.1) \bigr\} \\ &\qquad= \bigl\{ \mbox{the solution of system } (3.2) \bigr\} , \\ (\mathrm{iii})& \quad \mathop{\lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0, \ldots,\Delta_{m} ( u(t_{m}^{ -} ) ) \to 0}}\limits _{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0, \ldots,\bar{\Delta}_{n} ( u(\bar{t}_{n}^{ -} ) ) \to 0} \bigl\{ \mbox{the solution of system } (1.1) \bigr\} \\ &\qquad= \bigl\{ \mbox{the solution of system } (3.3) \bigr\} \end{aligned}$$
Therefore, we give the definition of a solution of system (1.1).
Definition 3.1
A function \(z(t):[a,T] \to \mathbb{R}\) is said to be a solution of the fractional Cauchy problem (1.1) if \({}_{H}\mathcal{J}_{a^{ +}}^{2 - q}z(a^{ +} ) = u_{2}\) and \({}_{H}D_{a^{ +}}^{q - 1}z(a^{ +} ) = u_{1}\), the equation condition \({}_{H}D_{a^{ +}}^{q}z(t) = f(t,z(t))\) for each \(t \in (a, T]\) is satisfied, the impulsive conditions \(\Delta ( {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}z ) |_{t = t_{k}} = \Delta_{k} ( z(t_{k}^{ -} ) ) \) (\(k = 1, 2, \ldots, m\)) and \(\Delta ( {}_{H}D_{a^{ +}}^{q - 1}z ) \vert _{t = \bar{t}_{l}} = \bar{\Delta}_{l} ( z(\bar{t}_{l}^{ -} ) ) \) (\(l =1, 2, \ldots, n\)) are satisfied, the restriction of \(z( \cdot )\) to the interval \((t'_{k},t'_{k + 1}] \) (\(k = 0,1, 2, \ldots, \Omega\)) is continuous, and conditions (i)-(iii) hold.
Using the equality \(\ln \frac{t}{t_{k}} = \int_{t_{k}}^{t} \frac{ds}{s}\) (\(k = 0, 1, 2, \ldots, m\)), define the piecewise function
$$\begin{aligned} \tilde{u}(t) ={}& \frac{1}{\Gamma (q)} \bigl( {}_{H}D_{a^{ +}}^{q - 1}u \bigl(t_{k}^{ +} \bigr) \bigr) \biggl( \int_{t_{k}}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{1}{\Gamma (q - 1)} \bigl( {}_{H} \mathcal{J}_{a^{ +}}^{2 - q}u\bigl(t_{k}^{ +} \bigr) \bigr) \biggl( \int_{t_{k}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{t_{k}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \quad\mbox{for } t \in (t_{k},t_{k + 1}] \ (\mbox{where } k = 0,1,2,\ldots,m). \end{aligned}$$
By Definition 2.2 we have
$$\begin{aligned} &\bigl[ {}_{H}D_{a^{ +}}^{q}\tilde{u}(t) \bigr]_{t \in (t_{k},t_{k + 1}]} \\ &\quad= \biggl\{ \frac{1}{\Gamma (2 - q)} \biggl( t\frac{d}{dt} \biggr)^{2} \int_{a}^{t} \biggl(\ln \frac{t}{\eta} \biggr)^{2 - q - 1} \biggl[ \frac{1}{\Gamma (q)} \bigl( {}_{H}D_{a^{ +}}^{q - 1}u \bigl(t_{k}^{ +} \bigr) \bigr) \biggl(\ln \frac{\eta}{t_{k}} \biggr)^{q - 1} \\ &\qquad{} + \frac{1}{\Gamma (q - 1)} \bigl( {}_{H}\mathcal{J}_{a^{ +}}^{2 - q} u\bigl(t_{k}^{ +} \bigr) \bigr) \biggl(\ln \frac{\eta}{ t_{k}}\biggr)^{q - 2} \\ &\qquad{}+ \frac{1}{\Gamma (q)} \int_{t_{k}}^{\eta} \biggl(\ln \frac{\eta}{ s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \frac{d\eta}{\eta} \biggr\} _{t \in (t_{k},t_{k + 1}]} \\ &\quad= \biggl\{ \frac{1}{\Gamma (2 - q)} \biggl( t\frac{d}{dt} \biggr)^{2} \int_{t_{k}}^{t} \biggl(\ln \frac{t}{\eta} \biggr)^{2 - q - 1} \biggl[ \frac{1}{\Gamma (q)} \bigl( {}_{H}D_{a^{ +}}^{q - 1}u \bigl(t_{k}^{ +} \bigr) \bigr) \biggl(\ln \frac{\eta}{t_{k}} \biggr)^{q - 1} \\ &\qquad{} + \frac{1}{\Gamma (q - 1)} \bigl( {}_{H} \mathcal{J}_{a^{ +}}^{2 - q}u\bigl(t_{k}^{ +} \bigr) \bigr) \biggl(\ln \frac{\eta}{ t_{k}}\biggr)^{q - 2} \\ &\qquad{}+ \frac{1}{\Gamma (q)} \int_{t_{k}}^{\eta} \biggl(\ln \frac{\eta}{ s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \frac{d\eta}{\eta} \biggr\} _{t \in (t_{k},t_{k + 1}]} \\ &\quad= \biggl\{ \frac{1}{\Gamma (2 - q)\Gamma (q)} \biggl( t\frac{d}{dt} \biggr)^{2} \int_{t_{k}}^{t} \biggl(\ln \frac{t}{\eta} \biggr)^{2 - q - 1} \biggl[ \int_{t_{k}}^{\eta} \biggl(\ln \frac{\eta}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \frac{d\eta}{\eta} \biggr\} _{t \in (t_{k},t_{k + 1}]} \\ &\quad= \biggl\{ \biggl( t\frac{d}{dt} \biggr)^{2} \biggl( \int_{t_{k}}^{t} \biggl(\ln \frac{t}{s}\biggr)f \bigl(s,u(s)\bigr)\frac{ds}{s} \biggr) \biggr\} _{t \in (t_{k},t_{k + 1}]} \\ &\quad= f\bigl(t,u(t)\bigr) \vert _{t \in (t_{k},t_{k + 1}]}. \end{aligned}$$
So, \(\tilde{u}(t)\) satisfies the condition of Hadamard fractional derivative and does not satisfy conditions (i)-(iii). Thus, we will assume that \(\tilde{u}(t)\) is an approximate solution to seek the exact solution of system (1.1). First, let us prove two useful conclusions.
Lemma 3.2
Let
\(q \in(1, 2)\), and let
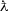 be a constant. System (3.1) is equivalent to the fractional integral equation
be a constant. System (3.1) is equivalent to the fractional integral equation
provided that the integral in (3.4) exists.
Proof
Necessity. We will verify that Eq. (3.4) satisfies the conditions of system (3.1).
For system (3.1), we have
$$\begin{aligned} &\lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0,\ldots,\Delta_{m} ( u(t_{m}^{ -} ) ) \to 0} \left \{ \textstyle\begin{array}{@{}l} {}_{H}D_{a^{ +}}^{q}u(t) = f(t,u(t)),\quad q \in (1,2),t \in (a,T] \mbox{ and}\\ \quad t \ne t_{k}\ (k = 1,2,\ldots,m), \\ \Delta ( {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u ) \vert _{t = t_{k}} = {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(t_{k}^{ +} ) - {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(t_{k}^{ -} ) = \Delta_{k} ( u(t_{k}^{ -} ) ),\\ \quad k = 1,2,\ldots,m, \\ {}_{H}D_{a^{ +}}^{q - 1}u(a^{ +} ) = u_{1},\qquad{}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(a^{ +} ) = u_{2} \end{array}\displaystyle \right . \\ &\quad\to \left \{ \textstyle\begin{array}{@{}l} {}_{H}D_{a^{ +}}^{q}u(t) = f(t,u(t)),\quad q \in (1,2),t \in (a,T], \\ {}_{H}D_{a^{ +}}^{q - 1}u(a^{ +} ) = u_{1}, \qquad{}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(a^{ +} ) = u_{2}. \end{array}\displaystyle \right . \end{aligned}$$
Therefore,
$$\begin{aligned} &\lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0,\ldots,\Delta_{m} ( u(t_{m}^{ -} ) ) \to 0} \bigl\{ \mbox{the solution of system } (3.1) \bigr\} \\ &\quad= \bigl\{ \mbox{the solution of system } (3.3) \bigr\} . \end{aligned}$$
(3.5)
Moreover, we easily verify that Eq. (3.4) satisfies condition (3.5).
Next, taking the Hadamard fractional derivative of Eq. (3.4) for each \(t \in (t_{k},t_{k + 1}] \) (\(k = 0,1, 2,\ldots, m\)), we have
So, Eq. (3.4) satisfies the Hadamard fractional derivative of system (3.1).
Finally, for each \(t_{k}\) (\(k = 1, 2,\ldots, m\)) in Eq. (3.4), we have
$$\begin{aligned} &{}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u \bigl(t_{k}^{ +} \bigr) - {}_{H} \mathcal{J}_{a^{ +}}^{2 - q}u\bigl(t_{k}^{ -} \bigr) \\ &\quad= \biggl\{ \frac{1}{\Gamma (2 - q)} \int_{a}^{t} \biggl(\ln \frac{t}{\eta} \biggr)^{2 - q - 1}u(\eta )\frac{d\eta}{\eta} \biggr\} _{t \to t_{k}^{ +}} - \biggl\{ \frac{1}{\Gamma (2 - q)} \int_{a}^{t} \biggl(\ln \frac{t}{\eta} \biggr)^{2 - q - 1}u(\eta )\frac{d\eta}{\eta} \biggr\} _{t = t_{k}^{ -}} \\ &\quad= \Delta_{k} \bigl( u\bigl(t_{k}^{ -} \bigr) \bigr). \end{aligned}$$
Therefore, Eq. (3.4) satisfies the impulsive conditions of (3.1). Thus, Eq. (3.4) satisfies all conditions of system (3.1).
Sufficiency. We will prove that the solutions of system (3.1) satisfy Eq. (3.4) by mathematical induction. By Definitions 2.1 and 2.2 the solution of system (3.1) satisfies
$$\begin{aligned} u(t) ={}& \frac{u_{1}}{\Gamma (q)}\biggl(\ln \frac{t}{a} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)}\biggl(\ln \frac{t}{a} \biggr)^{q - 2} + \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \quad\mbox{for } t \in (a,t_{1}]. \end{aligned}$$
(3.6)
Using (3.6) and Definitions 2.1 and 2.2, we get \({}_{H}D_{a^{ +}}^{q - 1}u(t_{1}^{ +} ) = {}_{H}D_{a^{ +}}^{q - 1}u(t_{1}^{ -} ) = u_{1} + \int_{a}^{t_{1}} f(s, u(s))\frac{ds}{s}\) and \({}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(t_{1}^{ +} ) = {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(t_{1}^{ -} ) + \Delta_{1} ( u(t_{1}^{ -} ) ) = u_{1}\ln \frac{t_{1}}{a} + u_{2} + \int_{a}^{t_{1}} (\ln \frac{t_{1}}{s})f(s,u(s))\frac{ds}{s} + \Delta_{1} ( u(t_{1}^{ -} ) )\). Therefore, the approximate solution for \(t \in (t_{1},t_{2}]\) is provided by
$$\begin{aligned} \tilde{u}(t) ={}& \frac{1}{\Gamma (q)} \bigl( {}_{H}D_{a^{ +}}^{q - 1}u \bigl(t_{1}^{ +} \bigr) \bigr) \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{1}{\Gamma (q - 1)} \bigl( {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u\bigl(t_{1}^{ +} \bigr) \bigr) \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{t_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ ={}& \frac{u_{1} + \int_{a}^{t_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}+ \frac{u_{1}\ln \frac{t_{1}}{a} + u_{2} + \int_{a}^{t_{1}} (\ln \frac{t_{1}}{s})f(s,u(s))\frac{ds}{s} + \Delta_{1} ( u(t_{1}^{ -} ) )}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{t_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \quad\mbox{for } t \in (t_{1},t_{2}]. \end{aligned}$$
(3.7)
Let \(e_{1}(t) = u(t) - \tilde{u}(t)\) for \(t \in (t_{1},t_{2}]\), where \(u(t)\) is the exact solution of system (3.1). Due to
$$\begin{aligned} \lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0}u(t) = {}&\frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \quad \mbox{for } t \in (t_{1},t_{2}], \end{aligned}$$
we obtain
$$\begin{aligned} &\lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0}e_{1}(t) \\ &\quad= \lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0} \bigl\{ u(t) - \tilde{u}(t) \bigr\} \\ &\quad= \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} + \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ &\qquad{}- \frac{u_{1} + \int_{a}^{t_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &\qquad{}- \frac{u_{1}\ln \frac{t_{1}}{a} + u_{2} + \int_{a}^{t_{1}} (\ln \frac{t_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\qquad{}- \frac{1}{\Gamma (q)} \int_{t_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \quad\mbox{for } t \in (t_{1},t_{2}]. \end{aligned}$$
(3.8)
By (3.8) we assume that
$$\begin{aligned} e_{1}(t) ={}& \sigma \bigl(\Delta_{1} \bigl( u \bigl(t_{1}^{ -} \bigr) \bigr)\bigr)\lim_{\Delta_{1} \to 0}e_{1}(t) \\ ={}& \sigma \bigl(\Delta_{1} \bigl( u\bigl(t_{1}^{ -} \bigr) \bigr)\bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{t_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{t_{1}}{a} + u_{2} + \int_{a}^{t_{1}} (\ln \frac{t_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{t_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\biggr]\quad \mbox{for } t \in (t_{1},t_{2}], \end{aligned}$$
where the function \(\sigma ( \cdot )\) is an undetermined function with \(\sigma (0) = 1\). Then,
$$\begin{aligned} u(t) ={}& \tilde{u}(t) + e_{1}(t) \\ ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} + \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ &{}+ \frac{\Delta_{1} ( u(t_{1}^{ -} ) )}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \bigl( 1 - \sigma \bigl(\Delta_{1} \bigl( u\bigl(t_{1}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{t_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{} - \frac{u_{1}\ln \frac{t_{1}}{a} + u_{2} + \int_{a}^{t_{1}} (\ln \frac{t_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{t_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\biggr] \quad\mbox{for } t \in (t_{1},t_{2}]. \end{aligned}$$
(3.9)
Using (3.9), we obtain \({}_{H}D_{a^{ +}}^{q - 1}u(t_{2}^{ +} ) = {}_{H}D_{a^{ +}}^{q - 1}u(t_{2}^{ -} ) = u_{1} + \int_{a}^{t_{2}} f(s,u(s))\frac{ds}{s}\) and
$$\begin{aligned} {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u \bigl(t_{2}^{ +} \bigr)&= {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u \bigl(t_{2}^{ -} \bigr) + \Delta_{2} \bigl( u \bigl(t_{2}^{ -} \bigr) \bigr) \\ &= u_{1}\ln \frac{t_{2}}{a} + u_{2} + \int_{a}^{t_{2}} \biggl(\ln \frac{t_{2}}{s} \biggr)f \bigl(s,u(s) \bigr)\frac{ds}{s} + \Delta_{1} \bigl( u \bigl(t_{1}^{ -} \bigr) \bigr) + \Delta_{2} \bigl( u \bigl(t_{2}^{ -} \bigr) \bigr). \end{aligned}$$
So, the approximate solution for \(t \in (t_{2},t_{3}]\) is given by
$$\begin{aligned} \tilde{u}(t) ={}& \frac{1}{\Gamma (q)} \bigl( {}_{H}D_{a^{ +}}^{q - 1}u \bigl(t_{2}^{ +} \bigr) \bigr) \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{1}{\Gamma (q - 1)} \bigl( {}_{H} \mathcal{J}_{a^{ +}}^{2 - q}u\bigl(t_{2}^{ +} \bigr) \bigr) \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{t_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ ={}& \frac{u_{1} + \int_{a}^{t_{2}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}+ \frac{u_{1}\ln \frac{t_{2}}{a} + u_{2} + \int_{a}^{t_{2}} (\ln \frac{t_{2}}{s})f(s,u(s))\frac{ds}{s} + \Delta_{1} ( u(t_{1}^{ -} ) ) + \Delta_{2} ( u(t_{2}^{ -} ) )}{\Gamma (q - 1)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{t_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \quad\mbox{for } t \in (t_{2},t_{3}]. \end{aligned}$$
(3.10)
Let \(e_{2}(t) = u(t) - \tilde{u}(t)\) for \(t \in (t_{2},t_{3}]\). By (3.6) and (3.9) the exact solution \(u(t)\) of system (3.1) satisfies
$$\begin{aligned}& \mathop{\lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0, }}\limits _{ \Delta_{2} ( u(t_{2}^{ -} ) ) \to 0}u(t) = \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\& \hphantom{\mathop{\lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0, }}\limits_{ \Delta_{2} ( u(t_{2}^{ -} ) ) \to 0}u(t)=}{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \quad\mbox{for } t \in (t_{2},t_{3}], \\& \lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0}u(t) \\& \quad= \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\& \qquad{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} + \frac{\Delta_{2} ( u(t_{2}^{ -} ) )}{\Gamma (q - 1)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\& \qquad{}- \bigl( 1 - \sigma \bigl(\Delta_{2} \bigl( u \bigl(t_{2}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl\{ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\& \qquad{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{t_{2}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\& \qquad{}- \frac{u_{1}\ln \frac{t_{2}}{a} + u_{2} + \int_{a}^{t_{2}} (\ln \frac{t_{2}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\& \qquad{}- \frac{1}{\Gamma (q)} \int_{t_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr\} \quad\mbox{for } t \in (t_{2},t_{3}], \\& \lim_{\Delta_{2} ( u(t_{2}^{ -} ) ) \to 0}u(t) = \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2}\\& \hphantom{\lim_{\Delta_{2} ( u(t_{2}^{ -} ) ) \to 0}u(t) =}{} + \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} + \frac{\Delta_{1} ( u(t_{1}^{ -} ) )}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\& \hphantom{\lim_{\Delta_{2} ( u(t_{2}^{ -} ) ) \to 0}u(t) =}{}- \bigl( 1 - \sigma \bigl(\Delta_{1} \bigl( u \bigl(t_{1}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl\{ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\& \hphantom{\lim_{\Delta_{2} ( u(t_{2}^{ -} ) ) \to 0}u(t) =}{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{t_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\& \hphantom{\lim_{\Delta_{2} ( u(t_{2}^{ -} ) ) \to 0}u(t) =}{}- \frac{u_{1}\ln \frac{t_{1}}{a} + u_{2} + \int_{a}^{t_{1}} (\ln \frac{t_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2}\\& \hphantom{\lim_{\Delta_{2} ( u(t_{2}^{ -} ) ) \to 0}u(t) =}{} - \frac{1}{\Gamma (q)} \int_{t_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr\} \quad\mbox{for } t \in (t_{2},t_{3}]. \end{aligned}$$
Therefore,
$$\begin{aligned} \mathop{\lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0, }}\limits _{\Delta_{2} ( u(t_{2}^{ -} ) ) \to 0}e_{2}(t) ={}& \mathop{\lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0,}}\limits _{\Delta_{2} ( u(t_{2}^{ -} ) ) \to 0} \bigl\{ u(t) - \tilde{u}(t) \bigr\} \\ ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{t_{2}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{t_{2}}{a} + u_{2} + \int_{a}^{t_{2}} (\ln \frac{t_{2}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{t_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}, \end{aligned}$$
(3.11)
$$\begin{aligned} \lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0}e_{2}(t) ={}& \lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0} \bigl\{ u(t) - \tilde{u}(t) \bigr\} \\ ={}& \sigma \bigl(\Delta_{2} \bigl( u\bigl(t_{2}^{ -} \bigr) \bigr)\bigr) \biggl\{ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ &{} - \frac{u_{1} + \int_{a}^{t_{2}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{} - \frac{u_{1}\ln \frac{t_{2}}{a} + u_{2} + \int_{a}^{t_{2}} (\ln \frac{t_{2}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{t_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\biggr\} , \end{aligned}$$
(3.12)
$$\begin{aligned} \lim_{\Delta_{2} ( u(t_{2}^{ -} ) ) \to 0}e_{2}(t) ={}& \lim_{\Delta_{2} ( u(t_{2}^{ -} ) ) \to 0} \bigl\{ u(t) - \tilde{u}(t) \bigr\} \\ ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} + \frac{\Delta_{1} ( u(t_{1}^{ -} ) )}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{\Delta_{1} ( u(t_{1}^{ -} ) )}{\Gamma (q - 1)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} - \frac{u_{1} + \int_{a}^{t_{2}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{t_{2}}{a} + u_{2} + \int_{a}^{t_{2}} (\ln \frac{t_{2}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{t_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ &{}- \bigl( 1 - \sigma \bigl(\Delta_{1} \bigl( u \bigl(t_{1}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl\{ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{t_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{t_{1}}{a} + u_{2} + \int_{a}^{t_{1}} (\ln \frac{t_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{t_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr\} . \end{aligned}$$
(3.13)
So, by (3.11)-(3.13) we obtain
$$\begin{aligned} e_{2}(t) ={}& \sigma \bigl(\Delta_{2} \bigl( u \bigl(t_{2}^{ -} \bigr) \bigr)\bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{t_{2}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{t_{2}}{a} + u_{2} + \int_{a}^{t_{2}} (\ln \frac{t_{2}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{t_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] + \frac{\Delta_{1} ( u(t_{1}^{ -} ) )}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{\Delta_{1} ( u(t_{1}^{ -} ) )}{\Gamma (q - 1)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \bigl( 1 - \sigma \bigl(\Delta_{1} \bigl( u\bigl(t_{1}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2}\\ &{} + \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{t_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1}\\ &{} - \frac{u_{1}\ln \frac{t_{1}}{a} + u_{2} + \int_{a}^{t_{1}} (\ln \frac{t_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{t_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \quad\mbox{for } t \in (t_{2},t_{3}]. \end{aligned}$$
Thus,
$$\begin{aligned} u(t) ={}& \tilde{u}(t) + e_{2}(t) \\ ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ &{}+ \frac{\Delta_{1} ( u(t_{1}^{ -} ) )}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} + \frac{\Delta_{2} ( u(t_{2}^{ -} ) )}{\Gamma (q - 1)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \bigl( 1 - \sigma \bigl(\Delta_{1} \bigl( u\bigl(t_{1}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{t_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{t_{1}}{a} + u_{2} + \int_{a}^{t_{1}} (\ln \frac{t_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{t_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \\ &{}- \bigl( 1 - \sigma \bigl(\Delta_{2} \bigl( u\bigl(t_{2}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{t_{2}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{t_{2}}{a} + u_{2} + \int_{a}^{t_{2}} (\ln \frac{t_{2}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{} - \frac{1}{\Gamma (q)} \int_{t_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\biggr] \quad\mbox{for } t \in (t_{2},t_{3}]. \end{aligned}$$
(3.14)
Letting \(t_{2} \to t_{1}\), we have
$$\begin{aligned}& \lim_{t_{2} \to t_{1}} \left \{ \textstyle\begin{array}{@{}l} {}_{H}D_{a^{ +}}^{q}u(t) = f(t,u(t)),\quad q \in (1,2),t \in (a,t_{3}] \mbox{ and } t \ne t_{1} \mbox{ and } t \ne t_{2}, \\ \Delta ( {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u ) \vert _{t = t_{k}} = {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(t_{k}^{ +} ) - {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(t_{k}^{ -} ) = \Delta_{k} ( u(t_{k}^{ -} ) ),\quad k = 1,2, \\ {}_{H}D_{a^{ +}}^{q - 1}u(a^{ +} ) = u_{1},\qquad {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(a^{ +} ) = u_{2}, \end{array}\displaystyle \right . \end{aligned}$$
(3.15)
$$\begin{aligned}& \quad\to \left \{ \textstyle\begin{array}{@{}l} {}_{H}D_{a^{ +}}^{q}u(t) = f(t,u(t)),\quad q \in (0,1),t \in (a,t_{3}] \mbox{ and } t \ne t_{1}, \\ \Delta ( {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u ) \vert _{t = t_{1}} = \Delta_{1} ( u(t_{1}^{ -} ) ) + \Delta_{2} ( u(t_{2}^{ -} ) ), \\ {}_{H}D_{a^{ +}}^{q - 1}u(a^{ +} ) = u_{1}, \qquad {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(a^{ +} ) = u_{2}. \end{array}\displaystyle \right . \end{aligned}$$
(3.16)
Using (3.9) and (3.14) in systems (3.16) and (3.15), respectively, we obtain
$$1 - \sigma (\Delta_{1} + \Delta_{2}) = 1 - \sigma ( \Delta_{1}) + 1 - \sigma (\Delta_{2}) \quad \forall \Delta_{1},\Delta_{2} \in \mathbb{R}. $$
Letting \(\rho (z) = 1 - \sigma (z)\) (\(\forall z \in \mathbb{R}\)), we have \(\rho (z + w) = \rho (z) + \rho (w) \) (\(\forall z,w \in \mathbb{R}\)). Therefore, 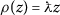 , where
, where  is a constant. So, by (3.9) and (3.14) we get
is a constant. So, by (3.9) and (3.14) we get
and
For \(t \in (t_{k},t_{k + 1}]\), suppose that
Using (3.19), we obtain \({}_{H}D_{a^{ +}}^{q - 1}u(t_{k + 1}^{ +} ) = {}_{H}D_{a^{ +}}^{q - 1}u(t_{k + 1}^{ -} ) = u_{1} + \int_{a}^{t_{k + 1}} f(s,u(s))\frac{ds}{s}\) and
$$\begin{aligned} {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u \bigl(t_{k + 1}^{ +} \bigr) &= {}_{H} \mathcal{J}_{a^{ +}}^{2 - q}u \bigl(t_{k + 1}^{ -} \bigr) + \Delta_{k + 1} \bigl( u \bigl(t_{k + 1}^{ -} \bigr) \bigr) \\ &= u_{1}\ln \frac{t_{k + 1}}{a} + u_{2} + \int_{a}^{t_{k + 1}} \biggl(\ln \frac{t_{k + 1}}{s} \biggr)f \bigl(s,u(s) \bigr)\frac{ds}{s} + \sum_{i = 1}^{k + 1} \Delta_{i} \bigl( u \bigl(t_{i}^{ -} \bigr) \bigr). \end{aligned}$$
So, the approximate solution for \(t \in (t_{k + 1},t_{k + 2}]\) is provided by
$$\begin{aligned} \tilde{u}(t) ={}& \frac{1}{\Gamma (q)} \bigl( {}_{H}D_{a^{ +}}^{q - 1}u \bigl(t_{k + 1}^{ +} \bigr) \bigr) \biggl( \int_{t_{k + 1}}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{1}{\Gamma (q - 1)} \bigl( {}_{H} \mathcal{J}_{a^{ +}}^{2 - q}u\bigl(t_{k + 1}^{ +} \bigr) \bigr) \biggl( \int_{t_{k + 1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{t_{k + 1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ =&{} \frac{u_{1} + \int_{a}^{k + 1} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{k + 1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}+ \frac{u_{1}\ln \frac{t_{k + 1}}{a} + u_{2} + \int_{a}^{t_{k + 1}} (\ln \frac{t_{k + 1}}{s})f(s,u(s))\frac{ds}{s} + \sum_{i = 1}^{k + 1} \Delta_{i} ( u(t_{i}^{ -} ) )}{\Gamma (q - 1)} \biggl( \int_{t_{k + 1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{t_{k + 1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \quad\mbox{for } t \in (t_{k + 1},t_{k + 2}]. \end{aligned}$$
(3.20)
Let \(e_{k + 1}(t) = u(t) - \tilde{u}(t)\) for \(t \in (t_{k + 1},t_{k + 2}]\). By (3.19) the exact solution \(u(t)\) of system (3.1) satisfies
Therefore,
$$\begin{aligned} &\lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0,\ldots,\Delta_{k + 1} ( u(t_{k + 1}^{ -} ) ) \to 0}e_{k + 1}(t) \\ &\quad= \lim_{\Delta_{1} ( u(t_{1}^{ -} ) ) \to 0,\ldots,\Delta_{k + 1} ( u(t_{k + 1}^{ -} ) ) \to 0} \bigl\{ u(t) - \tilde{u}(t) \bigr\} \\ &\quad= \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\qquad{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{k + 1} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t_{k + 1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &\qquad{}- \frac{u_{1}\ln \frac{t_{k + 1}}{a} + u_{2} + \int_{a}^{t_{k + 1}} (\ln \frac{t_{k + 1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t_{k + 1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\qquad{}- \frac{1}{\Gamma (q)} \int_{t_{k + 1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\quad \mbox{for } t \in (t_{k + 1},t_{k + 2}]. \end{aligned}$$
(3.22)
So, by (3.21) and (3.22) we obtain
Thus,
So, the solution of system (3.1) satisfies Eq. (3.4).
So, system (3.1) is equivalent to Eq. (3.4). The proof is now completed. □
Lemma 3.3
Let
\(q \in(1, 2)\), and let
ħ
be a constant. System (3.2) is equivalent to the fractional integral equation
$$ u(t) = \left \{ \textstyle\begin{array}{@{}l} \frac{u_{1}}{\Gamma (q)} ( \int_{a}^{t} \frac{ds}{s} )^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} ( \int_{a}^{t} \frac{ds}{s} )^{q - 2} \\ \quad{}+ \frac{1}{\Gamma (q)}\int_{a}^{t} (\ln \frac{t}{s})^{q - 1}f(s,u(s))\frac{ds}{s} \quad\textit{for } t \in (a,\bar{t}_{1}], \\ \frac{u_{1}}{\Gamma (q)} ( \int_{a}^{t} \frac{ds}{s} )^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} ( \int_{a}^{t} \frac{ds}{s} )^{q - 2} + \frac{1}{\Gamma (q)}\int_{a}^{t} (\ln \frac{t}{s})^{q - 1}f(s,u(s))\frac{ds}{s} \\ \quad{}+ \sum_{j = 1}^{l} \frac{\bar{\Delta}_{j} ( u(\bar{t}_{j}^{ -} ) )}{\Gamma (q)} ( \int_{\bar{t}_{j}}^{t} \frac{ds}{s} )^{q - 1} - \sum_{j = 1}^{l} \hbar \bar{\Delta}_{j} ( u(\bar{t}_{j}^{ -} ) ) [ \frac{u_{1}}{\Gamma (q)} ( \int_{a}^{t} \frac{ds}{s} )^{q - 1} \\ \quad{}+ \frac{u_{2}}{\Gamma (q - 1)} ( \int_{a}^{t} \frac{ds}{s} )^{q - 2} + \frac{1}{\Gamma (q)}\int_{a}^{t} (\ln \frac{t}{s})^{q - 1}f(s,u(s))\frac{ds}{s} \\ \quad{} - \frac{u_{1} + \int_{a}^{\bar{t}_{j}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} ( \int_{\bar{t}_{j}}^{t} \frac{ds}{s} )^{q - 1} - \frac{u_{1}\ln \frac{\bar{t}_{j}}{a} + u_{2} + \int_{a}^{\bar{t}_{j}} (\ln \frac{\bar{t}_{j}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} ( \int_{\bar{t}_{j}}^{t} \frac{ds}{s} )^{q - 2} \\ \quad{}- \frac{1}{\Gamma (q)}\int_{\bar{t}_{j}}^{t} (\ln \frac{t}{s})^{q - 1}f(s,u(s))\frac{ds}{s} ] \quad\textit{for } t \in (\bar{t}_{l},\bar{t}_{l + 1}], 1 \le l \le n \end{array}\displaystyle \right . $$
(3.23)
provided that the integral in (3.23) exists.
Proof
Necessity. We will verify that Eq. (3.23) satisfies the conditions of system (3.2).
For system (3.2), there exists an implicit condition
$$\begin{aligned} &\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0, \ldots,\bar{\Delta}_{n} ( u(\bar{t}_{n}^{ -} ) ) \to 0} \left \{ \textstyle\begin{array}{@{}l} {}_{H}D_{a^{ +}}^{q}u(t) = f(t,u(t)),\quad q \in (1,2),t \in (a,T] \mbox{ and}\\ \quad t \ne \bar{t}_{l}\ (l = 1,2,\ldots,n), \\ \Delta ( {}_{H}D_{a^{ +}}^{q - 1}u ) \vert _{t = \bar{t}_{l}} = {}_{H}D_{a^{ +}}^{q - 1}u(\bar{t}_{l}^{ +} ) - {}_{H}D_{a^{ +}}^{q - 1}u(\bar{t}_{l}^{ -} ) = \bar{\Delta}_{l} ( u(\bar{t}_{l}^{ -} ) ),\\ \quad l = 1,2,\ldots,n, \\ {}_{H}D_{a^{ +}}^{q - 1}u(a^{ +} ) = u_{1},\qquad{}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(a^{ +} ) = u_{2}, \end{array}\displaystyle \right . \\ &\quad\to \left \{ \textstyle\begin{array}{@{}l} {}_{H}D_{a^{ +}}^{q}u(t) = f(t,u(t)),\quad q \in (1,2),t \in (a,T], \\ {}_{H}D_{a^{ +}}^{q - 1}u(a^{ +} ) = u_{1},\qquad {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(a^{ +} ) = u_{2}, \end{array}\displaystyle \right . \end{aligned}$$
that is,
$$\begin{aligned} &\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0, \ldots,\bar{\Delta}_{n} ( u(\bar{t}_{n}^{ -} ) ) \to 0} \bigl\{ \mbox{the solution of system } (3.2) \bigr\} \\ &\quad= \bigl\{ \mbox{the solution of system } (3.3) \bigr\} . \end{aligned}$$
(3.24)
Obviously, Eq. (3.23) satisfies condition (3.24).
Next, taking the Hadamard fractional derivative to Eq. (3.23) for each \(t \in (\bar{t}_{l},\bar{t}_{l + 1}] \) (\(l = 0,1, 2,\ldots, n\)), we have
$$\begin{aligned} {}_{H}D_{a^{ +}}^{q}u(t) ={}& {}_{H}D_{a^{ +}}^{q} \Biggl\{ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} + \sum _{j = 1}^{l} \frac{\bar{\Delta}_{j} ( u(\bar{t}_{j}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{j}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \sum_{j = 1}^{l} \hbar \bar{ \Delta}_{j} \bigl( u\bigl(\bar{t}_{j}^{ -} \bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{j}} f(s,u(s))\frac{ds}{s}}{ \Gamma (q)} \biggl( \int_{\bar{t}_{j}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{\bar{t}_{j}}{a} + u_{2} + \int_{a}^{\bar{t}_{j}} (\ln \frac{\bar{t}_{j}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{j}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{j}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \Biggr\} \\ ={}& f\bigl(t,u(t)\bigr)_{t \ge a} \vert _{t \in (\bar{t}_{l},\bar{t}_{l + 1}]} \\ &{}- \Biggl\{ \sum _{j = 1}^{l} \hbar \bar{\Delta}_{j} \bigl( u\bigl(\bar{t}_{j}^{ -} \bigr) \bigr) \bigl[ f \bigl(t,u(t)\bigr)_{t \ge a} - f\bigl(t,u(t)\bigr)_{t \ge \bar{t}_{j}} \bigr] \Biggr\} _{t \in (\bar{t}_{l},\bar{t}_{l + 1}]} \\ =&{} f\bigl(t,u(t)\bigr) \vert _{t \in (\bar{t}_{l},\bar{t}_{l + 1}]}. \end{aligned}$$
So, Eq. (3.23) satisfies the Hadamard fractional derivative of system (3.2).
Finally, for each \(\bar{t}_{l} \) (\(l = 1, 2,\ldots, n\)) in Eq. (3.23), we have
$$\begin{aligned} &{}_{H}D_{a^{ +}}^{q - 1}u\bigl(\bar{t}_{l}^{ +} \bigr) - {}_{H}D_{a^{ +}}^{q - 1}u\bigl( \bar{t}_{l}^{ -} \bigr) \\ &\quad= \biggl\{ \frac{1}{\Gamma (2 - q)} \biggl( t\frac{d}{dt} \biggr) \int_{a}^{t} \biggl(\ln \frac{t}{\eta} \biggr)^{1 - q}u(\eta )\frac{d\eta}{\eta} \biggr\} _{t \to \bar{t}_{l}^{ +}} \\ &\qquad{}- \biggl\{ \frac{1}{\Gamma (2 - q)} \biggl( t\frac{d}{dt} \biggr) \int_{a}^{t} \biggl(\ln \frac{t}{\eta} \biggr)^{1 - q}u(\eta )\frac{d\eta}{\eta} \biggr\} _{t = \bar{t}_{l}^{ -}} \\ &\quad= \bar{\Delta}_{l} \bigl( u\bigl(\bar{t}_{l}^{ -} \bigr) \bigr). \end{aligned}$$
Therefore, Eq. (3.23) satisfies the impulsive conditions of (3.2). Thus, Eq. (3.23) satisfies all conditions of (3.2).
Sufficiency. We will prove that the solutions of system (3.2) satisfy Eq. (3.23) by mathematical induction. For \(t \in (a,t_{1}]\), by Definitions 2.1 and 2.2, the solution of system (3.2) satisfies
$$\begin{aligned} u(t) ={}& \frac{u_{1}}{\Gamma (q)}\biggl(\ln \frac{t}{a} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)}\biggl(\ln \frac{t}{a} \biggr)^{q - 2} + \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\quad \mbox{for } t \in (a,\bar{t}_{1}]. \end{aligned}$$
(3.25)
By (3.25) and Definitions 2.1 and 2.2 we have
$${}_{H}D_{a^{ +}}^{q - 1}u \bigl(\bar{t}_{1}^{ +} \bigr) = {}_{H}D_{a^{ +}}^{q - 1}u \bigl( \bar{t}_{1}^{ -} \bigr) = u_{1} + \int_{a}^{\bar{t}_{1}} f \bigl(s,u(s) \bigr)\frac{ds}{s} + \bar{\Delta}_{1} \bigl( u \bigl(\bar{t}_{1}^{ -} \bigr) \bigr) $$
and
$${}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u \bigl( \bar{t}_{1}^{ +} \bigr) = {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u \bigl(\bar{t}_{1}^{ -} \bigr) = u_{1} \biggl( \int_{a}^{\bar{t}_{1}} \frac{ds}{s} \biggr) + u_{2} + \int_{a}^{\bar{t}_{1}} \biggl(\ln \frac{\bar{t}_{1}}{s} \biggr)f \bigl(s,u(s) \bigr)\frac{ds}{s}. $$
Therefore, the approximate solution for \(t \in (\bar{t}_{1},\bar{t}_{2}]\) is provided by
$$\begin{aligned} \bar{u}(t) ={}& \frac{1}{\Gamma (q)} \bigl( {}_{H}D_{a^{ +}}^{q - 1}u \bigl(\bar{t}_{1}^{ +} \bigr) \bigr) \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{1}{\Gamma (q - 1)} \bigl( {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u \bigl(\bar{t}_{1}^{ +} \bigr) \bigr) \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{} + \frac{1}{\Gamma (q)} \int_{\bar{t}_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ ={}& \frac{u_{1} + \int_{a}^{\bar{t}_{1}} f(s,u(s))\frac{ds}{s} + \bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}+ \frac{u_{1}\ln \frac{\bar{t}_{1}}{a} + u_{2} + \int_{a}^{\bar{t}_{1}} (\ln \frac{\bar{t}_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{\bar{t}_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \quad\mbox{for } t \in (\bar{t}_{1},\bar{t}_{2}]. \end{aligned}$$
(3.26)
Let \(\bar{e}_{1}(t) = u(t) - \bar{u}(t)\) for \(t \in (\bar{t}_{1},\bar{t}_{2}]\). Due to
$$\begin{aligned} \lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0}u(t) ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\quad \mbox{for } t \in ( \bar{t}_{1},\bar{t}_{2}], \end{aligned}$$
we have
$$\begin{aligned} &\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0}\bar{e}_{1}(t) \\ &\quad= \lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0} \bigl\{ u(t) - \bar{u}(t) \bigr\} \\ &\quad= \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\qquad{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &\qquad{}- \frac{u_{1}\ln \frac{\bar{t}_{1}}{a} + u_{2} + \int_{a}^{\bar{t}_{1}} (\ln \frac{\bar{t}_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\qquad{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\quad \mbox{for } t \in ( \bar{t}_{1},\bar{t}_{2}]. \end{aligned}$$
Therefore, we assume that
$$\begin{aligned} \bar{e}_{1}(t) ={}& \delta \bigl(\bar{\Delta}_{1} \bigl( u \bigl(\bar{t}_{1}^{ -} \bigr) \bigr)\bigr)\lim _{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0}\bar{e}_{1}(t) \\ ={}& \delta \bigl(\bar{\Delta}_{1} \bigl( u\bigl( \bar{t}_{1}^{ -} \bigr) \bigr)\bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{1}} f(s,u(s))\frac{ds}{s}}{ \Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{\bar{t}_{1}}{a} + u_{2} + \int_{a}^{\bar{t}_{1}} (\ln \frac{\bar{t}_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\biggr], \end{aligned}$$
where \(\delta ( \cdot )\) is an undetermined function with \(\delta (0) = 1\). So,
$$\begin{aligned} u(t) ={}& \bar{u}(t) + \bar{e}_{1}(t) \\ ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} + \frac{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \bigl( 1 - \delta \bigl(\bar{\Delta}_{1} \bigl( u\bigl( \bar{t}_{1}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{1}} f(s,u(s))\frac{ds}{s}}{ \Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{\bar{t}_{1}}{a} + u_{2} + \int_{a}^{\bar{t}_{1}} (\ln \frac{\bar{t}_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \quad\mbox{for } t \in (\bar{t}_{1},\bar{t}_{2}]. \end{aligned}$$
(3.27)
By (3.27) we obtain
$${}_{H}D_{a^{ +}}^{q - 1}u \bigl(\bar{t}_{2}^{ +} \bigr) = {}_{H}D_{a^{ +}}^{q - 1}u \bigl( \bar{t}_{2}^{ -} \bigr) + \bar{\Delta}_{2} \bigl( u \bigl(\bar{t}_{2}^{ -} \bigr) \bigr) = u_{1} + \int_{a}^{\bar{t}_{2}} f \bigl(s,u(s) \bigr)\frac{ds}{s} + \bar{\Delta}_{1} \bigl( u \bigl(\bar{t}_{1}^{ -} \bigr) \bigr) + \bar{\Delta}_{2} \bigl( u \bigl(\bar{t}_{2}^{ -} \bigr) \bigr) $$
and
$${}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u\bigl( \bar{t}_{2}^{ +} \bigr) = {}_{H} \mathcal{J}_{a^{ +}}^{2 - q}u\bigl(\bar{t}_{2}^{ -} \bigr) = u_{1}\ln \frac{\bar{t}_{2}}{a} + u_{2} + \bar{ \Delta}_{1} \bigl( u\bigl(\bar{t}_{1}^{ -} \bigr) \bigr)\ln \frac{\bar{t}_{2}}{\bar{t}_{1}} + \int_{a}^{\bar{t}_{2}} \ln \frac{\bar{t}_{2}}{s}f\bigl(s,u(s) \bigr)\frac{ds}{s}. $$
So, the approximate solution for \(t \in (\bar{t}_{2},\bar{t}_{3}]\) is given by
$$ \begin{aligned}[b] \bar{u}(t) ={}& \frac{1}{\Gamma (q)} \bigl( {}_{H}D_{a^{ +}}^{q - 1}u \bigl(\bar{t}_{2}^{ +} \bigr) \bigr) \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{1}{\Gamma (q - 1)} \bigl( {}_{H} \mathcal{J}_{a^{ +}}^{2 - q}u\bigl(\bar{t}_{2}^{ +} \bigr) \bigr) \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{\bar{t}_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\\ ={}& \frac{u_{1} + \int_{a}^{\bar{t}_{2}} f(s,u(s))\frac{ds}{s} + \bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) + \bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}+ \frac{u_{1}\ln \frac{\bar{t}_{2}}{a} + u_{2} + \bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) )\ln \frac{\bar{t}_{2}}{\bar{t}_{1}} + \int_{a}^{\bar{t}_{2}} (\ln \frac{\bar{t}_{2}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2}\\ &{}+ \frac{1}{\Gamma (q)} \int_{\bar{t}_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\quad \mbox{for } t \in ( \bar{t}_{2},\bar{t}_{3}]. \end{aligned} $$
(3.28)
Let \(\bar{e}_{2}(t) = u(t) - \bar{u}(t)\) for \(t \in (\bar{t}_{2},\bar{t}_{3}]\). By (3.27) the exact solution \(u(t)\) of system (3.2) satisfies
$$\begin{aligned}& \mathop{\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0, }}\limits _{\bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) ) \to 0}u(t) = \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2}\\& \hphantom{\mathop{\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0, }}\limits _{\bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) ) \to 0}u(t) =}{} + \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\quad \mbox{for } t \in ( \bar{t}_{2},\bar{t}_{3}], \\& \lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0}u(t) \\& \quad= \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\& \qquad{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} + \frac{\bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\& \qquad{}- \bigl( 1 - \delta \bigl(\bar{\Delta}_{2} \bigl( u\bigl( \bar{t}_{2}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\& \qquad{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{2}} f(s,u(s))\frac{ds}{s}}{ \Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\& \qquad{}- \frac{u_{1}\ln \frac{\bar{t}_{2}}{a} + u_{2} + \int_{a}^{\bar{t}_{2}} (\ln \frac{\bar{t}_{2}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\& \qquad{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \quad\mbox{for } t \in (\bar{t}_{2},\bar{t}_{3}], \\& \lim_{\bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) ) \to 0}u(t) \\& \quad= \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\& \qquad{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} + \frac{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\& \qquad{}- \bigl( 1 - \delta \bigl(\bar{\Delta}_{1} \bigl( u\bigl( \bar{t}_{1}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2}\\& \qquad{} + \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{1}} f(s,u(s))\frac{ds}{s}}{ \Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\& \qquad{}- \frac{u_{1}\ln \frac{\bar{t}_{1}}{a} + u_{2} + \int_{a}^{\bar{t}_{1}} (\ln \frac{\bar{t}_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\& \qquad{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \quad\mbox{for } t \in (\bar{t}_{2},\bar{t}_{3}]. \end{aligned}$$
Therefore,
$$\begin{aligned} &\mathop{\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0, }}\limits _{ \bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) ) \to 0}\bar{e}_{2}(t) = \mathop{\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0, }}\limits _{\bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) ) \to 0} \bigl\{ u(t) - \bar{u}(t) \bigr\} \\ &\hphantom{\mathop{\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0, }}\limits _{ \bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) ) \to 0}\bar{e}_{2}(t)}= \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\hphantom{\mathop{\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0, }}\limits _{ \bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) ) \to 0}\bar{e}_{2}(t)=}{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{2}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &\hphantom{\mathop{\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0, }}\limits _{ \bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) ) \to 0}\bar{e}_{2}(t)=}{} - \frac{u_{1}\ln \frac{\bar{t}_{2}}{a} + u_{2} + \int_{a}^{\bar{t}_{2}} (\ln \frac{\bar{t}_{2}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\hphantom{\mathop{\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0, }}\limits _{ \bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) ) \to 0}\bar{e}_{2}(t)=}{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\quad \mbox{for } t \in ( \bar{t}_{2},\bar{t}_{3}], \end{aligned}$$
(3.29)
$$\begin{aligned} &\lim_{\bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) ) \to 0}\bar{e}_{2}(t) \\ &\quad= \lim_{\bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) ) \to 0} \bigl\{ u(t) - \bar{u}(t) \bigr\} \\ &\quad= \frac{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} - \frac{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} - \frac{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) )}{\Gamma (q - 1)}\ln \frac{\bar{t}_{2}}{\bar{t}_{1}} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\qquad{}+ \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} + \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ &\qquad{}- \frac{u_{1} + \int_{a}^{\bar{t}_{2}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &\qquad{}- \frac{u_{1}\ln \frac{\bar{t}_{2}}{a} + u_{2} + \int_{a}^{\bar{t}_{2}} (\ln \frac{\bar{t}_{2}}{s})f(s,u(s))\frac{ds}{s}}{ \Gamma (q - 1)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\qquad{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \\ &\qquad{}- \bigl( 1 - \delta \bigl(\bar{\Delta}_{1} \bigl( u\bigl( \bar{t}_{1}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\qquad{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{1}} f(s,u(s))\frac{ds}{s}}{ \Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &\qquad{}- \frac{u_{1}\ln \frac{\bar{t}_{1}}{a} + u_{2} + \int_{a}^{\bar{t}_{1}} (\ln \frac{\bar{t}_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\qquad{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\biggr] \quad\mbox{for } t \in (\bar{t}_{2},\bar{t}_{3}], \end{aligned}$$
(3.30)
$$\begin{aligned} &\lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0}\bar{e}_{2}(t) \\ &\quad= \lim_{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) \to 0} \bigl\{ u(t) - \bar{u}(t) \bigr\} \\ &\quad= \delta \bigl(\bar{\Delta}_{2} \bigl( u\bigl( \bar{t}_{2}^{ -} \bigr) \bigr)\bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\qquad{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{2}} f(s,u(s))\frac{ds}{s}}{ \Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &\qquad{}- \frac{u_{1}\ln \frac{\bar{t}_{2}}{a} + u_{2} + \int_{a}^{\bar{t}_{2}} (\ln \frac{\bar{t}_{2}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\qquad{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\biggr] \quad\mbox{for } t \in (\bar{t}_{2},\bar{t}_{3}]. \end{aligned}$$
(3.31)
So, by (3.29)-(3.31) we obtain
$$\begin{aligned} \bar{e}_{2}(t) = {}&\frac{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} - \frac{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} - \frac{\Delta_{1} ( u(\bar{t}_{1}^{ -} ) )\ln \frac{\bar{t}_{2}}{\bar{t}_{1}}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \delta \bigl(\bar{\Delta}_{2} \bigl( u\bigl( \bar{t}_{2}^{ -} \bigr) \bigr)\bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{2}} f(s,u(s))\frac{ds}{s}}{ \Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{\bar{t}_{2}}{a} + u_{2} + \int_{a}^{\bar{t}_{2}} (\ln \frac{\bar{t}_{2}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \\ &{}- \bigl( 1 - \delta \bigl(\bar{\Delta}_{1} \bigl( u\bigl( \bar{t}_{1}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{1}} f(s,u(s))\frac{ds}{s}}{ \Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{\bar{t}_{1}}{a} + u_{2} + \int_{a}^{\bar{t}_{1}} (\ln \frac{\bar{t}_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \quad\mbox{for } t \in (\bar{t}_{2},\bar{t}_{3}]. \end{aligned}$$
(3.32)
Thus,
$$\begin{aligned} u(t) ={}& \bar{u}(t) + \bar{e}_{2}(t) \\ ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} + \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ &{} + \frac{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{\bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \bigl( 1 - \delta \bigl(\bar{\Delta}_{1} \bigl( u\bigl( \bar{t}_{1}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{1}} f(s,u(s))\frac{ds}{s}}{ \Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{\bar{t}_{1}}{a} + u_{2} + \int_{a}^{\bar{t}_{1}} (\ln \frac{\bar{t}_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \\ &{}- \bigl( 1 - \delta \bigl(\bar{\Delta}_{2} \bigl( u\bigl( \bar{t}_{2}^{ -} \bigr) \bigr)\bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{2}} f(s,u(s))\frac{ds}{s}}{ \Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{\bar{t}_{2}}{a} + u_{2} + \int_{a}^{\bar{t}_{2}} (\ln \frac{\bar{t}_{2}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \quad\mbox{for } t \in (\bar{t}_{2},\bar{t}_{3}]. \end{aligned}$$
(3.33)
Letting \(\bar{t}_{2} \to \bar{t}_{1}\), we have
$$\begin{aligned} &\lim_{\bar{t}_{2} \to \bar{t}_{1}} \left \{ \textstyle\begin{array}{@{}l} {}_{H}D_{a^{ +}}^{q}u(t) = f(t,u(t)),\quad q \in (1,2),t \in (a,\bar{t}_{3}] \mbox{ and } t \ne \bar{t}_{1} \mbox{ and } t \ne \bar{t}_{2}, \\ \Delta ( {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u ) \vert _{t = \bar{t}_{l}} = {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(\bar{t}_{l}^{ +} ) - {}_{H}\mathcal{J}_{a^{ +}}^{1 - q}u(\bar{t}_{l}^{ -} ) = \bar{\Delta}_{l} ( u(\bar{t}_{l}^{ -} ) ), \quad l = 1,2, \\ {}_{H}D_{a^{ +}}^{q - 1}u(a^{ +} ) = u_{1},\qquad {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(a^{ +} ) = u_{2} \end{array}\displaystyle \right . \end{aligned}$$
(3.34)
$$\begin{aligned} &\quad\to \left \{ \textstyle\begin{array}{@{}l} {}_{H}D_{a^{ +}}^{q}u(t) = f(t,u(t)),\quad q \in (0,1),t \in (a,\bar{t}_{3}] \mbox{ and } t \ne \bar{t}_{1}, \\ \Delta ( {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u ) \vert _{t = \bar{t}_{1}} = \bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) ) + \bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) ), \\ {}_{H}D_{a^{ +}}^{q - 1}u(a^{ +} ) = u_{1},\qquad {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u(a^{ +} ) = u_{2}. \end{array}\displaystyle \right . \end{aligned}$$
(3.35)
Using (3.27) and (3.33) in systems (3.35) and (3.34), respectively, we have
$$1 - \delta (\bar{\Delta}_{1} + \bar{\Delta}_{2}) = 1 - \delta (\bar{\Delta}_{1}) + 1 - \delta (\bar{\Delta}_{2}) \quad \forall \bar{\Delta}_{1},\bar{\Delta}_{2} \in \mathbb{R}. $$
Letting \(\gamma (z) = 1 - \delta (z) \) (\(\forall z \in \mathbb{R}\)), we have \(\gamma (z + w) = \gamma (z) + \gamma (w)\) (\(\forall z,w \in \mathbb{R}\)). Therefore, \(\gamma (z) = \hbar z\), where ħ is a constant. So, by (3.27) and (3.33) we get
$$\begin{aligned} u(t) ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} + \frac{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \hbar \bar{\Delta}_{1} \bigl( u\bigl(\bar{t}_{1}^{ -} \bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{} - \frac{u_{1}\ln \frac{\bar{t}_{1}}{a} + u_{2} + \int_{a}^{\bar{t}_{1}} (\ln \frac{\bar{t}_{1}}{s})f(s,u(s))\frac{ds}{s}}{ \Gamma (q - 1)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr]\quad \mbox{for } t \in (\bar{t}_{1},\bar{t}_{2}], \end{aligned}$$
and
$$\begin{aligned} u(t) ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} + \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ &{}+ \frac{\bar{\Delta}_{1} ( u(\bar{t}_{1}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{\bar{\Delta}_{2} ( u(\bar{t}_{2}^{ -} ) )}{\Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \hbar \bar{\Delta}_{1} \bigl( u\bigl(\bar{t}_{1}^{ -} \bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{} - \frac{u_{1}\ln \frac{\bar{t}_{1}}{a} + u_{2} + \int_{a}^{\bar{t}_{1}} (\ln \frac{\bar{t}_{1}}{s})f(s,u(s))\frac{ds}{s}}{ \Gamma (q - 1)} \biggl( \int_{\bar{t}_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr] \\ &{}- \hbar \bar{\Delta}_{2} \bigl( u\bigl(\bar{t}_{2}^{ -} \bigr) \bigr) \biggl[ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{\bar{t}_{2}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{} - \frac{u_{1}\ln \frac{\bar{t}_{2}}{a} + u_{2} + \int_{a}^{\bar{t}_{2}} (\ln \frac{\bar{t}_{2}}{s})f(s,u(s))\frac{ds}{s}}{ \Gamma (q - 1)} \biggl( \int_{\bar{t}_{2}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{\bar{t}_{2}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr]\quad \mbox{for } t \in (\bar{t}_{2},\bar{t}_{3}]. \end{aligned}$$
Due to similarity of the proof with Lemma 3.2, the rest of proof is omitted.
So, system (3.2) is equivalent to Eq. (3.23). The proof is now completed. □
Theorem 3.4
Let
\(q \in(1, 2)\), and let
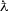 , ħ
be two constants. System (1.1) is equivalent to the fractional integral equation
, ħ
be two constants. System (1.1) is equivalent to the fractional integral equation
provided that the integral in (3.36) exists.
Proof
Necessity. We will verify that Eq. (3.36) satisfies the conditions of system (1.1).
First, we can easily verify that Eq. (3.36) satisfies the three implicit conditions (i)-(iii) by Lemmas 3.2 and 3.3.
Second, the proof that Eq. (3.36) satisfies the Hadamard fractional derivative and impulsive conditions of system (1.1) is similar to that of Lemma 3.2 and is omitted.
Sufficiency. We will prove that the solutions of system (3.1) satisfy Eq. (3.36) by mathematical induction. For \(t \in [a,t'_{1}]\), it is clear that the solution of system (1.1) satisfies Eq. (3.36) with
$$\begin{aligned} u(t) ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f \bigl(s,u(s) \bigr)\frac{ds}{s}\quad \mbox{for } t \in \bigl[a,t'_{1} \bigr]. \end{aligned}$$
(3.37)
For \(t \in (t'_{1},t'_{2}]\), there exist three cases \(t'_{1} = t_{1} < \bar{t}_{1}\), \(t'_{1} = \bar{t}_{1} < t_{1}\), and \(t'_{1} = t_{1} = \bar{t}_{1}\). For the two cases (\(t'_{1} = t_{1} < \bar{t}_{1}\) and \(t'_{1} = \bar{t}_{1} < t_{1}\)), we can verify that the solution of (1.1) satisfies Eq. (3.36) for \(t \in (t'_{1},t'_{2}]\) by Lemmas 3.2 and 3.3, respectively. Hence, we will consider the case \(t'_{1} = t_{1} = \bar{t}_{1}\). Using (3.37), we have
$$\begin{aligned}& {}_{H}D_{a^{ +}}^{q - 1}u \bigl(t_{1}^{\prime +} \bigr) = {}_{H}D_{a^{ +}}^{q - 1}u \bigl(t_{1}^{\prime -} \bigr) + \bar{\Delta}_{1} \bigl( u \bigl(t_{1}^{\prime -} \bigr) \bigr) = u_{1} + \int_{a}^{t'_{1}} f \bigl(s,u(s) \bigr)\frac{ds}{s} + \bar{\Delta}_{1} \bigl( u \bigl(t_{1}^{\prime -} \bigr) \bigr) \quad\mbox{and} \\& \begin{aligned}[b] {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u \bigl(t_{1}^{\prime +} \bigr) &= {}_{H} \mathcal{J}_{a^{ +}}^{2 - q}u \bigl(t_{1}^{\prime -} \bigr) + \Delta_{1} \bigl( u \bigl(t_{1}^{\prime -} \bigr) \bigr) \\ &= u_{1}\ln \frac{t'_{1}}{a} + u_{2} + \int_{a}^{t'_{1}} \ln \frac{t'_{1}}{s}f \bigl(s,u(s) \bigr)\frac{ds}{s} + \Delta_{1} \bigl( u \bigl(t_{1}^{\prime -} \bigr) \bigr). \end{aligned} \end{aligned}$$
Therefore, the approximate solution of system (1.1) for \(t \in (t'_{1},t'_{2}]\) is given by
$$\begin{aligned} \hat{u}(t) ={}& \frac{1}{\Gamma (q)} \bigl( {}_{H}D_{a^{ +}}^{q - 1}u \bigl(t_{1}^{\prime +} \bigr) \bigr) \biggl( \int_{t'_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{1}{\Gamma (q - 1)} \bigl( {}_{H} \mathcal{J}_{a^{ +}}^{2 - q}u\bigl(t_{1}^{\prime +} \bigr) \bigr) \biggl( \int_{t'_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{t'_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ =&{} \frac{u_{1} + \int_{a}^{t'_{1}} f(s,u(s))\frac{ds}{s} + \bar{\Delta}_{1} ( u(t_{1}^{\prime -} ) )}{\Gamma (q)} \biggl( \int_{t'_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}+ \frac{u_{1}\ln \frac{t'_{1}}{a} + u_{2} + \int_{a}^{t'_{1}} \ln \frac{t'_{1}}{s}f(s,u(s))\frac{ds}{s} + \Delta_{1} ( u(t_{1}^{\prime -} ) )}{\Gamma (q - 1)} \biggl( \int_{t'_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{t'_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \quad\mbox{for } t \in \bigl(t'_{1},t'_{2}\bigr]. \end{aligned}$$
(3.38)
Let \(\hat{e}_{1}(t) = u(t) - \hat{u}(t)\) for \(t \in (t'_{1},t'_{2}]\). By Lemmas 3.2 and 3.3 the exact solution \(u(t)\) of system (1.1) satisfies
Therefore,
$$\begin{aligned} \mathop{\lim_{\Delta_{1} ( u(t_{1}^{\prime -} ) ) \to 0, }}\limits _{ \bar{\Delta}_{1} ( u(t_{1}^{\prime -} ) ) \to 0}\hat{e}_{1}(t) ={}& \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{t'_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t'_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{t'_{1}}{a} + u_{2} + \int_{a}^{t'_{1}} \ln \frac{t'_{1}}{s}f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t'_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}- \frac{1}{\Gamma (q)} \int_{t'_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \quad\mbox{for } t \in \bigl(t'_{1},t'_{2}\bigr], \end{aligned}$$
(3.39)
$$\begin{aligned} \lim_{\Delta_{1} ( u(t_{1}^{\prime -} ) ) \to 0}\hat{e}_{1}(t) ={}& \bigl[ 1 - \hbar \bar{\Delta}_{1} \bigl( u \bigl(t_{1}^{\prime -} \bigr) \bigr) \bigr] \biggl\{ \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} - \frac{u_{1} + \int_{a}^{t'_{1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t'_{1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}- \frac{u_{1}\ln \frac{t'_{1}}{a} + u_{2} + \int_{a}^{t'_{1}} (\ln \frac{t'_{1}}{s})f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t'_{1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{} - \frac{1}{\Gamma (q)} \int_{t'_{1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \biggr\} \quad\mbox{for } t \in \bigl(t'_{1},t'_{2}\bigr], \end{aligned}$$
(3.40)
By (3.39)-(3.41) we get
Then,
Next, for \(t \in (t'_{k},t'_{k + 1}]\) (\(k =1, 2, \ldots, \Omega\)), suppose that
By (3.43) we have
$$\begin{aligned} {}_{H}D_{a^{ +}}^{q - 1}u \bigl(t_{k + 1}^{\prime +} \bigr) &= {}_{H}D_{a^{ +}}^{q - 1}u \bigl(t_{k + 1}^{\prime -} \bigr) + \sum_{k_{1} + 1}^{(k + 1)_{1}} \bar{ \Delta}_{j} \\ &= u_{1} + \int_{a}^{t'_{k + 1}} f \bigl(s,u(s) \bigr)\frac{ds}{s} + \sum_{j = 1}^{(k + 1)_{1}} \bar{ \Delta}_{j} \bigl( u \bigl(\bar{t}_{j}^{ -} \bigr) \bigr) \end{aligned}$$
and
$$\begin{aligned}[b] {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u \bigl(t_{k + 1}^{\prime +} \bigr) ={}& {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u\bigl(t_{k + 1}^{\prime -} \bigr) + \sum_{k_{0} + 1}^{(k + 1)_{0}} \Delta_{i} \bigl( u\bigl(t_{i}^{ -} \bigr) \bigr) \\ ={}& u_{1} \int_{a}^{t'_{k + 1}} \frac{ds}{s} + u_{2} + \int_{a}^{t'_{k + 1}} \ln \frac{t'_{k + 1}}{s}f\bigl(s,u(s) \bigr)\frac{ds}{s} + \sum_{i = 1}^{(k + 1)_{0}} \Delta_{i} \bigl( u\bigl(t_{i}^{ -} \bigr) \bigr) \\ &{}+ \sum_{j = 1}^{k_{1}} \bar{\Delta}_{j} \bigl( u\bigl(\bar{t}_{j}^{ -} \bigr) \bigr)\ln \frac{t'_{k + 1}}{\bar{t}_{j}}. \end{aligned} $$
Therefore, the approximate solution of system (1.1) for \(t \in (t'_{k + 1},t'_{k + 2}]\) is given by
$$\begin{aligned} \hat{u}(t) ={}& \frac{1}{\Gamma (q)} \bigl( {}_{H}D_{a^{ +}}^{q - 1}u \bigl(t_{k + 1}^{\prime +} \bigr) \bigr) \biggl( \int_{t'_{k + 1}}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{1}{\Gamma (q - 1)} \bigl( {}_{H}\mathcal{J}_{a^{ +}}^{2 - q}u\bigl(t_{k + 1}^{\prime +} \bigr) \bigr) \biggl( \int_{t'_{k + 1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &{}+ \frac{1}{\Gamma (q)} \int_{t'_{k + 1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ ={}& \frac{u_{1} + \int_{a}^{t'_{k + 1}} f(s,u(s))\frac{ds}{s} + \sum_{j = 1}^{(k + 1)_{1}} \bar{\Delta}_{j} ( u(\bar{t}_{j}^{ -} ) )}{ \Gamma (q)} \biggl( \int_{t'_{k + 1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &{}+ \frac{u_{1}\ln \frac{t'_{k + 1}}{a} + u_{2} + \int_{a}^{t'_{k + 1}} \ln \frac{t'_{k + 1}}{s}f(s,u(s))\frac{ds}{s} + \sum_{i = 1}^{(k + 1)_{0}} \Delta_{i} ( u(t_{i}^{ -} ) ) + \sum_{j = 1}^{k_{1}} \bar{\Delta}_{j} ( u(\bar{t}_{j}^{ -} ) )\ln \frac{t'_{k + 1}}{\bar{t}_{j}}}{\Gamma (q - 1)} \\ &{}\times\biggl( \int_{t'_{k + 1}}^{t} \frac{ds}{s} \biggr)^{q - 2} + \frac{1}{\Gamma (q)} \int_{t'_{k + 1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s}\quad \mbox{for } t \in \bigl(t'_{k + 1},t'_{k + 2}\bigr]. \end{aligned}$$
(3.44)
Let \(\hat{e}_{k + 1}(t) = u(t) - \hat{u}(t)\) for \(t \in (t'_{k + 1},t'_{k + 2}]\). By (3.43) the exact solution of system (1.1) satisfies
Therefore,
$$\begin{aligned} &\mathop{\lim_{\Delta_{i} ( u(t_{i}^{ -} ) ) \to 0,\bar{\Delta}_{j} ( u(\bar{t}_{j}^{ -} ) ) \to 0}}\limits _{\mathrm{for\ all}\ i\ \mathrm{and}\ j}\hat{e}_{k + 1}(t) \\ &\quad= \mathop{\lim_{\Delta_{i} ( u(t_{i}^{ -} ) ) \to 0,\bar{\Delta}_{j} ( u(\bar{t}_{j}^{ -} ) ) \to 0 }}\limits _{\mathrm{for\ all}\ i\ \mathrm{and}\ j} \bigl\{ u(t) - \hat{u}(t) \bigr\} \\ &\quad= \frac{u_{1}}{\Gamma (q)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 1} + \frac{u_{2}}{\Gamma (q - 1)} \biggl( \int_{a}^{t} \frac{ds}{s} \biggr)^{q - 2} + \frac{1}{\Gamma (q)} \int_{a}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \\ &\qquad{}- \frac{u_{1} + \int_{a}^{t'_{k + 1}} f(s,u(s))\frac{ds}{s}}{\Gamma (q)} \biggl( \int_{t'_{k + 1}}^{t} \frac{ds}{s} \biggr)^{q - 1} \\ &\qquad{} - \frac{u_{1}\int_{a}^{t'_{k + 1}} \frac{ds}{s} + u_{2} + \int_{a}^{t'_{k + 1}} \ln \frac{t'_{k + 1}}{s}f(s,u(s))\frac{ds}{s}}{\Gamma (q - 1)} \biggl( \int_{t'_{k + 1}}^{t} \frac{ds}{s} \biggr)^{q - 2} \\ &\qquad{}- \frac{1}{\Gamma (q)} \int_{t'_{k + 1}}^{t} \biggl(\ln \frac{t}{s} \biggr)^{q - 1}f\bigl(s,u(s)\bigr)\frac{ds}{s} \quad\mbox{for } t \in \bigl(t'_{k + 1},t'_{k + 2}\bigr], \end{aligned}$$
(3.45)
By (3.45) and (3.46) we have
Thus,
So, system (1.1) is equivalent to the integral equation (3.36). The proof is now completed. □
Corollary 3.5
Let
\(q \in (1, 2)\), and let
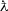 , ħ
be two constants. System (1.2) is equivalent to the fractional integral equation
, ħ
be two constants. System (1.2) is equivalent to the fractional integral equation
provided that the integral in (3.48) exists.
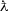 be a constant. System (3.1) is equivalent to the fractional integral equation
be a constant. System (3.1) is equivalent to the fractional integral equation


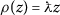 , where
, where  is a constant. So, by (3.9) and (3.14) we get
is a constant. So, by (3.9) and (3.14) we get 






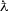 , ħ
be two constants. System (1.1) is equivalent to the fractional integral equation
, ħ
be two constants. System (1.1) is equivalent to the fractional integral equation










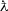 , ħ
be two constants. System (1.2) is equivalent to the fractional integral equation
, ħ
be two constants. System (1.2) is equivalent to the fractional integral equation


 , ħ are two constants. Next, we will verify that Eq. (4.2) satisfies all conditions of system (4.1).
, ħ are two constants. Next, we will verify that Eq. (4.2) satisfies all conditions of system (4.1).


