1 Introduction

Hibernation allows small mammals to minimize metabolic energy costs at a time when a scarcity of food and cold environmental temperatures endanger normal life. By hibernating, animals can reduce their energy requirements by at least ninety percent and survive for many months while slowly catabolizing body lipid reserves [1]. Hibernation constitutes an effective strategy of animals in order to survive cold environments and limited availability of food [2].

Biological resources are renewable resources. Clark [3] considered the economic and biological aspects of renewable resources management. In recent years, the optimal management of renewable resources, which has a direct relationship to sustainable development, has been studied extensively by many authors [4–8]. Especially, the predator-prey models with harvesting have been investigated by many papers [9–14]. Li and Wang [14] considered dynamics of an Ivlev-type predator-prey system with constant rate harvesting

$$ \left \{ \textstyle\begin{array}{l} \frac{dx(t)}{dt}=x(t)(1-x(t-\tau))-y(t)(1-e^{-rx(t)}-h), \\ \frac{dy(t)}{dt}= \beta y(t)(\alpha-1-\alpha e^{-rx(t)}), \end{array}\displaystyle \right . $$
(1.1)

where \(x(t)\) denotes the density of the prey population at time t. \(y(t)\) denotes the density of the predator population at time t. The biological meanings of the parameters can be found in [14]. There is a vast amount of literature on the applications of impulsive differential equations to investigate predator-prey systems and SI system [15–22]. Jiao et al. [20] also considered a three-dimensional predator-prey model with impulsive diffusion and harvesting on predator as follows:

$$ \left \{ \textstyle\begin{array}{l} \left . \textstyle\begin{array}{l} \frac{dx(t)}{dt}=x(t)(a-bx(t))-\beta x(t)y_{1}(t), \\ \frac{dy_{1}(t)}{dt}=k\beta x(t)y_{1}(t)-a_{1}y_{1}(t), \\ \frac{dy_{2}(t)}{dt}=y_{2}(t)(a_{2}-b_{2}y_{2}(t)), \end{array}\displaystyle \right \} \quad t\neq(n-1+l) \tau, t\neq n\tau, \\ \left . \textstyle\begin{array}{l} \triangle x(t)=-p_{1}x(t), \\ \triangle y_{1}(t)=0 , \\ \triangle y_{2}(t)= -p_{2} y_{2}(t), \end{array}\displaystyle \right \} \quad t= (n-1+l)\tau, n= 1,2, \ldots, \\ \left . \textstyle\begin{array}{l} \triangle x(t)=0, \\ \triangle y_{1}(t)=D(y_{2}(t)-y_{1}(t)) , \\ \triangle y_{2}(t)= D(y_{1}(t)-y_{2}(t)), \end{array}\displaystyle \right \}\quad t= n\tau, n= 1,2, \ldots, \end{array}\displaystyle \right . $$
(1.2)

where they suppose that system (1.2) is composed of two patches connected by diffusion and occupied by species \(x(t)\) and \(y_{i}(t)\) (\(i = 1, 2\)). \(x(t)\) and \(y_{i}(t)\) (\(i = 1, 2\)) represent the density of prey species in Patch 1 and the density of predator species in Patch i (\(i = 1, 2\)), respectively. The biological meanings of the parameters can be found in [20].

The hibernation constitutes an effective strategy of animals in order to survive cold environments and limited availability of food, it is a universal phenomenon in biological world. However, there are few papers considering and investigating mathematical models with winter hibernation. In this paper, we introduce the phenomenon of hibernation and focus on a periodic impulsive switched predator-prey system with hibernation and birth pulse.

The organization of this paper is as follows. In the next section, we introduce the model and background concepts. In Section 3, some important lemmas are presented. In Section 4, we give the globally asymptotically stable conditions of a prey-extinction periodic solution of system (2.1) and the permanent condition of system (2.1). In Section 5, a brief discussion and the simulations are given to conclude this work.

2 The model

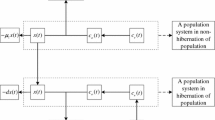
In this section, a periodic impulsive switched predator-prey system with hibernation and birth pulse is modeled by the nonlinear impulsive differential equation

$$ \left \{ \textstyle\begin{array}{l} \left . \textstyle\begin{array}{l} \frac{dx(t)}{dt}=x(t)(a-bx(t))-\beta_{1}x(t) y(t), \\ \frac{dy(t)}{dt}=k_{1}\beta_{1}x(t) y(t)-d_{1} y(t), \end{array}\displaystyle \right \} \quad t\in(n \tau,(n+l)\tau], \\ \left . \textstyle\begin{array}{l} \triangle x(t)=0, \\ \triangle y(t)=y(t)(a_{1}-b_{1} y(t)), \end{array}\displaystyle \right \} \quad t= (n+l)\tau,n \in Z^{+}, \\ \left . \textstyle\begin{array}{l} \frac{dx(t)}{dt}=-d_{2}x(t)-\beta_{2}x(t) y(t), \\ \frac{dy(t)}{dt}=k_{2}\beta_{2}x(t) y(t)-d_{3}y(t), \end{array}\displaystyle \right \}\quad t\in( (n+l)\tau, (n+1)\tau], \\ \left . \textstyle\begin{array}{l} \triangle x(t)=-\mu x(t), \\ \triangle y(t)=-\mu_{1}y(t), \end{array}\displaystyle \right \}\quad t= (n+1)\tau, n \in Z^{+}, \end{array}\displaystyle \right . $$
(2.1)

where the total population is divided into two subpopulations: prey population \(x(t)\) and predator population \(y(t)\). It is assumed that the prey population is hibernator, and the predators depend on prey as their source of food; if there is no prey, the predator population will disappear. The impulsive period is divided into hibernation and non-hibernation. The predator population is birth pulse in their non-hibernation of the prey population. Intrinsic rate of natural increase and density dependence rate of prey population are denoted by a and b, respectively. \(d_{1}\) is the natural death rate of the predator population. The predator population consumes the prey population with predation coefficients \(\beta_{1}\) in the non-hibernation period of prey population. \(k_{1}\) is the rate of conversion of nutrients into the predator population. \(d_{2}>0\) is the natural death rate of the prey population in the hibernation period of prey population. The predator population is birth pulse as intrinsic rate of natural increase and density dependence rate of prey population are denoted by \(a_{1}\) and \(b_{1}\) respectively at moments \(t=(n+l)\tau\), \(0< l<1\), \(n\in Z^{+}\), that is, the predator population is born in non-hibernation of prey population, and the predator population cannot have birth ability in hibernation of prey population. \(d_{3}>0\) is the natural death rate of the predator population in the hibernation period of prey population. The predator population consumes prey population with predation coefficients \(\beta_{2}\) in the hibernation period of prey population. \(k_{2}\) is the rate of conversion of nutrients into the predator population in the hibernation period of prey population. \(0<\mu<1\) is the harvesting coefficient of the prey population at moments \(t=(n+1)\tau\), \(n\in Z^{+}\). \(0<\mu_{1}<1\) is the harvesting coefficient of the predator population at moments \(t=(n+1)\tau\), \(n\in Z^{+}\). Time interval \((n\tau,(n+l)\tau]\) is the non-hibernation of prey population. Time interval \(((n+l)\tau,(n+1)\tau]\) is the hibernation of prey population.

3 Some lemmas

The solution of system (2.1), denoted by \(X(t)=(x(t),y(t))^{T}\), is a non-smooth function \(X: R_{+}\rightarrow R_{+}^{2}\), \(X(t)\) is continuous on \((n\tau,(n+l)\tau]\) and \(((n+l)\tau,(n+1)\tau ]\), \(n\in Z_{+}\). \(X(n\tau^{+})=\lim_{t\rightarrow n\tau^{+} }X(t)\) and \(X((n+l)\tau ^{+})=\lim_{t\rightarrow(n+l)\tau^{+} }X(t)\) exist. Obviously the global existence and uniqueness of solutions of system (2.1) are guaranteed by the smoothness properties of f, which denotes the mapping defined by the right-hand side of system (2.1) (see Lakshmikantham et al. [23]).

Lemma 3.1

For each solution \((x(t),y(t))\) of system (2.1), there exists a constant \(M>0\) such that \(x(t)\leq M\), \(y(t)\leq M \) with all t large enough.

Proof

Define \(V(t)=kx(t)+y(t)\), \(k=\max\{k_{1},k_{2}\}\), and \(d=\min\{d_{1},d_{2},d_{3}\}\). When \(t\in( n\tau,(n+l)\tau]\), we have

$$D^{+}V(t)+dV(t)\leq kx(t)\bigl[a-bx(t)\bigr]-(d_{1}-d )y(t) \leq\frac{k(a+d)^{2}}{4b}, $$

when \(t\in( (n+l)\tau,(n+1)\tau]\), we have

$$D^{+}V(t)+dV(t)\leq-k(d_{2}-d )x(t)-(d_{3}-d )y(t)\leq\delta_{1}< 0. $$

Then, taking \(\delta=\frac{k(a+d)^{2}}{4b}\), when \(t\neq n\tau\), \(t\neq (n+l)\tau\), we have

$$D^{+}V(t)+dV(t)\leq\delta. $$

When \(t=(n+l)\tau\), \(V((n+l)\tau^{+})= V((n+l)\tau)-b[y(t)-\frac{a_{1}}{2b_{1}}]^{2}+\frac {a_{1}^{2}}{4b_{1}}\leq V((n+l)\tau)+\zeta\), where \(\zeta=\frac{a_{1}^{2}}{4b_{1}}\). When \(t=(n+1)\tau\), \(V((n+1)\tau^{+})= (1-\mu)x((n+1)\tau)+(1-\mu_{1})y((n+1)\tau) \leq V((n+1)\tau)\). By the lemma of [24], for \(t\in(n\tau,(n+l)\tau]\) and \(t\in( (n+l)\tau,(n+1)\tau]\), we have

$$\begin{aligned} V(t)&\leq V(0)\exp(-dt)+\int^{t}_{0}\delta\exp \bigl(-d(t-s)\bigr)\,ds+\sum_{0< (n+l)\tau< t}\zeta e^{-d(t-(n+l)\tau)} \\ &=V(0)\exp(-dt)+\frac{\delta}{d}\bigl(1-\exp(-dt)\bigr)+\zeta\frac{e^{-d(t-l\tau )}-e^{-d(t-(n+l)\tau)}}{1-e^{-dl\tau}} \\ &< V(0)\exp(-dt)+\frac{\delta}{d}\bigl(1-\exp(-dt)\bigr)+\frac{\zeta e^{-d(t-l\tau )}}{1-e^{-dl\tau}}+ \frac{\zeta e^{dl\tau}}{e^{dl\tau}-1} \\ &\leq V(0)\exp(-dt)+\frac{\zeta e^{-d(t-l\tau)}}{1-e^{-dl\tau}}+\frac {\zeta e^{dl\tau}}{e^{dl\tau}-1} \\ &\rightarrow\frac{\zeta e^{dl\tau}}{e^{dl\tau}-1}\quad \mbox{as }t\rightarrow\infty. \end{aligned}$$

So \(V(t)\) is uniformly ultimately bounded. Hence, by the definition of \(V(t)\), we have that there exists a constant \(M>0\) such that \(x(t)\leq M\), \(y(t)\leq M\) for t large enough. The proof is complete. □

If \(x(t)=0\), we can easily have the subsystem of system (2.1) as follows:

$$ \left \{ \textstyle\begin{array}{l} \frac{dy(t)}{dt}=-d_{1}y(t), \quad t\in(n\tau,(n+l)\tau], \\ \triangle y(t)=y(t)(a_{1}-b_{1} y(t)),\quad t= (n+l)\tau,n\in Z^{+}, \\ \frac{dy(t)}{dt}=-d_{3}y(t), \quad t\in( (n+l)\tau, (n+1)\tau], \\ \triangle y(t)=-\mu_{1}y(t),\quad t= (n+1)\tau, n\in Z^{+}. \end{array}\displaystyle \right . $$
(3.1)

We can easily obtain the analytic solution of system (3.1) between pulses, i.e.,

$$ y(t)= \left \{ \textstyle\begin{array}{l@{\quad}l} y(n\tau^{+})e^{-d_{1}(t-n\tau)}, &t\in(n\tau,(n+l)\tau], \\ y((n+l)\tau^{+})e^{-d_{3}(t-(n+l)\tau)},&t\in((n+l)\tau,(n+1)\tau]. \end{array}\displaystyle \right . $$
(3.2)

Considering the second and fourth equations of system (3.1), we have the stroboscopic map of system (3.1)

$$\begin{aligned} y\bigl((n+1)\tau^{+}\bigr) =&(1-\mu_{1})y \bigl(n\tau^{+}\bigr)e^{-[d_{1}l\tau+d_{3}(1-l)\tau ]} \\ &{}+(1-\mu_{1})y\bigl(n\tau^{+}\bigr)e^{-[d_{1}l\tau+d_{3}(1-l)\tau ]} \bigl[a_{1}-b_{1}y\bigl(n\tau^{+} \bigr)e^{-d_{1}l\tau}\bigr]. \end{aligned}$$
(3.3)

Two fixed points of (3.3) are obtained as \(P_{1}(0)\) and \(P_{2}(y^{\ast})\), where

$$ y^{\ast}=\frac{(1-\mu_{1})(a_{1}+1)e^{-[d_{1}l\tau+d_{3}(1-l)\tau ]}-1}{(1-\mu_{1})be^{-d_{1}(1-l)\tau}\times e^{-[d_{1}l\tau +d_{3}(1-l)\tau]}},\quad (1-\mu_{1}) (a_{1}+1)e^{-[d_{1}l\tau+d_{3}(1-l)\tau ]}>1. $$
(3.4)

Lemma 3.2

[25]

Consider the following difference equation:

$$ z\bigl((t+1)\bigr)=F\bigl(z(t)\bigr) . $$
(3.5)

\(z^{\ast}\) satisfies

$$ z^{\ast}=F\bigl(z^{\ast}\bigr), $$
(3.6)

then \(z^{\ast}\) is called equilibrium of (3.5), and if

$$ {\biggl.\frac{\partial F(z)}{\partial z}\biggr|_{z=z^{\ast}}}< 1, $$
(3.7)

then the unique equilibrium \(z^{\ast}\) of (3.5) is globally asymptotically stable. Otherwise, it is not stable.

Lemma 3.3

  1. (i)

    If \((1-\mu_{1})(a_{1}+1)e^{-(d_{1}l\tau+d_{3}(1-l)\tau)}<1\), the fixed point \(P_{1}(0)\) of (3.3) is globally asymptotically stable.

  2. (ii)

    If \((1-\mu_{1})(a_{1}+1)e^{-(d_{1}l\tau+d_{3}(1-l)\tau)}>1\), the fixed point \(P_{2}(y^{\ast})\) of (3.3) is globally asymptotically stable.

Proof

Making notation as

$$\begin{aligned} F\bigl(y\bigl(n\tau^{+}\bigr)\bigr) =&(1- \mu_{1})y\bigl(n\tau^{+}\bigr)e^{-[d_{1}l\tau+d_{3}(1-l)\tau]} \\ &{}+(1-\mu_{1})y\bigl(n\tau^{+}\bigr)e^{-[d_{1}l\tau+d_{3}(1-l)\tau ]} \bigl[a_{1}-b_{1}y\bigl(n\tau^{+} \bigr)e^{-d_{1}l\tau}\bigr], \end{aligned}$$
(3.8)

then

$$ {\biggl.\frac{\partial F(y(n\tau^{+}))}{\partial y(n\tau^{+})}\biggr|_{y(n\tau ^{+})=0}}=(1-\mu_{1}) (a_{1}+1)e^{-[d_{1}l+d_{3}(1-l)]\tau}< 1 $$
(3.9)

and

$$ {\biggl.\frac{\partial F(y(n\tau^{+}))}{\partial y(n\tau^{+})}\biggr|_{y(n\tau ^{+})=y^{\ast}}}=2-(1-\mu_{1}) (a_{1}+1)e^{-[d_{1}l+d_{3}(1-l)]\tau}< 1. $$
(3.10)

From Lemma 3.2, we obtain that the fixed points \(P(0)\) and \(P(y^{\ast })\) of (3.3) are stable, and then they are globally asymptotically stable. □

It is well known that the following lemma can easily be proved.

Lemma 3.4

  1. (i)

    If \((1-\mu_{1})(a_{1}+1)e^{-[d_{1}l+d_{3}(1-l)]\tau}<1\), the triviality periodic solution of system (3.1) is globally asymptotically stable.

  2. (ii)

    If \((1-\mu_{1})(a_{1}+1)e^{-[d_{1}l+d_{3}(1-l)]\tau}>1\), the periodic solution \(\widetilde{y(t)}\) of system (3.1) is globally asymptotically stable, where \(\widetilde{y(t)}\) is defined as

    $$ \widetilde{y(t)}= \left \{ \textstyle\begin{array}{l@{\quad}l} y^{\ast}e^{-d_{1}(t-n\tau)},& t\in(n\tau,(n+l)\tau], \\ (e^{-d_{1}l\tau}y^{\ast})e^{-d_{3}(t-(n+l)\tau)},&t\in((n+l)\tau ,(n+1)\tau], \end{array}\displaystyle \right . $$
    (3.11)

    and \(y^{\ast}\) is defined as (3.4).

4 Dynamics for system (2.1)

Theorem 4.1

Let \((x(t),y(t))\) be any solution of system (2.1). If

$$(1-\mu_{1}) (a_{1}+1)e^{-[d_{1}l+d_{3}(1-l)]\tau}< 1 $$

and

$$\ln\frac{1}{1-\mu}>al\tau-d_{2}(1-l)\tau-\frac{\beta_{1}y^{\ast }}{d_{1}}\times \bigl(1-e^{-d_{1}l\tau}\bigr) -\frac{\beta_{2}e^{-d_{1}l\tau}y^{\ast}}{d_{1}} \bigl(1-e^{-d_{3}(1-l)\tau}\bigr) $$

hold, then the prey-extinction boundary periodic solution \((0,\widetilde {y(t)})\) of (2.1) is globally asymptotically stable, where \(y^{\ast}\) is defined as (3.4).

Proof

First, we prove the local stability. Defining \(x_{1}(t)=x(t)\), \(y_{1}(t)=y(t)-\widetilde{y(t)}\), then we have the following linearly similar system for system (2.1) which concerns one periodic solution \((0, \widetilde{y(t)})\) to

$$\left( \textstyle\begin{array}{@{}c@{}} \frac{dx(t)}{dt} \\ \frac{dy(t)}{dt} \end{array}\displaystyle \right) = \left( \textstyle\begin{array}{@{}c@{\quad}c@{}} a-\beta_{1} \widetilde{y(t)} & 0 \\ k_{1}\beta_{1}\widetilde{y(t)}& -d_{1} \end{array}\displaystyle \right) \left( \textstyle\begin{array}{@{}c@{}} x(t)\\ y(t) \end{array}\displaystyle \right), \quad t\in\bigl(n\tau,(n+l)\tau\bigr] $$

and

$$\left( \textstyle\begin{array}{@{}c@{}} \frac{dx(t)}{dt} \\ \frac{dy(t)}{dt} \end{array}\displaystyle \right) = \left( \textstyle\begin{array}{@{}c@{\quad}c@{}} -d_{2}-\beta_{2} \widetilde{y(t)} & 0 \\ k_{2}\beta_{2}\widetilde{y(t)}& -d_{3} \end{array}\displaystyle \right) \left( \textstyle\begin{array}{@{}c@{}} x(t)\\ y(t) \end{array}\displaystyle \right),\quad t\in\bigl(n\tau,(n+l)\tau\bigr]. $$

It is easy to obtain the fundamental solution matrix

$$\Phi(t)= \left( \textstyle\begin{array}{@{}c@{\quad}c@{}} \exp(\int^{t}_{0}(a-\beta_{1}\widetilde{y(s)})\,ds) & 0 \\ \ast& \exp(-d_{1}t) \end{array}\displaystyle \right),\quad t\in\bigl(n\tau,(n+l)\tau\bigr]. $$

There is no need to calculate the exact form of ∗, as it is not required in the analysis that follows, and

$$\Phi(t)= \left( \textstyle\begin{array}{@{}c@{\quad}c@{}} \exp(\int^{t}_{0}(-d_{2}-\beta_{2}\widetilde{y(t)})\,ds) & 0 \\ \star& \exp(-d_{3}t) \end{array}\displaystyle \right), \quad t\in\bigl((n+l)\tau,(n+1) \tau\bigr]. $$

There is no need to calculate the exact form of ⋆, as it is not required in the analysis that follows.

The linearization of the third and fourth equations of (2.1) is

$$\left( \textstyle\begin{array}{@{}c@{}} x((n+l)\tau^{+}) \\ y((n+l)\tau^{+}) \end{array}\displaystyle \right) = \left( \textstyle\begin{array}{@{}c@{\quad}c@{}} 1 & 0 \\ 0& 1+ a_{1} \end{array}\displaystyle \right) \left( \textstyle\begin{array}{@{}c@{}} x((n+l)\tau) \\ y((n+l)\tau) \end{array}\displaystyle \right), $$

and the linearization of the seventh and eighth equations of (2.1) is

$$\left( \textstyle\begin{array}{@{}c@{}} x((n+1)\tau^{+}) \\ y((n+1)\tau^{+}) \end{array}\displaystyle \right) = \left( \textstyle\begin{array}{@{}c@{\quad}c@{}} 1-\mu& 0 \\ 0& 1-\mu_{1} \end{array}\displaystyle \right) \left( \textstyle\begin{array}{@{}c@{}} x((n+1)\tau) \\ y((n+1)\tau) \end{array}\displaystyle \right). $$

The stability of the periodic solution \((0,\widetilde{y(t)})\) is determined by the eigenvalues of

$$M= \left( \textstyle\begin{array}{@{}c@{\quad}c@{}} 1 & 0 \\ 0& 1+ a_{1} \end{array}\displaystyle \right) \left( \textstyle\begin{array}{@{}c@{\quad}c@{}} 1-\mu& 0 \\ 0& 1-\mu_{1} \end{array}\displaystyle \right) \Phi(\tau), $$

where

$$\begin{aligned} \lambda_{1} =&(1-\mu)e^{\int^{l\tau}_{0}(a-\beta_{1}\widetilde {y(s)})\,ds-\int^{\tau}_{l\tau}[d_{2}+\beta_{2}\widetilde{y(s)}]\,ds} \\ =&(1-\mu)e^{al\tau-d_{2}(1-l)\tau-\frac{\beta_{1}y^{\ast}}{d_{1}}\times (1-e^{-d_{1}l\tau}) -\frac{\beta_{2}e^{-d_{1}l\tau}y^{\ast}}{d_{1}} (1-e^{-d_{3}(1-l)\tau})} \end{aligned}$$

and

$$\lambda_{2}=(1-\mu_{1}) (1+a_{1})e^{-[d_{1}l\tau+d_{3}(1-l)\tau]}. $$

According to the Floquet theory [24], if \(| \lambda_{1}|<1\) and \(| \lambda_{2}|<1\), i.e.,

$$\ln\frac{1}{1-\mu}> al\tau-d_{2}(1-l)\tau-\frac{\beta_{1}y^{\ast }}{d_{1}}\times \bigl(1-e^{-d_{1}l\tau}\bigr) -\frac{\beta_{2}e^{-d_{1}l\tau}y^{\ast}}{d_{1}} \bigl(1-e^{-d_{3}(1-l)\tau}\bigr) $$

and

$$\ln(1-\mu_{1}) (1+a_{1})< d_{1}l \tau+d_{3}(1-l)\tau $$

hold, then \((0,\widetilde{y(t)})\) is locally stable, where \(y^{\ast}\) is defined as (3.4).

In the following, we will prove the global attraction. Choose \(\varepsilon>0\) such that

$$\rho=(1-\mu)e^{\int^{l\tau}_{0}[a-\beta_{1}(\widetilde{y(s)}+\varepsilon )]\,ds-\int^{\tau}_{l\tau}[d_{2}+\beta_{2}(\widetilde{y(s)}+\varepsilon)]\,ds}< 1. $$

From the first and fifth equations of (2.1), we notice that

$$\frac{dy(t)}{dt}\leq d_{1}y(t) $$

and

$$\frac{dy(t)}{dt}\leq-d_{3}y(t), $$

so we consider the following impulsive differential equation:

$$ \left \{ \textstyle\begin{array}{l} \frac{dy_{2}(t)}{dt}=-d_{1}y_{2}(t), \quad t\in(n\tau,(n+l)\tau], \\ \triangle y_{2}(t)=y_{2}(t)(a_{1}-b_{1} y_{2}(t)),\quad t= (n+l)\tau,n\in Z^{+}, \\ \frac{dy_{2}(t)}{dt}=-d_{3}y_{2}(t), \quad t\in( (n+l)\tau, (n+1)\tau], \\ \triangle y_{2}(t)=-\mu_{1}y(t),\quad t= (n+1)\tau, n\in Z^{+}. \end{array}\displaystyle \right . $$
(4.1)

From Lemma 3.4 and the comparison theorem of impulsive equation [24], we have \(y(t)\leq y_{2}(t)\) and \(y_{2}(t)\rightarrow\widetilde{y(t)}\) as \(t\rightarrow\infty\). Then

$$ y(t)\leq y_{2}(t)\leq\widetilde{y(t)}+\varepsilon $$
(4.2)

for all t large enough, for convenience we may assume that (4.2) holds for all \(t\geq0\). From (2.1) and (4.2), we get

$$ \left \{ \textstyle\begin{array}{l} \frac{dx(t)}{dt}\leq x(t)[(a-\beta_{1}(\widetilde{y(t)}+\varepsilon ))-bx(t)], \quad t\in(n\tau,(n+l)\tau], \\ \triangle x(t)=0,\quad t=(n+l)\tau,n\in Z^{+}, \\ \frac{dx(t)}{dt}\leq-[d_{2}+\beta_{2}(\widetilde{y(t)}+\varepsilon )]x(t), \quad t\in((n+l)\tau, (n+1)\tau], \\ \triangle x(t)=-\mu x(t),\quad t= (n+1)\tau, n\in Z^{+}. \end{array}\displaystyle \right . $$
(4.3)

So

$$x\bigl((n+1)\tau\bigr)\leq x\bigl(n\tau^{+}\bigr) (1- \mu)e^{\int^{\tau}_{0}[a-\beta _{1}(\widetilde{y(s)}+\varepsilon)]\,ds-\int^{\tau}_{l\tau}[d_{2}+\beta _{2}(\widetilde{y(s)}+\varepsilon)]\,ds}. $$

Hence \(x(n\tau)\leq x(0^{+})\rho^{n}\) and \(x(n\tau)\rightarrow0\) as \(n\rightarrow\infty\), therefore \(x(t)\rightarrow0\) as \(t\rightarrow\infty\).

Next we prove that \(y(t)\rightarrow\widetilde{y(t)}\) as \(t\rightarrow\infty\). For \(\varepsilon<\min\{\frac{d_{1}}{k_{1}\beta _{1}},\frac{d_{3}}{k_{2}\beta_{2}}\}\), there must exist \(t_{0}>0\) such that \(0< x(t)<\varepsilon\) for all \(t\geq t_{0}\). Without loss of generality, we may assume that \(0< x(t)<\varepsilon\) for all \(t\geq{0}\), then for system (2.1) we have

$$ -d_{1}y(t)\leq\frac{dy(t)}{dt}\leq-[d_{1}-k_{1} \beta_{1}\varepsilon ]y(t) $$
(4.4)

and

$$ -d_{3}y(t)\leq\frac{dy(t)}{dt}\leq-[d_{3}-k_{2} \beta_{2}\varepsilon ]y(t). $$
(4.5)

Then we have \(z_{2}(t)\leq y(t)\leq z_{1}(t)\) and \(z_{1}(t)\rightarrow\widetilde{y(t)}\), \(z_{2}(t)\rightarrow \widetilde{z_{2}(t)}\) as \(t\rightarrow\infty\). While \(z_{1}(t)\) and \(z_{2}(t)\) are the solutions of

$$ \left \{ \textstyle\begin{array}{l} \frac{dz_{1}(t)}{dt}=-d_{1}z_{1}(t),\quad t\in(n\tau,(n+l)\tau], \\ \triangle z_{1}(t)=z_{2}(t)(a_{1}-b_{1} z_{1}(t)),\quad t= (n+l)\tau,n\in Z^{+}, \\ \frac{dz_{1}(t)}{dt}=-d_{3}z_{1}(t), \quad t\in( (n+l)\tau, (n+1)\tau], \\ \triangle z_{1}(t)=-\mu_{1}z_{1}(t),\quad t= (n+1)\tau, n\in Z^{+} \end{array}\displaystyle \right . $$
(4.6)

and

$$ \left \{ \textstyle\begin{array}{l} \frac{dz_{1}(t)}{dt}=-[d_{1}-k_{1}\beta_{1}\varepsilon]z_{1}(t), \quad t\in(n\tau,(n+l)\tau], \\ \triangle z_{2}(t)=z_{2}(t)(a_{1}-b_{1} z_{2}(t)),\quad t= (n+l)\tau,n\in Z^{+}, \\ \frac{dz_{2}(t)}{dt}=-[d_{3}-k_{2}\beta_{2}\varepsilon]z_{2}(t), \quad t\in( (n+l)\tau, (n+1)\tau], \\ \triangle z_{2}(t)=-\mu_{1}z_{2}(t),\quad t= (n+1)\tau, n\in Z^{+}, \end{array}\displaystyle \right . $$
(4.7)

respectively,

$$ \widetilde{z_{2}(t)}= \left \{ \textstyle\begin{array}{l@{\quad}l} z_{2}^{\ast}e^{-(d_{1}-k_{1}\beta_{1}\varepsilon)(t-n\tau)},& t\in(n\tau ,(n+l)\tau], \\ (e^{-(d_{1}-k_{1}\beta_{1}\varepsilon)(t-n\tau)l\tau}z_{2}^{\ast })e^{-(d_{3}-k_{2}\beta_{2}\varepsilon)(t-(n+l)\tau)},&t\in((n+l)\tau ,(n+1)\tau], \end{array}\displaystyle \right . $$
(4.8)

where \(z_{2}^{\ast}\) is defined as

$$\begin{aligned} \begin{aligned}[b] &z_{2}^{\ast}=\frac{(1-\mu_{1})(a_{1}+1)e^{-[(d_{1}-k_{1}\beta _{1}\varepsilon)l\tau+(d_{3}-k_{2}\beta_{2}\varepsilon)(1-l)\tau]}-1}{ (1-\mu_{1})be^{-[(d_{1}-k_{1}\beta_{1}\varepsilon)l\tau +(d_{3}-k_{2}\beta_{2}\varepsilon)(1-l)\tau]}\times e^{-(d_{1}-k_{1}\beta_{1}\varepsilon)l\tau}}, \\ &\quad (1-\mu_{1}) (a_{1}+1)e^{-[(d_{1}-k_{1}\beta_{1}\varepsilon)l\tau +(d_{3}-k_{2}\beta_{2}\varepsilon)(1-l)\tau]}>1. \end{aligned} \end{aligned}$$
(4.9)

Therefore, for any \(\varepsilon_{1}>0\), there exists \(t_{1}\), \(t>t_{1}\), such that

$$\widetilde{y(t)}-\varepsilon_{1}< y(t)< \widetilde{z_{2}(t)}+ \varepsilon_{1}. $$

Let \(\varepsilon\rightarrow0\), so we have

$$\widetilde{y(t)}-\varepsilon_{1}< y(t)< \widetilde{y(t)}+ \varepsilon_{1} $$

for t large enough, which implies \(y(t)\rightarrow \widetilde{y(t)}\) as \(t\rightarrow\infty\). This completes the proof. □

The next work is the investigation of permanence of system (2.1). Before starting our theorem, we give the following definition.

Definition 4.2

System (2.1) is said to be permanent if there are constants \(m,M >0 \) (independent of initial value) and a finite time \(T_{0}\) such that for all solutions \((x(t), y(t))\) with all initial values \(x(0^{+})>0\), \(y(0^{+})>0\), \(m\leq x(t)\leq M\), \(m\leq y(t)\leq M\) hold for all \(t\geq T_{0}\). Here \(T_{0}\) may depend on the initial values \((x(0^{+}), y(0^{+}))\).

Theorem 4.3

Let \((x(t),y(t))\) be any solution of system (2.1). If

$$(1-\mu_{1}) (a_{1}+1)e^{-[d_{1}l+d_{3}(1-l)]\tau}< 1 $$

and

$$\ln\frac{1}{1-\mu}< al\tau-d_{2}(1-l)\tau-\frac{\beta_{1}y^{\ast }}{d_{1}}\times \bigl(1-e^{-d_{1}l\tau}\bigr) -\frac{\beta_{2}e^{-d_{1}l\tau}y^{\ast}}{d_{1}} \bigl(1-e^{-d_{3}(1-l)\tau}\bigr) $$

hold, then system (2.1) is permanent.

Proof

Suppose \((x(t), y(t))\) is a solution of (2.1) with \(x(0)>0\), \(y(0)>0\). By Lemma 3.1, we have proved that there exists a constant \(M >0\) such that \(x(t)\leq M\), \(y(t)\leq M\) for t large enough, we may assume \(x(t)\leq M\), \(y(t)\leq M\) for \(t\geq0\). From Theorem 4.1, we know \(y(t)>\widetilde{y(t)}-\varepsilon_{2}\) for all t large enough and \(\varepsilon_{2}> 0\), so \(y(t)\geq e^{-d_{1}l\tau}y^{\ast }(1+e^{-d_{3}(1-l)\tau})-\varepsilon_{2}=m_{2}\) for t large enough. Thus, we only need to find \(m_{1}>0\) such that \(x(t)\geq m_{1}\) for t large enough, we will do it in what follows.

By the conditions of this theorem, we can select \(m_{3}>0\), \(\varepsilon_{1}> 0\) small enough such that \(m_{3}<\min \{\frac{d_{1}}{k_{1}\beta_{1}},\frac{d_{3}}{k_{2}\beta_{2}}\}\), \(\sigma=al\tau-\beta_{1}\varepsilon-\beta_{2}\varepsilon -d_{2}(1-l)\tau-\frac{\beta_{1}z^{\ast}}{d_{1}-k_{1}\beta _{1}m_{3}}\times(1-e^{-(d_{1}-k_{1}\beta_{1}m_{3})l\tau}) -\frac{\beta_{2}e^{-(d_{1}-k_{1}\beta_{1}m_{3})l\tau}z^{\ast }}{d_{1}-k_{1}\beta_{1}m_{3}} (1-e^{-(d_{3}-k_{2}\beta _{2}m_{3})(1-l)\tau})> 0\) and

$$z^{\ast}=\frac{(1-\mu_{1})(a_{1}+1)e^{-[(d_{1}-k_{1}\beta _{1}m_{3})l\tau+(d_{3}-k_{2}\beta_{2}m_{3})(1-l)\tau]}-1}{(1-\mu _{1})be^{-[(d_{1}-k_{1}\beta_{1}m_{3})l\tau+(d_{3}-k_{2}\beta _{2}m_{3})(1-l)\tau]}\times e^{-(d_{1}-k_{1}\beta_{1}m_{3})l\tau}}, $$

\((1-\mu_{1})(a_{1}+1)e^{-[(d_{1}-k_{1}\beta_{1}m_{3})l\tau +(d_{3}-k_{2}\beta_{2}m_{3})(1-l)\tau]}>1\). We will prove that \(x(t)< m_{3}\) cannot hold for \(t\geq 0\). Otherwise,

$$ \left \{ \textstyle\begin{array}{l} \frac{dy(t)}{dt}< -(d_{1}-k_{1}\beta_{1}m_{3}) y(t), \quad t\in(n\tau,(n+l)\tau], \\ \triangle y(t)=y(t)(a_{1}-b_{1} y(t)),\quad t= (n+l)\tau,n\in Z^{+}, \\ \frac{dy(t)}{dt}< -(d_{3}-k_{2}\beta_{2}m_{3})y(t), \quad t\in( (n+l)\tau, (n+1)\tau], \\ \triangle y(t)=-\mu_{1}y(t),\quad t= (n+1)\tau, n\in Z^{+}. \end{array}\displaystyle \displaystyle \displaystyle \right . $$
(4.10)

By Lemma 3.4, we have \(y(t)\geq z(t)\) and \(z(t)\rightarrow\overline{z(t)}\), \(t\rightarrow\infty\), where \(z(t)\) is the solution of

$$ \left \{ \textstyle\begin{array}{l} \frac{dz(t)}{dt}=-(d_{1}-k_{1}\beta_{1}m_{3}) z(t), \quad t\in(n\tau,(n+l)\tau], \\ \triangle z(t)=z(t)(a_{1}-b_{1} z(t)),\quad t= (n+l)\tau,n\in Z^{+}, \\ \frac{dz(t)}{dt}=-(d_{3}-k_{2}\beta_{2}m_{3})z(t), \quad t\in( (n+l)\tau, (n+1)\tau], \\ \triangle z(t)=-\mu_{1}z(t),\quad t= (n+1)\tau, n\in Z^{+} \end{array}\displaystyle \right . $$
(4.11)

and

$$ \overline{z(t)}= \left \{ \textstyle\begin{array}{l@{\quad}l} z^{\ast}e^{-(d_{1}-k_{1}\beta_{1}m_{3})(t-n\tau)}, &t\in(n\tau,(n+l)\tau ], \\ (e^{-(d_{1}-k_{1}\beta_{1}m_{3})(t-n\tau)l\tau}z^{\ast })e^{-(d_{3}-k_{2}\beta_{2}m_{3})(t-(n+l)\tau)},&t\in((n+l)\tau,(n+1)\tau ], \end{array}\displaystyle \right . $$
(4.12)

where \(z^{\ast}\) is defined as

$$\begin{aligned}& z^{\ast}=\frac{(1-\mu_{1})(a_{1}+1)e^{-[(d_{1}-k_{1}\beta_{1}m_{3})l\tau +(d_{3}-k_{1}\beta_{1}m_{3})(1-l)\tau]}-1}{(1-\mu _{1})be^{-[(d_{1}-k_{1}\beta_{1}m_{3})l\tau+(d_{3}-k_{1}\beta _{1}m_{3})(1-l)\tau]}\times e^{-(d_{1}-k_{1}\beta_{1}m_{3})l\tau}}, \\& \quad (1-\mu_{1}) (a_{1}+1)e^{-[(d_{1}-k_{1}\beta_{1}m_{3})l\tau +(d_{3}-k_{2}\beta_{2}m_{3})(1-l)\tau]}>1. \end{aligned}$$
(4.13)

Therefore, there exists \(T_{1}>0\) such that

$$y(t)\leq z(t)\leq\overline{z(t)}+\varepsilon_{1} $$

and

$$ \left \{ \textstyle\begin{array}{l} \frac{dx(t)}{dt}\geq x(t)[(a-\beta_{1}(\overline{z(t)}+\varepsilon _{1}))-bx(t)], \quad t\in(n\tau,(n+l)\tau], \\ \triangle x(t)=0,\quad t=(n+l)\tau,n\in Z^{+}, \\ \frac{dx(t)}{dt}\geq-[d_{2}+\beta_{2}(\overline{z(t)}+\varepsilon )]x(t), \quad t\in((n+l)\tau, (n+1)\tau], \\ \triangle x(t)=-\mu x(t),\quad t= (n+1)\tau, n\in Z^{+}. \end{array}\displaystyle \right . $$
(4.14)

For \(t\geq T_{1}\), let \(N_{1}\in N\) and \(N_{1}\tau> T_{1}\). Integrating (4.14) on \((n\tau,(n+1)\tau)\), \(n\geq N_{1}\), we have

$$\begin{aligned} x\bigl((n+1)\tau\bigr) \geq& x\bigl(n\tau^{+}\bigr) (1- \mu)e^{\int^{(n+l)\tau}_{n\tau}[a-\beta_{1}(\overline {z(s)}+\varepsilon)]\,ds-\int^{(n+1)\tau}_{(n+l)\tau} [d_{2}+\beta_{2}(\overline{z(s)}+\varepsilon)]\,ds} \\ =&(1-\mu_{1})x\bigl(n\tau^{+}\bigr)e^{\sigma}, \end{aligned}$$

then \(x((N_{1}+k)\tau)\geq (1-\mu_{1})^{k}x(N_{1}\tau^{+})e^{k\sigma}\rightarrow\infty\), as \(k\rightarrow\infty\), which is a contradiction to the boundedness of \(x(t)\). Hence there exists \(t_{1}>0\) such that \(x(t)\geq m_{1}\). The proof is complete. □

5 Discussion

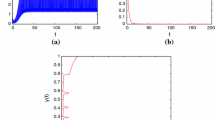
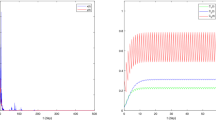
In this paper, according to the fact, a periodic impulsive switched predator-prey system with hibernation and birth pulse is proposed and investigated, we analyzed global asymptotic stability of the prey-extinction periodic solution of system (2.1) and obtained the conditions for the permanence of system (2.1). If it is assumed that \(x(0)=0.1\), \(y(0)=0.1\), \(a=2\), \(b=0.8\), \(d_{1}=0.5\), \(d_{2}=0.5\), \(d_{3}=0.4\), \(\beta_{1}=0.6\), \(k_{1} =0.3\), \(\beta_{2}=0.3\), \(k_{2}=0.4\), \(\mu =0.7\), \(\mu_{1}=0\), \(l=0.8\), \(\tau=1\), then the prey-extinction periodic solution \((0,\widetilde{y(t)})\) of system (2.1) is globally asymptotically stable (see Figure 1). If we assume that \(x(0)=0.1\), \(y(0)=0.1\), \(a=2\), \(b=0.8\), \(d_{1}=0.5\), \(d_{2}=0.5\), \(d_{3}=0.4\), \(\beta_{1}=0.6\), \(k_{1} =0.3\), \(\beta_{2}=0.3\), \(k_{2}=0.4\), \(\mu =0.5\), \(\mu_{1}=0\), \(l=0.8\), \(\tau=1\), then system (2.1) is permanent (see Figure 2).

Figure 1
figure 1

Globally asymptotically stable prey-extinction periodic solution of system ( 2.1 ) with \(\pmb{x(0)=0.1}\) , \(\pmb{y(0)=0.1}\) , \(\pmb{a=2}\) , \(\pmb{b=0.8}\) , \(\pmb{d_{1}=0.5}\) , \(\pmb{d_{2}=0.5}\) , \(\pmb{d_{3}=0.4}\) , \(\pmb{\beta_{1}=0.6}\) , \(\pmb{k_{1} =0.3}\) , \(\pmb{\beta _{2}=0.3}\) , \(\pmb{k_{2}=0.4}\) , \(\pmb{\mu=0.7}\) , \(\pmb{l=0.8}\) , \(\pmb{\tau=1}\) . (a) Time-series of \(x(t)\); (b) time-series of \(y(t)\); (c) the phase portrait of the globally asymptotically stable prey-extinction periodic solution of system (2.1).

Full size image
Figure 2
figure 2

The permanence of system ( 2.1 ) with \(\pmb{x(0)=0.1}\) , \(\pmb{y(0)=0.1}\) , \(\pmb{a=2}\) , \(\pmb{b=0.8}\) , \(\pmb{d_{1}=0.5}\) , \(\pmb{d_{2}=0.5}\) , \(\pmb{d_{3}=0.4}\) , \(\pmb{\beta_{1}=0.6}\) , \(\pmb{k_{1} =0.3}\) , \(\pmb{\beta _{2}=0.3}\) , \(\pmb{k_{2}=0.4}\) , \(\pmb{\mu=0.5}\) , \(\pmb{l=0.8}\) , \(\pmb{\tau=1}\) . (a) Time-series of \(x(t)\); (b) time-series of \(y(t)\); (c) the phase portrait of the permanence of system (2.1).

Full size image

From the simulation experiment of Figures 1 and 2, the parameter μ affects the dynamical behaviors of system (2.1). If all parameters of system (2.1) are fixed, when \(\mu=0.7\), the prey population of system (2.1) goes extinct; when \(\mu=0.5\), system (2.1) is permanent. From Theorem 4.1 and Theorem 4.3, we can easily deduce that there must exist a threshold \(\mu^{\ast}\). If \(\mu >\mu^{\ast}\), the prey-extinction periodic solution \((0,\widetilde {y(t)})\) of system (2.1) is globally asymptotically stable. If \(\mu<\mu^{\ast}\), system (2.1) is permanent. That is to say, impulsive harvesting rate of the prey population plays an important role in system (2.1). The impulsive harvesting rate of the prey population will also reduce the predator population. It tells us that destroying or excessive exploiting of the prey population will cause extinction of the predator population. Our results also provide reliable tactic basis for the practical biological economics management and the protection of biodiversity.