Survival and ergodicity of a stochastic Holling-III predator–prey model with Markovian switching in an impulsive polluted environment

Abstract

Based on the effects of white noise and colored noise, we propose a stochastic Holling-III predator–prey model in an impulsive polluted environment. Firstly, we prove an existence and uniqueness theorem of the presented model. Secondly, we establish sufficient criteria of extinction, nonpersistence in mean, and weak persistence in mean for both prey and predator species. Thirdly, with the aid of Lyapunov functions, we prove that this system is ergodic and has a unique stationary distribution under certain conditions. Finally, we verify the theoretical results by performing some numerical simulations.

1 Introduction

Environmental pollution from various industries attracts more and more demographers and ecologists because it has seriously threatened the survival of humans and other exposed living organisms [2, 26, 38]. In the early years, the survival analysis of populations in the polluted environment was carried out by establishing deterministic models. For example, Hallam et al. [3, 6–8] used some deterministic models to show the effects of toxicant on populations, He and Wang [10, 11] analyzed the dynamics of two single-species models in polluted environments, and so on.

The deterministic models are not suitable for modeling the ubiquitous noise-driven systems, so stochastic models in the polluted environment are frequently used to explore the dynamics behavior of species [27]. Generally, there are two main types of environmental noise, white noise and colored noise. For white noise-driven models, Gard [5] investigated a stochastic single-species model to explain the influence of the toxicant on organisms and compared it to the corresponding deterministic model. Liu and Wang [20] studied the dynamics of stochastic single-species population models with and without pollution. Wei et al. [36, 37] further investigated the stochastic single-species population model in a polluted environment. In addition, Lv et al. [23] introduced a new impulsive stochastic chemostat model. On the other hand, to illustrate the switching between two or more environmental regimes, it is meaningful to consider the influence of colored noise on the population [4, 32]. Liu and Wang [21] proposed a stochastic single-specie model under regime switching. Moreover, a stochastic two-species model is presented in [44]. For the dynamics behaviors of the populations with environmental toxins and noises, we also refer the readers to [22, 34, 39, 43] and references therein.

Many models mentioned are based on the Lotka–Volterra model with linear functional responses. However, these models ignore some important natural phenomena (compared with the models with nonlinear functional responses), especially for the predator–prey case [9, 28]. To this end, Holling [12, 13] proposed the most widely used functional responses and classified them into three basic types (denoted types I, II, and III). As a typical nonlinear functional response, Holling type III [29] has a powerful role in describing the predation behavior of vertebrates, for example, some predators learn more special skills for hunting or prey handling. Recently, some important models with Holling type III has been discussed. For instance, Huang et al. [14] established a prey–predator model with Holling-III response function and a prey refuge to show that the refuge has a steadying influence on prey–predator interactions. Su et al. [33] indicated that both periodically varying environment and stochastically released natural enemies have a great impact on the survival of the species by using the predator–prey system with generalized Holling-III type functional response. Wu and Li [40] combined Holling-III type with Hassell–Varley type functional responses to demonstrate the permanence and global attractivity of a discrete predator–prey system. More recently, Sengupta et al. [30] analyzed the dynamics of the deterministic and stochastic models with Holling-III response function, respectively.

To the best of our knowledge, there are rare results on the effects of pollution inputs and noise fluctuations for the dynamics behavior of Holling-III predator–prey systems. Undoubtedly, the theoretical analysis of Holling type-III is more challenging than other functional responses because its nonlinear form is more complicated. In this paper, we are devoted to two main goals:

• to analyze the long-time behavior of stochastic Holling-III predator–prey systems with regime switching in an impulsive polluted environment, and

• to investigate the effects of pollution inputs and noise fluctuations on the dynamics of predators and preys.

In particular, when the considered model of this paper reduces to that of [30], our conditions in Theorem 3.2 are more convenient to verify the weak persistence in the mean of predator species in comparison with [30, Theorem 4.4].

This paper is organized as follows. In Sect. 2, we begin to state our model and prepare some preliminaries including the existence of a unique positive solution. In Sect. 3, we obtain some sufficient conditions of the extinction and weak persistence in mean for two species. In Sect. 4, we investigate the existence and uniqueness of stationary distribution. In Sect. 5, we present numerical simulations confirming our theoretical results. Finally, in the last section, we give a brief conclusion.

2 The model and preliminaries

We begin this section by stating the stochastic Holling-III predator–prey model with Markovian switching in an impulsive polluted environment step by step and prepare some preliminaries including the existence and uniqueness theorem.

2.1 The model

First, let us introduce the deterministic Holling-III predator–prey model [41]

$$ \textstyle\begin{cases} \mathrm{d}x(t) = [a_{1}x(t)-b_{1}x(t)^{2}- \frac{\alpha x(t)^{2}}{1+\beta x(t)^{2}}y(t) ] \,\mathrm{d}t, \\ \mathrm{d}y(t) = [-a_{2}y(t)-b_{2}y(t)^{2}+ \frac{k\alpha x(t)^{2}}{1+\beta x(t)^{2}}y(t) ] \,\mathrm{d}t \end{cases} $$

(2.1)

with the initial value $(x(0),y(0)) \in \mathbb{R}_{+}^{2}$, where $x(t)$ and $y(t)$ denote the population densities of prey and predator species at time t, respectively, $a_{1}$ and $a_{2}$ stand for the intrinsic growth rate of prey population and the death rate of predator population, respectively. Both $b_{1}$ and $b_{2}$ represent intraspecific coefficients of competition. The nonlinear function $\frac{\alpha x^{2}}{1+\beta x^{2}}$ is the Holling-III functional response, where α stands for the predation rate of predators on prey populations, β denotes the handling time of predators for each prey that is consumed, and k denotes the conversion rate concerning the number of newborn predators for each captured prey. All parameters of the model are positive.

Taking into account the impact of environmental pollution on species [3, 6–8], most of the existing studies assume that the exogenous input of toxicant is continuous. However, the actual situation is that the toxin is released in regular pulses; for example, the factories drain sewage into rivers on a regular basis. Therefore we focus on the case of toxic exogenous pulse input and then obtain the following model:

$$ \textstyle\begin{cases} \left.\textstyle\begin{array}{l} \mathrm{d}x(t) = [a_{1}x(t)-b_{1}x(t)^{2}- \frac{\alpha x(t)^{2}}{1+\beta x(t)^{2}}y(t) \\ \phantom{\mathrm{d}x(t) =} {} -r_{1}C_{1}(t)x(t)]\,\mathrm{d}t, \\ \mathrm{d}y(t) = [-a_{2}y(t)-b_{2}y(t)^{2}+ \frac{k\alpha x(t)^{2}}{1+\beta x(t)^{2}}y(t) \\ \phantom{\mathrm{d}y(t) =}{} -r_{2}C_{2}(t)y(t)]\,\mathrm{d}t, \\ \mathrm{d}C_{i}(t) = [e_{i}C_{E}(t)-(g_{i}+m_{i})C_{i}(t)]\,\mathrm{d}t, \\ \mathrm{d}C_{E}(t) = -hC_{E}(t)\,\mathrm{d}t, \end{array}\displaystyle \right\} \quad t\neq n\rho, n\in \mathbb{N}, \\ \left.\textstyle\begin{array}{l} \bigtriangleup x(t)=0,\qquad \bigtriangleup y(t)=0, \\ \bigtriangleup C_{i}(t)=0\quad (i=1, 2), \qquad\bigtriangleup C_{E}(t)=u, \end{array}\displaystyle \right\} \quad t=n\rho, n\in \mathbb{N}, \end{cases} $$

(2.2)

where $\bigtriangleup \chi (t) = \chi (t^{+}) - \chi (t)$ with $\chi = x,y,C_{1},C_{2},C_{E}$, $C_{1}(t)$, $C_{2}(t)$, and $C_{E}(t)$ stand for the concentrations of toxicant in the organism of the prey, predator, and environment at time t, respectively, $r_{1}$ and $r_{2}$ denote the dose-response of the prey and predator to the toxicant, respectively, $e_{i}$ is the uptake rate of toxicant from environment, $g_{i}$ and $m_{i}$ indicate the excretion and depuration rates of toxicant, respectively, h is the loss rate of toxicant, and u and ρ represent the toxicant input amount and the period of the exogenous toxicant input, respectively. Here we assume that the environmental capacity is large enough so that the effects of toxins excreted by the organism into the environment have negligible influences on the concentration of environmental toxins.

Now we further take the white noise into consideration. Following the approach used in [15, 17, 19], the parameters $a_{1}$ and $-a_{2}$ of system (2.2) are perturbed with

$$\begin{aligned} a_{1}\rightarrow a_{1}+\sigma _{1} \dot{B}_{1}(t) \quad \text{and}\quad -a_{2}\rightarrow -a_{2}+\sigma _{2} \dot{B}_{2}(t), \end{aligned}$$

where the dot denotes the time formal derivative, $B_{1}(t)$ and $B_{2}(t)$ are mutually independent one-dimensional standard Brownian motions defined on the complete probability space $(\Omega,\mathcal{F},\{\mathcal{F}_{t}\}_{t\geq 0},\mathbb{P})$, and $\sigma _{i}^{2}\ (i = 1, 2)$ are the intensities of the white noises. Thus system (2.2) becomes the stochastic Holling-III predator–prey model in the impulsive polluted environment

$$ \textstyle\begin{cases} \left.\textstyle\begin{array}{l} \mathrm{d}x(t) = [a_{1}x(t)-b_{1}x(t)^{2}- \frac{\alpha x(t)^{2}}{1+\beta x(t)^{2}}y(t) \\ \phantom{\mathrm{d}x(t) =}{} -r_{1}C_{1}(t)x(t)] \,\mathrm{d}t + \sigma _{1}x(t) \,\mathrm{d}B_{1}(t), \\ \mathrm{d}y(t) = [-a_{2}y(t)-b_{2}y(t)^{2}+ \frac{k\alpha x(t)^{2}}{1+\beta x(t)^{2}}y(t) \\ \phantom{\mathrm{d}y(t) =}{} -r_{2}C_{2}(t)y(t)] \,\mathrm{d}t + \sigma _{2}y(t) \,\mathrm{d}B_{2}(t), \\ \mathrm{d}C_{i}(t) = [e_{i}C_{E}(t)-(g_{i}+m_{i})C_{i}(t)] \,\mathrm{d}t, \\ \mathrm{d}C_{E}(t) = -hC_{E}(t) \,\mathrm{d}t, \end{array}\displaystyle \right\}\quad t\neq n\rho, n\in \mathbb{N}, \\ \left.\textstyle\begin{array}{l} \bigtriangleup x(t)=0, \qquad\bigtriangleup y(t)=0, \\ \bigtriangleup C_{i}(t)=0 \quad(i=1, 2),\qquad \bigtriangleup C_{E}(t)=u, \end{array}\displaystyle \right\} \quad t=n\rho, n\in \mathbb{N}. \end{cases} $$

(2.3)

It is worth pointing out that there are many phenomena that cannot be modeled by Brownian motion-driven stochastic differential equations (SDEs) [45]; for example, when the growth environment of some species changes significantly, their birth and death rates will be much different [1, 46]. In general, the switching among different environments is memoryless, and the waiting time of the next switch obeys an exponential distribution. Hence these random changes can be described by a continuous-time Markov chain $\xi (t)$, $t>0$, taking values in a finite-state space $\mathbb{S}=\{1, 2, \ldots,N\}$ with the generator $\Gamma =(\gamma _{ij})_{N\times N}$ given by

$$\begin{aligned} \mathbb{P} \bigl\{ \xi (t+\Delta t)=j|\xi (t)=i \bigr\} = \textstyle\begin{cases} \gamma _{ij}\Delta t + o(\Delta t) & \text{if } i\neq j, \\ 1+\gamma _{ii}\Delta t + o(\Delta t) & \text{if } i=j, \end{cases}\displaystyle \end{aligned}$$

where $\gamma _{ij}>0$ is the transition rate from state i to state j if $i\neq j$, and $\gamma _{ii}=-\sum_{j\neq i}\gamma _{ij}$. Finally, model (2.3) can be formulated as

$$ \textstyle\begin{cases} \left.\textstyle\begin{array}{l} \mathrm{d}x(t) = [a_{1}(\xi (t))x(t)-b_{1}(\xi (t))x(t)^{2}- \frac{\alpha (\xi (t))x(t)^{2}}{1+\beta (\xi (t))x(t)^{2}}y(t) \\ \phantom{\mathrm{d}x(t) =}{} -r_{1}(\xi (t))C_{1}(t)x(t)] \,\mathrm{d}t + \sigma _{1}( \xi (t))x(t) \,\mathrm{d}B_{1}(t), \\ \mathrm{d}y(t) = [-a_{2}(\xi (t))y(t)-b_{2}(\xi (t))y(t)^{2}+ \frac{k(\xi (t))\alpha (\xi (t))x(t)^{2}}{1+\beta (\xi (t))x(t)^{2}}y(t) \\ \phantom{\mathrm{d}y(t) =}{} -r_{2}(\xi (t))C_{2}(t)y(t)] \,\mathrm{d}t + \sigma _{2}( \xi (t))y(t) \,\mathrm{d}B_{2}(t), \\ \mathrm{d}C_{i}(t) = [e_{i}C_{E}(t)-(g_{i}+m_{i})C_{i}(t)] \,\mathrm{d}t, \\ \mathrm{d}C_{E}(t) = -hC_{E}(t) \,\mathrm{d}t, \end{array}\displaystyle \right\}\quad t\neq n\rho, n\in \mathbb{N}, \\ \left.\textstyle\begin{array}{l} \bigtriangleup x(t)=0,\qquad \bigtriangleup y(t)=0, \\ \bigtriangleup C_{i}(t)=0\quad (i=1, 2), \qquad\bigtriangleup C_{E}(t)=u, \end{array}\displaystyle \right\} \quad t=n\rho, n\in \mathbb{N}, \end{cases} $$

(2.4)

where all functions $a_{i}, b_{i}, r_{i}, \sigma _{i}\ (i=1, 2)$ and $\alpha, \beta, k$ are $\mathbb{R}_{+}$-valued. In addition, we assume that $\xi (t)$ is irreducible and independent of Brownian motions $B_{i}(t)\ (i=1,2)$. In fact, the Markov chain $\xi (t)$ has a unique stationary distribution $\pi =(\pi _{1}, \pi _{2},\ldots,\pi _{N})\in \mathbb{R}^{1\times N}$, which can be obtained by solving the linear equation $\pi \Gamma =0$ subject to $\sum^{N}_{j=1}\pi _{j}=1$ and $\pi _{j}>0, j\in \mathbb{S}$. As a result, for any vector $\theta =(\theta (1), \ldots, \theta (N))^{T}$, $\lim_{t\rightarrow \infty }\frac{1}{t}\int ^{t}_{0}\theta (\xi (s)) \,\mathrm{d}s=\sum_{i\in \mathbb{S}}\pi _{i}\theta (i)$. In reality, environmental noise has little effect on the toxin concentration of the organism, so we assume that the parameters $e_{i}$, $g_{i}$, $m_{i}$, and h are independent of noises.

2.2 Preliminaries

For convenience, define $f^{*}=\limsup_{t\rightarrow \infty }f(t),\ f_{*}=\liminf_{t\rightarrow \infty }f(t)$, $\langle f\rangle = \frac{1}{t} \int ^{t}_{0}f(s) \,\mathrm{d}s$, $\check{g}=\max_{i\in \mathbb{S}}g(i)$, and $\hat{g}=\min_{i\in \mathbb{S}}g(i)$. For the subsystem of model (2.4),

$$ \textstyle\begin{cases} \left.\textstyle\begin{array}{l} \mathrm{d}C_{i}(t)=[e_{i}C_{E}(t)-(g_{i}+m_{i})C_{i}(t)] \,\mathrm{d}t, \\ \mathrm{d}C_{E}(t)=-hC_{E}(t) \,\mathrm{d}t, \end{array}\displaystyle \right\}\quad t\neq n\rho, n\in \mathbb{N}, \\ \bigtriangleup C_{i}(t)=0\quad (i=1, 2),\qquad \bigtriangleup C_{E}(t)=u,\quad t=n \rho, n\in \mathbb{N} \end{cases} $$

(2.5)

with initial values $C_{i}(0)\in (0,1)\ (i=1, 2)$ and $C_{E}(0)\in (0,1)$, the following lemma is taken from [18].

Lemma 2.1

For subsystem (2.5), we have:

• (1) it admits a unique positive ρ-periodic solution $(\overline{C}_{1}(t), \overline{C}_{2}(t), \overline{C}_{E}(t))^{T}$;

• (2) for any $\varepsilon >0$ and sufficiently large t,

  $$\begin{aligned} \overline{C}_{i}(t)-\varepsilon < C_{i}(t)< \overline{C}_{i}(t)+ \varepsilon,\quad i=1, 2; \end{aligned}$$

  (2.6)

• (3) and

  $$\begin{aligned} \lim_{t\rightarrow \infty } \frac{1}{t} \int _{0}^{t} C_{i}(s) \,\mathrm{d}s = \lim_{t\rightarrow \infty } \frac{1}{t} \int _{0}^{t} \overline{C}_{i}(s) \, \mathrm{d}s = \frac{e_{i}u}{h(g_{i}+m_{i})\rho } =: \frac{G_{i}}{\rho },\quad i=1, 2. \end{aligned}$$

  (2.7)

Because $C_{1}(t)$, $C_{2}(t)$, and $C_{E}(t)$ can be obtained only from (2.5), system (2.4) reduces to the subsystem

$$ \textstyle\begin{cases} \mathrm{d}x(t)=[a_{1}(\xi (t))x(t)-b_{1}(\xi (t))x(t)^{2}- \frac{\alpha (\xi (t))x(t)^{2}}{1+\beta (\xi (t))x(t)^{2}}y(t) \\ \phantom{\mathrm{d}x(t)=}{} -r_{1}(\xi (t))C_{1}(t)x(t)] \,\mathrm{d}t+\sigma _{1}(\xi (t))x(t) \,\mathrm{d}B_{1}(t), \\ \mathrm{d}y(t)=[-a_{2}(\xi (t))y(t)-b_{2}(\xi (t))y(t)^{2}+ \frac{k(\xi (t))\alpha (\xi (t))x(t)^{2}}{1+\beta (\xi (t))x(t)^{2}}y(t) \\ \phantom{\mathrm{d}x(t)=}{} -r_{2}(\xi (t))C_{2}(t)y(t)] \,\mathrm{d}t+\sigma _{2}(\xi (t))y(t) \,\mathrm{d}B_{2}(t) \end{cases} $$

(2.8)

with initial values

$$\begin{aligned} x(0)>0,\qquad y(0)>0\quad\text{and}\quad \xi (0)\in \mathbb{S}. \end{aligned}$$

(2.9)

Subsystem (2.8) can be written as the SDE

$$\begin{aligned} \mathrm{d}z(t)=f \bigl(z(t), \xi (t) \bigr) \,\mathrm{d}t + g \bigl(z(t), \xi (t) \bigr) \,\mathrm{d}B(t) \end{aligned}$$

(2.10)

with initial value $(z(0),\xi (0)) = (z_{0},\xi _{0})$, where the drift coefficient $f: \mathbb{R}^{n}\times \mathbb{S}\rightarrow \mathbb{R}^{n}$, the diffusion coefficient $g: \mathbb{R}^{n}\times \mathbb{S}\rightarrow \mathbb{R}^{n\times d}$, and $B(t)$ is a d-dimensional Brownian motion. Let $D(z, k)=g(z, k)g(z, k)^{T}=(d_{ij}(z, k))$. For a a twice continuously differentiable function $V(z, k): \mathbb{R}^{n}\times \mathbb{S}\rightarrow \mathbb{R}$, we define the diffusion operator $\mathcal{L}$ by

$$\begin{aligned} \mathcal{L}V(z, k) = \sum^{n}_{i=1}f_{i}(z, k) \frac{\partial V(z, k)}{\partial z_{i}} + \frac{1}{2}\sum^{n}_{i,j=1}d_{ij}(z, k)\frac{\partial ^{2}V(z, k)}{\partial z_{i}z_{j}} + \sum^{N}_{l=1} \gamma _{kl}V(z, l). \end{aligned}$$

(2.11)

We end this section with the following existence and uniqueness theorem.

Theorem 2.1

For any given initial value $(x(0), y(0), \xi (0))\in \mathbb{R}^{2}_{+}\times \mathbb{S}$, there exists a unique global solution to system (2.8), and $(x(t), y(t), \xi (t))\in \mathbb{R}^{2}_{+}\times \mathbb{S}$ a.s.

Proof

Since both the drift and diffusion coefficients of equation (2.8) satisfy the local Lipschitz condition, there is a unique local solution $(x(t), y(t), \xi (t))$ on $t\in [0, \tau _{e})$, where $\tau _{e}$ denotes the explosion time (see [25]). To verify that the solution is global, we need to prove that $\tau _{e}=\infty$ a.s. Let $m_{0}>1$ be sufficiently large such that $x(0), y(0) \in [1/m_{0}, m_{0}]$. For each integer $m\geq m_{0}$, define the stopping time

$$\begin{aligned} \tau _{m}=\inf \biggl\{ t\in [0,\tau _{e}):\min \bigl\{ x(t), y(t) \bigr\} \leq \frac{1}{m} \text{ or } \max \bigl\{ x(t), y(t) \bigr\} \geq m \biggr\} \end{aligned}$$

with convention $\inf \emptyset =+\infty$. It is clear that $\tau _{m}$ increases as $m\rightarrow \infty$. Let $\tau _{\infty }=\lim_{m\rightarrow \infty }\tau _{m}$, so that $\tau _{\infty }\leq \tau _{e}$. Thus we only need to prove that $\tau _{\infty }=\infty$ a.s. If this were not true, then there would be constants $T>0$ and $\epsilon \in (0,1)$ such that $\mathbb{P}\{\tau _{\infty }\leq T\}>\epsilon$ and an integer $m_{1}\geq m_{0}$ such that

$$\begin{aligned} \mathbb{P}\{\tau _{m}\leq T \}\geq \epsilon, \quad\forall m \geq m_{1}. \end{aligned}$$

(2.12)

Define the $C^{2}$-function V: $\mathbb{R}_{+}^{2}\times \mathbb{S}\rightarrow \mathbb{R}_{+}$ as follows:

$$\begin{aligned} V(x,y,i)=(x-1-\ln x)+(y-1-\ln y). \end{aligned}$$

According to the definition of the operator $\mathcal{L}$ (see (2.11)) and the vertex formula of quadratic functions, we have

$$\begin{aligned} & \mathcal{L}V(x,y,i) \\ &\quad= \biggl(1-\frac{1}{x} \biggr) \biggl[a_{1}(i)x - b_{1}(i)x^{2} - \frac{\alpha (i) x^{2}y}{1+\beta (i) x^{2}} - r_{1}(i)C_{1}x \biggr] + \frac{1}{2} \sigma _{1}(i)^{2} \\ &\qquad{} + \biggl(1-\frac{1}{y} \biggr) \biggl[-a_{2}(i)y - b_{2}(i)y^{2} + \frac{k(i)\alpha (i) x^{2}y}{1+\beta (i) x^{2}} - r_{2}(i)C_{2}y \biggr] + \frac{1}{2} \sigma _{2}(i)^{2} \\ &\quad\leq - b_{1}(i)x^{2} + \bigl(a_{1}(i)+b_{1}(i) \bigr)x - b_{2}(i)y^{2} + \biggl(b_{2}(i)+\alpha (i)+\frac{k(i)\alpha (i)}{\beta (i)} \biggr)y \\ &\qquad{} + a_{2}(i) + r_{1}(i)C_{1} + r_{2}(i)C_{2} + \frac{1}{2} \bigl( \sigma _{1}(i)^{2}+\sigma _{2}(i)^{2} \bigr) \leq H, \end{aligned}$$

where H is a finite positive constant. Then the generalized Itô’s formula [25] yields

$$\begin{aligned} \mathrm{d}V\leq H \,\mathrm{d}t + \sigma _{1}(i) \bigl(x(t)-1 \bigr) \,\mathrm{d}B_{1}(t) + \sigma _{2}(i) \bigl(y(t)-1 \bigr) \, \mathrm{d}B_{2}(t), \end{aligned}$$

which implies

$$\begin{aligned} & \mathbb{E} \bigl[V \bigl(x(\tau _{m}\wedge T),y(\tau _{m}\wedge T), \xi (\tau _{m}\wedge T) \bigr) \bigr] \\ &\quad\leq \mathbb{E} \bigl[V \bigl(x(0),y(0),\xi (0) \bigr) \bigr] + HT, \end{aligned}$$

(2.13)

where $\tau _{m}\wedge T = \min \{\tau _{m}, T\}$. On the other hand, set $\Omega _{m}=\{\tau _{m}\leq T \}$ for $m\geq m_{1}$, so $\mathbb{P}(\Omega _{m})\geq \epsilon$ by (2.12). Note that for all $\omega \in \Omega _{m}$, at least one of $x(\tau _{m},\omega )$ and $y(\tau _{m},\omega )$ equals either m or $1/m$. Then

$$\begin{aligned} V \bigl(x(\tau _{m},\omega ),y(\tau _{m},\omega ),\xi ( \tau _{m}, \omega ) \bigr) \geq (m-1-\ln m ) \wedge \biggl( \frac{1}{m}-1-\ln \frac{1}{m} \biggr). \end{aligned}$$

Reviewing (2.13), we can claim that

$$\begin{aligned} \mathbb{E} \bigl[V \bigl(x(0),y(0),\xi (0) \bigr) \bigr] + HT &\geq \mathbb{E} \bigl[1_{\Omega _{m}}V \bigl(x(\tau _{m},\omega ),y(\tau _{m}, \omega ),\xi (\tau _{m},\omega ) \bigr) \bigr] \\ &\geq \epsilon \biggl[ (m-1-\ln m ) \wedge \biggl(\frac{1}{m}-1- \ln \frac{1}{m} \biggr) \biggr], \end{aligned}$$

where $1_{\Omega _{m}}$ is the indicator function of the set $\Omega _{m}$. Letting $m\rightarrow \infty$ leads to

$$\begin{aligned} \infty > \mathbb{E} \bigl[V \bigl(x(0),y(0),\xi (0) \bigr) \bigr] + HT = \infty, \end{aligned}$$

a contradiction, so that $\tau _{\infty }=\infty$ a.s. The proof is complete. □

Remark 2.1

By the existence and uniqueness theorem it follows from [42, Lemma 1] that the solution $(x(t), y(t), \xi (t))$ of (2.8) satisfies

$$\begin{aligned} &\limsup_{t\rightarrow \infty } \bigl[x(t)+y(t) \bigr] < \infty\quad \text{a.s.}, \\ &\lim_{t\rightarrow \infty }\frac{1}{t} \int ^{t}_{0}\sigma _{1} \bigl( \xi (s) \bigr)x(s) \,\mathrm{d}B_{1}(s) = 0 \quad\text{a.s.}, \\ &\lim_{t\rightarrow \infty }\frac{1}{t} \int ^{t}_{0}\sigma _{2} \bigl( \xi (s) \bigr)y(s) \,\mathrm{d}B_{2}(s) = 0 \quad\text{a.s}. \end{aligned}$$

3 Extinction and persistence

This section aims to investigate the extinction, nonpersistence in mean, and weak persistence in mean of both prey $x(t)$ and predator $y(t)$ separately.

Definition 3.1

([21, 35])

The population $z(t)$ is called:

• (1) extinct if $\lim_{t\rightarrow \infty }z(t)=0$ a.s.;

• (2) nonpersistent in mean if $\limsup_{t\rightarrow \infty } \frac{1}{t}\int _{0}^{t} z(s) \,\mathrm{d}s= 0$ a.s.; and

• (3) weakly persistent in mean if $\limsup_{t\rightarrow \infty } \frac{1}{t}\int _{0}^{t} z(s) \,\mathrm{d}s > 0$ a.s.

For convenience, we define

$$\begin{aligned} & A_{1} = \sum^{N}_{i=1} \pi _{i} \biggl[a_{1}(i)-\frac{1}{2} \sigma _{1}^{2}(i) \biggr],\qquad B_{1}= \bigl\langle r_{1} \bigl(\xi (t) \bigr) \overline{C}_{1}(t) \bigr\rangle _{*}, \\ & A_{2} = \sum^{N}_{i=1} \pi _{i} \biggl[-a_{2}(i)-\frac{1}{2} \sigma _{2}^{2}(i)+\frac{k(i)\alpha (i)}{\beta (i)} \biggr],\qquad B_{2}= \bigl\langle r_{2} \bigl(\xi (t) \bigr)\overline{C}_{2}(t) \bigr\rangle _{*}, \\ & A_{3} = \sum^{N}_{i=1} \pi _{i} \biggl[ a_{1}(i) - a_{2}(i) - \frac{\sigma ^{2}_{1}(i)}{2} - \frac{\sigma ^{2}_{2}(i)}{2} - \frac{ ( 2\sqrt{\delta k(i)\alpha (i)} - ( a_{1}(i) + b_{1}(i) ) )^{2}}{4(b_{1}(i)-\delta \beta (i))} \biggr] \\ &\phantom{A_{3} =}{} - \bigl\langle r_{1} \bigl(\xi (t) \bigr)\overline{C}_{1}(t) \bigr\rangle _{*}- \bigl\langle r_{2} \bigl(\xi (t) \bigr) \overline{C}_{2}(t) \bigr\rangle _{*} - \delta. \end{aligned}$$

Theorem 3.1

The prey $x(t)$ of (2.8) is

• (1) extinct if $A_{1}- B_{1}<0$;

• (2) nonpersistent in mean if $A_{1}- B_{1}=0$; and

• (3) weakly persistent in mean if $A_{1}- B_{1}>0$.

Proof

Applying generalized Itô’s formula to (2.8) yields

$$\begin{aligned} \frac{1}{t}\ln \frac{x(t)}{x(0)}={}&\frac{1}{t} \int ^{t}_{0} \biggl[a_{1} \bigl( \xi (s) \bigr)-\frac{1}{2}\sigma _{1}^{2} \bigl(\xi (s) \bigr)-b_{1} \bigl(\xi (s) \bigr)x(s)- \frac{\alpha (\xi (s))x(s)y(s)}{1+\beta (\xi (s))x(s)^{2}} \biggr] \, \mathrm{d}s \\ &{} -\frac{1}{t} \int ^{t}_{0}r_{1} \bigl(\xi (s) \bigr)C_{1}(s) \,\mathrm{d}s+ \frac{M_{1}(t)}{t}, \end{aligned}$$

(3.1)

$$\begin{aligned} \frac{1}{t}\ln \frac{y(t)}{y(0)}={}&\frac{1}{t} \int ^{t}_{0} \biggl[-a_{2} \bigl( \xi (s) \bigr)-\frac{1}{2}\sigma ^{2}_{2} \bigl(\xi (s) \bigr)-b_{2} \bigl(\xi (s) \bigr)y(s) \\ &{} + \frac{k(\xi (s))\alpha (\xi (s))x(s)^{2}}{1+\beta (\xi (s))x(s)^{2}} \biggr] \,\mathrm{d}s - \frac{1}{t} \int ^{t}_{0}r_{2} \bigl(\xi (s) \bigr)C_{2}(s) \,\mathrm{d}s + \frac{M_{2}(t)}{t}, \end{aligned}$$

(3.2)

where $M_{i}(t)=\int ^{t}_{0}\sigma _{i}(\xi (s)) \,\mathrm{d}B_{i}(s)\ (i=1,2)$ satisfy (see [24, Theorem 3.4])

$$\begin{aligned} \lim_{t\rightarrow \infty }\frac{M_{i}(t)}{t}=0\quad \text{a.s.}, i=1, 2. \end{aligned}$$

(3.3)

Firstly, it follows from equation (3.1) that

$$\begin{aligned} \frac{1}{t}\ln \frac{x(t)}{x(0)}\leq \frac{1}{t} \int ^{t}_{0} a_{1} \bigl( \xi (s) \bigr)- \frac{1}{2}\sigma _{1}^{2} \bigl(\xi (s) \bigr) - r_{1} \bigl(\xi (s) \bigr)C_{1}(s) \,\mathrm{d}s + \frac{M_{1}(t)}{t}. \end{aligned}$$

(3.4)

Using (3.3) and the ergodicity of $\xi (t)$, we obtain

$$\begin{aligned} \biggl[\frac{1}{t}\ln \frac{x(t)}{x(0)} \biggr]^{*} \leq A_{1}-B_{1}< 0\quad \text{a.s.}, \end{aligned}$$

which implies that $\lim_{t\rightarrow \infty }x(t)=0$ a.s., so the prey $x(t)$ is extinct, and (1) is proved.

Secondly, for given $\epsilon > 0$ small, there exists a constant $\widetilde{T}>0$ such that for all $t>\widetilde{T}$,

$$ \begin{aligned} & \frac{1}{t} \int ^{t}_{0} a_{1} \bigl(\xi (s) \bigr)- \frac{1}{2} \sigma _{1}^{2} \bigl(\xi (s) \bigr) \, \mathrm{d}s \leq A_{1}+\frac{\epsilon }{2}, \\ & \frac{1}{t} \int ^{t}_{0} r_{1} \bigl(\xi (s) \bigr)C_{1}(s) \,\mathrm{d}s \geq B_{1}- \frac{\epsilon }{2}. \end{aligned} $$

(3.5)

Inserting (3.5) into (3.1) leads to

$$\begin{aligned} \frac{1}{t}\ln \frac{x(t)}{x(0)}\leq A_{1}-B_{1}+ \epsilon - \frac{1}{t} \int ^{t}_{0}\hat{b}_{1}x(s) \, \mathrm{d}s + \frac{M_{1}(t)}{t}. \end{aligned}$$

By [19, Lemma 2], if $A_{1}-B_{1}\geq 0$, then

$$\begin{aligned} \bigl\langle x(t) \bigr\rangle ^{*} \leq \frac{A_{1}-B_{1}+\epsilon }{\hat{b}_{1}} \quad \text{a.s}. \end{aligned}$$

(3.6)

In particular, when $A_{1}-B_{1}=0$, it follows from (3.6) and the arbitrariness of ϵ that $\langle x(t) \rangle ^{*} = 0$ a.s., which states that the prey $x(t)$ is nonpersistent in mean. So (2) is proved.

Thirdly, taking the upper limits of both sides of (3.1) shows

$$\begin{aligned} \biggl[\frac{1}{t}\ln \frac{x(t)}{x(0)} \biggr]^{*} \geq A_{1} - B_{1} - \biggl\langle b_{1} \bigl(\xi (t) \bigr)x(t) + \biggl( \frac{\alpha ^{2}(\xi (t))}{4\beta (\xi (t))}+1 \biggr)y(t) \biggr\rangle ^{*}. \end{aligned}$$

(3.7)

Recalling that $x(t)^{*} < \infty$ a.s. (see Remark 2.1), we get that the left side of (3.7) is nonpositive. Then

$$\begin{aligned} \check{b}_{1} \bigl\langle x(t) \bigr\rangle ^{*} + \biggl( \frac{\check{\alpha }^{2}}{4\hat{\beta }}+1 \biggr) \bigl\langle y(t) \bigr\rangle ^{*} \geq A_{1}-B_{1}>0, \end{aligned}$$

(3.8)

which shows that $\langle x(t)\rangle ^{*} > 0$. Otherwise, for all $\omega \in \{\omega: \langle x(t,\omega )\rangle ^{*} =0 \}$, estimate (3.8) gives $\langle y(t)\rangle ^{*} > 0$. However, since $\frac{k(\xi )\alpha (\xi )x^{2}}{1+\beta (\xi )x^{2}} \leq \frac{\check{k} \check{\alpha } x}{2\hat{\beta }^{1/2}}, x \in \mathbb{R}_{+}$, another equation (3.2) yields

$$\begin{aligned} \biggl[\frac{\ln y(t,\omega )}{t} \biggr]^{*} \leq -\sum _{i \in \mathbb{S}}\pi _{i} \biggl[a_{2}(i) + \frac{\sigma ^{2}_{2}(i)}{2} \biggr] < 0 \quad \text{a.s.}, \end{aligned}$$

which shows that $\langle y(t)\rangle ^{*} = 0$, a contradiction, so $\langle x(t)\rangle ^{*} >0$ a.s., that is, the prey $x(t)$ is weakly persistent in mean. Hereto, all conclusions of the theorem are proved. □

Theorem 3.2

The predator $y(t)$ of (2.8) is

• (1) extinct if $A_{2}- B_{2}<0$;

• (2) nonpersistent in mean if $A_{2}- B_{2}=0$; and

• (3) weakly persistent in mean if there exists a constant $\delta \in (0, \frac{\hat{b}_{1}}{\check{\beta }})$ such that $A_{3}>0$.

Proof

Firstly, using equation (3.2), we have

$$\begin{aligned} \frac{1}{t}\ln \frac{y(t)}{y(0)}\leq{}& \frac{1}{t} \int ^{t}_{0} -a_{2} \bigl( \xi (s) \bigr) - \frac{1}{2}\sigma ^{2}_{2} \bigl(\xi (s) \bigr) + \frac{k(\xi (s))\alpha (\xi (s))}{\beta (\xi (s))} \\ &{} - r_{2} \bigl(\xi (s) \bigr)C_{2}(s) \,\mathrm{d}s + \frac{M_{2}(t)}{t}. \end{aligned}$$

(3.9)

Analogously, taking the upper limits on both sides of (3.9) yields

$$\begin{aligned} \biggl[\frac{1}{t}\ln \frac{y(t)}{y(0)} \biggr]^{*} \leq A_{2}-B_{2}< 0\quad \text{a.s.}, \end{aligned}$$

which implies that $\lim_{t\rightarrow \infty }y(t)=0$ a.s., and thus (1) is proved.

Secondly, for given $\epsilon > 0$ small, there exists a constant $\widetilde{T}>0$ such that for all $t>\widetilde{T}$,

$$ \begin{aligned}& \frac{1}{t} \int ^{t}_{0} -a_{2} \bigl(\xi (s) \bigr) - \frac{1}{2} \sigma _{2}^{2} \bigl(\xi (s) \bigr) + \frac{k(\xi (s))\alpha (\xi (s))}{\beta (\xi (s))} \,\mathrm{d}s \leq A_{2}+ \frac{\epsilon }{2}, \\ &\frac{1}{t} \int ^{t}_{0}r_{2} \bigl(\xi (s)C_{2}(s) \bigr) \,\mathrm{d}s \geq B_{2}- \frac{\epsilon }{2}. \end{aligned} $$

(3.10)

Inserting (3.10) into (3.2), we arrive at

$$\begin{aligned} \frac{1}{t}\ln \frac{y(t)}{y(0)}\leq A_{2}-B_{2}+ \epsilon - \frac{1}{t} \int ^{t}_{0}\hat{b}_{2}y(s) \,\mathrm{d}s + \frac{M_{2}(t)}{t}. \end{aligned}$$

If $A_{2}-B_{2}\geq 0$, then

$$\begin{aligned} \bigl\langle y(t) \bigr\rangle ^{*} \leq \frac{A_{2}-B_{2}+\epsilon }{\hat{b}_{2}} \quad \text{a.s}. \end{aligned}$$

(3.11)

In particular, if $A_{2}-B_{2}=0$, then follows from (3.11) and the arbitrariness of ϵ that $\langle y(t)\rangle ^{*} = 0$ a.s., and thus (2) is proved.

Finally, by (3.1), (3.2), and the first equation of (2.8) we get

$$\begin{aligned} & \frac{1}{t}\ln \frac{x(t)}{x(0)}+\frac{1}{t}\ln \frac{y(t)}{y(0)}-\frac{(x(t)-x(0))}{t} \\ &\quad=\frac{1}{t} \int ^{t}_{0} \biggl[- \frac{\alpha (\xi (s))x(s)y(s)}{1+\beta (\xi (s))x^{2}(s)} + \frac{k(\xi (s))\alpha (\xi (s))x^{2}(s)}{1+\beta (\xi (s))x^{2}(s)} + \frac{\alpha (\xi (s))x^{2}(s)y(s)}{1+\beta (\xi (s))x^{2}(s)} \biggr] \,\mathrm{d}s \\ &\qquad{} +\frac{1}{t} \int ^{t}_{0} \biggl[a_{1} \bigl(\xi (s) \bigr)-r_{1} \bigl(\xi (s) \bigr)C_{1}(s) - \frac{1}{2} \sigma ^{2}_{1} \bigl(\xi (s) \bigr)-a_{2} \bigl(\xi (s) \bigr)-r_{2} \bigl(\xi (s) \bigr)C_{2}(s) \\ &\qquad{} -\frac{1}{2}\sigma ^{2}_{2} \bigl(\xi (s) \bigr)+b_{1} \bigl(\xi (s) \bigr)x^{2}(s)- \bigl[b_{1} \bigl(\xi (s) \bigr)+a_{1} \bigl(\xi (s) \bigr)-r_{1} \bigl(\xi (s) \bigr)C_{1}(s) \bigr]x(s) \\ &\qquad{} -b_{2} \bigl(\xi (s) \bigr)y(s) \biggr] \,\mathrm{d}s + \frac{M_{1}(t)}{t}+ \frac{M_{2}(t)}{t} - \frac{1}{t} \int ^{t}_{0}\sigma _{1} \bigl(\xi (s) \bigr)x(s) \,\mathrm{d}B_{1}(s). \end{aligned}$$

Applying the reverse Young inequality

$$\begin{aligned} mn \geq 2\sqrt{\delta m} - \delta n^{-1},\quad \delta, m, n > 0, \end{aligned}$$

(3.12)

we get $\frac{k \alpha x^{2}}{1 + \beta x^{2}} \geq 2\sqrt{\delta k \alpha }x - \delta (1 + \beta x^{2}), x \in \mathbb{R}_{+}$. Then, using the inequality $-\frac{\alpha x}{1 + \beta x^{2}}y \geq - \frac{(1+\beta )\alpha }{2\beta }y, x,y \in \mathbb{R}_{+}$, we derive that

$$\begin{aligned} & \frac{1}{t}\ln \frac{x(t)}{x(0)}+\frac{1}{t}\ln \frac{y(t)}{y(0)} \\ &\quad\geq \frac{1}{t} \int ^{t}_{0} \biggl[a_{1} \bigl(\xi (s) \bigr) - r_{1} \bigl(\xi (s) \bigr)C_{1}(s) - \frac{1}{2}\sigma ^{2}_{1} \bigl(\xi (s) \bigr)-a_{2} \bigl(\xi (s) \bigr) -r_{2} \bigl(\xi (s) \bigr)C_{2}(s) \\ &\qquad{} - \frac{1}{2}\sigma ^{2}_{2} \bigl(\xi (s) \bigr) - \frac{ (2\sqrt{\delta k(\xi (s))\alpha (\xi (s))} - [b_{1}(\xi (s))+a_{1}(\xi (s)) ] )^{2}}{4[b_{1}(\xi (s))-\delta \beta (\xi (s))]} - \delta \biggr] \,\mathrm{d}s \\ &\qquad{} -\frac{1}{t} \int ^{t}_{0} \biggl[b_{2} \bigl(\xi (s) \bigr)+ \frac{[1+\beta (\xi (s))]\alpha (\xi (s))}{2\beta (\xi (s))} \biggr]y(s) \,\mathrm{d}s + \frac{M_{1}(t)}{t} + \frac{M_{2}(t)}{t} \\ & \qquad{}-\frac{1}{t} \int ^{t}_{0}\sigma _{1} \bigl(\xi (s) \bigr)x(s) \,\mathrm{d}B_{1}(s) - \frac{x(0)}{t}, \end{aligned}$$

where we used the vertex formula of quadratic functions. On the other hand, Remark 2.1 reads

$$\begin{aligned} \biggl[ \frac{1}{t}\ln \frac{x(t)}{x(0)}+\frac{1}{t}\ln \frac{y(t)}{y(0)} \biggr]^{*} \leq 0 \quad \text{and} \quad \biggl[ \frac{1}{t} \int ^{t}_{0}\sigma _{1} \bigl(\xi (s) \bigr)x(s) \,\mathrm{d}B_{1}(s) \biggr]^{*} = 0. \end{aligned}$$

Thus $\langle y(t)\rangle ^{*} > 0$ a.s. Hereto, all conclusions of this theorem are proved. □

Remark 3.1

According to Theorems 3.1 and 3.2, we can observe that

• (1) the greater the values of $\sigma _{i}\ (i=1,2)$, the greater the risk of extinction of $x(t)$ and $y(t)$; see Figs. 1 and 2(a);

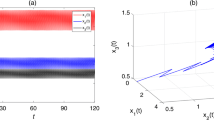
  Figure 1

  

  The sample paths of stochastic model (5.1) with $\pi = (0.9,0.1)$, $a_{1} = (0.62,0.8)$, $b_{1} = (0.021,0.04)$, $\alpha = 0.2$, $\beta = 0.1$, $r_{1} = 0.9$, $\sigma _{1} = 1$, $a_{2} = (0.2,0.4)$, $b_{2} = 0.04$, $k = 0.2$, $r_{2} = 0.8$, $\sigma _{2} = 0.2$, $\rho = 1.2$, $x_{0} = 5$, $y_{0} = 4$

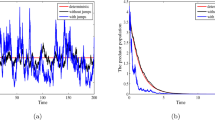
  Figure 2

  

  The sample paths of stochastic model (5.1), where (a) $\pi = (0.9,0.1)$, $a_{1} = (0.62,0.8)$, $b_{1} = (0.021,0.04)$, $\alpha = 0.2$, $\beta = 0.1$, $r_{1} = 0.9$, $\sigma _{1} = 0.1$, $a_{2} = (0.2,0.4)$, $b_{2} = 0.04$, $k = 0.2$, $r_{2} = 0.8$, $\sigma _{2} = 0.1$, $\rho = 1.2$, $x_{0} = 5$, $y_{0} = 4$; (b) $\pi = (0.1,0.9)$, $a_{1} = (0.62,0.8)$, $b_{1} = (0.021,0.04)$, $\alpha = 0.2$, $\beta = 0.1$, $r_{1} = 0.9$, $\sigma _{1} = 1$, $a_{2} = (0.2,0.4)$, $b_{2} = 0.04$, $k = 0.2$, $r_{2} = 0.8$, $\sigma _{2} = 0.2$, $\rho = 1.2$, $x_{0} = 5$, $y_{0} = 4$

• (2) the distribution π of Markov chain $\xi (t)$ plays a significant role in the survival of $x(t)$ and $y(t)$; see Figs. 1 and 2(b);

• (3) the smaller the value of the impulsive input period ρ, the greater the risk of extinction $x(t)$ and $y(t)$; see Figs. 1 and 3.

  Figure 3

  

  The sample paths of stochastic model (5.1) with $\pi = (0.9,0.1)$, $a_{1} = (0.62,0.8)$, $b_{1} = (0.021,0.04)$, $\alpha = 0.2$, $\beta = 0.1$, $r_{1} = 0.9$, $\sigma _{1} = 1$, $a_{2} = (0.2,0.4)$, $b_{2} = 0.04$, $k = 0.2$, $r_{2} = 0.8$, $\sigma _{2} = 0.2$, $\rho = 1.86$, $x_{0} = 5$, $y_{0} = 4$

Remark 3.2

When model (2.4) of this paper reduces to [30, model (5)], compared with [30, Theorem 4.4(3)], Theorem 3.2(3) is more convenient to verify the weak persistence in the mean of predator species $y(t)$, because the conditions of Theorem 3.2(3) are only related to the parameters of equation (2.4).

4 Stationary distribution

In this section, we prove that the solution of model (2.8) has a unique stationary distribution under certain conditions. To facilitate its proof, we will first prove a useful lemma.

Lemma 4.1

([31, 45])

Suppose that all of the following conditions hold:

• (1) $\gamma _{ij}>0$ for all $i\neq j$;

• (2) For all $k\in \mathbb{S}$, the symmetric $D(\cdot, k)$ admits a constant $\varrho \in (0, 1]$ such that

  $$ \varrho \vert \zeta \vert ^{2}\leq \zeta ^{T}D(z, k) \zeta \leq \varrho ^{-1} \vert \zeta \vert ^{2}, \quad\zeta, z \in \mathbb{R}^{n}; $$

• (3) There exists a bounded open set $\mathcal{D}\subset \mathbb{R}^{n}$ with a regular boundary satisfying that for all $k\in \mathbb{S}$, there exists a twice continuously differentiable function $V(\cdot, k): \mathcal{D}^{c}\rightarrow \mathbb{R}_{+}$ such that for some $\varsigma >0$,

  $$\begin{aligned} \mathcal{L}V(z, k)\leq -\varsigma,\quad (z, k)\in \mathcal{D}^{c} \times \mathbb{S}. \end{aligned}$$

Then the solution $(z(t),\xi (t))$ of (2.10) is ergodic and positive recurrent, that is, it has a unique stationary distribution.

Theorem 4.1

If there exists a constant $\delta \in (0, \frac{\hat{b}_{1}}{\check{\beta }})$ such that $\lambda:=\sum_{i=1}^{N}\pi _{i}\Phi _{i}>0$, where $\Phi _{i} = a_{1}(i) - r_{1}(i)(\overline{C}_{1}(t))^{*} -a_{2}(i) -r_{2}(i)( \overline{C}_{2}(t))^{*} - \frac{1}{2}(\sigma _{1}^{2}(i)+\sigma _{2}^{2}(i)) - \delta - \frac{(b_{1}(i)+a_{1}(i)-2\sqrt{\delta k(i)\alpha (i)})^{2}}{4(b_{1}(i)- \delta \beta (i))} -\frac{(b_{2}(i)-a_{2}(i))^{2}}{4b_{2}(i)}$, then the solution $(x(t), y(t), \xi (t))$ of model (2.8) is ergodic and has a unique stationary distribution in $\mathbb{R}^{2}_{+}\times \mathbb{S}$.

Proof

To use Lemma 4.1, we need to verify its three conditions. The first two conditions of Lemma 4.1 can be easily verified by the same proof of [31], so we omit it. Thus we mainly verify condition (3) of Lemma 4.1. For simplicity, define the $C^{2}$-function $U: \mathbb{R}_{+}^{2} \rightarrow \mathbb{R}$ as

$$\begin{aligned} U(x,y)=-M(\ln x-x+\ln y-y)+\frac{1}{2}(\check{k}x+y)^{2}, \end{aligned}$$

where $M=\frac{2}{\lambda }\max \{2,\sup_{(x,y)\in \mathbb{R}^{2}_{+}} \{ -\frac{d_{1}}{2}x^{3}+d_{2}x^{2}-\frac{d_{3}}{2}y^{3}+ \frac{d_{4}}{2}y^{2}\} \}>0$, and the positive constants $d_{i}\ (i = 1,2,3,4)$ will be fixed later. Based on the fact that $U(x,y)$ has a unique minimum point $U(x^{*},y^{*})$, we proceed to define the Lyapunov function $V:\mathbb{R}_{+}^{2}\times \mathbb{S}\rightarrow \mathbb{R}_{+}$ as

$$\begin{aligned} V(x,y,i)&=-M(\ln x-x+\ln y-y)+\frac{1}{2}(\check{k}x+y)^{2}-U \bigl(x^{*},y^{*} \bigr)+M \bigl( \omega _{i}+ \vert \omega \vert \bigr) \\ &=: V_{1}(x,y)+V_{2}(x,y)-U \bigl(x^{*}, y^{*} \bigr)+V_{3}(i), \end{aligned}$$

where $\omega =(\omega _{1}, \omega _{1}, \ldots, \omega _{N})$, $|\omega |=( \omega _{1}^{2} + \omega _{2}^{2} + \cdots + \omega _{N}^{2} )^{1/2}$ with $\omega _{i}\ (i\in \mathbb{S})$ to determined later. For sufficiently large t, taking into account (2.6) and using generalized Itô’s formula, together with the facts $\frac{\alpha }{1+\beta x^{2}} xy \leq \alpha xy$, $-\frac{k\alpha x^{2}}{1+\beta x^{2}} \leq -2\sqrt{\delta k \alpha }x + \delta (1+\beta x^{2})$, $\frac{k \alpha x^{2}}{1 + \beta x^{2}}y \leq \frac{k \alpha }{2 \beta ^{1/2}}xy$ for all $\delta,x,y \in \mathbb{R}_{+}$, as well as the vertex formula of quadratic functions, we have

$$\begin{aligned} & \mathcal{L}V_{1}(x,y,i) \\ &\quad=-M \biggl[ \biggl( \frac{1}{x} - 1 \biggr) \biggl( \bigl[a_{1}(i)-r_{1}(i)C_{1}(t) \bigr]x - b_{1}(i)x^{2} - \frac{\alpha (i)x^{2}y}{1+\beta (i)x^{2}} \biggr) - \frac{1}{2}\sigma _{1}^{2}(i) \\ &\qquad{} + \biggl( \frac{1}{y} - 1 \biggr) \biggl(- \bigl[a_{2}(i) + r_{2}(i)C_{2}(t) \bigr]y - b_{2}(i)y^{2} + \frac{k(i)\alpha (i)x^{2}y}{1+\beta (i)x^{2}} \biggr) - \frac{1}{2} \sigma _{2}^{2}(i) \biggr] \\ &\quad\leq M \biggl(\check{\alpha } + \frac{\check{k} \check{\alpha }}{2 \hat{\beta }^{1/2}} \biggr)xy - M \biggl( a_{1}(i) - r_{1}(i)C_{1}(t) - a_{2}(i) - r_{2}(i)C_{2}(t) - \delta \\ &\qquad{} - \frac{1}{2} \bigl(\sigma _{1}^{2}(i)+\sigma _{2}^{2}(i) \bigr) - \frac{(b_{1}(i)+a_{1}(i)-2\sqrt{\delta k(i)\alpha (i)})^{2}}{4(b_{1}(i)-\delta \beta (i))} -\frac{(b_{2}(i)-a_{2}(i))^{2}}{4b_{2}(i)} \biggr) \\ &\quad\leq M \biggl(\check{\alpha } + \frac{\check{k} \check{\alpha }}{2 \hat{\beta }^{1/2}} \biggr)xy - M\Phi _{i}, \end{aligned}$$

(4.1)

where

$$\begin{aligned} \Phi _{i} = {}&a_{1}(i) - r_{1}(i)\bigl(\overline{C}_{1}(t)\bigr)^{*} -a_{2}(i) -r_{2}(i)\bigl( \overline{C}_{2}(t)\bigr)^{*} - \frac{1}{2}\bigl(\sigma _{1}^{2}(i)+\sigma _{2}^{2}(i)\bigr) - \delta\\ &{} - \frac{(b_{1}(i)+a_{1}(i)-2\sqrt{\delta k(i)\alpha (i)})^{2}}{4(b_{1}(i)-\delta \beta (i))} -\frac{(b_{2}(i)-a_{2}(i))^{2}}{4b_{2}(i)}. \end{aligned}$$

Using generalized Itô’s formula again, we have

$$\begin{aligned} & \mathcal{L}V_{2}(x,y,i) \\ &\quad= (\check{k}x+y) \biggl( \check{k} \bigl[a_{1}(i)-r_{1}(i)C_{1}(t) \bigr]x - \check{k}b_{1}(i)x^{2} - \frac{\check{k}\alpha (i)x^{2}y}{1+\beta (i)x^{2}} \\ &\qquad{} - \bigl[a_{2}(i)+r_{2}(i)C_{2}(t) \bigr]y-b_{2}y^{2}+ \frac{k\alpha (i)x^{2}y}{1+\beta (i)x^{2}} \biggr) + \frac{1}{2} \bigl( \check{k}^{2}\sigma _{1}^{2}x^{2} + \sigma _{2}^{2}y^{2} \bigr) \\ &\quad\leq - \check{k}^{2}b_{1}(i)x^{3} + \check{k}^{2} \biggl(a_{1}(i) + \frac{1}{2}\sigma _{1}^{2}(i) \biggr)x^{2} - b_{2}(i)y^{3} + \frac{1}{2} \sigma _{2}^{2}(i) y^{2} + \check{k}a_{1}(i)xy \end{aligned}$$

(4.2)

and

$$\begin{aligned} \mathcal{L}V_{3}(i)=M\sum _{j=1}^{N}\gamma _{ij}\omega _{j}. \end{aligned}$$

(4.3)

On the other hand, we can observe that

$$\begin{aligned} \sum_{i=1}^{N}\pi _{i}=1 \quad \text{and}\quad \pi \bigl[\Phi -( \pi \Phi )\mathbb{I}_{N} \bigr]=0, \end{aligned}$$

where $\Phi =(\Phi _{1},\Phi _{2},\ldots,\Phi _{N})^{T}$ and $\mathbb{I}_{N}=(1,1,\ldots,1)^{T}\in R^{N}$. Since Φ is irreducible, there exists a solution $\omega =(\omega _{1},\omega _{2},\ldots,\omega _{N})^{T}$ to the following equation (see [16, Lemma 2.3]):

$$\begin{aligned} \Gamma \omega =\Phi -(\pi \Phi )\mathbb{I}_{N}, \end{aligned}$$

which implies that

$$\begin{aligned} -\Phi _{i}+\sum_{j=1}^{N} \gamma _{ij}\omega _{j}=-\sum_{j=1}^{N} \pi _{j}\Phi _{j}=-\lambda,\quad i = 1,2,\ldots,N. \end{aligned}$$

(4.4)

Now, combining (4.1)–(4.4), we arrives at

$$\begin{aligned} \mathcal{L}V(x,y,i)\leq -M\lambda -d_{1}x^{3}+d_{2}x^{2}-d_{3}y^{3}+d_{4}y^{2}+d_{5}xy, \end{aligned}$$

where $d_{1}=\check{k}^{2}\hat{b}_{1}$, $d_{2}=\check{k}^{2}( \check{a}_{1} + \frac{1}{2}\check{\sigma }^{2}_{1} )$, $d_{3}=\hat{b}_{2}$, $d_{4} = \frac{1}{2}\check{\sigma }^{2}_{2}$, and $d_{5}=M( \check{\alpha } + \frac{\check{k} \check{\alpha }}{2 \hat{\beta }^{1/2}} ) + \check{k} \check{a}_{1}$. To verify condition (3) of Lemma 4.1, we consider the bounded closed subset

$$\begin{aligned} \mathcal{D}_{\varepsilon } = \biggl\{ (x,y)\in \mathbb{R}^{2}_{+} | \varepsilon \leq x\leq \frac{1}{\varepsilon }, \varepsilon \leq y\leq \frac{1}{\varepsilon } \biggr\} , \end{aligned}$$

where ε is sufficiently small such that

$$\begin{aligned} & 0< \varepsilon < \min \biggl\{ \frac{M\lambda }{4d_{5}}, \frac{d_{3}}{2d_{5}}, \frac{d_{1}}{2d_{5}} \biggr\} , \end{aligned}$$

(4.5)

$$\begin{aligned} & 1-M\lambda +M_{1} \leq \min \biggl\{ \frac{d_{1}}{2\varepsilon _{3}}, \frac{d_{3}}{2\varepsilon _{3}} \biggr\} , \end{aligned}$$

(4.6)

where

$$\begin{aligned} M_{1}=\sup_{(x,y)\in \mathbb{R}^{2}_{+}} \biggl\{ - \frac{d_{1}}{2}x^{3}+d_{2}x^{2}- \frac{d_{3}}{2}y^{3}+d_{4}y^{2}+ \frac{d_{5}}{2} \bigl(x^{2}+y^{2} \bigr) \biggr\} . \end{aligned}$$

Finally, it remains to prove

$$\begin{aligned} \mathcal{L}V(x,y,i)\leq -1,\quad (x,y,i)\in \mathcal{D}_{\varepsilon }^{c} \times \mathbb{S}, \end{aligned}$$

where the complement $\mathcal{D}^{c}_{\varepsilon }$ can be split as $\mathcal{D}^{c}_{\varepsilon } = \mathcal{D}_{\varepsilon }^{1} \cup \mathcal{D}_{\varepsilon }^{2} \cup \mathcal{D}_{\varepsilon }^{3} \cup \mathcal{D}_{\varepsilon }^{4}$ with

$$\begin{aligned} &\mathcal{D}_{\varepsilon }^{1}= \bigl\{ (x,y)\in \mathbb{R}^{2}_{+} | 0< x< \varepsilon \bigr\} ,\qquad \mathcal{D}_{\varepsilon }^{2}= \bigl\{ (x,y) \in \mathbb{R}^{2}_{+} | 0< y< \varepsilon \bigr\} , \\ &\mathcal{D}_{\varepsilon }^{3}= \biggl\{ (x,y)\in \mathbb{R}^{2}_{+} | x> \frac{1}{\varepsilon } \biggr\} ,\qquad \mathcal{D}_{\varepsilon }^{4}= \biggl\{ (x,y) \in \mathbb{R}^{2}_{+} | y>\frac{1}{\varepsilon } \biggr\} . \end{aligned}$$

Case 1: $(x,y,i)\in \mathcal{D}_{\varepsilon }^{1}\times \mathbb{S}$. It follows from the estimate $xy\leq \varepsilon y\leq \varepsilon (1+y^{3})$, the definition of M, and (4.5) that

$$\begin{aligned} \mathcal{L}V(x,y,i)\leq{}& {-}M\lambda -d_{1}x^{3}+d_{2}x^{2}-d_{3}y^{3}+d_{4}y^{2}+ \varepsilon d_{5}+\varepsilon d_{5}y^{3} \\ \leq{}&{ -}\frac{M\lambda }{4}- \biggl(\frac{M\lambda }{4}-\varepsilon d_{5} \biggr)- \biggl(\frac{d_{3}}{2}-\varepsilon d_{5} \biggr)y^{3} -\frac{M\lambda }{2} \\ &{} -\frac{d_{1}}{2}x^{3} +d_{2}x^{2} - \frac{d_{3}}{2}y^{3}+d_{4}y^{2} \\ \leq {}&{-}\frac{M\lambda }{4} \leq -1 \quad \text{on } \mathcal{D}^{1}_{ \varepsilon } \times \mathbb{S}. \end{aligned}$$

Case 2: $(x,y,i)\in \mathcal{D}_{\varepsilon }^{2}\times \mathbb{S}$. Since $xy\leq \varepsilon x\leq \varepsilon (1+x^{3})$, we also have

$$\begin{aligned} \mathcal{L}V(x,y,i)\leq{}& {-}M\lambda -d_{1}x^{3}+d_{2}x^{2}-d_{3}y^{3}+d_{4}y^{2}+ \varepsilon d_{5}+\varepsilon d_{5}x^{3} \\ \leq{}&{ -}\frac{M\lambda }{4}- \biggl(\frac{M\lambda }{4}-\varepsilon d_{5} \biggr)- \biggl(\frac{d_{1}}{2}-\varepsilon d_{5} \biggr)x^{3} -\frac{M\lambda }{2} \\ &{} -\frac{d_{1}}{2}x^{3} +d_{2}x^{2} - \frac{d_{3}}{2}y^{3}+d_{4}y^{2} \\ \leq{}&{ -}\frac{M\lambda }{4} \leq -1 \quad\text{on } \mathcal{D}^{2}_{ \varepsilon } \times \mathbb{S}. \end{aligned}$$

Case 3: $(x,y,i)\in \mathcal{D}_{\varepsilon }^{3}\times \mathbb{S}$. Based on (4.6), we have

$$\begin{aligned} \mathcal{L}V(x,y,i)&\leq -M\lambda -d_{1}x^{3}+d_{2}x^{2}-d_{3}y^{3}+d_{4}y^{2}+d_{5} \biggl(\frac{x^{2}}{2}+\frac{y^{2}}{2} \biggr) \\ &\leq -M\lambda -\frac{d_{1}}{2}x^{3} -\frac{d_{1}}{2}x^{3} +d_{2}x^{2} -\frac{d_{3}}{2}y^{3} +d_{4}y^{2} +d_{5} \biggl(\frac{x^{2}}{2}+ \frac{y^{2}}{2} \biggr) \\ &\leq -M\lambda -\frac{d_{1}}{2\varepsilon ^{3}} +M_{1} \leq -1\quad \text{on } \mathcal{D}^{3}_{\varepsilon }\times \mathbb{S}. \end{aligned}$$

Case 4: $(x,y,i)\in \mathcal{D}_{\varepsilon }^{4}\times \mathbb{S}$. Similarly,

$$\begin{aligned} \mathcal{L}V(x,y,i)&\leq -M\lambda -\frac{d_{3}}{2}y^{3} - \frac{d_{1}}{2}x^{3}+d_{2}x^{2} - \frac{d_{3}}{2}y^{3} +d_{4}y^{2} +d_{5} \biggl(\frac{x^{2}}{2}+\frac{y^{2}}{2} \biggr) \\ &\leq -M\lambda -\frac{d_{3}}{2\varepsilon ^{3}}+M_{1} \leq -1\quad \text{on } \mathcal{D}^{4}_{\varepsilon }\times \mathbb{S}. \end{aligned}$$

To summarize, condition (3) of Lemma 4.1 is satisfied. Therefore we obtain the desired assertion. □

5 Numerical simulations

In this section, we perform some numerical simulations to verify the theoretical results established in the previous sections.

Example 5.1

Consider the following stochastic Holling-III predator–prey model with Markovian switching in an impulsive polluted environment:

$$ \textstyle\begin{cases} \left.\textstyle\begin{array}{l} \mathrm{d}x = [ a_{1}(\xi (t))x - b_{1}(\xi (t))x^{2}- \frac{\alpha x^{2}y}{1+\beta x^{2}} - r_{1}C_{1}x ] \,\mathrm{d}t \\ \phantom{\mathrm{d}x = }{}+ \sigma _{1} x \,\mathrm{d}B_{1}(t), \\ \mathrm{d}y = [ -a_{2}(\xi (t))y-b_{2}y^{2}+ \frac{k\alpha x^{2}y}{1+\beta x^{2}} - r_{2}C_{2}y ] \,\mathrm{d}t\\ \phantom{\mathrm{d}y = }{} + \sigma _{2} y \,\mathrm{d}B_{2}(t), \\ \mathrm{d}C_{1} = (0.4C_{E} - 1.1C_{1}) \,\mathrm{d}t, \\ \mathrm{d}C_{2} = (0.2C_{E} - 0.4C_{2}) \,\mathrm{d}t, \\ \mathrm{d}C_{E} =-0.4C_{E} \,\mathrm{d}t, \end{array}\displaystyle \right\}\quad t\neq n\rho, n\in \mathbb{N}, \\ \bigtriangleup x(t)=0,\qquad \bigtriangleup y(t)=0,\qquad \bigtriangleup C_{1}(t)=0,\\ \bigtriangleup C_{2}(t)=0,\qquad \bigtriangleup C_{E}(t)=0.3, \quad t=n\rho, n \in \mathbb{N,} \end{cases} $$

(5.1)

with the initial value $(x(0), y(0), C_{1}(0), C_{2}(0), C_{E}(0)) = (x_{0},y_{0},0.03,0.03,0.3)$, where $\xi (t)$ is a Markov chain with $\xi (0) = 1$ and state space $\mathbb{S} = \{1,2\}$.

(i) In Fig. 1, we take $\pi = (0.9,0.1)$, $a_{1} = (0.62,0.8)$, $b_{1} = (0.021,0.04)$, $\alpha = 0.2$, $\beta = 0.1$, $r_{1} = 0.9$, $\sigma _{1} = 1$, $a_{2} = (0.2,0.4)$, $b_{2} = 0.04$, $k = 0.2$, $r_{2} = 0.8$, $\sigma _{2} = 0.2$, $\rho = 1.2$, $x_{0} = 5$, $y_{0} = 4$. By simple calculation, $A_{1} - B_{1} = -183/2750 < 0$ and $A_{2} - B_{2} = -9/100 < 0$. Theorems 3.1 and 3.2 indicate that both $x(t)$ and $y(t)$ will go to extinction. Figure 1 is consistent with the result.

(ii) In Fig. 2(a), we take $\pi = (0.9,0.1)$, $a_{1} = (0.62,0.8)$, $b_{1} = (0.021,0.04)$, $\alpha = 0.2$, $\beta = 0.1$, $r_{1} = 0.9$, $\sigma _{1} = 0.1$, $a_{2} = (0.2,0.4)$, $b_{2} = 0.04$, $k = 0.2$, $r_{2} = 0.8$, $\sigma _{2} = 0.1$, $\rho = 1.2$, $x_{0} = 5$, $y_{0} = 4$. The only difference between the parameters of Figs. 1 and 2(a) is the noise intensities $\sigma _{1}$ and $\sigma _{2}$. Because $A_{1} - B_{1} = 524/1223 > 0$ and $A_{2} - B_{2} = -3/40 < 0$, Theorems 3.1 and 3.2 show that $x(t)$ is weakly persistent in mean and $y(t)$ is extinct. Figure 2(a) supports the result.

(iii) In Fig. 2(b), we take $\pi = (0.1,0.9)$, $a_{1} = (0.62,0.8)$, $b_{1} = (0.021,0.04)$, $\alpha = 0.2$, $\beta = 0.1$, $r_{1} = 0.9$, $\sigma _{1} = 1$, $a_{2} = (0.2,0.4)$, $b_{2} = 0.04$, $k = 0.2$, $r_{2} = 0.8$, $\sigma _{2} = 0.2$, $\rho = 1.2$, $x_{0} = 5$, $y_{0} = 4$. The only difference between the parameters of Figs. 1 and 2(b) is the distribution π of the Markov chain $\xi (t)$. Based on $A_{1} - B_{1} = 213/2750 > 0$ and $A_{2} - B_{2} = -1/4 < 0$, Theorems 3.1 and 3.2 imply that $x(t)$ is weakly persistent in mean and $y(t)$ is extinct. Figure 2(b) confirms the result.

(iv) In Fig. 3, we take $\pi = (0.9,0.1)$, $a_{1} = (0.62,0.8)$, $b_{1} = (0.021,0.04)$, $\alpha = 0.2$, $\beta = 0.1$, $r_{1} = 0.9$, $\sigma _{1} = 1$, $a_{2} = (0.2,0.4)$, $b_{2} = 0.04$, $k = 0.2$, $r_{2} = 0.8$, $\sigma _{2} = 0.2$, $\rho = 1.86$, $x_{0} = 5$, $y_{0} = 4$. The only difference between the parameters of Figs. 1 and 3 is the impulsive input period ρ. Since $A_{1} - B_{1} = 59/9776 > 0$ and $A_{2} - B_{2} = -1/775 < 0$, Theorems 3.1 and 3.2 reveal that $x(t)$ is weakly persistent in mean and $y(t)$ is extinct, which coincides with Fig. 3.

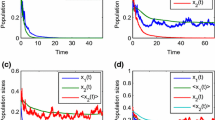
(v) In Fig. 4, we take $\pi = (0.9,0.1)$, $a_{1} = (0.78,0.72)$, $b_{1} = (0.52, 0.48)$, $\alpha = 0.98$, $\beta = 0.84$, $r_{1} = 0.1$, $\sigma _{1} = 0.1$, $a_{2} = (0.24,0.18)$, $b_{2} = 0.1$, $k = 0.86$, $r_{2} = 0.1$, $\sigma _{2} = 0.2$, $\rho = 4$, $x_{0} = 1.4$, $y_{0} = 1.6$. By simple calculation, $A_{1} - B_{1} = 1048/1375 > 0$ and $A_{3} = 496/3919 > 0$ when $\delta =\frac{\check{b}_{1}}{2\beta } = 2/7$. Thus Theorems 3.1 and 3.2 state that both $x(t)$ and $y(t)$ are weakly persistent in mean, which is illustrated in Fig. 4(a). On the other hand, if $\delta =\frac{\check{b}_{1}}{2\beta } = 2/7$, then $\lambda = 611/7556 > 0$. Hence Theorem 4.1 indicates that model (5.1) has a unique stationary distribution, which is confirmed by Figs. 4(c) and 4(d).

Figure 4

(a), (b) The sample paths of stochastic model (5.1) with $\pi = (0.9,0.1)$, $a_{1} = (0.78,0.72)$, $b_{1} = (0.52, 0.48)$, $\alpha = 0.98$, $\beta = 0.84$, $r_{1} = 0.1$, $\sigma _{1} = 0.1$, $a_{2} = (0.24,0.18)$, $b_{2} = 0.1$, $k = 0.86$, $r_{2} = 0.1$, $\sigma _{2} = 0.2$, $\rho = 4$, $x_{0} = 1.4$, $y_{0} = 1.6$; (c), (d) The density function diagrams of $x(t)$ and $y(t)$, respectively

6 Conclusions and future work

In this paper, we explore a stochastic Holling-III predator–prey system and regime switching in an impulsive polluted environment.

The major contributions of this work are:

• We obtain sufficient conditions for the extinction, nonpersistence in mean, and weak persistence in mean. More specifically, for the prey $x(t)$, $A_{1}-B_{1}$ is the threshold of the extinction and weak persistence in mean. That is, if $A_{1}-B_{1}<0$, then $x(t)$ is extinct; if $A_{1}-B_{1}>0$, then $x(t)$ is weakly persistent in mean. For the predator $y(t)$, if $A_{2}-B_{2}<0$, then $y(t)$ is extinct; if there exists a constant $\delta \in (0, \frac{\hat{b}_{1}}{\check{\beta }})$ such that $A_{3}>0$, then $y(t)$ is weakly persistent in mean.

• From Theorems 3.1 and 3.2 we can see that both intensities $\sigma _{i}\ (i = 1,2)$ of white noise and the distribution π of Markov chain $\xi (t)$ are related to the values of $A_{1}$ and $A_{2}$, which will change the survival of $x(t)$ and $y(t)$. To be specific, the greater the values of $\sigma _{i}\ (i=1,2)$, the greater the risk of extinction of $x(t)$ and $y(t)$; see Figs. 1 and 2(a). Also, the distribution π of Markov chain $\xi (t)$ plays a significant role in the survival of $x(t)$ and $y(t)$; see Figs. 1 and 2(b). In addition, the smaller the value of impulsive input period ρ, the greater the risk of extinction of $x(t)$ and $y(t)$; see Figs. 1 and 3.

• Finally, we discuss the positive recurrence and ergodicity of the stochastic model, namely, there exists a unique stationary distribution under some conditions by constructing Lyapunov functions.

Nowadays, environmental pollution has become a concern of people around the world. And environmental noise makes a huge difference to the biological systems in real life. Besides Holling type, we can also consider the stochastic models with other meaningful functional responses under regime switching, such as Beddington–DeAngelis type and Watt type. Furthermore, we will try to collect the real data to validate our theoretical results and explain biological significance.