Abstract
The Riccati-Bernoulli sub-ODE method is firstly proposed to construct exact traveling wave solutions, solitary wave solutions, and peaked wave solutions for nonlinear partial differential equations. A Bäcklund transformation of the Riccati-Bernoulli equation is given. By using a traveling wave transformation and the Riccati-Bernoulli equation, nonlinear partial differential equations can be converted into a set of algebraic equations. Exact solutions of nonlinear partial differential equations can be obtained by solving a set of algebraic equations. By applying the Riccati-Bernoulli sub-ODE method to the Eckhaus equation, the nonlinear fractional Klein-Gordon equation, the generalized Ostrovsky equation, and the generalized Zakharov-Kuznetsov-Burgers equation, traveling solutions, solitary wave solutions, and peaked wave solutions are obtained directly. Applying a Bäcklund transformation of the Riccati-Bernoulli equation, an infinite sequence of solutions of the above equations is obtained. The proposed method provides a powerful and simple mathematical tool for solving some nonlinear partial differential equations in mathematical physics.
Similar content being viewed by others
1 Introduction
Nonlinear partial differential equations (NLPDEs) are known to describe a wide variety of phenomena not only in physics, but also in biology, chemistry, and several other fields. The investigation of traveling wave solutions for NLPDEs plays an important role in the study of nonlinear physical phenomena. In recent years, many powerful methods were used to construct traveling wave solutions of NLPDEs. For example, the inverse scattering method [1], the Bäcklund and Darboux transformation method [2], the homotopy perturbation method [3], the first integral method [4–6], the \(( \frac{{{G}'}}{G} )\)-expansion method [7–9], the sub-equation method [10, 11], Hirota’s method [12], the homogeneous balance method [13–15], the variational iteration method [16, 17], the tanh-sech method [18], the Jacobi elliptic function method [19], the modified simple equation method [20–23], the \(\exp(-\Phi(\xi))\)-expansion method [24], the alternative functional variable method [25], and so on.
Many well-known NLPDEs can be handled by those traditional methods. However, there is no unified method which can be used to deal with all types of NLPDEs. Moreover, we always encounter the fractional NLPDEs, the NLPDEs which have nonlinear terms of any order or peaked wave solutions. It is significant to construct traveling wave solutions of NLPDEs by a uniform method. Based on those problems, the Riccati-Bernoulli sub-ODE method is firstly presented.
In this paper, the Riccati-Bernoulli sub-ODE method is proposed to construct traveling wave solutions, solitary wave solutions, and peaked wave solutions of NLPDEs. By using a traveling wave transformation and the Riccati-Bernoulli equation, NLPDEs can be converted into a set of algebraic equations. Exact solutions of NLPDEs can be obtained by solving the set of algebraic equations. The Eckhaus equation, the nonlinear fractional Klein-Gordon equation, the generalized Ostrovsky equation, and the generalized Zakharov-Kuznetsov-Burgers (ZK-Burgers) equation are chosen to illustrate the validity of the Riccati-Bernoulli sub-ODE method. A Bäcklund transformation of the Riccati-Bernoulli equation is given. If we get a solution of NLPDEs, we can search for a new infinite sequence of solutions of the NLPDEs by using a Bäcklund transformation.
The remainder of this paper is organized as follows: the Riccati-Bernoulli sub-ODE method is described in Section 2. In Section 3, a Bäcklund transformation of the Riccati-Bernoulli equation is given. In Sections 4-7, we apply the Riccati-Bernoulli sub-ODE method to the Eckhaus equation, the nonlinear fractional Klein-Gordon equation, the generalized Ostrovsky equation, and the generalized ZK-Burgers equation, respectively. In Section 8, our results are compared with the first integral method, the \(( \frac{{{G}'}}{G} )\)-expansion method, and physical explanations of the obtained solutions are discussed. In Section 9, some conclusions and directions for future work are given.
2 Description of the Riccati-Bernoulli sub-ODE method
Let there be given a NLPDE, say, in two variables,
where P is in general a polynomial function of its arguments, the subscripts denote the partial derivatives. The Riccati-Bernoulli sub-ODE method consists of three steps.
Step 1. Combining the independent variables x and t into one variable
with
where the localized wave solution \(u ( \xi )\) travels with speed V, by using Eqs. (2) and (3), one can transform Eq. (1) to an ODE
where \({u}'\) denotes \(\frac{du}{d\xi}\).
Step 2. Suppose that the solution of Eq. (4) is the solution of the Riccati-Bernoulli equation
where a, b, c, and m are constants to be determined later.
From Eq. (5) and by directly calculating, we get
Remark
When \(ac\ne0\) and \(m=0\), Eq. (5) is a Riccati equation. When \(a\ne0\), \(c=0\), and \(m\ne1\), Eq. (5) is a Bernoulli equation. Obviously, the Riccati equation and Bernoulli equation are special cases of Eq. (5). Because Eq. (5) is firstly proposed, we call Eq. (5) the Riccati-Bernoulli equation in order to avoid introducing new terminology.
Equation (5) has solutions as follows:
Case 1. When \(m=1\), the solution of Eq. (5) is
Case 2. When \(m\ne1\), \(b=0\), and \(c=0\), the solution of Eq. (5) is
Case 3. When \(m\ne1\), \(b\ne0\), and \(c=0\), the solution of Eq. (5) is
Case 4. When \(m\ne1\), \(a\ne 0\), and \({{b}^{2}}-4ac<0\), the solutions of Eq. (5) are
and
Case 5. When \(m\ne1\), \(a\ne0\), and \({{b}^{2}}-4ac>0\), the solutions of Eq. (5) are
and
Case 6. When \(m\ne1\), \(a\ne0\), and \({{b}^{2}}-4ac=0\), the solution of Eq. (5) is
where C is an arbitrary constant.
Step 3. Substituting the derivatives of u into Eq. (4) yields an algebraic equation of u. Noticing the symmetry of the right-hand item of Eq. (5) and setting the highest power exponents of u to equivalence in Eq. (4), m can be determined. Comparing the coefficients of \({{u}^{i}}\) yields a set of algebraic equations for a, b, c, and V. Solving the set of algebraic equations and substituting m, a, b, c, V, and \(\xi=k ( x+Vt )\) into Eq. (8)-(15), we can get traveling wave solutions of Eq. (1).
In the subsequent section, we will give a Bäcklund transformation of the Riccati-Bernoulli equation and some applications to illustrate the validity of the Riccati-Bernoulli sub-ODE method.
3 Bäcklund transformation of the Riccati-Bernoulli equation
When \({{u}_{n-1}} ( \xi )\) and \({{u}_{n}} ( \xi )\) (\({{u}_{n}} ( \xi )={{u}_{n}} ( {{u}_{n-1}} ( \xi ) )\)) are the solutions of Eq. (5), we get
namely
Integrating above equation once with respect to ξ and simplifying it, we get
where \({{A}_{1}}\) and \({{A}_{2}}\) are arbitrary constants.
Equation (16) is a Bäcklund transformation of Eq. (5). If we get a solution of Eq. (5), we can search for new infinite sequence of solutions of Eq. (5) by using Eq. (16). Then an infinite sequence of solutions of Eq. (1) is obtained.
4 Application to the Eckhaus equation
The Eckhaus equation reads
where \(\psi =\psi ( x,t )\) is a complex-valued function of two real variables x, t.
The Eckhaus equation was found [26] as an asymptotic multiscale reduction of certain classes of nonlinear Schrödinger type equations. A lot of the properties of the Eckhaus equation were obtained [27]. The Eckhaus equation can be linearized by making some transformations of dependent variables [28]. An exact traveling wave solution of the Eckhaus equation was obtained by the \(( \frac{{{G}'}}{G} )\)-expansion method [8] and the first integral method [5].
In this section, new type of exact traveling wave solutions of the Eckhaus equation are obtained by using the Riccati-Bernoulli sub-ODE method.
Using the traveling wave transformation
Eq. (17) is reduced to
where
and k, α, β are real constants to be determined later.
Suppose that the solution of Eq. (19) is the solution of Eq. (5). Substituting Eqs. (5) and (6) into Eq. (19), we get
Setting \(m=-1\) and \(c=0\), Eq. (21) becomes
Setting each coefficient of \({{u}^{j}}\) (\(j=1,3,5\)) to zero, we get
Notice that \(k\ne0\), otherwise we can only get trivial solution.
Case A. If \(b=0\), from Eqs. (23a)-(23c) and (5), we get
where C is an arbitrary real constant.
Case A-1. When \(ka=-1\), we get exact traveling wave solutions of Eq. (17),
where C and α are arbitrary real constants.
Case A-2. When \(ka=-\frac{1}{3}\), we get exact traveling wave solutions of Eq. (17),
where C and α are arbitrary real constants.
Case B. If \(b\ne0\), from Eqs. (23a)-(23c), we get
Case B-1. When \(b=-\frac{\sqrt{{{\alpha}^{2}}+\beta}}{k}\) and \(a=-\frac{1}{k}\), from Eqs. (10) and (18), we get an exact traveling wave solution of Eq. (17),
where C, α, and β are arbitrary real constants.
Especially, if we choose \(C={{C}_{1}}=\frac{1}{\sqrt{{{\alpha}^{2}}+\beta}}\), Eq. (28) becomes
where α and β are arbitrary real constants.
If we choose \(C={{C}_{2}}=-\frac{1}{\sqrt{{{\alpha}^{2}}+\beta}}\), Eq. (28) becomes
where α and β are arbitrary real constants.
Case B-2. When \(b=\frac{\sqrt{{{\alpha }^{2}}+\beta}}{k}\) and \(a=-\frac{1}{k}\), from Eqs. (10) and (18), we get an exact traveling wave solution of Eq. (17),
where C, α, and β are arbitrary real constants.
Especially, if we choose \(C={{C}_{3}}=\frac{1}{\sqrt{{{\alpha}^{2}}+\beta}}\), Eq. (31) becomes
where α and β are arbitrary real constants.
If we choose \(C={{C}_{4}}=-\frac{1}{\sqrt{{{\alpha}^{2}}+\beta}}\), Eq. (31) becomes
where α and β are arbitrary real constants.
Applying Eq. (16) to \({{\psi}_{j}} ( x,t ) \) (\(j=1,2,\ldots,8\)), we can get an infinite sequence of solutions of Eq. (17). For example, by applying Eq. (16) to Eq. (32), we get a new solution of Eq. (17),
where \({{A}_{1}}\), \({{A}_{2}}\), α, and β are arbitrary real constants.
5 Application to the nonlinear fractional Klein-Gordon equation
The nonlinear fractional Klein-Gordon equation [23] reads
where β and γ are known constants.
As is well known, linear and nonlinear Klein-Gordon equations model many problems in classical and quantum mechanics, solitons and condensed matter physics. For example, the nonlinear sine Klein-Gordon equation models a Josephson junction, the motion of rigid pendula attached to a stretched wire, and dislocations in crystals [17, 29–31]. A non-local version of these equations are properly described by the fractional version of them. Exact traveling wave solutions of the nonlinear fractional Klein-Gordon equation were obtained by the homotopy perturbation method [29] and the first integral method [6].
In this section, exact traveling wave solutions of the nonlinear fractional Klein-Gordon equation are obtained by using the Riccati-Bernoulli sub-ODE method.
Using the transformation
with
where l and λ are constants to be determined later, Eq. (35) becomes
Suppose that the solution of Eq. (38) is the solution of Eq. (5). Substituting Eq. (6) into Eq. (38), we get
Setting \(m=0\), Eq. (39) is reduced to
Setting each coefficient of \({{u}^{i}} \) (\(i=0,1,2,3\)) to zero, we get
Solving Eqs. (41a)-(41d), we get
Case A. When \(\frac{\beta}{{{\lambda}^{2}}-{{l}^{2}}}>0\), substituting Eqs. (42a)-(42c) and (37) into Eqs. (11) and (12), we get exact traveling wave solutions of Eq. (35),
and
where C, l, and λ are arbitrary constants.
Case B. When \(\frac{\beta}{{{\lambda}^{2}}-{{l}^{2}}}<0\), substituting Eqs. (42a)-(42c) and (37) into Eqs. (13) and (14), we get exact traveling wave solutions of Eq. (35),
and
where C, l, and λ are arbitrary constants.
Applying Eq. (16) to \({{u}_{j}} ( x,t ) \) (\(j=1,2,\ldots,8 \)), we can get an infinite sequence of solutions of Eq. (35). For example, by applying Eq. (16) to \({{u}_{j}} ( x,t ) \) (\(j=1,2,\ldots,8\)) once, we get new solutions of Eq. (35),
where \({{A}_{1}}\), \({{A}_{2}}\), C, l, and λ are arbitrary real constants.
6 Application to the generalized Ostrovsky equation
The generalized Ostrovsky equation reads
where β, ε, and δ are known constants.
The generalized Ostrovsky equation is a model for the weakly nonlinear surface and internal waves in a rotating ocean. Exact peaked wave solutions were obtained by the undetermined coefficient method [32].
In this section, exact peaked wave solutions of the generalized Ostrovsky equation are obtained by using the Riccati-Bernoulli sub-ODE method.
Using the transformation
with
where k and V are the wave number and wave speed, respectively, Eq. (45) becomes
Suppose that the solution of Eq. (48) is the solution of Eq. (5). From Eqs. (5) and (6), we get
Substituting Eqs. (5), (6), and (49) into Eq. (48), we get
where
Setting \(m=2\) and \(c=0\), Eq. (50) is reduced to
Setting each coefficient of \({{u}^{j}} \) (\(j=0,1,2\)) to zero, we get
Solving Eqs. (52a)-(52c), we get
Substituting Eqs. (53a)-(53c) and (47) into Eq. (10), we get exact peaked wave solutions of Eq. (45),
where C is an arbitrary constant.
Similar to Sections 4 and 5, by using a Bäcklund transformation, we can get an infinite sequence of solutions of the generalized Ostrovsky equation. It being a similar process, we omit it.
7 Application to the generalized ZK-Burgers equation
The generalized ZK-Burgers equation [33] reads
where α, β, γ, σ, and λ are known constants.
The generalized ZK-Burgers equation retains the strong nonlinear aspects of the governing equation in many practical transport problems such as nonlinear waves in a medium with low-frequency pumping or absorption, transport and dispersion of pollutants in rivers, and sediment transport. Wang et al. obtained a solitary wave of the generalized ZK-Burgers equation with a positive fractional power term by using the HB method and with the aid of sub-ODEs [33].
In this section, exact traveling wave solutions of the generalized ZK-Burgers equation are obtained by using the Riccati-Bernoulli sub-ODE method.
Using the transformation
with
where k, l, n, and V are constants to be determined later, Eq. (55) becomes
Suppose that the solution of Eq. (55) is the solution of Eq. (5). Noticing \({u}'\ne0\) and \(k\ne0\), otherwise we can only get trivial solution. Substituting Eqs. (5), (6), and (7) into Eq. (58), we get
where
Setting \(m=1-\frac{\lambda}{2}\) and \(c=0\), Eq. (59) is reduced to
Setting each coefficient of \({{u}^{j}}\) (\(j=0,\frac{\lambda }{2},\lambda \)) to zero, we get
Solving Eqs. (62a)-(62c), we get
Substituting Eqs. (63a)-(63c) and (57) into Eq. (10), we get exact traveling wave solutions of Eq. (55),
where C, l, and n are arbitrary constants.
Equation (64) is new type of traveling wave solution of the generalized ZK-Burgers equation. Especially, if we choose \(C={{C}_{1}}=\frac{\rho ( \lambda+4 )}{\sigma }\sqrt{\frac{-\alpha}{2\rho ( {{\lambda}^{2}}+3\lambda+2 )}}\), we get the solitary wave solutions of Eq. (55),
where l, n are arbitrary constants and
If we choose \(C={{C}_{2}}=-\frac{\rho ( \lambda+4 )}{2\sigma }\sqrt{\frac{-2\alpha}{\rho ( {{\lambda}^{2}}+3\lambda+2 )}}\), we get the solitary wave solutions of Eq. (55),
where l and n are arbitrary constants.
Similar to Sections 4 and 5, by using a Bäcklund transformation, we can get an infinite sequence of solutions of the generalized ZK-Burgers equation. It being a similar process, we omit it.
8 Comparisons and explanations of the solutions
In this section, the physical interpretation of the results of Sections 4-7 are given, respectively. We will compare the Riccati-Bernoulli sub-ODE method with the \(( \frac{{{G}'}}{G} )\)-expansion method, the first integral method, and so on. Some of our obtained exact solutions are in the figures represented with the aid of Maple software.
(1) The Eckhaus equation:
Applying the Riccati-Bernoulli sub-ODE method, Eqs. (25), (26), (28), (31), and (34) are new types of exact traveling wave solutions of the Eckhaus equation. Equations (29), (30), (32), and (33), which are expressed by the hyperbolic functions, are a kind of kink-type envelope solitary solutions. They could not be obtained by the method presented in Ref. [27]. Equation (26), which is expressed by the rational functions, could not be obtained by the \(( \frac{{{G}'}}{G} )\)-expansion method [8] and the first integral method [5].
(2) The nonlinear fractional Klein-Gordon equation:
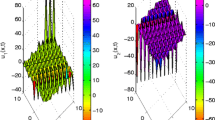
Applying the Riccati-Bernoulli sub-ODE method and comparing our results with Golmankhaneh’s results [29], it is easy to find that \({{u}_{j}} ( x,t ) \) (\(j=1,\ldots,8 \)) are new and identical to results by the first integral method [6]. \({{u}_{j}} ( x,t ) \) (\(j=1,2,3,4 \)), which are expressed by the trigonometric functions, are periodic wave solutions. \({{u}_{j}} ( x,t ) \) (\(j=5,6,7,8 \)), which are expressed by the hyperbolic functions, are a kind of kink-type envelope solitary solutions. The shape of \(u={{u}_{1}} ( x,t )\) is represented in Figure 1 with \(\alpha=\frac{1}{90}\), \(\beta=1\), \(\gamma=1\), \(\lambda=\frac{9}{5}\), \(C=0\) and \(l=\frac{3}{2}\) within the interval \(-5\le x\le5\) and \(0\le t\le\frac{1}{2}\). The shape of \(u={{u}_{5}} ( x,t )\) is represented in Figure 2 with \(\alpha=\frac{1}{5}\), \(\beta=-1\), \(\gamma =1\), \(\lambda=2\), \(C=0\), and \(l=1\) within the interval \(-6\le x\le6\) and \(0\le t\le6\).
Graph of solution \(\pmb{u={{u}_{1}} ( x,t )}\) of the nonlinear fractional Klein-Gordon equation for \(\pmb{\alpha =\frac{1}{90}}\) , \(\pmb{\beta=1}\) , \(\pmb{\gamma=1}\) , \(\pmb{\lambda=\frac{9}{5}}\) , \(\pmb{C=0}\) , and \(\pmb{l=\frac{3}{2}}\) . The left figure shows the 3-D plot and the right figure shows the 2-D plot for \(t=0\).
Graph of solution \(\pmb{u={{u}_{5}} ( x,t )}\) of the nonlinear fractional Klein-Gordon equation for \(\pmb{\alpha =\frac{1}{5}}\) , \(\pmb{\beta=-1}\) , \(\pmb{\gamma=1}\) , \(\pmb{\lambda=2}\) , \(\pmb{C=0}\) , and \(\pmb{l=1}\) . The left figure shows the 3-D plot and the right figure shows the 2-D plot for \(t=0\).
(3) The generalized Ostrovsky equation:
Applying the Riccati-Bernoulli sub-ODE method, it is easy to find that our results are identical to results presented in Ref. [32]. \(u={{u}_{1,2}} ( x,t )\) are peaked wave solutions of the generalized Ostrovsky equation. The shape of \(u={{u}_{1}} ( x,t )\) is represented in Figure 3 with \(\delta=6\), \(\beta =6\), \(\varepsilon=1\), \(\lambda=2\), and \(C=\frac{1}{10}\) within the interval \(-5\le x,t\le5\).
(4) The generalized ZK-Burgers equation:
By applying the Riccati-Bernoulli sub-ODE method to the generalized ZK-Burgers equation, we find that if λ is a positive fraction, our results degenerate to the results of Ref. [33]. Moreover, we enlarge the value range of parameters λ of the generalized ZK-Burgers equation so that the parameter λ can be an arbitrary constant (\(\lambda\ne-1,-2,-4\)). \({{u}_{j}} ( x,t ) \) (\(j=1,\ldots,6 \)) are exact traveling wave solutions of the generalized ZK-Burgers equation. \({{u}_{j}} ( x,t ) \) (\(j=3,4,5,6 \)), which are expressed by the hyperbolic functions, are a kind of kink-type envelope solitary solutions. The shape of \(u={{u}_{1}} ( x,t )\) is represented in Figure 4 with \(\alpha=\beta=\gamma=l=n=y=z=1\), \(\lambda=-\sqrt{2}\) and \(\sigma =2\) within the interval \(-5\le x,t\le5\).
Moreover, by using a Bäcklund transformation, we can get an infinite sequence of solutions of these NLPDEs which cannot be obtained by the \(( \frac{{{G}'}}{G} )\)-expansion method and the first integral method. The graphical demonstrations of some obtained solutions are shown in Figures 1-4.
9 Conclusions
The Riccati-Bernoulli sub-ODE method is successfully used to establish exact traveling wave solutions, solitary wave solutions and peaked wave solutions of NLPDEs. A Bäcklund transformation of the Riccati-Bernoulli equation is given. By applying a Bäcklund transformation of the Riccati-Bernoulli equation to the NLPDEs, an infinite sequence of solutions of the NLPDEs is obtained. The Eckhaus equation, the nonlinear fractional Klein-Gordon equation, the generalized Ostrovsky equation, and the generalized ZK-Burgers equation are chosen to illustrate the validity of the Riccati-Bernoulli sub-ODE method. Many well-known NLPDEs can be handled by this method. The performance of this method is found to be simple and efficient. The availability of computer systems like Maple facilitates the tedious algebraic calculations. The Riccati-Bernoulli sub-ODE method is also a standard and computable method, which allows us to perform complicated and tedious algebraic calculations.
It is well known that it is difficult to propose an uniform analytical method for all types of the NLPDEs, and the Riccati-Bernoulli sub-ODE method is no exception. Similar to the first integral method, the \(( \frac{{{G}'}}{G} )\)-expansion method and the homogeneous balance method, the Riccati-Bernoulli sub-ODE method is used to obtain exact solutions of the form of Eq. (1). Constructing more powerful sub-ODE and Bäcklund transformations is future work and aims to search for exact solutions of NLPDEs
References
Ablowitz, MJ, Clarkson, PA: Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, New York (1991)
Rogers, C, Schief, WK: Bäcklund and Darboux Transformation Geometry and Modern Applications in Solitons Theory. Cambridge University Press, Cambridge (2002)
He, JH: An approximate solution technique depending on an artificial parameter: a special example. Commun. Nonlinear Sci. Numer. Simul. 3, 92-97 (1998)
Feng, ZS: The first-integral method to study the Burgers-Korteweg-de Vries equation. J. Phys. A, Math. Gen. 35, 343-349 (2002)
Taghizadeh, N, Mirzazadeh, M, Filiz, T: The first-integral method applied to the Eckhaus equation. Appl. Math. Lett. 25, 798-802 (2012)
Lu, B: The first integral method for some time fractional differential equations. J. Math. Anal. Appl. 395, 684-693 (2012)
Wang, ML, Li, XZ, Zhang, JL: The \(( \frac{{G'}}{G} )\)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 372, 417-423 (2008)
Zhang, H: New application of the \(( \frac{{G'}}{G})\)-expansion method. Commun. Nonlinear Sci. Numer. Simul. 14, 3220-3225 (2009)
Khan, K, Akbar, MA: Study of analytical method to seek for exact solutions of variant Boussinesq equations. SpringerPlus 3, 324-340 (2014)
Xu, SL, Liang, JC: Exact soliton solutions to a generalized nonlinear Schrödinger equation. Commun. Theor. Phys. 53, 159-165 (2010)
Wang, ML: Applications of F-expansion to periodic wave solutions for a new Hamiltonian amplitude equation. Chaos Solitons Fractals 24, 1257-1268 (2005)
Hirota, R: Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 27, 1192-1194 (1971)
Wang, ML: Solitary wave solutions for variant Boussinesq equations. Phys. Lett. A 199, 169-172 (1995)
Wang, ML, Zhou, YB: Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. A 216, 67-75 (1996)
Bai, CL: Extended homogeneous balance method and Lax pairs, Bäcklund transformation. Commun. Theor. Phys. 37, 645-648 (2002)
He, JH: An new approach to nonlinear partial differential equations. Commun. Nonlinear Sci. Numer. Simul. 2, 230-235 (1997)
Yusufoglu, E: The variational iteration method for studying the Klein-Gordon equation. Appl. Math. Lett. 21, 669-674 (2008)
Wazwaz, AM: The tanh method: exact solutions of the sine-Gordon and the sinh-Gordon equations. Appl. Math. Comput. 167, 1196-1210 (2005)
Yan, ZL: Abunbant families of Jacobi elliptic function solutions of the-dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 18, 299-309 (2003)
Khan, K, Akbar, MA, Rayhanul Islam, SM: Exact solutions for \((1+1)\)-dimensional nonlinear dispersive modified Benjamin-Bona-Mahony equation and coupled Klein-Gordon equations. SpringerPlus 3, 724-731 (2014)
Khan, K, Akbar, MA: Solitary wave solutions of some coupled nonlinear evolution equations. J. Sci. Res. 6, 273-284 (2014)
Khan, K, Akbar, MA: Traveling wave solutions of the \((2+1)\)-dimensional Zoomeron equation and the Burgers equations via the MSE method and the Exp-function method. Ain Shams Eng. J. 5, 247-256 (2014)
Ahmed, MT, Khan, K, Akbar, MA: Study of nonlinear evolution equations to construct traveling wave solutions via modified simple equation method. Phys. Rev. Res. Int. 3, 490-503 (2013)
Khan, K, Akbar, MA: The \(\exp(-\Phi(\xi))\)-expansion method for finding travelling wave solutions of Vakhnenko-Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 5, 72-83 (2014)
Zerarka, A, Ouamane, S, Attaf, A: Construction of exact solutions to a family of wave equations by the functional variable method. Waves Random Complex Media 21, 44-56 (2011)
Calogero, F, Eckhaus, W: Nonlinear evolution equations, rescalings, model PDEs and their integrability: I. Inverse Probl. 3, 229-262 (1987)
Calogero, F, Lillo, SD: The Eckhaus PDE \(i{{\psi }_{t}}+{{\psi }_{xx}}+2{{( {{| \psi |}^{2}} )}_{x}}\psi +{{| \psi |}^{4}}\psi =0\). Inverse Probl. 4, 633-682 (1987)
Calogero, F: The evolution partial differential equation \({{u}_{t}}={{u}_{xxx}}+3( {{u}_{xx}}{{u}^{2}}+3u_{x}^{2}u )+3{{u}_{x}}{{u}^{4}}\). J. Math. Phys. 28, 538-555 (1987)
Golmankhaneh, AK, Baleanu, D: On nonlinear fractional Klein-Gordon equation. Signal Process. 91, 446-451 (2011)
El-Sayed, S: The decomposition method for studying the Klein-Gordon equation. Chaos Solitons Fractals 18, 1025-1030 (2003)
Odibat, Z, Momani, SA: Numerical solution of sine-Gordon equation by variational iteration method. Phys. Lett. A 370, 437-440 (2007)
Lu, Y: A simple method for solving nonlinear wave equations for their peaked soliton solutions and its applications. Acta Phys. Sin. 58, 7452-7456 (2009)
Wang, ML, Li, LX, Li, EQ: Exact solitary wave solutions of nonlinear evolutions with a positive fractional power term. Commun. Theor. Phys. 61, 7-14 (2014)
Acknowledgements
The research is supported by the National Natural Science Foundation of China (11372252, 11372253 and 11432010) and the Fundamental Research Funds for the Central Universities (3102014JCQ01035).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors completed the paper together. All authors read and approved the final manuscript.
Rights and permissions
Open Access This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly credited.
About this article
Cite this article
Yang, XF., Deng, ZC. & Wei, Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv Differ Equ 2015, 117 (2015). https://doi.org/10.1186/s13662-015-0452-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-015-0452-4