Hybrid cubic and hyperbolic b-spline collocation methods for solving fractional Painlevé and Bagley-Torvik equations in the Conformable, Caputo and Caputo-Fabrizio fractional derivatives

Abstract

In this paper, we approximate the solution of fractional Painlevé and Bagley-Torvik equations in the Conformable (Co), Caputo (C), and Caputo-Fabrizio (CF) fractional derivatives using hybrid hyperbolic and cubic B-spline collocation methods, which is an extension of the third-degree B-spline function with more smoothness. The hybrid B-spline function is flexible and produces a system of band matrices that can be solved with little computational effort. In this method, three parameters m, η, and λ play an important role in producing accurate results. The proposed methods reduce to the system of linear or nonlinear algebraic equations. The stability and convergence analysis of the methods have been discussed. The numerical examples are presented to illustrate the applications of the methods and compare the computed results with those obtained using other methods.

1 Introduction

Studying fractional calculus is an old topic that goes back to Leibniz (1695) and Euler (1730) [1–3]. The analysis of noninteger derivatives and integrals offers an excellent method to explain the memory and inherited properties of complex systems. Several existing arbitrary-order derivatives in fractional calculus are typically classified into singular and nonsingular [4–8]. A new effective description of the nonsingular kernel was applied in [8–14].

In general, an analytical solution of the fractional differential equation is difficult. Consequently, the Painlevé and Bagley-Torvik equations do not always have solutions in closed forms that can be obtained by analytical approaches. Numerical methods to find an approximate solution and qualitative behaviors of the solution for fractional differential equation have been investigated in [15–33] and some references therein.

In recent years, the search for numerical methods for approximating the solution to fractional equations has become a topic of interest in applied sciences and engineering. Several mathematicians have recently developed numerical methods for approximating solutions to fractional differential equations involving Caputo-Fabrizio derivatives see [11, 13, 14], and [16].

The B-spline interpolator function is considered one of the most effective methods for interpolating smooth functions, especially compared to other techniques, such as finite element, finite volume, and finite difference methods [14, 34–37]. We also know that the non-polynomial spline function has certain advantages over the polynomial spline function due to its increased smoothness and parameter dependence, leading to improved approximation of solutions see [26, 33, 38–40], and the references therein.

If the solution of the differential equation is an exponential function, then the exponential B-spline interpolator function provides a better approximation compared to the polynomial B-spline function. The advantage of using the hybrid B-spline is that it has three free parameters, λ, m, and κ, that can be determined so that the numerical method produces results with better accuracy. The main reason for writing this article is to create a B-spline function that is a combination of third-order B-spline and hyperbolic B-spline function to approximate the solutions of Painlevé and Bagley-Torvik equations in the Conformable, Captuo, and Caputo-Fabrizio fractional derivative. It also studies of convergence and stability of the numerical method.

We consider the Bagley-Torvik equation in the following form:

$$ \textstyle\begin{cases} \eta _{1}(x)u''(x)+\eta _{2}(x) _{x}D_{0}^{\alpha}u(x)+\eta _{3}(x)u'(x) \\ \quad {} +\eta _{4}(x)_{x}D_{0}^{\beta}u(x)+\eta _{5}(x) u(x)=f(x), \\ u'(0)-\omega _{1}=u(1)-\omega _{2}=0, \end{cases} $$

(1)

where $\alpha =1.5$, $\beta =0.5$, and fractional Painlevé of the first type as:

$$ \textstyle\begin{cases} \eta _{1}(x) _{x}D_{0}^{\alpha}u(x)-6u^{2}(x)-x=f(x), \\ u'(0)-\omega _{1}=u(1)-\omega _{2}=0, \end{cases} $$

(2)

and also Painlevé fractional differential equation of the second type as follows:

$$ \textstyle\begin{cases} \eta _{1}(x) _{x}D_{0}^{\alpha}u(x)-2 u^{3}(x)-xu(x)-x=f(x), & \\ u'(0)-\omega _{1}=u(1)-\omega _{2}=0, & \end{cases} $$

(3)

where, $_{x}D_{0}^{\alpha}$ and $_{x}D_{0}^{\beta}$ are one of the derivatives of Conformable or Caputo or Caputo-Fabrizio also $x\in [0,1]$, $\alpha \in (1,2]$, and $\beta \in (0,1]$. The functions of $\eta _{i}(x), {i=1,2,3,4,5}$, and $f(x)\in C([0,1])$ are continuous, and the function $u(x)$ is also the solution that must be approximated. The fractional Bagley-Torvik equation with derivatives of order 0.5 or 1.5 determines the movement of real physical structures, a plate immersed in gas in fluid together with a Newtonian fluid, simultaneously [18] and [41]. In mathematical physics, such as statistical mechanics, plasma physics, nonlinear waves, quantum gravity, quantum field theory, general relativity, nonlinear optics, and fiber optics, the Painlevé fractional differential equation appears in [19] and [20]. Some of the physical phenomena experienced by physical laboratories do not always have solutions in closed forms, e.g, the fractional Bagley-Torvik and Painleveé equations.

The cubic B-spline function for approximating the solution of Painlevé and Bagley-Torvik equations in the Captuo, Caputo-Fabrizio, and Conformable fractional sense concerning boundary set conditions has been studied in [14], but the convergence of the given numerical method has not been discussed. Several good papers [28, 29, 33] have used spline approximation methods to approximate the solution of fractional Bagley-Torvik equation.

In [21], the reproducing kernel space method for approximating the solution of Bagley-Trovick fractional differential equation is analyzed. A hybrid of block-pulse functions and Chebyshev polynomials based on operational matrices for approximating the solution of fractional differential equations has been studied and analyzed in [42].

The existence of positive and negative solutions of the Bagley-Torvik fractional differential equation and the derivative properties of these solutions have been studied in [22]. The Taylor matrix method for approximating the solution of Bagley-Trovick equation in fluid mechanics is developed in [31]. Cubic spline method for approximating the solution of fractional boundary value problems has been developed in [26]. The Chebyshev collocation method for approximating the solution of fractional Bagley-Torvik equation is introduced in [23].

In [24], the homotopy perturbation method was applied for approximating the solution of Bagley-Torvik equation as a prototype fractional differential equation with two derivatives. The exponential integrators method for numerical solution of the Bagley-Torvik equation was discussed in [30].

The Adomian decomposition method for solving initial value problem of Bagley-Torvik equation is also discussed in [32]. Fractional linear multistep method and a predictor-corrector method of the Adams type, which was based on finite difference methods for initial value problem of the Bagley-Torvik equation, are discussed in [27]. The Legendre operational matrix method for fractional differential equation is applied in [43], and the combination of collocation points and first-order Bessel functions, which is called the Bessel-collocation method for boundary value problem of Bagley-Torvik equation, is discussed in [25]. Recently, some numerical methods have been employed for approximating the solutions of the fractional two-point boundary value problems in both linear and nonlinear types, for example, the cubic B-spline interpolation method [34], the cubic B-spline method, the finite difference technique [35], the B-spline collocation method for solving conformable initial value problems of nonsingular and singular types [36], and well-posedness and numerical simulations employing Legendre-shifted spectral approach for Caputo-Fabrizio fractional stochastic integro differential equations [13]. The solvability of a nonlocal problem with integral transmitting condition for mixed type equation with the Caputo fractional derivative [44] and an extended Caputo fractional derivative operator with its applications [45] are also discussed. An approximate analytic view of physical and biological models in the setting of the Caputo operator via the Elzaki transform decomposition method is shown in [46].

In [15] and [16], iterative reproducing kernel and spline functions have been used to study and develop Bagley-Torvik and Painlevé equations with fractional order.

Many approaches have been developed for solving the fractional differential equations. These methods include: solutions of variable-order fractional differential equations by reproducing the kernel method [47], numerical solutions of fractional differential equations of the Lane-Emden type by reproducing the kernel Hilbert space [48], the reproducing kernel method for approximate solutions of fractional order boundary value problems [49], a collocation shooting method [50], implicit finite difference approximation for time-fractional diffusion equations [51], fractional model and numerical algorithms for predicting COVID-19 with isolation and quarantine strategies [52], Sinc approximation for the numerical solution of a nonlinear fractional pantograph equation [53], matrix approach to discrete fractional calculus [54], and the weighted and shifted Grünwald difference operators [55].

The main objective of this study is to utilize a hybrid of hyperbolic and cubic B-spline functions to solve equations (1)-(3), which results are more accurate compared with some other methods. The first aim of the present work is to explore the cubic hyperbolic B-spline interpolation with multiple parameters and produce the error of approximate hyperbolic spline. The second aim is to introduce a new approximate technique to find solutions of fractional boundary value problem and demonstrate the convergence analysis for this technique. Also, the main advantage of our algorithm is that it can be used directly without using assumption or transformation formulae. The solutions can be obtained with high accuracy compared with other numerical techniques. Also, the proposed method is easy to implement.

This paper consists of four sections. In Sect. 2, we describe basic definitions and the hybrid B-spline. The solutions of fractional Painlevé and Bagley-Torvik equations are approximated using the hybrid B-spline in Sect. 3. Stability and convergence analysis is proved in Sect. 4. In Sect. 5, the numerical examples are given to illustrate the applications of the method, and the computed results are also compared with another known method described in [14, 30, 54].

2 Basic definitions and description of the methods

In this section, we recall some definitions and properties of the fractional calculus theory used in this paper. There are several definitions of a fractional derivative of order $\alpha >0$, such as Riemann-Liouville, Grünwald-Letnikove, Caputo, Conformable, and Caputo-Fabrizio fractional derivatives. In the present work, Caputo, Caputo-Fabrizio, and Conformable fractional derivatives are used for formulating the problem. All these details have been quoted in References [1–19] and [33–36].

The Sobolev space of one-order on (a, b) is defined as follows:

$$ H^{1}(a, b)= \bigl\{ u(x)|u(x)\in L^{2}(a, b), u'\in L^{2}(a,b) \bigr\} , $$

where the $L^{2}(a,b)$ is the square-integrable functions on $(a, b)$.

Here, we give some required definitions and properties of the fractional derivative and the B-spline function.

Definition 1

Let $u(x)$ be a function defined on $(a,b)$, then the Riemann-Liouville fractional derivative has the following form

$$ \textstyle\begin{cases} ^{R}_{x}D_{a}^{\alpha }(u(x))= \frac{1}{\Gamma (m-\alpha )} \frac{d^{m}}{dx^{m}}\int _{a}^{x}(x-t)^{m-\alpha -1}u(t)\,dt, \\ \quad \alpha >0, m-1< \alpha < m, \end{cases} $$

(4)

where $\Gamma (\cdot)$ is the gamma function.

Definition 2

The right and left Riemann-Liouville fractional integrals

$$\begin{aligned}& ^{R}_{x}D_{a+}^{-\alpha}u(x)= \frac{1}{\Gamma (\alpha )} \int _{a}^{x}(x-t)^{ \alpha -1}u(t)\,dt, \quad \alpha >0,\\& ^{R}_{x}D_{b-}^{-\alpha}u(x)= \frac{1}{\Gamma (\alpha )} \int _{x}^{b}(t-x)^{ \alpha -1}u(t)\,dt, \quad \alpha >0. \end{aligned}$$

Definition 3

Let $u(x)$ be a function defined on $(a,b)$, then the Caputo fractional derivative has the following form

$$ \textstyle\begin{cases} ^{C}_{x}D^{\alpha }(u(x))= \frac{1}{\Gamma (m-\alpha )} \int _{a}^{x} (x-t)^{m-\alpha -1}u^{(m)}(t)\,dt, \\ \quad \alpha >0, m-1< \alpha < m. \end{cases} $$

(5)

Definition 4

The Grünwald definition for the fractional derivative is defined in the following form:

$$ A^{\alpha}_{h,p} \bigl(u(x) \bigr)=\lim \frac{1}{h^{\alpha}}\sum_{k=0}^{\infty}g_{ \alpha ,k}u \bigl(x-(k-p)h \bigr), $$

(6)

where $A^{\alpha}_{h,p} (u(x))=^{R}_{x}D_{a}^{\alpha }(u(x))+O(h)$, and $g_{\alpha ,k}= \frac{\Gamma (k-\alpha )}{\Gamma (-\alpha )\Gamma (k+1)}$.

Definition 5

The weighted and shifted Grünwald difference operator is as follows.

Let $u(x)\in L^{1}(R), _{\infty}\!D^{ \alpha +2}_{x} (u(x))$, and its Fourier transform belongs to $L^{1}(R)$,

$$ \textstyle\begin{cases} _{a}D^{ \alpha}_{h,p,q}u(x)= \frac{\vartheta}{h^{\alpha}} \sum_{k=0}^{[ \frac{x-a}{h}]+p} g_{\alpha ,k}u(x-(k-p)h) \\ \hphantom{_{a}D^{ \alpha}_{h,p,q}u(x)}\quad +\frac{(1-\vartheta )}{h^{\alpha}}\sum_{k=0}^{[\frac{x-a}{h}]+q} g_{ \alpha ,k}u(x-(k-q)h)+O(h^{2}), \\ _{b}D^{ \alpha}_{h,p,q}u(x)= \frac{\vartheta}{h^{\alpha}} \sum_{k=0}^{[ \frac{b-x}{h}]+p} g_{\alpha ,k}u(x+(k-p)h) \\ \hphantom{_{b}D^{ \alpha}_{h,p,q}u(x)}\quad +\frac{(1-\vartheta )}{h^{\alpha}}\sum_{k=0}^{[\frac{b-x}{h}]+q} g_{ \alpha ,k}u(x+(k-q)h)+O(h^{2}), \end{cases} $$

(7)

where $x\in R$, $\vartheta \in [0,1]$, also p, and $q, (p\neq q)$ are integers and symmetric.

Definition 6

Let $u(x)\in H^{1}(a,b)$, $\alpha \in (m-1,m]$, $m\in N$ and $\alpha \geq 0$, then the Caputo-Fabrizio fractional derivative of order α is written as:

$$ \textstyle\begin{cases} ^{CF}_{x}D_{a}^{\alpha }(u(x))= \frac{1}{(m-\alpha )} \int _{a}^{x} u(t)^{(m)}\exp( \frac{m-\alpha -1}{m-\alpha}(x-t))\,dt, \\ \quad \alpha >0, m-1< \alpha \leq m, x\geq a. \end{cases} $$

(8)

Definition 7

If $u(x)$ is m-differentiable for all $x\geq a> 0$, then the Conformable fractional derivative with order α is

$$ \textstyle\begin{cases} ^{Co}_{x}D_{a}^{\alpha }(u(x))= \lim_{\eta \rightarrow 0} \frac{u^{(\lceil \alpha \rceil -1)}(x+\eta x^{\lceil \alpha \rceil -\alpha})-u^{(\lceil \alpha \rceil -1)}(x)}{\eta}, \\ \quad a>0, m-1< \alpha \leq m, m\in N, \end{cases} $$

(9)

indeed,

$$ ^{Co}_{x}D_{a}^{\alpha } \bigl(u(x) \bigr)=x^{(\lceil \alpha \rceil -\alpha )}u^{( \lceil \alpha \rceil )}(x), $$

(10)

and the Conformable fractional integral is the following

$$ ^{Co}\boldsymbol{J}_{a}^{\alpha }u(x)= \int _{a}^{x} (t-a)^{ \alpha -1}u(t)\,dt, $$

(11)

where $0<\alpha \leq 1$, and $\lceil \alpha \rceil$ is the smallest integer greater than or equal to α.

Let us consider a mesh with nodal points $x_{i}$ on $[a,b]$ such that:

$$ \Delta :a=x_{0}< x_{1}< x_{2}< \cdots < x_{n-1}< x_{n}=b, $$

where $h=\frac{b-a}{n}$, $x_{i}=a+ih$, for $i=0(1)n$. Suppose

$$ \dots < x_{-2} < x_{-1} < x_{0} < x_{1} < x_{2} < \cdots $$

is a sequence of knots on R. Zero-order B-splines are piecewise constants defined by:

$$ B_{i}^{0}(x)= \textstyle\begin{cases} 1, & x_{i}\leq x\leq x_{i+1}, \\ 0, & \text{otherwise,} \end{cases} $$

(12)

and polynomial B-splines of order $k\geq 1$ are defined recursively in the following form:

$$ B_{i}^{k}(x)= \biggl( \frac{x-x_{i}}{x_{i+k}-x_{i}} \biggr)B_{i}^{k-1}(x)+ \biggl( \frac{x_{i+k+1}-x}{x_{i+k+1}-x_{i+1}} \biggr)B_{i+1}^{k-1}(x). $$

(13)

The hyperbolic B-splines are defined by:

$$ H_{i}^{0}(x)= \textstyle\begin{cases} 1, & x_{i}\leq x\leq x_{i+1}, \\ 0, & \text{otherwise,} \end{cases} $$

(14)

generally, for $k\geq 1$,

$$ H_{i}^{k}(x)= \frac{\sinh (x)(m(x-x_{i}))}{\sinh (x)(\eta (x_{i+k}-x_{i}))}H_{i}^{k-1}(x)+ \frac{\sinh (x)(m(x_{i+k+1}-x))}{\sinh (x)(\eta (x_{i+k+1}-x_{i+1}))}H_{i+1}^{k-1}(x), $$

(15)

where, m and η are the positive real numbers, and a hybrid cubic B-spline basis function is also established using a linear combination of the cubic B-spline basis function and hyperbolic cubic B-spline basis as follows:

$$ T_{i}^{3}(x)=\lambda B_{i}^{k}(x)+(1-\lambda )H_{i}^{k}(x), $$

(16)

hither, the parameter $\lambda \in R$ is a free parameter to control the global shape of curve. The hybrid B-spline basis function reduces to cubic hyperbolic B-spline and cubic B-spline function when $\lambda =0$ and 1, respectively. The finite difference approach yields the solution only at the selected points, but the spline function has the flexibility to get the approximation at any point in the domain with more accurate results compared to the usual finite difference method. The advantage of using hybrid B-spline is the free parameters that play an important role in the implementation of the method and also affect the results to be obtained up to a desired level of accuracy. An appropriate choice of the parameter rises the order of accuracy of the scheme. Suppose the estimate solution $S(x)$ to the exact solution $u(x)$ at point $x_{i}$, respectively, is defined as:

$$ S(x) =\sum_{i=-1}^{n+1}C_{i}T_{i}^{3}(x),\quad x\in [x_{0},x_{n}], $$

(17)

here, $T_{i}^{3}(x)$ are hybrid cubic B-spline basis functions, and $C_{i}$ are unknown real coefficients. The values of $T_{i}^{3}(x)$ and its derivatives $T_{i}^{\prime \,3}(x)$, $T_{i}^{\prime \prime \,3}(x)$ at the nodal points can be simplified as:

$$ \textstyle\begin{cases} S(x_{i})= p_{1}C_{i-1} + p_{2}C_{i} + p_{1}C_{i+1}, & \\ S'(x_{i})= p_{3}C_{i-1} + p_{4}C_{i+1}, & \\ S''(x_{i})= p_{5}C_{i-1} + p_{6}C_{i} + p_{5}C_{i+1}, & \end{cases} $$

(18)

where

$$ \textstyle\begin{cases} p_{1}=\frac{\lambda }{6}-(-1+\lambda ) \text{csch}(h \eta ) \text{csch}(2 h \eta ) \text{csch}(3 h \eta ) \text{sinh}^{3}(h m), & \\ p_{2}=\frac{2 \lambda }{3}- \frac{2 (-1+\lambda ) \text{cosh}(h m) \text{csch}^{3}(h \eta ) \text{sinh}^{3}(h m)}{2 \text{cosh}(h \eta )+\text{cosh}(3 h \eta )}, & \\ p_{3}=\frac{\lambda }{2 h}- \frac{3 m (-1+\lambda ) \text{csch}^{3}(h \eta ) \text{sinh}(h m) \text{sinh}(2 h m)}{4 (2 \text{cosh}(h \eta )+\text{cosh}(3 h \eta ))},\qquad p_{4}=-p_{3},& \\ p_{5}= \frac{8 \lambda +16 \lambda \text{cosh}(2 h \eta )+3 h^{2} m^{2} (-1+\lambda ) \text{csch}^{3}(h \eta ) \text{sech}(h \eta ) (\text{sinh}(h m)-3 \text{sinh}(3 h m))}{8 h^{2} (1+2 \text{cosh}(2 h \eta ))}, & \\ p_{6}=-\frac{2 \lambda }{h^{2}}+ \frac{6 m^{2} (-1+\lambda ) \text{cosh}^{3}(h m) \text{csch}^{3}(h \eta ) \text{sinh}(h m)}{2 \text{cosh}(h \eta )+\text{cosh}(3 h \eta )}. & \end{cases} $$

3 Hybrid B-spline solution for fractional Bagley-Torvik and Painlevé equations

3.1 Bagley-Torvik equation regarding Conformable fractional derivative approach

Now, we are ready to start the implementation of our method using the properties of Conformable fractional derivative and Hybrid cubic B-spline functions. Let $u(x)$ be the analytical and $\overline{u}(x)$ be the numerical solutions for Painlevé and Bagley-Torvik equations. The value of $u''(x)$, $^{Co}_{x}D_{0}^{\frac{3}{2}}u(x)$, $u'(x)$, $_{x}D_{0}^{ \frac{1}{2}}u(x)$, $u(x)$, approximate at $x=x_{i}$ where $i=0,1,\ldots,n$, as follows

$$ \textstyle\begin{cases} \overline{u}(x_{i})=S(x_{i})=p_{1}C_{i-1} + p_{2}C_{i} + p_{1}C_{i+1}, & \\ ^{Co}_{x}D_{0}^{\frac{1}{2}}\overline{u}(x_{i})=^{Co}_{x}D_{0}^{ \frac{1}{2}}S(x_{i})=x^{\frac{1}{2}}(p_{3}C_{i-1} + p_{4}C_{i+1}), & \\ ^{Co}_{x}D_{0}^{\beta}\overline{u}(x_{i})=^{Co}_{x}D_{0}^{\beta}S(x_{i})=x^{1- \beta}(p_{3}C_{i-1} + p_{4}C_{i+1}),\quad \beta \in (0,1] & \\ \overline{u}'(x_{i})=S'(x_{i})= p_{3}C_{i-1}+ p_{4}C_{i+1},& \\ ^{Co}_{x}D_{0}^{\frac{3}{2}}\overline{u}(x_{i})=^{Co}_{x}D_{0}^{ \frac{3}{2}}S(x_{i})=x^{\frac{1}{2}}(p_{5}C_{i-1}+p_{6}C_{i}+ p_{5}C_{i+1}), & \\ \overline{u}''(x_{i})=S''(x_{i})=p_{5}C_{i-1}+p_{6}C_{i}+ p_{5}C_{i+1} & \\ ^{Co}_{x}D_{0}^{\alpha}\overline{u}(x_{i})=^{Co}_{x}D_{0}^{\alpha}S(x_{i})=x^{2- \alpha}(p_{5}C_{i-1}+p_{6}C_{i}+ p_{5}C_{i+1}),\quad \alpha \in (1,2]. & \end{cases} $$

(19)

To obtain the approximate solution (1) with boundary conditions by putting (17) in (1), we use the following system for $i=0,1,\ldots,n$,:

$$ \bigl(\delta _{-1}(x_{i})C_{i-1} + \delta _{0}(x_{i})C_{i} + \delta _{1}(x_{i})C_{i+1} \bigr)=f_{i}, $$

(20)

and the boundary conditions as:

$$ \textstyle\begin{cases} \overline{u'}(0)=p_{3}C_{-1}+ p_{4}C_{1}=\omega _{1}, & \\ \overline{u}(1)=p_{1}C_{n-1}+ p_{2}C_{n}+p_{1}C_{n+1}=\omega _{2},& \end{cases} $$

(21)

this system can be written in the following matrix-vector form:

$$ AX=B, $$

(22)

where,

$$\begin{aligned}& X=[C_{-1},C_{0},\ldots,C_{n+1}]^{t},\qquad B=[\omega _{1},f_{0},\ldots,f_{n}, \omega _{2}]^{t},\qquad f_{i}=f(x_{i}),\quad i=0,1, \ldots,n, \\& A= \begin{pmatrix} p_{3} & 0 & p_{4} & & & & \\ \delta _{-1}(x_{0}) & \delta _{0}(x_{0})&\delta _{1}(x_{0}) & & & & \\ & \delta _{-1}(x_{1}) & \delta _{0}(x_{1})&\delta _{1}(x_{1}) & & & \\ & & \ddots &\ddots & \ddots & & \\ & & & &\delta _{-1}(x_{n}) & \delta _{0}(x_{n})&\delta _{1}(x_{n}) \\ & & & &p_{1} & p_{2} & p_{1} \end{pmatrix}, \\& \textstyle\begin{cases} \delta _{-1}(x_{i})=\eta _{1}(x_{i})p_{5}+\eta _{2}(x_{i})(x_{i})^{0.5}p_{5}+ \eta _{3}(x_{i})p_{3}+\eta _{4}(x_{i})(x_{i})^{0.5}p_{3}+\eta _{5}(x_{i})p_{1}, & \\ \delta _{0}(x_{i})=\eta _{1}(x_{i})p_{6}+\eta _{2}(x_{i})(x_{i})^{0.5}p_{6}+ \eta _{5}(x_{i})p_{2}, & \\ \delta _{1}(x_{i})=\eta _{1}(x_{i})p_{5}+\eta _{2}(x_{i})(x_{i})^{0.5}p_{5}+ \eta _{3}(x_{i})p_{4}+\eta _{4}(x_{i})(x_{i})^{0.5}p_{4}+\eta _{5}(x_{i})p_{1}, & \end{cases}\displaystyle \end{aligned}$$

(23)

also, since A is strictly diagonally dominant [37], to find the values of $C_{-1}, C_{0}, \ldots, C_{n+1}$ in vector X, we can solve the system of equations (22) as follows:

$$ X=A^{-1}B. $$

(24)

The numerical solution can be calculated after substituting the values of λ and $C_{i}, \text{for } i=-1,0,1,\ldots,n,n+1$, in equation (17).

3.2 Painlevé equations regarding Conformable fractional derivative approach

In this portion, we consider equations (2) and (3) regarding the Conformable approach. Substituting the values of (17) in equations (2) and (3) of Painlevé equations at $x_{i}$, we get:

$$ \textstyle\begin{cases} \sum_{i=-1}^{n+1}C_{i}(\eta _{1}(x_{i}) ^{Co}_{x}D_{0}^{\alpha}T_{i}^{3}(x)-6(T_{i}^{3}(x_{i}))^{2})-x_{i}=f(x_{i}),& \\ p_{3}C_{-1}+ p_{4}C_{1}=\omega _{1}, & \\ p_{1}C_{n-1}+ p_{2}C_{n}+p_{1}C_{n+1}=\omega _{2}, & \end{cases} $$

(25)

and

$$ \textstyle\begin{cases} \sum_{i=-1}^{n+1}C_{i}(\eta _{1}(x_{i}) ^{Co}_{x}D_{0}^{\alpha}T_{i}^{3}(x)-2(T_{i}^{3}(x_{i}))^{3}-x_{i}T_{i}^{3}(x_{i}))-x_{i}=f(x_{i}),& \\ p_{3}C_{-1}+ p_{4}C_{1}=\omega _{1}, & \\ p_{1}C_{n-1}+ p_{2}C_{n}+p_{1}C_{n+1}=\omega _{2}, & \end{cases} $$

(26)

equations (25) and (26) construct nonlinear systems, which can be solved by Newton’s iteration method. We also used the software Mathematica 9.0 to obtain the numerical solutions.

4 Stability and convergence analysis

System (22) obtained using the hybrid cubic hyperbolic B-spline and cubic B-spline functions cannot be solved exactly. However, we can calculate the solutions that are close to the exact solution when small errors are introduced into the input functions. Specifically, we need to prove that the difference between these solutions always depends on the coefficients of the linear system; that means, the method is stable. Let δA and δB be small perturbations in A and B. Let ϕ be the solution to the system

$$ (A+\delta A)\phi =B+\delta B, $$

(27)

also let A be nonsingular and $\|\delta A\|<\frac{1}{2\|A^{-1}\|}$, then $A+\delta A$ is nonsingular and

$$ \bigl\Vert (A+\delta A)^{-1} \bigr\Vert \leq 2 \bigl\Vert (A)^{-1} \bigr\Vert . $$

Using (22) and (27), we get

$$\begin{aligned} &X-\phi = A^{-1}B-(A+\delta A)^{-1}(B+ \delta B), \end{aligned}$$

(28)

$$\begin{aligned} &(A+\delta A) (X-\phi ) =(A+\delta A)A^{-1}B-(B+\delta B), \end{aligned}$$

(29)

$$\begin{aligned} &(A+\delta A) (X-\phi ) = \bigl(B+\delta AA^{-1}B \bigr)-(B+\delta B), \end{aligned}$$

(30)

$$\begin{aligned} &(A+\delta A) (X-\phi )=\delta AX-\delta B, \end{aligned}$$

(31)

$$\begin{aligned} &(X-\phi )=(A+\delta A)^{-1}(\delta AX-\delta B), \end{aligned}$$

(32)

and we know that A is strictly diagonally dominant and also

$$ \bigl\Vert A^{-1} \bigr\Vert \leq \nu < \infty . $$

(33)

It implies that

$$ \bigl\Vert (X-\phi ) \bigr\Vert = \bigl\Vert (A+\delta A)^{-1} \bigr\Vert \bigl( \Vert \delta AX \Vert + \Vert \delta B \Vert \bigr)=2 \nu \bigl( \Vert \delta A \Vert \Vert X \Vert + \Vert \delta B \Vert \bigr). $$

This shows the stability of the system (the norm used is infinite norm).

Let $u(x)$ be the exact solution of (1)-(3) and $S(x_{i})= S_{i}$ be an approximation to $u_{i} = u(x_{i})$ obtained by the hybrid b-spline function $S_{i}(x) \in C^{\infty}[a,b]$, by algebraic manipulation of relations (17) and (18), when $\lambda =0$, we get the consistency relations between the spline approximation and its derivatives at the nodal points in the following form:

$$ \textstyle\begin{cases} \frac{h^{2}}{6}[S''_{i-1}+4S''_{i}+S''_{i+1}]=u_{i+1}-2u_{i}+u_{i-1}, & i=1,\ldots,n-1, \quad \mathbf{(I)} \\ -2h ( S'_{i-1}+4 S'_{i}+ S'_{i+1} )= (6 u_{i-1}-6 u_{i+1} ), &i=1,\ldots,n-1. \quad \mathbf{(II)} \end{cases} $$

(34)

Lemma 1

The local truncation errors $x_{i}$ associated with the equation (34) for $i=1,\ldots,n-1$. are given by

$$\begin{aligned} &\bigl\vert S''_{i}-u''_{i} \bigr\vert = \frac{h^{2}}{12}u^{(4)}_{i}+O \bigl(h^{4} \bigr), \end{aligned}$$

(35)

$$\begin{aligned} &\bigl\vert S'_{i}-u'_{i} \bigr\vert =\frac{h^{4}}{180}u^{(5)}_{i} +O \bigl(h^{5} \bigr). \end{aligned}$$

(36)

Proof

See [40]. □

4.1 The hybrid B-spline method for fractional Painlevé and Bagley-Trovik equations in the Caputo fractional sense

Substitute the numerical point solution of Bagley-Trovik equation at $x=x_{i}$, where $i=0,1,\ldots,n$, is as follows

$$ \textstyle\begin{cases} \eta _{1}(x_{i})u(x)''|_{x=x_{i}}+\eta _{2}(x_{i}) ^{C}_{x}D_{0}^{\alpha}(u(x))|_{x=x_{i}}+\eta _{3}(x_{i})u(x)'|_{x=x_{i}} \\ \quad {}+\eta _{4}(x_{i}) ^{C}_{x}D_{0}^{\beta}(u(x))|_{x=x_{i}}+\eta _{5}(x_{i}) u(x)'|_{x=x_{i}}= f_{i}, \\ u'(0)-\omega _{1}=u(1)-\omega _{2}=0,\quad i=0,2,3,\ldots,n-1. \end{cases} $$

(37)

Considering each subinterval $[x_{j-1},x_{j}]$ of partition $[0,x_{i}]$, for $t\in [x_{j-1},x_{j}]$ and using the properties of the Caputo fractional derivative and Hybrid cubic B-spline functions for $1< \alpha <2$ gives

$$\begin{aligned} ^{C}_{x}D_{0}^{\alpha} \bigl(u(x) \bigr)|_{x=x_{i}} =& \frac{1}{\Gamma (2-\alpha )}\sum _{j=1}^{i} \int _{x_{j-1}}^{x_{j}}(x_{i}-t)^{1- \alpha}u''(t) \,dt, \end{aligned}$$

(38)

and for $0< \beta <1$, we also get

$$\begin{aligned} ^{C}_{x}D_{0}^{\beta} \bigl(u(x) \bigr)|_{x=x_{i}} =&\frac{1}{\Gamma (1-\beta )} \sum _{j=1}^{i} \int _{x_{j-1}}^{x_{j}}(x_{i}-t)^{-\beta}u'(t) \,dt. \end{aligned}$$

(39)

Using equation (17) and Lemma 1, we obtain the following relation

$$\begin{aligned} \textstyle\begin{cases} ^{C}_{x}D_{0}^{\alpha}(u(x))|_{x=x_{i}}=\frac{1}{\Gamma (2-\alpha )} \sum_{j=1}^{i}\int _{(j-1)h}^{jh}(\sum_{j=-1}^{i+1}C_{j}(T_{j}^{3}(t))'' \\ \hphantom{^{C}_{x}D_{0}^{\alpha}(u(x))|_{x=x_{i}}}\quad +O(h^{2}))(x_{i}-t)^{1-\alpha}\,dt, \end{cases}\displaystyle \end{aligned}$$

(40)

since $(x_{i}-t)^{1-\alpha}$ does not change sign on $[(j-1)h, jh]$, using the weighted mean value theorem to establish an integral formula and applying to each integration of the last summation, we get

$$ \textstyle\begin{cases} \int _{(j-1)h}^{jh}(\sum_{j=-1}^{i+1}C_{j}(T_{j}^{3}(t))''+O(h^{2}))(x_{i}-t)^{1- \alpha}\,dt \\ \quad =(\sum_{j=-1}^{i+1}C_{j}(T_{j}^{3}(\overline{\eta}))''+O(h^{2}))\int _{(j-1)h}^{jh}(x_{i}-t)^{1- \alpha}\,dt \\ \quad =\sum_{j=1}^{i}(p_{5}C_{j-1} + p_{6}C_{j} + p_{5}C_{j+1})+O(h^{2})) \int _{(j-1)h}^{jh}(x_{i}-t)^{1-\alpha}\,dt, & \end{cases} $$

(41)

where $\overline{\eta}\in [(j-1)h, jh]$. After simple calculations, equations (40) and (41) become

$$ \textstyle\begin{cases} ^{C}_{x}D_{0}^{\alpha}(u(x))|_{x=x_{i}} \\ \quad =\frac{1}{\Gamma (3-\alpha )}\sum_{j=1}^{i}((p_{5}C_{j-1} + p_{6}C_{j} + p_{5}C_{j+1})+O(h^{2}))) \\ \qquad {}((x_{i}-jh+h)^{2-\alpha}-(x_{i}-jh)^{2-\alpha}) \\ \quad =\frac{1}{\Gamma (3-\alpha )}\sum_{j=1}^{i}((x_{i}-jh+h)^{2-\alpha}-(x_{i}-jh)^{2- \alpha}) \\ \qquad {}((p_{5}C_{j-1} + p_{6}C_{j} + p_{5}C_{j+1}))) \\ \qquad {}+\frac{1}{\Gamma (3-\alpha )}\sum_{j=1}^{i}((x_{i}-jh+h)^{2-\alpha}-(x_{i}-jh)^{2- \alpha})(O(h^{2})) \\ \quad = \frac{h^{2-\alpha}}{\Gamma (3-\alpha )}\sum_{j=1}^{i}((i-j+1)^{2- \alpha}-(i-j)^{2-\alpha}) \\ \qquad {} (p_{5}C_{j-1} + p_{6}C_{j} + p_{5}C_{j+1}) \\ \qquad {}+\frac{1}{\Gamma (3-\alpha )}\sum_{j=1}^{i}((i-j+1)^{2-\alpha}-(i-j)^{2- \alpha})O(h^{4-\alpha}). \end{cases} $$

(42)

Following the same technique on $0< \beta <1$, we get

$$\begin{aligned}& \textstyle\begin{cases} D^{\beta}(u(x))|_{x=x_{i}} \\ \quad= \frac{h^{1-\beta}}{\Gamma (2-\beta )}\sum_{j=1}^{i}((i-j+1)^{1-\beta}-(i-j)^{1- \beta})(\sum_{j=-1}^{i+1}C_{j}(T_{j}^{3}(t))') \\ \qquad {}+\frac{1}{\Gamma (2-\alpha )}\sum_{j=1}^{i}((i-j+1)^{1-\beta}-(i-j)^{1- \beta})O(h^{5-\beta}). \end{cases}\displaystyle \\& \textstyle\begin{cases} ^{C}_{x}D_{0}^{\beta}(u(x))|_{x=x_{i}} \\ \quad =\frac{h^{1-\beta}}{\Gamma (2-\beta )}\sum_{j=1}^{i}((i-j+1)^{1-\beta}-(i-j)^{1- \beta})(p_{3}C_{j-1} + p_{4}C_{j+1}) \\ \qquad {}+\frac{1}{\Gamma (2-\alpha )}\sum_{j=1}^{i}((i-j+1)^{1-\beta}-(i-j)^{1- \beta})O(h^{5-\beta}). \end{cases}\displaystyle \end{aligned}$$

(43)

To shorten a little the size of this section, we will omit truncation error here to approximate the Painlevé and Bagley-Trovik regarding the Caputo fractional sense. Anyhow, substituting (42) and (43) in (37) at $i=0,1,2,\ldots,n$, where the attached linear or nonlinear systems are obtained as follows:

$$ \textstyle\begin{cases} \eta _{1}(x_{i})((p_{5}C_{i-1} + p_{6}C_{i} + p_{5}C_{i+1})) \\ \quad {}+\eta _{2}(x_{i}) \frac{h^{2-\alpha}}{\Gamma (3-\alpha )}\sum_{j=1}^{i}((i-j+1)^{2- \alpha}-(i-j)^{2-\alpha})(p_{5}C_{j-1} + p_{6}C_{j} + p_{5}C_{j+1}) \\ \quad {}+\eta _{3}(x_{i})(p_{3}C_{i-1} + p_{4}C_{i+1}) \\ \quad {}+\eta _{4}(x_{i}) \frac{h^{1-\beta}}{\Gamma (2-\beta )}\sum_{j=1}^{i}((i-j+1)^{1-\beta}-(i-j)^{1- \beta})((p_{3}C_{j-1} + p_{4}C_{j+1})) \\ \quad {}+\eta _{5}(x_{i}) (p_{1}C_{i-1} + p_{2}C_{i} + p_{1}C_{i+1})= f_{i}. \end{cases} $$

(44)

Hither, substituting (42) in fractional Painlevé of the (I) and (II), we have the following nonlinear systems

$$ \begin{aligned} &\eta _{1}(x_{i}) \frac{h^{2-\alpha}}{\Gamma (3-\alpha )}\sum_{j=1}^{i} \bigl((i-j+1)^{2- \alpha}-(i-j)^{2-\alpha} \bigr) \\ &\quad(p_{5}C_{j-1} + p_{6}C_{j} + p_{5}C_{j+1})-6(u_{i})^{2}-x_{i}= f_{i},& \end{aligned} $$

(45)

and

$$ \begin{aligned} &\eta _{1}(x_{i}) \frac{h^{2-\alpha}}{\Gamma (3-\alpha )}\sum_{j=1}^{i} \bigl((i-j+1)^{2- \alpha}-(i-j)^{2-\alpha} \bigr) \\ &\quad(p_{5}C_{j-1} + p_{6}C_{j} + p_{5}C_{j+1})-2(u_{i})^{3}-x_{i}u_{i}= f_{i}, \end{aligned} $$

(46)

for $i=0,1,2,\ldots,n$.

Relations (45) and (46) become nonlinear systems in the following form as:

$$ F \bigl[x_{i},S_{i},S''_{i} \bigr]=0. $$

(47)

Anyhow, in the general case, we have the following nonlinear systems

$$ F \bigl[x_{i},S_{i},S'_{i},S''_{i} \bigr]=0,\quad i=0,1,2,\ldots,n. $$

(48)

By the end of this subsection, we can obtain the approximate solutions by solving the linear system or nonlinear system (48), and also to solve it, we use the Newton method or the Mathematica command like (FindRoot).

4.2 Bagley-Torvik and Painlevé equations regarding Caputo-Fabrizio fractional derivative approach

Using the Caputo-Fabrizio fractional derivative for $1< \alpha <2$ and considering each subinterval $[x_{j-1},x_{j}]$ of partition $[0,x_{i}]$, for $t\in [x_{j-1},x_{j}]$, we get

$$\begin{aligned} ^{CF}_{x}D_{0}^{\alpha } \bigl(u(x) \bigr)|_{x=x_{i}} =&\frac{1}{(2-\alpha )} \sum _{j=1}^{i} \int _{x_{j-1}}^{x_{j}}e^{\frac{1-\alpha}{2-\alpha}(x_{i}-t)}u''(t) \,dt, \end{aligned}$$

(49)

and also for $0< \beta <1$, we get

$$\begin{aligned} ^{CF}_{x}D_{0}^{\beta } \bigl(u(x) \bigr)|_{x=x_{i}} =&\frac{1}{(1-\beta )}\sum _{j=1}^{i} \int _{x_{j-1}}^{x_{j}}e^{\frac{-\beta}{1-\beta}(x_{i}-t)}u'(t) \,dt. \end{aligned}$$

(50)

Finally, we approximate the exact solution (1)-(3) by the hybrid B-spline function as:

$$\begin{aligned}& \textstyle\begin{cases} \eta _{1}(x_{i})(p_{5}C_{i-1}+p_{6}C_{i}+ p_{5}C_{i+1}) \\ \quad {}+\eta _{2}(x_{i}) \frac{1}{(\alpha -1)}\sum_{j=1}^{i}(e^{\frac{(1-\alpha )h}{2-\alpha}(i-j)}(1-e^{ \frac{1-\alpha}{2-\alpha}h})(p_{5}C_{j-1}+p_{6}C_{j}+ p_{5}C_{j+1}) \\ \quad {}+\eta _{3}(x_{i})( p_{3}C_{i-1}+ p_{4}C_{i+1}) \\ \quad {}+\eta _{4}(x_{i}) (\frac{-1}{(\beta )})\sum_{j=1}^{i}(e^{\frac{\beta h}{1-\beta}(j-i)}(1-e^{ \frac{-\beta }{1-\beta}h})(p_{3}C_{j-1}+ p_{4}C_{j+1}) \\ \quad {}+\eta _{5}(x_{i}) (p_{1}C_{i-1} + p_{2}C_{i} + p_{1}C_{i+1})= f_{i},\quad i=0,1,2,\ldots,n, \end{cases}\displaystyle \end{aligned}$$

(51)

$$\begin{aligned}& \textstyle\begin{cases} \eta _{1}(x_{i}) \frac{1}{(\alpha -1)}\sum_{j=1}^{i}(e^{\frac{(1-\alpha )h}{2-\alpha}(i-j)}(1-e^{ \frac{1-\alpha}{2-\alpha}h})(p_{5}C_{j-1}+p_{6}C_{j}+ p_{5}C_{j+1}) \\ \quad {}- 6 (p_{1}C_{i-1} + p_{2}C_{i} + p_{1}C_{i+1})^{2}-x_{i}= f_{i}, \quad i=0,1,2,\ldots,n, \end{cases}\displaystyle \end{aligned}$$

(52)

$$\begin{aligned}& \textstyle\begin{cases} \eta _{1}(x_{i}) \frac{1}{(\alpha -1)}\sum_{j=1}^{i}(e^{\frac{(1-\alpha )h}{2-\alpha}(i-j)}(1-e^{ \frac{1-\alpha}{2-\alpha}h})(p_{5}C_{j-1}+p_{6}C_{j}+ p_{5}C_{j+1}) \\ \quad {}- 2 (p_{1}C_{i-1} + p_{2}C_{i} + p_{1}C_{i+1})^{3}-x_{i}(p_{1}C_{i-1} + p_{2}C_{i} + p_{1}C_{i+1})-x_{i}= f_{i}, \\ \quad i=0,1,2,\ldots,n. \end{cases}\displaystyle \end{aligned}$$

(53)

However, the above systems with boundary conditions (21) convert to the following nonlinear system with $n+3$ equations and $n+3$ unknowns

$$ F[x_{i},p_{1}C_{i-1} + p_{2}C_{i} + p_{1}C_{i+1},p_{3}C_{i-1}+ p_{4}C_{i+1},p_{5}C_{i-1}+p_{6}C_{i}+ p_{5}C_{i+1}]=0, $$

(54)

for $i=0,1,2,\ldots,n$.

4.3 Convergence analysis

In this section, we discuss the convergence analysis of hybrid cubic and hyperbolic B-spline. Let $u(x)$ be the exact solution of the problem and $S(x)\in C^{\infty}[0,T]$ be the hybrid B-spline approximation to $u(x)$ satisfying in $S(x_{i})=u(x_{i})$, $i=0,1,\ldots,n-1$. We should approximate the error $\|u(x)-S(x)\|$. Let us assume that $\hat{S}(x)$ is the computed hybrid B-spline approximation to $S(x)$. To estimate $\|u(x)-S(x)\|$, we will estimate $\|u(x)-\hat{S}(x)\|$ and $\|\hat{S}(x)-S(x)\|$ separately.

First, we consider the Painlevé equations with the Conformable derivative and then discretize it with the hybrid B-spline function as follows:

$$\begin{aligned}& \textstyle\begin{cases} \eta _{1}(x_{i})x_{i}^{2-\alpha}S''(x_{i})-6S^{2}(x_{i})-x_{i}=f(x_{i}), & \\ S'(0)-\omega _{1}=S(1)-\omega _{2}=0, & \end{cases}\displaystyle \end{aligned}$$

(55)

$$\begin{aligned}& \textstyle\begin{cases} \eta _{1}(x_{i}) x_{i}^{2-\alpha}S''(x_{i})-2 S^{3}(x_{i})-x_{i}S(x_{i})-x_{i}=f(x_{i}), & \\ S'(0)-\omega _{1}=S(1)-\omega _{2}=0. & \end{cases}\displaystyle \end{aligned}$$

(56)

By discretizing the Bagley-Torvik equation with the Conformable derivative, the following linear system is obtained.

$$ \textstyle\begin{cases} \eta _{1}(x)S''(x)+\eta _{2}(x) x^{\frac{1}{2}}S''(x)+\eta _{3}(x)S'(x) \\ \quad {}+\eta _{4}(x)x^{\frac{1}{2}}S'(x)+\eta _{5}(x) S(x)=f(x), \\ S'(0)-\omega _{1}=S(1)-\omega _{2}=0. \end{cases} $$

(57)

We investigate the convergence analysis for the conformable fractional derivative and also for Caputo and Caputo-Fabrizio fractional derivatives that are similar.

We also obtain a linear or nonlinear system of equations, the convergence of which we analyzed on the nonlinear system. In general, we have the following system:

$$ \textstyle\begin{cases} F(x_{i},u(x_{i}),u'(x_{i}),u''(x_{i}))=0, \quad i=0,1,2,\ldots,n, \\ u'(x_{0})=\omega _{1}, \qquad u(x_{n})=\omega _{2}. \end{cases} $$

(58)

By substituting (17) in (58) at $x_{i}, i=0,1,2,\ldots,n$, the attached nonlinear system of order $(n+3)$ is obtained as:

$$ \textstyle\begin{cases} F(x_{i},S(x_{i}),S'(x_{i}),S''(x_{i}))=0, \quad i=0,1,2,\ldots,n, \\ S'(x_{0})=\omega _{1}, \qquad S(x_{n})=\omega _{2}. \end{cases} $$

(59)

Equations (59) construct a nonlinear system, which can be solved by Newton’s iteration method.

Lemma 2

Let $\hat{S}(x)$ be the unique spline interpolation to $S(x)$, and also suppose that partial derivatives of F exist and $|\frac{\partial F}{\partial u}|\leq k_{1}$, $|\frac{\partial F}{\partial u'}|\leq k_{2}$, $| \frac{\partial F}{\partial u''}|\leq k_{3}$, for some constants $k_{1}$, $k_{2}$ and $k_{3}$. Then for $0 \leq i \leq n$, we have:

$$ \bigl\vert F \bigl(x_{i},S(x_{i}),S'(x_{i}),S''(x_{i}) \bigr)- F \bigl(x_{i},\hat{S}(x_{i}), \hat{S}'(x_{i}),\hat{S}''(x_{i}) \bigr) \bigr\vert \leq O \bigl(h^{2} \bigr). $$

(60)

Proof

For $0\leq i\leq n$, we get

$$\begin{aligned} &F \bigl(x_{i},S(x_{i}),S'(x_{i}),S''(x_{i}) \bigr)- F \bigl(x_{i},\hat{S}(x_{i}), \hat{S}'(x_{i}),\hat{S}''(x_{i}) \bigr) \\ &\quad =F \bigl(x_{i},S(x_{i}),S'(x_{i}),S''(x_{i}) \bigr)-F \bigl(x_{i},\hat{S}(x_{i}),S'(x_{i}),S''(x_{i}) \bigr) \\ &\qquad +F \bigl(x_{i},\hat{S}(x_{i}),S'(x_{i}),S''(x_{i}) \bigr)-F \bigl(x_{i},S(x_{i}), \hat{S}'(x_{i}),S''(x_{i}) \bigr) \\ &\qquad +F \bigl(x_{i},S(x_{i}),\hat{S}'(x_{i}),S''(x_{i}) \bigr)+ F \bigl(x_{i},S(x_{i}),S'(x_{i}), \hat{S}''(x_{i}) \bigr) \\ &\qquad -F \bigl(x_{i},S(x_{i}),S'(x_{i}), \hat{S}''(x_{i}) \bigr) - F \bigl(x_{i},\hat{S}(x_{i}), \hat{S}'(x_{i}), \hat{S}''(x_{i}) \bigr). \end{aligned}$$

(61)

Now using the mean value theorem for there parts of the above relation there exist $\xi _{i}$, $\varsigma _{i}$ and $\nu _{i}$ such that

$$\begin{aligned}& F \bigl(x_{i},S(x_{i}),S'(x_{i}),S''(x_{i}) \bigr)-F \bigl(x_{i},\hat{S}(x_{i}),S'(x_{i}),S''(x_{i}) \bigr)= \frac{\partial F}{\partial u}(\xi _{i}) \bigl(S(x_{i})- \hat{S}(x_{i}) \bigr),\\& F \bigl(x_{i},S(x_{i}),S'(x_{i}),S''(x_{i}) \bigr)-F \bigl(x_{i},S(x_{i}),\hat{S}'(x_{i}),S''(x_{i}) \bigr)= \frac{\partial F}{\partial u'}(\varsigma _{i}) \bigl(S'(x_{i})- \hat{S}'(x_{i}) \bigr),\\& F \bigl(x_{i},S(x_{i}),S'(x_{i}),S''(x_{i}) \bigr)+ F \bigl(x_{i},S(x_{i}),S'(x_{i}), \hat{S}''(x_{i}) \bigr)= \frac{\partial F}{\partial u''}(\nu _{i}) \bigl(S''(x_{i})- \hat{S}''(x_{i}) \bigr), \end{aligned}$$

using Theorem 1 in [14], (42)-(43), and Lemma 1, one obtained:

$$ \textstyle\begin{cases} u(x_{i})=\overline{u}(x_{i})+O(h^{4}), \\ ^{Co}_{x}D_{0}^{\beta}u(x)=^{Co}_{x}D_{0}^{\beta}\overline{u}(x)+O(h^{5- \beta}),\quad \beta \in (0,1], & \\ u'(x)= \overline{u}'(x)+O(h^{4}), \\ ^{Co}_{x}D_{0}^{\alpha}u(x)=^{Co}_{x}D_{0}^{\alpha}\overline{u}(x)+O(h^{4- \alpha}),\quad \alpha \in (1,2], \\ u''(x_{i})=\overline{u}''(x_{i})+O(h^{2}), \end{cases} $$

the maximum truncation error for approximations is $O(h^{2})$. From [56], we have $|S(x_{i})-\hat{S}(x_{i})|\equiv O(h^{4})$, $|S'(x_{i})-\hat{S}'(x_{i})| \equiv O(h^{3})$, $|S''(x_{i})-\hat{S}''(x_{i})|\equiv O(h^{2})$, and taking the absolute value of the above relationship, we get

$$\begin{aligned} &\bigl\vert F \bigl(x_{i},S(x_{i}),S'(x_{i}),S''(x_{i}) \bigr)- F \bigl(x_{i},\hat{S}(x_{i}), \hat{S}'(x_{i}),\hat{S}''(x_{i}) \bigr) \bigr\vert \\ &\quad \leq k_{1} \bigl\vert S(x_{i})-\hat{S}(x_{i}) \bigr\vert + k_{2} \bigl\vert S'(x_{i})- \hat{S}'(x_{i}) \bigr\vert + k_{3} \bigl\vert S''(x_{i})- \hat{S}''(x_{i}) \bigr\vert \\ &\quad \leq k_{1}O \bigl(h^{4} \bigr)+k_{2}O \bigl(h^{3} \bigr)+k_{3}O \bigl(h^{2} \bigr) \equiv O \bigl(h^{2} \bigr). \end{aligned}$$

(62)

 □

Theorem 1

Let $u(x)\in C^{\infty}[0,T]$ be the exact solution (1)-(3) and $S(x)$ be the hyperbolic B-spline approximation to $u(x)$, then we have

$$ \bigl\Vert u(x)-S(x) \bigr\Vert \leq O \bigl( h^{2} \bigr). $$

Proof

Since $\hat{S}(x)$ is an interpolation to $u(x)$, there is a finite constant $\varrho _{1}$ independent of h that we get

$$ \bigl\Vert u(x)-\hat{S}(x) \bigr\Vert \leq \varrho _{1} h^{2}\equiv O \bigl(h^{2} \bigr), $$

now using the triangular inequality and Lemma 1, we can obtain the following results

$$ \bigl\Vert u(x)-S(x) \bigr\Vert \leq \bigl\Vert u(x)-\hat{S}(x) \bigr\Vert + \bigl\Vert \hat{S}(x)-S(x) \bigr\Vert \equiv O \bigl(h^{2} \bigr). $$

 □

5 Numerical results

In this section, we have implemented our methods for solving some of the Bagley-Torvik and Painlevé fractional differential equations with different values of λ, m, η, h, and α. We have obtained linear or nonlinear algebraic systems, and to solve it, we can employ Mathematica command like “FindRoot”. The findroot command depends on the initial guess of the interval that contains the value of the unknowns, which can be obtained from boundary conditions or other methods such as a Bisection method. The maximum absolute errors in solutions of the methods are tabulated in tables, and one can compare them with the methods described in [14, 30, 54]. The convergence order (C.O.) is obtained by

$$ C.O.=\log _{2}\frac{E(h)}{E(\frac{h}{2})}, $$

(63)

where $E(h)$ is the maximum absolute error. Numerical results derived by the proposed method and MATHEMATICA 9 solver are seen in tables and graphs.

Example 1

Consider the following Bagley-Torvik fractional boundary value problem in Caputo approach:

$$\begin{aligned} &u''(x)+D^{\frac{3}{2}}u(x)+u(x)= \gamma (\gamma -1)x^{\gamma -2}+ \frac{\Gamma (\gamma +1)}{\Gamma (\gamma -\frac{1}{2})}x^{\gamma - \frac{3}{2}}+x^{\gamma},\\ &\quad x\in [0,1], u(0)=0,u'(0)=0. \end{aligned}$$

The exact solution is given by $u(x)=x^{\gamma}$. The maximum absolute errors are compared with the methods described in [30] and [54]. To compare the numerical results with [30] and [54], we have taken $n = 8,16,32,64,128,256,512$, $\lambda =0,5,0.6,0.9$, and $\gamma =3,4$ in Tables 1 and 2. The convergence order of Example 1 for $n=10$, $\lambda =0,5,0.6$, is compared with order 2 in Fig. 1.

Figure 1

The convergence order of Example 1 for $n=10$, $\lambda =0,5,0.6$, $m=1$, $\eta =1$, is compared with order 2

Table 1 Observed maximum absolute errors of Caputo fractional derivative for the Example 1, $\eta =1$, $m=1$ and $\gamma =3$

Table 2 Observed maximum absolute errors of Caputo fractional derivative for the Example 1, $\eta =1$, $m=1$ and $\gamma =4$

Example 2

Consider the Bagley-Torvik fractional equation in Caputo, Conformable, and Caputo-Fabrizio approaches:

The Bagley-Torvik equation in the Caputo approach:

$$ \textstyle\begin{cases} u''(x)+^{C}_{x}D_{0}^{\frac{3}{2}}u(x)+u'(x)+^{C}_{x}D_{0}^{ \frac{1}{2}}u(x)+u(x) \\ \quad =6x+3x^{2}+x^{3}-8\sqrt{\frac{x^{3}}{\pi}}+\frac{16}{5}\sqrt{ \frac{x^{5}}{\pi}}, \quad x\in [0,1], \\ u'(0)=0,\qquad u(1)=1. \end{cases} $$

(64)

The Bagley-Torvik equation in the Caputo-Fabrizio approach:

$$ \textstyle\begin{cases} u''(x)+^{CF}_{x}D_{0}^{\frac{3}{2}}u(x)+u'(x)+^{CF}_{x}D_{0}^{ \frac{1}{2}}u(x)+u(x) \\ \quad =-42x+3x^{2}+x^{3}+88-96e^{-x}, \quad x\in [0,1], \\ u'(0)=0,\qquad u(1)=1. \end{cases} $$

(65)

The Bagley-Torvik equation in the Conformable approach:

$$ \textstyle\begin{cases} u''(x)+^{Co}_{x}D_{0}^{\frac{3}{2}}u(x)+u'(x)+^{Co}_{x}D_{0}^{ \frac{1}{2}}u(x)+u(x) \\ \quad =6x+6x^{\frac{3}{2}}+3x^{2}+x^{3}+3x^{\frac{5}{2}}, \quad x\in [0,1], \\ u'(0)=0,\qquad u(1)=1. \end{cases} $$

(66)

The exact solution is given by $u(x)=x^{3}$. The absolute errors of $x_{i}$ with $h=\frac{1}{10}$ are compared with the methods from [14] in Table 3. The relative errors of our method for $n = 10$, $\lambda =0,5$, $m=1$, and $\eta =1$ with method in [14] are plotted in Fig. 2.

Figure 2

The relative errors of our method for $n = 10$, $\lambda =0,5$, $m=1$, and $\eta =1$ with the Conformable derivative

Table 3 Observed absolute errors of Example 2, regarding $\lambda =0.5$, $m=1$ and $\eta =1$

Example 3

Consider the Painlevé fractional equation in Caputo, Conformable, and Caputo-Fabrizio approaches:

$$\begin{aligned}& \textstyle\begin{cases} ^{C}_{x}D_{0}^{\alpha}u(x)-6u^{2}(x)=f(x),\quad x\in [0,1], \\ u'(0)=0,\qquad u(1)=-\alpha . \end{cases}\displaystyle \end{aligned}$$

(67)

$$\begin{aligned}& \textstyle\begin{cases} ^{CF}_{x}D_{0}^{\alpha}u(x)-6u^{2}(x)= f(x), \quad x\in [0,1], \\ u'(0)=0,\qquad u(1)=-\alpha . \end{cases}\displaystyle \end{aligned}$$

(68)

$$\begin{aligned}& \textstyle\begin{cases} ^{Co}_{x}D_{0}^{\alpha}u(x)-6u^{2}(x)=f(x), \quad x\in [0,1], \\ u'(0)=0,\qquad u(1)=-\alpha . \end{cases}\displaystyle \end{aligned}$$

(69)

The exact solution is given by $u(x)=\alpha \cos (\pi x)$. The absolute errors for $h=\frac{1}{10}$, $\lambda =0$, $m=1$, $\eta =1$, $\alpha =1.5,1.6,1.7,1.8,1.9$ are compared with the methods from [14] in Tables 4 and 5. The convergence orders (C.O.) with $n=4,8,16,32,64,128,256,512,1024$, and $\alpha =1.1,1.6,1.9$ are displayed in Table 6. The graphs of numerical solutions regarding the Caputo-Fabrizio approach with different values of $\alpha =1.2,1.4,1.6,1.8$, $\lambda =0.5$, $m=1$, and $\eta =1$, are plotted in Fig. 3.

Figure 3

The Exact and the numerical solutions regarding the Caputo-Fabrizio approach with different values of $\alpha =1.2,1.4,1.6,1.8$, $\lambda =0.5$, $m=1$, and $\eta =1$

Table 4 Observed absolute errors of Example 3,regarding Conformable derivative by using our method with $\lambda =0$, $n=10$, $m=1$ and $\eta =1$

Table 5 Observed absolute errors of Example 3 in [14] regarding Conformable derivative

Table 6 Observed maximum absolute errors of the Example 3 for $\lambda =0.9$, $m=1$ and $\eta =1$ regarding Conformable derivative

Example 4

Consider the Painlevé fractional equation in Caputo, Conformable and Caputo-Fabrizio approaches:

$$\begin{aligned}& \textstyle\begin{cases} ^{C}_{x}D_{0}^{\alpha}u(x)-2u^{3}(x)-xu(x)=f(x),\quad x\in [0,1], \\ u'(0)=0,\qquad u(1)=-\alpha . \end{cases}\displaystyle \end{aligned}$$

(70)

$$\begin{aligned}& \textstyle\begin{cases} ^{CF}_{x}D_{0}^{\alpha}u(x)-2u^{3}(x)-xu(x)= f(x),\quad x\in [0,1], \\ u'(0)=0,\qquad u(1)=-\alpha . \end{cases}\displaystyle \end{aligned}$$

(71)

$$\begin{aligned}& \textstyle\begin{cases} ^{Co}_{x}D_{0}^{\alpha}u(x)-2u^{3}(x)-xu(x)=f(x), \quad x\in [0,1], \\ u'(0)=0,\qquad u(1)=-\alpha . \end{cases}\displaystyle \end{aligned}$$

(72)

The exact solution is given by $u(x)=2x^{3}-3x^{2}+x+\alpha$. The absolute errors with different values $\alpha =1.5,1.9$, $\lambda =1$, $\eta =1$, $m=1$ and $h=\frac{1}{10}$ are compared with the method [14] in Table 7.

Table 7 Observed absolute errors of Example 4, regarding Conformable derivative

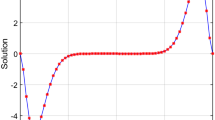
The graphs of numerical solutions regarding Caputo approach with different value of $\alpha =1.1,1.3,1.5,1.7,1.9$, $\lambda =0.5$, $m=1$, $\eta =1$, and $h=\frac{1}{20}$, are plotted in Fig. 4.

Figure 4

The numerical solutions regarding the Caputo approach with different values of $\alpha =1.1,1.3,1.5,1.7,1.9$, $\lambda =0.5$, $m=1$, $\eta =1$, and the exact solutions

Here, the algorithm of the hybrid B-spline method for Example 2 is given with the Conformable derivative, and the algorithm is written similarly for other derivatives such as Caputo and Caputo-Fabrizio approaches.

Algorithm 1

Approximate solutions of equation (66) with Conformable approach using the hybrid B-spline function.

ClearAll

In[1]: $\omega _{1}=0;\omega _{2}=1;\eta _{1}(x)=1;\eta _{2}(x)=1;\eta _{3}(x)=1; \eta _{4}(x)=1;\eta _{5}(x)=1;\lambda =0.5;\eta =1;m=1$;

In[2]: $u(x)=x^{3};f(x)=6x+6x^{\frac{3}{2}}+3x^{2}+x^{3}+3x^{\frac{5}{2}}$;

In[3]: Define the Conformable fractional derivative $^{Co}_{x}D_{a}^{\alpha }(u(x))$ using equation (10).

In[4]: Define the hybrid cubic B-spline basis functions $T_{i}^{3}(x)$. using equations (12)-(16).

In[5]: $\overline{u}(x) =\sum_{i=-1}^{n+1}C_{i}T_{i}^{3}(x)$.

In[6]: $\text{Do}[x_{i}=i*h; \text{equations}_{i} =\overline{u}''(x_{i})+^{Co}_{x}D_{0}^{ \frac{3}{2}}\overline{u}(x_{i})+\overline{u}'(x_{i}) +^{Co}_{x}D_{0}^{ \frac{1}{2}}\overline{u}(x_{i})+\overline{u}(x_{i})-f(x_{i})==0,\{i=0,n \}]$;

In[7]: $\text{boundary1}=\sum_{i=-1}^{n+1}C_{i}T_{i}^{3'}(0)==0$;

Out[7]: $-5C_{-1}+5C_{1}==0$;

In[8]: $\text{boundary2}=\sum_{i=-1}^{n+1}C_{i}T_{i}^{3}(1)==1$;

Out[8]: $\frac{1}{6}(C_{-1}+4C_{0}+C_{1})==1$;

(^∗Approximate solutions are obtained using the hybrid B-spline function by solving the system of 13 equations and 13 unknowns with the help of Mathematica version 9 software.^∗)

In[9]: Solutions=Solve[$\{\text{boundary1},\text{equations}_{0}, \text{equations}_{1},\ldots,\text{equations}_{10},\text{boundary2}\}$, $\{C_{-1},C_{0},\ldots,C_{10},C_{11}\}$];

Out[9]: $-9.5894539103510313295\times 10^{-21}$, $-9.6375615386799582263\times 10^{-21}$, $-9.5894539103510313295\times 10^{-21}$, 0.0059999999999999999908, 0.023999999999999999991, 0.059999999999999999992, 0.11999999999999999999, 0.20999999999999999999, 0.33600000000000000000, 0.50400000000000000000, 0.72000000000000000000, 0.99000000000000000000.

(^∗Approximate solutions $\overline{u}(x)$ are obtained^∗)

End.

6 Conclusion

Computational methods for solving the fractional Bagley-Torvik and Painlevé equations were proposed with the conformable, Captuo, and Caputo-Fabrizio fractional sense concerning boundary set conditions. The fractional differential equation term in the fractional Painlevé and Bagley-Torvik equations were discretized using the hybrid B-spline function. The first aim of the paper is to illuminate that the hybrid B-spline is a solver for several appointed forms without using any transformation or limiting assumptions. This algorithm is implemented straightforwardly. Second, this method is a simple method to apply and includes some parameters, such as m, η, and λ, which increase the accuracy of the method. Third, it could be applied to other types of linear and nonlinear or singular and regular fractional problems. The novel approaches are applied to approximate the outcomes for fractional-order and integral-order problems. The obtained results show that the method used to approximate the solution of various problems of partial differential equations and integral equations in the light of fractional derivative is effective and appropriate. The feasibility of the numerical algorithm was illustrated with four examples, and the approximated results were compared with the methods in [14, 30, 54].