Abstract
In this paper, we approximate the solution of fractional Bagley–Torvik equation by using the exponential spline function and the shifted Grünwald difference operator. The proposed methods reduce to the system of algebraic equations. The convergence analysis of the methods has been discussed. The numerical examples are presented to illustrate the applications of the methods and to compare the computed results with the other methods.
Similar content being viewed by others
1 Introduction
Fractional calculus is an old topic in mathematical analysis, which goes back to Leibniz (1695) and Euler (1730) (see [15, 16]). In recent years, the numerical solution of fractional equations has become a popular topic in applied sciences control and engineering. Bagley–Torvik equation appears in the modeling of the motion of a rigid plate submerged in a Newtonian fluid [6]. Existence and uniqueness theorem for Bagley–Torvik equation with Dirichlet boundary condition is given in [5]. In this article, the exponential spline will be employed to obtain the approximate solution of Bagley–Torvik equation with Caputo derivative
subject to boundary conditions
Here, \(D^{\alpha }\) is the Caputo derivative, \(f(x)\) is a continuous function, \(\omega _{i}\) (\(i=1,2\)), η̅, μ are real constants, and \(m = 1\) or 2. In general, it is difficult to solve most of the fractional differential equations analytically. Therefore, numerical methods to find an approximate solution and qualitative behaviors of the solution for fractional differential equation have been investigated by authors in [1–9, 11, 14, 19–25, 27–29], and some references therein. The reproducing kernel method is employed for the fractional order differential equations in [1–3]. In [21], numerical solution of boundary value problem of fractional Bagley–Torvik equation is given in the reproducing kernel space. In [14], the authors study the numerical approach based on operational matrices of fractional differential equations with a hybrid of block-pulse functions and Chebyshev polynomials. The existence of positive and negative solutions and properties of their derivatives for the generalized Bagley–Torvik fractional differential equation is given in [24]. Numerical solution of the fractional Bagley–Torvik equation arising in fluid mechanics based on Taylor matrix method is given in [11]. In [29] the numerical solutions for fractional boundary value problem have been found by cubic spline polynomials. The numerical scheme for solving two-point fractional Bagley–Torvik equation using the Chebyshev collocation method has been solved in [22]. In [23] the Bagley–Torvik equation as a prototype fractional differential equation with two derivatives is investigated by means of homotopy perturbation method. The numerical solution to the Bagley–Torvik equation by exponential integrators is discussed in [9]. Also Adomian decomposition method for solving the initial value problem of Bagley–Torvik equation is discussed in [19], fractional linear multistep method and a predictor-corrector method of Adams type based on finite difference methods for initial value problem of Bagley–Torvik equation are discussed in [8]; Legendre operational matrix method for fractional differential equation is applied in [20]; and a combination of collocation points and first-order Bessel functions, which is called Bessel-collocation method for boundary value problem of Bagley–Torvik equation, is discussed in [27]. Quadratic spline solution for boundary value problem of fractional order is applied in [28], and an exponential spline technique for solving fractional boundary value problem is employed in [4].
The first aim of the present work is to explore exponential spline interpolation with multiple parameters and to produce the error of approximate exponential spline. The second aim is to introduce a new approximate technique to find solutions of fractional boundary value problem, and we demonstrate the convergence analysis for this technique.
In [10], the authors tried to approximate the solution of nonlinear fractional differential pantograph equations by sinc interpolation. At first, they have transformed the problem into a nonlinear integral equation with some delay terms and the kernel of this integral equation is weakly singular for the case \(0<\alpha <1\), thus the solution is weakly singular and the numerical methods cannot achieve high accuracy in approximating solutions. The main advantage of our algorithm is that it can be used directly without using assumption or transformation formulae.
This paper is organized into four sections. In Sect. 2, we describe basic definitions and the nonpolynomial spline method to approximate the solutions of fractional Bagley–Torvik equation. Convergence analysis is proved in Sect. 3. In Sect. 4, the numerical examples are given to illustrate the applications of the method, and also the computed results are compared with another known method in [4, 9, 17, 21, 28, 29].
2 Basic definitions and description of the methods
In this section, we recall some definitions and properties of the fractional calculus theory, which are used in this paper. There are several definitions of a fractional derivative of order \(\alpha >0\), such as Riemann–Liouville, Grunwald–Letnikov, and Caputo. In the present work, Caputo and Grunwald–Letnikov fractional derivatives are used for the formulation of the problem.
Definition 1
Let \(u(x)\) be a function defined on \((a,b)\), then the Riemann–Liouville fractional derivative is of the following form [5]:
where Γ is the gamma function.
Definition 2
The left Riemann–Liouville fractional integral [5]
Definition 3
Let \(u(x)\) be a function defined on \((a,b)\), then the Caputo fractional derivative is of the following form [5]:
Definition 4
The Grunwald definition for the fractional derivative is defined in the following form [5]:
where \(A^{\alpha }_{h,p} (u(x))=^{R}D^{\alpha }(u(x))+O(h) \) and \(g_{\alpha ,k}= \frac{\varGamma (k-\alpha )}{\varGamma (-\alpha )\varGamma (k+1)}\).
Definition 5
The weighted and shifted Grünwald difference operator is as follows [25]. Let \(u(x)\in L^{1}(R)\), \({}_{ \infty } D^{ \alpha +2}_{x} (u(x))\), and its Fourier transform belongs to \(L^{1}(R)\),
where \(x\in R\), \(\vartheta \in [0,1] \), also p and q (\(p\neq q\)) are integers and symmetric.
Let us consider a mesh with nodal points \(x_{i}\) on \([a,b]\) such that
where \(h=\frac{b-a}{n}\), \(x_{i}=a+ih\) for \(i=0(1)n\).
Let \(u(x)\) be the exact solution of (1) and \(S_{i}\) be an approximation to \(u_{i} = u(x_{i})\) obtained by the exponential spline function \(Q_{i}(x) \in C^{\infty }[a,b]\) passing through the points \((x_{i}, S _{i} )\) and \((x_{i+1}, S_{i+1}) \). Then in each subinterval the parametric spline segment \(Q_{i}(x)\) has the following form (see [12, 18, 26]):
where β is a free parameter of the spline functions which can be real or pure imaginary and which will be used to raise the accuracy of the method, see [26].
To derive the coefficients \(a_{i_{k}}, k=1, 2, 3, 4\), of equation (6), we first define
By algebraic manipulation we get
where \(\theta =h\beta \). Applying the continuity of the first derivative of \(Q'_{i}(x )=Q'_{i-1}(x )\) at \(x=x_{i}\) for \(i=1,\ldots,n-1\), we get the following consistency relation:
where
For the development of consistency relations between the exponential spline approximation and its derivatives at the nodal points, we consider the following four relations:
After a simple calculation, we obtain the values of coefficients, and using the second-order derivative continuity at the knots \(x_{i}\), for \(i=1,\ldots,n-1\), we get
where
In the limiting case, when \(\theta \to 0\), relations (9) and (11) reduce into the ordinary cubic spline relation:
The proposed differential Eq. (1) in the mesh point \((x_{i})\) may be discretized by
Lemma 1
The local truncation error\(x_{i}\)associated with equations (9) and (11) for\(i=1,\ldots,n-1\)in the limiting case when\(\theta \to 0\)is given by
Proof
The above expressions can be obtained by expanding the terms \(M_{i+1}\), \(M_{i-1}\), \(m_{i+1}\), \(m_{i-1}\), \(u_{i+1}\), and \(u_{i-1}\) about the points \(x_{i}\) in relations (12) using Taylor series respectively. Moreover,
In a similar manner, we get
□
2.1 Cubic and exponential splines method for approximate fractional Bagley–Torvik equation
In this section, we give some methods to approximate \(D^{\alpha }(u(x))|_{x=x _{i}}\) by using spline function.
Method I. The discrete approximation of the Caputo fractional derivative \(D^{\alpha }(u(x))\) can be obtained by a cubic spline (in the limiting case when \(\theta \to 0\), the relations of exponential spline reduce into ordinary cubic spline relation) formula as follows (see [12] and [13]):
Using the Caputo fractional derivative for \(1< \alpha <2\), we get
Using a piecewise technique, the following equation is obtained using equation (21) and Lemma 1:
Since \((x_{i}-\eta )^{1-\alpha }\) does not change sign on \([(j-1)h, jh]\), by the weighted mean value theorem for integrals and by applying to each integration of the last summation, we get
where \(\overline{\eta }\in [(j-1)h, jh]\). After simple calculations, equations (6), (10), and (22) become
Using [12] and [13], we have \(\|Q''-u'' \| _{\infty }=O(h^{2})\). Also we obtain the following relation for \(i = 1, 2, \ldots , n-1\):
where \(\overline{a}_{in}=\overline{c}_{in}=\overline{b}_{i1}= \overline{d}_{i1}=0\) for \(i=1, 2, \ldots,n\). Also we approximate \(u_{i}\) by \(\hat{u_{i}}\) and \(m_{i}\) by \(\hat{m_{i}}\) such that \(\hat{u_{i}}\) and \(\hat{m_{i}}\) for \(i = 1, 2, \ldots,n\) satisfy system (11). We get
Finally, we approximate the exact solution \(u_{i}\) by the natural cubic spline function \(\widehat{Q_{i}}(x) \) for \(i = 1, 2, \ldots,n\). In the matrix notation, we get
where \(\overline{A}=(\overline{a}_{ij})\), \(\overline{B}=(\overline{b}_{ij})\), \(\overline{C}=(\overline{c}_{ij})\), and \(\overline{D}=(\overline{d} _{ij})\). Now, the values \(\hat{ M_{i}}\) and \(\hat{ m_{i}} \) are determined as the solutions of linear systems (12)(I) and (12)(II). We approximate \(\hat{m_{0}}=\frac{-3\hat{u}_{0}+4 \hat{u}_{1}-\hat{u}_{2}}{2h}\), \(\hat{m_{n}}=\frac{3\hat{u}_{n-2}-4\hat{u}_{n-1}-\hat{u}_{n}}{2h}\), and also, by using boundary conditions, we approximate \(\hat{ M_{i}}\) for \(i=0, n\). We need the following lemma.
Lemma 2
The matricesWandZare obtained with the help of systems (9) and (11) invertible.
Proof
The values \(\hat{M}_{i}\) are determined as the solutions of the following linear system:
Also the values \(\hat{m}_{i}\) are determined as follows:
Also, for determining the values \(\hat{M}_{i}\) and \(\hat{m}_{i}\), in the limiting case when \(\theta \to 0\), by using relations (12), the matrices W and Z are strictly diagonally-dominant matrices, then the matrices W and Z are invertible. Hence,
Therefore, from (26) and (29) we obtain
□
Method II. Suppose that \(M_{j}=Q''(x_{j})\) is approximated \(u''(x_{j})\) in the subintervals \([(j-1)h,jh]\) for \(i=1,2,3,\ldots,n-1\) and \(j=1,2,\ldots,i\). Also, by using equation (23), the following recurrence relation is obtained:
Bagley–Torvik equation (1)–(2) for \(1< \alpha <2\) can be discretized as follows:
Finally, we approximate the exact solution \(u_{i}\) by the natural cubic spline function \(\widehat{Q_{i}}(x) \) for \(i = 1,2,\ldots,n\). In the matrix notation, we get
where \(\rho =\frac{1}{\varGamma (3-\alpha )}\sum_{j=1}^{i}((i-j+1)^{2- \alpha }-(i-j)^{2-\alpha })\).
Hence, from (29) and (32) we also obtain
Method III. In this section, we approximate the exact solution by use of the Caputo fractional derivative for \(0< \alpha <1\) as follows:
Using a piecewise technique, equation (34) becomes
Since \((x_{i}-\eta )^{-\alpha }\) does not change sign on \([(j-1)h, jh]\), by the weighted mean value theorem for integrals and by applying to each integration of the last summation, we get
After simple calculations, from equations (34) and (36) we get
where \(a_{i_{k}}\) for \(i=1,2,3,4\) are given in relation (8).
The values \(M_{j}, j=0,1,2,\ldots,n \), are determined by using (9) with natural boundary conditions \(M_{0}=Q''(a)=M_{n}=Q''(b)=0\); in consequence, we approximate \(u_{i}\) by \(\hat{u_{i}}\) and \(M_{i}\) by \(\hat{M_{i}}\) so that \(\hat{u_{i}}\) and \(\hat{M_{i}}\) for \(i = 1,2,\ldots,n-1\) satisfy system (9). We get
This implies that
where \(\dot{\lambda }=(\dot{\lambda }_{ij})=\ddot{\lambda }=( \ddot{\lambda }_{ij})=\tilde{\lambda }=(\tilde{\lambda }_{ij})=\bar{ \lambda }=(\bar{\lambda }_{ij})=((i-j+1)^{1-\alpha }-(i-j)^{1-\alpha })\) for \(i=1,2,\ldots,n-1\) such that \((\dot{\lambda }_{i0})=(\dot{\lambda }_{in})=( \ddot{\lambda }_{i0})=(\ddot{\lambda }_{i1})=(\tilde{\lambda }_{i0})=( \tilde{\lambda }_{in})=(\bar{\lambda }_{i0})=(\bar{\lambda }_{i1})=0\). In the matrix notation, we get
where \(\hat{M}=(\hat{M_{1}},\hat{M_{1}},\ldots,\hat{M_{n}})^{t}\), \(\hat{U}=(\hat{u_{1}},\hat{u_{2}},\ldots,\hat{u_{n}})^{t} \), and \(F= (f_{1},f_{2},\ldots,f_{n})^{t}\). By using (29) and (41), we have
such that
2.2 The weighted and shifted Grünwald difference operator and exponential spline function
Method IV. In this section, we would like to develop a numerical method based on the methods in references [4, 25, 29], and [28]. Also we investigate the convergence analysis of this method. Let \(U = (u_{i})\), \(S = (s_{i})\), \(C = (c_{i})\), \(T = (t_{i})\), and \(E = (e_{i}) = U-S=U-Q_{i}(x) \) be \((n-1)\)-dimensional column vectors. We used the weighted and shifted Grünwald difference operator and exponential spline function. By using consistency relation (12)(I) and using the boundary condition, we get the system of algebraic equations
where
We assume that \(F=(f_{1},f_{2},f_{3},\ldots,f_{n-1})^{t}\), \(S=(s_{1},s_{2},s_{3},\ldots,s_{n-1})^{t}\)
where
Substituting equation (46) into equation (43), we obtain
and
Now the error equation can be written as follows:
In order to get a bound on \(\|E\|\) (the infinite norm), we need the following lemma.
Lemma 3
AssumeAto be an\((n-1)\times (n-1)\)matrix with\(\|A\|_{\infty }<1\), then the matrix\((I-A)\)is invertible in addition to\(\|(I-A)^{-1}\| _{\infty }\leq \frac{1}{1-\|A\|_{\infty }}\).
From equation (52), it can be written that
Using the above lemma and (53), we get
provided that \(\|N^{-1}\|(h^{2-\alpha }\|B\|\| G_{1}\|+h^{2-\alpha } \|B\|\| G_{2}\|+|\mu | h^{2}\|B\|)<1\). Also from equation (18) we have \(\|T\|=\frac{1}{12}h^{4}P_{4}\), where
and \(\|B\|=1\). It was shown in [29], where \(\| G_{1}\| \leq 2|\overline{\eta }|\vartheta \), \(\|G_{2}\|\leq 2|\overline{\eta }|(1-\vartheta )\) for \(0<\alpha <1\) and \(\| G_{1}\|\leq 4|\overline{\eta }|\vartheta \), \(\|G_{2}\|\leq 4|\overline{\eta }|(1-\vartheta )\) for \(1<\alpha <2\). Also in [18] it was shown that \(\|N^{-1}\|\leq \frac{(b-a)^{2}}{8h ^{2}}\).
By substituting the values of \(\|B\|\), \(\|G_{1}\|\), \(\|G_{2}\|\), and \(\|N^{-1}\|\) in equation (54), we get
provided \((b-a)^{2}(2|\overline{\eta }|h^{-\alpha }\vartheta +2|\overline{ \eta }|h^{-\alpha }(1-\vartheta )+|\mu |)<8\) for \(0<\alpha <1\) and \(0\leq \vartheta \leq 1\).
Theorem 1
Let\(Q_{\Delta }(x,\beta )=Q(x)\in C^{\infty }[a, b]\)be the unique nonpolynomial spline which interpolates\(u(x)\)with relations (9) and (11). Then the following error estimates hold for cubic spline (in the limiting case when\(\theta \to 0\)):
Proof
See [13] and [18]. Now, by using [13] we approximate \(u_{i}\) by cubic spline \(\widehat{Q} _{i}\) where
and
We known that \(\widehat{u}_{0}\), \(\widehat{u}_{n}\), \(\widehat{M}_{0}\), and \(\widehat{M}_{n}\) are known from boundary conditions. The notations \(\hat{M}=(\widehat{M}_{0}, \widehat{M}_{1}, \widehat{M}_{2}, \ldots, \widehat{M}_{n-1}, \widehat{M}_{n})^{T}\), \(\hat{U}=(\widehat{u}_{0}, \widehat{u}_{1}, \widehat{u}_{2}, \ldots, \widehat{u}_{n-1}, \widehat{u} _{n})^{T}\), and by using (12)(II), we get \(\widehat{m}=( \widehat{m}_{0}, \widehat{m}_{1},\widehat{m}_{2}, \ldots, \widehat{m} _{n-1},\widehat{m}_{n})^{T}\), and also \(D^{\alpha }(u(x))|_{x=x_{i}}\), \(i=0,1,2,\ldots,n\), are taken from (5). Therefore, by using (57) and (55), we get
It follows \(\|E\|\rightarrow 0\) as \(h\rightarrow 0\). Therefore the convergence of this method has been established. □
3 Convergence analysis
In this section, we discuss the convergence analysis of exponential spline Method III. Convergence analyses of Method I and Method II are similar. So, first we write equation (41) in the points of \(x_{i}\), \(i=1,2,\ldots,n-1\):
Now, using the results obtained in (18), we have
Equations (60) construct a nonlinear system, which can be solved by Newton’s iterations method. Let \(u(x)\) be the exact solution of the problem and \(Q(x)\in C^{\infty }[0,T]\) be the exponential spline approximation to \(u(x)\) satisfied in \(Q(x_{i})=u(x_{i})\), \(i=1,2,\ldots,n-1\), and \(Q''(x_{i})=u''(x_{i})\), \(i=0,n\). We should approximate the error \(\|u(x)-Q(x)\|\). Let us assume that \(\hat{Q}(x)\) is the computed spline approximation to \(Q(x)\). To estimate \(\|u(x)-Q(x)\|\), we will estimate \(\|u(x)-\hat{Q}(x) \|\) and \(\|\hat{Q}(x)-Q(x)\|\) separately.
Lemma 4
Let\(\hat{Q}(x)\)be the unique spline interpolation to\(Q(x)\), and also suppose that partial derivatives ofFexist and\(|\frac{\partial F}{ \partial u}|\leq k_{1}\), \(|\frac{\partial F}{\partial u''}|\leq k_{2}\)for some constants\(k_{1}\)and\(k_{2}\). Then, for\(0 \leq i \leq n\), we have
Proof
For \(1\leq i\leq n-1\), we get
Now, using the mean value theorem for two parts of the above relation, there exist \(\xi _{i}\) and \(\nu _{i}\) such that
Using relation (57), we have \(|Q(x_{i})-\hat{Q}(x_{i})| \equiv O(h^{4})\), \(|Q''(x_{i})-\hat{Q}''(x_{i})|\equiv O(h^{2})\), and taking the absolute value, we obtain
□
Theorem 2
Let\(u(x)\in C^{2}[0,T]\)be the exact solution (1) and\(Q(x)\)be the exponential spline approximation to\(u(x)\), then we have
Proof
Since \(\hat{Q}(x)\) is an interpolation to \(u(x)\), thus there is a finite constant \(\varrho _{1}\) independent of h that we get
where \(\varrho _{1}\) is a finite constant. Now, using the triangular inequality and Lemma 1, we can obtain the results as follows:
We can prove the convergence analysis for Method I and Method II in the same manner. □
4 Numerical results
In this section, we have implemented our methods for solving some of the Bagley–Torvik differential equations with different values of \(h=\frac{1}{8}, \frac{1}{16}, \frac{1}{32}, \frac{1}{64}, \frac{1}{128}, \frac{1}{256}, \frac{1}{512}, \frac{1}{1024}\), and \(\alpha =0, 0.2,0.3,0.4,0.5, 0.9\). The maximum absolute errors in solutions of the methods are tabulated in tables. We compute the absolute error for examples and compare them with the methods in [4, 9, 17, 21, 28, 29]. The convergence order (C.O.) is obtained by
where \(E(h)\) is the maximum absolute error. Numerical results can be derived by using MATHEMATICA 9.
Example 1
Consider the following boundary value problem [29]:
where
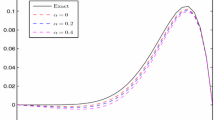
the exact solution is given by the relation \(u(x)=x^{4}(x-1)\). The maximum absolute errors of Method III and Method IV are presented in Tables 1 and 3, and also compare the computed results with the method [29] in Table 2.
Example 2
Consider the following boundary value problem:
where the exact solution is given by the relation \(u(x)=x^{6}(1-x^{2})\). The maximum absolute errors of Method III and Method IV are presented in Tables 7 and 4. Also compare the computed results with the methods [28] and [4] in Tables 5 and 6.
Example 3
Consider the following Bagley–Torvik fractional boundary value problem:
the exact solution is given by \(u(x)=x^{3}-x\). The numerical solutions are computed by Methods I and IV. In order to compare the solutions with [21] in Table 9, we have taken \(n=10,20\), and 40 in Table 8. The absolute error and the order of convergence for \(n = 4,8,16,32,64,128,256\), and 512 are given in Table 10.
Example 4
Consider the following Bagley–Torvik fractional boundary value problem:
The exact solution is given by \(u(x)=x^{\gamma }\). The absolute errors are compared with the methods [9] and [17]. In order to compare the solutions with [9], we have taken \(n = 8,16,32,64,128,256,512, 1024\) and \(\gamma =3,4\) in Tables 11 and 12.
5 Conclusion
Computational methods for solving the fractional Bagley–Torvik equation were proposed. The fractional differential equation term in the fractional Bagley–Torvik equation was discretized using the exponential spline function and the shifted Grünwald difference operator. Also we obtain the four numerical schemes based on the exponential spline. The convergence analyses of the shifted Grünwald difference and the exponential spline are discussed. The feasibility of the numerical algorithms was illustrated with four examples, and the approximated results were compared with the methods in [4, 9, 17, 21, 28, 29].
References
Akgül, A.: A new method for approximate solutions of fractional order boundary value problems. Neural Parallel Sci. Comput. 22(1–2), 223–237 (2014)
Akgül, A., Inc, M., Karatas, E., Baleanu, D.: Numerical solutions of fractional differential equations of Lane–Emden type by an accurate technique. Adv. Differ. Equ. 2015, 220 (2015)
Akgül, A., Mustafa, I., Baleanu, D.: On solutions of variable-order fractional differential equations. Int. J. Optim. Control 7(1), 112–116 (2017)
Akram, G., Tariq, H.: An exponential spline technique for solving fractional boundary value problem. Calcolo 53, 545–558 (2016)
Al-Mdallal, Q.M., Syam, M.I., Anwar, M.N.: A collocation shooting method for solving fractional boundary value problems. Commun. Nonlinear Sci. Numer. Simul. 15(12), 3814–3822 (2010)
Bagley, R.L., Torvik, P.J.: On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 51(2), 294–298 (1984)
Diego Murio, A.: Implicit finite difference approximation for time fractional diffusion equations. Comput. Math. Appl. 56, 1138–1145 (2008)
Diethelm, K., Ford, J.: Numerical solution of the Bagley–Torvik equation. BIT Numer. Math. 42, 490–507 (2002)
Esmaeili, S.: The numerical solution to the Bagley–Torvik equation by exponential integrators. Sci. Iran. 24(6), 2941–2951 (2017)
Ghasemi, M., Jalilian, Y., Trujillo, J.J.: Existence and numerical simulation of solutions for nonlinear fractional pantograph equations. Int. J. Comput. Math. 94(10), 2041–2062 (2017)
Gülsu, M., Öztürk, Y., Anapali, A.: Numerical solution of the fractional Bagley–Torvik equation arising in fluid mechanics. Int. J. Comput. Math. 94(1), 173–184 (2017)
Jalilian, R., Tahernezhad, T.: Exponential spline method for approximation solution of Fredholm integro-differential equation. Int. J. Comput. Math. https://doi.org/10.1080/00207160.2019.1586891
Maleknejad, Kh., Rashidinia, J., Jalilian, H.: Nonpolynomial spline functions and quasilinearization. Filomat 32(11) (2018)
Maleknejad, Kh., Torkzadeh, L.: Hybrid functions approach for the fractional Riccati differential equation. Filomat 30(9), 2453–2463 (2016)
Oldham, K.B., Spanier, J.: The Fractional Calculus. Academic Press, New York (1974)
Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1990)
Podlubny, I.: Matrix approach to discrete fractional calculus. Fract. Calc. Appl. Anal. 3(4), 359–386 (2000)
Rashidinia, J., Jalilian, R.: Non-polynomial spline for solution of boundary-value problems in plate deflection theory. Int. J. Comput. Math. 84, 1483–1494 (2007)
Ray, S.S., Bera, R.K.: Analytical solution of the Bagley Torvik equation by Adomian decomposition method. Appl. Math. Comput. 168, 398–410 (2005)
Saadatmandi, A., Dehghan, M.: A new operational matrix for solving fractional-order differential equations. Comput. Math. Appl. 59, 1326–1336 (2010)
Sakar, M.G., Sald, O., Akgül, A.: A novel technique for fractional Bagley–Torvik equation. Proc. Natl. Acad. Sci. India Sect. A https://doi.org/10.1007/s40010-018-0488-4
Saw, V., Kumar, S.: Numerical scheme for solving two point fractional Bagley–Torvik equation using Chebyshev collocation method. WSEAS Trans. Syst. 17, 166–177 (2018)
Sayevand, Kh., Mirzaee, F.: A unique continuous solution for the Bagley–Torvik equation. CJMS 1(1), 47–51 (2012)
Staněk, S.: Two-point boundary value problems for the generalized Bagley–Torvik fractional differential equation. Cent. Eur. J. Math. 11(3), 574–593 (2013)
Tian, W., Zhou, H., Deng, W.: A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 84, 1703–1727 (2015)
Van Daele, M., Vanden Berghe, G., De Meyer, H.: A smooth approximation for the solution of a fourth-order boundary value problem based on nonpolynomial splines. J. Comput. Appl. Math. 51, 383–394 (1994)
Yüzbaş, Ş.: Numerical solution of the Bagley–Torvik equation by the Bessel collocation method. Math. Methods Appl. Sci. 36, 300–312 (2013)
Zahra, W.K., Elkholy, S.M.: Quadratic spline solution for boundary value problem of fractional order. Numer. Algorithms 59, 373–391 (2012)
Zahra, W.K., Elkholy, S.M.: Cubic spline solution of fractional Bagley–Torvik equation. Electron. J. Math. Anal. Appl. 1(2), 230–241 (2013)
Acknowledgements
The authors are grateful to the reviewers for their helpful, valuable comments and suggestions in the improvement of this manuscript.
Availability of data and materials
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Abbreviations
Not applicable.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Emadifar, H., Jalilian, R. An exponential spline approximation for fractional Bagley–Torvik equation. Bound Value Probl 2020, 20 (2020). https://doi.org/10.1186/s13661-020-01327-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-020-01327-2