1 Introduction

Leibnitz created arbitrary-order derivatives shortly after integer-order derivatives, and this topic has attracted the interest of numerous academics recently. As soon as its potential was known, fractional calculus (FC) quickly replaced classical calculus as the preferred modeling tool for practical issues. FC theory provides a superbly methodical framework for understanding the physical world. The specific explanation it offers for nonlinear complex systems has recently attracted the attention of numerous experts. Using fractional models of differential equations has the benefit of being nonlocal, which can be used in any model. Locality is preserved by derivatives of integer order, but nonlocality is introduced by those of fractional order. This demonstrates that the future state of a physical system is dependent on not only its current state but also its past states. Models built with the use of fractional-order derivatives are thus more accurate representations of reality. Classical derivatives and fractional derivatives are both mathematical concepts related to the rate of change of a function, but they differ in their definition and application. While classical derivatives deal with integer orders and provide information about instantaneous rates of change, fractional derivatives extend this concept to noninteger orders, offering a way to model systems with memory or long-range dependence. Fractional calculus is a field that has found applications in diverse scientific and engineering disciplines [1].

However, the fractional order varies based on time and space. The scenario leads to a rapidly expanding field of FPDEs with fractional operators of variable order. Several potent numerical approaches were established in the scientific literature, and numerous eminent scholars contributed to this topic. These techniques include the adomian decomposition method (ADM), the homotopy perturbation method (HPM), the homotopy analysis method (HAM), the collocation method, the Sumudu transform method (STM), the conformable Shehu homotopy perturbation method (CSHPM), the conformable q-Shehu homotopy analysis transform method (Cq-SHATM), the conformable sumudu decomposition method, the conformable Laplace decomposition method, and the differential transform method (DTM) [2–32].

In recent years, there have been studies on ST in the literature [33–40]. Using the q-homotopy Shehu analysis transform method (q-HSATM), we analyze and find an approximated analytical solution for the time-fractional NWS equation in the current framework. The methodology under consideration has been tweaked, and it is now a sophisticated hybrid of q-HATM and the Shehu transform (ST). Since q-HATM is a modified method of HAM, it avoids the need for linearization, discretization, and perturbation, and it also requires less memory and fewer calculations than traditional HAM and no complicated polynomials, integrations, or physical parameters. Recently, many researchers have found it to be highly helpful in interpreting results for many types of nonlinear problems due to its consistency and effectiveness. Srivastava et al. determine the q-HATM solution for the model of the vibration equation and analyze its behavior [41]. Veeresha et al. examine the approximation of an analytical solution for a smoking epidemic model of fractional order [42]. Singh et al. suggest that the efficiency of q-HATM may be shown in the coupled system [43]. Numerical simulations of the Gardner and Cahn–Hilliard equations are presented by Prakasha et al., who verify that the proposed method is more accurate than alternative classical techniques [44]. Veeresha et al. provide an illustrative example of the novel numerical surfaces used in the mathematical model of cancer chemotherapy [45]. The solution for the combined modified Boussinesq and approximate long wave was reported by Veeresha et al. [46]. Using the energy-dependent Schrödinger potential as an example, Veeresha et al. demonstrated the superior performance of the suggested strategy over the coupled fractional reduced differential transform method (CFRDTM) for solving the associated coupled equation [47]. The proposed method is also being considered by many researchers as a means to obtain an approximate analytical solution to a wide range of issues [48, 49].

The fluctuations in the sand, the lines on seashells, and many other striped patterns like these can be modeled by amplitude equations. The NWSE is one of the most important amplitude equations in applied sciences. It shows how stripes appear in two-dimensional systems [50–53]. The NWSE has the form [50, 51, 54]

$$ \frac{\partial ^{\alpha} u}{\partial t^{\alpha}} =a \frac{\partial ^{2} u}{ \partial x^{2}} +hu-c u^{m},\quad 0< \alpha < 1, t\geq 0,x\in \mathbb{R}, $$
(1)

where m is a positive integer, a, h and c real numbers.

The Shehu transform is used to solve linear equations such as the Laplace transform. However, to solve nonlinear equations, q-homotopy analysis must be used together with a numerical method such as the transform method. Therefore, in this study, the Shehu transform and the q-homotopy analysis transformation method were combined. This paper aims to present a new method, the q-SHATM and to use it to obtain new numerical solutions for a NWS equation.

In light of developments, this paper proposes to investigate the use of the q-HSATM to solve the time-fractional Newell–Whitehead–Segel equation numerically, and to compare the results with those obtained using a more recent technique.

The first aim of this study is to introduce the q-homotopy Shehu analysis transform method. The second aim is to solve a time-fractional Newell–Whitehead–Segel equation for the first time with the newly produced hybrid method. Several previously unmentioned solutions in the literature are retrieved and their graphic characteristics are plotted in their entirety. The main motivation of writing this paper is to obtain the new numerical solutions of a time-fractional Newell–Whitehead–Segel equation by using a new hybrid method, namely the q-homotopy Shehu analysis transform method (q-HSATM). Also, it has been observed that the results obtained from the table give better results than the LTDM [50] in the literature.

The structure of this paper is as follows. In Sect. 2, we provide a quick recap of some of the preliminary definitions of the Caputo fractional derivative and other conclusions that can be helpful in the study of fractional differential equations. Considering the issue at hand, a potential q-HSATM solution procedure is presented in Sect. 3. Convergence of the suggested approach is given in Sect. 4. The approximate solutions are found using q-HSATM on several numerical test situations presented in Sect. 5. Section 6 contains the discussion and results. Finally, the conclusion is given.

2 Preliminaries

Several fundamental definitions are provided in this section.

Definition 1

([19, 55, 56])

The Riemann–Liouville fractional integral is described as

$$ I^{a} f ( x ) = \textstyle\begin{cases} \frac{1}{\Gamma (a)} \int _{0}^{x} ( x-t )^{a-1} f ( t )\,dt, &a>0, x>0,\\ I^{0} f ( x ) =f ( x ), &a=0. \end{cases} $$
(2)

Definition 2

([19, 55, 56])

The Caputo fractional derivative (CFD) is given by

$$ D^{a} f ( x ) = I^{a-n} D^{n} f ( x ) = \frac{1}{ \Gamma (n-a)} \int _{0}^{x} (x-t)^{n-a-1} f^{ ( n )} (t)\,dt, $$
(3)

where \({n -1< a \leq n}\), \({n \in N}\), \({x >0}\), \({f \in C_{-1}^{n} }\).

Definition 3

([57])

The Mittag–Leffler function \({E}_{{a}}\) is defined as

$$ E_{a} ( z ) = \sum_{n=0}^{\infty} \frac{z^{a}}{ \Gamma (na+1)}, \quad a>0. $$
(4)

Definition 4

([33])

The Shehu transform (ST) of the function \({f}({t})\) is given by

$$ S \bigl[ f(t) \bigr] = V [ s,u ] = \int _{0}^{\infty} f ( t ) e^{- \frac{s t}{u}}\,dt,\quad s>0,u>0. $$
(5)

Definition 5

([33])

If \({V} ( {s}, {u} )\) is the ST of the function \({f}({t})\), then the ST of CFD is defined by

$$ S \bigl[ D^{\alpha} f ( t ) \bigr] = \biggl( \frac{s }{u } \biggr)^{\alpha} \mathrm{V} ( s,u ) - \sum_{k=0}^{n-1} \biggl( \frac{s }{u } \biggr)^{\alpha -k-1} f^{ ( k )} ( 0 ),\quad n-1< \alpha \leq n. $$
(6)

3 The methodology of the q-homotopy Shehu analysis transform method

In this section, the q-HSATM for nonlinear FPDEs is presented. In order to illustrate the technique for the suggested method, the nonlinear FPDEs are written in standard operator form

$$ D_{t}^{a} u ( x,t ) + A u ( x,t ) +Nu ( x,t ) =g ( x,t ), \quad t>0,n-1< \alpha \leq n, $$
(7)

with the initial condition

$$ u ( x,0 ) =h ( x ), $$
(8)

where A is a linear operator, N is a nonlinear operator, \(g(x,t)\) is a source term, and \({D}_{{t}}^{{a}}\) is a time-fractional derivative operator of order α.

Now, by performing a Shehu transform on Eq. (7) and using the initial condition, it is acquired as

$$ S \bigl[ u ( x,t ) \bigr] - \sum_{k=0}^{n-1} \biggl( \frac{s }{u } \biggr)^{-k-1} \frac{\partial ^{k} u(x,t)}{ \partial t^{k}} \bigg| _{t=0} + \biggl( \frac{u}{s} \biggr)^{\alpha} S \bigl[ A u ( x,t ) + Nu ( x,t ) -g(x,t) \bigr] =0. $$
(9)

The nonlinear operator by the assistance of HAM for a real function \({\varphi} ({x}, {t}; {q})\) is defined as

$$\begin{aligned} N \bigl[ \varphi (x,t;q) \bigr] ={}& S \bigl[ \varphi (x,t;q) \bigr] - \frac{u}{s} \varphi (x,t;q) \bigl( 0^{+} \bigr) \end{aligned}$$
(10)
$$\begin{aligned} &{} + \biggl( \frac{u}{s} \biggr)^{\alpha} \bigl\{ S \bigl[ A u ( x,t ) + Nu ( x,t ) -g(x,t) \bigr] \bigr\} , \end{aligned}$$
(11)

where \({q\epsilon} [ {0}, \frac{{1}}{ {n}} ] \).

This establishes a homotopy as follows:

$$ ( 1-nq ) S \biggl[ \varphi ( x,t;q ) - \frac{u}{s} \varphi ( x,t;q ) \bigl( 0^{+} \bigr) \biggr] =hq H ( x,t ) N \bigl[ \varphi ( x,t;q ) \bigr], $$
(12)

where, \({h\neq 0}\) is an auxiliary parameter and S represents the Shehu transform. For \({q}={0}\) and \({q}= \frac{{1}}{ {n}}\), the results in Eq. (12) are, respectively, provided as

$$ \varphi ( x,t;0 ) = u_{0} ( x,t ), \qquad \varphi \biggl( x,t; \frac{1}{n} \biggr) =u ( x,t ) . $$
(13)

Therefore, by amplifying q from 0 to \(\frac{{1}}{{n}}\), the solution \({\varphi} ( {x}, {t}; {q} )\) converges from \({u}_{{0}} ( {x}, {t} )\) to the solution \({u} ( {x}, {t} )\). Employing the Taylor theorem around q and expanding \({\varphi} ( {x}, {t}; {q} )\), it is obtained as

$$ \varphi ( x, t; q ) = u_{0} ( x, t ) + \sum _{i =1}^{\infty} u_{m} ( x, t ) q^{m}, $$
(14)

where

$$ u_{m} ( x, t ) = \frac{1}{m !} \frac{\partial ^{m} \varphi ( x, t; q )}{\partial q^{m}} \bigg| _{q =0}. $$
(15)

Equation (14) converges at \({q}= \frac{{1}}{ {n}}\) for the appropriate \({u}_{{0}} ( {x}, {t} )\), n, and h. Then, we have one of the solutions of the original nonlinear equation of the form

$$ u ( x, t ) = u_{0} ( x, t ) + \sum_{m =1}^{\infty} u_{m} ( x, t ) \biggl( \frac{1}{n} \biggr)^{m}. $$
(16)

If we differentiate the zeroth-order deformation Eq. (13) m times with respect to q and we divide by m!, respectively, then for \(q=0\), it is obtained as

$$ S \bigl[ u_{m} ( x,t ) - k_{m} u_{m-1} ( x,t ) \bigr] =h H ( x,t ) \mathcal{R}_{m} ( \overrightarrow{u}_{m-1} ), $$
(17)

where the vectors are defined by

$$ \overrightarrow{u}_{m} = \bigl\{ u_{0} ( x,t ), u_{1} ( x,t ),\dots , u_{m} ( x,t ) \bigr\} . $$
(18)

When the inverse Shehu transform to Eq. (17) is applied, then it is obtained as

$$ u_{m} ( x, t ) = k_{m} u_{m -1} ( x, t ) + h S ^{-1} \bigl[ H ( x, t ) \mathcal{R}_{m} ( \overrightarrow{u}_{m -1} ) \bigr], $$
(19)

where

$$\begin{aligned} \mathcal{R}_{m} ( \overrightarrow{u}_{m -1} ) =& S \bigl[ u_{m -1} ( x, t ) \bigr] - \biggl( 1- \frac{k_{m}}{n} \biggr) \frac{u }{s} u_{0} ( x,t ) + \biggl( \frac{u}{ s} \biggr)^{\alpha} S \bigl( A u_{m -1} ( x, t ) \\ &{} + H_{m -1} ( x, t ) - \mathrm{g} ( x, t ) \bigr) \end{aligned}$$
(20)

and

$$ k_{m} = \textstyle\begin{cases} 0, & m \leq 1,\\ n, & m >1. \end{cases} $$
(21)

Here, \({H}_{{m}}\) is a homotopy polynomial and presented as

$$ H_{m -1} = \frac{1}{ ( m -1 ) !} \frac{\partial ^{m -1} \varphi ( x, t; q )}{\partial q^{m -1}} \bigg| _{q =0} $$
(22)

and

$$\begin{aligned}& \varphi ( x, t; q ) = \varphi _{0} + q \varphi _{1} + q^{2} \varphi _{2} +\cdots , \end{aligned}$$
(23)
$$\begin{aligned}& u_{m} ( x, t ) = ( k_{m} +h ) u_{m -1} ( x, t ) - \biggl( 1- \frac{k_{m}}{n} \biggr) \frac{u }{s} u_{0} ( x,t ) + h S ^{-1} \biggl[ \biggl( \biggl( \frac{u}{s} \biggr)^{\alpha} S \bigl( A u_{m -1} ( x, t ) \\& \hphantom{u_{m} ( x, t ) =}{} + H_{m -1} ( x, t ) -g ( x,t ) \bigr) \biggr]. \end{aligned}$$
(24)

By utilizing q-HSATM, the series solution is defined by

$$ u ( x, t ) = \sum_{i=0}^{\infty} u_{m} ( x, t ) \biggl( \frac{1}{n} \biggr)^{m}. $$
(25)

4 Convergence analysis

Theorem 1

(Uniqueness Theorem [42, 58])

The solution for the nonlinear fractional differential Eq. (7) obtained by q-HSATM is unique for \(\forall {\alpha} {\epsilon} ({0},{1})\), where \({\alpha} =({n}+{\hslash} )+{\hslash} ({\rho} +{\delta} ){T}\).

Proof

The solution of nonlinear FPDEs Eq. (7) is presented as

$$ u ( x, t ) = \sum_{i=0}^{\infty} u_{m} ( x, t ) \biggl( \frac{1}{n} \biggr)^{m}, $$
(26)

where

$$\begin{aligned}& u_{m} ( x, t ) = ( k_{m} +h ) u_{m -1} ( x, t ) - \biggl( 1- \frac{k_{m}}{n} \biggr) \frac{u }{s} u_{0} ( x,t ) \\& \hphantom{u_{m} ( x, t ) =}{}+ h S ^{-1} \biggl[ \biggl( \biggl( \frac{u}{s} \biggr)^{\alpha} S \bigl( A u_{m -1} ( x, t ) + H_{m -1} ( x, t ) - g ( x,t ) \bigr) \biggr) \biggr]. \end{aligned}$$
(27)

Assume that u and w are two different solutions of Eq. (7), then with the help of the aforementioned equation, we obtain

$$\begin{aligned} \vert {u}-{w} \vert =& \biggl\vert ( {n}+{h} ) ( {u}-{w} ) \\ &{} + {h} {S}^{-{1}} \biggl[ \biggl( \frac{{u}}{ {s}} \biggr)^{{\alpha}} {S} \bigl( {A} ( {u}-{w} ) +{N} ( {u}- {w} ) \bigr) \biggr] \biggr\vert . \end{aligned}$$
(28)

Now, using the convolution theorem for the Shehu transform, it is obtained as

$$\begin{aligned} \vert {u}-{w} \vert \leq& ( {n}+ {h} ) \vert {u}-{w} \vert +{h} \int _{{0}}^{{t}} \bigl( \bigl\vert {A} ( {u}-{w} ) \bigr\vert +{N} ( {u}-{w} ) \bigr) \frac{ ( {t}-{\tau} )^{{\alpha}}}{ {\Gamma }({1}+{\alpha} )} {\,d\tau} \\ \leq& ( {n}+{h} ) \vert {u}- {w} \vert \\ &{}+{h} \int _{{0}}^{{t}} \bigl( {\rho} \vert {u}-{w} \vert +{\delta} \vert {u}-{w} \vert \bigr) \frac{ ( {t}-{\tau} )^{{\alpha}}}{ {\Gamma }({1}+{\alpha} )} {d \tau}. \end{aligned}$$
(29)

Then, using the integral mean-value theorem, it yields

$$\begin{aligned} \vert {u}-{w} \vert \leq& ( {n}+ {h} ) \vert {u}-{w} \vert +{h} \bigl( {\rho} \vert {u}-{w} \vert + {\delta} \vert {u}-{w} \vert \bigr) {T} \\ \leq& {\alpha} \vert {u}-{w} \vert . \end{aligned}$$
(30)

As a result, we have \(( 1- \tau ) \vert w-u \vert \leq 0\). As \(\tau \in ( 0,1 )\), \(\vert w-u \vert =0\), which implies that \(w =u\). Hence, the solution is unique. □

Theorem 2

(Convergence theorem [58])

Assume that X is a Banach space and \({F}: {X} {\rightarrow} {X}\) is a nonlinear mapping. If the inequality

$$ \bigl\Vert {G}({a})-{G}({h}) \bigr\Vert \leq {\gamma} \Vert {a}-{h} \Vert , \quad\forall {a}, {b}\in {X} $$
(31)

exists, then G has a fixed point in view of Banach fixed point theory [59]. Furthermore, for the arbitrary choice of \({a}_{{0}}\), \({b}_{{0}} {\in} {X}\), the sequence created by the q-HSATM converges to a fixed point of G and

$$ \Vert {w}_{{m}} - {w}_{{n}} \Vert \leq \frac{{\gamma}^{{n}}}{ {1}-{\gamma}} \Vert {w}_{{1}} - {w}_{{0}} \Vert ,\quad \forall {a}, {b}\in {X}. $$
(32)

Proof

Let us take a Banach space (\(C[J]\), \(\Vert . \Vert \)) of all continuous functions on J with the norm expressed as \(\Vert g(t) \Vert = \max_{t\in J} \vert g(t) \vert \).

Now, we demonstrate that the sequence \(\{ w_{n} \}\) is a Cauchy sequence in the Banach space:

$$\begin{aligned} \Vert w_{m} - w_{n} \Vert =& \max_{t\in J} \vert w_{m} - w_{n} \vert \\ =& \max_{t\in J} \biggl\vert ( n+h ) ( w_{m-1} - w_{n-1} ) + h ( {}_{c} S_{\alpha} )^{-1} \biggl[ \biggl( \frac{u}{s} \biggr)^{\alpha} S \bigl( A ( w_{m-1} - w_{n-1} ) \\ &{} +N ( w_{m-1} - w_{n-1} ) \bigr) \biggr] \biggr\vert \\ \leq& \max_{t\in J} \biggl[ ( n+h ) \vert w_{m-1} - w_{n-1} \vert +h ( {}_{c} S_{\alpha} )^{-1} \biggl[ \biggl( \frac{u}{ s} \biggr)^{\alpha} S\bigl(A \vert w_{m-1} - w_{n-1} \vert \biggr] \\ &{} +N \vert w_{m-1} - w_{n-1} \vert \bigr) \biggr] \bigg]. \end{aligned}$$
(33)

Now, utilizing the convolution theorem for the Shehu transform, it is obtained as

$$\begin{aligned} \Vert w_{m} - w_{n} \Vert \leq& \max _{t\in J} \biggl[ ( n+h ) \vert w_{m-1} - w_{n-1} \vert + ( n+h ) \vert w_{m-1} - w_{n-1} \vert \\ &{}+h \int _{0}^{t} \bigl( A \vert w_{m-1} - w_{n-1} \vert +N \vert w_{m-1} - w_{n-1} \vert \bigr) \frac{ ( t-\eta )^{\alpha}}{\alpha}\,d\eta \biggr] \\ \leq& \max_{t\in J} \biggl[ ( n+h ) \vert w_{m-1} - w_{n-1} \vert + ( n+h ) \vert w_{m-1} - w_{n-1} \vert \\ &{} +h \int _{0}^{t} \bigl( \rho \vert w_{m-1} - w_{n-1} \vert + \delta \vert w_{m-1} - w_{n-1} \vert \bigr) \frac{ ( t-\eta )^{\alpha}}{\alpha}\,d\eta \biggr]. \end{aligned}$$
(34)

Next, by the application of the integral mean-value theorem [59], it is obtained as

$$\begin{aligned} \Vert w_{m} - w_{n} \Vert \leq& \max _{t\in J} \bigl[ ( n+h ) \vert w_{m-1} - w_{n-1} \vert +h\bigl( \rho \vert w_{m-1} - w_{n-1} \vert + \delta \vert w_{m-1} - w_{n-1} \vert \bigr)T \bigr] \\ \leq& \tau \Vert w_{m-1} - w_{n-1} \Vert . \end{aligned}$$
(35)

Let \(m=n+1\), then we obtain

$$ \Vert w_{n+1} - w_{n} \Vert \leq \tau \Vert w_{n} - w_{n-1} \Vert \leq \tau ^{2} \Vert w_{n-1} - w_{n-2} \Vert \leq \cdots \leq \tau ^{n} \Vert w_{1} - w_{0} \Vert . $$
(36)

By using the triangular inequality, we have

$$\begin{aligned} \Vert w_{m} - w_{n} \Vert \leq& \Vert w_{n+1} - w_{n} \Vert + \Vert w_{n+2} - w_{n+1} \Vert +\cdots + \Vert w_{m} - w_{m-1} \Vert \\ \leq& \bigl[ \tau ^{n} + \tau ^{n+1} +\cdots + \tau ^{m-1} \bigr] \Vert w_{1} - w_{0} \Vert \\ \leq& \tau ^{n} \bigl[ 1+ \tau + \tau ^{2} +\cdots + \tau ^{m-n-1} \bigr] \Vert w_{1} - w_{0} \Vert \\ \leq& \tau ^{n} \biggl[ \frac{1- \tau ^{m-n-1}}{1- \tau} \biggr] \Vert w_{1} - w_{0} \Vert . \end{aligned}$$
(37)

Since \(\tau \in ( 0,1 )\), \(1- \tau ^{m-n-1} <1\), then we obtain

$$ \Vert w_{m} - w_{n} \Vert \leq \frac{\tau ^{n}}{1- \tau} \Vert w_{1} - w_{0} \Vert . $$
(38)

For \(\Vert w_{1} - w_{0} \Vert <\infty \), so as \(m\rightarrow \infty \) then \(\Vert w_{m} - w_{n} \Vert \rightarrow 0\). Thus, the sequence \(\{ w_{n} \}\) is a Cauchy sequence in \(C[J]\), and so the sequence is convergent. □

5 The numerical solutions of the time-fractional Newell–Whitehead–Segel equation

Let us assune \(a =1\), \(h =2\), \(c =3\), and \(m=2\) for the nonlinear time-fractional Newell–Whitehead–Segel equation (NTFNWSE) [52, 60]:

$$ \frac{\partial ^{\alpha} u(x,t)}{\partial t^{\alpha}} = \frac{\partial ^{2} u(x,t)}{\partial x^{2}} +2u(x,t)-3 u^{2} (x,t),\quad 0< \alpha < 1 $$
(39)

with initial condition

$$ u ( x, 0 ) = \beta , $$
(40)

where β is an arbitrary constant.

Now, by applying the Shehu transform to Eq. (39) and by using Eq. (40), then it is obtained as

$$ S \bigl[ u ( \mathrm{x},\mathrm{t} ) \bigr] - \frac{u}{s} u ( \mathrm{x},0 ) - \biggl( \frac{u}{s} \biggr)^{\alpha} S \biggl[ \frac{\partial ^{2} u ( x,t )}{ \partial x^{2}} +2u ( x,t ) -3 u^{2} ( x,t ) \biggr] =0. $$
(41)

The nonlinear operator by using Eq. (41) is described by

$$\begin{aligned} {N} \bigl[ {\varphi} ( {x}, {t}; {q}) \bigr] =& {S} \bigl[ {\varphi} ( {x}, {t}; {q}) \bigr] - \frac{{u}}{ {s}} {u}({x}, {0}) \\ &{}- \biggl( \frac{{u}}{ {s}} \biggr)^{{\alpha}} {S} \biggl[ \frac{{\partial}^{{2}} {\varphi} ( {x}, {t}; {q})}{{\partial x}^{{2}}} +{2 \varphi} ( {x}, {t}; {q}) -{3 u}^{{2}} {\varphi} ( {x}, {t}; {q}) \biggr]. \end{aligned}$$
(42)

By applying the proposed algorithm, the mth-order deformation equation is defined by

$$ {S} \bigl[ {u}_{{m}} ( {x}, {t} ) - {k}_{{m}} {u}_{{m}-{1}} ( {x}, {t} ) \bigr] ={h} \mathcal{{R}}_{{m}} ( \overrightarrow{ {u}}_{{m}-{1}} ), $$
(43)

where

$$\begin{aligned} \mathcal{R}_{ m} ( \overrightarrow{u}_{m-1} ) =& S \bigl[ \overrightarrow{u}_{m-1} ( x,\mathrm{t} ) \bigr] - \frac{u}{s} u ( \mathrm{x},0 ) - \biggl( 1- \frac{\mathrm{k}_{\mathrm{m}}}{\mathrm{n}} \biggr) \biggl( \frac{u}{s} \biggr)^{\alpha} \\ &{}\times S \Biggl[ \frac{\partial ^{2} u_{m-1} (x,t)}{\partial x^{2}} +2 u_{m-1} (x,t) -3 \sum _{i=0}^{m-1} u_{i} (x,t) u_{m-1-i} (x,t) \Biggr]. \end{aligned}$$
(44)

On applying the inverse Shehu transform to Eq. (43), it is obtained as

$$ {u}_{{m}} ( {x}, {t} ) = {k}_{{m}} {u}_{{m}-{1}} ( {x}, {t} ) + {h S}^{-{1}} \bigl[ { \mathcal{R}}_{{m}} ( \overrightarrow{{u}}_{{m}-{1}} ) \bigr]. $$
(45)

By the use of the initial condition, it is acquired as

$$ {u}_{{0}} ( {x}, {t} ) = { \beta}. $$
(46)

To find the values of \(u_{1} ( x,t )\), putting \(m=1\) in Eq. (45), it is obtained as

$$ {u}_{{1}} ( {x}, {t} ) = \frac{{h} ( {3} {\beta}^{{2}} -{2} {\beta} ) {t}^{{\alpha}}}{ {\Gamma} ( {\alpha} +{1} )}. $$
(47)

Similarly, to find values of \(u_{2} ( x,\mathrm{t} )\), putting \(m=2\) in Eq. (45), it is found as

$$ {u}_{{2}} ( {x}, {t} ) = \frac{{h} ( {n}+{h} ) ( {3} {\beta}^{{2}} -{2} {\beta} ) {t}^{{\alpha}}}{ {\Gamma} ( {\alpha} +{1} )} - \frac{{h}^{{2}} ( -{18} {\beta}^{{3}} +{18} {\beta}^{{2}} -{4} {\beta} ) {t}^{{2 \alpha}}}{ {\Gamma} ( {2}{\alpha} +{1} )}. $$
(48)

In this way, the other terms are generated. Thus, the q-HSATM solution of Eq. (39) has the form

$$\begin{aligned} {u} ( {x}, {t} ) =& {\beta} + \frac{{h} ( {3} {\beta}^{{2}} -{2} {\beta} ) {t}^{{\alpha}}}{ {\Gamma} ( {\alpha} +{1} )} + \frac{{h}({n}+{h})}{{\Gamma} ( {\alpha} +{1} )} \bigl( {3} { \beta}^{{2}} -{2} {\beta} \bigr) {t}^{{\alpha}} \\ &{}- \frac{{h}^{{2}} ( -{18} {\beta}^{{3}} +{18} {\beta}^{{2}} -{4} {\beta} ) {t}^{{2 \alpha}}}{ {\Gamma} ( {2}{\alpha} +{1} )}. \end{aligned}$$
(49)

Substituting the values of \(\alpha =1\), \(n=1\), \(h=- 1\) in Eq. (49), the obtained results \(\sum_{m=1}^{M} u_{m} ( x,t ) ( \frac{1}{ n} )^{m}\) converge to the analytical solutions \(u ( x,t ) = \frac{- \frac{2}{3} \beta \exp (2\mathrm{t})}{- \frac{2}{3} + \beta - \beta \exp (2\mathrm{t})}\) of NTFNWSE when \(M\rightarrow \infty \).

Figure 1 demonstrates a 3D graph of the q-HSATM solution, the exact solution, and the absolute error in Eq. (49) for \(h =-1\), \(n =1\), \(\alpha =1\), \(\beta =1\).

Figure 1
figure 1

(a) \(u ( x, t )\) solution of q-HSATM (b) Exact solution of \(u ( x, t )\) (c) Nature of absolute error \(= \vert u_{\mathrm{exact}} - u_{q-H S ATM} \vert \) at \(h =-1\), \(n =1\), \(\alpha =1\), \(\beta =1 \)

Full size image

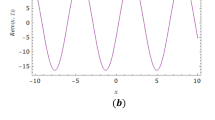
Figure 2 shows a 2D graph of Eq. (49) for different values of α.

Figure 2
figure 2

\(u ( x,t )\) solution of q-HSATM with respect to t when \(\forall \mathrm{x} \in \mathbbm{{}\mathbb{R}\mathbbm{}}\) and \(\beta =1\) with different values of α

Full size image

Table 1 shows the comparison of the absolute errors of the methods ATHPM, LTDM, and q-HSATM.

Table 1 Comparative study between ATHPM [61], LTDM [50], and q-HSATM for the numerical solutions \({u} ( {x}, {t} )\) at \({\alpha} ={1}\) and \({\beta} ={0}.{01}\)
Full size table

6 Result and discussion

For Eq. (39), the graphs of the temperature \({u}({x}, {t})\) for different values of \({\alpha} ={0}.{9}\), \({\alpha} ={0}.{7}\), \({\alpha} ={0}.{6}\), and \({\alpha} ={1}\) are drawn. Figure 1 shows three-dimensional graphs of the q-HSATM solution, the exact solution, and the absolute error at \({h} =-{1}\), \({n} ={1}\), \({\alpha} ={1}\), \({\beta} ={1} \). For increasing values of t, the two-dimensional graphs of the numerical solutions to this equation for various values α and the value \({\beta} ={1}\) are depicted in Fig. 2. Figure 2 shows that the temperature \({u}({x}, {t})\) rises as any values of the space variable x and the time variable t increases. It can be seen in Fig. 2 that as the α value approaches one, the temperature \({u}({x}, {t})\) converges. It is shown in Table 1 that the absolute errors of the third-order q-HSATM solution were obtained. Table 1 indicates that the absolute error increases significantly when any values of the space variable x and the value of time t increases. Table 1 demonstrates that while the q-HSATM yields the same results as ATHPM, it yields far more robust results than LTDM.

7 Conclusion

This work investigates the performance of NTFNWSE using q-HSATM. It is imperative to illustrate the influence of the fractional operator incorporated into the model being examined. Furthermore, the MAPLE software has been utilized to construct 2D and 3D graphs that depict the solutions to this equation for different values of α. The variability of the general structure of surface graphs created by the Maple software for Eq. (39) is evident. In addition, MAPLE software was used to obtain the graphs of the numerical solutions of this equation for the various α and \(\beta =1\) values. For NTFNWSE, it is observed that the general structure of surface graphs plotted in Maple software differs. The numerical solutions for NTFNWSE have been quickly and successfully obtained. Therefore, it may be extrapolated that q-HSATM is overly effective and robust for obtaining numerical solutions for various fractional nonlinear partial differential equations.