Abstract
This paper deals with the numerical treatment of a singularly perturbed unsteady Burger–Huxley equation. We linearize the problem using the Newton–Raphson–Kantorovich approximation method. We discretize the resulting linear problem using the implicit Euler method and specially fitted finite difference method for time and space variables, respectively. We provide the stability and convergence analysis of the method, which is first-order parameter uniform convergent. We present several model examples to illustrate the efficiency of the proposed method. The numerical results depict that the present method is more convergent than some methods available in the literature.
Similar content being viewed by others
1 Introduction
We consider the following unsteady nonlinear singularly perturbed Burger–Huxley equation:
with left boundary \(\Im _{l}= \lbrace (s,t ):s=0,t\in \Im _{t} \rbrace \), initial boundary \(\Im _{i}= \lbrace (s,t ):t=0,s\in \Im _{s} \rbrace \), and right boundary \(\Im _{r}= \lbrace (s,t ):s=1,t\in \Im _{t} \rbrace \), where ε is a small singular perturbation parameter such that \(0 < \varepsilon \ll 1\), \(\alpha \ge 1\), \(\lambda \ge 0\), \(\theta \in (0,1)\), and \(\partial \Im =\Im _{l}\cup \Im _{i}\cup \Im _{r}\), The functions \(\wp _{0}(t)\), \(\wp _{1}(t)\), and \(y_{0}(s) \) are assumed to be sufficiently smooth, bounded, and independent of ε. Equation (1) shows a prototype model for describing the interaction between nonlinear convection effects, reaction mechanisms, and diffusion transport. This equation has many intriguing phenomena such as bursting oscillation [1], population genetics [2], interspike [3], bifurcation, and chaos [4]. Several membrane models based on the dynamics of potassium and sodium ion fluxes can be found in [5].
In [6–16] and references therein, the authors constructed various analytical and numerical methods for the Burger equations. The Burger–Huxley equation, in which the highest order derivative term is affected by a small parameter ε \((0<\varepsilon \ll 1)\), is classified as the singularly perturbed Burger–Huxley equation (SPBHE). The presence of ε and the nonlinearity in the problem lead to severe difficulties in approximating the solution of the problem. For instance, due to the presence of ε, the solution reveals boundary/sharp interior layer(s), and it is tough to find a stable numerical approximation. While solving SPBHE, unless specially designed meshes are used, the presented methods in [6–16] and other standard numerical methods fail to give acceptable results. This limitation of the conventional numerical methods has encouraged researchers to develop robust numerical techniques that perform well enough independently of ε. Kaushik and Sharma [17] investigated problem (1) using the finite difference method (FDM) on the piecewise uniform Shishkin mesh. In [18] a monotone hybrid finite difference operator on a piecewise uniform Shishkin mesh is employed to find the approximate solution for problem (1). An upwind FDM on an adaptive nonuniform grid to find an approximate solution for problem (1) is suggested by Liu et al. [19]. In [20–23] the authors proposed a parameter uniform numerical method based on fitted operator techniques for problem (1).
However, the development of the solution methodologies for problem (1) is at an infant stage. This limitation motivated us to construct a parameter uniform numerical scheme for solving problem (1) based on the fitted operator approach. The proposed method is an ε-uniformly convergent numerical algorithm that does not require a priori knowledge of the location and breadth of the boundary layer(s), which in turn increases the difficulty of finding the free oscillation solution of the problem under consideration. Also, the proposed method requires less computational effort to solve the families of the problem under consideration.
2 A priori estimates for the solution of the continuous problem
Lemma 2.1
(maximum principle)
If \(y\arrowvert _{\partial \Im}\ge 0\) and \((\textit{\pounds}_{\varepsilon} ) y\arrowvert _{\Im}\ge 0\), then \(y\arrowvert _{\overline{\Im}}\ge 0\).
Proof
See [18]. □
Lemma 2.2
(stability estimate)
The solution \(y(s,t)\) of Eq. (1) is bounded, that is,
Proof
See [18]. □
3 Formulation of the numerical scheme
3.1 Quasi-linearization technique
Equation (1) can be rewritten as
where \(g(s, t, y(s, t), \frac{\partial y}{\partial s}(s,t))=-\alpha y \frac{\partial y}{\partial s}+\lambda (1-y ) (y- \theta ) \) is a nonlinear function of s, t, \(y(s,t)\), \(\frac{\partial y}{\partial s}(s,t)\).
To linearize the semilinear term of Eq. (1), we choose a reasonable initial approximation \(y^{0}(s,t) \) for the function \(y(s, t)\) in the term \(g(s, t, y(s, t), \frac{\partial y}{\partial s}(s,t))\) that satisfies both initial and boundary conditions and is obtained by the separation-of-variables method of the homogeneous part of the problem under consideration; it is given by
Now we apply the Newton–Raphson–Kantorovich approximation technique to the nonlinear term \(g(s, t, y(s, t), \frac{\partial y}{\partial s}(s,t))\) of Eq. (2), which can be linearized as
where \(\lbrace y^{(m)} \rbrace ^{\infty}_{m=0}\) is a sequence of approximate solutions of \(g(s, t, y^{(m)}(s, t), \frac{\partial y^{(m)}}{\partial s}(s,t))\).
For simplicity, we denote \({y^{(m+1)}}=\hat{y}\) and substitute Eq. (3) into Eq. (2), which yields
where
3.2 Temporal semidiscretization
Now we apply the implicit Euler method with uniform mesh \(\Im ^{M}_{\tau }= \lbrace j\tau , 0< j\le M, \tau =T/M \rbrace \) to Eq. (4) in temporal variable:
Clearly, the operator \((I+\tau \text{\pounds}^{M}_{\varepsilon} ) \) satisfies the maximum principle, which confirms the stability of the semidiscrete equation (5).
Lemma 3.1
(Local Error Estimate)
The local truncation error estimate \(e_{j+1}=\hat{y}(s,t_{j+1})-\hat{Y}(s,t_{j+1})\) of the solution of Eq. (5) is bounded by
and the global error estimate in the temporal direction is given by
where C is a positive constant independent of ε and τ.
Proof
See [23]. □
Lemma 3.2
The derivative of the solution \(Y^{j+1}(s)\) of Eq. (5) is bounded by
Proof
See [18]. □
Rewrite Eq. (5) as
where
3.3 Spatial semidiscretization
In this section, we use the finite difference method for the spatial discretization of problem (6) with a uniform step size. For right boundary layer problem, by the theory of singular perturbations [24] the asymptotic solution of the zeroth-order approximation for problem (6) is given as
where \(Y^{j+1}_{0}(s)\) is the solution of the reduced problem
Taking the first terms in Taylor’s series expansion for \(\gamma (s)\) about the point 1, Eq. (7) becomes
Now we divide the interval \([0, 1]\) into N equal parts with \(\ell =1/N\) yielding a space mesh \(\Im ^{N}_{s}= \lbrace 0 = s_{0}, s_{1}, s_{2},\dots , s_{N} = 1 \rbrace \). Then we have \(s_{i}=i\ell \), \(i=0,1,2,\dots ,N\). By considering Eq. (8) at \(s_{i} = i\ell \) as \(\ell \rightarrow 0\) we obtain
where \(\rho =\frac{\ell}{\varepsilon ^{2}}\).
Let \(Y^{j+1}(s)\) be a smooth function in the interval \([0, 1]\). Then by applying Taylor’s series we have
and
Adding Eq. (10) and Eq. (11), we get
and
Substituting \(\frac{\ell ^{4}}{12}\frac{d^{6}Y^{j+1}_{i}}{ds^{6}}\) from Eq. (13) into Eq. (12), we obtain
where \(R=\frac{\ell ^{4}}{20}\frac{d^{4}Y^{j+1}_{i}}{ds^{4}}- \frac{13\ell ^{6}}{302400}\frac{d^{8}Y^{j+1}_{i}}{ds^{8}}+O(\ell ^{(10)})\).
Now from Eq. (6) we have
where we approximate \(\frac{dY^{j+1}_{i-1}}{ds}\), \(\frac{dY^{j+1}_{i}}{ds} \), and \(\frac{dY^{j+1}_{i+1}}{ds}\) using nonsymmetric finite differences [25]:
Substituting Eq. (16) into Eq. (15), we obtain
Inserting Eq. (17) into Eq. (14) and rearranging, we get
Introducing a constant fitting factor \(\sigma (\rho )\) in Eq. (18), we obtain
Multiplying (19) by ℓ and taking the limit as \(\ell \rightarrow 0\), we get
Using Eq. (9), we have
Using the above expressions in Eq. (20), we get
On simplifying, we get
which is the required value of the constant fitting factor \(\sigma (\rho )\). Finally, using Eq. (19) and the value of \(\sigma (\rho )\) given by Eq. (21), we get
where
For sufficiently small mesh sizes, the above matrix is nonsingular, and \(\vert \chi ^{c}_{i} \vert \ge \vert \chi ^{c}_{i} \vert + \vert \chi ^{+}_{i} \vert \). Hence by [26] the matrix χ is an M-matrix and has an inverse. Therefore Eq. (22) can be solved by the matrix inverse with given boundary conditions.
4 Convergence analysis
Lemma 4.1
If \(Y_{i}^{j+1} \ge 0\) on \(i=0,N\) and \(\textit{\pounds}^{N,M}Y_{i}^{j+1}\ge 0\) on \(\overline{\Im}^{N,M}\), then \(Y_{i}^{j+1}\ge 0\) at each point of \(\overline{\Im}^{N,M}\).
Lemma 4.2
The solution \(Y^{j+1}_{i}\) of the discrete scheme in (22) on \(\overline{\Im}^{N,M}\) satisfies the following bound:
where \(Q(s_{i})\ge Q^{*}>0\).
Hence Lemma 4.2 confirms that the discrete scheme (22) is uniformly stable in supremum norm.
Lemma 4.3
If \(Y\in C^{3}(I)\), then the local truncation error in space discretization is given as
Proof
By definition
Using relation (22) with \(W=\frac{\gamma (0)}{2}\coth (\frac{\gamma (1)\rho}{2} ) \), we get
Thus we obtain the desired result. □
Lemma 4.4
Let \(Y(s_{i},t_{j+1})\) be the solution of problem (6), and let \(Y^{j+1}_{i}\) be the solution of the discrete problem (22). Then we have the following estimate:
Proof
Rewrite Eq. (22) in matrix vector form as
where \(Z = ( \chi _{i,j} ) \), \(0\le j\le M-1\), \(1 \le i \le N-1 \), is the tridiagonal matrix with
and \(H = (\mu ^{j+1}_{i})\) is the column vector with \((\mu ^{j+1}_{i})=\frac{1}{30} ( \vartheta ^{j+1}_{i-1}+28 \vartheta ^{j+1}_{i}+\vartheta ^{j+1}_{i+1} ) \), \(i =1,2,\dots ,N-1\), with local truncation error
We also have
where \(\overline{Y}= ( \overline{Y}_{0},\overline{Y}_{1},\dots , \overline{Y}_{N} ) ^{t}\) and \(\top (\ell )= (\top _{1}(\ell ),\top _{2}(\ell ),\dots ,\top _{N}( \ell ) )^{t} \) are the actual solution and the local truncation error, respectively.
From Eqs. (23) and (24) we get
Then Eq. (25) can be written as
where \(E=\overline{Y}-Y= ( \top _{0},\top _{1},\top _{2},\dots ,\top _{N} )^{t} \). Let S be the sum of elements of the ith row of Z. Then we have
where \(B_{i0}=\Gamma _{i}=\frac{1}{30} ( \vartheta ^{j+1}_{i-1}+28 \vartheta ^{j+1}_{i}+\vartheta ^{j+1}_{i+1} )\).
Since \(0<\varepsilon \ll 1\), for sufficiently small ℓ, the matrix Y is irreducible and monotone. Then it follows that \(Z^{-1}\) exists and its elements are nonnegative [27]. Hence from Eq. (26) we obtain
and
Let \(\overline{\chi}_{ki}\) be the \(( ki )\)th element of \(Z^{-1}\). Since \(\overline{\chi}_{ki}\ge 0\), by the definition of multiplication of matrices with its inverses we have
Therefore it follows that
for some i0 between 1 and \(N-1\), and \(B_{i0}=\Gamma _{i}\). From equations (23), (27), and (28) we obtain
which implies
Therefore
This implies that the spatial semidiscretization process is convergent of second order. □
Theorem 4.5
Let \(y(s,t)\) be the solution of problem (1), and let \(Y^{j}_{i}\) be the numerical solution obtained by the proposed scheme (22). Then we have the following error estimate for the totally discrete scheme:
Proof
By combining the result of Lemmas 3.1 and 4.4 we obtain the required bound. □
5 Numerical examples, results, and discussion
In this section, we consider three model problems to verify the theoretical findings of the proposed method. As the exact solutions of the considered examples are not known, we calculate the maximum absolute error for each ε given in [28] by
and the corresponding order of convergence for each ε by
For all N and τ, the ε-uniform maximum error and the corresponding ε-uniform order of convergence are calculated using
Example 5.1
Consider the following SPBHE:
Example 5.2
Consider the following SPBHE:
Example 5.3
Consider the following SPBHE:
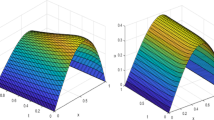
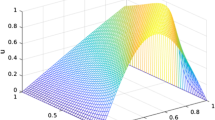
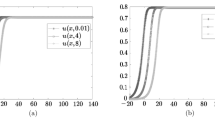
The \(E^{N,\tau}_{\varepsilon} \) \(E^{N,\tau} \), and \(r^{N,\tau} \) for Examples 5.1, 5.2,and 5.3 are tabulated for various values of ε, M, and N in Tables 1–4. These results show that the proposed scheme reveals the parameter uniform convergence of first order. Besides, the numerical results depict that the proposed method gives better results than those in [17–19, 23]. The 3D view of the numerical solution of Examples 5.1 and 5.2 at \(N=64\), \(M=40\), and \(\varepsilon =2^{-18}\) are plotted in Fig. 1. The effects of ε and the time step on the solution profile for the considered problems are displayed in Figs. 2 and 3, respectively. The log-log plots of maximum absolute errors for Examples 5.1–5.3 are plotted in Fig. 4. This figure shows that the obtained theoretical rate of convergence of the proposed method agrees with numerical experiments.
6 Conclusion
We have presented a parameter uniform numerical scheme for the singularly perturbed unsteady Burger–Huxley equation. The developed scheme constitutes the implicit Euler in the time direction and specially fitted finite difference method in the space direction. Theoretical and numerical stability and parameter uniform convergence analysis of the developed scheme is presented. The presented method is shown to be ε-uniformly convergent with convergence order \(O(\tau + \ell ^{2})\). Several model examples are presented to illustrate the efficiency of the proposed method. The proposed scheme gives more accurate numerical results than those in [17–19, 23].
Availability of data and materials
There are no associated data arising from this work.
Abbreviations
- FDM:
-
Finite difference method
References
Duan, L., Lu, Q.: Bursting oscillations near codimension-two bifurcations in the Chay neuron model. Int. J. Nonlinear Sci. Numer. Simul. 7(1), 59–64 (2006)
Aronson, D.G., Weinberger, H.F.: Multidimensional nonlinear diffusion arising in population genetics. Adv. Math. 30(1), 33–76 (1978)
Liu, S., Fan, T., Lu, Q.: The spike order of the winnerless competition (WLC) model and its application to the inhibition neural system. Int. J. Nonlinear Sci. Numer. Simul. 6(2), 133–138 (2005)
Zhang, G.-J., Xu, J.-X., Yao, H., Wei, R.-X.: Mechanism of bifurcation-dependent coherence resonance of an excitable neuron model. Int. J. Nonlinear Sci. Numer. Simul. 7(4), 447–450 (2006)
Lewis, E., Reiss, R., Hamilton, H., Harmon, L., Hoyle, G., Kennedy, D.: An electronic model of the neuron based on the dynamics of potassium and sodium ion fluxes. In: Neural Theory and Modeling, pp. 154–189 (1964)
Ismail, H.N., Raslan, K., Abd Rabboh, A.A.: Adomian decomposition method for Burger’s–Huxley and Burger’s–Fisher equations. Appl. Math. Comput. 159(1), 291–301 (2004)
Javidi, M., Golbabai, A.: A new domain decomposition algorithm for generalized Burger’s–Huxley equation based on Chebyshev polynomials and preconditioning. Chaos Solitons Fractals 39(2), 849–857 (2009)
Estevez, P.: Non-classical symmetries and the singular manifold method: the Burgers and the Burgers–Huxley equations. J. Phys. A, Math. Gen. 27(6), 2113 (1994)
Krisnangkura, M., Chinviriyasit, S., Chinviriyasit, W.: Analytic study of the generalized Burger’s–Huxley equation by hyperbolic tangent method. Appl. Math. Comput. 218(22), 10843–10847 (2012)
Satsuma, J., Ablowitz, M., Fuchssteiner, B., Kruskal, M.: Topics in soliton theory and exactly solvable nonlinear equations. Phys. Rev. Lett. (1987)
Wang, X., Zhu, Z., Lu, Y.: Solitary wave solutions of the generalised Burgers–Huxley equation. J. Phys. A, Math. Gen. 23(3), 271 (1990)
Hashim, I., Noorani, M.S.M., Al-Hadidi, M.S.: Solving the generalized Burgers–Huxley equation using the Adomian decomposition method. Math. Comput. Model. 43(11–12), 1404–1411 (2006)
Hashim, I., Noorani, M., Batiha, B.: A note on the Adomian decomposition method for the generalized Huxley equation. Appl. Math. Comput. 181(2), 1439–1445 (2006)
Khattak, A.J.: A computational meshless method for the generalized Burger’s–Huxley equation. Appl. Math. Model. 33(9), 3718–3729 (2009)
Mohammadi, R.: B-spline collocation algorithm for numerical solution of the generalized Burger’s–Huxley equation. Numer. Methods Partial Differ. Equ. 29(4), 1173–1191 (2013)
Sari, M., Gürarslan, G.: Numerical solutions of the generalized Burgers-Huxley equation by a differential quadrature method. Math. Probl. Eng. 2009, Article ID 370765 (2009)
Kaushik, A., Sharma, M.: A uniformly convergent numerical method on non-uniform mesh for singularly perturbed unsteady Burger–Huxley equation. Appl. Math. Comput. 195(2), 688–706 (2008)
Gupta, V., Kadalbajoo, M.K.: A singular perturbation approach to solve Burgers–Huxley equation via monotone finite difference scheme on layer-adaptive mesh. Commun. Nonlinear Sci. Numer. Simul. 16(4), 1825–1844 (2011)
Liu, L.-B., Liang, Y., Zhang, J., Bao, X.: A robust adaptive grid method for singularly perturbed Burger–Huxley equations. Electron. Res. Arch. 28(4), 1439 (2020)
Kabeto, M.J., Duressa, G.F.: Accelerated nonstandard finite difference method for singularly perturbed Burger–Huxley equations. BMC Res. Notes 14(1), 446, 1–7 (2021)
Jima, K.M., File, D.G.: Implicit finite difference scheme for singularly perturbed Burger–Huxley equations. J. Partial Differ. Equ. 35, 87–100 (2022)
Derzie, E.B., Munyakazi, J.B., Dinka, T.G.: Parameter-uniform fitted operator method for singularly perturbed Burgers–Huxley equation. J. Math. Model., 1–20 (2022). https://doi.org/10.22124/jmm.2022.21484.1883
Daba, I.T., Duressa, G.F.: Uniformly convergent computational method for singularly perturbed unsteady Burger–Huxley equation. MethodsX 9, 101886 (2022)
O’Malley, R.E.: Singular Perturbation Methods for Ordinary Differential Equations. Applied Mathematical Sciences, vol. 89. Springer, Berlin (1991)
Ranjan, R., Prasad, H.S.: A novel approach for the numerical approximation to the solution of singularly perturbed differential-difference equations with small shifts. J. Appl. Math. Comput. 65(1), 403–427 (2018)
Nichols, N.K.: On the numerical integration of a class of singular perturbation problems. J. Optim. Theory Appl. 60(3), 2050034 (1989)
File, G., Reddy, Y.N.: Terminal boundary-value technique for solving singularly perturbed delay differential equations. J. Taibah Univ. Sci. 8(3), 289–300 (2014)
Daba, I.T., Duressa, G.F.: Collocation method using artificial viscosity for time dependent singularly perturbed differential–difference equations. Math. Comput. Simul. 192, 201–220 (2022)
Acknowledgements
The authors would like to thank the anonymous referees for their helpful comments, which improved the quality of this paper.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
Conceptualization: I.T.Daba & G.F. Duressa; Investigation and formal analysis: I.T.Daba & G.F. Duressa; Software programming: I.T.Daba; Visualization: I.T.Daba & G.F. Duressa; Writing- original draft: I.T.Daba; Writing- review & editing: G.F. Duressa.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Daba, I.T., Duressa, G.F. Fitted numerical method for singularly perturbed Burger–Huxley equation. Bound Value Probl 2022, 102 (2022). https://doi.org/10.1186/s13661-022-01681-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-022-01681-3