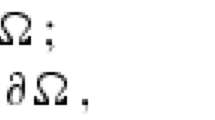1 Introduction

The \((p,q)\)-Laplacian comes from a general reaction-diffusion system that has a wide spectrum of applications in physics and related sciences such as biophysics, plasma physics, solid-state physics, fractional quantum mechanics in the study of particles on stochastic fields, fractional superdiffusion and fractional white-noise limit, etc. (see [1, 5–7, 23–25, 31, 32] and the references therein).

Recently, Motreanu [20] proved the existence of solutions (generalized and weak) for

$$ \textstyle\begin{cases} -\operatorname{div} ( \vert \nabla u \vert ^{p-2}\nabla u-\mu \vert \nabla u \vert ^{q-2}\nabla u )=f(x,\rho \star u,\nabla (\rho \star u))&\text{in } \Omega , \\ u=0&\text{on } \partial \Omega , \end{cases} $$

under suitable condition of f and ρ, where he overcame the lack of ellipticity.

Here, with the inspiration of [20], the multiplicity of nontrivial solutions for the nonstandard Dirichlet problem with an anisotropic competing \((p, q)\)-Laplacian

$$ \textstyle\begin{cases} -\overset{N}{\underset{i=1}{\sum}}\frac{\partial }{\partial x_{i}} ( \vert \frac{\partial u}{\partial x_{i}} \vert ^{p_{i}-2}- \mu \vert \frac{\partial u}{\partial x_{i}} \vert ^{q_{i}-2} ) \frac{\partial u}{\partial x_{i}} =f(x, \phi \star u,\nabla (\phi \star u))&\text{in } \Omega , \\ u=0&\text{on } \partial \Omega , \end{cases} $$
(1.1)

is proved, where Ω is a bounded smooth domain in \(\mathbb{R}^{N}\), \(N\geq 3\), with a Lipschitz boundary ∂Ω, \(f:\Omega \times \mathbb{R}\times \mathbb{R}^{N}\to \mathbb{R}\) is a Carathéodory function, \(\phi \in L^{1}(\mathbb{R}^{N})\), \(u\in W_{0}^{1,\overrightarrow{p}}(\Omega )\), and the convolution \(\phi \star u(x)\) is defined by

$$ \phi \star u(x):= \int _{\mathbb{R}^{N}}\phi (x-y)u(y)\,dy\quad \text{for a.e. } x\in \mathbb{R}^{N}. $$

We set \(\overrightarrow{p}:=(p_{1},\ldots , p_{N})\) and \(\overrightarrow{q}:=(q_{1},\ldots , q_{N})\) where

$$ \begin{aligned} &1< p_{1}, p_{2},\ldots ,p_{N}, \quad \sum^{N}_{i=1} \frac{1}{p_{i}}>1, \\ &1< q_{1}, q_{2}, \ldots , q_{N}, \quad \sum ^{N}_{i=1}\frac{1}{q_{i}}>1. \end{aligned} $$

Let p̅ and q̅ denote the harmonic means \(\overline{p}= N/ (\sum^{N}_{i=1}\frac{1}{p_{i}} )\) and \(\overline{q}= N/ (\sum^{N}_{i=1}\frac{1}{q_{i}} )\), respectively, and define

$$\begin{aligned}& p^{\star }:=\frac{N}{ (\sum^{N}_{i=1}\frac{1}{p_{i}} )-1}= \frac{N\overline{p}}{N-\overline{p}},\qquad q^{\star }:= \frac{N}{ (\sum^{N}_{i=1}\frac{1}{q_{i}} )-1}= \frac{N\overline{q}}{N-\overline{q}}, \\& p_{\infty}:=\max \bigl\{ p_{+},p^{\star }\bigr\} \quad \text{and}\quad p_{+}:=\max \{p_{i}: i=1,\ldots , N\}. \end{aligned}$$

We define an order as follows:

$$ \overrightarrow{q}\leq \overrightarrow{p} \quad \text{if and only if}\quad q_{i}\leq p_{i}\quad \text{for all } i=1,\ldots , N. $$
(1.2)

Throughout the paper, we assume that

$$ \overrightarrow{q}\leq \overrightarrow{p},\qquad q_{N} < q^{\star },\qquad p_{N}< p^{ \star }\quad \text{and}\quad q^{\star }< p^{\star }. $$
(1.3)

Also, we assume

\((H_{1})\):

\(|f(x,t,\xi )|\leq \sigma (x)+c_{1}|t|^{p^{+}-1}+c_{2} \overset{N}{\underset{i=1}{\sum}}|\xi _{i}|^{p_{i}-1}\) for a.e. \(x\in \Omega \) and for all \((t,\xi )\in \mathbb{R}\times \mathbb{R}^{N}\), where \(\xi =(\xi _{1},\ldots ,\xi _{N})\), \(\sigma \in L^{\gamma '}(\Omega )\) for \(\gamma \in (1,p^{+})\), \(\gamma '=\frac{\gamma}{\gamma -1}\) and constants \(c_{1}\geq 0\), \(c_{2}\geq 0\), satisfying

$$ \Vert \phi \Vert _{L^{1}(\mathbb{R}^{N})}^{p^{+}-1} c_{1}S_{p^{+}}+c_{2}\Pi < 1, $$
(1.4)

where \(\Pi =\max_{1\leq i\leq N}\{S^{\prime}_{p_{i}}\|\phi \|^{p_{i}-1}_{L^{1}( \mathbb{R}^{N})}\}\) and \(S^{\prime}_{p_{i}}\) is the Sobolev constant for the embedding \(W_{0}^{1,p_{i}}(\Omega )\subset L^{p_{i}}(\Omega )\) for \(i=1,\ldots , N\).

The differential operator in (1.1), i.e.,

$$ u\to \overset{N}{\underset{i=1}{\sum}} \frac{\partial }{\partial x_{i}} \biggl( \biggl\vert \frac{\partial u}{\partial x_{i}} \biggr\vert ^{p_{i}-2}-\mu \biggl\vert \frac{\partial u}{\partial x_{i}} \biggr\vert ^{q_{i}-2} \biggr) \frac{\partial u}{\partial x_{i}} $$

is the difference of the anisotropic degenerated p-Laplacian and q-Laplacian. In fact, the negative anisotropic ϱ-Laplacian (for \(\varrho =p,q\))

$$ -\Delta _{\overrightarrow{\varrho}}: W_{0}^{1, \overrightarrow{\varrho}}(\Omega )\to W^{-1,\overrightarrow{\varrho}^{ \prime}(\Omega )} $$

is expressed as

$$ \langle -\Delta _{\overrightarrow{\varrho}}u,v\rangle = \overset{N}{\underset{i=1}{\sum }} \int _{\Omega} \frac{\partial }{\partial x_{i}} \biggl\vert \frac{\partial u}{\partial x_{i}} \biggr\vert ^{\varrho _{i}-2} \frac{\partial u}{\partial x_{i}}\cdot \frac{\partial v}{\partial x_{i}}\,dx $$

for all \(u,v\in W_{0}^{1,\overrightarrow{\varrho}}(\Omega )\), where \(\overrightarrow{\varrho}:=(\varrho _{1},\ldots ,\varrho _{N})\) and \(\overrightarrow{\varrho}^{\prime}:=( \frac{\varrho _{1}}{\varrho _{1}-1},\ldots , \frac{\varrho _{N}}{\varrho _{N}-1})\).

Since \(1< q_{1}\), \(\overrightarrow{q}<\overrightarrow{p}\), \(p_{N}<\infty \), the continuous embedding \(W_{0}^{1,\overrightarrow{p}}(\Omega )\hookrightarrow W_{0}^{1, \overrightarrow{q}}(\Omega )\) holds and the operator \(-\Delta _{\overrightarrow{p}}+\mu \Delta _{\overrightarrow{q}}\) is well defined on \(W_{0}^{1,\overrightarrow{p}}(\Omega )\).

The sign of \(-\Delta _{\overrightarrow{p}}+\mu \Delta _{\overrightarrow{q}}\) for \(\mu >0\) and sufficiently large is different from \(\mu >0\) and sufficiently small. This makes it difficult to study (1.1). We owe essential ideas to [20] to overcome the lack of ellipticity, monotonicity, and variational structure in problem (1.1) (see [18–20, 22]). Therefore, for problem (1.1), the existence of a solution is proved by Theorem 1.1.

Theorem 1.1

Suppose that \((H_{1})\) holds. Then, there exists a generalized solution to problem (1.1). In particular, if \(\mu \leq 0\), there exists a weak solution to problem (1.1).

The rest of the paper is organized as follows: In Sect. 2, the suitable function spaces and some lemmas are recalled. In Sect. 3, the associated Nemytskij operator is introduced and then we show the anisotropic competing \((p,q)\)-Laplacian (1.1) has a solution, i.e., the proof of Theorem 1.1 is presented.

2 Function space

Consider the anisotropic Sobolev spaces \(W^{1,\overrightarrow{p}}(\Omega )\), with the norm

$$ \Vert u \Vert _{W^{1,\overrightarrow{p}}(\Omega )}:= \int _{\Omega } \bigl\vert u(x) \bigr\vert \,dx+ \sum _{i=1}^{N} \biggl( \int _{\Omega } \biggl\vert \frac{\partial u}{\partial x_{i}} \biggr\vert ^{p_{i}}\,dx \biggr)^{\frac{1}{p_{i}}}, $$

and \(W^{1,\overrightarrow{p}}_{0}(\Omega )\) with the norm

$$ \begin{aligned} \Vert u \Vert _{W^{1,\overrightarrow{p}}_{0}(\Omega )}&:=\sum _{i=1}^{N} \biggl( \int _{\Omega } \biggl\vert \frac{\partial u}{\partial x_{i}} \biggr\vert ^{p_{i}}\,dx \biggr)^{\frac{1}{p_{i}}} \\ &=\sum_{i=1}^{N} \Vert u \Vert _{W^{1,p_{i}}_{0}(\Omega )}. \end{aligned} $$

Note that \(W^{1,\overrightarrow{p}}_{0}(\Omega )\) is a reflexive and uniformly convex Banach space (see [26–28] and references therein for more details or more literature in [2, 4, 8–14, 30]). Here, is an embedding theorem [15, Theorem 1].

Theorem 2.1

Let \(\Omega \subset \mathbb{R}^{N}\) be an open bounded domain with Lipschitz boundary. If

$$ p_{i}>1, \quad \textit{for all } i=1,\ldots ,N, \qquad \sum _{i=1}^{N} \frac{1}{p_{i}}>1, $$

then for all \(r\in [1,p_{\infty}]\), there is a continuous embedding \(W_{0}^{1,\overrightarrow{p}}(\Omega )\subset L^{r}(\Omega )\). For \(r< p_{\infty}\), the embedding is compact.

Note that the Sobolev space \(W^{1,\overrightarrow{p}}_{0}(\Omega )\) is embedded in \(W^{1,\overrightarrow{p}}(\mathbb{R}^{N})\) by identifying every \(u\in W^{1,\overrightarrow{p}}_{0}(\Omega )\) with its extension equal to zero outside Ω. Thus, one can define the convolution \(\phi \star u\) of \(\phi \in L^{1}(\mathbb{R}^{N})\) with \(u\in W^{1,\overrightarrow{p}}_{0} (\Omega )\) (see [3, Sect. 4.4 and Sect. 9.1]) by

$$ \phi \star u(x)= \int _{\mathbb{R}^{N}}\phi (x-y)u(y)\,dy\quad \text{for a.e. } x\in \mathbb{R}^{N}. $$

Also,

$$ \frac{\partial}{\partial x_{i}}(\phi \star u) =\phi \star \frac{\partial u}{\partial x_{i}}\in L^{p_{i}}\bigl(\mathbb{R}^{N}\bigr), \text{for all} i=1,2,\ldots , N. $$

Remark 2.2

Assume \(\phi \in L^{1}(\mathbb{R}^{N})\) with \(u\in W^{1,\overrightarrow{p}}_{0} (\Omega )\), then

  1. (i)
    $$ \Vert \phi \star u \Vert _{L^{r}(\mathbb{R}^{N})}\leq \Vert \phi \Vert _{L^{1}( \mathbb{R}^{N})} \Vert u \Vert _{L^{r}(\Omega )} $$
    (2.1)

    whenever \(r\in [1,p^{\star }]\);

  2. (ii)
    $$ \biggl\Vert \phi \star \frac{\partial u}{\partial x_{i}} \biggr\Vert _{L^{p_{i}}( \mathbb{R}^{N})}\leq \Vert \phi \Vert _{L^{1}(\mathbb{R}^{N})} \biggl\Vert \frac{\partial u}{\partial x_{i}} \biggr\Vert _{L^{p_{i}}(\Omega )} $$
    (2.2)

    for all \(i=1,\ldots , N\);

  3. (iii)

    By (2.2), we have

    $$ \begin{aligned} \Vert \phi \star u \Vert _{W_{0}^{1\overrightarrow{p}}(\mathbb{R}^{N})}={}& \sum_{i=1}^{N} \biggl( \int _{\mathbb{R}^{N}} \biggl\vert \frac{\partial (\phi \star u)}{\partial x_{i}} \biggr\vert ^{p_{i}}\,dx \biggr)^{ \frac{1}{p_{i}}} \\ ={}& \sum_{i=1}^{N} \biggl\Vert \frac{\partial (\phi \star u)}{\partial x_{i}} \biggr\Vert _{L^{p_{i}}( \mathbb{R}^{N})} \\ \leq {}& \sum_{i=1}^{N} \Vert \phi \Vert _{L^{1}(\mathbb{R}^{N})} \biggl\Vert \frac{\partial u}{\partial x_{i}} \biggr\Vert _{L^{p_{i}}(\mathbb{R}^{N})} \\ = {}& \Vert \phi \Vert _{L^{1}(\mathbb{R}^{N})}\sum_{i=1}^{N} \biggl\Vert \frac{\partial u}{\partial x_{i}} \biggr\Vert _{L^{p_{i}}(\mathbb{R}^{N})} \\ ={}& \Vert \phi \Vert _{L^{1}(\mathbb{R}^{N})} \Vert u \Vert _{W_{0}^{1\overrightarrow{p}}( \mathbb{R}^{N})}. \end{aligned} $$
    (2.3)

Before ending this section we require a generalized solution for (1.1).

Definition 2.3

A function \(u\in W^{1,\overrightarrow{p}}_{0}(\Omega )\) is called a generalized solution to problem (1.1) if there exists a sequence \(\{u_{n}\}_{n\geq 1}\) in \(W^{1,\overrightarrow{p}}_{0}(\Omega )\) such that

  1. (I)

    \(u_{n}\rightharpoonup u\) in \(W^{1,\overrightarrow{p}}_{0}(\Omega )\) as \(n\to \infty \);

  2. (II)

    \(-\Delta _{\overrightarrow{p}}u_{n}+\mu \Delta _{\overrightarrow{q}}u_{n}-f (\cdot , \phi \star u_{n}(\cdot ),\nabla (\phi \star \nabla u)(\cdot )) \rightharpoonup 0\) in \(W^{-1,\overrightarrow{p}^{\prime}}(\Omega )\) as \(n\to \infty \);

  3. (III)

    \(\lim_{n\to \infty}\langle -\Delta _{\overrightarrow{p}}u_{n}+ \mu \Delta _{\overrightarrow{q}}u_{n}, u_{n}-u\rangle =0\).

Remark 2.4

Assume u is a weak solution of (1.1), i.e., u satisfies

$$ \bigl\langle (-\Delta _{\overrightarrow{p}}+\mu \Delta _{ \overrightarrow{q}} ) (u),v\bigr\rangle _{W_{0}^{1,\overrightarrow{p}}( \Omega )}= \int _{\Omega }f\bigl(x,\phi \star u(x),\nabla \bigl(\phi \star u(x) \bigr)\bigr)v(x)\,dx $$

for all \(v\in W^{1,\overrightarrow{p}}_{0}(\Omega )\). Set \(u_{n} = u\) for all n, then any weak solution is a generalized solution to problem (1.1).

3 Weak and generalized solutions

Here, we study the behavior of the Nemytskij operator and construct a sequence (by the Galerkin basis of the space) that converges strongly to the generalized (weak) solution of (1.1) when \(\mu \geq 0\) (\(\mu <0\)). First, we recall an embedding result.

Since \(\overrightarrow{q}<\overrightarrow{p}\) and Ω is bounded then

$$ \begin{aligned} & W_{0}^{1\overrightarrow{p}}(\Omega )\quad \text{is continuously embedded in } W_{0}^{1\overrightarrow{q}}( \Omega ) \quad \text{and } \\ &W^{-1,\overrightarrow{q}^{\prime}}(\Omega )\quad \text{is continuously embedded in } W^{-1,\overrightarrow{p}^{\prime}}( \Omega ). \end{aligned} $$
(3.1)

Assume the operator \(A: W_{0}^{1,\overrightarrow{p}}(\Omega )\to W^{-1,\overrightarrow{p}^{ \prime}}(\Omega ) \) (see (1.1)) is defined by

$$ \bigl\langle A(u),v\bigr\rangle =\langle -\Delta _{\overrightarrow{p}}u+\mu \Delta _{\overrightarrow{q}}u,v\rangle - \int _{\Omega}f\bigl(x, \phi \star u(x), \nabla (\phi \star u) (x) \bigr)v(x)\,dx. $$
(3.2)

Lemma 3.1

The operator A defined by (3.2) is continuous, when (\(H_{1}\)) holds.

Proof

Define the operator

$$ T: W_{0}^{1,\overrightarrow{p}}(\Omega )\to L^{p^{+}}(\Omega )\times L^{p_{1}}( \Omega )\times \cdots \times L^{p_{N}}(\Omega ) $$

by \(T(u)=(\phi \star u |_{\Omega}, \nabla (\phi \star u) |_{ \Omega})\). Relations (2.1) and (2.3) imply that T is linear and continuous. By (\(H_{1}\)) and Krasnoselskii’s theorem [16], the Nemytskii operator

$$ \begin{aligned} \mathcal{N}:{}&L^{p^{+}}(\Omega )\times \bigl(L^{{p_{1}}}( \Omega )\times \cdots \times L^{{p_{N}}}(\Omega ) \bigr)\to L^{{p^{+}}^{ \prime}}(\Omega ) \\ &{}(v,,w_{1},\ldots ,w_{N})\mapsto f\bigl(\cdot ,v(\cdot ),w_{1}(\cdot ), \ldots ,w_{N}(\cdot )\bigr) \end{aligned} $$

is well defined and continuous and so the composition operator

$$ W_{0}^{1,\overrightarrow{p}}(\Omega )\to L^{{p^{+}}^{\prime}}( \Omega ), \qquad u\mapsto f\bigl(\cdot ,\phi \star u(\cdot ),\nabla (\phi \star u) ( \cdot )\bigr) $$
(3.3)

is continuous. Note that \(L^{{p^{+}}^{\prime}}(\Omega )\) is continuously embedded in \(W^{-1,{p^{+}}^{\prime}}(\Omega )\).

The operator \(-\Delta _{\overrightarrow{\varrho}}: W_{0}^{1, \overrightarrow{\varrho}}(\Omega )\to W^{-1,\overrightarrow{\varrho}^{ \prime}}(\Omega ) \) (for \(\varrho =p,q\)) is continuous. Therefore, embedding (3.1) implies \(-\Delta _{\overrightarrow{p}}+\mu \Delta _{\overrightarrow{q}}: W_{0}^{1 \overrightarrow{p}}(\Omega )\to W^{-1,\overrightarrow{p}^{\prime}}( \Omega ) \) is continuous and finally the operator A is continuous. □

Assume \(\{X_{n}\}\) (vector subspaces of \(W_{0}^{1,\overrightarrow{p}}(\Omega )\)) is a Galerkin basis for the separable Banach space \(W_{0}^{1,\overrightarrow{p}}(\Omega )\), i.e.,

  1. (i)

    \(\dim (X_{n})<\infty \), for all n;

  2. (ii)

    \(X_{n}\subset X_{n+1}\), for all n;

  3. (iii)

    \(\overline{\underset{n}{\cup}X_{n}}=W_{0}^{1,\overrightarrow{p}}( \Omega )\).

A consequence of Brouwer’s fixed-point theorem will resolve each approximate problem on \(X_{n}\). Due to this, we construct a sequence \(\{u_{n}\}\) by the next Proposition.

Proposition 3.2

Assume (\(H_{1}\)) holds. Then, for each \(n\geq 1\) there exists \(u_{n}\in X_{n}\) such that

$$ \begin{aligned} \bigl\langle (-\Delta _{\overrightarrow{p}}+ \mu \Delta _{ \overrightarrow{q}} ) (u_{n}),v\bigr\rangle _{W_{0}^{1, \overrightarrow{p}}(\Omega )} = \int _{\Omega }f\bigl(x,\phi \star u_{n}(x), \nabla \bigl(\phi \star u_{n}(x)\bigr)\bigr)v(x)\,dx \end{aligned} $$
(3.4)

for all \(v\in X_{n}\). In addition, \(\{u_{n}\}_{n\geq 1}\) is bounded in \(W_{0}^{1,\overrightarrow{p}}(\Omega )\).

Proof

We define \(A_{n}:X_{n}\to X_{n}^{\star }\) by

$$ \begin{aligned} &\bigl\langle A_{n}(u),v\bigr\rangle _{X_{n}} \\ &\quad =\bigl\langle (-\Delta _{\overrightarrow{p}}+\mu \Delta _{ \overrightarrow{q}} ) (u),v\bigr\rangle _{W_{0}^{1,\overrightarrow{p}}( \Omega )}- \int _{\Omega }f\bigl(x,\phi \star u(x),\nabla \bigl(\phi \star u(x) \bigr)\bigr)v(x)\,dx \end{aligned} $$

for all \(u,v\in X_{n}\) and all \(n\in \mathbb{N}\). The operator \(A_{n}\) is continuous (by Lemma 3.1) and

$$ \begin{aligned} &\bigl\langle A_{n}(v),v\bigr\rangle _{X_{n}} \\ &\quad =\overset{N}{\underset{i=1}{\sum}} \int _{\Omega } \biggl( \biggl\vert \frac{\partial v}{\partial x_{i}} \biggr\vert ^{p_{i}}-\mu \biggl\vert \frac{\partial v}{\partial x_{i}} \biggr\vert ^{q_{i}} \biggr)\,dx - \int _{ \Omega }f\bigl(x,\phi \star v(x),\nabla \bigl(\phi \star v(x) \bigr)\bigr)v(x)\,dx \\ &\quad \geq \overset{N}{\underset{i=1}{\sum}} \Vert v \Vert _{W_{0}^{1,{p_{i}}}( \Omega )}^{p_{i}} -\mu \overset{N}{\underset{i=1}{\sum}} \vert \Omega \vert ^{ \frac{p_{i}-q_{i}}{p_{i}}} \Vert v \Vert _{W_{0}^{1,{p_{i}}}(\Omega )}^{q_{i}}- \Vert \sigma \Vert _{L^{\gamma ^{\prime}}(\Omega )} \Vert v \Vert _{L^{\gamma}(\Omega )} \\ & \qquad {}-c_{1} \Vert \phi \star v \Vert ^{p^{+}-1}_{L^{p^{+}}(\Omega )} \Vert v \Vert _{L^{p^{+}}( \Omega )}-c_{2}\overset{N}{\underset{i=1}{ \sum}} \Vert \phi \star v \Vert _{W_{0}^{1,{p_{i}}}( \Omega )}^{p_{i}-1} \Vert v \Vert _{L^{p_{i}}(\Omega )} \end{aligned} $$

for all \(v\in X_{n}\), by (\(H_{1}\)) and the Hölder inequality. Now (2.1), (2.3), and Sobolev embedding show that

$$\begin{aligned}& \bigl\langle A_{n}(v) ,v\bigr\rangle _{X_{n}} \\& \quad = \overset{N}{\underset{i=1}{\sum}} \int _{\Omega } \biggl( \biggl\vert \frac{\partial v}{\partial x_{i}} \biggr\vert ^{p_{i}}-\mu \biggl\vert \frac{\partial v}{\partial x_{i}} \biggr\vert ^{q_{i}} \biggr)\,dx \\& \qquad {} - \int _{\Omega }f\bigl(x,\phi \star v(x),\nabla \bigl(\phi \star v(x) \bigr)\bigr)v(x)\,dx \\& \quad \geq \overset{N}{\underset{i=1}{\sum}} \Vert v \Vert _{W_{0}^{1,{p_{i}}}( \Omega )}^{p_{i}} -\mu \overset{N}{\underset{i=1}{\sum}} \vert \Omega \vert ^{ \frac{p_{i}-q_{i}}{p_{i}}} \Vert v \Vert _{W_{0}^{1,{p_{i}}}(\Omega )}^{q_{i}}- \Vert \sigma \Vert _{L^{\gamma ^{\prime}}(\Omega )} \Vert v \Vert _{L^{\gamma}(\Omega )} \\& \qquad {} -c_{1} \Vert \phi \Vert ^{p^{+}-1}_{L^{1}(\mathbb{R}^{N})} \Vert v \Vert ^{p^{+}}_{L^{p^{+}}( \Omega )}-c_{2}\overset{N}{ \underset{i=1}{\sum}} \Vert \phi \Vert ^{p_{i}-1}_{L^{1}( \mathbb{R}^{N})} \Vert v \Vert _{W_{0}^{1,{p_{i}}}(\Omega )}^{p_{i}-1} \Vert v \Vert _{L^{p_{i}}( \Omega )} \\& \quad \geq \overset{N}{\underset{i=1}{\sum}} \Vert v \Vert _{W_{0}^{1,{p_{i}}}( \Omega )}^{p_{i}} -\mu \overset{N}{\underset{i=1}{\sum}} \vert \Omega \vert ^{ \frac{p_{i}-q_{i}}{p_{i}}} \Vert v \Vert _{W_{0}^{1,{p_{i}}}(\Omega )}^{q_{i}}-S_{ \gamma} \Vert \sigma \Vert _{L^{\gamma ^{\prime}}(\Omega )} \Vert v \Vert _{W_{0}^{1, \overrightarrow{p}}(\Omega )} \\& \qquad {} -c_{1}S_{p^{+}} \Vert \phi \Vert ^{p^{+}-1}_{L^{1}(\mathbb{R}^{N})} \sum_{i=1}^{N} \Vert v \Vert ^{p_{i}}_{W_{0}^{1,p_{i}}(\Omega )}-c_{2} \overset{N}{\underset{i=1}{\sum }} S'_{p_{i}} \Vert \phi \Vert ^{p_{i}-1}_{L^{1}( \mathbb{R}^{N})} \Vert v \Vert _{W_{0}^{1,{p_{i}}}(\Omega )}^{p_{i}} \\& \quad \geq \overset{N}{\underset{i=1}{\sum}} \Vert v \Vert _{W_{0}^{1,{p_{i}}}( \Omega )}^{p_{i}} -\mu \overset{N}{\underset{i=1}{\sum}} \vert \Omega \vert ^{ \frac{p_{i}-q_{i}}{p_{i}}} \Vert v \Vert _{W_{0}^{1,{p_{i}}}(\Omega )}^{q_{i}}-S_{ \gamma} \Vert \sigma \Vert _{L^{\gamma ^{\prime}}(\Omega )} \Vert v \Vert _{W_{0}^{1, \overrightarrow{p}}(\Omega )} \\& \qquad {} - \bigl( \Vert \phi \Vert _{L^{1}(\mathbb{R}^{N})}^{p^{+}-1} c_{1}S_{p^{+}}+c_{2} \Pi \bigr)\overset{N}{ \underset{i=1}{\sum}} \Vert v \Vert _{W_{0}^{1,{p_{i}}}( \Omega )}^{p_{i}}, \end{aligned}$$
(3.5)

for all \(x\in X_{n}\), where \(|\Omega |\) is the Lebesgue measure of Ω.

Assume \(\lambda _{1,\overrightarrow{p}}>0\) denotes the first eigenvalue of the negative anisotropic p-Laplacian on \(W_{0}^{1,\overrightarrow{p}}(\Omega )\) that is given by

$$ \lambda _{1,\overrightarrow{p}}=\min \biggl\{ \frac{\overset{N}{\underset{i=1}{\sum}}\int _{\Omega} \vert \frac{\partial u}{\partial x_{i}} \vert ^{p_{i}}\,dx}{ \Vert u \Vert _{L^{p^{+}}(\Omega )}^{p^{+}}}: u\in W_{0}^{1,\overrightarrow{p}}(\Omega )\backslash \{0\} \biggr\} . $$
(3.6)

See [15, Theorem 3] or [17, Theorem 2] for more details. By (1.4) (recall that \(S_{p^{+}}=\lambda _{1,\overrightarrow{p}}^{-\frac{1}{p^{+}}}\)) and \(p_{i}>q_{i}>1\) and \(p^{+}>q^{+}>1\), for \(i=1,\ldots ,N\), for \(R = R(n)>0\) sufficiently large we obtain

$$ \bigl\langle A_{n}(v),v\bigr\rangle _{X_{n}}\geq 0\quad \text{whenever } v\in X_{n} \text{ with } \Vert v \Vert _{W_{0}^{1,\overrightarrow{p}}(\Omega )}=R. $$

As a consequence of Brouwer’s fixed-point theorem (see, e.g., [29, p. 37]) (since \(X_{n}\) is a finite-dimensional space) there exists \(u_{n} \in X_{n}\) solving the equation \(A_{n}(u_{n})=0\) and this shows that \(u_{n}\in X_{n}\) is a solution for problem (3.4).

\(\{u_{n}\}_{n\geq 1}\) is bounded in \(W_{0}^{1,\overrightarrow{p}}(\Omega )\). To show this, let \(v=u_{n}\in X_{n}\) in (3.5), then

$$\begin{aligned}& \overset{N}{\underset{i=1}{\sum}} \Vert v \Vert _{W_{0}^{1,{p_{i}}}( \Omega )}^{p_{i}} -c_{1}S_{p^{+}} \Vert \phi \Vert ^{p^{+}-1}_{L^{1}( \mathbb{R}^{N})}\sum_{i=1}^{N} \Vert v \Vert ^{p_{i}}_{W_{0}^{1,p_{i}}(\Omega )} \\& \qquad {} -c_{2}\overset{N}{\underset{i=1}{\sum}} S'_{p_{i}} \Vert \phi \Vert ^{p_{i}-1}_{L^{1}(\mathbb{R}^{N})} \Vert v \Vert _{W_{0}^{1,{p_{i}}}( \Omega )}^{p_{i}} \\& \quad \leq \mu \overset{N}{\underset{i=1}{\sum}} \vert \Omega \vert ^{ \frac{p_{i}-q_{i}}{p_{i}}} \Vert v \Vert _{W_{0}^{1,{p_{i}}}(\Omega )}^{q_{i}}+S_{ \gamma} \Vert \sigma \Vert _{L^{\gamma ^{\prime}}(\Omega )} \Vert v \Vert _{W_{0}^{1, \overrightarrow{p}}(\Omega )}. \end{aligned}$$

Since \(p_{i}>q_{i}>1\) and \(p^{+}>q^{+}>1\), for \(i=1,\ldots ,N\), then (1.4) shows that \(\{u_{n}\}_{n\geq 1}\) is bounded in \(W_{0}^{1,\overrightarrow{p}}(\Omega )\). □

Now, we can prove the existence of the solution of problem (1.1), i.e., we present the proof of Theorem 1.1.

Proof

Assume \(\{u_{n}\}_{n\geq 1}\subset W_{0}^{1,\overrightarrow{p}}(\Omega )\) is given by Proposition 3.2 that is bounded in \(W_{0}^{1,\overrightarrow{p}}(\Omega )\) and the reflexively, there exists a subsequence still denoted by \(\{u_{n}\}_{n\geq 1}\) that is bounded and

$$ u_{n}\rightharpoonup u \quad \text{in } W_{0}^{1,\overrightarrow{p}}( \Omega ) $$
(3.7)

with some \(u\in W_{0}^{1,\overrightarrow{p}}(\Omega )\). The continuity of the operator in (3.3), shows that the sequence \(\{f(\cdot ,\phi \star u_{n},\nabla (\phi \star u_{n}))\}_{n\geq 1}\) is bounded in \(L^{\overrightarrow{p}^{\prime}}\). Suppose

$$ -\Delta _{\overrightarrow{p}}u_{n}+\mu \Delta _{\overrightarrow{q}}u_{n}-f\bigl( \cdot ,\phi \star u_{n},\nabla (\phi \star u_{n})\bigr)\rightharpoonup \eta\quad \text{in } W^{-1,\overrightarrow{p}^{\prime}}(\Omega ) $$
(3.8)

with some \(\eta \in W^{-1,\overrightarrow{p}^{\prime}}(\Omega )\), by the reflexivity of \(W^{-1,\overrightarrow{p}^{\prime}}(\Omega )\).

Assume \(v\in \bigcup_{n\geq 1}X_{n}\). Fix an integer \(m\geq 1\) such that \(v\in X_{m}\). Proposition 3.2 provides that (3.4) holds for all \(n\geq m\). Letting \(n\to \infty \) in (3.4), by means of (3.8) we obtain

$$ \langle \eta ,v\rangle\geq 0 \quad \text{for all} v\in \bigcup _{n\geq 1}X_{n}. $$

By the density of \(\bigcup_{n\geq 1}X_{n}\) in \(W^{1,\overrightarrow{p}}_{0}(\Omega )\) (see (iii) in the definition of the Galerkin basis), it turns out that \(\eta =0\) and so in \(W^{-1,\overrightarrow{p}^{\prime}}(\Omega )\) we have

$$ -\Delta _{\overrightarrow{p}}u_{n}+\mu \Delta _{\overrightarrow{q}}u_{n}-f\bigl( \cdot ,\phi \star u_{n},\nabla (\phi \star u_{n})\bigr)\rightharpoonup 0. $$
(3.9)

Letting \(v=u_{n}\) in (3.4), we obtain

$$ \langle -\Delta _{\overrightarrow{p}}u_{n}+\mu \Delta _{ \overrightarrow{q}}u_{n},u_{n}\rangle - \int _{\Omega }f\bigl( \cdot ,\phi \star u_{n},\nabla ( \phi \star u_{n})\bigr)\,dx=0 $$
(3.10)

for all \(n\geq 1\), while (3.9) gives

$$ \langle -\Delta _{\overrightarrow{p}}u_{n}+\mu \Delta _{ \overrightarrow{q}}u_{n},u_{n}\rangle - \int _{\Omega }f\bigl( \cdot ,\phi \star u_{n},\nabla ( \phi \star u_{n})\bigr)\,dx\to 0 $$
(3.11)

as \(n\to \infty \). Together, (3.10) and (3.11) yield

$$ \langle -\Delta _{\overrightarrow{p}}u_{n}+\mu \Delta _{ \overrightarrow{q}}u_{n},u_{n}-u\rangle - \int _{\Omega }f\bigl( \cdot ,\phi \star u_{n},\nabla ( \phi \star u_{n})\bigr) (u_{n}-u)\,dx\to 0 $$
(3.12)

as \(n\to \infty \). Theorem 2.1 and (3.7) imply that \(u_{n}\to u\) strongly in \(L^{p}(\Omega )\), and since \(\{f(\cdot ,\phi \star u_{n},\nabla (\phi \star u_{n}))\}\) is bounded, then

$$ \lim_{n\to \infty} \int _{\Omega }f\bigl(\cdot ,\phi \star u_{n},\nabla ( \phi \star u_{n})\bigr) (u_{n}-u)\,dx= 0. $$
(3.13)

By inserting (3.13) into (3.12) we obtain

$$ \lim_{n\to \infty}\langle -\Delta _{\overrightarrow{p}}u_{n}+ \mu \Delta _{\overrightarrow{q}}u_{n},u_{n}-u\rangle =0. $$
(3.14)

Thus, the conditions of Definition 2.3 are satisfied and this implies that \(u\in W_{0}^{1,\overrightarrow{p}}(\Omega )\) is a generalized solution to problem (1.1).

Now, we prove the existence of a weak solution in the case \(\mu \leq 0\). Assume u is a generalized solution to problem (1.1) and \(\{u_{n}\}_{n\geq 1}\) satisfy the conditions of Definition 2.3 with respect to u. We obtain

$$ \begin{aligned} &\langle -\Delta _{\overrightarrow{p}}u_{n},u_{n}-u \rangle _{W_{0}^{1,\overrightarrow{p}}(\Omega )} \\ &\quad \leq \langle -\Delta _{\overrightarrow{p}}u_{n},u_{n}-u\rangle _{W_{0}^{1, \overrightarrow{p}}(\Omega )} -\mu \langle -\Delta _{ \overrightarrow{q}}u_{n}+\Delta _{\overrightarrow{q}}u,u_{n}-u \rangle _{W_{0}^{1,\overrightarrow{p}}(\Omega )} \\ &\quad = \langle -\Delta _{\overrightarrow{p}}u_{n}+\mu \Delta _{ \overrightarrow{q}}u_{n},u_{n}-u\rangle _{W_{0}^{1,\overrightarrow{p}}( \Omega )} -\mu \langle \Delta _{\overrightarrow{q}}u,u_{n}-u\rangle _{W_{0}^{1, \overrightarrow{p}}(\Omega )} \end{aligned} $$

by the monotonicity of \(-\Delta _{\overrightarrow{q}}\) and hence,

$$ \limsup_{n\to \infty}\langle \Delta _{\overrightarrow{p}}u_{n},u_{n}-u \rangle _{W_{0}^{1,\overrightarrow{p}}(\Omega )}\leq 0. $$

Then, \(u_{n}\to u\) strongly in \(W^{1,\overrightarrow{p}}(\Omega )\) (see, e.g., [21, Proposition 2.72]). The continuity of A (Lemma 3.1), shows \(A(u_{n})\to A(u)\) in \(W^{-1,\overrightarrow{p}^{\prime}}(\Omega )\) and condition (II) of Definition 2.3, shows \(A(u) = 0\). This shows that

$$ \bigl\langle (-\Delta _{\overrightarrow{p}}+\mu \Delta _{ \overrightarrow{q}} ) (u),v\bigr\rangle _{W_{0}^{1,\overrightarrow{p}}( \Omega )}= \int _{\Omega }f\bigl(x,\phi \star u(x),\nabla \bigl(\phi \star u(x) \bigr)\bigr)v(x)\,dx $$

for all \(v\in W^{1,\overrightarrow{p}}_{0}(\Omega )\), which means u is a weak solution to problem (1.1). □