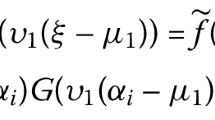Abstract
In this paper, we obtain necessary and sufficient conditions for the oscillation of solutions to a second-order neutral differential equation with impulses. Two examples are provided to show the effectiveness and feasibility of the main results. Our main tool is Lebesgue’s dominated convergence theorem.
Similar content being viewed by others
1 Introduction
Nowadays impulsive differential equations are attracting a lot of attention. They appear in the study of several real world problems (see, for instance, [1, 2, 15]). In general, it is well known that several natural phenomena are driven by differential equations, but the description of some real world problems subjected to sudden changes in their stated became very interesting from the mathematical point of view because they should be described considering systems of differential equations with impulses. Examples of the aforementioned phenomena are related to mechanical systems, biological systems, population dynamics, pharmacokinetics, theoretical physics, biotechnology processes, chemistry, engineering, and control theory.
We also stress that the modeling of these phenomena is suitably formulated by evolutive partial differential equations; moreover, moment problem approaches appear also as a natural instrument in control theory of neutral type systems; see [16, 20, 34] and [13], respectively.
The literature related to impulsive differential equations is very wide. Here we mention some recent developments in this field.
In [28], Shen and Wang considered impulsive differential equations of the following form:
where and for , and obtained sufficient conditions that ensure the oscillation and asymptotic behavior of the solutions of problem (1.1).
In [12], Graef et al. considered the problem
assuming that (that is, \(q(\iota )\) is piecewise continuous in \([\iota _{0},\infty )\)), obtained sufficient conditions for the oscillation of the solutions of problem (1.2).
In [27], Shen and Zou obtained oscillation criteria for first-order impulsive neutral delay differential equations of the form
obtaining sufficient conditions that ensure the oscillation of the solutions of (1.3) under the assumptions that and \(b_{k}\leq \frac{I_{k}(u)}{u}\leq 1\).
Karpuz et al. in [14] extended the results contained in [27] by taking the nonhomogeneous counterpart of system (1.3) with variable delays.
Oscillation and nonoscillation properties for a class of second-order neutral impulsive differential equations with constant coefficients and constant delays were studied by Tripathy and Santra in [30], where the authors considered the problem
Other necessary and sufficient conditions for the oscillation of a class of second-order neutral impulsive systems were established in [32], where Tripathy and Santra studied systems of the form
In [32], in particular, the authors are interested in oscillating systems that, after a perturbation by instantaneous change of state, remain oscillating.
In [26], Santra and Tripathy investigated the oscillatory behavior of the solutions for first-order impulsive neutral delay differential equations of the form
for different values of the neutral coefficient q.
We also mention the paper [24] in which Santra and Dix, using Lebesgue’s dominated convergence theorem, obtained necessary and sufficient conditions for the oscillation of the solutions of the following second-order neutral differential equation with impulses:
where
In line with the contents of [24], Tripathy and Santra in [31] examined oscillation and nonoscillation properties for the solutions of the following class of forced impulsive nonlinear neutral differential systems:
for different values of \(q(\iota )\) and obtained sufficient conditions for the existence of positive bounded solutions of system (1.8).
Finally, we mention the recent work [33] in which Tripathy and Santra obtained some characterizations for the oscillation of solutions of the following second-order neutral impulsive differential system:
where \(w(\iota )=u(\iota )+q(\iota )u(\zeta (\iota ))\) and \(-1< q(\iota )\leq 0\).
For further details on neutral impulsive differential equations and for recent results related to the oscillation theory for ordinary differential equations, we refer the reader to the papers [3–6, 8, 9, 11, 21–23, 25, 29, 35] and to the references therein. In particular, the study of oscillation of half-linear/Emden–Fowler (neutral) differential equations with deviating arguments (delayed or advanced arguments or mixed arguments) has numerous applications in physics and engineering (e.g., half-linear/Emden–Fowler differential equations arise in a variety of real world problems such as in the study of p-Laplace equations, non-Newtonian fluid theory, the turbulent flow of a polytropic gas in a porous medium, and so forth); see, e.g., the papers [7, 10, 16–20] for more details.
Motivated by the aforementioned findings, in this paper we prove necessary and sufficient conditions for the oscillation of solutions to a second-order nonlinear impulsive differential system of the form
where
the functions g, r, r̃, p, q, ν, ζ are continuous and satisfy the conditions stated below; the sequence \(\{\phi _{k}\}\) satisfies \(0<\phi _{1}<\phi _{2}<\cdots <\phi _{k}< \to \infty \) as \(k\to \infty \); and α is the quotient of two positive odd integers.
In this paper we use the following assumptions:
-
(a)
, , \(\nu (\iota )<\iota \), \(\zeta (\iota )<\iota \), \(\lim_{\iota \to \infty}\nu (\iota )=\infty \), \(\lim_{\iota \to \infty}\zeta (\iota )=\infty \).
-
(b)
, , \(\nu (\iota )>\iota \), \(\zeta (\iota )<\iota \), \(\lim_{\iota \to \infty}\zeta (\iota )=\infty \).
-
(c)
, ; \(0< p(\iota )\), \(0\leq r(\iota )\), \(0\leq \tilde{r}(\iota )\) for all \(\iota \geq 0\); \(\sum r(\iota )\) is not identically zero in any interval \([b,\infty )\).
-
(d)
with \(0\leq q(\iota )\leq a<1\);
-
(e)
is nondecreasing and \(g(\iota )\iota >0\) for \(\iota \neq 0\).
-
(f)
\(\lim_{\iota \to \infty}P(\iota )=\infty \), where \(P(\iota )=\int _{0}^{\iota }p^{-1/\alpha}(s) \,\mathrm{d}s\).
2 Preliminary results
For the sake of simplicity, we set
Lemma 2.1
Suppose that (a)–(f) hold for \(\iota \geq \iota _{0} \), and let u be an eventually positive solution of (1.10)–(1.11). Then w satisfies
Proof
Let u be an eventually positive solution. Then \(w(\iota )>0\) and there exists \(\iota _{0} \geq 0\) such that \(u(\iota )>0\), \(u(\nu (\iota ))>0\), \(u(\zeta (\iota ))>0\) for all \(\iota \geq \iota _{0} \). Then (1.10)–(1.11) gives that
which shows that \(p(\iota ) (w'(\iota ) )^{\alpha}\) is nonincreasing for \(\iota \geq \iota _{0} \), including jumps of discontinuity. Next we claim that for \(w>0\), \(p(\iota ) (w'(\iota ) )^{\alpha}\) is positive for \(\iota \geq \iota _{1} >\iota _{0} \). If not, letting \(p(\iota ) (w'(\iota ) )^{\alpha}\leq 0\) for \(\iota \geq \iota _{1} \), we can choose \(c>0\) such that
that is,
Integrating both sides from \(\iota _{1} \) to ι, we get
Taking limit on both sides as \(\iota \to \infty \), we have \(\lim_{\iota \to \infty}w(\iota )\leq -\infty \), which leads to a contradiction to \(w(\iota )>0\). Hence, \(p(\iota ) (w'(\iota ) )^{\alpha}>0\) for \(\iota \geq \iota _{1} \), that is, \(w'(\iota )>0\) for \(\iota \geq \iota _{1} \). This completes the proof. □
Lemma 2.2
Suppose that (a)–(f) hold for \(\iota \geq \iota _{0} \), and let u be an eventually positive solution of (1.10)–(1.11). Then w satisfies
Proof
Assume that u is an eventually positive solution of (1.10)–(1.11). Then \(w(\iota )>0\) and there exists \(\iota \geq \iota _{1} >\iota _{0} \) such that
Hence w satisfies (2.3) for \(\iota \geq \iota _{1} \). □
3 Main results
In Theorem 3.1 we use a constant β, the quotient of two odd positive integers with \(\beta >\alpha \), for which
The existence of such a constant can be established by taking \(g(\iota )=|\iota |^{\delta}\operatorname{sgn}(\iota )\) with \(\beta <\delta \).
Theorem 3.1
Let (b)–(f) and (3.1) hold for \(\iota \geq \iota _{0} \). Then every solution of (1.10)–(1.11) is oscillatory if and only if
Proof
Let u be an eventually positive solution of (1.10)–(1.11). Then \(w(\iota )>0\) and there exists \(\iota _{0} \geq 0\) such that \(u(\iota )>0\), \(u(\nu (\iota ))>0\), \(u(\zeta (\iota ))>0\) for all \(\iota \geq \iota _{0} \). Thus, Lemmas 2.1 and 2.2 hold for \(\iota \geq \iota _{1} \). By Lemma 2.1, there exists \(\iota _{2}>\iota _{1} \) such that \(w'(\iota )>0\) for all \(\iota \geq \iota _{2}\). Then there exist \(\iota _{3}>\iota _{2}\) and \(c>0\) such that \(w(\iota )\geq c\) for all \(\iota \geq \iota _{3}\). Next, using Lemma 2.2, we get \(u(\iota )\geq (1-a)w(\iota )\) for all \(\iota \geq \iota _{3}\) and (1.10)–(1.11) become
Integrating (3.3) from ι to ∞, we get
Since \(p(\iota ) (w'(\iota ) )^{\alpha}\) is positive and nondecreasing, \(\lim_{\iota \to \infty} p(\iota ) (w'(\iota ) )^{\alpha}\) exists, and it is finite and positive. Then
that is,
Since
then we use (3.5) in (3.4) to get
Next, if we set \(K=\frac {g_{0}[c(1-a)]}{c^{\beta}}\), where \(g_{0}[c(1-a)]= \min \{g[c(1-a)]\}\), the above inequality becomes
Using (b) and the fact that \(w(\iota )\) is nondecreasing, we have
i.e.,
Integrating both sides from \(\iota _{3}\) to ∞, we get
due to \(\beta >\alpha \), which is a contradiction to (3.2) and hence the sufficiency part of the theorem is proved.
Next we prove the necessary part by a contrapositive argument. If (3.2) does not hold, then for every \(\varepsilon >0\) there exists \(\iota \geq \iota _{0} \), for which
where \(2\varepsilon = [\max \{g(\frac {1}{1-a})\} ]^{-1/\alpha}>0\).
Let us define the set
and \(\Phi : V\rightarrow V\) as
Now we prove that \((\Phi u)(\iota )\in V\). For \(u(\iota )\in V\),
and further, for \(u(\iota )\in V\),
Hence Φ maps from V to V.
Now we are going to find a fixed point for Φ in V, which will give an eventually positive solution of (1.10)–(1.11).
First we define a sequence of functions in V by
Here we see \(u_{1}(\iota )\geq u_{0}(\iota )\) for each fixed ι and \(\frac {1}{2}\leq u_{n-1}(\iota )\leq u_{n}(\iota )\leq \frac {1}{1-a}\) for \(\iota \geq Y\) for all \(n\geq 1\). Thus \({u_{n}}\) converges point-wise to a function u. By Lebesgue’s dominated convergence theorem u is a fixed point of Φ in V, which shows that it has a nonoscillatory solution. This completes the proof of the theorem. □
In Theorem 3.2 we take a constant β, the quotient of two odd positive integers with \(\beta < \alpha \), for which
The existence of such a constant can be established by taking \(g(\iota )=|\iota |^{\delta}\operatorname{sgn}(\iota )\) with \(\beta >\delta \). The assumption upon β can be withdrawn by taking \(|u|^{\beta}\operatorname{sgn}(u)\) instead of \(u^{\beta}\).
Theorem 3.2
Let (a), (c)–(f), and (3.6) hold for \(\iota \geq \iota _{0} \). Then every solution of (1.10)–(1.11) is oscillatory if
Proof
Let \(u(\iota )\) be an eventually positive solution of (1.10)–(1.11). Then, proceeding as in the proof of Theorem 3.1, we have \(\iota _{2}>\iota _{1} >\iota _{0} \) such that inequality (3.4) holds for all \(\iota \geq \iota _{2}\). Using (e), there exists \(\iota _{3}>\iota _{2}\) for which \(P(\iota )-P(\iota _{3})\geq \frac {1}{2} P(\iota )\) for \(\iota \geq \iota _{3}\). Integrating (3.4) from \(\iota _{3}\) to ι, we have
that is,
Since \(p(\iota ) (w'(\iota ) )^{\alpha}\) is nonincreasing and positive, then there exist \(c>0\) and \(\iota _{4}>\iota _{3}\) such that \(p(\iota ) (w'(\iota ) )^{\alpha}\leq c^{\alpha}\) for \(\iota \geq \iota _{4}\). Integrating the relation \(w'(\iota ) \leq cp^{-1/\alpha}(\iota )\) from \(\iota _{4}\) to ι, we have
that is,
Using (3.6) and (3.9), we obtain
Using (3.10) in (3.8), we obtain
Hence,
where
Now,
and
which shows that \(U(\iota )\) is nonincreasing on \([\iota _{4},\infty )\) and \(\lim_{\iota \to \infty}U(\iota )\) exists. Using (3.11) and (a), we find
To estimate the discontinuity of \(U^{1-\beta /\alpha}\), we use a Taylor polynomial of order 1 from the function \(h(u)=u^{1-\beta /\alpha}\), with \(0<\beta <\alpha \), about \(u=a\):
Then
Now, integrating (3.13) from \(\iota _{4}\) to ι, we have
that is,
which contradicts (3.7). This completes the proof. □
Example 3.1
Consider the neutral differential equations
Here \(\alpha = 1/3\), \(p(\iota )=1\), \(0< q(\iota )=e^{-\iota}<1\) \(\nu (\iota )= \iota -2\), \(\phi _{k}=3^{k}\) for , \(g(\iota )=\iota ^{7/3}\). For \(\beta =5/3\), we have \(\delta =7/3>\beta =5/3>\alpha =1/3\) and \(g(\iota )/\iota ^{\beta}=\iota ^{2/3}\), which are increasing functions. Now we check (3.2). We have
So, all the conditions of Theorem 3.1 hold. Thus, each solution of (3.14)–(3.15) is oscillatory.
Example 3.2
Consider the neutral differential equations
Here \(\alpha = 11/3\), \(p(\iota )=e^{-\iota}\), \(0< q(\iota )=e^{-\iota}<1\), \(\nu (\iota )= \iota -2\), \(\phi _{k}=k\) for , \(P(\iota )= \int _{0}^{\iota }e^{3s/11} \,ds=\frac{11}{3}(e^{3\iota /11}-1)\), \(g(\iota )=\iota ^{1/3}\). For \(\beta =7/3\), we have \(\delta =1/3<\beta =7/3<\alpha =11/3\) and \(g(\iota )/\iota ^{\beta}=\iota ^{-2}\), which are decreasing functions. Now we check (3.7). We have
So, all the conditions of Theorem 3.2 hold, and therefore each solution of (3.16)–(3.17) is oscillatory.
4 Conclusions
In this work, we have undertaken the problem by taking a second-order highly nonlinear neutral impulsive differential system and established necessary and sufficient conditions for the oscillation of (1.10)–(1.11) when the neutral coefficient lies in \([0,1)\). It would be of interest to investigate the oscillation of (1.10)–(1.11) with different neutral coefficients; see, e.g., the papers [17–19] for more details. Furthermore, it is also interesting to analyze the oscillation of (1.10)–(1.11) with a nonlinear neutral term; see, e.g., the paper [10] for more details.
Availability of data and materials
Not applicable.
References
Agarwal, R.P., O’Regan, D., Saker, S.H.: Oscillation and Stability of Delay Models in Biology. Springer, New York (2014)
Bainov, D.D., Simeonov, P.S.: Impulsive Differential Equations: Asymptotic Properties of the Solutions. Series on Advances in Mathematics for Applied Sciences, vol. 28. World Scientific, Singapore (1995)
Bazighifan, O., Ruggieri, M., Santra, S.S., Scapellato, A.: Qualitative properties of solutions of second-order neutral differential equations. Symmetry 12(9), 1520 (2020). https://doi.org/10.3390/sym12091520
Bazighifan, O., Ruggieri, M., Scapellato, A.: An improved criterion for the oscillation of fourth-order differential equations. Mathematics 8(4), 610 (2020). https://doi.org/10.3390/math8040610
Berezansky, L., Braverman, E.: Oscillation of a linear delay impulsive differential equations. Commun. Appl. Nonlinear Anal. 3, 61–77 (1996)
Berezansky, L., Domoshnitsky, A., Koplatadze, R.: Oscillation, Nonoscillation, Stability and Asymptotic Properties for Second and Higher Order Functional Differential Equations. Chapman & Hall/CRC Press, Boca Raton (2020)
Bohner, M., Hassan, T.S., Li, T.: Fite-Hille-Wintner-type oscillation criteria for second-order half-linear dynamic equations with deviating arguments. Indag. Math. 29(2), 548–560 (2018)
Diblik, J.: Positive solutions of nonlinear delayed differential equations with impulses. Appl. Math. Lett. 72, 16–22 (2017)
Diblik, J., Svoboda, Z., Smarda, Z.: Retract principle for neutral functional differential equation. Nonlinear Anal., Theory Methods Appl. 71(12), 1393–1400 (2009)
Džurina, J., Grace, S.R., Jadlovská, I., Li, T.: Oscillation criteria for second-order Emden-Fowler delay differential equations with a sublinear neutral term. Math. Nachr. 293(5), 910–922 (2020)
Ghosh, T., Santra, S.S., Scapellato, A.: Oscillation results for second-order neutral delay differential equations. AIP Conf. Proc. 2425, 210005 (2022)
Graef, J.R., Shen, J.H., Stavroulakis, I.P.: Oscillation of impulsive neutral delay differential equations. J. Math. Anal. Appl. 268, 310–333 (2002)
Infusino, M., Kuhlmann, S.: Infinite dimensional moment problem: open questions and applications. In: Contemp. Math., vol. 697, pp. 187–201. Am. Math. Soc., Providence (2017)
Karpuz, B., Ocalan, O.: Oscillation criteria for a class of first-order forced differential equations under impulse effects. Adv. Dyn. Syst. Appl. 7(2), 205–218 (2012)
Lakshmikantham, V., Bainov, D.D., Simeonov, P.S.: Oscillation Theory of Impulsive Differential Equations. World Scientific, Singapore (1989)
Li, T., Pintus, N., Viglialoro, G.: Properties of solutions to porous medium problems with different sources and boundary conditions. Z. Angew. Math. Phys. 70(3), Art. 86, pp. 1–18 (2019)
Li, T., Rogovchenko, Y.V.: Oscillation of second-order neutral differential equations. Math. Nachr. 288(10), 1150–1162 (2015)
Li, T., Rogovchenko, Y.V.: Oscillation criteria for second-order superlinear Emden-Fowler neutral differential equations. Monatshefte Math. 184(3), 489–500 (2017)
Li, T., Rogovchenko, Y.V.: On the asymptotic behavior of solutions to a class of third-order nonlinear neutral differential equations. Appl. Math. Lett. 105, Art. 106293, pp. 1–7 (2020)
Li, T., Viglialoro, G.: Boundedness for a nonlocal reaction chemotaxis model even in the attraction-dominated regime. Differ. Integral Equ. 34(5–6), 315–336 (2021)
Luo, Z., Jing, Z.: Periodic boundary value problem for first-order impulsive functional differential equations. Comput. Math. Appl. 55, 2094–2107 (2008)
Ruggieri, M., Santra, S.S., Scapellato, A.: On nonlinear impulsive differential systems with canonical and non-canonical operators. Appl. Anal. (2021). https://doi.org/10.1080/00036811.2021.1965586
Ruggieri, M., Santra, S.S., Scapellato, A.: Oscillatory behavior of second-order neutral differential equations. Bull. Braz. Math. Soc. (2021). https://doi.org/10.1007/s00574-021-00276-3
Santra, S.S., Dix, J.G.: Necessary and sufficient conditions for the oscillation of solutions to a second-order neutral differential equation with impulses. Nonlinear Stud. 27(2), 375–387 (2020)
Santra, S.S., Scapellato, A.: Some conditions for the oscillation of second-order differential equations with several mixed delays. J. Fixed Point Theory Appl. 24(2), 18 (2022)
Santra, S.S., Tripathy, A.K.: On oscillatory first order nonlinear neutral differential equations with nonlinear impulses. J. Appl. Math. Comput. 59, 257–270 (2019). https://doi.org/10.1007/s12190-018-1178-8
Shen, J., Zou, Z.: Oscillation criteria for first order impulsive differential equations with positive and negative coefficients. J. Comput. Appl. Math. 217, 28–37 (2008)
Shen, J.H., Wang, Z.C.: Oscillation and asymptotic behaviour of solutions of delay differential equations with impulses. Ann. Differ. Equ. 10(1), 61–68 (1994)
Tripathy, A.K.: Oscillation criteria for a class of first order neutral impulsive differential-difference equations. J. Appl. Anal. Comput. 4, 89–101 (2014)
Tripathy, A.K., Santra, S.S.: Characterization of a class of second order neutral impulsive systems via pulsatile constant. Differ. Equ. Appl. 9(1), 87–98 (2017)
Tripathy, A.K., Santra, S.S.: On the forced impulsive oscillatory nonlinear neutral systems of the second order. Nonlinear Oscil. 23(2), 274–288 (2020)
Tripathy, A.K., Santra, S.S.: Necessary and sufficient conditions for oscillation of a class of second order impulsive systems. Differ. Equ. Dyn. Syst. 30(2), 433–450 (2022)
Tripathy, A.K., Santra, S.S.: Necessary and sufficient conditions for oscillations to a second-order neutral differential equations with impulses. Kragujev. J. Math. 47(1), 81–93 (2023)
Viglialoro, G., Woolley, T.E.: Solvability of a Keller-Segel system with signal-dependent sensitivity and essentially sublinear production. Appl. Anal. 99(14), 2507–2525 (2020)
Yu, J., Yan, J.: Positive solutions and asymptotic behavior of delay differential equations with nonlinear impulses. J. Math. Anal. Appl. 207, 388–396 (1997)
Acknowledgements
The researchers would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project. The authors are very grateful to the anonymous referees for their detailed comments and valuable suggestions.
Funding
For this paper, no direct funding was received.
Author information
Authors and Affiliations
Contributions
All authors have contributed equally to this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Santra, S.S., Scapellato, A. & Moaaz, O. Second-order impulsive differential systems of mixed type: oscillation theorems. Bound Value Probl 2022, 67 (2022). https://doi.org/10.1186/s13661-022-01648-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-022-01648-4