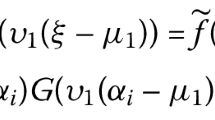Second-order impulsive differential systems with mixed and several delays

Abstract

In this work, we present new necessary and sufficient conditions for the oscillation of a class of second-order neutral delay impulsive differential equations. Our oscillation results complement, simplify and improve recent results on oscillation theory of this type of nonlinear neutral impulsive differential equations that appear in the literature. An example is provided to illustrate the value of the main results.

1 Introduction

Nowadays impulsive differential equations are attracting a lot of attention. They appear in the study of several real world problems (see, for instance, [1–3]). In general, it is well known that several natural phenomena are driven by differential equations. However, the description of some real world problems requires studies on systems of differential equations with impulses, a subject very interesting from a mathematical point of view. Examples of the aforementioned phenomena are related to mechanical systems, biological systems, population dynamics, pharmacokinetics, theoretical physics, biotechnology processes, chemistry, engineering, control theory (we also stress that in the modeling of these phenomena is suitably formulated by evolutive partial differential equations and, moreover, moment problem approaches appear also as a natural instrument in control theory of neutral type systems; see [4–6] and [7], respectively).

The literature related to impulsive differential equations is very wide. Here we mention some recent developments in this field.

In [8], Shen and Wang considered impulsive differential equations of the following form:

$$ \textstyle\begin{cases} u'(\iota )+r(\iota )u(\iota -\nu )=0,\quad \iota \neq \phi _{k} , \iota \geq \iota _{0}, \\ u(\phi _{k}^{+})-u(\phi _{k} ^{-})=I_{k}(u(\phi _{k} )), \quad k\in \mathbb{N}, \end{cases} $$

(1)

where $r\in C(\mathbb{R},\mathbb{R})$ and $I_{k}\in C(\mathbb{R},\mathbb{R})$ for $k\in \mathbb{N}$, and obtained sufficient conditions that ensure the oscillation and the asymptotic behaviour of the solutions of the problem (1).

In [9], Graef et al. considered the problem

$$ \textstyle\begin{cases} (u(\iota )-q(\iota )u(\iota -\zeta ) )'+r(\iota ) \vert u( \iota -\nu ) \vert ^{\lambda }\operatorname{sgn} u(\iota -\nu )=0,\quad \iota \geq \iota _{0}, \\ u(\phi _{k} ^{+})=b_{k} u(\phi _{k} ), \quad k\in \mathbb{N}, \end{cases} $$

(2)

assuming that $q(\iota )\in PC([\iota _{0},\infty ),\mathbb{R}_{+})$ (that is, $q(\iota )$ is piecewise continuous in $[\iota _{0},\infty )$), obtained sufficient conditions for the oscillation of the solutions of the problem (2).

In [10], Shen and Zou obtained oscillation criteria for first-order impulsive neutral delay differential equations of the form

$$ \textstyle\begin{cases} (u(\iota )-q(\iota )u(\iota -\zeta ) )'+r(\iota )u(\iota - \nu _{1})-v(\iota )u(\iota -\nu _{2})=0, \quad \nu _{1}\geq \nu _{2}>0, \\ u(\phi _{k} ^{+})=I_{k}(u(\phi _{k} )),\quad k\in \mathbb{N}, \end{cases} $$

(3)

obtaining sufficient conditions that ensure the oscillation of the solutions of (3) under the assumptions that $q(\iota )\in PC([\iota _{0},\infty ),\mathbb{R}_{+})$ and $b_{k}\leq \frac{I_{k}(u)}{u}\leq 1$.

Karpuz et al. in [11] extended the results contained in [10] by taking the nonhomogeneous counterpart of the system (3) with variable delays.

Oscillation and nonoscillation properties for a class of second-order neutral impulsive differential equations with constant coefficients and constant delays were studied by Tripathy and Santra in [12], where the authors considered the problem

$$ \textstyle\begin{cases} (u(\iota )-qu(\iota -\zeta ) )''+ru(\iota -\nu )=0,\quad \iota \neq \phi _{k} , k\in \mathbb{N}, \\ \Delta (u(\phi _{k})-qu(\phi _{k}-\zeta ))'+\tilde{r}u(\phi _{k}-\nu )=0,\quad k\in \mathbb{N}. \end{cases} $$

(4)

Other necessary and sufficient conditions for the oscillation of a class of second-order neutral impulsive systems were established in [13], where Tripathy and Santra studied systems of the form

$$ \textstyle\begin{cases} (p(\iota )(u(\iota )+q(\iota )u(\iota -\zeta ))' )'+r( \iota )g(u(\iota -\nu )), \quad \iota \neq \phi _{k} , k\in \mathbb{N}, \\ \Delta (p(\phi _{k})(u(\phi _{k})+q(\phi _{k})u(\phi _{k}-\zeta ))')+r( \phi _{k})g(u(\phi _{k}-\nu ))=0,\quad k\in \mathbb{N}. \end{cases} $$

(5)

In [13], in particular, the authors are interested with oscillating systems that, after a perturbation by instantaneous change of state, remain oscillating.

In [14], Santra and Tripathy investigated the oscillatory behaviour of the solutions for first-order impulsive neutral delay differential equations of the form

$$ \textstyle\begin{cases} (u(\iota )-q(\iota )u(\iota -\zeta ))'+r(\iota )g(u(\iota -\nu ))=0, \quad \iota \neq \phi _{k} , \iota \geq \iota _{0}, \\ u(\phi _{k} ^{+})=I_{k}(u(\phi _{k} )),\quad k\in \mathbb{N}, \\ u(\phi _{k}^{+}-\tau )=I_{k}(u(\phi _{k}-\tau )),\quad k\in \mathbb{N}, \end{cases} $$

(6)

for different values of the neutral coefficient q.

We also mention Ref. [15] in which Santra and Dix, using Lebesgue’s dominated convergence theorem, obtained necessary and sufficient conditions for the oscillation of the solutions of the following second-order neutral differential equations with impulses:

$$ \textstyle\begin{cases} (p(\iota )(w'(\iota ))^{\gamma } )'+\sum_{j=1}^{m} r_{j}( \iota )g_{j}(u(\nu _{j}(\iota )))=0, \quad \iota \geq \iota _{0}, \iota \neq \phi _{k}, k\in \mathbb{N}, \\ \Delta (p(\phi _{k})(w'(\phi _{k}))^{\gamma })+\sum_{j=1}^{m} \widetilde{r}_{j}(\phi _{k})g_{j}(u(\nu _{j}(\phi _{k})))=0, \end{cases} $$

(7)

where

$$ w(\iota )=u(\iota )+q(\iota )u\bigl(\zeta (\iota )\bigr),\qquad \Delta u(a)= \lim _{s\to a^{+}}u(s)-\lim_{s\to a^{-}}u(s),\quad -1\leq q(\iota ) \leq 0. $$

In line with the contents of [15], Tripathy and Santra in [16] examined oscillation and nonoscillation properties for the solutions of the following class of forced impulsive nonlinear neutral differential systems:

$$ \textstyle\begin{cases} (p(\iota )(u(\iota )+q(\iota )u(\iota -\zeta ))')'+r(\iota )g(u( \iota -\nu ))=f(\iota ), \quad \iota \neq \phi _{k}, k\in \mathbb{N}, \\ \Delta (p(\phi _{k})(u(\phi _{k})+q(\phi _{k})u(\phi _{k}-\zeta ))')+ \tilde{r}(\phi _{k})g(u(\phi _{k}-\nu ))=\tilde{f}(\phi _{k}),\quad k \in \mathbb{N}, \end{cases} $$

(8)

for different values of $q(\iota )$ and obtained sufficient conditions for the existence of positive bounded solutions of system (8).

Finally we mention recent work [17] in which Tripathy and Santra obtained some characterizations for the oscillation of solutions of the following second-order neutral impulsive differential system:

$$ \textstyle\begin{cases} (p(\iota )(w'(\iota ))^{\gamma })'+\sum_{j=1}^{m} r_{j}(\iota ) x^{ \alpha _{j}}(\nu _{j}(\iota ))=0,\quad \iota \geq \iota _{0}, \iota \neq \phi _{k} , \\ \Delta (p(\phi _{k})(w'(\phi _{k}))^{\gamma })+\sum_{j=1}^{m} h_{j}( \phi _{k})x^{\alpha _{j}}(\nu _{j}(\phi _{k}))=0, \quad k\in \mathbb{N} , \end{cases} $$

(9)

where $w(\iota )=u(\iota )+q(\iota )u(\zeta (\iota ))$ and $-1< q(\iota )\leq 0$.

For further details on neutral impulsive differential equations and for recent results related to the oscillation theory for ordinary differential equations, we refer the reader to Refs. [18–43] and to the references therein. In particular, the study of oscillation of half-linear/Emden–Fowler (neutral) differential equations with deviating arguments (delayed or advanced arguments or mixed arguments) has numerous applications in physics and engineering (e.g., half-linear/Emden–Fowler differential equations arise in a variety of real world problems such as in the study of p-Laplace equations and in chemotaxis models); see, e.g., Refs. [4, 34–37, 39, 40, 42, 43] for more details. In particular, by using different methods, the following work was concerned with the oscillation of various classes of half-linear/Emden–Fowler differential equations and half-linear/Emden–Fowler differential equations with different neutral coefficients (e.g., Ref. [33] was concerned with neutral differential equations assuming that $0\leq q(\iota )<1$ and $q(\iota )>1$; Ref. [34] was concerned with neutral differential equations assuming that $0\leq q(\iota )<1$; Ref. [36] was concerned with neutral differential equations assuming that $q(\iota )$ is nonpositive; Rewfs. [37, 41] were concerned with neutral differential equations in the case where $q(\iota )>1$; Ref. [40] was concerned with neutral differential equations assuming that $0\leq q(\iota )\leq q_{0}<\infty$ and $q(\iota )>1$; Ref. [42] was concerned with neutral differential equations in the case where $0\leq q(\iota )\leq q_{0}<\infty$; Ref. [43] was concerned with neutral differential equations in the case when $0\leq q(\iota )= q_{0}\neq 1$; whereas Ref. [39] was concerned with differential equations with a nonlinear neutral term assuming that $0\leq q(\iota )\leq a<1$), which has the same research topic as that of this paper.

Motivated by the aforementioned findings, in this paper we prove necessary and sufficient conditions for the oscillation of solutions to a second-order nonlinear impulsive differential system in the form

$$\begin{aligned}& \bigl(p(\iota ) \bigl(w'(\iota ) \bigr)^{\alpha } \bigr)' +\sum_{j=1}^{m} r_{j}( \iota )u^{\beta }\bigl(\nu _{j}(\iota ) \bigr)=0, \quad \iota \geq \iota _{0}, \iota \neq \phi _{k}, k\in \mathbb{N}, \end{aligned}$$

(10)

$$\begin{aligned}& \Delta \bigl(p(\phi _{k}) \bigl(w'(\phi _{k}) \bigr)^{\alpha } \bigr) + \sum_{j=1}^{m} \tilde{r}_{j}(\phi _{k})u^{\beta }\bigl(\nu _{j}(\phi _{k})\bigr)=0 , \end{aligned}$$

(11)

where

$$ w(\iota )=u(\iota )+q(\iota )u\bigl(\zeta (\iota )\bigr),\qquad \Delta u(a)= \lim _{s\to a^{+}}u(s)-\lim_{s\to a^{-}}u(s), $$

the functions $r_{j}$, $\tilde{r}_{j}$, p, q, $\nu _{j}$, ζ are continuous that satisfy the conditions stated now;

• (a) $\nu _{j}\in C([0,\infty ),\mathbb{R})$, $\zeta \in C^{2}([0,\infty ),\mathbb{R})$, $\nu _{j}(\iota )<\iota$, $\zeta (\iota )<\iota$, $\lim_{\iota \to \infty }\nu _{j}(\iota )=\infty$, $\lim_{\iota \to \infty }\zeta (\iota )=\infty$.

• (b) $\nu _{j}\in C([0,\infty ),\mathbb{R})$, $\zeta \in C^{2}([0,\infty ),\mathbb{R})$, $\nu _{j}(\iota )>\iota$, $\zeta (\iota )<\iota$, $\lim_{\iota \to \infty }\zeta (\iota )=\infty$.

• (c) $p\in C^{1}([0,\infty ),\mathbb{R})$, $r_{j},\tilde{r}_{j}\in C([0,\infty ),\mathbb{R})$; $0< p(\iota )$, $0\leq r_{j}(\iota )$, $0\leq \tilde{r}_{j}(\iota )$, for all $\iota \geq 0$ and $j=1,2,\dots ,m$; $\sum r_{j}(\iota )$ is not identically zero in any interval $[b,\infty )$.

• (d) $q\in C^{2}([0,\infty ),\mathbb{R_{+}})$ with $0\leq q(\iota )\leq a<1$.

• (e) $\lim_{\iota \to \infty }P(\iota )=\infty$ where $P(\iota )=\int _{0}^{\iota }p^{-1/\alpha }(s) \,\mathrm{d}s$.

• (f) α and β are the quotients of two positive odd integers and the sequence $\{\phi _{k}\}$ satisfies $0<\phi _{1}<\phi _{2}<\cdots <\phi _{k}\to \infty$ as $k\to \infty$.

2 Preliminary results

To make our notations simpler, we set

$$\begin{aligned} &R_{1}(\iota )= \sum_{j=1}^{m} r_{j}(\iota ) \bigl((1-a)w \bigl(\nu _{j}( \iota ) \bigr) \bigr)^{\beta }; \\ &R_{(1,k)}= \sum_{j=1}^{m} \tilde{r}_{j}(\phi _{k}) \bigl((1-a)w \bigl( \nu _{j}(\phi _{k}) \bigr) \bigr)^{\beta } . \end{aligned}$$

Lemma 2.1

Suppose (a)–(f) hold for $\iota \geq \iota _{0}$, and u is an eventually positive solution of (10)–(11). Then w satisfies

$$\begin{aligned}& 0< w(\iota ),\qquad w'(\iota )>0,\quad \textit{and} \quad \bigl(p(\iota ) \bigl(w'( \iota ) \bigr)^{\alpha } \bigr)'\leq 0 \quad \textit{for } \iota \geq \iota _{1} . \end{aligned}$$

(12)

Proof

Let u be an eventually positive solution. Then $w(\iota )>0$ and there exists $\iota _{0}\geq 0$ such that $u(\iota )>0$, $u(\nu _{j}(\iota ))>0$, $u(\zeta (\iota ))>0$ for all $\iota \geq \iota _{0}$ and $j=1,2,\dots ,m$. Then (10)–(11) gives

$$ \begin{gathered} \bigl(p(\iota ) \bigl(w'( \iota ) \bigr)^{\alpha } \bigr)' = -\sum _{j=1}^{m} r_{j}( \iota )u^{\beta } \bigl(\nu _{j}(\iota )\bigr)\leq 0 \quad \text{for } \iota \neq \phi _{k}, \\ \Delta \bigl(p(\phi _{k}) \bigl(w'(\phi _{k}) \bigr)^{\alpha } \bigr) =- \sum_{j=1}^{m} \tilde{r}_{j}(\phi _{k})u^{\beta }\bigl(\nu _{j}(\phi _{k})\bigr) \leq 0\quad \text{for }k\in \mathbb{N} , \end{gathered} $$

(13)

which shows that $p(\iota ) (w'(\iota ) )^{\alpha }$ is non-increasing for $\iota \geq \iota _{0}$, including jumps of discontinuity. Next we claim that, for $w>0$, $p(\iota ) (w'(\iota ) )^{\alpha }$ is positive for $\iota \geq \iota _{1}>\iota _{0}$. If not, letting $p(\iota ) (w'(\iota ) )^{\alpha }\leq 0$ for $\iota \geq \iota _{1}$, we can choose $c>0$ such that

$$ p(\iota ) \bigl(w'(\iota ) \bigr)^{\alpha }\leq -c , $$

that is,

$$ w'(\iota )\leq (-c)^{1/\alpha }p^{-1/\alpha }(\iota ) . $$

Integrating both sides from $\iota _{1}$ to ι we get

$$ w(\iota )-w(\iota _{1})-\sum_{k=1}^{\infty }w'( \phi _{k})\leq (-c)^{1/ \alpha } \bigl(P(\iota )-P(\iota _{1}) \bigr). $$

Taking the limit in both sides as $\iota \to \infty$, we have $\lim_{\iota \to \infty }w(\iota )\leq -\infty$, that is, $w(\iota )\leq 0$ which leads to a contradiction to $w(\iota )>0$. Hence, $p(\iota ) (w'(\iota ) )^{\alpha }>0$ for $\iota \geq \iota _{1}$ i.e., $w'(\iota )>0$ for $\iota \geq \iota _{1}$. This completes the proof. □

Lemma 2.2

Suppose (a)–(f) hold for $\iota \geq \iota _{0}$, and u is an eventually positive solution of (10)–(11). Then w satisfies

$$\begin{aligned} u(\iota )\geq (1-a)w(\iota )\quad \textit{for } \iota \geq \iota _{1}. \end{aligned}$$

(14)

Proof

Assume that u is an eventually positive solution of (10)–(11). Then $w(\iota )>0$ and there exists $\iota \geq \iota _{1}>\iota _{0}$ such that

$$\begin{aligned} u(\iota )&= w(\iota )-q(\iota )u\bigl(\zeta (\iota )\bigr) \\ &\geq w(\iota )-q(\iota )w\bigl(\zeta (\iota )\bigr) \\ &\geq w(\iota )-q(\iota )w(\iota ) \\ &= \bigl(1-q(\iota ) \bigr)w(\iota ) \\ &\geq (1-a)w(\iota ) . \end{aligned}$$

Hence w satisfies (14) for $\iota \geq \iota _{1}$. □

Remark 2.1

The above two lemmas hold for any $\alpha >\beta$ or $\alpha <\beta$.

3 Main results

Theorem 3.1

Let (b)–(f) hold for $\iota \geq \iota _{0}$ and $\beta > \alpha$. Then every solution of (10)–(11) is oscillatory if and only if

$$ \int _{0}^{\infty }p^{-1/\alpha }(s) \Biggl[ \int _{s}^{\infty }\sum_{j=1}^{m} r_{j}(\psi ) \,\mathrm{d}\psi +\sum_{\phi _{k}\geq s} \sum_{j=1}^{m} \tilde{r}_{j}(\phi _{k}) \Biggr]^{1/\alpha } \,\mathrm{d}s =\infty . $$

(15)

Proof

Let u be an eventually positive solution of (10)–(11). Then $w(\iota )>0$ and there exists $\iota _{0}\geq 0$ such that $u(\iota )>0$, $u(\nu _{j}(\iota ))>0$, $u(\zeta (\iota ))>0$ for all $\iota \geq \iota _{0}$ and $j=1,2,\dots ,m$. Thus, Lemmas 2.1 and 2.2 hold for $\iota \geq \iota _{1}$. By Lemma 2.1, there exists $\iota _{2}>\iota _{1}$ such that $w'(\iota )>0$ for all $\iota \geq \iota _{2}$. Then there exist $\iota _{3}>\iota _{2}$ and $c>0$ such that $w(\iota )\geq c$ for all $\iota \geq \iota _{3}$. Next using Lemma 2.2, we get $u(\iota )\geq (1-a)w(\iota )$ for all $\iota \geq \iota _{3}$ and (10)–(11) become

$$ \begin{gathered} \bigl(p(\iota ) \bigl(w'( \iota ) \bigr)^{\alpha } \bigr)' + R_{1}(\iota )\leq 0 \quad \text{for } \iota \neq \phi _{k}, \\ \Delta \bigl(p(\phi _{k}) \bigl(w'(\phi _{k}) \bigr)^{\alpha } \bigr) + R_{(1,k)} \leq 0\quad \text{for }k=1,2,\dots . \end{gathered} $$

(16)

Integrating (16) from ι to ∞ we get

$$\begin{aligned} &\bigl[p(s) \bigl(w'(s) \bigr)^{\alpha }\bigr]_{\iota }^{\infty }+ \int _{\iota }^{\infty }R_{1}(s) \,\mathrm{d}s+ \sum_{\phi _{k} \geq \iota } R_{(1,k)} \leq 0 . \end{aligned}$$

Note that $p(\iota ) (w'(\iota ) )^{\alpha }$ is positive and non-decreasing. So, $\lim_{\iota \to \infty } p(\iota ) (w'(\iota ) )^{\alpha }$ finitely exists and is positive. Therefore,

$$ \begin{aligned} p(\iota ) \bigl(w'(\iota ) \bigr)^{\alpha }& \geq \int _{\iota }^{\infty }R_{1}(s) \,\mathrm{d}s+ \sum_{\phi _{k} \geq \iota } R_{(1,k)} , \end{aligned} $$

that is,

$$ \begin{aligned} w'(\iota ) &\geq p^{-1/\alpha }(\iota ) \biggl[ \int _{\iota }^{\infty }R_{1}(s) \,\mathrm{d}s + \sum_{\phi _{k} \geq \iota } R_{(1,k)} \biggr]^{1/\alpha } \\ &= (1-a)^{\beta /\alpha } p^{-1/\alpha }(\iota ) \Biggl[ \int _{\iota }^{\infty }\sum_{j=1}^{m} r_{j}(s)w^{\beta } \bigl(\nu _{j}(s) \bigr) \, \mathrm{d}s +\sum_{\phi _{k}\geq \iota } \sum _{j=1}^{m} \tilde{r}_{j} (\phi _{k}) w^{\beta } \bigl(\nu _{j}(\phi _{k}) \bigr) \Biggr]^{1/\alpha } . \end{aligned} $$

(17)

Using (b) and the fact that $w(\iota )$ is non-decreasing,

$$\begin{aligned} w'(\iota ) &\geq (1-a)^{\beta /\alpha }p^{-1/\alpha }(\iota ) \Biggl[ \int _{ \iota }^{\infty }\sum_{j=1}^{m} r_{j}(s) \,\mathrm{d}s + \sum_{\phi _{k} \geq \iota } \sum _{j=1}^{m} \tilde{r}_{j} (\phi _{k}) \Biggr]^{1/\alpha } w^{\beta /\alpha }(\iota ) , \end{aligned}$$

that is,

$$\begin{aligned} \frac{w'(\iota )}{w^{\beta /\alpha }(\iota )} &\geq (1-a)^{\beta / \alpha } p^{-1/\alpha }(\iota ) \Biggl[ \int _{\iota }^{\infty }\sum_{j=1}^{m} r_{j}(s) \,\mathrm{d}s + \sum_{\phi _{k}\geq \iota } \sum _{j=1}^{m} \tilde{r}_{j} (\phi _{k}) \Biggr]^{1/\alpha } . \end{aligned}$$

By integrating over $\iota _{3}$ and ∞ both side, we have

$$\begin{aligned} &(1-a)^{\beta /\alpha } \int _{\iota _{3}}^{\infty }p^{-1/\alpha }(s) \Biggl[ \int _{s}^{\infty }\sum_{j=1}^{m} r_{j}(\psi ) \,\mathrm{d}\psi + \sum_{ \phi _{k}\geq \iota } \sum_{j=1}^{m} \tilde{r}_{j} ( \phi _{k}) \Biggr]^{1/ \alpha } \,\mathrm{d}s\\ &\quad \leq \int _{\iota _{3}}^{\infty }\frac{w'(s)}{w^{\beta /\alpha }(s)} \,\mathrm{d}s < \infty \end{aligned}$$

due to $\beta >\alpha$, which is a contradiction to (15) and hence the sufficient part of the theorem is proved.

Next we prove necessary part by contrapositive argument. If (15) does not hold, then for every $\varepsilon >0$ there exists $\iota \geq \iota _{0}$ for which

$$\begin{aligned} \int _{\iota }^{\infty }p^{-1/\alpha }(s) \Biggl[ \int _{s}^{\infty }\sum_{j=1}^{m} r_{j}(\psi ) \,\mathrm{d}\psi +\sum_{\phi _{k}\geq s} \sum_{j=1}^{m} \tilde{r}_{j}(\phi _{k}) \Biggr]^{1/\alpha } \,\mathrm{d}s< \varepsilon \quad \text{for } \iota \geq T, \end{aligned}$$

where $2\varepsilon = [\frac{1}{1-a} ]^{-\beta /\alpha }>0$. Let us define a set

$$ V= \biggl\{ u\in C\bigl([0,\infty \bigr)): \frac{1}{2}\leq u(\iota )\leq \frac{1}{1-a} \text{ for all } \iota \geq T \biggr\} $$

and $\Phi : V\rightarrow V$ as

$$ (\Phi u) (\iota )= \textstyle\begin{cases} 0 &\text{if } \iota \leq T, \\\frac{1+a}{2(1-a)}-q(\iota )u(\zeta (\iota )) \\ \quad {}+ \int _{\iota }^{\iota }p^{-1/\alpha }(s) [\int _{s}^{\infty }\sum_{j=1}^{m} r_{j}(\psi )u^{\beta }(\nu _{j}(\psi )) \,\mathrm{d}\psi \\ \quad {}+\sum_{\phi _{k} \geq s} \sum_{j=1}^{m} \tilde{r}_{j}(\phi _{k})u^{\beta }(\nu _{j}( \phi _{k})) ]^{1/\alpha } \,\mathrm{d}s &\text{if } \iota >T . \end{cases} $$

Next, we prove $(\Phi u)(\iota )\in V$. For $u(\iota )\in V$,

$$\begin{aligned} (\Phi u) (\iota )&\leq \frac{1+a}{2(1-a)}\\ &\quad {}+ \int _{T}^{\iota }p^{-1/ \alpha }(s) \Biggl[ \int _{s}^{\infty }\sum_{j=1}^{m} r_{j}(\psi ) \biggl( \frac{1}{1-a} \biggr)^{\beta } \, \mathrm{d}\psi +\sum_{\phi _{k}\geq s} \sum _{j=1}^{m} \tilde{r}_{j}(\phi _{k}) \biggl(\frac{1}{1-a} \biggr)^{\beta } \Biggr]^{1/\alpha } \,\mathrm{d}s \\ &\leq \frac{1+a}{2(1-a)}+ \biggl(\frac{1}{1-a} \biggr)^{\beta /\alpha } \times \varepsilon \\ &=\frac{1+a}{2(1-a)} +\frac{1}{2}= \frac{1}{1-a} \end{aligned}$$

and further, for $u(\iota )\in V$,

$$\begin{aligned} (\Phi u) (\iota )\geq \frac{1+a}{2(1-a)} - q(\iota ).\frac{1}{1-a}+0 \geq \frac{1+a}{2(1-a)} - \frac{a}{1-a} =\frac{1}{2} . \end{aligned}$$

Hence Φ maps V into V.

Now we are going to find a fixed point for Φ in V which will give an eventually positive solution of (10)–(11).

First we define a sequence of functions in V by

$$\begin{aligned}& u_{0}(\iota )=0 \quad \text{for } \iota \geq \iota _{0}, \\& u_{1}(\iota )=(\Phi u_{0}) (\iota )= \textstyle\begin{cases} 0 &\text{if } \iota < T, \\ \frac{1}{2} &\text{if } \iota \geq T, \end{cases}\displaystyle \\& u_{n+1}(\iota ) = (\Phi u_{n}) (\iota )\quad \text{for }n \geq 1, \iota \geq T. \end{aligned}$$

Here we see $u_{1}(\iota )\geq u_{0}(\iota )$ for each fixed ι and $\frac{1}{2}\leq u_{n-1}(\iota )\leq u_{n}(\iota )\leq \frac{1}{1-a}$, $\iota \geq T$ for all $n\geq 1$. Thus ${u_{n}}$ converges point-wise to a function u. By Lebesgue’s dominated convergence theorem u is a fixed point of Φ in V, which shows that there has a non-oscillatory solution. This completes the proof the theorem. □

Theorem 3.2

Let (a), (c)–(f) hold for $\iota \geq \iota _{0}$ and $\beta < \alpha$. Then every solution of (10)–(11) is oscillatory if and only if

$$ \begin{aligned} \Biggl[ \int _{0}^{\infty }\sum_{j=1}^{m} r_{j}(\psi )\bigl[(1-a) P \bigl(\nu _{j}( \psi ) \bigr) \bigr]^{\beta } \,\mathrm{d}\psi +\sum_{k=1}^{\infty } \sum_{j=1}^{m} \tilde{r}_{j}(\phi _{k})\bigl[(1-a)P \bigl(\nu _{j}(\phi _{k}) \bigr)\bigr]^{\beta } \Biggr]=\infty . \end{aligned} $$

(18)

Proof

Let $u(\iota )$ be an eventually positive solution of (10)–(11). Then, proceeding as in the proof of Theorem 3.1 we have $\iota _{2}>\iota _{1}>\iota _{0}$ such that (17) holds for all $\iota \geq \iota _{2}$. Using (e), there exists $\iota _{3}>\iota _{2}$ for which $P(\iota )-P(\iota _{3})\geq \frac{1}{2} P(\iota )$ for $\iota \geq \iota _{3}$. Integrating (17) from $\iota _{3}$ to ι, we have

$$ \begin{aligned} w(\iota )-w(\iota _{3})&\geq \int _{\iota _{3}}^{\iota }p^{-1/\alpha }(s) \biggl[ \int _{s}^{\infty }R_{1}(\kappa )\,\mathrm{d} \kappa + \sum_{\phi _{k} \geq s} R_{(1,k)} \biggr]^{1/\alpha } \,\mathrm{d}s \\ &\geq \int _{\iota _{3}}^{\iota }p^{-1/\alpha }(s) \biggl[ \int _{\iota }^{\infty }R_{1}(\kappa )\,\mathrm{d} \kappa + \sum_{\phi _{k} \geq \iota } R_{(1,k)} \biggr]^{1/\alpha } \,\mathrm{d}s, \end{aligned} $$

that is,

$$\begin{aligned} w(\iota )&\geq \bigl(P(\iota )-P(\iota _{3})\bigr) \biggl[ \int _{\iota }^{\infty }R_{1}( \kappa )\,\mathrm{d} \kappa + \sum_{\phi _{k} \geq \iota } R_{(1,k)} \biggr]^{1/ \alpha } \\ &\geq \frac{1}{2} P(\iota ) \biggl[ \int _{\iota }^{\infty }R_{1}(\kappa ){ \mathrm{d}} \kappa + \sum_{\phi _{k} \geq \iota } R_{(1,k)} \biggr]^{1/\alpha }. \end{aligned}$$

(19)

Hence,

$$\begin{aligned} w(\iota )\geq \frac{1}{2}P(\iota )U^{1/\alpha }(\iota ) \quad \text{for } \iota \geq \iota _{3} \end{aligned}$$

where

$$\begin{aligned} U(\iota )= \int _{\iota }^{\infty }\sum_{j=1}^{m} r_{j}(\kappa ) \bigl((1-a)w \bigl(\nu _{j}(\kappa ) \bigr) \bigr)^{\beta } \,\mathrm{d}\kappa +\sum_{\phi _{k} \geq \iota } \sum_{j=1}^{m} \tilde{r}_{j}(\phi _{k}) \bigl((1-a)w \bigl( \nu _{j}(\phi _{k}) \bigr) \bigr)^{\beta } . \end{aligned}$$

Now,

$$\begin{aligned} U'(\iota )&=-\sum_{j=1}^{m} r_{j}(\iota ) \bigl((1-a)w \bigl(\nu _{j}( \iota ) \bigr) \bigr)^{\beta } \\ &\leq -\frac{1}{2^{\beta }} \sum_{j=1}^{m} r_{j}(\iota )\bigl[(1-a)P \bigl( \nu _{j}(\iota ) \bigr) \bigr]^{\beta }U^{\beta /\alpha } \bigl(\nu _{j}(\iota ) \bigr)\leq 0 \end{aligned}$$

(20)

and

$$\begin{aligned} \quad \Delta U(\phi _{k})= -\frac{1}{2^{\beta }} \sum _{j=1}^{m} r_{j}( \phi _{k})\bigl[(1-a)P \bigl(\nu _{j}(\phi _{k}) \bigr)\bigr]^{\beta }U^{\beta / \alpha }\bigl(\nu _{j}(\phi _{k}) \bigr)\leq 0, \end{aligned}$$

(21)

which shows that $U(\iota )$ is non-increasing on $[\iota _{4},\infty )$ and $\lim_{\iota \to \infty }U(\iota )$ exists. Using (20) and (a), we find

$$\begin{aligned} \bigl[U^{1-\beta /\alpha }(\iota ) \bigr]'&= (1-\beta / \alpha )U^{-\beta / \alpha }(\iota )U'(\iota ) \\ &\leq -\frac{1-\beta /\alpha }{2^{\beta }} \sum_{j=1}^{m} r_{j}(\iota )\bigl[(1-a)P \bigl(\nu _{j}(\iota ) \bigr) \bigr]^{\beta }U^{\beta /\alpha } \bigl(\nu _{j}( \iota ) \bigr)U^{-\beta /\alpha }(\iota ) \\ &\leq -\frac{1-\beta /\alpha }{2^{\beta }} \sum_{j=1}^{m} r_{j}(\iota )\bigl[(1-a)P \bigl(\nu _{j}(\iota ) \bigr) \bigr]^{\beta } . \end{aligned}$$

(22)

To estimate the discontinuity of $U^{1-\beta /\alpha }$, we use the first-order Taylor polynomial approximation $h(u)=u^{1-\beta /\alpha }$, with $0<\beta <\alpha$ and $u=a$:

$$\begin{aligned} b^{1-\beta /\alpha }-a^{1-\beta /\alpha }\leq (1-\beta /\alpha )a^{- \beta /\alpha }(b-a) . \end{aligned}$$

Then

$$\begin{aligned} \Delta U^{1-\beta /\alpha }(\phi _{k})&\leq (1-\beta /\alpha )U^{- \beta /\alpha }(\phi _{k})\Delta U(\phi _{k}) \\ &\leq -\frac{1-\beta /\alpha }{2^{\beta }} \sum_{j=1}^{m} r_{j}(\phi _{k})\bigl[(1-a)P \bigl(\nu _{j}(\phi _{k}) \bigr)\bigr]^{\beta } . \end{aligned}$$

Integrating (22) from $\iota _{3}$ to ι we have

$$\begin{aligned} \bigl[U^{1-\beta /\alpha }(s) \bigr]_{\iota _{4}}^{\iota }-\sum _{\phi _{k} \geq \iota } &\Delta \bigl[U^{1-\beta /\alpha }(\phi _{k}) \bigr] \leq - \frac{1-\beta /\alpha }{2^{\beta }} \int _{\iota _{3}}^{\iota }\sum_{j=1}^{m} r_{j}(s)\bigl[(1-a)P \bigl(\nu _{j}(s) \bigr) \bigr]^{\beta }\,\mathrm{d}s, \end{aligned}$$

that is,

$$\begin{aligned} &\frac{1-\beta /\alpha }{2^{\beta }} \Biggl[ \int _{0}^{\infty }\sum_{j=1}^{m} r_{j}(s)\bigl[(1-a) P \bigl(\nu _{j}(s) \bigr) \bigr]^{\beta } \,\mathrm{d}s+\sum_{k=1}^{\infty } \sum_{j=1}^{m} \tilde{r}_{j}(\phi _{k})\bigl[(1-a)P \bigl(\nu _{j}( \phi _{k}) \bigr)\bigr]^{\beta } \Biggr] \\ &\quad \leq - \bigl[U^{1-\beta /\alpha }(s) \bigr]_{\iota _{3}}^{\iota }< U^{1- \beta /\alpha }( \iota _{3})< \infty \end{aligned}$$

which contradicts (18). This completes the proof the theorem. □

Example 3.1

Consider the neutral differential equations

$$\begin{aligned}& \bigl( \bigl( \bigl(u(\iota )+e^{-\iota }u\bigl(\zeta (\iota )\bigr) \bigr)' \bigr)^{1/3} \bigr)'+\iota \bigl(u(\iota -2)\bigr)^{5/3} + (\iota +1) \bigl(u(\iota -3) \bigr)^{5/3}=0 , \end{aligned}$$

(23)

$$\begin{aligned}& \bigl( \bigl( \bigl(u\bigl(3^{k}\bigr)+e^{-3^{k}}u \bigl(\zeta \bigl(3^{k}\bigr)\bigr) \bigr)' \bigr)^{1/3} \bigr)'+(\iota +2) \bigl(u\bigl(3^{k}-2 \bigr)\bigr)^{5/3} + (\iota +3) \bigl(u\bigl(3^{k}-3\bigr) \bigr)^{5/3}=0 . \end{aligned}$$

(24)

Here $\alpha = 1/3$, $p(\iota )=1$, $0< q(\iota )=e^{-\iota }<1$, $\nu _{j}(\iota )=\iota -(j+1)$, $\phi _{k}=3^{k}$ for $k \in \mathbb{N}$ with index $j=1,2$. For $\beta =5/3$, we have $\beta =5/3>\alpha =1/3$. To check (15) we have

$$\begin{aligned} & \int _{\iota _{0}}^{\infty } \Biggl[ \frac{1}{p(s)} \Biggl[ \int _{s}^{\infty }\sum_{j=1}^{m} r_{j}(\psi ) \,d\psi +\sum_{\phi _{k}\geq s} \sum _{j=1}^{m} \tilde{r}_{j}(\phi _{k}) \Biggr] \Biggr]^{1/\alpha } \,ds \\ &\quad \geq \int _{\iota _{0}}^{\infty } \Biggl[ \frac{1}{p(s)} \Biggl[ \int _{s}^{\infty }\sum_{j=1}^{m} r_{j}(\psi ) \,d\psi \Biggr] \Biggr]^{1/\alpha } \,ds \\ &\quad \geq \int _{\iota _{0}}^{\infty } \biggl[ \frac{1}{p(s)} \biggl[ \int _{s}^{\infty }r_{1}(\psi ) \,d\psi \biggr] \biggr]^{1/\alpha } \,ds \\ &\quad\geq \int _{2}^{\infty } \biggl[ \int _{s}^{\infty }\psi \,d\psi \biggr]^{3} \,ds=\infty . \end{aligned}$$

So, all the conditions of Theorem 3.1 hold. Thus, each solution of (23)–(24) is oscillatory.

Example 3.2

Consider the neutral differential equations

$$\begin{aligned}& \bigl(e^{-\iota } \bigl( \bigl(u(\iota )+e^{-\iota }u \bigl(\zeta (\iota )\bigr) \bigr)' \bigr)^{11/3} \bigr)' +\frac{1}{\iota +1}\bigl(u(\iota -2)\bigr)^{7/3} + \frac{1}{\iota +2}\bigl(u(\iota -3)\bigr)^{7/3}=0 , \end{aligned}$$

(25)

$$\begin{aligned}& \bigl(e^{-k} \bigl( \bigl(u(k)+e^{-k}u\bigl(\zeta (k)\bigr) \bigr)' \bigr)^{11/3} \bigr)' + \frac{1}{\iota +4}\bigl(u(k-2)\bigr)^{7/3} + \frac{1}{\iota +5} \bigl(u(k-3)\bigr)^{7/3}=0 . \end{aligned}$$

(26)

Here $\alpha = 11/3$, $p(\iota )=e^{-\iota }$, $0< q(\iota )=e^{-\iota }<1$, $\nu _{j}(\iota )=\iota -(j+1)$, $\phi _{k}=k$ for $k \in \mathbb{N}$ with index $j=1,2$, $P(\iota )= \int _{0}^{\iota }e^{3s/11} \,ds=\frac{11}{3}(e^{3\iota /11}-1)$. For $\beta =7/3$, we have $\beta =7/3<\alpha =11/3$. To check (18) we have

$$\begin{aligned} &\frac{1}{(2)^{\beta }} \Biggl[ \int _{0}^{\infty }\sum_{j=1}^{m} r_{j}( \psi )\bigl[(1-a) P \bigl(\nu _{j}(\psi ) \bigr) \bigr]^{\beta } \,d\psi +\sum_{k=1}^{\infty } \sum_{j=1}^{m} \tilde{r}_{j}(\phi _{k})\bigl[(1-a)P \bigl(\nu _{j}( \phi _{k}) \bigr)\bigr]^{\beta } \Biggr] \\ &\quad\geq \frac{1}{(2)^{7/3}} \int _{0}^{\infty }\sum_{j=1}^{m} r_{j}( \psi )\bigl[(1-a) P \bigl(\nu _{j}(\psi ) \bigr) \bigr]^{\beta } \,d\psi \\ &\quad \geq \frac{1}{(2)^{7/3}} \int _{0}^{\infty }r_{1}(\psi )\bigl[(1-a) P \bigl( \nu _{1}(\psi ) \bigr)\bigr]^{\beta } \,\mathrm{d}\psi \\ &\quad= \frac{1}{(2)^{7/3}} \int _{0}^{\infty }\frac{1}{\psi +1} \biggl[(1-a) \frac{11}{3} \bigl(e^{3(\psi -2)/11}-1 \bigr) \biggr]^{7/3} \,d\psi =\infty . \end{aligned}$$

So, all the conditions of Theorem 3.2 hold, and therefore, each solution of (25)–(26) is oscillatory.

4 Conclusions

In this work, we studied second-order highly nonlinear neutral impulsive differential systems and established necessary and sufficient conditions for the oscillation of (10)–(11) when the neutral coefficient lies in $[0, 1)$. It would be of interest to examine the oscillation of (10)–(11) with different neutral coefficients; see, e.g., Refs. [33, 36, 37, 40–43] for more details. Furthermore, it is also interesting to analyze the oscillation of (10)–(11) with a nonlinear neutral term; see, e.g., Ref. [39] for more details.