Stability and Hopf bifurcation of a predator-prey model

Abstract

In this paper, we study a class of predator-prey model with Holling-II functional response. Firstly, by using linearization method, we prove the stability of nonnegative equilibrium points. Secondly, we obtain the existence, direction, and stability of Hopf bifurcation by using Poincare–Andronov Hopf bifurcation theorem. Finally, we demonstrate the validity of our results by numerical simulation.

1 Introduction

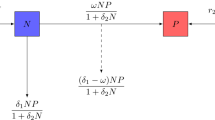
Population ecology is a discipline in which dynamic systems are involved in species, populations, and how these groups interact with the environment. Population ecology primarily studies how species population size changes over time and space. Since Lotka–Volterra’s groundbreaking work in the 1920s, the predator-prey model has become one of the most important research topics in mathematical ecology for nearly a century. At the same time, mathematicians used the theory of dynamics to analyze the differential equations based on a predator-prey model. Hsu and Huang in [4] got some results on the global stability of a predator-prey system. Xiao and Ruan have investigated the global analysis in a predator-prey system with nonmonotonic functional response (we can see [10]). In addition, there are some scholars who applied bifurcation theory in dynamics based on models. In [7], Li and Li considered the Hopf bifurcation of a predator-prey model with time delay and stage structure for the prey. Song studied the stability and Hopf bifurcation of a predator-prey model with stage structure and time delay for the prey (see [8]). There are also many related studies, and we can find them in [5, 11] etc. In this paper, we consider the Gause-type model raised by Caughley and Lawton in [1]. Namely, we are concerned with the predator-prey model with Holling-II functional response

$$ \textstyle\begin{cases} \frac{dN}{dT} =Ng(N)-\frac{aNP}{1+ahN},\\ \frac{dP}{dT}= \frac{caNP}{1+ahN}-mP \end{cases} $$

(1.1)

under positive initial conditions $N(0)> 0$, $P(0)> 0$. The average growth rate of a typical prey species is assumed to be a logistic model

$$ g(N)=R \biggl( 1-\frac{N}{K} \biggr), $$

where N is the prey population density, P is the predator population density, K is the environmental capacity, a is the prey capture rate, h is the capture time, m is the predator’s intrinsic mortality, and c denotes the conversion efficiency of ingested prey into the predator. When the predator density is low, the prey density increases, the individual’s predation rate is the largest. For more details on the background about system (1.1), we can see [6].

Let

$$ x=\frac{N}{RK}, \qquad y=\frac{P}{hKR^{2}}, \qquad t=RT, $$

system (1.1) is dimensionless to

$$ \textstyle\begin{cases} {x}'=x(1-x)-\frac{xy}{x+\alpha },\\ {y}'=\frac{rxy}{x+\alpha }-\sigma y \end{cases} $$

(1.2)

with

$$ \alpha =\frac{1}{ahkR}, \qquad \sigma =\frac{m}{R}, \qquad r= \frac{c}{hR}. $$

2 Preliminary analysis

In this section, we are concerned with the preliminary analysis of system (1.2), namely the boundedness of the solutions and the stability of each nonnegative equilibrium point of system (1.2). Note that the Jacobian of (1.2) is

$$ J= \begin{bmatrix} -2x+1-\frac{ya}{-(x+2)^{2}}&-\frac{x}{x+\alpha }\\ \frac{ry\alpha }{(x+\alpha )^{2}}& \frac{rx}{x+\alpha }-\sigma \end{bmatrix}. $$

We cannot find the diagonal matrix L, so that $LJ+J^{T}L=0$ is established, so system (1.2) is not conservative. Due to the boundedness of the functional response, we can find that

$$ \lim_{(x,y)\rightarrow (0,0)}\frac{dx}{dt}=\lim_{(x,y)\rightarrow (0,0)} \frac{dy}{dt}=0. $$

Assume

$$ \frac{dx}{dt}(0,0)=\frac{dy}{dt}(0,0)=0, $$

then these functions

$$ (x,y)\in \mathbb{R}_{+}^{2}:= \bigl\{ (x,y)\in \mathbb{R}^{2} :x> 0,y>0 \bigr\} . $$

In fact, direct calculations indicate that system (1.2) satisfies the Lipschitz condition.

2.1 Boundedness of solution

Theorem 2.1

All the solutions of system (1.2) are uniformly bounded on $\mathbb{R}_{+}^{2}$.

Proof

We define a function

$$ \tau =rx+y, $$

then

$$ \frac{d\tau }{dt}=r\frac{dx}{dt}+\frac{dy}{dt}. $$

For each $\eta < \sigma$,

$$\begin{aligned} \frac{d\tau }{dt}+\eta \tau &=rx(1-x)-\frac{rxy}{x+\alpha }+ \frac{rxy}{x+ \alpha }-\sigma y+\eta (rx+y) \\ &= rx(1+\eta -x )+y(\eta -\sigma ) \\ &\leq \frac{r(1+\eta )^{2}}{4}. \end{aligned}$$

Upon that we can find $\varphi > 0~$ such that

$$ \frac{d\tau }{dt}+\eta \tau =\varphi . $$

Through the above equation, we have $\frac{d\tau }{dt}+\eta \tau \leq \varphi$, which implies that

$$ \tau (t)\leq e^{-\eta t}\tau (0)+\frac{\varphi }{\eta } \bigl(1-e^{-\tau t}\bigr) \leq \max \biggl\{ \tau (0), \frac{\varphi }{\eta } \biggr\} =M. $$

Moreover, we have

$$ \lim_{t\rightarrow \infty }\tau (t)\leq M. $$

 □

2.2 Stability analysis

In this section, we analyze the stability of the nonnegative equilibrium points for system (1.2). It is easy to get the nonnegative equilibrium points of system (1.2): $E_{0} (0,0)$, $E_{1}(1,0)$, and $E_{*}(x^{*},y ^{*})$ with $x^{*}=\frac{\sigma \alpha }{r-\sigma }$, $y^{*}=(1-x^{*})(x ^{*}+\alpha )$, and $r>\sigma (\alpha +1)$ ensures system (1.2) has a unique positive equilibrium point $E_{*}(x^{*},y^{*})$.

2.2.1 Stability analysis of the equilibrium $E_{0}(0,0)$

Theorem 2.2

The equilibrium $E_{0}(0,0)$ is unstable.

Proof

The Jacobi matrix of (1.2) at $E_{0}(0,0)$ is

$$ J_{0}= \begin{bmatrix} 1 & 0 \\ 0 & -\sigma \end{bmatrix} . $$

Then the characteristic equation of $J_{0}$ is

$$ \mu ^{2}-P\mu +Q=0 $$

with

$$ P=1-\sigma ,\qquad Q=-\sigma . $$

Clearly, $E_{0}(0,0)$ is a saddle point which is unstable. □

2.2.2 Stability analysis of the equilibrium $E_{1}(1,0)$

Theorem 2.3

• (1) The equilibrium $E_{1}(1,0)$ is locally asymptotically stable if $r< (1+\alpha )\sigma$.

• (2) System (1.2) enters into transcritical bifurcation around $r=(1+\alpha )\sigma$.

• (3) The equilibrium $E_{1}(1,0)$ is globally asymptotically stable if $r<\sigma -1$.

Proof

(1) The Jacobian of (1.2) at $E_{1}(1,0)$ is

$$ J_{1}= \begin{bmatrix} -1&-\frac{1}{1+\alpha } \\ 0 & \frac{r}{1+\alpha }-\sigma \end{bmatrix} . $$

Then the characteristic equation of $J_{1}$ is

$$ \mu ^{2}-P\mu +Q=0 $$

with

$$ P=\frac{r}{1+\alpha }-\sigma -1,\qquad Q=\sigma -\frac{r}{1+\alpha }. $$

If $r< (1+\alpha )\sigma$, we have $P< 0$ and $Q> 0$. Therefore, the equilibrium point $E_{1}(1,0)$ is locally asymptotically stable.

(2) The one of eigenvalues of $J_{1}$ will be 0 if $\operatorname{det} J_{1}=0$, which gives $r=(1+\alpha )\sigma$. If Ω and Φ denote the eigenvectors corresponding to the eigenvalue 0 of the matrices $J_{1}$ and $J_{1}^{T}$, respectively.

Let

$$ \varOmega =(\varPsi _{1}, \varPsi _{2})^{T},\qquad \varPhi =(0,\varpi _{2})^{T}, $$

where $\varPsi _{1}=-\frac{1}{1+\alpha }\varPsi _{2}$, and $\varPsi _{2}$, $\varpi _{2}$ are two nonzero numbers.

Now

$$ \varPhi ^{T}\bigl[F_{r}(X_{1},r)\bigr]=0, $$

where $X_{1}=(1,0)$. According to Sotomayor’s theory in [9], system (1.2) does not attain any saddle-node bifurcation around $E_{1}(1,0)$.

Again

$$ \varPhi ^{T}\bigl[DF_{r }(X_{1},r)\varOmega \bigr] =\frac{\varPsi _{2}\varpi _{2}}{1+\alpha }\neq 0 $$

and

$$ \varPhi ^{T}\bigl[D^{2}F_{r}(X_{1},r) (\varOmega ,\varOmega )\bigr]\neq 0, $$

where

$$ \bigl[DF_{r}(X_{1},r)\bigr]= \begin{bmatrix} 0 &0 \\ 0 &\frac{1}{1+\alpha } \end{bmatrix} , $$

and

$$ D^{2}F(X,r)= \begin{bmatrix} \bigtriangledown \frac{\partial F_{1}}{\partial x } & \bigtriangledown \frac{\partial F_{2}}{\partial x } \\ \bigtriangledown \frac{\partial F_{1}}{\partial y } &\bigtriangledown \frac{\partial F_{2}}{\partial y } \end{bmatrix} \in \mathbb{R}^{2\times 2\times 2} $$

with

$$ \bigtriangledown \frac{\partial F_{i}}{\partial x}= \biggl(\frac{\partial ^{2}F_{i}}{\partial x^{2}} , \frac{\partial ^{2}F_{i}}{\partial x\partial y}\biggr)^{T}, \qquad \bigtriangledown \frac{\partial F_{i}}{\partial y}= \biggl(\frac{ \partial ^{2}F_{i}}{\partial x\partial y} ,\frac{\partial ^{2}F_{i}}{ \partial y^{2}} \biggr)^{T} $$

for $i=1,2$. Then, according to the same theorem [9], system (1.2) experiences transcritical bifurcation at $r=(1+\alpha )\sigma$ around the axial equilibrium $E_{1}(1,0)$.

(3) Let $(x,y)\in \mathbb{R}_{+}^{2}:= \{ (x,y)\in \mathbb{R} ^{2} :x> 0,y> 0 \}$ and consider the function $V:\mathbb{R}_{x} ^{2}\rightarrow \mathbb{R}$,

$$ V(x,y)=\frac{1}{2}(x-1)^{2}+\frac{1}{2}y^{2}+y. $$

(2.1)

The derivative of (2.1) along system (1.2) is

$$\begin{aligned} \frac{dV}{dt} &=(x-1){x}'+y{y}'+y' \\ &=(x-1)\biggl[x(1-x)-\frac{xy}{x+\alpha }\biggr]+y\biggl(\frac{rxy}{x+\alpha }- \sigma y\biggr)+\biggl(\frac{rxy}{x+ \alpha }-\sigma y\biggr) \\ &=-(1-x)^{2}x-\frac{(x-1)xy}{x+\alpha }+\frac{rxy^{2}}{x+\alpha }- \sigma y^{2}+\frac{rxy}{x+\alpha }-\sigma y \\ &\leq \frac{xy}{x+\alpha }+ry^{2}-\sigma y^{2}+ry- \sigma y \leq y(1+r-\sigma )+y^{2}(r-\sigma ), \end{aligned}$$

if $\sigma >1+r$, then $\frac{dV}{dt}<0$, and $E_{1}(1,0)$ is globally asymptotically stable. □

2.2.3 Stability analysis of the positive equilibrium $E _{*}(x^{*},y^{*})$

The Jacobi matrix of (1.2) at $E_{*}(x^{*},y^{*})$ is

$$ J_{*}= \begin{bmatrix} \frac{\sigma r-\sigma ^{2} -\sigma (r+\sigma )\alpha }{(r-\sigma )r}&-\frac{ \sigma }{r} \\ r-\sigma \alpha -\sigma & 0 \end{bmatrix} . $$

Then the characteristic equation of $J_{*}$ is

$$ \mu ^{2}+P\mu +Q=0 $$

(2.2)

with

$$ P=-\frac{\sigma r-\sigma ^{2}-\sigma (r+\sigma )\alpha }{(r-\sigma )r},\qquad Q=\frac{\sigma r-\sigma ^{2}(\alpha +1)}{r}. $$

If $r>\sigma (\alpha +1)$, we have $Q>0$, by simple calculations, we get the following theorem.

Theorem 2.4

Let $\alpha <1$. If $r> \frac{\sigma (1+\alpha )}{1-\alpha }$, then the eigenvalue of Eq. (2.2) has a pair of negative real parts, that is, the positive equilibrium point $E_{*}(x^{*},y^{*})$ is locally asymptotically stable. If $\sigma (\alpha +1)< r<\frac{\sigma (1+ \alpha )}{1-\alpha }$, then $E_{*}(x^{*},y^{*})$ is unstable.

3 The analysis of the Hopf bifurcation

In this section, we consider the Hopf bifurcation of system (1.2) at $(x^{*},y^{*})$ by setting the parameter of bifurcation as r. Define $r_{0}=\frac{\sigma (1+\alpha )}{1-\alpha }$. Let $\mu =\delta (r) \pm \omega (r)i$ be the two roots of Eq. (2.2), by calculating, we can get

$$\begin{aligned}& \delta (r)=\frac{\sigma r-\sigma ^{2}-\sigma (r+\sigma )\alpha }{2(r- \sigma )r }, \\& \omega (r)=\frac{\alpha }{2}\sqrt{\frac{\sigma r-\sigma ^{2}-\sigma (r+\sigma )\alpha }{(r-\sigma )r}- \frac{4(\sigma r-\sigma ^{2}-\sigma \alpha )}{r}}. \end{aligned}$$

According to Mainul’s theory in [2], we know that if $\operatorname{tr}J_{*}=0$, then both eigenvalues of Eq. (2.2) will be purely imaginary provided $\operatorname{det}J_{*}>0$. Therefore, the implicit function theorem implies that a Hopf bifurcation occurs where a periodic orbit is created as the stability of the equilibrium point $E_{*}$ changes. Now, let $\operatorname{tr}J_{*}=0$, we have

$$ \operatorname{det}J_{*}=\frac{\sigma (1+\alpha ^{2})}{1+\alpha }. $$

Obviously, $\operatorname{det}J_{*}>0$, which should be positive in order to get a Hopf bifurcation. In order to obtain more details of the Hopf bifurcation at $(x^{*},y^{*})$, we need to do a further analysis to system (1.2). Let $\widetilde{x}=x-x^{*}$, $\widetilde{y}=y-y^{*}$, we transform the equilibrium $(x^{*},y^{*})$ of system (1.2) to ($0,0$) of a new system. For the sake of simplicity, we denote x̃, ỹ by x, y, respectively. Thus, system (1.2) is transformed to

$$ \textstyle\begin{cases} {x}' =(x^{*}+x)(1-x-x^{*})-\frac{(x+x^{*})(y+y^{*})}{(x+x^{*})+\alpha },\\ {y}'=\frac{r(x+x^{*})(y+y^{*})}{(x+x^{*})+\alpha }-\sigma (y+y ^{*}). \end{cases} $$

(3.1)

Rewrite system (3.1) as

$$ \binom{x'{(t)}}{y'{(t)}}=J\binom{x}{y}+\binom{f(x,y,r)}{g(x,y,r)}, $$

(3.2)

where

$$\begin{aligned} f(x,y,r)= {}&A_{1}x^{2}+A_{2}xy+A_{3}y^{2}+A_{4}x^{3}+A_{5}x^{2}y+A_{6}xy ^{2}+A_{7}y^{3} \\ &{}+o\bigl( \vert x \vert ^{4}+ \vert x \vert ^{3} \vert y \vert + \vert x \vert ^{2} \vert y \vert ^{2}+ \vert x \vert ^{3} \vert y \vert \bigr), \\ g(x,y,r)={} &B_{1}x^{2}+B_{2}xy+B_{3}y^{2}+B_{4}x^{3}+B_{5}x^{2}y+B_{6}xy ^{2}+B_{7}y^{3} \\ &{}+o\bigl( \vert x \vert ^{4}+ \vert x \vert ^{3} \vert y \vert + \vert x \vert ^{2} \vert y \vert ^{2}+ \vert x \vert ^{3} \vert y \vert \bigr) \end{aligned}$$

with

$$\begin{aligned} A_{1} &=\frac{(r-\sigma -\sigma r)(r-\sigma )\alpha }{\sigma ^{2}\alpha }-1, \qquad A_{2}= \frac{(r-\sigma )^{2}}{2\sigma ^{2}\alpha }, \\ A_{4} &=\frac{(r-\sigma -\sigma r)(r-\sigma )^{2} }{\sigma ^{2}\alpha }, \qquad A_{5}= \frac{(r-\sigma )^{3}}{3\sigma ^{3}\alpha ^{2} }, \\ B_{1} &=-\frac{r(r-\sigma -\sigma r)(r-\sigma )}{\sigma ^{2}\alpha }, \qquad B_{2}= \frac{r(r-\sigma )^{2}}{2\sigma ^{2}\alpha }, \\ B_{4} &=\frac{r(r-\sigma -\sigma r)(r-\sigma )^{2}}{\sigma ^{3}\alpha ^{2}}, \qquad B_{5}=- \frac{r(r-\sigma )^{3}}{3\sigma ^{3}\alpha ^{2}}, \\ A_{3} &=A_{6}=A_{7}=B_{3}=B_{6}=B_{7}=0. \end{aligned}$$

Define

$$ T= \begin{bmatrix} 1 &0 \\ T_{1} & T_{2} \end{bmatrix} $$

with

$$\begin{aligned}& T_{1}=\frac{\sigma r-\sigma ^{2}-\sigma (r+\sigma )\alpha }{2(r-\sigma )\alpha }, \\& T_{2}=\frac{\alpha }{2}\sqrt{\frac{\sigma r-\sigma ^{2}-\sigma (r+ \sigma )\alpha }{(r-\sigma )r}- \frac{4(\sigma r-\sigma ^{2}-\sigma \alpha )}{r}}. \end{aligned}$$

If

$$ \begin{bmatrix} 1 \\ T_{1}-T_{2}i \end{bmatrix} \mu =\delta (r)\pm \omega (r)i, $$

and

$$ T^{-1}= \begin{bmatrix} 1 & 0 \\ -\frac{T_{1}}{T_{2}}& \frac{1}{T_{2}} \end{bmatrix} . $$

Through further transform, we have

$$ \begin{bmatrix} X \\ Y \end{bmatrix} =T^{-1} \begin{bmatrix} x \\ y \end{bmatrix} , $$

namely

$$ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} X \\ T_{1}X+T_{2}Y \end{bmatrix} . $$

Thus, system (3.2) can be transformed into

$$ \begin{bmatrix} X'{(t)} \\ Y'{(t)} \end{bmatrix} =T^{-1}JT+T^{-1} \begin{bmatrix} F(X,T_{1}X+T_{2}Y,r) \\ G(X,T_{1}X+T_{2}Y,r) \end{bmatrix} $$

with

$$\begin{aligned} F(X,Y,r)= {}&C_{1}X^{2}+C_{2}XY+C_{3}Y^{2}+C_{4}X^{3}+C_{5}X^{2}Y+C_{6}XY ^{2}+C_{7}Y^{3} \\ &{}+o\bigl( \vert X \vert ^{4}+ \vert X \vert ^{3} \vert Y \vert + \vert X \vert ^{2} \vert Y \vert ^{2}+ \vert X \vert ^{3} \vert Y \vert \bigr), \\ G(X,Y,r)={} &D_{1}X^{2}+D_{2}XY+D_{3}Y^{2}+D_{4}X^{3}+D_{5}X^{2}Y+D_{6}XY ^{2}+D_{7}Y^{3} \\ &{}+o\bigl( \vert X \vert ^{4}+ \vert X \vert ^{3} \vert Y \vert + \vert X \vert ^{2} \vert Y \vert ^{2}+ \vert X \vert ^{3} \vert Y \vert \bigr), \end{aligned}$$

where

$$\begin{aligned} C_{1} &= \biggl(\frac{(r-\sigma -\sigma r)(r-\sigma )\alpha }{\sigma ^{2} \alpha }-1 \biggr) \bigl(1+T_{1}+T_{1}^{2}\bigr), \qquad C_{2}=\frac{(r-\sigma )^{2}(T _{2}+2T_{1}T_{2})}{2\sigma ^{2}\alpha }, \\ C_{4} &=\frac{(r-\sigma -\sigma r)(r-\sigma )^{2}(1+T_{1}+T_{1}^{2}+T _{1}^{3}) }{\sigma ^{2}\alpha },\qquad C_{5}= \frac{(r-\sigma )^{3}(T_{2}+2T _{1}T_{2}+3T_{1}^{2}T_{2})}{3\sigma ^{3}\alpha ^{2} }, \\ D_{1} &=-\frac{T_{1}}{T_{2}}C_{1}+ \frac{r(r-\sigma -\sigma r)(1+T_{1}+T _{1})}{T_{2}\alpha \sigma ^{2}},\qquad D_{2}=-\frac{T_{1}}{T_{2}}C_{2}+ \frac{(r- \sigma )^{2}r(1+2T_{1})}{2\sigma ^{2}\alpha }, \\ D_{4} &=-\frac{T_{1}}{T_{2}}C_{4}+ \frac{r(r-\sigma -\sigma r)(r- \sigma )^{2}(1+T_{1}+T_{1}^{2}+T_{1}^{3})}{T_{2}\sigma ^{3}\alpha ^{2}}, \\ D_{5} &=-\frac{T_{1}}{T_{2}}C_{5}- \frac{r(r-\sigma )^{3}(1+2T_{1}+3T _{1}^{2})}{3\sigma ^{3}\alpha ^{2}}, \\ C_{3} &=C_{6}=C_{7}=D_{3}=D_{6}=D_{7}=0. \end{aligned}$$

Performing polar transformation on system (1.2) according to the technique in [6], we have

$$\begin{aligned} {\rho }'(r) &=\delta (r)\rho +a(r)\rho ^{3}+\cdots , \\ \theta '(r) &=\omega (r)+b(r)\rho ^{2}+\cdots . \end{aligned}$$

The Taylor expansion of equations above at $r=r_{0}$ are

$$\begin{aligned} {\rho }' &=\delta (r_{0}) (r-r_{0})\rho +a(r_{0})\rho ^{3}+o\bigl((r-r_{0})^{2} \rho ,(r-r_{0})\rho ^{3},\rho ^{5} \bigr), \\ {\theta }' &=\omega (r_{0}) +\omega (r_{0}) (r-r_{0}) +b(r_{0})\rho ^{2}+o\bigl((r-r_{0}),(r-r_{0})r^{2},r^{4} \bigr). \end{aligned}$$

In order to investigate the stability of the periodic solution, we need to calculate the sign of the coefficient $a(r_{0})$, which is given by

$$\begin{aligned} a(r_{0})= {}&\frac{1}{16}\bigl[{F}'_{XXX}+{F}'_{XYY}+{G}'_{XXX}+{G}'_{YYY} \bigr] \\ &{}+\frac{1}{16\omega _{0}}\bigl[F'_{XY} \bigl(F'_{XX}+F'_{YY} \bigr)-G'_{XY}\bigl(G'_{XX}+G'_{YY} \bigr)-F'_{XX}G'_{XX}+F'_{YY}G'_{YY} \bigr]. \end{aligned}$$

Calculate the partial derivative of the bifurcation at $(X,Y,r)=(0,0,r _{0})$ when $\omega _{0}=\omega (r_{0})$, we have

$$\begin{aligned} a(r_{0})= {}&\frac{1}{8}\biggl[3C_{4}+C_{6}+D_{5}-3 \frac{T_{10}}{T_{20}}C_{7}\biggr] \\ &{}+\frac{1}{8\omega _{0}}\bigl[C_{2}(C_{1}+C_{3})-D_{2}(D_{1}+D_{3})-2C_{1} ^{2}D_{1}^{2}+2C_{3}^{2}D_{3}^{2} \bigr]. \end{aligned}$$

The explicit calculation of $a(r_{0})$ can be found in [3]. According to Poincare–Andronow’s Hopf bifurcation theory and the above calculations of $a(r_{0})$, we get the further result.

Theorem 3.1

Set $r>\sigma (\alpha +1)$ and $\alpha <1$ hold. If $a(r_{0})<0$, the periodic solution of the Hopf bifurcation from $(x^{*},y^{*})$ is asymptotically stable, the Hopf bifurcation is subcritical. If $a(r_{0})>0$, the periodic solution of the bifurcation is unstable, and the Hopf bifurcation is supercritical.

4 Numerical simulations

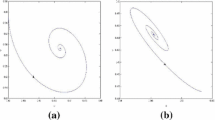
In this section, we perform numerical simulations about system (1.2). Figure 1 shows that $E_{0}(0,0)$ is a saddle point which is unstable and $E_{1}(1,0)$ is also a saddle point when we set $r=0.4$, $\alpha =0.2$, $\sigma =0.3$. We also can observe that $E_{*}(x^{*},y^{*})$ is locally asymptotically stable when $\alpha <1$ and $r> \frac{\sigma (1+ \alpha )}{1-\alpha }$.

Figure 1

$E_{0}(0,0)$ is a saddle point

The equilibrium point $E_{1}(1,0)$ is globally asymptotically stable. In order to make sure $\sigma > \frac{r}{1+\alpha }$, we set $r=0.4$, $\alpha =0.2$, $\sigma =0.35$, as shown in Fig. 2.

Figure 2

$E_{1}(1,0)$ is globally asymptotically stable

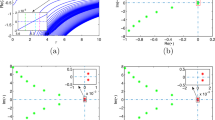
Let $\alpha =0.2$, $\sigma =0.3$, we have $r_{0}=0.45$. When $r=0.45$, system (1.2) emits a Hopf bifurcation at $(x^{*},y^{*})$. And by further calculation, we have $a(r_{0})\approx -1.833<0$, the Hopf bifurcation is subcritical and the periodic solution of the Hopf bifurcation at $(x^{*},y^{*})$ is asymptotically stable, see Fig. 3.

Figure 3

Hopf bifurcation at $r_{0}=0.45$