Abstract
Considering the effect of variable viscosity and the phenomenon of flow separation, the MHD Cu/Ag-Water nanofluids through a permeable wedge are investigated. The governing equations of flow and energy are reduced by similarity transformations and then solved numerically by the shooting method. It is found that dual solutions exist for negative pressure gradient. Compared with the Ag-Water nanofluid, the flow separation occurs later for injection, while it occurs earlier for suction in the Cu-Water nanofluid. The outcomes also specify that suction and small variable viscosity parameters delay the separation for the two nanofluids.
Similar content being viewed by others
1 Introduction
Because of the low thermal conductivity, there is a limit to the heat transfer performance of the classical heat transfer fluids such as water, ethylene glycol, and engine oil. The thermal conductivity of metals, however, is extremely higher compared with the conventional heat transfer fluids. A nanofluid, which was first proposed by Choi and Eastman [1], is a fluid that is created by the distribution of solid particles with dimensions less than 100 nm in base fluid. Choi noticed that the addition of one percent of nanoparticles by volume to the usual fluids increases the thermal conductivity of the fluid up to approximately twice. Comprehensive literature on the applications of nanofluids can be found in papers [2–5]. Magnetic nanofluid is a magnetic colloidal suspension of carrier liquid and magnetic nanoparticles. The advantage of the magnetic nanofluid is that fluid flow and heat transfer can be controlled by an external source, which makes it applicable to modern metallurgical and metal-working processes such as electronic packing, thermal engineering, and aerospace. Therefore many researchers have been contributing to the study of magneto-hydrodynamic (MHD) nanofluid flow [6–8].
On the other hand, the study of the flow field in a boundary adjacent to the wedge, an essential part in the area of fluid dynamics and heat transfer, is very important in many thermal engineering applications like geothermal systems, crude oil extraction, thermal insulation heat exchangers, the storage of nuclear waste, etc. Falkner and Skan [9] were the first to analyze the steady laminar flow over a wedge, and they proposed a well-known Falkner-Skan equation to describe the flow over a wedge, which has provided many fruitful sources of information about the behavior of incompressible boundary layers. Since then, many researchers have devoted themselves to investigating the same problem and gained lots of valuable results, see [10–16]. In the past decade, Su and Zheng [17] analyzed the Hall effect on MHD flow and heat transfer of nanofluids over a stretching wedge in the presence of velocity slip and Joule heating. Srinivasacharya et al. [18] investigated the steady laminar magnetohydrodynamic (MHD) flow, heat and mass transfer characteristics in a nanofluid over a wedge in the presence of a variable magnetic field. Khan et al. [19] presented the locally similar solutions for the unsteady two-dimensional Falkner-Skan flow of MHD Carreau nanofluid past a static/moving wedge in the presence of convective boundary condition. They found that an increment in the pressure gradient parameter depreciates the heat and mass transfer rate both for shear thinning and shear thickening fluids.
All the above-mentioned literature about MHD nanofluids flowing past a wedge only considered the accelerating or constant flow case, with positive or constant pressure gradient. In both cases, there exists no separation point in the velocity profile. However, many early researchers [20–23] pointed out that for the decelerating flow case, with negative pressure gradient, two solutions occurred in the well-known Falkner-Skan equation. Hence separation may happen in the decelerating flow. As the results pointed out in the reference [24], the occurrence of flow separation has several undesirable effects, and it leads to an increase in the drag on a body immersed in the flow. In order to reduce the drag force, injection on the boundary layer flow has been introduced and proved to be an effective way [25].
Motivated by the above research, this paper aims to explore the flow and heat transfer of MHD nanofluid past a permeable wedge with suction or injection, considering the occurrence of flow separation and variable viscosity. The physical properties of the nanofluids may change significantly with temperature [26–28]. To more accurately depict the flow behavior and heat transfer, it is necessary to take the variation of viscosity with temperature into account. By means of similarity reductions, the nonlinear equations are solved numerically by the shooting method. Besides, the effects of the governing parameters on the separation point, dimensionless velocity, temperature, skin friction coefficient, and local Nusselt number are graphically presented and discussed in detail.
2 Formulation
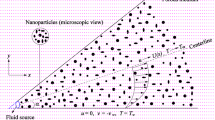
We consider a steady two-dimensional laminar flow and heat transfer of viscous incompressible MHD Cu/Ag-Water nanofluids past a permeable wedge with temperature-dependent viscosity. The coordinate system is selected in such a way that the x-axis is aligned with the flow on the surface of the wedge and the y-axis is taken normal to it, as shown in Figure 1. The inclined angle of the wedge is taken as \(\Omega= \beta\pi\). The free stream velocity \(U_{e} ( x ) = U_{0} x^{m}\), where \(U_{0}\) is constant and m is a pressure gradient parameter related in the inclined angle βπ by \(m = \beta/(2-\beta)\). A variable magnetic field of strength \(B ( x ) = B_{0} x^{(m-1)/2}\) is applied along the y-direction, where \(B_{0}\) is constant. It is assumed that the temperature on the wedge surface is a constant \(T_{w}\) and the ambient temperature is \(T_{\infty}\). \(V_{w} \) is the velocity of suction (\(V_{w} <0\)) or injection (\(V_{w} >0\)). Further, the magnetic Reynolds number is assumed to be small so that the induced magnetic field can be neglected in comparison with the applied magnetic field. The base fluid water and the nanoparticles are also assumed to be in thermal equilibrium, and there is no slippage between them.
With the above assumptions, using Boussinesq and boundary layer approximations, the governing equations for the continuity, momentum, and energy can be expressed as follows:
with the boundary conditions
Here \((u, v)\) are the velocity components along the x and y directions, respectively, T is the temperature, and σ is the electrical conductivity. The effective dynamic viscosity \(\mu_{\mathit {nf}}\), the effective density \(\rho_{\mathit {nf}}\), the thermal diffusivity \(\alpha _{n}\), and the heat capacity \((\rho C_{p} )_{\mathit {nf}}\) of the nanofluids are defined as in [29, 30]
where ϕ is the solid volume fraction of nanoparticles. The thermal conductivity of nanofluids restricted to spherical nanoparticles is approximated by the Maxwell-Garnett (MG) model [31]:
in which the subscripts nf, f, and s represent the thermophysical properties of the nanofluid, base fluid, and nano solid particles, respectively.
Note that the viscosity of base fluid \(\mu_{f}\) is not constant, but vary as a function of temperature given by the following [24, 32]:
where \(a=\gamma/ \mu_{\infty}\) and \(T_{r} = T_{\infty} - \gamma ^{-1}\), \(\mu_{\infty}\), a constant, is the cold free stream viscosity, a and \(T_{r} \) are constants related to the reference state, and γ is a thermal property of the fluid. For nanofluids, \(a>0\). To solve Eqs. (1), (2), and (3) subjected to the boundary conditions (4) and (5), we introduce the stream function \(\psi(x,y)\) (\(u= {\partial \psi} / \partial y\), \(v=-\partial\psi/\partial x \)) and the similarity variables as
Then Eqs. (1)-(3) are reduced to
where
prime denotes differentiation with respect to η, \(\upsilon_{ \infty}\) is the cold free stream kinematic viscosity, the magnetic field parameter \(M= \sigma B_{0}^{2} / U_{\infty} \rho_{\mathit {nf}}\), the Prandtl number \(P_{r} = \upsilon_{\infty} (\rho C_{p} )_{f} / k_{f}\), and the variable viscosity parameter \(\theta_{r} =( T_{r} - T_{\infty } )/( T_{w} - T_{\infty} )\).
According to the definition of \(\theta_{r}\), we obtain \(\mu_{f} = \mu_{\infty} /[1-\theta(\eta)/ \theta_{r} ]\). Since the viscosity of liquids decreases with increasing temperature, \(\theta_{r}\) is negative for nanofluids. When \(\theta_{r} \rightarrow-\infty\), \(\mu_{f} \rightarrow\mu_{\infty}\), i.e., the viscosity variation in the boundary layer is negligible.
The boundary conditions (4) and (5) can be converted into
where \(f_{w} =- V_{w} \sqrt{2x/[ ( m+1 ) \upsilon_{ \infty} U_{e} ]}\), \(f_{w} <0 \) for injection and \(f_{w} >0\) for suction, while \(f_{w} =0\) for impermeable wedge surface.
The quantities of physical interest are the skin friction coefficient \(C_{f}\) and the local Nusselt number \(\mathit {Nu}_{x}\), which are defined as [24]
where \(\tau_{w}\) is the wall shear stress on the surface and \(q_{w}\) is the surface heat flux. Using the similarity transformation (12), we obtain
where \(\mathit {Re}_{x} = U_{e} x/ \upsilon_{\infty}\) is the local Reynolds number. So, \(f^{\prime\prime} ( 0 ) \) represents the skin friction coefficient \(C_{f} \) and \(- \theta' ( 0 ) \) represents the local Nusselt number \(\mathit {Nu}_{x}\).
3 Results and discussion
Numerical solutions to the nonlinear ordinary differential Eqs. (13) and (14) with the boundary conditions (15) and (16) can be obtained by the shooting method. In order to acquire the sufficiently accurate numerical solutions, the convergence criterion 10−6 is used in the iterative process. To confirm the accuracy of the applied numerical method, values of \(f^{\prime\prime} ( 0 ) \) and \(- \theta' ( 0 ) \) for different values of the Falkner-Skan exponent m with \(P_{r} =0.73 \) and \(f_{w} =0 \) were compared with the established results of the research carried out by Watanabe [33] and Deka et al. [24]. The results were found in good agreement (see Table 1).
In the present work, MHD mixed convection flow and heat transfer past a permeable wedge immersed in nanofluids with variable viscosity are conducted. Two different nanoparticles, namely, copper (Cu) and silver (Ag), with water as the base fluid are considered in this study. The Prandtl number of the base fluid was kept at constant as \(P_{r} =6.2\). The thermophysical properties of water and Cu/Ag nanoparticles are given in Table 2.
Figure 2 shows the skin friction \(f''(0)\) of Cu/Ag-Water nanofluids as a function of m for representative values of \(f_{w} \) when \(\theta_{r} =-2\), \(\phi=0.05 \), \(M=0\). It is seen that there is only one solution when \(m\geq0\), two solutions when \(m_{C} \leq m<0\), and no solution when \(m< m_{C}\). Here \(m_{C}\) is the critical value. In addition, the skin friction coefficient \(f''(0)\) almost vanishes when \(m< m_{C}\) for the two nanofluids. In the range \(m_{C} \leq m<0\), there exist two values of \(f^{\prime\prime} ( 0 ) \). One is \(f^{\prime\prime} ( 0 ) \geq0\) and the other is \(f^{\prime\prime} ( 0 ) <0\). Physically, \(f ^{\prime\prime} ( 0 ) >0\) means that the nanofluid exerts a drag force on the wedge, while \(f^{\prime\prime} ( 0 ) <0\) means the opposite and \(f^{\prime\prime} ( 0 ) \approx0\) at \(m_{C}\) means there is no wall shear stress and the flow will separate completely at this point. From Figure 2 we can also see that the flow separation is delayed as the value of \(f_{w} \) increases. Hence suction delays the separation. Further, compared with the Ag-Water nanofluid, the flow separation occurs later for injection, while it occurs earlier for suction in the Cu-Water nanofluid.
Figure 3 depicts the skin friction \(f''(0)\) of Cu/Ag-Water nanofluids as a function of m for representative values of \(\theta_{r} \) with \(f_{w} =\pm0.2 \), \(\phi=0.05\), \(M=0\). From Figure 3, we can see that the separation is delayed with smaller value of \(- \theta_{r}\) for both suction (\(f_{w} =0.2\)) and injection (\(f_{w} =-0.2\)). Besides, the adverse critical values \(-m _{c}\) of Cu-Water are a bit lower than those of Ag-Water for suction, but we found just the opposite for injection for each fixed \(\theta_{r}\), which is consistent with the results of Figure 2. Critical values \(m_{C}\) with representative values of \(f_{w}\) or \(\theta_{r} \) are shown in Table 3.
The velocity and temperature profiles of the first and second solutions for various values of pressure gradient parameter m for the two nanofluids are shown in Figure 4 and Figure 5, respectively when \(\phi=0.05\), \(f_{w} =1\), \(\theta_{r} =-2\), \(P_{r} =6.2\) and \(M=0\). From Figure 4, it is observed that for the first solution, an increase in m leads to an increase in the flow velocity profiles near the surface of the wedge. Most importantly, the boundary layer thickness becomes thinner with an increase in m, which means that a higher velocity gradient occurs at the surface. In addition, for accelerated flows with positive pressure gradient (\(m>0\)), no point of inflection occurs in the velocity profiles. For decelerated flows with negative pressure gradient (\(m<0\)), however, we obtain velocity profile with a point of inflection. The second solution profiles prove the existence of dual solutions for decelerated flows. Furthermore, both the magnitude of the reverse flow (second solution) velocity and the boundary layer thickness increase with a decrease in the adverse pressure gradient parameter (−m). From Figure 4 we can also see that the velocity of Cu-Water is lower than Ag-Water for every single m in the first solution. But a cross point is found in the second solution, which means that the velocity of Cu-Water is larger than that of Ag-Water for small dimensionless η, but it is just opposite for larger η. From Figure 5 we can find that the influence of pressure gradient parameter m on the temperature profiles is much less than that on velocity profiles for the two nanofluids. Also, the temperature of Cu-Water nanofluid is slightly lower than that of Ag-Water nanofluid for each fixed m. It is worth noting that dual solutions also exist in the temperature profiles for decelerated flows (\(m<0\)).
Velocity and temperature profiles of Cu-Water nanofluid for different values of ϕ are presented in Figure 6 and Figure 7, respectively. It was verified that the Ag-Water nanofluid has similar velocity and temperature profiles for different values of ϕ. Here we only discuss the velocity and temperature profiles of Cu-Water nanofluid against ϕ. It can be seen from Figure 6 that both the velocity and temperature profiles increase with the increasing solid volume fraction of nanoparticles ϕ for suction (\(f _{w}=0.5\)). For injection (\(f _{w}=-0.5\)), however, the temperature profile declines with an increase in the nanoparticle volume fraction for smaller η, but it is just the opposite for larger η within the boundary layer. Figure 6 also shows that the velocity profile in the presence of suction (\(f _{w}=0.5\)) is larger than that in the presence of injection (\(f _{w}=-0.5\)), while the temperature profile is just the opposite. So, suction accelerates the fluid motion and reduces the temperature of the nanofluid along the wall. Figure 7 depicts the temperature profile of Cu-Water nanofluid for various values of ϕ when \(\theta_{r} =-2,- \infty\). Figure 7 tells us that for a fixed ϕ, the velocity profile is larger, while the temperature profile is lower for \(\theta_{r}=-2\) than that for \(\theta_{r}=-\infty\). This can be physically explained that the temperature difference of the permeable wedge and the ambient nanofluid within the boundary layer decreases as the value of \(- \theta_{r}\) increases. Thus the nanofluid viscosity increases, which results in declining of the velocity profile and thickening of the boundary layer thickness.
Figure 8 illustrates the effect of M on the velocity and temperature profiles of Cu-Water nanofluid when \(m= 0.2\), \(\phi=0.05\), \(f_{w} = \pm 0.5\), \(\theta_{r}=-2\), and \(P _{r}=6.2\). The effect of M on the two profiles of Ag-Water nanofluid was found to be similar to that of Cu-Water nanofluid, neglected here. It can be seen from Figure 8 that the velocity profile is an increasing function of M, while the temperature profile is just the opposite. Also, it can be seen that the velocity profile is larger in the presence of suction (\(f _{w} =0.5\)) than that in the presence of injection (\(f _{w}=-0.5\)), while the opposite is true for the temperature profile, which coincides with the result of Figure 6.
Figures 9 and 10 depict the skin friction and the rate of heat transfer coefficients as a function of \(f _{w}\) for various values of m, respectively. It is observed that both the skin friction coefficient \(f^{\prime\prime} ( 0 ) \) and the rate of heat transfer coefficient \(- \theta' ( 0 ) \) increase with an increase in values of \(f _{w}\) or pressure gradient parameter m. Hence suction enhances heat transfer and skin friction, while the effect of injection is just the opposite. The Cu-Water nanofluid has a larger skin friction coefficient but a slightly lower rate of heat transfer coefficient than that of Ag-Water nanofluid for deep injection (\(f _{w}<-0.5\)), while the opposite is true for suction (\(f _{w}>0\)). Note that the effect of m on the rate of heat transfer coefficient is much less than that on the skin friction coefficient and almost vanishes when \(f _{w}=-1.25\).
4 Conclusions
The boundary layer flow of Cu-Water and Ag-Water nanofluids passing through a permeable wedge with variable viscosity under the effects of MHD was investigated numerically in present study. Unlike other papers involving a similar problem, this paper takes flow separation into account and compares the effects of several important parameters on two different nanofluids, namely, Cu-Water nanofluid and Ag-Water nanofluid. The main observations of this study are summarized below:
-
Dual solutions exist for negative pressure gradient (\(m<0\)) for the two nanofluids.
-
Suction and small variable viscosity parameter delay the flow separation for the two nanofluids.
-
Compared with the Ag-Water nanofluid, the flow separation occurs later for injection, while it occurs earlier for suction in the Cu-Water nanofluid.
-
Suction enhances heat transfer and skin friction, while the effect of injection is just the opposite for the two nanofluids.
References
Choi, SUS, Eastman, JA: Enhancing thermal conductivity of fluids with nanoparticles. Mater. Sci. 231, 99-105 (1995)
Hussein, AM, Bakar, RA, Kadirgama, K: Study of forced convection nanofluid heat transfer in the automotive cooling system. Case Stud. Therm. Eng. 2, 50-61 (2014)
Frank, M, Drikakis, D, Asproulis, N: Thermal conductivity of nanofluid in nanochannels. Microfluid. Nanofluid. 19(5), 1011-1017 (2015)
Serna, J: Heat and mass transfer mechanisms in nanofluids boundary layers. Int. J. Heat Mass Transf. 92, 173-183 (2016)
Hayat, T, Khan, MI, Waqas, M, Alsaedi, A: Newtonian heating effect in nanofluid flow by a permeable cylinder. Results Phys. 7, 256-262 (2017)
Hatami, M, Sheikholeslami, M, Hosseini, M, Ganji, DD: Analytical investigation of MHD nanofluid flow in non-parallel walls. J. Mol. Liq. 194(2), 251-259 (2014)
Hayat, T, Imtiaz, M, Alsaedi, A: MHD 3D flow of nanofluid in presence of convective conditions. J. Mol. Liq. 212, 203-208 (2015)
Mabood, F, Khan, WA: Analytical study for unsteady nanofluid MHD flow impinging on heated stretching sheet. J. Mol. Liq. 219, 216-223 (2016)
Falkner, VM, Skan, SW: Some approximate solutions of the boundary layer equations. Philos. Mag. 12, 865-896 (1931)
Yih, KA: MHD forced convection flow adjacent to a non-isothermal wedge. Int. Commun. Heat Mass Transf. 26(6), 819-827 (1999)
Martin, MJ, Boyd, ID: Falkner-skan flow over a wedge with slip boundary conditions. J. Thermophys. Heat Transf. 24(2), 263-270 (2010)
Sattar, MA: A local similarity transformation for the unsteady two-dimensional hydrodynamic boundary layer equations of a flow past a wedge. Int. J. Appl. Math. Mech. 7(1), 15-28 (2011)
Kandasamy, R, Muhaimin, I, Khamis, AB, Roslan, RB: Unsteady Hiemenz flow of Cu-nanofluid over a porous wedge in the presence of thermal stratification due to solar energy radiation: Lie group transformation. Int. J. Therm. Sci. 65, 196-205 (2013)
Turkyilmazoglu, M: Slip flow and heat transfer over a specific wedge: an exactly solvable Falkner-Skan equation. J. Eng. Math. 92(1), 73-81 (2015)
Raju, CSK, Sandeep, NA: Comparative study on heat and mass transfer of the Blasius and Falkner-Skan flow of a bio-convective Casson fluid past a wedge. Eur. Phys. J. Plus 131(11), 405 (2016)
Raju, CSK, Sandeep, N: Nonlinear radiative magnetohydrodynamic Falkner-Skan flow of Casson fluid over a wedge. Alex. Eng. J. 55(3), 2045-2054 (2016)
Su, X, Zheng, L: Hall effect on MHD flow and heat transfer of nanofluids over a stretching wedge in the presence of velocity slip and Joule heating. Cent. Eur. J. Phys. 11(12), 1694-1703 (2013)
Srinivasacharya, D, Mendu, U, Venumadhav, K: MHD boundary layer flow of a nanofluid past a wedge. Proc. Eng. 127, 1064-1070 (2015)
Khan, M, Azam, M, Munir, A: On unsteady Falkner-Skan flow of MHD Carreau nanofluid past a static/moving wedge with convective surface condition. J. Mol. Liq. 230, 48-58 (2017)
Hartree, DR: On an equation occurring in Falkner and Skan’s approximate treatment of the equations of the boundary layer. Proc. Camb. Philos. Soc. 33(2), 223-239 (1937)
Stewartson, K: Further solutions of the Falkner-Skan equation. Math. Proc. Camb. Philos. Soc. 50(3), 454-465 (1954)
Steinheuer, J: Similar solutions for the laminar wall jet in a decelerating outer flow. AIAA J. 6(11), 2198-2200 (1968)
Cebeci, T, Keller, HB: Shooting and parallel shooting methods for solving the Falkner-Skan boundary-layer equation. J. Comput. Phys. 7(2), 289-300 (1971)
Deka, RK, Basumatary, M: Effect of variable viscosity on flow past a porous wedge with suction or injection: new results. Afr. Math. 26(7), 1263-1279 (2015)
Schlichting, H, Gersten, K: Boundary-Layer Theory. McGraw-Hill, New York (1979)
Khamis, S, Makinde, DO, Nkansah-Gyekye, Y: Unsteady flow of variable viscosity Cu-Water and Al2O3-Water nanofluids in a porous pipe with buoyancy force. Int. J. Numer. Methods Heat Fluid Flow 25(7), 1638-1657 (2015)
Makinde, OD, Iskander, T, Mabood, F, Khan, WA, Tshehla, MS: MHD Couette-Poiseuille flow of variable viscosity nanofluids in a rotating permeable channel with Hall effects. J. Mol. Liq. 221, 778-787 (2016)
Huda, AB, Akbar, NS, Beg, OA, Khan, MY: Dynamics of variable-viscosity nanofluid flow with heat transfer in a flexible vertical tube under propagating waves. Results Phys. 7, 413-425 (2017)
Brinkman, HC: The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 20(4), 571 (1952)
Sourtiji, E, Gorji-Bandpy, M, Ganji, DD, Hosseinizadeh, SF: Numerical analysis of mixed convection heat transfer of Al2O3-Water nanofluid in a ventilated cavity considering different positions of the outlet port. Mindfulness 5(4), 381-391 (2014)
Garnett, JCM: Colours in metal glasses and in metallic films. Philos. Trans. R. Soc. Lond. 203, 385-420 (1904)
Soundalgekar, VM, Takhar, HS, Das, UN, Deka, RK, Sarmah, A: Effect of variable viscosity on boundary layer flow along a continuously moving plate with variable surface temperature. Heat Mass Transf. 40(5), 421-424 (2004)
Watanabe, T: Thermal boundary layer over a wedge with uniform suction or injection in forced flow. Acta Mech. 83(3), 119-126 (1990)
Acknowledgements
This work was supported by the Science and Technology Major Project of Fujian Province (grant number 2011HZ006-1), Construction of Scientific and Technological Innovation Platform of Fujian Province (grant number 2011H2008), and Special Funds for the University Development from Central Finance of China in 2012 and 2016.
Author information
Authors and Affiliations
Contributions
All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Xu, X., Chen, S. Dual solutions of a boundary layer problem for MHD nanofluids through a permeable wedge with variable viscosity. Bound Value Probl 2017, 147 (2017). https://doi.org/10.1186/s13661-017-0877-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-017-0877-7