A regularization method for solving the G-variational inequality problem and fixed-point problems in Hilbert spaces endowed with graphs

Abstract

This article considers and investigates a variational inequality problem and fixed-point problems in real Hilbert spaces endowed with graphs. A regularization method is proposed for solving a G-variational inequality problem and a common fixed-point problem of a finite family of G-nonexpansive mappings in the framework of Hilbert spaces endowed with graphs, which extends the work of Tiammee et al. (Fixed Point Theory Appl. 187, 2015) and Kangtunyakarn, A. (Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 112:437–448, 2018). Under certain conditions, a strong convergence theorem of the proposed method is proved. Finally, we provide numerical examples to support our main theorem. The numerical examples show that the speed of the proposed method is better than some recent existing methods in the literature.

1 Introduction

Assume that H is a real Hilbert space with an inner product $\langle \cdot , \cdot \rangle$ and its induced norm $\| \cdot \|$. Let C be a nonempty, closed, and convex subset of H and $\mathcal{T}:C \rightarrow C$ be a nonlinear mapping. A point $x\in C$ is called a fixed point of $\mathcal{T}$ if $\mathcal{T}x=x$. Let $F(\mathcal{T}):= \{x\in C: \mathcal{T}x=x\}$ be the set of fixed points of $\mathcal{T}$. The mapping $\mathcal{T}$ is nonexpansive if $\Vert \mathcal{T}x-\mathcal{T}y \Vert \leq \Vert x-y \Vert$ for all $x,y \in C$.

Denote by $G = (V(G), E(G))$ a directed graph, where $V(G)$ and $E(G)$ are the set of its vertices and edges, respectively. Assuming that G has no parallel edges, we denote $G^{-1}$ as the directed graph derived from G by reversing the direction of its edges, i.e.,

$$ E\bigl(G^{-1}\bigr) = \bigl\{ (x, y) : (y, x) \in E(G)\bigr\} . $$

In 2008, Jachymski [1] studied fixed-point theory in a metric space endowed with a directed graph by combining the concepts of fixed-point theory and graph theory. The following contractive-type mapping with a directed graph was proposed. Given a metric space $(X, d)$, let G be a directed graph such that the set of its vertices $V(G) = X$ and the set of its edges $E(G)$ consists of all loops, i.e., $\triangle = \{(x, x) : x \in X\} \subseteq E(G)$. A mapping $T : X \rightarrow X$ is said to be a G-contraction if it preserves the edges of G, i.e.,

$$ x,y\in X,\quad (x,y)\in E(G) \quad \Rightarrow \quad \bigl(T(x),T(y)\bigr)\in E(G) $$

and there exists $\alpha \in (0, 1)$ such that for any $x, y \in X$,

$$ (x,y)\in E(G) \quad \Rightarrow\quad d\bigl(T(x),T(y)\bigr)\leq \alpha d(x,y). $$

The generalized Banach contraction principle in a metric space endowed with a directed graph was also established.

Given a nonempty convex subset C of a Banach space X and a directed graph G with $V(G) = C$, then $T : C \rightarrow C$ is said to be G-nonexpansive if the following conditions hold:

• 1. T is edge preserving, i.e., $(x, y)\in E(G) \Rightarrow (Tx, Ty) \in E(G)$ for any $x, y \in C$;

• 2. $(x, y) \in E(G) \Rightarrow \|Tx - Ty\| \leq \| x - y\|$ for any $x, y \in C$.

This mapping was proposed by Tiammee et al. [2] in 2015. Moreover, Tiammee et al. [2] also introduced Property G and the following Halpern iteration process for finding the set of fixed points of G-nonexpansive mappings in Hilbert spaces endowed with a directed graph. Suppose C has Property G. Let $\{ x_{n} \}$ be a sequence generated by $x_{0}=u\in C$ and

$$ x_{n+1}=\beta _{n}u+(1-\beta _{n})Tx_{n},\quad n\geq 0, $$

(1)

where $\{\beta _{n}\} \subseteq [0,1]$ and $T : C\rightarrow C$ is a G-nonexpansive mapping. If $\{x_{n}\}$ is dominated by $P_{F(T)}x_{0}$ and $\{x_{n}\}$ dominates $x_{0}$, then $\{x_{n}\}$ converges strongly to $P_{F(T)}x_{0}$ under some suitable control conditions.

In 2017, Kangtunyakarn [3] suggested G-S-mapping generated by a finite family of G-nonexpansive mappings and finite real numbers and introduced the following Halpern iteration associated with G-S-mapping for solving the fixed-point problem of a finite family of G-nonexpansive mappings in Hilbert spaces endowed with graphs. Let $\{ x_{n} \}$ be a sequence generated by $x_{0}=u\in C$ and

$$ x_{n+1}=\beta _{n}u+(1-\beta _{n})Sx_{n},\quad n\geq 0, $$

(2)

where $\{\beta _{n}\} \subseteq [0,1]$, and S is a G-S-mapping. He showed that the sequence $\{x_{n}\}$ generated by (2) converges strongly to a point in $F(S)=\bigcap_{i=1}^{N}F(T_{i})$ under some suitable control conditions. Furthermore, in the past few years, several iterative methods have been introduced for solving the fixed-point problem of G-nonexpansive mappings; see [4–8] and the references therein.

For a given nonlinear operator $\bar{A} : C \to H$, we consider the following variational inequality problem of solving $x \in C$ such that

$$ \langle y-x, \bar{A}x\rangle \geq 0, $$

(3)

for all $y\in C$. Denote by $VI ( C,\bar{A} )$ the set of solutions of the variational inequality (3). The variational inequalities were introduced in [9, 10], which has been extensively studied in the literature; see [11–13]. It is well known that ũ solves the problem (3) if and only if ũ solves the equation

$$ \tilde{u}=P_{C}(I-\lambda \bar{A})\tilde{u},\quad \forall \lambda > 0. $$

This work focuses on the following G-variational inequality problem in Hilbert spaces endowed with graphs, which Kangtunyakarn introduced [14] in 2020. In order to propose this problem, he combined the concept of problem (3) with graph theory. Given a directed graph G with $V ( G )=C$, the G-variational inequality problems is to find a point $x^{\ast }\in C$ such that

$$ \bigl\langle y-x^{\ast },Ax^{\ast }\bigr\rangle \geq 0, $$

(4)

for all $y\in C$ with $( x^{\ast },y ) \in E ( G )$, where A is a mapping from C to H. We denote by $G\text{-}VI ( C,A )$ the set of all solutions of (4).

Moreover, he also introduced the following G-α-inverse strongly monotone in Hilbert spaces endowed with graphs: A mapping $A: C\rightarrow H$ is said to be G-α-inverse strongly monotone if there exists a positive number α such that

$$ \langle Ax-Ay,x-y\rangle \geq \alpha \Vert Ax-Ay \Vert ^{2}, $$

for all $x,y\in C$ with $( x,y ) \in E ( G )$. For more information on the G-variational inequality problem and G-α-inverse strongly monotone, see [14].

Furthermore, the following method for solving the G-variational inequality problems and the fixed-point problem of a G-nonexpansive mapping in Hilbert spaces endowed with graphs were also introduced in [14]. Let $\{ x_{n} \}$ be a sequence generated by $x_{0}=u\in C$ and

$$ x_{n+1}=\alpha _{n}u+\beta _{n}P_{C} ( I-\lambda A ) x_{n}+ \gamma _{n}Sx_{n}, \quad n\geq 0, $$

(5)

where $\{ \alpha _{n} \} , \{ \beta _{n} \} , \{ \gamma _{n} \} \subseteq [ 0,1 ]$ with $\alpha _{n}+\beta _{n}+\gamma _{n}=1$, $\lambda \in ( 0,2\alpha )$, $S:C\rightarrow C$ is a G-nonexpansive mapping, and $A:C\rightarrow H$ is a G-α-inverse strongly monotone operator with $A^{-1}(0) \neq \emptyset$. Under certain conditions, a strong convergence result of the algorithm (5) in Hilbert spaces endowed with graphs was shown.

In this paper, motivated by Tiammee et al. [2], Kangtunyakarn [3], and Kangtunyakarn [14], we study the G-variational inequality problem (4) and introduce a new method for solving the G-variational inequality problem (4) and fixed-point problems of a finite family of G-nonexpansive mappings in Hilbert spaces endowed with graphs as follows: Given $u=x_{0}\in C$, let the sequences $\{x_{n}\}$ be defined by

$$ x_{n+1}=P_{C}(I -\lambda A) \bigl(\beta _{n}u+(1-\beta _{n})Sx_{n}\bigr), \quad n\geq 0, $$

(6)

where $\{\beta _{n}\} \subseteq [0,1]$, $\lambda \in (0,2\alpha )$, $A:C\rightarrow H$ is a G-α-inverse strongly monotone operator with $A^{-1}(0) \neq \emptyset$, and S is a G-S-mapping generated by a finite family of G-nonexpansive mappings and finite real numbers. We note that the proposed method (6) reduces to the iteration process (2) when $A = 0$, $P_{C}=I$ and reduces to the iteration process (1) when $A = 0$, $P_{C}=I$, $N=1$ and $\alpha _{1}^{N}=1$. Under suitable conditions, a strong convergence theorem of the proposed method is proved. In the last section, we provide numerical examples to support our main theorem. The main result extends and improves the corresponding results. We made the following contributions to this research.

• The proposed method is constructed around the Halpern iteration process in [15] and the regularization technique in [16]. In this case, our main results is to solve a common solution of the G-variational inequality problem ($G\text{-}VI ( C,A )$) and the fixed-point problems of a finite family of G-nonexpansive mappings ($\bigcap_{i=1}^{N}F(T_{i})$), while the results in Tiammee et al. [2] and Kangtunyakarn [3] are to solve a solution of the fixed-point problem of a G-nonexpansive mapping ($F(T)$) and a common solution of the fixed-point problems of a finite family of G-nonexpansive mappings ($\bigcap_{i=1}^{N}F(T_{i})$), respectively.

• Under certain mild conditions, the strong convergence of the iterative sequences generated by the proposed method is established in Hilbert spaces endowed with graphs.

• Numerical examples in finite- and infinite-dimensional spaces are provided to demonstrate the convergence behavior of our proposed method and the comparison to the Halpern-type algorithms proposed in Algorithm 5 of Kangtunyakarn [14]. It is shown that the proposed iterative method has a faster convergence speed (in terms of CPU time and the number of iterations) than Algorithm 5 of Kangtunyakarn [14] (see Sect. 4).

This paper is organized as follows. In Sect. 2, we first recall some basic definitions and lemmas. In Sect. 3, we propose a modified regularization method and analyze its convergence. In Sect. 4, some numerical experiments are provided.

2 Preliminaries

For the purpose of proving our theorem, we provide several definitions and lemmas in this section. For convenience, the following notations are used throughout the paper:

• H denotes a real Hilbert space with an inner product $\langle \cdot , \cdot \rangle$ and an induced norm $\| \cdot \|$;

• C denotes a nonempty, closed, and convex subset of H;

• $x_{n} \rightarrow q$ denotes the strong convergence of a sequence $\{x_{n}\}$ to q in H;

• $x_{n} \rightharpoonup q$ denotes the weak convergence of a sequence $\{x_{n}\}$ to q in H;

• $G= ( V ( G ) ,E ( G ) )$ denotes a directed graph with $V ( G ) =C$ and $E(G)$ is convex.

Recall that the (nearest point) projection $P_{C}$ from H onto C assigns to each $x \in H$, there exists the unique point $P_{C}x \in C$ satisfying the property

$$ \Vert x- P_{C}x \Vert = \min_{y \in C} \Vert x- y \Vert . $$

The fact that H satisfies Opial’s condition is well known, i.e., for any sequence $\{x_{n} \}$ with $x_{n} \rightharpoonup x$, the inequality

$$ \lim_{n \rightarrow \infty} \inf \Vert x_{n}-x \Vert < \lim _{n \rightarrow \infty} \inf \Vert x_{n}-y \Vert $$

holds for every $y \in H$ with $y \neq x$.

Lemma 2.1

([17]) For any $u \in H$ and $v \in C$, $P_{C}u=v$ if and only if the inequality $\langle u-v, v-w \rangle \geq 0$ holds for all $w \in C$.

Lemma 2.2

For every $p,q\in H$. If $\Vert p+q \Vert = \Vert p \Vert + \Vert q \Vert$, there exists $s> 0$ such that $q=sp$ or $p=sq$.

Lemma 2.3

([18]) Let $\{z_{n}\}$ be a sequence of nonnegative real numbers satisfying

$$ z_{n+1} \leq (1- a_{n})z_{n} + \tau _{n}, \quad \forall n \geq 0, $$

where $\{a_{n}\}$ is a sequence in $(0,1)$ and $\{\tau _{n}\}$ is a sequence of real numbers. If the following conditions hold:

• (1) $\sum_{n=1}^{\infty} a_{n} = \infty$;

• (2) $\limsup_{n \rightarrow \infty} \frac{\tau _{n}}{a_{n}} \leq 0$ or $\sum_{n=1}^{\infty} |\tau _{n} |< \infty$,

then, $\lim_{n \rightarrow \infty} z_{n} = 0$.

The following basic definitions of domination in graphs ([19, 20]) are needed to prove the main theorem.

Given G a directed graph, a set $X \subseteq V(G)$ is called a dominating set if there exists $x \in X$ such that $(x, z) \in E(G)$ for every $z \in V(G) \setminus X$, and we say that x dominates z or z is dominated by x. Let $z \in V(G)$, a set $X \subseteq V(G)$ is dominated by z if $(z, x) \in E(G)$ for any $x \in X$ and we say that X dominates z if $(x, z) \in E(G)$ for all $x \in X$. This work assumes that $E(G)$ contains all loops.

Definition 2.4

(Property G [2])

Let X be a normed space. A nonempty $C \subset X$ is said to have the Property G if every sequence $\{x_{n}\}$ in C converging weakly to $x \in C$, there is a subsequence $\{x_{n_{k}}\}$ of $\{x_{n}\}$ such that $({x_{n_{k}}}, x) \in E(G)$ for all $k \in \mathbb{N}$.

Theorem 2.5

([2]) Let X be a normed space, and G be a directed graph with $V(G) = X$. Let $T: X \rightarrow X$ be a G-nonexpansive mapping. If X has a Property G, then T is continuous.

Theorem 2.6

([2]) Let C have the Property G. If $T: C \rightarrow C$ is a G-nonexpansive mapping, and $F(T)\times F(T)\subseteq E(G)$, then $F(T)$ is closed and convex.

Definition 2.7

([2]) A graph G is called transitive if for any $x, y, z \in V(G)$ such that $(x, y)$ and $(y, z)$ are in $E(G)$, then $(x, z) \in E(G)$.

Lemma 2.8

([14]) Let G be transitive with $E(G) = E(G^{-1})$ and let $A:C \to H$ be a G-α-inverse strongly monotone mapping with ${A^{ - 1}}(0) \ne \emptyset$. Then, G-$VI(C,A)=A^{-1}(0)=F(P_{C}(I- \lambda A))$, for all $\lambda >0$.

Lemma 2.9

([14]) Let C have a property G and let $A:C\rightarrow H$ be a G-α-inverse strongly monotone mapping with $F ( P_{C} ( I-\lambda A ) ) \times F ( P_{C} ( I-\lambda A ) ) \subseteq E ( G )$, for all $\lambda \in ( 0,2\alpha )$. Then, $F(P_{C} ( I-\lambda A ))$ is closed and convex.

In 2017, Kangtunyakarn [3] introduced the G-S-mapping generated by a finite family of nonlinear mappings and finite real numbers as follows.

Definition 2.10

([3]) For every $i=1,2,\ldots,N$, let $T_{i}$ be a mapping of C into itself. For each $k=1,2,\ldots,N$, let $\alpha _{k} = (\alpha _{1}^{k},\alpha _{2}^{k},\alpha _{3}^{k})$ where $\alpha _{1}^{k},\alpha _{2}^{k},\alpha _{3}^{k} \in [0,1]$ and $\alpha _{1}^{k}+\alpha _{2}^{k}+\alpha _{3}^{k}=1$. Define the mapping $S:C\rightarrow C$ as follows:

$$\begin{aligned}& \mathcal{L}_{0} =I \\& \mathcal{L}_{1} =\alpha _{1}^{1}T_{1} \mathcal{L}_{0}+\alpha _{2}^{1} \mathcal{L}_{0}+\alpha _{3}^{1}I, \\& \mathcal{L}_{2} =\alpha _{1}^{2}T_{2} \mathcal{L}_{1}+\alpha _{2}^{2} \mathcal{L}_{1}+\alpha _{3}^{2}I, \\& \mathcal{L}_{3} =\alpha _{1}^{3}T_{3} \mathcal{L}_{2}+\alpha _{2}^{3} \mathcal{L}_{2}+\alpha _{3}^{3}I, \\& \vdots \\& \mathcal{L}_{N-1} =\alpha _{1}^{N-1}T_{N-1} \mathcal{L}_{N-2}+\alpha _{2}^{N-1} \mathcal{L}_{N-2}+\alpha _{3}^{N-1}I, \\& S =\mathcal{L}_{N}=\alpha _{1}^{N}T_{N} \mathcal{L}_{N-1}+\alpha _{2}^{N} \mathcal{L}_{N-1}+\alpha _{3}^{N}I. \end{aligned}$$

This mapping is called the G-S-mapping generated by $T_{1},T_{2},\ldots,T_{N}$ and $\alpha _{1},\alpha _{2},\ldots,\alpha _{N}$.

Lemma 2.11

([3]) Let $\{T_{i}\}^{N}_{i=1} : C \to C$ be a G-nonexpansive mapping with $\bigcap_{i=1}^{N}F(T_{i})$ the dominating set. Let $\alpha _{k}=(\alpha _{1}^{k},\alpha _{2}^{k},\alpha _{3}^{k})$, where $\alpha _{1}^{k},\alpha _{2}^{k},\alpha _{3}^{k}\in [0,1]$ with $\alpha _{1}^{k}+\alpha _{2}^{k}+\alpha _{3}^{k}=1$ for all $k=1,2,\ldots,N$ and $\alpha _{1}^{k}\in (0,1)$ for all $k=1,2,\ldots,N-1$ and $\alpha _{1}^{N}\in (0,1]$, $\alpha _{2}^{k}, \alpha _{3}^{k}\in [0,1]$ for all $k=1,2,\ldots,N$. Let $S:C\to C$ be a G-S-mapping generated by $T_{1},T_{2},\ldots,T_{N}$ and $\alpha _{1}, \alpha _{2},\ldots,\alpha _{N}$. Then, $F(S)=\bigcap_{i=1}^{N}F(T_{i})$ and S is a G-nonexpansive mapping.

Lemma 2.12

([3]) Let C have the Property G. If $T:C\to C$ is a G-nonexpansive mapping, then $I-T$ is demiclosed at zero.

3 Main results

In this section, we establish a strong convergence theorem of a regularization algorithm designed to solve the G-variational inequality problem and the fixed-point problem of a finite family of G-nonexpansive mappings in a Hilbert space endowed with graphs.

Theorem 3.1

Let H be a Hilbert space and $C \subset H$ be nonempty, closed, and convex. Suppose a directed graph G with $V(G)=C$ has Property G, and it is transitive with $E(G) = E(G^{-1})$ is convex. Let $A : C \to H$ be a G-α-inverse strongly monotone operator with $A^{-1}(0)\neq \emptyset$. Let $\{T_{i}\}^{N}_{i=1} : C \to C$ be a G-nonexpansive mapping with $\bigcap_{i=1}^{N}F(T_{i})$ the dominating set. Let $\alpha _{k}=(\alpha _{1}^{k},\alpha _{2}^{k},\alpha _{3}^{k})$, where $\alpha _{1}^{k},\alpha _{2}^{k},\alpha _{3}^{k}\in [0,1]$ with $\alpha _{1}^{k}+\alpha _{2}^{k}+\alpha _{3}^{k}=1$ for all $k=1,2,\ldots,N$ and $\alpha _{1}^{k}\in (0,1)$ for all $k=1,2,\ldots,N-1$ and $\alpha _{1}^{N}\in (0,1]$, $\alpha _{2}^{k}, \alpha _{3}^{k}\in [0,1]$ for all $k=1,2,\ldots,N$. Let $S:C\to C$ be a G-S-mapping generated by $T_{1},T_{2},\ldots,T_{N}$ and $\alpha _{1}, \alpha _{2},\ldots,\alpha _{N}$. Assume that

$$ \Omega =\bigcap_{i=1}^{N}F(T_{i}) \cap G\textit{-} VI(C,A)\neq \emptyset $$

with $\bigcap_{i=1}^{N}F(T_{i})\times \bigcap_{i=1}^{N}F(T_{i}) \subseteq E(G)$ and $G\textit{-} VI(C,A)\times G\textit{-} VI(C,A) \subseteq E(G)$, and there exists $x_{0}\in C$ such that $(x_{0},T_{1}x_{0}) \in E(G)$. Let $\{x_{n}\}$ be a sequence generated by $x_{0} = u \in C$ and

$$ x_{n+1}=P_{C}(I -\lambda A) \bigl(\beta _{n}u+(1-\beta _{n})Sx_{n}\bigr),\quad n\geq 0, $$

(7)

where $\{\beta _{n}\} \subseteq [0,1]$ and $\lambda \in (0,2\alpha )$.

If the following conditions hold:

• (i) $\lim_{n \rightarrow \infty} \beta _{n}= 0$ and $\sum_{n=1}^{\infty}\beta _{n}=\infty$;

• (ii) $\sum_{n=1}^{\infty}|\beta _{n+1} - \beta _{n}|< \infty$;

• (iii) $(T_{i}x,T_{i+1}x)\in E(G)$ for all $i=1,2,\ldots,N-1$ and $x\in C$,

then, $\{x_{n}\}$ converges strongly to $P_{\Omega}x_{0}$, where $P_{\Omega}$ is a metric projection on Ω, $P_{\Omega}x_{0}$ is dominated by $\{x_{n}\}$, $P_{\Omega}x_{0}$ is dominated by $x_{0}$, and $\{x_{n}\}$ dominates $x_{0}$.

Proof

First, we show that

$$ \bigl\Vert P_{C} ( I-\lambda A ) x-P_{C} ( I-\lambda A ) y \bigr\Vert \leq \Vert x-y \Vert , $$

(8)

for all $x,y\in C$ with $( x,y ) \in E ( G )$. Indeed, letting $x,y\in C$ with $( x,y ) \in E ( G )$, we have

$$\begin{aligned} \bigl\Vert P_{C} ( I-\lambda A ) x-P_{C} ( I-\lambda A ) y \bigr\Vert ^{2}\leq {}& \bigl\Vert x-y-\lambda ( Ax-Ay ) \bigr\Vert ^{2} \\ ={}& \Vert x-y \Vert ^{2}-2\lambda \langle x-y,Ax-Ay\rangle \\ & {}+\lambda ^{2} \Vert Ax-Ay \Vert ^{2} \\ \leq {}& \Vert x-y \Vert ^{2}-\lambda ( 2\alpha -\lambda ) \Vert Ax-Ay \Vert ^{2} \\ \leq {}& \Vert x-y \Vert ^{2}. \end{aligned}$$

(9)

From Lemmas 2.8 and 2.9, we have G-$VI(C,A)$ is closed and convex. From Lemmas 2.11 and 2.12, we have $F(S)=\bigcap_{i=1}^{N}F(T_{i})$ is closed and convex. Then, Ω is closed and convex. Moreover, from $\bigcap_{i=1}^{N}F(T_{i})\neq \emptyset$ and Lemma 2.11, we have $\bigcap_{i=1}^{N}F(T_{i})=F(S)$ and S is a G-nonexpansive mapping.

Next, we will show that $( x_{n},x_{n+1} )\in E(G)$ for all $n \geq 0$.

Put $x^{*}=P_{\Omega }x_{0}$. Since $x^{*}$ is dominated by $\{ x_{n} \}$, we have $( x_{n},x^{*} ) \in E ( G )$ for all $n \geq 0$.

Since $x^{*}$ is dominated by $\{ x_{0} \}$, we have $( x_{0},x^{*} ) \in E ( G )$.

Since $\{x_{n}\}$ dominates $x_{0}$, we have $( x_{n},x_{0} ) \in E ( G )$ for all $n \geq 0$.

Since $E(G)=E(G^{-1})$ and $( x_{n},x_{0} ) \in E ( G )$, then $( x_{0},x_{n} ) \in E ( G )$ for all $n \geq 0$.

By the transitivity of $E(G)$ and since $( x_{n},x^{*} )$, $(x^{*},x_{0})$, $( x_{0},x_{n+1} )$ are in $E(G)$, then $( x_{n},x_{n+1} )\in E(G)$ for all $n \geq 0$.

Putting $y_{n}=\beta _{n}u+(1-\beta _{n})Sx_{n}$ for all $n \geq 0$, it follows that $x_{n+1}=P_{C}(I -\lambda A)y_{n}$ for all $n \geq 0$.

We now claim that $(x_{0},Sx_{n})$, $(x_{n},Sx_{n})$, and $(x_{n},y_{n})$ are in $E(G)$ for all $n \geq 0$.

Since $E(G)=E(G^{-1})$ and $(x_{0},x^{*}) \in E(G)$, we have $(x^{*}, x_{0}) \in E(G)$.

We now prove this result by using mathematical induction. By continuing in the same direction as in Theorem 3.1 [3], we have $(x_{0}, Sx_{0})\in E(G)$.

Since $(x_{0},x_{0})$, $(x_{0},Sx_{0})\in E(G)$, and $E(G)$ is convex, we have $(x_{0}, y_{0})\in E(G)$.

Since S is G-nonexpansive and $(x_{0},x_{1})\in E(G)$, we obtain $(Sx_{0}, Sx_{1})\in E(G)$.

By the transitivity of $E(G)$ and since $(x_{0}, Sx_{0})$, $(Sx_{0}, Sx_{1})$ are in $E(G)$, we obtain $(x_{0}, Sx_{1})\in E(G)$.

As $E(G)$ is convex and $(x_{0},x_{0})$, $(x_{0},Sx_{1})$ are in $E(G)$, we have $(x_{0}, y_{1})\in E(G)$.

By the transitivity of $E(G)$ and since $(x_{1},x_{0})$, $(x_{0},Sx_{1})$ are in $E(G)$, we have $(x_{1}, Sx_{1})\in E(G)$.

By the transitivity of $E(G)$ and since $(x_{1},x_{0})$, $(x_{0}, y_{1})$ are in $E(G)$, we have $(x_{1}, y_{1})\in E(G)$.

Suppose that $(x_{0},Sx_{k}) \in E(G)$ for all $k \geq 0$. Since $(x_{0},x_{0})$, $(x_{0},Sx_{k})\in E(G)$ and $E(G)$ is convex, we have $(x_{0}, y_{k})\in E(G)$ for all $k \geq 0$.

Since S is G-nonexpansive and $(x_{k},x_{k+1}) \in E(G)$ for all $k \geq 0$, we obtain $(Sx_{k}, Sx_{k+1})\in E(G)$ for all $k \geq 0$.

By the transitivity of $E(G)$ and since $(x_{0}, Sx_{k})$, $(Sx_{k}, Sx_{k+1})$ are in $E(G)$ for all $k \geq 0$, we obtain $(x_{0}, Sx_{k+1})\in E(G)$ for all $k \geq 0$.

As $E(G)$ is convex and $(x_{0},x_{0})$, $(x_{0},Sx_{k+1})$ are in $E(G)$ for all $k \geq 0$, we have $(x_{0}, y_{k+1})\in E(G)$ for all $k \geq 0$.

By the transitivity of $E(G)$ and since $(x_{k+1},x_{0})$, $(x_{0}, y_{k+1})$ are in $E(G)$ for all $k \geq 0$, we have $(x_{k+1}, y_{k+1})\in E(G)$ for all $k \geq 0$.

By the transitivity of $E(G)$ and since $(x_{k+1},x_{0})$, $(x_{0},Sx_{k+1})$ are in $E(G)$ for all $k \geq 0$, we have $(x_{k+1}, Sx_{k+1})\in E(G)$ for all $k \geq 0$.

From induction, we obtain that $(x_{0},Sx_{n})$, $(x_{n},Sx_{n})$, and $(x_{n},y_{n})$, are in $E(G)$ for all $n \geq 0$. Moreover, By the transitivity of $E(G)$ and since $(x^{*},x_{0})$, $(x_{0},y_{n})$ are in $E(G)$, we have $(x^{*}, y_{n})\in E(G)$ for all $n \geq 0$.

From Lemma 2.8, we obtain $G\text{-}VI ( C,A ) = A^{-1}(0)$. Then, $x^{*} \in A^{-1}(0)$. Since $Ax^{*} = 0$, we have

$$\begin{aligned} \bigl\Vert {P_{C}} (I - \lambda A )y_{n} - x^{*} \bigr\Vert ^{2} &\leq \bigl\Vert {y_{n}} - x^{*} - \lambda A{y_{n}} \bigr\Vert ^{2} \\ &= { \bigl\Vert {{y_{n}} - {x^{*}}} \bigr\Vert ^{2}} - 2\lambda \bigl\langle {{y_{n}} - {x^{*}},A{y_{n}} - A{x^{*}}} \bigr\rangle + { \lambda ^{2}} { \Vert {A{y_{n}}} \Vert ^{2}} \\ &\leq \bigl\Vert {y_{n}} - x^{*} \bigr\Vert ^{2} - 2\lambda { \bigl\Vert A{y_{n}} - A{x^{*}} \bigr\Vert ^{2}} + {\lambda ^{2}} { \Vert {A{y_{n}}} \Vert ^{2}} \\ &= { \bigl\Vert {y_{n}} - x^{*} \bigr\Vert ^{2}} - \lambda (2\alpha - \lambda ){ \Vert {A{y_{n}}} \Vert ^{2}} \\ &\leq { \bigl\Vert {y_{n}} - x^{*} \bigr\Vert ^{2}}. \end{aligned}$$

(10)

From the definition of ${x_{n}}$, (10), and since S is a G-nonexpansive mapping, we have

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \leq {}& \bigl\Vert y_{n}-x^{*} \bigr\Vert \\ \leq {}& \bigl\Vert \beta _{n}u+(1-\beta _{n})Sx_{n}-x^{*} \bigr\Vert \\ \leq{}& \alpha _{n} \bigl\Vert u-x^{*} \bigr\Vert +(1- \beta _{n}) \bigl\Vert Sx_{n}-x^{*} \bigr\Vert \\ \leq {}& \alpha _{n} \bigl\Vert u-x^{*} \bigr\Vert +(1- \beta _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert \\ \leq {}& \max \bigl\{ \bigl\Vert u-x^{*} \bigr\Vert , \bigl\Vert x_{1}-x^{*} \bigr\Vert \bigr\} . \end{aligned}$$

(11)

By using mathematical induction, we conclude that the sequences $\{ x_{n} \}$, $\{ P_{C} ( I-\lambda A ) y_{n} \}$, and $\{ Sx_{n} \}$ are all bounded.

From the definition of $x_{n}$ and (9), we have

$$\begin{aligned} \Vert x_{n+1}-x_{n} \Vert \leq{} & \bigl\Vert P_{C} ( I-\lambda A ) y_{n}-P_{C} ( I-\lambda A ) y_{n-1} \bigr\Vert \\ \leq {}& \Vert y_{n}- y_{n-1} \Vert \\ \leq {}& \bigl\Vert \beta _{n}u+(1-\beta _{n})Sx_{n}- \alpha _{n-1}u-(1-\alpha _{n-1})Sx_{n-1} \bigr\Vert \\ \leq {}& \vert \beta _{n}-\alpha _{n-1} \vert \Vert u \Vert + (1-\beta _{n}) \Vert Sx_{n}-Sx_{n-1} \Vert + \vert \beta _{n}-\alpha _{n-1} \vert \Vert Sx_{n-1} \Vert \\ \leq{} & (1-\beta _{n}) \Vert x_{n}-x_{n-1} \Vert +2M \vert \beta _{n}-\alpha _{n-1} \vert , \end{aligned}$$

where $M=\max_{n\in \mathbb{N}}\{\|u\|, \|Sx_{n}\|\}$. Applying Lemma 2.3, and conditions (i) and (ii), we have

$$ \lim_{n \rightarrow \infty} \Vert x_{n+1}-x_{n} \Vert =0. $$

(12)

Since $x_{n+1}=P_{C}(I-\lambda A)y_{n}$, then we also have

$$ \lim_{n \rightarrow \infty} \bigl\Vert P_{C}(I- \lambda A)y_{n}-x_{n} \bigr\Vert =0. $$

(13)

By the nonexpansiveness of $P_{C}$, we obtain

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}={}& \bigl\Vert P_{C}(I-\lambda A)y_{n}-P_{C}(I- \lambda A)x^{*} \bigr\Vert ^{2} \\ \leq{} & \bigl\Vert (I-\lambda A)y_{n}-(I-\lambda A)x^{*} \bigr\Vert ^{2} \\ ={}& \bigl\Vert y_{n}-x^{*}-\lambda \bigl(Ay_{n}-Ax^{*} \bigr) \bigr\Vert ^{2} \\ ={}& \bigl\Vert y_{n}-x^{*} \bigr\Vert ^{2}-2 \lambda \bigl\langle y_{n}-x^{*},Ay_{n}-Ax^{*} \bigr\rangle +\lambda ^{2} \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert ^{2}. \end{aligned}$$

(14)

From the definition of $y_{n}$ and since S is G-nonexpansive, we have

$$\begin{aligned} \bigl\Vert y_{n}-x^{*} \bigr\Vert ^{2}\leq {}& \beta _{n} \bigl\Vert u-x^{*} \bigr\Vert ^{2}+(1-\beta _{n}) \bigl\Vert Sx_{n}-x^{*} \bigr\Vert ^{2} \\ \leq {}&\beta _{n} \bigl\Vert u-x^{*} \bigr\Vert ^{2}+(1-\beta _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2} \\ \leq {}&\beta _{n} \bigl\Vert u-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}. \end{aligned}$$

(15)

From (14) and (15), we obtain

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \leq {}&\beta _{n} \bigl\Vert u-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}-2 \lambda \bigl\langle y_{n}-x^{*},Ay_{n}-Ax^{*} \bigr\rangle \\ &{}+\lambda ^{2} \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert ^{2} \\ \leq {}&\beta _{n} \bigl\Vert u-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}-2\lambda \alpha \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert ^{2} \\ &{}+\lambda ^{2} \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert ^{2} \\ \leq {}&\beta _{n} \bigl\Vert u-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}-\lambda (2\alpha - \lambda ) \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert ^{2} . \end{aligned}$$

It follows that

$$\begin{aligned} \lambda (2\alpha -\lambda ) \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert ^{2}\leq {}& \beta _{n} \bigl\Vert u-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}- \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2} \\ \leq {}& \beta _{n} \bigl\Vert u-x^{*} \bigr\Vert ^{2}+ \bigl( \bigl\Vert x_{n}-x^{*} \bigr\Vert + \bigl\Vert x_{n+1}-x^{*} \bigr\Vert \bigr) \Vert x_{n+1}-x_{n} \Vert . \end{aligned}$$

From the condition (i) and (12), we obtain

$$ \lim_{n \rightarrow \infty} \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert =0. $$

(16)

From the definition of $P_{C}(I-\lambda A)$, we have

$$\begin{aligned} \bigl\Vert P_{C}(I-\lambda A)y_{n}- x^{*} \bigr\Vert ^{2}\leq {}& \bigl\Vert P_{C}(I-\lambda A)y_{n}-P_{C}(I- \lambda A)x^{*} \bigr\Vert ^{2} \\ \leq {}& \bigl\langle (I-\lambda A)y_{n}- (I-\lambda A)x^{*},P_{C}(I- \lambda A)y_{n}- x^{*} \bigr\rangle \\ = {}& \frac {1}{2} \bigl[ \bigl\Vert (I-\lambda A)y_{n}- (I- \lambda A)x^{*} \bigr\Vert ^{2} + \bigl\Vert P_{C}(I-\lambda A)y_{n}-x^{*} \bigr\Vert ^{2} \\ &{}- \bigl\Vert (I-\lambda A)y_{n}- (I-\lambda A)x^{*}- \bigl(P_{C}(I-\lambda A)y_{n}- x^{*}\bigr) \bigr\Vert ^{2} \bigr] \\ \leq {}& \frac {1}{2} \bigl[ \bigl\Vert y_{n}- x^{*} \bigr\Vert ^{2} + \bigl\Vert P_{C}(I-\lambda A)y_{n}-x^{*} \bigr\Vert ^{2} \\ &{}- \bigl\Vert y_{n}-P_{C}(I-\lambda A)y_{n}- \lambda \bigl(Ay_{n}-Ax^{*}\bigr) \bigr\Vert ^{2} \bigr] \\ \leq {}& \frac {1}{2} \bigl[ \beta _{n} \bigl\Vert u-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2} + \bigl\Vert P_{C}(I-\lambda A)y_{n}-x^{*} \bigr\Vert ^{2} \\ &{}- \bigl\Vert y_{n}-P_{C}(I-\lambda A)y_{n} \bigr\Vert ^{2}- \lambda ^{2} \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert ^{2} \\ &{}+2\lambda \bigl\langle y_{n}-P_{C}(I-\lambda A)y_{n}, Ay_{n}-Ax^{*} \bigr\rangle \bigr] \\ \leq {}& \frac {1}{2} \bigl[ \beta _{n} \bigl\Vert u-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2} + \bigl\Vert P_{C}(I-\lambda A)y_{n}-x^{*} \bigr\Vert ^{2} \\ &{}- \bigl\Vert y_{n}-P_{C}(I-\lambda A)y_{n} \bigr\Vert ^{2}- \lambda ^{2} \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert ^{2} \\ &{}+2\lambda \bigl\Vert y_{n}-P_{C}(I-\lambda A)y_{n} \bigr\Vert \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert \bigr]. \end{aligned}$$

It follows that

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}={}& \bigl\Vert P_{C}(I-\lambda A)y_{n}- x^{*} \bigr\Vert ^{2} \\ \leq {}& \beta _{n} \bigl\Vert u-x^{*} \bigr\Vert ^{2}+ \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2} - \bigl\Vert y_{n}-P_{C}(I- \lambda A)y_{n} \bigr\Vert ^{2} \\ &{}- \lambda ^{2} \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert ^{2}+2\lambda \bigl\Vert y_{n}-P_{C}(I- \lambda A)y_{n} \bigr\Vert \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert . \end{aligned}$$

(17)

From (17), we have

$$\begin{aligned} \bigl\Vert y_{n}-P_{C}(I-\lambda A)y_{n} \bigr\Vert ^{2} \leq {}& \beta _{n} \bigl\Vert u-x^{*} \bigr\Vert ^{2}+ \bigl( \Vert x_{n}-z \Vert + \Vert x_{n+1}-z \Vert \bigr) \Vert x_{n+1}-x_{n} \Vert \\ &{}+2\lambda \bigl\Vert y_{n}-P_{C}(I-\lambda A)y_{n} \bigr\Vert \bigl\Vert Ay_{n}-Ax^{*} \bigr\Vert . \end{aligned}$$

(18)

From the condition (i) and (12), (16), and (18), we have

$$ \lim_{n \rightarrow \infty} \bigl\Vert P_{C}(I- \lambda A)y_{n}-y_{n} \bigr\Vert =0. $$

(19)

Since

$$ \Vert y_{n}-x_{n} \Vert \leq \bigl\Vert y_{n}-P_{C}(I-\lambda A)y_{n} \bigr\Vert + \bigl\Vert P_{C}(I-\lambda A)y_{n}-x_{n} \bigr\Vert , $$

from (13) and (19), we have

$$ \lim_{n \rightarrow \infty} \Vert y_{n}-x_{n} \Vert =0. $$

(20)

From the definition of $y_{n}$, condition (i), and (20), we obtain

$$ \lim_{n \rightarrow \infty} \Vert x_{n}-Sx_{n} \Vert =0. $$

(21)

Since $\{x_{n}\}$ is bounded in a Hilbert space H and C has the property G, without loss of generality, we may assume that there is a subsequence $\{x_{n_{k}}\}$ of $\{x_{n}\}$ with $\{x_{n_{k}}\} \rightharpoonup \omega$ for some $\omega \in C$ and $(x_{n_{k}}, \omega ) \in E(G)$. Since $\lim_{n \rightarrow \infty} \Vert y_{n}-x_{n} \Vert =0$, then we obtain $y_{n_{k}} \to \omega$ as $k \to \infty$. By Lemma 2.12 and (21), we obtain $\omega \in F(S)$. This implies that

$$ \omega \in \bigcap_{i=1}^{N}F(T_{i}). $$

(22)

By the transitivity of $E(G)$ and $(y_{n_{k}},x_{n_{k}})$, $(x_{n_{k}}, \omega )$ being in $E(G)$, we obtain $(y_{n_{k}}, \omega )\in E(G)$ for all $k \in \mathbb{N}$. Assume that $\omega \neq P_{C}(I-\lambda A)\omega$. From Opial’s condition, (9), (19), and $(y_{n_{k}}, \omega )\in E(G)$, we obtain

$$\begin{aligned} \liminf_{k \rightarrow \infty} \Vert y_{n_{k}} - \omega \Vert < {}& \liminf_{k \rightarrow \infty} \bigl\Vert y_{n_{k}} - P_{C}(I-\lambda A)\omega \bigr\Vert \\ \leq{} & \liminf_{k \rightarrow \infty} \bigl( \bigl\Vert y_{n_{k}} - P_{C}(I- \lambda A)y_{n_{k}} \bigr\Vert + \bigl\Vert P_{C}(I-\lambda A)y_{n_{k}} - P_{C}(I- \lambda A) \omega \bigr\Vert \bigr) \\ \leq {}& \liminf_{k \rightarrow \infty} \Vert y_{n_{k}} - \omega \Vert . \end{aligned}$$

This is a contradiction. Then, $\omega \in F(P_{C}(I-\lambda A))$. Therefore, from Lemma 2.8, we have

$$ w \in G\text{-} VI(C,A). $$

(23)

From (22) and (23), we can conclude that $\omega \in \Omega$.

Since $x_{n_{k}} \rightharpoonup \omega$ and $\omega \in \Omega$, we have

$$ \limsup_{n\rightarrow \infty }\bigl\langle x_{n}-x^{*},x_{0}-x^{*} \bigr\rangle =\lim_{k\rightarrow \infty } \bigl\langle x_{n_{k}}-x^{*},x_{0}-x^{*} \bigr\rangle =\bigl\langle \omega -x^{*},x_{0}-x^{*} \bigr\rangle \leq 0, $$

(24)

where $x^{*}=P_{\Omega}x_{0}$. From the definition of $x_{n}$ and (10), we have

$$\begin{aligned} \bigl\Vert x_{n+1}-x^{*} \bigr\Vert ^{2}={}& \bigl\Vert P_{C}(I-\lambda A)y_{n}-P_{C}(I- \lambda A)x^{*} \bigr\Vert ^{2} \\ \leq {}& \bigl\Vert y_{n}-x^{*} \bigr\Vert ^{2} \\ \leq {}&(1-\beta _{n}) \bigl\Vert x_{n}-x^{*} \bigr\Vert ^{2}+2\beta _{n}\bigl\langle x_{n+1}-x^{*},x_{0}-x^{*} \bigr\rangle . \end{aligned}$$

Applying Lemma 2.3, (24), and the condition (i), we can conclude that the sequence $\{x_{n}\}$ converges strongly to $x^{*}=P_{\Omega}x_{0}$. This completes the proof. □

In our main results, if we choose $N=1$ and $\alpha _{1}^{N}=1$, then we obtain the following result.

Corollary 3.2

Let C have the Property G and G be transitive with $E(G) = E(G^{-1})$. Let $A : C \to H$ be a G-α-inverse strongly monotone operator with $A^{-1}(0)\neq \emptyset$. Let $T : C \to C$ be a G-nonexpansive mapping. Assume that

$$ \Omega =F(T)\cap G\textit{-} VI(C,A)\neq \emptyset $$

with $F(T)\times F(T)\subseteq E(G)$ and $G\textit{-} VI(C,A)\times G\textit{-} VI(C,A) \subseteq E(G)$, and there exists $x_{0}\in C$ such that $(x_{0},Tx_{0})\in E(G)$. Let $\{x_{n}\}$ be a sequence generated by $x_{0} = u \in C$ and

$$ \textstyle\begin{cases} x_{0}\in C, \\ y_{n}=\beta _{n}u+(1-\beta _{n})Tx_{n} \\ x_{n+1}=P_{C}(I -\lambda A)y_{n}, \quad n\geq 0, \end{cases} $$

(25)

where $\{\beta _{n}\} \subseteq [0,1]$ and $\lambda \in (0,2\alpha )$.

If the following conditions hold:

• (i) $\lim_{n \rightarrow \infty} \beta _{n}= 0$ and $\sum_{n=1}^{\infty}\beta _{n}=\infty$;

• (ii) $\sum_{n=1}^{\infty}|\beta _{n+1} - \beta _{n}|< \infty$,

then, $\{x_{n}\}$ converges strongly to $P_{\Omega}x_{0}$, where $P_{\Omega}$ is a metric projection on Ω, $P_{\Omega}x_{0}$ is dominated by $\{x_{n}\}$, $P_{\Omega}x_{0}$ is dominated by $x_{0}$, and $\{x_{n}\}$ dominates $x_{0}$.

Taking $A=0$ and $P_{C}=I$ in Theorem 3.1, then we obtain the following result.

Corollary 3.3

Let C have the Property G and G be transitive with $E(G) = E(G^{-1})$. Let $\{T_{i}\}^{N}_{i=1} : C \to C$ be a G-nonexpansive mapping with $\bigcap_{i=1}^{N}F(T_{i})$ the dominating set. Let $\alpha _{k}=(\alpha _{1}^{k},\alpha _{2}^{k},\alpha _{3}^{k})$, where $\alpha _{1}^{k},\alpha _{2}^{k},\alpha _{3}^{k}\in [0,1]$ with $\alpha _{1}^{k}+\alpha _{2}^{k}+\alpha _{3}^{k}=1$ for all $k=1,2,\ldots,N$ and $\alpha _{1}^{k}\in (0,1)$ for all $k=1,2,\ldots,N-1$ and $\alpha _{1}^{N}\in (0,1]$, $\alpha _{2}^{k}, \alpha _{3}^{k}\in [0,1]$ for all $k=1,2,\ldots,N$. Let $S:C\to C$ be a G-S-mapping generated by $T_{1},T_{2},\ldots,T_{N}$ and $\alpha _{1}, \alpha _{2},\ldots,\beta _{n}$. Assume that

$$ \Omega =\bigcap_{i=1}^{N}F(T_{i}) \cap G\textit{-} VI(C,A)\neq \emptyset $$

with $\bigcap_{i=1}^{N}F(T_{i})\times \bigcap_{i=1}^{N}F(T_{i}) \subseteq E(G)$, and there exists $x_{0}\in C$ such that $(x_{0},T_{1}x_{0})$. Let $\{x_{n}\}$ be a sequence generated by $x_{0} = u \in C$ and

$$ \textstyle\begin{cases} x_{0}\in C, \\ x_{n+1}=\beta _{n}u+(1-\beta _{n})Sx_{n}, \quad n\geq 0, \end{cases} $$

(26)

where $\{\beta _{n}\} \subseteq [0,1]$.

If the following conditions hold:

• (i) $\lim_{n \rightarrow \infty} \beta _{n}= 0$ and $\sum_{n=1}^{\infty}\beta _{n}=\infty$;

• (ii) $\sum_{n=1}^{\infty}|\beta _{n+1} - \beta _{n}|< \infty$;

• (iii) $(T_{i}x,T_{i+1}x)\in E(G)$ for all $i=1,2,\ldots,N-1$ and $x\in C$,

then, $\{x_{n}\}$ converges strongly to $P_{\Omega}x_{0}$, where $P_{\Omega}$ is a metric projection on Ω, $P_{\Omega}x_{0}$ is dominated by $\{x_{n}\}$, $P_{\Omega}x_{0}$ is dominated by $x_{0}$, and $\{x_{n}\}$ dominates $x_{0}$.

Taking $A=0$, $P_{C}=I$, $N=1$, and $\alpha _{1}^{N}=1$ in Theorem 3.1, then we obtain the following result.

Corollary 3.4

Let C have the Property G and G be transitive with $E(G) = E(G^{-1})$. Let $T : C \to C$ be a G-nonexpansive mapping. Assume that $F(T)\neq \emptyset$ with $F(T)\times F(T)\subseteq E(G)$, and there exists $x_{0}\in C$ such that $(x_{0},Tx_{0})$. Let $\{x_{n}\}$ be a sequence generated by $x_{0} = u \in C$ and

$$ \textstyle\begin{cases} x_{0}\in C, \\ x_{n+1}=\beta _{n}u+(1-\beta _{n})Tx_{n}, \quad n\geq 0, \end{cases} $$

(27)

where $\{\beta _{n}\} \subseteq [0,1]$.

If the following conditions hold:

• (i) $\lim_{n \rightarrow \infty} \beta _{n}= 0$ and $\sum_{n=1}^{\infty}\beta _{n}=\infty$;

• (ii) $\sum_{n=1}^{\infty}|\beta _{n+1} - \beta _{n}|< \infty$,

then, $\{x_{n}\}$ converges strongly to $P_{F(T)}x_{0}$, where $P_{F(T)}$ is a metric projection on $F(T)$, $P_{F(T)}x_{0}$ is dominated by $\{x_{n}\}$, $P_{F(T)}x_{0}$ is dominated by $x_{0}$, and $\{x_{n}\}$ dominates $x_{0}$.

Remark 1

We have the following consequences of Theorem 3.1:

• 1. The results of Kangtunyakarn [3] is a special case of Theorem 3.1 by taking $A=0$ and $P_{C}=I$.

• 2. The results of Tiammee et al. [2] is a special case of Theorem 3.1 by taking $A=0$, $P_{C}=I$, $N=1$, and $\alpha _{1}^{N}=1$.

4 Examples and numerical results

In this section, we provide some numerical examples to support our obtained result. To obtain these results, we recall some lemmas as follows.

Lemma 4.1

[14] Let $G= ( V ( G ) ,E ( G ) )$ be a directed graph with $V ( G ) =C$ dominating z for all $z\in C$. Let $E(G)$ be convex and G be a transitive with $E(G) = E(G^{-1})$. Let $S:C\rightarrow C$ be a G-nonexpansive mapping with $F ( S ) \neq \emptyset$ and $F ( S ) \times F ( S ) \subseteq E ( G )$. Then,

(i) $I-S$ is G-$\frac{1}{2}$-inverse strongly monotone;

(ii) G-$VI ( C,I-S ) =F ( S )$.

We now provide an example to support our main result.

Example 4.2

Let $H = \mathbb{R}$ and $C = [0, 1.5 ]$ with the usual norm $\|x - y\| = |x - y|$ and let $G = (V(G), E(G))$ be a directed graph such that $V(G) = C$, $E(G) = \{(x, y) : x, y \in [0, 1] \text{ with } |x - y| < 1 \}$. For every $i=1,2,\ldots,N$, define the mapping $T_{i} : [0, 1.5 ] \rightarrow [0, 1.5 ]$ by

$$ T_{i}x= \textstyle\begin{cases} \frac {x}{2^{i}} + (1-\frac {1}{2^{i}} )\frac {1}{2}& \text{if } x \in [0,1], \\ 0 &\text{if } x \in (1,1.5] . \end{cases} $$

(28)

Let $S:[0, 1.5 ]\to [0, 1.5 ]$ be a G-S-mapping generated by $T_{1},T_{2},\ldots,T_{N}$ and $\alpha _{1}, \alpha _{2},\ldots,\alpha _{n}$, where

$$ \alpha _{i}= \biggl( \frac {1}{5^{i}},\frac {5^{i}-1}{5^{i}} \biggl( \frac {6^{i}-1}{6^{i}} \biggr),\frac {5^{i}-1}{5^{i}} \biggl( \frac {1}{6^{i}} \biggr) \biggr) $$

for all $i=1,2,\ldots,N$ and let $A: [ 0, 1.5 ] \rightarrow \mathbb{R}$ be a mapping defined by

$$ Ax=x-\frac {x^{2}}{4}-\frac {7}{16}, $$

(29)

for all $x\in [ 0, 1.5 ]$.

Suppose that the sequence $\{x_{n}\}$ is generated by $u=x_{0}=\frac{1}{6}$ and

$$ x_{n+1}=P_{[0,1.5]}\biggl(I - \frac {1}{6}A \biggr) \bigl(\beta _{n}u+(1-\beta _{n})Sx_{n} \bigr), $$

(30)

where $\beta _{n}=\frac {1}{2n+2}$ for all $n\geq 0$.

Then, the sequence $\{x_{n}\}$ converges strongly to $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}x_{0}=\{ \frac{1}{2}\}$.

Solution. It is clear that $A^{-1}(0) \neq \emptyset$, since $\frac{1}{2} \in A^{-1}(0)$ and $E(G)=E(G^{-1})$. Let $x,y \in [0,1.5]$ with $(x,y)\in E(G)$. It is easy to check that $T_{i}$ is a G-nonexpansive mapping for all $i = 1,2,\ldots,N$ such that $\bigcap_{i=1}^{N}F(T_{i})=\{ \frac{1}{2} \}$. However, it is not nonexpansive, as $|x-y|<|T_{i}x-T_{i}y|$ for all $i=1,2,\ldots,N$, where $x=1$, $y= 1.1$. Let $v\in V(G)-\bigcap_{i=1}^{N}F(T_{i})$. Since $\frac{1}{2}\in \bigcap_{i=1}^{N}F(T_{i})$, we have $|\frac{1}{2}-v|<1$. It follows that $\bigcap_{i=1}^{N}F(T_{i})$ is the dominating set. Let $x\in V(G)=[1,1.5]=[0,1]\cup (1,1.5]$. Then,

Case $x\in [0,1]$. Then,

$$ T_{i}x=\frac {x}{2^{i}} + \biggl(1-\frac {1}{2^{i}} \biggr) \frac {1}{2} \quad \text{and}\quad T_{i+1}x=\frac {x}{2^{i+1}} + \biggl(1- \frac {1}{2^{i+1}} \biggr)\frac {1}{2}, $$

for all $i=1,2,\ldots,N-1$. Since $[0,1]$ is convex, we have $T_{i}x,T_{i+1}x\in [0,1]$ for all $i=1,2,\ldots,N-1$. Observe that

$$ \vert T_{i+1}x-T_{i}x \vert =\frac {1}{2^{i+1}} \biggl\vert \frac {1}{2}-x \biggr\vert \leq 1. $$

Then, $(T_{i+1}x, T_{i}x)\in E(G)$ for all $i=1,2,\ldots,N-1$.

Case $x\in (1,1.5]$. It is obvious that $|T_{i}x-T_{i+1}x|<1$. Then, $(T_{i}x, T_{i+1}x)\in E(G)$ for all $i=1,2,\ldots,N-1$.

It is easy to check that $\mathcal{T}$ is a G-nonexpansive mapping, where $\mathcal{T}x=\frac {x^{2}}{4}+\frac {7}{16}$ for all $x\in [ 0,1 ]$.

Since $Ax=x-\frac {x^{2}}{4}-\frac {7}{16}= ( I-\mathcal{T} ) x$ for all $x\in [ 0,1 ]$, $\mathcal{T}$ is a G-nonexpansive mapping and from Lemma 4.1, we have A is G-$\frac {1}{2}$-inverse strongly monotone. Then, $\bigcap_{i=1}^{N}F(T_{i})\cap G\text{-}VI ( C,A ) = \{ \frac {1}{2} \}$.

For every $z\in [ 0,1 ]$, we have

$$\begin{aligned} \biggl( I-\frac {1}{6}A \biggr) z =&z-\frac {1}{6}Az \\ =&z-\frac {1}{6} \biggl( z-\frac {z^{2}}{4}-\frac {7}{16} \biggr) \\ =&\frac {5z}{6}+\frac {1}{6} \biggl( \frac {z^{2}}{4}+ \frac {7}{16} \biggr) \\ =&\frac {5z}{6}+\frac {1}{6} \biggl( \frac {z^{2}}{4}+ \frac {3}{4}\cdot \frac {28}{48} \biggr) \in [ 0,1 ]. \end{aligned}$$

From the definition of $P_{C}$, we have

$$ P_{[0,1.5]} \biggl( I-\frac {1}{6}A \biggr) z\in [ 0,1 ], $$

(31)

for all $z\in [ 0,1 ]$.

Putting $x_{0}=\frac{1}{6}$ and $y_{n}=\beta _{n}u+(1-\beta _{n})Sx_{n}$ for all $n \geq 0$, from (31), we have $P_{[0,1.5]} ( I-\frac {1}{4}A ) x_{0}\in [ 0,1 ]$. This implies that $T_{1}x_{0}\in [0,1]$ and $|x_{0}-T_{1}x_{0}|<1$. This implies that $(x_{0},T_{1}x_{0})\in E(G)$.

From the definition of S and $x_{0}=\frac{1}{6}$, we have $Sx_{0}\in [0,1]$. It follows that $(x_{0},Sx_{0})\in E(G)$.

From $x_{0}, Sx_{0}\in [0,1]$ and the definition of $y_{n}$, we have $y_{0}\in [0,1]$ for all $n\geq 0$.

From (31) and $y_{0}\in [0,1]$, we have $P_{[0,1.5]} ( I-\frac {1}{6}A ) y_{0}\in [ 0,1 ]$. This implies that $x_{1}\in [ 0,1 ]$.

Continuing in this way, we have $x_{n}\in [ 0,1 ]$ for all $n \geq 0$.

Since $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}x_{0}=\{ \frac{1}{2}\}$ and $x_{n}\in [ 0,1 ]$ for all $n \geq 0$, we have $|x_{n}-\frac{1}{2}|<1$. This implies that $(x_{n},P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}x_{0})\in E(G)$. Then, $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}x_{0}$ is dominated by $\{x_{n}\}$.

It is obvious that $\{x_{n}\}$ dominates $x_{0}$ and also $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}x_{0}$ is dominated by $x_{0}$, where $x_{0}=\frac{1}{6}$. From Theorem 3.1, we have the sequence $\{x_{n}\}$ converging strongly to $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}x_{0}=\{ \frac{1}{2}\}$.

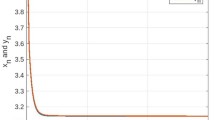
We first start with the initial point $x_{0}=\frac{1}{6}$. Our testing procedure takes $|x_{n+1}-x_{n}| \leq 1\mathrm{E}-12$ as the stopping condition. Now, a convergence of the algorithm (30) is shown in Table 1 and visualized in Figs. 1 and 2.

Figure 1

Visualization of the first one hundred rounds of algorithm (30) in Example 4.2

Figure 2

Visualization of the error $| x_{n} - x_{n+1} |$ of algorithm (30) in Example 4.2

Table 1 Convergence of the algorithm (30) in Example 4.2

Next, a comparison of algorithm (30) and algorithm (5) of [14] is provided, focusing on CPU time and the number of iterations for different initial points, as detailed in Table 2. Moreover, Our testing procedure takes $|x_{n+1}-x_{n}| \leq 1\mathrm{E}-6$ as the stopping condition.

Table 2 Numerical values of algorithm (30) and algorithm (5) of [14]

Remark 2

By observing the convergence behavior of Algorithm (30) in Example 4.2, we conclude that

• 1. Table 1 and Figs. 1 and 2 show that $\{x_{n}\}$ converges to a solution, i.e., $x_{n}\to 1/2\in \Omega$. The convergence of $\{x_{n}\}$ of Example 4.2 can be guaranteed by Theorem 3.1.

• 2. The values of the sequence $\{x_{n}\}$ with respect to n are also plotted in Fig. 1, demonstrating that $(x_{n},x_{0}), (x_{n+1},x_{n})\in E(G)$.

• 3. For every $i = 1,2,\ldots,N$, $T_{i}$ are G-nonexpansive mappings but not nonexpansive.

• 4. From Table 2, we see that the sequence generated by our algorithm (30) has better convergence than algorithm (5) of [14] in terms of the number of iterations and the CPU time.

Next, we give an example in the infinite-dimensional space $l_{2}$ to support some results as follows.

Example 4.3

Let $C:= \{\mathbf{x}=(x_{1}, x_{2}, x_{3},\ldots)\in l_{2}: \|\mathbf{x}\|_{l_{2}} \leq 1 \text{ and } x_{i}\in [0,1] \text{ for } i=1,2,3,\ldots\}$ with the norm $\|\mathbf{x}\|_{l_{2}}= (\sum_{i=1}^{\infty}|x_{i}|^{2} )^{1/2}$ and the inner product $\langle \mathbf{x}, \mathbf{y}\rangle = \sum_{i=1}^{\infty}x_{i}y_{i}$ for $\mathbf{y}=(y_{1}, y_{2}, y_{3},\ldots)\in l_{2}: \|\mathbf{y}\|_{l_{2}} \leq 1 \text{ and } y_{i}\in [0,1]$. Let $G = (V(G), E(G))$ be such that $V(G) = C$, $E(G) = \{(\mathbf{x}, \mathbf{y}) :x_{i}, y_{i}\in [0, \frac{1}{3}] \text{ with }\|\mathbf{x}-\mathbf{y}\|_{l_{2}}\leq \frac{1}{5} \text{ for } i= 1,2,3,\ldots \}$. Define the mapping $T:C\to C$ by

$$ T\mathbf{x}= \biggl(\frac {1}{2}x_{1}^{2}, \frac {3}{8}x_{2}^{2},0, 0, 0, \ldots \biggr),\quad \forall \mathbf{x} \in C. $$

(32)

Suppose that the sequence $\{\mathbf{x}_{n}\}$ is generated by $\mathbf{u}=\mathbf{x}_{0}= (\frac{1}{6}, \frac{1}{8},0,0,0,\ldots )$ and

$$ \mathbf{x}_{n+1}=\beta _{n}\mathbf{u}+(1- \beta _{n})T\mathbf{x}_{n}, $$

(33)

where $\beta _{n}=\frac {1}{2n+2}$ for all $n\geq 0$. Then, the sequence $\{\mathbf{x}_{n}\}$ converges strongly to $P_{F(T)}\mathbf{x}_{0}$.

Solution. We can easily show that T is a G-nonexpansive mapping with $F(T)=\{\mathbf{0}\}$, where $\mathbf{0}=(0,0,0,0,0,\ldots)$ is the null vector on $l_{2}$. From the definition of T and $\mathbf{u}=\mathbf{x}_{0}= (\frac{1}{6}, \frac{1}{8},0,0,0,\ldots )$, we have $(\mathbf{x}_{0},T\mathbf{x}_{0})\in E(G)$. Since $P_{F(T)}\mathbf{x}_{0}=\{\mathbf{0}\}$ and the definition of $\mathbf{x}_{n}$, we have $\|\mathbf{x}_{n}-\mathbf{0}\|_{l_{2}} \leq \frac{1}{5}$. It follows that $(\mathbf{x}_{n},P_{F(T)}\mathbf{x}_{0})\in E(G)$. Then, $P_{F(T)}\mathbf{x}_{0}$ is dominated by $\{\mathbf{x}_{n}\}$. It is obvious that $\{\mathbf{x}_{n}\}$ dominates $\mathbf{x}_{0}$ and also $P_{F(T)}\mathbf{x}_{0}$ is dominated by $\{\mathbf{x}_{0}\}$. From Corollary 3.4, we have the sequence $\{\mathbf{x}_{n}\}$ converging strongly to $P_{F(T)}\mathbf{x}_{0}=\{\mathbf{0}\}$. We first start with the initial point $\mathbf{x}_{0}= (\frac{1}{6}, \frac{1}{8},0,0,0,\ldots )$. The stopping criterion for our testing method is taken as $\|\mathbf{x}_{n+1}-\mathbf{x}_{n}\|_{l_{2}} \leq 1\mathrm{E}-9$. Now, a convergence of the algorithm (33) is shown in Table 3 and visualized in Fig. 3.

Figure 3

Visualization of the convergence and error $\| x_{n+1} - x_{n} \|_{l_{2}}$ of algorithm (33) in Example 4.3

Table 3 Convergence of the algorithm (33) in Example 4.3

Remark 3

By observing the convergence behavior of Algorithm (30) in Example 4.3, we conclude that it converges to a solution, i.e., $\mathbf{x}_{n}\to \mathbf{0}\in F(T)$.

Next, we provide a numerical example to support our results in a two-dimensional space.

Example 4.4

Let $H=\mathbb{R}^{2}$ and $C = [-2, 2] \times [-2, 2]$. Let $G = (V(G), E(G))$ be a directed graph, where $V(G) = C$ and $E(G) = \{(\textbf{x},\textbf{y})=((x_{1}, x_{2}), (y_{1},y_{2})) : \textbf{x}, \textbf{y} \in [-1, 1]\times [-1,1]\}$. Let $P_{C}:H \to C$ be a metric projection defined by

$$ P_{C}(z_{1}, z_{2})=\bigl(\max \bigl\{ \min \{z_{1}, 2 \}, -2\bigr\} , \max \bigl\{ \min \{z_{2},2 \},-2\bigr\} \bigr), $$

(34)

for all $\textbf{z}=(z_{1},z_{2})\in H$.

For every $i=1,2,\ldots,N$, let $T_{i} : C \rightarrow C$ be mappings defined by

$$ T_{i}(x_{1}, x_{2})= \biggl( \frac {x_{1}}{3^{i}} + \biggl(1- \frac {1}{3^{i}} \biggr)\frac {1}{2}, \frac {x_{2}}{2^{i+1}} + \biggl(1- \frac {1}{2^{i+1}} \biggr)\frac {1}{4} \biggr), $$

(35)

for all $x_{1}, x_{2}\in C$.

Let $S: C\to C$ be a G-S-mapping generated by $T_{1},T_{2},\ldots,T_{N}$ and $\alpha _{1}, \alpha _{2},\ldots,\alpha _{n}$, where

$$ \alpha _{i}= \biggl( \frac {1}{5^{i}},\frac {5^{i}-1}{5^{i}} \biggl( \frac {6^{i}-1}{6^{i}} \biggr),\frac {5^{i}-1}{5^{i}} \biggl( \frac {1}{6^{i}} \biggr) \biggr), $$

for all $i=1,2,\ldots,N$

and let $A:C \rightarrow H$ be a mapping defined by

$$ A(x_{1},x_{2})= \biggl( x_{1}- \frac {x_{1}^{3}}{4}-\frac {15}{32}, \frac {x_{2}}{5}-\frac {1}{20} \biggr), $$

(36)

for all $(x_{1},x_{2})\in C$.

Suppose that the sequence $\{\textbf{x}^{n}\}$ is generated by $\textbf{u}=\textbf{x}^{0}=(x^{0}_{1}, x^{0}_{2})=(1,0)$ and

$$ \textbf{x}^{n+1}=P_{C}\biggl(I- \frac {1}{2}A\biggr) \bigl(\beta _{n}\textbf{u}+(1-\beta _{n})S \textbf{x}^{n}\bigr), $$

(37)

where $\beta _{n}=\frac{1}{2n+4}$ for all $n\geq 0$.

Then, the sequence $\{x^{n}\}$ converges strongly to $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}\textbf{x}^{0}=\{ (\frac{1}{2}, \frac{1}{4} )\}$.

Solution. It is clear that $A^{-1}(0,0) \neq \emptyset$, since $(\frac{1}{2}, \frac{1}{4} ) \in A^{-1}(0,0)$ and $E(G)=E(G^{-1})$. Let $\textbf{x},\textbf{y}\in C$ with $(\textbf{x},\textbf{y})\in E(G)$, where $\textbf{x}=(x_{1}, x_{2})$ and $\textbf{y}= (y_{1},y_{2})$. Then, we have $\textbf{x},\textbf{y}\in [ -1, 1 ]\times [ -1, 1 ]$. It is easy to verify that $T_{i}$ are G-nonexpansive mappings for all $i = 1,2,\ldots,N$ such that $\bigcap_{i=1}^{N}F(T_{i})=\{ (\frac{1}{2}, \frac{1}{4} ) \}$.

From the definition of the mapping A, it is obvious that A is $G\text{-}\frac{1}{2}$-inverse strongly monotone and $G\text{-} VI(C,A)=\{ (\frac{1}{2}, \frac{1}{4} )\}$. Therefore, $\bigcap_{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)=\{ (\frac{1}{2}, \frac{1}{4} )\}$.

From the definition of $T_{i }$ and $\textbf{x}\in [-1, 1] \times [-1, 1]$, we have

$$ T_{i}\textbf{x}= \biggl( \frac {x_{1}}{3^{i}} + \biggl(1- \frac {1}{3^{i}} \biggr)\frac {1}{2}, \frac {x_{2}}{2^{i+1}} + \biggl(1- \frac {1}{2^{i+1}} \biggr)\frac {1}{4} \biggr) $$

and

$$ T_{i+1}\textbf{x}= \biggl( \frac {x_{1}}{3^{i+1}} + \biggl(1- \frac {1}{3^{i+1}} \biggr)\frac {1}{2}, \frac {x_{2}}{2^{i+2}} + \biggl(1- \frac {1}{2^{i+2}} \biggr)\frac {1}{4} \biggr), $$

for all $i=1,2,\ldots,N-1$. Since $[ -1, 1 ]$ is convex, we have $T_{i}\textbf{x},T_{i+1}\textbf{x}\in [ -1, 1 ]\times [ -1, 1 ]$ for all $i=1,2,\ldots,N-1$. Then, $(T_{i+1}\textbf{x}, T_{i}\textbf{x})\in E(G)$ for all $i=1,2,\ldots,N-1$.

Putting $\textbf{u}=\textbf{x}^{0}=(0,1)\in [ -1, 1 ]\times [ -1, 1 ]$ and the definition of $T_{1}$, we obtain $T_{1}\textbf{x}^{0}\in [ -1, 1 ]\times [ -1, 1 ]$. This implies that $(\textbf{x}^{0},T_{1}\textbf{x}^{0})\in E(G)$. From the definition of S, we have, $S\textbf{x}^{0}\in [ -1, 1 ]\times [ -1, 1 ]$.

Since $\textbf{u}=\textbf{x}^{0}=(1,0)$, $S\textbf{x}^{0}=(1,0)$, $\beta _{n}=\frac{1}{2n+4}$ for all $n\geq 0$, we have

$$ \bigl(\beta _{0}\textbf{u}+(1-\beta _{0})S \textbf{x}^{0} \bigr) = (1, 0) $$

and it follows that

$$ \biggl(I-\frac {1}{2}A\biggr) \bigl(\beta _{0} \textbf{u}+(1-\beta _{0})S\textbf{x}^{0} \bigr) = (0.859375, 0.025000). $$

(38)

From (34) and (38), we have

$$ \textbf{x}^{1}=\bigl(x^{1}_{1},x^{2}_{1} \bigr)=P_{C}\biggl(I-\frac {1}{2}A\biggr) \bigl(\beta _{0} \textbf{u}+(1-\beta _{0})S\textbf{x}^{0} \bigr) = (0.859375, 0.025000). $$

(39)

It follows from (39) that $\textbf{x}^{1} \in [ -1, 1 ]\times [ -1, 1 ]$.

Since $\textbf{u}=(1,0)$, $S\textbf{x}^{1}=(0.8114583,0.0587500)$, $\beta _{n}=\frac{1}{2n+4}$ for all $n\geq 0$, we have

$$ \bigl(\beta _{1}\textbf{u}+(1-\beta _{1})S \textbf{x}^{1} \bigr) = (0.8428819, 0.0489583) $$

and it follows that

$$ \biggl(I-\frac {1}{2}A\biggr) \bigl(\beta _{1} \textbf{u}+(1-\beta _{1})S\textbf{x}^{1} \bigr) = (0.7306692, 0.0690625). $$

(40)

From (34) and (40), we have

$$ \textbf{x}^{2}=\bigl(x^{2}_{1},x^{2}_{2} \bigr)=P_{C}\biggl(I-\frac {1}{2}A\biggr) \bigl(\beta _{1} \textbf{u}+(1-\beta _{1})S\textbf{x}^{1}\bigr) = (0.7306692, 0.0690625). $$

(41)

It follows from (41) that $\textbf{x}^{2} \in [ -1, 1 ]\times [ -1, 1 ]$.

Continuing in this way, we have $\textbf{x}^{n}=(x_{1}^{n}, x_{2}^{n})\in [ -1, 1 ]\times [ -1, 1 ]$ for all $n \geq 0$. This implies that $(\textbf{x}^{n},\textbf{x}^{0}) \in E(G)$.

From $\bigcap_{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)= \{(\frac{1}{2}, \frac{1}{4})\}$, it is easy to see that $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}\textbf{x}^{0} \in [ -1, 1 ]\times [ -1, 1 ]$.

Since $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}\textbf{x}^{0} \in [ -1, 1 ]\times [ -1, 1 ]$ and $\textbf{x}^{n} \in [ -1, 1 ]\times [ -1, 1 ]$ for all $n \geq 0$, we have $(\textbf{x}^{n},P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)} \textbf{x}^{0} )\in E(G)$. Then, $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}\textbf{x}^{0}$ is dominated by $\{\textbf{x}^{n}\}$.

It is obvious that $\{\textbf{x}^{n}\}$ dominates $\textbf{x}^{0}$ and also $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}\textbf{x}^{0}$ is dominated by $\textbf{x}^{0}$, where $\textbf{x}^{0}=\{(\frac{1}{2}, \frac{1}{4})\}$. From Theorem 3.1, we have the sequence $\{\textbf{x}^{n}\}$ converging strongly to $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}\textbf{x}^{0}=\{( \frac{1}{2}, \frac{1}{4})\}$.

Now, a convergence of the algorithm (37) is shown in Table 4 and visualized in Figs. 4 and 5.

Figure 4

Visualization of the convergence of the algorithm (37) in Example 4.4

Figure 5

Error plotting of algorithm (37) in Example 4.4

Table 4 Convergence of the algorithm (37) in Example 4.2

Remark 4

For the provided Example 4.4, we have the following observations:

• 1. Table 4 and Figs. 4 and 5 show that $\{\textbf{x}^{n}\}$ converges to $(\frac{1}{2}, \frac{1}{4})$. The convergence of $\{\textbf{x}^{n}\}$ in Example 4.4 can be guaranteed by Theorem 3.1.

• 2. The values of the sequence $\{\textbf{x}^{n}\}$ with respect to n are also plotted in Fig. 4, showing that $(\textbf{x}^{n},\textbf{x}^{0}), (\textbf{x}^{n+1},\textbf{x}^{n})\in E(G)$.

In the following example, we investigate the metric projection onto a half-space $H\_(\alpha ,\beta ):\{z\in H:\langle \alpha , z \rangle \leq \beta \}$, where $\alpha \in H$, $\alpha \neq 0$ and $\beta \in \mathbb{R}$. It is obvious that

$$ P_{H\_(\alpha ,\beta )}x= \textstyle\begin{cases} x-\frac {\langle \alpha , x \rangle - \beta }{ \Vert \alpha \Vert ^{2}}\alpha , &\text{if} \langle \alpha , x \rangle > \beta , \\ x, &\text{if} \langle \alpha , x \rangle \leq \beta . \end{cases} $$

(42)

Equality (42) is clear if $x\in H\_(\alpha ,\beta )$, i.e., $\langle \alpha , x \rangle \leq \beta$ (see, [21] for more details).

Example 4.5

Let $H=\mathbb{R}^{2}$ and $C = \{(x_{1},x_{2})\in \mathbb{R}^{2}:-3x_{1}+x_{2}\leq 9\}$. Then, we obtain

$$ P_{C}(x_{1}, x_{2})= \textstyle\begin{cases} (\frac {x_{1}+3x_{2}-27}{10}, \frac {3x_{1}+9x_{2}+9}{10} ), &\text{if} -3x_{1}+x_{2}> 9, \\ (x_{1},x_{2}), &\text{if} -3x_{1}+x_{2}\leq 9, \end{cases} $$

(43)

for all $(x_{1},x_{2})\in \mathbb{R}^{2}$.

Let $G = (V(G), E(G))$ be a directed graph, where $V(G) = C$ and $E(G) = \{(\textbf{x},\textbf{y})=((x_{1}, x_{2}), (y_{1},y_{2})) : \textbf{x}, \textbf{y} \in [0, 1]\times [0,1]\}$.

For every $i=1,2,\ldots,N$, let $T_{i} : C \rightarrow C$ be mappings defined by

$$ T_{i}(x_{1}, x_{2})= \biggl( \frac {x^{2}_{1}}{5^{i}}, \frac {x_{2}}{2^{i}} + \biggl(1-\frac {1}{2^{i}} \biggr) \frac {1}{2} \biggr), $$

(44)

for all $(x_{1},x_{2})\in C$.

Let $S: C\to C$ be a G-S-mapping generated by $T_{1},T_{2},\ldots,T_{N}$ and $\alpha _{1}, \alpha _{2},\ldots,\alpha _{n}$, where

$$ \alpha _{i}= \biggl( \frac {1}{5^{i}},\frac {5^{i}-1}{5^{i}} \biggl( \frac {6^{i}-1}{6^{i}} \biggr),\frac {5^{i}-1}{5^{i}} \biggl( \frac {1}{6^{i}} \biggr) \biggr), $$

for all $i=1,2,\ldots,N$ and let $A:C \rightarrow H$ be a mapping defined by

$$ A(x_{1},x_{2})= \biggl( x_{1}- \frac {x_{1}^{3}}{4}, \frac {4x_{2}}{5}- \frac {2}{5} \biggr), $$

(45)

for all $(x_{1},x_{2})\in C$.

Suppose that the sequence $\{\textbf{x}^{n}\}$ is generated by $\textbf{u}=\textbf{x}^{0}=(x^{0}_{1}, x^{0}_{2})=(1,0)$ and

$$ \textbf{x}^{n+1}=P_{C}\biggl(I- \frac {1}{2}A\biggr) \bigl(\beta _{n}\textbf{u}+(1-\beta _{n})S \textbf{x}^{n}\bigr), $$

(46)

where $\beta _{n}=\frac{1}{2n+4}$ for all $n\geq 0$.

Then, the sequence $\{x^{n}\}$ converges strongly to $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}\textbf{x}^{0}=\{ (0,\frac{1}{2} )\}$.

Solution. It is clear that $A^{-1}(0,0) \neq \emptyset$, since $(0,\frac{1}{2} ) \in A^{-1}(0,0)$ and $E(G)=E(G^{-1})$. Let $\textbf{x},\textbf{y}\in C$ with $(\textbf{x},\textbf{y})\in E(G)$, where $\textbf{x}=(x_{1}, x_{2})$ and $\textbf{y}= (y_{1},y_{2})$. Then, we have $\textbf{x},\textbf{y}\in [0, 1 ]\times [ 0, 1 ]$. It is easy to verify that $T_{i}$ are G-nonexpansive mappings for all $i = 1,2,\ldots,N$ such that $\bigcap_{i=1}^{N}F(T_{i})=\{ (0,\frac{1}{2} ) \}$.

From the definition of the mapping A, it is obvious that A is $G\text{-}\frac{1}{2}$-inverse strongly monotone and $G\text{-} VI(C,A)=\{ (0,\frac{1}{2} )\}$. Therefore, $\bigcap_{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)=\{ (0, \frac{1}{2} )\}$.

From the definition of $T_{i }$, it is obvious that $T_{i}\textbf{x},T_{i+1}\textbf{x}\in [ 0, 1 ]\times [ 0, 1 ]$ for all $i=1,2,\ldots,N-1$. Then, $(T_{i+1}\textbf{x}, T_{i}\textbf{x})\in E(G)$ for all $i=1,2,\ldots,N-1$.

Putting $\textbf{u}=\textbf{x}^{0}=(1,0)\in [ 0, 1 ]\times [ 0, 1 ]$ and the definition of $T_{i}$, we obtain $T_{1}\textbf{x}^{0}\in [ 0, 1 ]\times [ 0, 1 ]$. This implies that $(\textbf{x}^{0},T_{1}\textbf{x}^{0})\in E(G)$. From the definition of S, we have, $S\textbf{x}^{0}\in [ 0, 1 ]\times [ 0, 1 ]$.

Since $\textbf{u}=\textbf{x}^{0}=(1,0)$, $S\textbf{x}^{0}=(1,0)$, and $\beta _{n}=\frac{1}{2n+4}$ for all $n\geq 0$, we have

$$ \bigl(\beta _{0}\textbf{u}+(1-\beta _{0})S \textbf{x}^{0} \bigr) = (1, 0) $$

and it follows that

$$ \biggl(I-\frac {1}{2}A\biggr) \bigl(\beta _{0} \textbf{u}+(1-\beta _{0})S\textbf{x}^{0} \bigr) = (0.6250000, 0.2000000). $$

(47)

From (43) and (47), we have

$$ \textbf{x}^{1}=\bigl(x^{1}_{1},x^{2}_{1} \bigr)=P_{C}\biggl(I-\frac {1}{2}A\biggr) \bigl(\beta _{0} \textbf{u}+(1-\beta _{0})S\textbf{x}^{0} \bigr) = (0.6250000, 0.2000000). $$

(48)

It follows from (48) that $\textbf{x}^{1}\in [ 0, 1 ]\times [ 0, 1 ]$.

Since $\textbf{u}=(1,0)$, $S\textbf{x}^{1}=(0.5156250,0.2300000)$, and $\beta _{n}=\frac{1}{2n+4}$ for all $n\geq 0$, we have

$$ \bigl(\beta _{1}\textbf{u}+(1-\beta _{1})S \textbf{x}^{1} \bigr) = (0.5963542, 0.1916667) $$

and it follows that

$$ \biggl(I-\frac {1}{2}A\biggr) \bigl(\beta _{1} \textbf{u}+(1-\beta _{1})S\textbf{x}^{1} \bigr) = (0.3246879, 0.3150000). $$

(49)

From (43) and (49), we have

$$ \textbf{x}^{2}=\bigl(x^{2}_{1},x^{2}_{2} \bigr)=P_{C}\biggl(I-\frac {1}{2}A\biggr) \bigl(\beta _{1} \textbf{u}+(1-\beta _{1})S\textbf{x}^{1}\bigr) = (0.3246879, 0.3150000). $$

(50)

It follows from (50) that $\textbf{x}^{2} \in [0, 1 ]\times [0, 1 ]$.

Continuing in this way, we have $\textbf{x}^{n}=(x_{1}^{n}, x_{2}^{n})\in [ 0, 1 ]\times [ 0, 1 ]$ for all $n \geq 0$. This implies that $(\textbf{x}^{n},\textbf{x}^{0}) \in E(G)$.

From $\bigcap_{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)= \{(0, \frac{1}{2}) \}$, it is easy to see that $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}\textbf{x}^{0} \in [ 0, 1 ]\times [ 0, 1 ]$.

Since $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}\textbf{x}^{0}\in [ 0, 1 ]\times [ 0, 1 ]$ and $\textbf{x}^{n} \in [ 0, 1 ]\times [ 0, 1 ]$ for all $n \geq 0$, we have $(\textbf{x}^{n},P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)} \textbf{x}^{0} )\in E(G)$. This implies that $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}\textbf{x}^{0}$ is dominated by $\{\textbf{x}^{n}\}$.

It is obvious that $\{\textbf{x}^{n}\}$ dominates $\textbf{x}^{0}$ and also $P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}\textbf{x}^{0}$ is dominated by $\textbf{x}^{0}$, where $\textbf{x}^{0}=\{(0, \frac{1}{2})\}$.

From Theorem 3.1, we have the sequence $\{\textbf{x}^{n}\}$ converging strongly to

$P_{\bigcap _{i=1}^{N}F(T_{i})\cap G\text{-} VI(C,A)}\textbf{x}^{0}=\{(0, \frac{1}{2})\}$.

Now, a convergence of the algorithm (46) is shown in Table 5 and visualized in Figs. 6 and 7.

Figure 6

Visualization of the convergence of the algorithm (46) in Example 4.4

Figure 7

Error plotting of algorithm (46) in Example 4.4

Table 5 Convergence of the algorithm (46) in Example 4.2

Remark 5

For the provided Example 4.5, we have the following observations:

• 1. Table 5 and Figs. 6 and 7 show that $\{\textbf{x}^{n}\}$ converges to $(0, \frac{1}{2})$. The convergence of $\{\textbf{x}^{n}\}$ in Example 4.5 can be guaranteed by Theorem 3.1.

• 2. The values of the sequence $\{\textbf{x}^{n}\}$ with respect to n are also plotted in Fig. 6, showing that $(\textbf{x}^{n},\textbf{x}^{0}), (\textbf{x}^{n+1},\textbf{x}^{n})\in E(G)$.