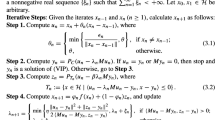A modified subgradient extragradient algorithm-type for solving quasimonotone variational inequality problems with applications

Abstract

In this article, we introduce an inertial-type algorithm that combines the extragradient subgradient method, the projection contraction method, and the viscosity method. The proposed method is used for solving quasimonotone variational inequality problems in infinite dimensional real Hilbert spaces such that it does not depend on the Lipschitz constant of the cost operator. Further, we prove the strong convergence results of the new algorithm. Our strong convergence results are achieved without imposing strict conditions on the control parameters and inertial factor of our algorithm. We utilize our algorithm to solve some problems in applied sciences and engineering such as image restoration and optimal control. Some numerical experiments are carried out to support our theoretical results. Our numerical illustrations show that our new method is more efficient than many existing methods.

1 Introduction

Throughout this article, let H be a real Hilbert space with inner product $\langle \cdot ,\cdot \rangle$ and its induced norm $\|\cdot \|$. Let Ψ be a nonempty closed and convex subset of H and $M:\Psi \to H$ be an operator. A variational inequality problem $VI(\Psi ,M)$ involves finding a point $g\in \Psi$ such that

$$\begin{aligned} \langle Mg, h-g\rangle \geq 0, \quad \forall h\in \Psi . \end{aligned}$$

(1.1)

The solution set of $VI(\Psi ,M)$ (1.1) shall be denoted by S. Diverse problems emanating from engineering, economics, mechanics, transportation, mathematical programming, etc. can be formulated as $VI(\Psi ,M)$ (1.1) (see, for example, [4, 5, 15, 22, 23, 28]). We use $S_{D}$ to denote a solution set of the dual variational inequality problem, that is, $S_{D}=\{g^{*}\in \Psi :\langle Mh,h-g^{*}\rangle \geq 0, \forall h\in \Psi \}$. It is easy to see that $S_{D}$ is a closed and convex subset of Ψ [41]. If M is continuous and Ψ is convex, then we obtain that $S_{D}\subseteq S$, and if M is continuous and quasimonotone, then $S=S_{D}$ [12]. The inclusion $S\subset S_{D}$ is not true if M is a continuous and quasimonotone mapping [56].

There are basically two well-known approaches for solving the variational inequality problems, namely, the regularized method and the projection method. In this article, our interest will be on the projection method [39]. For any $g\in H$, there exists a unique point z in Ψ such that

$$ \Vert g-z \Vert =\inf \bigl\{ \Vert g-h \Vert :h\in \Psi \bigr\} ,\quad \text{where } z=P_{\Psi }g, $$

and $P_{\Psi}:H\to \Psi$ is called a metric projection from H into Ψ.

It is well known that the variational inequality problem $VI(\Psi ,M)$ (1.1) can be transformed into a fixed point problem as follows:

$$\begin{aligned} g^{*}=P_{\Psi}(I-\tau M)g^{*}, \end{aligned}$$

(1.2)

where $P_{\Psi}:H\to \Psi$ is the metric projection and $\tau >0$, see [43]. The simplest projection method to find the solution of $VI(\Psi ,M)$ (1.1) is the projection gradient method (PGM) defined as follows:

$$ g_{m+1}=P_{\Psi}(g_{m}-\tau Mg_{m}). $$

(1.3)

Observe that just one projection onto the feasible set is required. However, the convergence of PGM to an element of S requires a slightly strong hypothesis that the operator is L-continuous and α-inverse strongly monotone with $\tau \in (0,\frac{2\alpha}{L^{2}})$. In [19], the authors observed that if the strong monotonicity assumption is relaxed to monotonicity, then the situation may become divergence. To overcome this challenge, Korpelevich [24] introduced the extragradient method (EGM) as follows:

$$\begin{aligned} \textstyle\begin{cases} h_{m}=P_{\Psi}(g_{m}-\tau Mg_{m}), \\ g_{m+1}=P_{\Psi}(g_{m}-\tau Mh_{m}), \end{cases}\displaystyle \end{aligned}$$

(1.4)

where M is a monotone operator that is L-Lipschitz continuous and $\tau \in (0,\frac{1}{L})$. It is well known that the sequence $\{g_{m}\}$ that is generated by (1.4) converges weakly to a point in S.

It is worthy to note that the calculation of the projection onto a closed convex set Ψ is equivalent to the solution of the minimum distance problem. It is not hard to see that EGM requires two calculations of the two projections onto Ψ in each iteration and the performance of the method may reduce if Ψ is a general closed and convex set. For some years now, the (EGM) has been modified and improved in diverse forms, see, e.g., [7–10, 27, 33, 42, 46] and the references in them.

To overcome the drawback in EGM, Censor et al. [8–10] introduced the subgradient extragradient method (SEGM) as follows:

$$\begin{aligned} \textstyle\begin{cases} h_{m}=P_{\Psi}(g_{m}-\tau Mg_{m}), \\ Z_{m}=\{g\in H|\langle g_{m}-\tau Mg_{m}-h_{m},g-h_{m}\rangle \leq 0\}, \\ g_{m+1}=P_{Z_{m}}(g_{m}-\tau Mh_{m}), \end{cases}\displaystyle \end{aligned}$$

(1.5)

where $\tau \in (0,\frac{1}{L})$, M is a monotone and L-Lipschitz continuous operator. This method replaces the two projections onto Ψ in EGM by one projection onto Ψ and one onto a half space. This may speed up the convergence of the algorithm.

The second modification of (EGM), which is known as Tseng’s extragradient method (TEGM), was developed by Tseng [48] as follows:

$$\begin{aligned} \textstyle\begin{cases} h_{m}=P_{\Psi}(g_{m}-\tau Mg_{m}), \\ g_{m+1}=h_{m}-\tau (Mh_{m}- Mg_{m}), \end{cases}\displaystyle \end{aligned}$$

(1.6)

where $\lambda \in (0,\frac{1}{L})$ and M is a monotone and L-Lipschitz continuous operator.

The third method which was introduced to overcome the limitation of (EGM) is known as the projection and contraction method (PCM). This method was introduced by He [18] as follows:

$$\begin{aligned} \textstyle\begin{cases} h_{m}=P_{\Psi}(g_{m}-\tau Mg_{m}), \\ v_{m}=(g_{m}-h_{m})-\tau (Mg_{m}-Mh_{m}), \\ g_{m+1}=g_{m}-\rho \beta _{m}v_{m}, \end{cases}\displaystyle \end{aligned}$$

(1.7)

where $\rho \in (0,2)$, $\tau \in (0,\frac{1}{L})$ and $\beta _{m}$ is defined as

$$ \beta _{m}=\frac{\langle g_{m}-h_{m},v_{m}\rangle}{ \Vert v_{m} \Vert ^{2}}. $$

The SEGM, TEGM, and PCM require only to calculate one projection onto the feasible set in each iteration. For some years now, these methods have been improved in various ways by different authors, see, e.g., [2, 39, 41, 49] and the references in them. Some authors have considered the combination of the subgradient extragradient method and the projection contraction method to obtain more efficient methods, see, for example, [39, 41].

It is worthy to note that the class of quasimonotone operators properly includes the classes of monotone and pseudomonotone operators which have been studied by many authors in the recent years, see, e.g., [2, 25, 30, 56]. In applied sciences and engineering, it will be more interesting to extend the methods of solving variational inequality problems to a more general class of quasimonotone operators. The broadness and the applicability of this operator have attracted a considerable amount of interest from researchers in the last few years. For instance, in [56], Ye and He introduced an algorithm with double projection for solving variational inequality problem involving quasimonotone operators in an infinite dimensional Euclidean space $\mathbb{R}^{m}$. In [30], Salhuddin extended the main EGM, which deals with monotone operators, to solving a variational inequality problem involving Lipschitz continuous and quasimonotone operators in infinite dimensional Hilbert spaces. In [25], Liu and Yang modified the EGM, SEGM, and TEGM using a new step size for approximating the solution variational inequality problems involving quasimonotone operators in real Hilbert spaces. Very recently, Alakoya et al. [2] improved the results of Lui and Yang [25] by introducing two inertial algorithms with self-adaptive step sizes for solving quasimonotone variational inequality problems. The authors obtained some strong convergence results without using some strict conditions used by Liu and Yang [25] in obtaining convergence results.

On the other hand, the concept of inertial technique was first studied by Polyak [29] as a process of acceleration for solving a smooth convex minimization problem. This technique is obtained from an implicit time discretization of a second-order dynamical system as heavy ball with friction. In recent years, the inertial technique has been wildly employed as the rate of convergence accelerator of algorithms for approximating the solution of several kinds of optimization problems (see [50] and the references in it). The inertial-type algorithms have been studied by several researchers, see, e.g., [2, 36–39, 41, 49] and the references in them.

It is well known that the strong convergence of iteration algorithms is more desirable and applicable than their weak convergence. Most results on variational inequality problems in the current literature deal with weak convergence. One of the techniques for obtaining the strong convergence results of an algorithm is by combining such an algorithm with the viscosity method.

Motivated and inspired by the works above, we introduce an inertial-type algorithm that combines the subgradient extragradient method, the projection contraction method, and the viscosity method. The proposed method is used for solving quasimonotone (or without monotonicity) variational inequality problems in infinite dimensional Hilbert spaces such that it does not depend on the Lipschitz constant of the cost operator. Further, we prove the strong convergence results of the new algorithm. We utilize our algorithm to solve some problems in applied sciences and engineering such as image restoration and optimal control. Some numerical experiments are carried out to support our theoretical results without using some existing restrictive assumptions. Our numerical illustrations show that our new method enjoys better speed of convergence than many existing methods.

The paper is organized as follows: We first recall some basic definitions and established results in Sect. 2. The convergence analysis of the proposed method is presented in Sect. 3. Numerical experiments and the applications of the proposed method are presented in Sect. 4. The summary of the obtained results is given in Sect. 5.

2 Preliminaries

In this section, we present some important notations, definitions, and results that will be useful in the sequel.

Let Ψ stand for a nonempty closed and convex subset of a real Hilbert space H. The weak and strong convergence of $\{g_{m}\}$ to g are written as $g_{m}\rightharpoonup g$ and $g_{m}\rightarrow g$, respectively. Assume that a subsequence $\{g_{m_{i}}\}$ of $\{g_{m}\}$ converges weakly to a point g, then g is known as the weak cluster point of $\{g_{m}\}$ and the set of such cluster points of $\{g_{m}\}$ is denoted by $\omega _{w}(g_{m})$.

Definition 2.1

An operator $M:H\to H$ is called:

($a_{1}$):

contraction if there exists a constant $c\in [0,1)$ such that

$$ \Vert Mg-Mh \Vert \leq c \Vert g-h \Vert ,\quad \forall g,h\in H; $$

($a_{2}$):

L-Lipschitz continuous if $L>0$ exists with

$$ \Vert Mg-Mh \Vert \leq L \Vert g-h \Vert ,\quad \forall g,h\in H; $$

($a_{3}$):

L-strongly monotone if $L>0$ exists with

$$ \langle Mg-Mh, g-h\rangle \geq L \Vert g-h \Vert ^{2},\quad \forall g,h\in H; $$

($a_{4}$):

monotone if

$$ \langle Mg-Mh, g-h\rangle \geq 0,\quad \forall g,h\in H; $$

($a_{5}$):

pseudomonotone if

$$ \langle Mh, g-h\rangle \geq 0\quad \implies \quad \langle Mg, g-h \rangle \geq 0,\quad \forall g,h\in H; $$

($a_{6}$):

quasimonotone if

$$ \langle Mh, g-h\rangle > 0\quad \implies \quad \langle Mg, g-h \rangle \geq 0, \quad \forall g,h\in H; $$

($a_{7}$):

sequentially weakly continuous if for any sequence $\{g_{m}\}$ that converges weakly to g the sequence $\{Mg_{m}\}$ weakly converges to Mg.

From the definition above, it is true that ($a_{3}$) ⇒ ($a_{4}$) ⇒ ($a_{5}$) ⇒ ($a_{6}$). However, the converses are not always true.

Lemma 2.1

([56])

If one of the following holds:

• (i) The mapping M is a pseudomonotone on Ψ and $S\neq \emptyset$;

• (ii) The mapping M is the gradient of U, where U is the differential quasiconvex function of the open set $V\supset \Psi$ and attains its global minimum on Ψ;

• (iii) The mapping M is quasimonotone on Ψ, $M\neq 0$ on ψ, and Ψ is bounded;

• (iv) The mapping M is quasimonotone on Ψ, $M\neq 0$ on Ψ, and there exists a positive number r such that, for all $g\in r$ with $\|g\|\geq r$, there exists $h\in \Psi$ such that $\|h\|\leq r$ and $\langle Mg, h-g\rangle \leq 0$;

• (v) The mapping M is quasimonotone on Ψ, $int \Psi$ is nonempty, and there exists $g^{*}\in S$ such that $Mg^{*}\neq 0$.

Then $S_{D}$ is nonempty.

Lemma 2.2

Let H be a real Hilbert space. Then, for each $g,h\in H$ and $\zeta \in \mathbb{R}$, we have

• (i) $\|g+h\|^{2}\leq \|g\|^{2}+2 \langle h,g+h\rangle$;

• (ii) $\|g+h\|^{2}= \|g\|^{2}+2\langle g,h\rangle +\|h\|^{2}$;

• (iii) $\|\zeta g+(1-\zeta )h\|^{2}=\zeta \|g\|^{2}+(1-\zeta )\|h\|^{2}- \zeta (1-\zeta )\|g-h\|^{2}$.

Lemma 2.3

([16])

Let Ψ be nonempty closed convex subset of a real Hilbert space H. Suppose $g\in H$ and $h\in \Psi$. Then $h=P_{\Psi }g\iff\langle g-h,h-w\rangle \geq 0$, $\forall w\in \Psi$.

Lemma 2.4

([16])

Let Ψ be a closed convex subset of a real Hilbert space H. If $g\in H$, then

• (i) $\|P_{\Psi }g-P_{\Psi }h\|\leq \langle P_{\Psi }g-P_{\Psi }h,g-h \rangle$, $\forall h\in H$;

• (ii) $\langle (I-P_{\Psi})g-(I-P_{\Psi})h,g-h\rangle \geq \|(I-P_{\Psi})g-(I-P_{ \Psi})h\|^{2}$, $\forall h\in H$;

• (iii) $\|P_{\Psi }g-h\|^{2}\leq \|g-h\|^{2}-\|g-P_{\Psi }g\|^{2}$, $\forall h\in H$.

Lemma 2.5

([51])

Let $\{u_{m}\}$ be a sequence of nonnegative real numbers such that

$$ u_{m+1}\leq (1-\nu _{m})u_{m}+\nu _{m} v_{m}+w_{m}, $$

where $\{\nu _{m}\}\subset (0,1)$ and $\{v_{m}\}$, $\{w_{m}\}$ satisfy the following conditions:

• (a) $\sum_{m=0}^{\infty}\nu _{m}=\infty$;

• (b) $\limsup_{m\to \infty}v_{m}\leq 0$;

• (c) $w_{m}\geq 0$, ∀m, $\sum_{m=0}^{\infty}w_{m}<\infty$. Then $\lim_{m\to \infty}u_{m}=0$.

Lemma 2.6

([26])

If there exists a subsequence $\{c_{m_{i}}\}$ of a nonnegative real numbers sequence $\{c_{m}\}$ such that $c_{m_{i}}< c_{m_{i}+1}$ for all $i\in \mathbb{N}$. Then there exists a nondecreasing sequence $\{s_{j}\}$ of $\mathbb{N}$ such that $\lim_{j\to \infty}s_{j}=\infty$ and the following inequalities are satisfied by all (sufficiently large) number $j\in \mathbb{N}$:

$$\begin{aligned} c_{s_{j}}\leq c_{s_{j}+1}\quad \textit{and}\quad c_{j}\leq c_{s_{j}+1}. \end{aligned}$$

(2.1)

3 Main results

In this section, we establish the convergence analysis of our proposed algorithm under the following assumptions:

($C_{1}$):

The self mapping f defined on a real Hilbert space H is a contraction with constant $c \in (0,1)$.

($C_{2}$):

The positive sequence $\{\xi _{m}\}$ satisfies $\lim_{m\to \infty}\frac{\xi _{m}}{a_{m}}=0$, where $\{a_{m}\}\in (0,1]$ such that $\sum_{m=1}^{\infty}a_{m}<\infty$.

($C_{3}$):

The sequence $\{b_{m}\}\subset (0,1)$ satisfies $\sum_{m=1}^{\infty}b_{m}=\infty$, $\lim_{m\to \infty}b_{m}=0$, and $0< b\leq b_{m}$.

($C_{4}$):

$S_{D}\neq \emptyset$.

($C_{5}$):

The operator M is Lipschitz continuous such that $L>0$;

($C_{6}$):

The operator M is sequentially weak continuous on Ψ.

($C_{7}$):

The operator M is quasimonotone on Ψ.

($C_{8}$):

If $g_{m}\rightharpoonup g^{*}$ and $\limsup_{m\to \infty}\langle Mg_{m},g_{m}\rangle \leq \langle Mg^{*},g^{*}\rangle$, then $\lim_{m\to \infty}\langle Mg_{m},g_{m}\rangle = \langle Mg^{*},g^{*} \rangle$.

Algorithm 3.1

____________________________________________________________________

Initialization: Given $\tau _{1} >0$, $\psi >0$, $\eta >1$, $\rho \in (0,\frac{2}{\eta} )$, $\mu \in (0,1)$, and let $g_{0},g_{1}\in H$ be arbitrary. Take $\{q_{m}\}\subset [0,\infty )$ with $\sum_{m=0}^{\infty}q_{m}<\infty$ and $\{p_{m}\}\in [1,\infty )$ such that $\lim_{m\to \infty}p_{m}=1$.

____________________________________________________________________

Iteration Steps: Compute $g_{m+1}$ as follows:

Step 1: Given the iterates $g_{m-1}$ and $\{g_{m}\}$ ($m\geq 1$), choose $\psi _{m}$ such that $0\leq \psi _{m}\leq \bar{\psi}_{m}$, where

$$\begin{aligned} \bar{\psi}_{m}&= \textstyle\begin{cases} \min \{\psi ,\frac{\xi _{m}}{ \Vert g_{m}-g_{m-1} \Vert } \} \quad \text{if } g_{m}\neq g_{m-1},\\ \psi , \quad \text{otherwise}. \end{cases}\displaystyle \end{aligned}$$

(3.1)

Step 2: Set

$$ t_{m}=(1-a_{m}) \bigl(g_{m}+\psi _{m}(g_{m}-g_{m-1})\bigr), $$

(3.2)

and compute

$$\begin{aligned} h_{m}&=P_{\Psi}(t_{m}-\tau _{m}Mt_{m}). \end{aligned}$$

(3.3)

If $t_{m}=h_{m}$ or $Mt_{m}=0$, then stop and $t_{m}$ is a solution. Otherwise, we go to Step 3.

Step 3: Compute

$$\begin{aligned} k_{m}&=P_{Z_{m}}(t_{m}-\rho \tau _{m}\delta _{m}Mh_{m}), \end{aligned}$$

(3.4)

where

$$\begin{aligned} &Z_{m}=\bigl\{ g\in H:\langle t_{m}-\tau _{m}Mt_{m}-h_{m},g-h_{m} \rangle \leq 0\bigr\} , \end{aligned}$$

(3.5)

$$\begin{aligned} &\delta _{m}=(1-\mu )\frac{\Vert t_{m}-h_{m} \Vert ^{2}}{ \Vert v_{m} \Vert ^{2}}, \end{aligned}$$

(3.6)

and

$$\begin{aligned} v_{m}=t_{m}-h_{m}-\tau _{m}(Mt_{m}-Mh_{m}). \end{aligned}$$

(3.7)

Step 4: Compute

$$\begin{aligned} g_{m+1}=(1-b_{m})k_{m}+b_{m}f(k_{m}). \end{aligned}$$

(3.8)

Update

$$\begin{aligned} \tau _{m+1}=&\textstyle\begin{cases} \min \{\frac{p_{m}\mu \Vert t_{m}-h_{m} \Vert }{ \Vert Mt_{m}-Mh_{m} \Vert }, \tau _{m}+q_{m} \} \quad \text{if } Mt_{m}\neq Mh_{m},\\ \tau _{m}+q_{m} \quad \text{otherwise}. \end{cases}\displaystyle \end{aligned}$$

(3.9)

Set $m:=m+1$ and return to Step 1.

____________________________________________________________________

Remark 3.2

Now, we highlight some of the advantages of new Algorithm 3.1 over some existing methods in the literature.

• (1) Our algorithm uses an efficient step size that was first introduced by Tan et al. [39]. It is not hard to see that the step size studied is quite different from those step sizes studied in many articles. To be precise, if $q_{m}=0$ and $p_{m}=1$ for all $m\geq 0$, then the considered step size reduces to the step size used by several methods (see, e.g., [14, 43, 44, 53–55]). Furthermore, if $q_{m}\neq 0$ and $p_{m}=1$, $\forall m\geq 0$, then the step size reduces to the step size in [25].

• (2) It is important to note that the additive step size in our method is updated explicitly and is permitted to increase at each iteration of algorithm, which makes it more implementable in practice.

• (3) The operators involved in our new algorithm are quasimonotone. This class of operators is wider than the classes of monotone and pseudomonotone operators. Hence, our method is more applicable than the methods for solving monotone and pseudomontone variational inequality problems used by many authors (see, e.g, [39, 41, 43, 44, 54, 55] and the references in them).

• (4) To speed up the convergence of our method, we embed a modified inertial term in our algorithm. Further, we prove our convergence results without the strict conditions imposed on the control parameter in the inertial term, i.e., $\lim_{m\to \infty}a_{m}=0$ and $\sum_{m=0}^{\infty}a_{m}=\infty$.

• (5) Our algorithm uses a nonmonotonic step size rule which allows it work without the prior knowledge of the Lipschitz constant of M. In practical application sense, this is preferable to the fixed-step algorithm studied in [11, 47]. Also, our algorithm does not require any line search rule.

• (6) The inertial term used in the algorithm [2, 41] has been studied by several authors in the literature. Recently, a more relaxed inertial term (3.3), which is considered in our proposed Algorithm 3.1, has been studied by a few authors (see, e.g., [39, 40, 45]). In this research direction, convergence analysis of these methods required that the relaxation parameter $a_{m}$ in the inertial term (3.3) is in (0,1). In this article, we improve upon the existing results in this direction by proving our convergence results such that the relaxation parameter $a_{m}$ is allowed to be chosen in (0,1]. This implies that the relaxation parameter can be chosen in a special case to be 1. Thus, our proposed algorithm improves several inertial algorithm types for solving variational inequality problems in the existing literature.

Lemma 3.3

([39, 52])

Suppose that M is L-Lipschitz continuous on H and $\{\tau _{m}\}$ is the sequence generated by (3.9), then there exists $\tau \in [\min \{\frac{\mu}{L},\tau _{1} \},\tau _{1}+ \sum_{m=1}^{\infty}q_{m} ]$ with $\tau =\lim_{m\to \infty}\tau _{m}$. Moreover,

$$ \Vert Mt_{m}-Mh_{m} \Vert \leq \frac{p_{m}\mu}{\tau _{m+1}} \Vert t_{m}-h_{m} \Vert . $$

(3.10)

Next we show the boundedness of the sequence $\{g_{m}\}$ generated by Algorithm 3.1.

Lemma 3.4

If $\{g_{m}\}$ is a sequence generated by Algorithm 3.1, then under assumptions $(C_{1})$–$(C_{5})$, $\{g_{m}\}$ is bounded.

Proof

Let $g^{*}\in S_{D}$. Then from (3.2) we have

$$\begin{aligned} \bigl\Vert t_{m}-g^{*} \bigr\Vert &= \bigl\Vert (1-a_{m}) \bigl(g_{m}+\psi _{m}(g_{m}-g_{m-1}) \bigr)-g^{*} \bigr\Vert \\ &= \bigl\Vert (1-a_{m}) \bigl(g_{m}-g^{*} \bigr)+(1-a_{m})\psi _{m}(g_{m}-g_{m-1})-a_{m}g^{*} \bigr\Vert \\ &\leq (1-a_{m}) \bigl\Vert g_{m}-g^{*} \bigr\Vert +(1-a_{m})\psi _{m} \Vert g_{m}-g_{m-1} \Vert +a_{m} \bigl\Vert g^{*} \bigr\Vert \\ &=(1-a_{m}) \bigl\Vert g_{m}-g^{*} \bigr\Vert +a_{m}\biggl[(1-a_{m})\frac{\psi _{m}}{a_{m}} \Vert g_{m}-g_{m-1} \Vert + \bigl\Vert g^{*} \bigr\Vert \biggr]. \end{aligned}$$

(3.11)

On the other hand, since by (3.1) we have

$$\begin{aligned} \frac{\psi _{m}}{a_{m}} \Vert g_{m}-g_{m-1} \Vert \leq \frac{\xi _{m}}{a_{m}} \to 0, \end{aligned}$$

(3.12)

which implies that $\lim_{m\to \infty}[(1-a_{m})\frac{\psi _{m}}{a_{m}}\|g_{m}-g_{m-1} \|+\|g^{*}\|]=\|g^{*}\|$, therefore there exists $K_{1}>0$ such that

$$\begin{aligned} (1-a_{m})\frac{\psi _{m}}{a_{m}} \Vert g_{m}-g_{m-1} \Vert + \bigl\Vert g^{*} \bigr\Vert \leq K_{1}. \end{aligned}$$

(3.13)

From (3.13) and (3.11), we obtain

$$\begin{aligned} \bigl\Vert t_{m}-g^{*} \bigr\Vert \leq (1-a_{m}) \bigl\Vert g_{m}-g^{*} \bigr\Vert +a_{m}K_{1}. \end{aligned}$$

(3.14)

Next, by (3.4), Lemma 2.4, and Lemma 2.2, we have

$$\begin{aligned} \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2}={}& \bigl\Vert P_{Z_{m}}(t_{m}-\rho \tau _{m}\delta _{m}Mh_{m})-g^{*} \bigr\Vert ^{2} \\ \leq{}& \bigl\Vert t_{m}-\rho \tau _{m}\delta _{m}Mh_{m}-g^{*} \bigr\Vert ^{2}- \Vert t_{m}- \rho \tau _{m}\delta _{m}Mh_{m}-k_{m} \Vert ^{2} \\ ={}& \bigl\Vert t_{m}-g^{*} \bigr\Vert ^{2}-2\rho \tau _{m}\delta _{m}\bigl\langle t_{m}-g^{*},Mh_{m} \bigr\rangle +\rho ^{2}\tau ^{2}_{m}\delta ^{2}_{m} \Vert Mh_{m} \Vert ^{2}- \Vert t_{m}-k_{m} \Vert ^{2} \\ &{}+2\rho \tau _{m}\delta _{m}\langle t_{m}-k_{m},Mh_{m}\rangle -\rho ^{2} \tau ^{2}_{m}\delta ^{2}_{m} \Vert Mh_{m} \Vert ^{2} \\ ={}& \bigl\Vert t_{m}-g^{*} \bigr\Vert ^{2}- \Vert t_{m}-k_{m} \Vert ^{2}-2 \rho \tau _{m}\delta _{m} \bigl\langle Mh_{m},k_{m}-g^{*} \bigr\rangle \\ ={}& \bigl\Vert t_{m}-g^{*} \bigr\Vert ^{2}- \Vert t_{m}-k_{m} \Vert ^{2}-2\rho \tau _{m}\delta _{m} \langle Mh_{m},k_{m}-h_{m} \rangle \\ &{}-2\rho \tau _{m}\delta _{m}\bigl\langle Mh_{m},h_{m}-g^{*} \bigr\rangle . \end{aligned}$$

(3.15)

Now, since $h_{m}\in \Psi$ and $g^{*}\in S_{D}$, we have $\langle Mh_{m},h_{m}-g^{*}\rangle \geq 0$ for all $n\geq 0$. Thus, from (3.15), we have

$$\begin{aligned} \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2}\leq \bigl\Vert t_{m}-g^{*} \bigr\Vert ^{2}- \Vert t_{m}-k_{m} \Vert ^{2}-2 \rho \tau _{m} \delta _{m}\langle Mh_{m},k_{m}-h_{m} \rangle . \end{aligned}$$

(3.16)

On the other hand, since $k_{m}\in Z_{m}$, we have

$$ \langle t_{m}-\tau _{m} Mt_{m}-h_{m},k_{m}-h_{m} \rangle \leq 0. $$

Hence,

$$\begin{aligned} -2\rho \tau _{m}\delta _{m}\langle Mh_{m},k_{m}-h_{m}\rangle ={}&2\rho \tau _{m}\delta _{m}\langle t_{m}-\tau _{m} Mt_{m}-h_{m},k_{m}-h_{m} \rangle \\ &{}-2\rho \tau _{m}\delta _{m}\bigl\langle t_{m}-h_{m}-\tau _{m}(Mt_{m}-Mh_{m}),k_{m}-h_{m} \bigr\rangle \\ \leq{}& -2\rho \tau _{m}\delta _{m}\bigl\langle t_{m}-h_{m}-\tau _{m}(Mt_{m}-Mh_{m}),k_{m}-h_{m} \bigr\rangle \\ ={}& -2\rho \tau _{m}\delta _{m}\langle v_{m},k_{m}-h_{m}\rangle \\ ={}& -2\rho \tau _{m}\delta _{m}\langle v_{m},t_{m}-h_{m} \rangle +2 \rho \tau _{m}\delta _{m}\langle v_{m},t_{m}-k_{m}\rangle . \end{aligned}$$

(3.17)

Now, we estimate $-2\rho \tau _{m}\delta _{m}\langle v_{m},t_{m}-h_{m}\rangle$ and $2\rho \tau _{m}\delta _{m}\langle v_{m},t_{m}-k_{m}\rangle$. From (3.7) and (3.9), we have

$$\begin{aligned} \langle v_{m},t_{m}-h_{m}\rangle &=\bigl\langle t_{m}-h_{m}-\tau _{m}(Mt_{m}-Mh_{m}),t_{m}-h_{m} \bigr\rangle \\ &\geq \Vert t_{m}-h_{m} \Vert ^{2}- \tau _{m} \Vert Mt_{m}-Mh_{m} \Vert \Vert t_{m}-h_{m} \Vert \\ &\geq \biggl(1-p_{m}\mu \frac{\tau _{m}}{\tau _{m+1}} \biggr) \Vert t_{m}-h_{m} \Vert ^{2}. \end{aligned}$$

(3.18)

By Lemma 3.3, we have that $\lim_{m\to \infty}\tau _{m}$ exists. Since $\lim_{m\to \infty}p_{m}=1$, we have $\lim_{m\to \infty}\frac{p_{m}\tau _{m}}{\tau _{m+1}}=1$. Now, since $\lim_{m\to \infty} (1-p_{m}\mu \frac{\tau _{m}}{\tau _{m+1}} )=1-\mu >\frac{1-\mu}{\eta}>0$, there exists $m_{0}\in \mathbb{N}$ such that

$$\begin{aligned} 1-p_{m}\mu \frac{\tau _{m}}{\tau _{m+1}}>\frac{1-\mu}{\eta}>0,\quad \forall m\geq m_{0}. \end{aligned}$$

(3.19)

Using (3.18) and (3.19), we have

$$\begin{aligned} \langle v_{m},t_{m}-h_{m}\rangle &= \frac{1-\mu}{\eta} \Vert t_{m}-h_{m} \Vert ^{2},\quad \forall m\geq m_{0}. \end{aligned}$$

(3.20)

Since $\delta _{m}=(1-\mu )\frac{\|t_{m}-h_{m}\|^{2}}{\|v_{m}\|^{2}}$, it implies

$$\begin{aligned} \Vert t_{m}-h_{m} \Vert ^{2}= \frac{\delta _{m} \Vert v_{m} \Vert ^{2}}{(1-\mu )}. \end{aligned}$$

(3.21)

By (3.20) and (3.21), we have

$$\begin{aligned} -2\rho \tau _{m}\delta _{m}\langle v_{m},t_{m}-h_{m} \rangle = \frac{-2\rho \delta ^{2}}{\eta} \Vert v_{m} \Vert ^{2},\quad \forall m \geq m_{0}. \end{aligned}$$

(3.22)

Next, by Lemma 2.2, we get

$$\begin{aligned} 2\rho \tau _{m}\delta _{m}\langle v_{m},t_{m}-h_{m} \rangle = \Vert t_{m}-k_{m} \Vert ^{2}+\rho \delta ^{2}_{m} \Vert v_{m} \Vert ^{2}- \Vert t_{m}-k_{m}-\rho \delta v_{m} \Vert ^{2}. \end{aligned}$$

(3.23)

Putting (3.22) and (3.23), we obtain

$$\begin{aligned} &-2\rho \tau _{m}\delta _{m}\langle Mh_{m},k_{m}-h_{m} \rangle \\ &\quad \leq \Vert t_{m}-k_{m} \Vert ^{2}- \Vert t_{m}-k_{m}-\rho \delta v_{m} \Vert ^{2}-\rho \biggl( \frac{2}{\eta}-\rho \biggr)\delta ^{2}_{m} \Vert v_{m} \Vert ^{2}. \end{aligned}$$

(3.24)

Using (3.7), we obtain

$$\begin{aligned} \Vert v_{m} \Vert &\leq \Vert t_{m}-k_{m} \Vert +\tau _{m} \Vert Mt_{m}-Mh_{m} \Vert \\ &\leq \Vert t_{m}-k_{m} \Vert +p_{m} \mu \frac{\tau _{m}}{\tau _{m+1}} \Vert t_{m}-k_{m} \Vert \\ &= \biggl(1+p_{m}\mu \frac{\tau _{m}}{\tau _{m+1}} \biggr) \Vert t_{m}-k_{m} \Vert . \end{aligned}$$

(3.25)

It follows from (3.25) that

$$\begin{aligned} \frac{1}{ \Vert v_{m} \Vert ^{2}}\geq \frac{1}{ (1+p_{m}\mu \frac{\tau _{m}}{\tau _{m+1}} )^{2} \Vert t_{m}-h_{m} \Vert ^{2}}. \end{aligned}$$

(3.26)

Thus, from (3.6) and (3.26), we obtain

$$\begin{aligned} \delta ^{2}_{m} \Vert v_{m} \Vert &= \frac{(1-\mu )^{2} \Vert t_{m}-h_{m} \Vert ^{4}}{ \Vert v_{m} \Vert ^{2}} \\ &\geq \frac{(1-\mu )^{2}}{ (1+p_{m}\mu \frac{\tau _{m}}{\tau _{m+1}} )^{2}} \Vert t_{m}-h_{m} \Vert ^{2}. \end{aligned}$$

(3.27)

Combining (3.16), (3.22), and (3.27), we have

$$\begin{aligned} \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2}\leq {}&\bigl\Vert t_{m}-g^{*} \bigr\Vert ^{2}- \Vert t_{m}-k_{m}-\rho \delta v_{m} \Vert ^{2} \\ &{}-\rho \biggl(\frac{2}{\eta}-\rho \biggr) \biggl( \frac{1-\mu}{1+p_{m}\mu \frac{\tau _{m}}{\tau _{m+1}}} \biggr)^{2} \Vert t_{m}-h_{m} \Vert ^{2},\quad \forall m\geq m_{0}. \end{aligned}$$

(3.28)

From (3.14) and (3.28), we obtain

$$\begin{aligned} \bigl\Vert k_{m}-g^{*} \bigr\Vert &\leq \bigl\Vert t_{m}-g^{*} \bigr\Vert \\ &\leq (1-a_{m}) \bigl\Vert g_{m}-g^{*} \bigr\Vert +a_{m}K_{1}. \end{aligned}$$

(3.29)

From (3.8) we get

$$\begin{aligned} \bigl\Vert g_{m+1}-g^{*} \bigr\Vert &= \bigl\Vert (1-b_{m})k_{m}+b_{m}f(k_{m})-g^{*} \bigr\Vert \\ &= \bigl\Vert b_{m}\bigl(f(k_{m})-g^{*} \bigr)+(1-b_{m}) \bigl(k_{m}-g^{*}\bigr) \bigr\Vert \\ &\leq b_{m} \bigl\Vert f(k_{m})-g^{*} \bigr\Vert +(1-b_{m}) \bigl\Vert k_{m}-g^{*} \bigr\Vert \\ &\leq b_{m} \bigl\Vert f(k_{m})-f \bigl(g^{*}\bigr) \bigr\Vert +b_{m} \bigl\Vert f \bigl(g^{*}\bigr)-g^{*} \bigr\Vert +(1-b_{m}) \bigl\Vert k_{m}-g^{*} \bigr\Vert \\ &\leq b_{m}c \bigl\Vert k_{m}-g^{*} \bigr\Vert +b_{m} \bigl\Vert f\bigl(g^{*} \bigr)-g^{*} \bigr\Vert +(1-b_{m}) \bigl\Vert k_{m}-g^{*} \bigr\Vert \\ &=\bigl(1-(1-c)b_{m}\bigr) \bigl\Vert k_{m}-g^{*} \bigr\Vert +b_{m} \bigl\Vert f\bigl(g^{*} \bigr)-g^{*} \bigr\Vert . \end{aligned}$$

(3.30)

Substituting (3.29) into (3.30), we have

$$\begin{aligned} \bigl\Vert g_{m+1}-g^{*} \bigr\Vert &\leq \bigl(1-(1-c)b_{m}\bigr)\bigl[(1-a_{m}) \bigl\Vert g_{m}-g^{*} \bigr\Vert +a_{m}K_{1} \bigr]+b_{m} \bigl\Vert f\bigl(g^{*}\bigr)-g^{*} \bigr\Vert . \end{aligned}$$

(3.31)

Since $a_{m}\subset (0,1)$, $b_{m}\subset (0,1)$, $0< b\leq b_{m}$, and $c\in (0,1)$, then it implies that $(1-(1-c)b_{m})<1$ and $(1-a_{m})<1$. Again, since $K_{1}>0$, (3.31) becomes

$$\begin{aligned} \bigl\Vert g_{m+1}-g^{*} \bigr\Vert &\leq \bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert +a_{m}K_{1}+b_{m} \bigl\Vert f \bigl(g^{*}\bigr)-g^{*} \bigr\Vert \\ &\leq \bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert +K_{1}+b_{m} \bigl\Vert f \bigl(g^{*}\bigr)-g^{*} \bigr\Vert \\ &=\bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert +b_{m}\frac{K_{1}}{b_{m}}+b_{m} \bigl\Vert f \bigl(g^{*}\bigr)-g^{*} \bigr\Vert \\ &=\bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert +b_{m} \biggl[\frac{K_{1}}{b_{m}}+ \bigl\Vert f \bigl(g^{*}\bigr)-g^{*} \bigr\Vert \biggr] \\ &\leq \bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert +b_{m} \biggl[\frac{K_{1}}{b}+ \bigl\Vert f \bigl(g^{*}\bigr)-g^{*} \bigr\Vert \biggr] \\ &\leq \bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert +(1-c)b_{m} \biggl[ \frac{K_{1}}{(1-c)b}+\frac{ \Vert f(g^{*})-g^{*} \Vert }{(1-c)} \biggr] \\ &\leq \max \biggl\{ \bigl\Vert g_{m}-g^{*} \bigr\Vert , \frac{K_{1}}{(1-c)b}+ \frac{ \Vert f(g^{*})-g^{*} \Vert }{(1-c)} \biggr\} \\ &\leq \cdots \\ &\leq \max \biggl\{ \bigl\Vert g_{0}-g^{*} \bigr\Vert , \frac{K_{1}}{(1-c)b}+ \frac{ \Vert f(g^{*})-g^{*} \Vert }{(1-c)} \biggr\} . \end{aligned}$$

This implies that $\{g_{m}\}$ is bounded. Furthermore, it follows that $\{k_{m}\}$, $\{f(k_{m})\}$, and $\{t_{m}\}$ are bounded. □

Lemma 3.5

Suppose that assumptions $(C_{1})$–$(C_{7})$ hold and $\{g_{m}\}$ is a sequence generated by Algorithm 3.1. If there exists a subsequence $\{g_{m_{i}}\}$ of $\{g_{m}\}$ with $g_{m_{i}}\rightharpoonup p^{*}\in H$ and $\lim_{m\to \infty}\|h_{m_{i}}-t_{m_{i}}\|=0$, then either $p^{*}\in S_{D}$ or $Mp^{*}=0$.

Proof

By Lemma 3.4, $\{t_{m}\}$ is bounded. Thus, the weak cluster point set of $\{t_{m}\}$ is nonempty. Let $p^{*}$ be a weak cluster point of $\{t_{m}\}$. Suppose that we take a subsequence $\{t_{m_{i}}\}$ of $\{t_{m}\}$ such that $t_{m_{i}}\rightharpoonup p^{*}\in \Psi$ as $i\to \infty$. From the hypothesis of the lemma, it implies that $h_{m_{i}}\rightharpoonup p^{*}\in \Psi$ as $i\to \infty$.

The following two cases will now be considered.

Case I: Assume that $\limsup_{i\to \infty}\|Mg_{m_{i}}\|=0$. Then

$$\lim_{i\to \infty}\| Mg_{m_{i}}\|=\liminf_{i\to \infty}\| Mg_{m_{i}}\|=0. $$

Since $h_{m_{i}}$ converges weakly to $p^{*}\in \Psi$ and M is weakly sequentially continuous on Ψ, it implies that $\{Mh_{m_{i}}\}$ converges weakly to $Np^{*}$. From the sequentially lower semicontinuity of the norm, we obtain

$$\begin{aligned} 0< \bigl\Vert Mp^{*} \bigr\Vert \leq \liminf_{i\to \infty} \Vert Mg_{m_{i}} \Vert =0. \end{aligned}$$

(3.32)

This implies that $Mp^{*}=0$.

Case II: Assume that $\limsup_{i\to \infty}\|Mg_{m_{i}}\|>0$. Then, without loss of generality, we can take $\lim_{i\to \infty}\|Mg_{m_{i}}\|=K_{2}>0$. This means that there exists $J>0$ such that $\|Mg_{m_{i}}\|>\frac{K_{2}}{2}$ for all $i\geq J$. Since $h_{m_{i}}=P_{\Psi}(t_{m_{i}}-\tau _{m_{i}}Mt_{m_{i}})$, by Lemma 2.3, we get

$$ \langle h_{m_{i}}-t_{m_{i}}+\tau _{m_{i}}Mt_{m_{i}},h-h_{m_{i}} \rangle \geq 0,\quad \forall h\in \Psi . $$

This implies that

$$ \langle t_{m_{i}}-h_{m_{i}},h-h_{m_{i}}\rangle \leq \tau _{m_{i}} \langle Mt_{m_{i}},h-h_{m_{i}}\rangle , \quad \forall h \in \Psi . $$

It follows that

$$\begin{aligned} &\frac{1}{\tau _{m_{i}}}\langle t_{m_{i}}-h_{m_{i}},h-h_{m_{i}} \rangle -\langle Mt_{m_{i}}- Mh_{m_{i}},h-h_{m_{i}}\rangle \\ &\quad \leq \langle Mh_{m_{i}},h-h_{m_{i}}\rangle ,\quad \forall h\in \Psi . \end{aligned}$$

(3.33)

Since $\lim_{m\to \infty}\|h_{m_{i}}-t_{m_{i}}\|=0$ and M is Lipschitz continuous on H, we have that $\lim_{m\to \infty}\|Mt_{m_{i}}-Mh_{m_{i}}\|=0$. Thus, from (3.33), we get

$$\begin{aligned} 0\leq \liminf_{i\to \infty}\langle Mh_{m_{i}},h-h_{m_{i}} \rangle \leq \limsup_{i\to \infty}\langle Mh_{m_{i}},h-h_{m_{i}} \rangle < +\infty . \end{aligned}$$

(3.34)

As a result of (3.34), the following cases are considered under Case II:

Case 1: Assume that $\limsup_{i\to \infty}\langle Mh_{m_{i}},h-h_{m_{i}}\rangle >0$, $\forall h\in \Psi$. Then we can take a subsequence $\{h_{m_{i_{j}}}\}$ of $\{h_{m_{i}}\}$ such that $\lim_{j\to \infty}\langle Mh_{m_{i_{j}}},h-h_{m_{i_{j}}} \rangle >0$. Hence, there exists $j_{0}\geq 1$ such that $\langle Mh_{m_{i_{j}}},h-h_{m_{i_{j}}}\rangle >0$, $\forall j\geq j_{0}$. From the quasimonotonicity of M on Ψ, it implies that $\langle Mh,h-h_{m_{i_{j}}}\rangle \geq 0$, $\forall h\in \Psi$, $j\geq j_{0}$. Consequently, by letting $j\to \infty$, we obtain $\langle Mh,h-p^{*}\rangle \geq 0$, $\forall h\in \Psi$. Thus, $p^{*}\in S_{D}$.

Case 2: Suppose that $\limsup_{i\to \infty}\langle Mh_{m_{i}},h-h_{m_{i}}\rangle =0$, $\forall h\in \Psi$. Then, by (3.34), we have

$$\begin{aligned} \lim_{i\to \infty}\langle Mh_{m_{i}},h-h_{m_{i}}\rangle =0,\quad \forall h\in \Psi , \end{aligned}$$

(3.35)

which implies that

$$\begin{aligned} \langle Mh_{m_{i}},h-h_{m_{i}}\rangle + \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}} \rangle \bigr\vert +\frac{1}{i+1}>0,\quad \forall h\in \Psi . \end{aligned}$$

(3.36)

Furthermore, since $\lim_{i\to \infty}\|Mg_{m_{i}}\|=K_{2}>0$, there exists $i_{0}\geq 1$ such that $\|Mh_{m_{i}}\|>\frac{K_{2}}{2}$, $\forall i\geq i_{0}$. Therefore, we can let $d_{m_{i}}=\frac{Mh_{m_{i}}}{\|Mh_{m_{i}}\|^{2}}$, $\forall i \geq i_{0}$. Hence $\langle Mh_{m_{i}},d_{m_{i}}\rangle =1$, $\forall i\geq i_{0}$. From (3.36) it follows that

$$\begin{aligned} \biggl\langle Mh_{m_{i}}, h+d_{m_{i}} \biggl[ \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}} \rangle \bigr\vert + \frac{1}{i+1} \biggr]-h_{m_{i}} \biggr\rangle >0, \end{aligned}$$

and due to the quasimonotonicity of M on H, we get

$$\begin{aligned} &\biggl\langle M \biggl(h+d_{m_{i}} \biggl[ \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}} \rangle \bigr\vert +\frac{1}{i+1} \biggr] \biggr), \\ & \quad {}h+d_{m_{i}} \biggl[ \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}} \rangle \bigr\vert + \frac{1}{i+1} \biggr]-h_{m_{i}} \biggr\rangle \geq 0. \end{aligned}$$

This means that

$$\begin{aligned}& \biggl\langle Mh,h+d_{m_{i}} \biggl[ \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}} \rangle \bigr\vert +\frac{1}{i+1} \biggr]-h_{m_{i}} \biggr\rangle \\& \quad \geq \biggl\langle Mh-M \biggl(h+d_{m_{i}} \biggl[ \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}} \rangle \bigr\vert + \frac{1}{i+1} \biggr] \biggr), \\& \qquad {} h+d_{m_{i}} \biggl[ \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}}\rangle \bigr\vert + \frac{1}{i+1} \biggr]-h_{m_{i}} \biggr\rangle \\& \quad \geq - \biggl\Vert Mh-M \biggl(h+d_{m_{i}} \biggl[ \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}} \rangle \bigr\vert + \frac{1}{i+1} \biggr] \biggr) \biggr\Vert \\& \qquad {}\times \biggl\Vert h+d_{m_{i}} \biggl[ \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}}\rangle \bigr\vert + \frac{1}{i+1} \biggr]-h_{m_{i}} \biggr\Vert \\& \quad \geq - L \biggl\Vert d_{m_{i}} \biggl[ \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}} \rangle \bigr\vert + \frac{1}{i+1} \biggr] \biggr\Vert \\& \qquad {}\times\biggl\Vert h+d_{m_{i}} \biggl[ \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}}\rangle \bigr\vert + \frac{1}{i+1} \biggr]-h_{m_{i}} \biggr\Vert \\& \quad \geq \frac{-L}{ \Vert Mh_{m_{i}} \Vert } \biggl( \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}} \rangle \bigr\vert +\frac{1}{i+1} \biggr) \\& \qquad {}\times \biggl\Vert h+d_{m_{i}} \biggl[ \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}}\rangle \bigr\vert + \frac{1}{i+1} \biggr]-h_{m_{i}} \biggr\Vert \\& \quad \geq \frac{-2L}{K_{2}} \biggl( \bigl\vert \langle Mh_{m_{i}},h-h_{m_{i}} \rangle \bigr\vert +\frac{1}{i+1} \biggr)K3 \end{aligned}$$

(3.37)

for some $K_{3}>0$, where $K_{3}$ is obtained from the boundedness of $\{h+d_{m_{i}} [|\langle Mh_{m_{i}},h-h_{m_{i}}\rangle |+ \frac{1}{i+1} ]-h_{m_{i}} \}$. Now, from (3.23), it follows that $\lim_{j\to \infty} (|\langle Mh_{m_{i}},h-h_{m_{i}} \rangle |+\frac{1}{i+1} )=0$. Hence, as $i\to \infty$ in (3.37), we obtain $\langle Mh,h-p^{*}\rangle$, $\forall h\in \Psi$. Thus, $p^{*}\in S_{D}$. □

Now, we present the strong convergence theorem of our Algorithm 3.1 as follows.

Theorem 3.6

Suppose that assumptions $(C_{1})$–$(C_{7})$ hold and $Mg\neq 0$, $\forall g\in H$. If $\{g_{m}\}$ is a sequence generated by Algorithm 3.1, then $\{g_{m}\}$ converges strongly to an element $g^{*}\in S_{D}\subset S$, where $g^{*}=P_{S_{D}}o f(g^{*})$.

Proof

Claim a:

$$\begin{aligned} & \Vert t_{m}-k_{m}-\rho \delta v_{m} \Vert ^{2}+\rho \biggl(\frac{2}{\eta}- \rho \biggr) \biggl( \frac{1-\mu}{1+p_{m}\mu \frac{\tau _{m}}{\tau _{m+1}}} \biggr)^{2} \Vert t_{m}-h_{m} \Vert ^{2} \\ &\quad \leq \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2}- \bigl\Vert g_{m+1}-g^{*} \bigr\Vert ^{2}+a_{m}K_{5}+b_{m}K_{4} \end{aligned}$$

(3.38)

for some $K_{4},K_{5}>0$. Indeed, for $g^{*}\in S_{D}$, using (3.8) and Lemma 2.2, we have

$$\begin{aligned} \bigl\Vert g_{m+1}-g^{*} \bigr\Vert ^{2} =& \bigl\Vert (1-b_{m})k_{m}+b_{m}f(k_{m})-g^{*} \bigr\Vert ^{2} \\ =& \bigl\Vert b_{m}\bigl(f(k_{m})-g^{*} \bigr)+(1-b_{m}) \bigl(k_{m}-g^{*}\bigr) \bigr\Vert ^{2} \\ \leq &b_{m} \bigl\Vert f(k_{m})-g^{*} \bigr\Vert ^{2}+(1-b_{m}) \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2} \\ \leq &b_{m}\bigl( \bigl\Vert f(k_{m})-f \bigl(g^{*}\bigr) \bigr\Vert + \bigl\Vert f\bigl(g^{*} \bigr)-g^{*} \bigr\Vert \bigr)^{2}+(1-b_{m}) \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2} \\ \leq &b_{m}\bigl(c \bigl\Vert k_{m}-g^{*} \bigr\Vert + \bigl\Vert f \bigl(g^{*}\bigr)-g^{*} \bigr\Vert \bigr)^{2}+(1-b_{m}) \bigl\Vert k_{m}-g^{*} \bigr\Vert \\ \leq &b_{m}\bigl( \bigl\Vert k_{m}-g^{*} \bigr\Vert + \bigl\Vert f\bigl(g^{*}\bigr)-g^{*} \bigr\Vert \bigr)^{2}+(1-b_{m}) \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2} \\ =& \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2}+b_{m}\bigl(2 \bigl\Vert k_{m}-g^{*} \bigr\Vert \cdot \bigl\Vert f\bigl(g^{*}\bigr)-g^{*} \bigr\Vert + \bigl\Vert f\bigl(g^{*}\bigr)-g^{*} \bigr\Vert ^{2}\bigr) \\ \leq & \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2}+b_{m}K_{4}, \end{aligned}$$

(3.39)

where $K_{4}=\sup_{m\geq 1}\{2\|k_{m}-g^{*}\|\cdot \|f(g^{*})-g^{*} \|+\|f(g^{*})-g^{*}\|^{2}\}$. Putting (3.28) into (3.39), we get

$$\begin{aligned} \bigl\Vert g_{m+1}-g^{*} \bigr\Vert ^{2} \leq & \bigl\Vert t_{m}-g^{*} \bigr\Vert ^{2}- \Vert t_{m}-k_{m}-\rho \delta v_{m} \Vert ^{2} \\ &{}-\rho \biggl(\frac{2}{\eta}-\rho \biggr) \biggl( \frac{1-\mu}{1+p_{m}\mu \frac{\tau _{m}}{\tau _{m+1}}} \biggr)^{2} \Vert t_{m}-h_{m} \Vert ^{2}+b_{m}K_{4}. \end{aligned}$$

(3.40)

Owing to (3.29), we obtain

$$\begin{aligned} \bigl\Vert t_{m}-g^{*} \bigr\Vert ^{2} \leq & \bigl((1-a_{m}) \bigl\Vert g_{m}-g^{*} \bigr\Vert +a_{m}K_{1} \bigr)^{2} \\ =&(1-a_{m})^{2} \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2}+a_{m}\bigl[2(1-a_{m})K_{1} \bigl\Vert g_{m}-g^{*} \bigr\Vert +a_{m}K^{2}_{1} \bigr] \\ \leq & \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2}+a_{m}K_{5}, \end{aligned}$$

(3.41)

where $K_{5}=\sup_{m\geq 1}\{2(1-a_{m})K_{1}\|g_{m}-g^{*}\|+a_{m}K^{2}_{1} \}$. Combining (3.40) and (3.41), we get

$$\begin{aligned} \bigl\Vert g_{m+1}-g^{*} \bigr\Vert ^{2} \leq & \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2}+a_{m}K_{5}- \Vert t_{m}-k_{m}- \rho \delta v_{m} \Vert ^{2} \\ &{}-\rho \biggl(\frac{2}{\eta}-\rho \biggr) \biggl( \frac{1-\mu}{1+p_{m}\mu \frac{\tau _{m}}{\tau _{m+1}}} \biggr)^{2} \Vert t_{m}-h_{m} \Vert ^{2}+b_{m}K_{4}, \end{aligned}$$

(3.42)

which implies that

$$\begin{aligned}& \Vert t_{m}-k_{m}-\rho \delta v_{m} \Vert ^{2}+\rho \biggl(\frac{2}{\eta}- \rho \biggr) \biggl( \frac{1-\mu}{1+p_{m}\mu \frac{\tau _{m}}{\tau _{m+1}}} \biggr)^{2} \Vert t_{m}-h_{m} \Vert ^{2} \\& \quad \leq \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2}- \bigl\Vert g_{m+1}-g^{*} \bigr\Vert ^{2} \\& \qquad {}+a_{m}K_{5}+b_{m}K_{4}. \end{aligned}$$

(3.43)

Claim b:

$$\begin{aligned} \bigl\Vert g_{m+1}-g^{*} \bigr\Vert ^{2} \leq& \bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2} \\ &{}+(1-c)b_{m} \biggl[\frac{2}{1-c}\bigl\langle f\bigl(g^{*}\bigr)-g^{*},g_{m+1}-g^{*} \bigr\rangle \biggr]+2a_{m}K_{6} \end{aligned}$$

for all $m\geq m_{0}$ and for some $K_{6}>0$.

Indeed, from (3.2) we have

$$\begin{aligned} \bigl\Vert t_{m}-g^{*} \bigr\Vert ^{2} =& \bigl\Vert (1-a_{m}) \bigl(g_{m}+\psi _{m}(g_{m}-g_{m-1})\bigr)-g^{*} \bigr\Vert ^{2} \\ \leq &(1-a_{m})^{2} \bigl\Vert g_{m}-g^{*}+\psi _{m}(g_{m}-g_{m-1})-a_{m}g^{*} \bigr\Vert ^{2} +2a_{m}\bigl\langle g^{*},g^{*}-t_{m} \bigr\rangle \\ \leq &(1-a_{m})^{2}\bigl( \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2}+2\psi _{m} \bigl\langle g_{m}-g_{m-1},g_{m}-g^{*}+ \psi _{m}(g_{m}-g_{m-1})\bigr\rangle \bigr) \\ &{}+2a_{m}\bigl\langle g^{*},g^{*}-t_{m} \bigr\rangle \\ \leq &(1-a_{m}) \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2}+2(1-a_{m})\psi _{m} \Vert g_{m}-g_{m-1} \Vert K_{6} \\ &{}+2a_{m}\bigl\langle g^{*},g^{*}-t_{m}\bigr\rangle , \end{aligned}$$

(3.44)

where $K_{6}=\sup_{m\geq 1}\{\|g_{m}-g^{*}+\psi _{m}(g_{m}-g_{m-1}) \|\}$. Now, from Lemma 2.2 and (3.8), we have

$$\begin{aligned} \bigl\Vert g_{m+1}-g^{*} \bigr\Vert ^{2} =& \bigl\Vert b_{m}f(k_{m})+(1-b_{m})k_{m}-g^{*} \bigr\Vert ^{2} \\ =& \bigl\Vert b_{m}\bigl(f(k_{m})-f \bigl(g^{*}\bigr)\bigr)+(1-b_{m}) \bigl(k_{m}-g^{*} \bigr)+b_{m}\bigl(f\bigl(g^{*}\bigr)-g^{*}\bigr) \bigr\Vert ^{2} \\ \leq & \bigl\Vert b_{m}\bigl(f(k_{m})-f \bigl(g^{*}\bigr)\bigr)+(1-b_{m}) \bigl(k_{m}-g^{*} \bigr) \bigr\Vert ^{2}+2b_{m} \bigl\langle f \bigl(g^{*}\bigr)-g^{*},g_{m+1}-g^{*}\bigr\rangle \\ \leq &b_{m} \bigl\Vert f(k_{m})-f \bigl(g^{*}\bigr) \bigr\Vert ^{2}+(1-b_{m}) \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2}+2b_{m} \bigl\langle f\bigl(g^{*}-g^{*}\bigr),g_{m+1}-g^{*} \bigr\rangle \\ \leq &b_{m}c^{2} \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2}+(1-b_{m}) \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2}+2b_{m} \bigl\langle f\bigl(g^{*}\bigr)-g^{*},g_{m+1}-g^{*} \bigr\rangle \\ \leq &b_{m}c \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2}+(1-b_{m}) \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2}+2b_{m} \bigl\langle f\bigl(g^{*} \bigr)-g^{*},g_{m+1}-g^{*}\bigr\rangle \\ \leq &\bigl(1-(1-c)b_{m}\bigr) \bigl\Vert k_{m}-g^{*} \bigr\Vert ^{2}+2b_{m}\bigl\langle f\bigl(g^{*}\bigr)-g^{*},g_{m+1}-g^{*} \bigr\rangle \\ \leq &\bigl(1-(1-c)b_{m}\bigr) \bigl\Vert t_{m}-g^{*} \bigr\Vert ^{2}+2b_{m}\bigl\langle f\bigl(g^{*} \bigr)-g^{*},g_{m+1}-g^{*} \bigr\rangle . \end{aligned}$$

(3.45)

Putting (3.44) into (3.45), we obtain

$$\begin{aligned} \bigl\Vert g_{m+1}-g^{*} \bigr\Vert ^{2} \leq &\bigl(1-(1-c)b_{m}\bigr)\bigl[(1-a_{m}) \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2}+2(1-a_{m}) \psi _{m} \Vert g_{m}-g_{m-1} \Vert K_{6} \\ &{}+2a_{m}\bigl\langle g^{*},g^{*}-t_{m} \bigr\rangle \bigr]+2b_{m}\bigl\langle f\bigl(g^{*} \bigr)-g^{*},g_{m+1}-g^{*} \bigr\rangle \\ \leq &\bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2} \\ &{}+2 \bigl(1-(1-c)b_{m}\bigr) (1-a_{m}) \psi _{m} \Vert g_{m}-g_{m-1} \Vert K_{6} \\ &{}+2a_{m}\bigl(1-(1-c)b_{m}\bigr)\bigl\langle g^{*},g^{*}-t_{m}\bigr\rangle \\ &{} +2 \bigl(1-(1-c)b_{m}\bigr)b_{m} \bigl\langle f \bigl(g^{*}\bigr)-g^{*},g_{m+1}-g^{*}\bigr\rangle \\ \leq &\bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2} \\ &{}+2 \bigl(1-(1-c)b_{m}\bigr) (1-a_{m}) \psi _{m} \Vert g_{m}-g_{m-1} \Vert K_{6} \\ &{}+2a_{m}\bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g^{*} \bigr\Vert \bigl\Vert g^{*}-t_{m} \bigr\Vert \\ &{} +2\bigl(1-(1-c)b_{m}\bigr)b_{m} \bigl\langle f \bigl(g^{*}\bigr)-g^{*},g_{m+1}-g^{*}\bigr\rangle \\ \leq &\bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2}+(1-c)b_{m} \frac{2}{1-c} \bigl\langle f\bigl(g^{*}\bigr)-g^{*},g_{m+1}-g^{*} \bigr\rangle \\ &{}+2\bigl(1-(1-c)b_{m}\bigr) \\ &{}\times a_{m} \biggl[(1-a_{m})\frac{\psi _{m}}{a_{m}} \Vert g_{m}-g_{m-1} \Vert K_{6}+2a_{m} \bigl\Vert g^{*} \bigr\Vert \bigl\Vert g^{*}-t_{m} \bigr\Vert \biggr] \\ \leq &\bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2}+(1-c)b_{m} \frac{2}{1-c} \bigl\langle f\bigl(g^{*}\bigr)-g^{*},g_{m+1}-g^{*} \bigr\rangle \\ &{}+2\bigl(1-(1-c)b_{m}\bigr) \\ &{}\times a_{m} \biggl[(1-a_{m})\frac{\psi _{m}}{a_{m}} \Vert g_{m}-g_{m-1} \Vert K_{6}+2a_{m} \bigl\Vert g^{*} \bigr\Vert \bigl\Vert g^{*}-t_{m} \bigr\Vert \biggr] \\ \leq &\bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2} \\ &{}+(1-c)b_{m} \biggl[ \frac{2}{1-c}\bigl\langle f\bigl(g^{*}\bigr)-g^{*},g_{m+1}-g^{*} \bigr\rangle \biggr] \\ &{}+2\bigl(1-(1-c)b_{m}\bigr)a_{m}K_{7} \\ \leq &\bigl(1-(1-c)b_{m}\bigr) \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2} \\ &{}+(1-c)b_{m} \biggl[ \frac{2}{1-c}\bigl\langle f\bigl(g^{*}\bigr)-g^{*},g_{m+1}-g^{*} \bigr\rangle \biggr] \\ &{}+2a_{m}K_{7}, \end{aligned}$$

(3.46)

where $K_{7}=\sup_{m\geq 1} \{(1-a_{m}) \frac{\psi _{m}}{a_{m}}\| g_{m}-g_{m-1}\|K_{6}+2a_{m}\| g^{*}\|\|g^{*}-t_{m} \| \}>0$.

Claim c: We now show that the sequence $\{\|g_{m}-g^{*}\|^{2}\}$ converges strongly to zero. To show this, we consider two possible cases on the sequence $\{\|g_{m}-g^{*}\|^{2}\}$.

Case A: There exists $N\in \mathbb{N}$ such that $\|g_{m+1}-g^{*}\|^{2}\leq \|g_{m}-g^{*}\|^{2}$ for all $m\geq N$. Since $\{\|g_{m}-g^{*}\|^{2}\}$ is bounded, it follows that $\{\|g_{m}-g^{*}\|^{2}\}$ converges, and hence

$$ \bigl\Vert g_{m}-g^{*} \bigr\Vert ^{2}- \bigl\Vert g_{m+1}-g^{*} \bigr\Vert ^{2}\to 0 \quad \text{as } m \to \infty . $$

Recalling that $\sum_{m=1}^{\infty}a_{m}<\infty$, $\lim_{m\to \infty}b_{m}=0$, $\rho \in (0,\frac{2}{\eta} )$, and $\lim_{m\to \infty} ( \frac{1-\mu}{1+p_{m}\mu \frac{\tau _{m}}{\tau _{m+1}}} )^{2}>0$, then from (3.43) it follows that

$$ \lim_{m\to \infty} \Vert t_{m}-k_{m}-\rho \delta v_{m} \Vert =0 \quad \text{and}\quad \lim_{m\to \infty} \Vert t_{m}-h_{m} \Vert =0. $$

(3.47)

For all $m\geq m_{0}$, we observe that $\|v_{m}\|\geq \frac{1-\mu}{\eta}\|t_{m}-h_{m}\|$, which implies that $\frac{1}{\|v_{m}\|}\leq \frac{\eta}{(1-\mu )\|t_{m}-h_{m}\|}$. Thus, we have

$$\begin{aligned} \Vert t_{m}-k_{m} \Vert \leq & \Vert t_{m}-k_{m}-\rho \delta v_{m} \Vert +\rho \delta _{m} \Vert v_{m} \Vert \\ =& \Vert t_{m}-k_{m}-\rho \delta v_{m} \Vert +\rho (1-\mu ) \frac{ \Vert t_{m}-h_{m} \Vert ^{2}}{ \Vert v_{m} \Vert } \\ \leq & \Vert t_{m}-k_{m}-\rho \delta v_{m} \Vert +\rho \eta \Vert t_{m}-h_{m} \Vert . \end{aligned}$$

Therefore, from (3.47) it follows that

$$\begin{aligned} \lim_{m\to \infty} \Vert t_{m}-k_{m} \Vert =0. \end{aligned}$$

(3.48)

Furthermore, from (3.2) we have

$$\begin{aligned} \Vert g_{m}-t_{m} \Vert =& \bigl\Vert (1-a_{m})\psi _{m}(g_{m}-g_{m-1})+a_{m}g_{m} \bigr\Vert \\ \leq &(1-a_{m})\psi _{m} \Vert g_{m}-g_{m-1} \Vert +a_{m} \Vert g_{m} \Vert \\ =&a_{m} \biggl((1-a_{m})\frac{\psi _{m}}{a_{m}} \Vert g_{m}-g_{m-1} \Vert + \Vert g_{m} \Vert \biggr). \end{aligned}$$

Thus,

$$\begin{aligned} \lim_{m\to \infty} \Vert g_{m}-t_{m} \Vert =0. \end{aligned}$$

(3.49)

Hence, using (3.48) and (3.49), we have

$$ \Vert k_{m}-g_{m} \Vert \leq \Vert k_{m}-t_{m} \Vert + \Vert t_{m}-g_{m} \Vert \to 0 \quad \text{as } m\to \infty . $$

(3.50)

Combining (3.8) and (3.50), we get

$$\begin{aligned} \Vert g_{m+1}-g_{m} \Vert \leq & \Vert g_{m+1}-k_{m} \Vert + \Vert k_{m}-g_{m} \Vert \\ =&b_{m} \bigl\Vert f(k_{m})-k_{m} \bigr\Vert + \Vert k_{m}-g_{m} \Vert . \end{aligned}$$

(3.51)

Since $\lim_{m\to \infty}b_{m}=0$, using (3.51), we obtain

$$\begin{aligned} \lim_{m\to \infty} \Vert g_{m+1}-g_{m} \Vert =0. \end{aligned}$$

(3.52)

Since $\{g_{m}\}$ is a bounded sequence, a subsequence $\{g_{m_{j}}\}$ of $\{g_{m}\}$ exists such that $\{g_{m_{j}}\}\rightharpoonup z\in H$ with

$$\begin{aligned} \limsup_{m\to \infty}\bigl\langle f\bigl(g^{*} \bigr)-g^{*},g_{m}-g^{*} \bigr\rangle =&\lim _{j\to \infty}\bigl\langle f\bigl(g^{*}\bigr)-g^{*},g_{m_{j}}-g^{*} \bigr\rangle \\ =&\bigl\langle f\bigl(g^{*}\bigr)-g^{*},z-g^{*} \bigr\rangle . \end{aligned}$$

(3.53)

Now, due to the hypothesis that $Mg\neq 0$ for all $g\in H$, we have $Mz\neq 0$ for all $z\in H$. Since $g_{m_{i}} \rightharpoonup z$ and by (3.47), it follows from Lemma 3.5 that $z\in S_{D}$. It is not hard to see that $P_{S_{D}}of$ is a contraction mapping. From the Banach contraction principle, we know that $P_{S_{D}}of$ has a unique fixed point, say $g^{*}\in H$. That is, $g^{*}P_{S_{D}}of(g^{*})$. By Lemma 2.3, we have

$$\begin{aligned} \bigl\langle f\bigl(g^{*}\bigr)-g^{*},z-g^{*}\bigr\rangle \leq 0. \end{aligned}$$

It follows that

$$\begin{aligned} \limsup_{m\to \infty} \bigl\langle f\bigl(g^{*} \bigr)-g^{*},g_{m}-g^{*} \bigr\rangle =\bigl\langle f\bigl(g^{*}\bigr)-g^{*},z-g^{*}\bigr\rangle \leq 0. \end{aligned}$$

(3.54)

Using (3.52) and (3.54), we have

$$\begin{aligned} \limsup_{m\to \infty} \bigl\langle f\bigl(g^{*} \bigr)-g^{*},g_{m+1}-g^{*} \bigr\rangle \leq& \limsup _{m\to \infty} \bigl\langle f\bigl(g^{*}\bigr)-g^{*},g_{m+1}-g_{m} \bigr\rangle \\ &{}+\limsup_{m\to \infty} \bigl\langle f\bigl(g^{*} \bigr)-g^{*},g_{m}-g^{*} \bigr\rangle \leq 0. \end{aligned}$$

(3.55)

By applying Lemma 2.5 to (3.46), we obtain $g_{m}\to g^{*}$ as $m\to \infty$.

Case B: There exists a subsequence $\{\|g_{m_{i}}-g^{*}\|\}$ of $\{\|g_{m}-g^{*}\|\}$ such that $\|g_{m_{i}}-g^{*}\|^{2}\leq \|g_{m_{i}+1}-g^{*}\|^{2}$ for all $i\in \mathbb{N}$. Now, by Lemma 2.6, a nondecreasing sequence $\{s_{j}\}$ of $\mathbb{N}$ such that $\lim_{j\to \infty}s_{j}=\infty$, and the following inequalities are satisfied for all $j\in \mathbb{N}$:

$$\begin{aligned} \bigl\Vert g_{s_{j}}-g^{*} \bigr\Vert ^{2}\leq \bigl\Vert g_{s_{j}+1}-g^{*} \bigr\Vert ^{2} \quad \text{and}\quad \bigl\Vert g_{j}-g^{*} \bigr\Vert ^{2}\leq \bigl\Vert g_{s_{j}+1}-g^{*} \bigr\Vert ^{2}. \end{aligned}$$

(3.56)

By (3.43), we have

$$\begin{aligned} & \Vert t_{s_{j}}-k_{s_{j}}-\rho \delta v_{s_{j}} \Vert ^{2}+\rho \biggl( \frac{2}{\eta}-\rho \biggr) \biggl( \frac{1-\mu}{1+p_{s_{j}}\mu \frac{\tau _{s_{j}}}{\tau _{s_{j}+1}}} \biggr)^{2} \Vert t_{s_{j}}-h_{s_{j}} \Vert ^{2} \\ &\quad \leq \bigl\Vert g_{s_{j}}-g^{*} \bigr\Vert ^{2}- \bigl\Vert g_{s_{j}+1}-g^{*} \bigr\Vert ^{2}+a_{s_{j}}K_{5}+b_{s_{j}}K_{4} \\ &\quad \leq a_{s_{j}}K_{5}+b_{s_{j}}K_{4}. \end{aligned}$$

This means that

$$ \lim_{j\to \infty} \Vert t_{s_{j}}-k_{s_{j}}-\rho \delta v_{s_{j}} \Vert =0 \quad \text{and} \quad \lim_{j\to \infty} \Vert t_{s_{j}}-h_{s_{j}} \Vert =0. $$

(3.57)

Using a similar proof as in Case A, we obtain

$$\begin{aligned} &\lim_{j\to \infty} \Vert t_{s_{j}}-k_{s_{j}} \Vert =0, \end{aligned}$$

(3.58)

$$\begin{aligned} &\lim_{j\to \infty} \Vert g_{s_{j}}-t_{s_{j}} \Vert =0, \end{aligned}$$

(3.59)

$$\begin{aligned} &\lim_{j\to \infty} \Vert g_{s_{j}+1}-g_{s_{j}} \Vert =0, \end{aligned}$$

(3.60)

and

$$\begin{aligned} \limsup_{j\to \infty} \bigl\langle f\bigl(g^{*} \bigr)-g^{*},g_{s_{j}+1}-g^{*} \bigr\rangle \leq 0. \end{aligned}$$

(3.61)

According to (3.46), we have

$$\begin{aligned} \bigl\Vert g_{s_{j}+1}-g^{*} \bigr\Vert ^{2} \leq & \bigl(1-(1-c)b_{s_{j}}\bigr) \bigl\Vert g_{s_{j}}-g^{*} \bigr\Vert ^{2} \\ &{}+(1-c)b_{s_{j}} \biggl[\frac{2}{1-c}\bigl\langle f\bigl(g^{*}\bigr)-g^{*},g_{s_{j}+1}-g^{*} \bigr\rangle \biggr]+2a_{s_{j}}K_{7}. \end{aligned}$$

(3.62)

Using (3.56) and (3.62), we have

$$\begin{aligned} \bigl\Vert g_{s_{j}+1}-g^{*} \bigr\Vert ^{2} \leq &\bigl(1-(1-c)b_{s_{j}}\bigr) \bigl\Vert g_{s_{j}+1}-g^{*} \bigr\Vert ^{2} \\ &{}+(1-c)b_{s_{j}} \biggl[\frac{2}{1-c}\bigl\langle f\bigl(g^{*}\bigr)-g^{*},g_{s_{j}-1}-g^{*} \bigr\rangle \biggr] \\ &{}+2a_{s_{j}}K_{7}. \end{aligned}$$

This implies that

$$\begin{aligned} \bigl\Vert g_{s_{j}+1}-g^{*} \bigr\Vert ^{2} \leq &\frac{2}{1-c}\bigl\langle f\bigl(g^{*} \bigr)-g^{*},g_{s_{j}-1}-g^{*} \bigr\rangle + \frac{2a_{s_{j}}K_{7}}{(1-c)b_{s_{j}}} \\ \leq &\frac{2}{1-c}\bigl\langle f\bigl(g^{*} \bigr)-g^{*},g_{s_{j}-1}-g^{*}\bigr\rangle + \frac{2a_{s_{j}}K_{7}}{(1-c)b}. \end{aligned}$$

Thus, we have

$$\begin{aligned} \limsup_{m\to \infty} \bigl\Vert g_{s_{j}+1}-g^{*} \bigr\Vert \leq 0. \end{aligned}$$

(3.63)

Combining (3.56) and (3.63), we obtain $\limsup_{m\to \infty}\|g_{j}-g^{*}\|\leq 0$, it follows that $g_{j}\to g^{*}$ as $j\to \infty$. This ends the proof. □

Remark 3.7

It is not hard to see that quasimonotonicity was not employed in Lemma 3.3. Also, only Case 2 of Lemma 3.5 is used. Now, we present the strong convergence result of our proposed Algorithm 3.1 without monotonicity.

Lemma 3.8

Suppose that assumptions $(C_{1})$–$(C_{6})$, $(C_{8})$ hold and $\{g_{m}\}$ is a sequence generated by Algorithm 3.1. If there exists a subsequence $\{g_{m_{i}}\}$ of $\{g_{m}\}$ with $g_{m_{i}}\rightharpoonup p^{*}\in H$ and $\lim_{m\to \infty}\|h_{m_{i}}-t_{m_{i}}\|=0$, then either $p^{*}\in S_{D}$ or $Mp^{*}=0$.

Proof

By (3.34) and using the same argument in Lemma (3.5), if we fix $h\in \Psi$, then we obtain $h_{m_{i}} \rightharpoonup p^{*}$, $p^{*}\in \Psi$ and

$$\begin{aligned} \liminf_{i\to \infty}\langle Mh_{m_{i}},h-h_{m_{i}} \rangle \geq 0. \end{aligned}$$

Next, a positive sequence $\{\epsilon _{m}\}$ such that $\lim_{m\to \infty}=0$ and

$$\begin{aligned} \langle Mh_{m_{i}},h-h_{m_{i}}\rangle +\epsilon _{m}>0,\quad \forall m\geq 0. \end{aligned}$$

This means that

$$\begin{aligned} \langle Mh_{m_{i}},h\rangle +\epsilon _{m}>\langle Mh_{m_{i}},h_{m_{i}} \rangle >0,\quad \forall m\geq 0. \end{aligned}$$

(3.64)

In particular, set $h=p^{*}$ in (3.64), we have

$$\begin{aligned} \bigl\langle Mh_{m_{i}},p^{*}\bigr\rangle +\epsilon _{m}>\langle Mh_{m_{i}},h_{m_{i}} \rangle >0,\quad \forall m \geq 0. \end{aligned}$$

(3.65)

Letting $m\to \infty$ in (3.65), from condition $(H_{6})$ and recalling that $h_{m_{i}}\rightharpoonup p^{*}$, we have

$$\begin{aligned} \bigl\langle Mp^{*},p^{*}\bigr\rangle \geq \limsup _{i\to \infty} \langle Mh_{m_{i}},h_{m_{i}}\rangle ,\quad \forall m\geq 0. \end{aligned}$$

By condition $(H_{8})$, we have $\lim_{i\to \infty}\langle Mh_{m_{i}},h_{m_{i}}\rangle = \langle Mp^{*},p^{*}\rangle$. Now, from (3.64) we have

$$\begin{aligned} \bigl\langle Mp^{*},h\bigr\rangle =&\lim_{i\to \infty} \bigl(\langle Mh_{m_{i}},h \rangle +\epsilon _{m}\bigr) \\ \geq &\liminf_{i\to \infty}\langle Mh_{m_{i}},h\rangle \\ =&\lim_{i\to \infty}\langle Mh_{m_{i}},h\rangle \\ =&\bigl\langle Mp^{*},p^{*}\bigr\rangle . \end{aligned}$$

It follows that

$$\begin{aligned} \bigl\langle Mp^{*},h-p^{*}\bigr\rangle \geq 0, \quad \forall h\in \Psi . \end{aligned}$$

(3.66)

This implies that $p^{*}\in S_{D}$. Consequently, we know that either $p^{*}\in S_{D}$ or $Mp^{*}=0$ as required. □

Theorem 3.9

Suppose that assumptions $(C_{1})$–$(C_{6})$, $(C_{8})$ hold and $Mg\neq 0$, $\forall g\in H$. If $\{g_{m}\}$ is a sequence generated by Algorithm 3.1, then $\{g_{m}\}$ converges strongly to an element $g^{*}\in S_{D}\subset S$, where $g^{*}=P_{S_{D}}o f(g^{*})$.

Proof

By using Lemma 3.5 and adopting the same approach in the proof of Theorem 3.6, we get the required result. □

4 Applications and numerical experiments

In this section, we consider the application of our proposed algorithm to image restoration problems and optimal control problems. Furthermore, we examine the efficiency of some iterative algorithm for solving quasimonotone variational inequality problems. Specifically, we numerically compare our proposed Algorithm 3.1 with Algorithms 3.2 of Alakoya et al. [2] (namely, Alakoya Alg. 3.2), Algorithm 3.1 of Liu and Yang [25] (namely, Liu and Yang Alg. 3.1), and Algorithm 2.1 of Ye and He [56] (namely, Ye and He Alg. 2.1). Throughout this section, the parameters of our proposed algorithm and the compared ones are as follows:

• For our Algorithm 3.1, let $\tau _{0}=0.6$, $\psi =0.5$, $\rho =1.6$, $\mu =0.5$, $a_{m}=\frac{1}{(n+1)^{2}}$, $b_{m}=\frac{1}{(m+1)}$, $q_{m}=\frac{1}{(m+1)^{1.1}}$, $p_{m}=\frac{(m+1)}{m}$, $\xi _{m}=\frac{100}{(m+1)^{3}}$, and $f(g)=\frac{g}{5}$.

• For Algorithm 3.2 of Alakoya et al. [2], let $\tau _{0}=0.6$, $\psi =0.5$, $\rho =1.6$, $\mu =0.5$, $b_{m}=\frac{1}{(m+1)}$, $q_{m}=\frac{1}{(m+1)^{1.1}}$, $\xi _{m}=\frac{100}{(m+1)^{3}}$, and $f(g)=\frac{g}{5}$.

• For Algorithm 3.1 of Liu and Yang [25], let $\tau _{0}=0.6$, $\mu =0.5$, $q_{m}=\frac{1}{(m+1)^{1.1}}$.

• For Algorithm 2.1 of Ye and He [56], let $\gamma =0.7$ and $\sigma =0.95$.

We perform all the numerical experiments on an HP laptop with Intel(R) Core(TM)i5-6200U CPU 2.3GHz with 5 GB RAM.

4.1 Application to image restoration problem

In recent years, compressive sensing (CS) has become one of the major techniques used by several authors for image/signal processing. Image restoration is one of the most popular classical inverse problems. This kind of problem has been deeply been studied in various applications such as image deblurring, remote sensing, astronomical imaging, digital photography, radar imaging, and microscopic imaging [20].

In this part of the article, we compare the performance our Algorithm 3.1 with Algorithm 2.1 of Ye and He [56], Algorithm 3.2 of Alakoya et al. [2], Algorithm 3.1 of Liu and Yang [25] for solving an image restoration problem, which involves reformation of an image that is degraded by blur and additive noise.

Example 4.1

Consider the $l_{1}$-norm regularization problem that has to do with finding the solution of the following continuous optimization problem:

$$\begin{aligned} \min_{g\in \mathbb{R}^{n}}\bigl\{ \Vert g \Vert _{1}:Ag=d\bigr\} , \end{aligned}$$

(4.1)

where A is a matrix of $m\times n$ ($n< m$) dimension, d is a vector in $\mathbb{R}^{m}$, and $\|g\|_{1}=\sum_{i=1}^{n}|g_{i}|$ is the $l_{1}$ norm of g. We can reconstruct expression (4.1) as the least absolute selection and shrinkage operator (LASSO) problem as follows [13, 32]:

$$\begin{aligned} \min_{g\in \mathbb{R}^{n}}\biggl\{ w \Vert g \Vert _{1}+ \frac{1}{2} \Vert d-Ag \Vert ^{2}_{2} \biggr\} , \end{aligned}$$

(4.2)

where $w>0$ denotes the balancing parameter. It is not hard to see that (4.2) is a convex unconstrained minimization problem that appears in image reconstruction and compress sensing, where the original image/signal is sparse in some orthogonal basis by the process

$$\begin{aligned} d=Ag+t, \end{aligned}$$

(4.3)

where $g\in \mathbb{R}^{n}$, g, t, and d are unknown original image, unknown additive random noise, and known degraded observation, respectively, and A is the blurring operation. The first iterative method used to the solve (4.2) was introduced by Figureido et al. [13]. After that, many iterative methods have been studied for this problem (see [13, 17, 31, 32] and the references in them). It is important to note that the LASSO problem (4.2) can be formulated as a variational inequality problem, that is, finding $g\in \mathbb{R}^{n}$ such that $\langle M(g),h-g\rangle \geq 0$ for all $h\in \mathbb{R}^{n}$, where $Mg=A^{T}(Ag-d)$ [31]. For this, M is monotone (hence M is quasimonotone) Lipschitz continuous with $L=\|A^{T}A\|$. Now, we let $\Psi =\mathbb{R}^{n}$. By so doing, it means that $Z_{m}$ defined in our proposed modified subgradient extragradient-type Algorithm 3.1 is equal to $\mathbb{R}^{n}$. Hence, our proposed Algorithm 3.1 coincides with this problem. For more details about the equivalence of model (4.2) to variational inequality problem, we refer the reader to [1, 3, 17, 21, 34, 35, 50] and the references in them.

Next, we aim at comparing the deblurring efficiency of our proposed Algorithm 3.1 with Algorithm 3.2 of Alakoya et al. [2], Algorithm 3.1 of Liu and Yang [25], and Algorithm 2.1 of Ye and He [56]. The test images are Peppers and Board of sizes $256\times 256$ each in the Image Processing Toolbox in the MATLAB. The image went through a Gaussian blur of size $8\times 8$ and standard deviation of $\sigma =4$. Now, to measure the performances of the algorithms, we use the signal-to-noise ratio (SNR) defined by

$$ SNR=30\log _{10} \biggl(\frac{ \Vert g \Vert _{2}}{ \Vert g-g^{*} \Vert _{2}} \biggr), $$

(4.4)

where $g^{*}$ is the restored image and g is the original image. We use Matlab2015a to write the programs with stopping criterion $E_{m}=\|g_{m+1}-g_{m}\|\leq 10^{-6}$.

The computation results of deblurring images of Peppers and Board are illustrated in the following Tables 1–2 and Figs. 1–4.

Figure 1

Degraded peppers and its restoration via various algorithms. (a) Original peppers; (b) Peppers degraded by motion blur and random noise; (c) Peppers restored by Algorithm 3.1; (d) Peppers restored by Alakoya Alg. 3.2; (e) Peppers restored by Liu and Yang Alg. 3.1 and (f) Peppers restored by Ye and He Alg. 2.1

Figure 2

Graph corresponding to Table 1

Figure 3

Degraded board and its restoration via various algorithms. (a) Original board; (b) Board degraded by motion blur and random noise; (c) Board restored by Algorithm 3.1; (d) Board restored by Alakoya Alg. 3.2; (e) Board restored by Liu and Yang Alg. 3.1 and (f) Board restored by Ye and He Alg. 2.1

Figure 4

Graph corresponding to Table 2

Table 1 Numerical comparison of various algorithms using their SNR values for peppers

Table 2 Numerical comparison of various algorithms using their SNR values for board

Note that the larger the value of the SNR, the better the quality of the restored images. From the numerical experiments presented in Tables 1–2 and Figs. 1–4, it is evident that our proposed Algorithm 3.1 appears more promising and competitive as it outperforms Algorithm 3.2 of Alakoya et al. [2], Algorithm 3.1 of Liu and Yang [25], and Algorithm 2.1 of Ye and He [56].

4.2 Application to optimal control problem

In this part of the article, we use our proposed Algorithm 3.1 to solve variational inequality arising in the optimal control problem. Now, we consider the following example when the terminal function is nonlinear. The initial controls $p_{0}(z)=p_{1}(z)$ are randomly taken in $[-1,1]$. We take the stopping criterion $E_{m}=\|g_{m+1}-g_{m}\|\leq 10^{-6}$.

Example 4.2

(See [6])

$$\begin{aligned} &\text{minimize}\quad -g_{1}(2)+\bigl(g_{2}(2) \bigr)^{2}, \\ &\text{subject to}\quad \dot{g_{1}}(z)=g_{2}(z), \\ &\hphantom{\text{subject to}}\quad \dot{g_{2}}(z)=x(z),\quad \forall z\in [0,2], \\ &\hphantom{\text{subject to}}\quad \dot{g_{1}}(0)=0 \qquad \dot{g_{2}}(0)=0, \\ &\hphantom{\text{subject to}}\quad s(z)\in [-1,1]. \end{aligned}$$

The exact solution of the problem in Example 4.2 is

$$\begin{aligned} s^{*}=\textstyle\begin{cases} 1, & \text{if } z\in [0,1.2); \\ -1, & \text{if } z\in [1.2,2]. \end{cases}\displaystyle \end{aligned}$$

Algorithm 3.1 took 0.0563 sec. to obtain the approximate solution at the 89 iteration. Figure 5 represents the approximate optimal control and the corresponding trajectories of Algorithm 3.1.

Figure 5

Optimal control (red) and random initial control (blue) on the left and optimal trajectories on the right for Example 4.2 generated by Algorithm 3.1

4.3 Numerical experiments

Here, we consider two numerical experiments in solving quasimonotone variational inequality problems. We illustrate the benefits and computing effectiveness of our proposed Algorithm 3.1 in comparison to some well known algorithms in the literature which includes: Algorithm 3.2 of Alakoya et al. [2], Algorithm 3.1 of Liu and Yang [25] and Algorithm 2.1 of Ye and He [56].

Example 4.3

(See [25])

Let $\Psi =[-1,1]$ and

$$\begin{aligned} Mg=\textstyle\begin{cases} 2g-1, & \text{if } g>1, \\ g^{2},& \text{if } g\in [-1,1], \\ -2g-1,& \text{if } g< 1. \end{cases}\displaystyle \end{aligned}$$

Then the mapping is M is quasimonotone and Lipschitz continuous with $S_{D}=\{-1\}$ and $S=\{-1,0\}$.

We take the stopping criterion $E_{m}=\|g_{m+1}-g_{m}\|\leq 10^{-6}$ and consider the following initial values for this experiment:

Case a: $(g_{0},g_{1})=(0.5,0.5)$;

Case b: $(g_{0},g_{1})=(-0.08,0.1)$;

Case c: $(g_{0},g_{1})=(0.1,0.9)$;

Case d: $(g_{0},g_{1})=(-5,-0.001)$.

We compare the convergence efficiency of our proposed Algorithm 3.1 with Algorithm 3.2 of Alakoya et al. [2], Algorithm 3.1 of Liu and Yang [25] and Algorithm 2.1 of Ye and He [56]. The graphs of errors against the iteration numbers in each case are plotted. We report the numerical results in Table 3 and Fig. 6.

Figure 6

Top left: Case a; top right: Case b; bottom left: Case c; bottom right: Case d

Table 3 Numerical results of Example 4.3

Example 4.4

(See [30])

Let $H=\ell _{2}$, where $\ell _{2}$ is a real Hilbert space whose elements are square summable sequences of real numbers, that is, $\ell _{2}=\{g=(g_{1},g_{2},\ldots ,g_{j},\ldots ),j=1,2,\ldots , \sum_{j=1}^{\infty}|g_{j}|^{2}<\infty \}$. Let $p,q\in \mathbb{R}$ be such that $q>p>\frac{q}{2} >0$. If $\Psi =\{g\in \ell _{2}:\|g\|\leq p\}$ and $Mg=(q-\|g\|)g$, then M is quasimonotone and Lipschitz continuous with $S_{D}={0}$. We set $p=3$ and $q=5$.

Wet take the stopping criterion $E_{m}=\|g_{m+1}-g_{m}\|\leq 10^{-5}$ and consider the following initial values for this experiment:

Case I: $g_{0}=g_{1}=(1,1,\ldots ,1_{50{,}000},0,0,\ldots )$;

Case II: $g_{0}=g_{1}=(2,2,\ldots ,2_{50{,}000},0,0,\ldots )$;

Case III: $g_{0}=g_{1}=(1,2,\ldots ,{50{,}000},0,0,\ldots )$;

Case IV: $g_{0}=g_{1}=(10,10,\ldots ,10_{50{,}000},0,0,\ldots )$.

We compare the convergence efficiency of our proposed Algorithm 3.1 with Algorithm 3.2 of Alakoya et al. [2], Algorithm 3.1 of Liu and Yang [25], and Algorithm 2.1 of Ye and He [56]. The graphs of errors against the iteration numbers in each case are plotted. We report the numerical results in Table 4 and Fig. 7.

Figure 7

Top left: Case I; top right: Case II; bottom left: Case III; bottom right: Case IV

Table 4 Numerical results of Example 4.4

5 Conclusion

In this paper, we constructed an inertial modified subgradient extragradient-type Algorithm 3.1 for solving variational inequality problems involving quasimonotone and Lipschitz continuous operators in a real Hilbert space. The step-size considered in our algorithm is explicitly and adaptively updated without prior knowledge of the Lipschitz constant of the operator. We proved the strong convergence results of our proposed algorithm under some mild assumptions imposed on the control parameters. We utilize our method to solve some problems in applied sciences and engineering such as image restoration and optimal control problems. We carried out several numerical experiments to show that our method outperforms many well known methods in the existing literature.