1 Introduction

Bernstein [1] introduced the famous Bernstein operators that are defined by

$$ B_{n} ( f;x ) =\sum_{j=0}^{n}b_{n,j} ( x ) f \biggl( \frac{j}{n} \biggr), $$
(1)

where \(f: [ 0,1 ] \rightarrow \mathbb{R}\) is a function, \(n\in \mathbb{N}:= \{ 1,2,\ldots \} \), \(x\in [ 0,1 ] \) and \(b_{n,j} ( x ) \) is defined by

$$ b_{n,j} ( x ) := \begin{pmatrix} n \\ j\end{pmatrix} x^{j} ( 1-x ) ^{n-j}, $$
(2)

where \(j\in \{ 0,1,2,\ldots,n \} \). Bernstein [1] proved that \(B_{n} ( f;x ) \) converges to \(f(x)\) uniformly on \([ 0,1 ] \) as \(n\rightarrow \infty \) for any continuous function \(f: [ 0,1 ] \rightarrow \mathbb{R}\mathbbm{.}\)

Among all linear positive operators, Bernstein operators are the most studied ones (see the monograph [2] for a survey of studies). This is due to their numerous applications in science and engineering, and also their favorable shape-preserving properties.

Since Bernstein operators possess favorable properties and are widely used in applications, there have been numerous generalizations and variants [3–8]. In particular, Ye et al. [9] introduced a new Bézier basis that is dependent on a shape parameter \(\lambda \in [ -1,1 ] \). Using this Bézier basis, new Bernstein-type operators (called λ-Bernstein operators) were introduced [3]

$$ B_{n,\lambda } ( f;x ) :=\sum_{j=0}^{n}b_{n,j} ( \lambda ;x ) f \biggl( \frac{j}{n} \biggr) , $$

where \(\lambda \in [ -1,1 ] \) and the Bézier basis is defined by [9]

$$\begin{aligned}& b_{n,0} ( \lambda ;x ) =b_{n,0} ( x ) - \frac {\lambda }{n+1}b_{n+1,1} ( x ) ,\\& b_{n,j} ( \lambda ;x ) =b_{n,j} ( x ) +\lambda \frac {n-2j+1}{n^{2}-1}b_{n+1,j} ( x ) -\lambda \frac {n-2j-1}{n^{2}-1}b_{n+1,j+1} ( x ),\\& b_{n,n} ( \lambda ;x ) =b_{n,n} ( x ) - \frac {\lambda }{n+1}b_{n+1,n} ( x ) , \end{aligned}$$

where \(b_{n,j} ( x ) \) is given by (2). Note that taking \(\lambda =0\), one has the well-known Bernstein operator given by (1). Moreover, introducing the shape parameter λ, one has more modeling flexibility. We refer to [10–14] for more details about λ-Bernstein operators and their variants.

Bernstein operators have favorable shape-preserving properties and studying them is crucial for applications in computer-aided design and computer graphics (see [3, 5, 15] for recent studies). It is well known that Bernstein operators have a convexity-preserving property [2]. Namely, \(B_{n} ( f ) \) is convex for every n, whenever \(f\in C [ 0,1 ] \) is convex. Moreover, Bernstein operators preserve monotonic functions i.e., \(B_{n} ( f ) \) is a decreasing (increasing) function for all \(n\in \mathbb{N} \) whenever \(f: [ 0,1 ] \rightarrow \mathbb{R} \) is a decreasing (increasing) function, respectively [2]. Temple [16] investigated the monotonicity of Bernstein operators with n. Namely, if f is a convex function on \([ 0,1 ] \), then \(B_{n} ( f;x ) \) are monotonic in n, meaning that for all \(n\in \mathbb{N}\) and \(x\in [ 0,1 ] \) the inequality \(B_{n+1} ( f;x ) \leq B_{n} ( f;x ) \) holds. The converse of this property also holds [2].

The main purpose of this paper is to investigate the shape-preserving properties of recently introduced λ-Bernstein operators. To this end, we introduce a new representation of \(B_{n,\lambda} ( f;x ) \) as a sum of a Bernstein operator \(B_{n} ( f;x ) \) and a sum of first order divided differences of f. With the help of this new expression, we show that λ-Bernstein operators preserve monotonic functions. On the other hand, we show by a counter example that the convexity-preserving property is not satisfied for some \(\lambda \in [ -1,1 ] \). However, a weaker result for the convexity-preserving property is proven. Finally, we show that the monotonicity of λ-Bernstein operators with n fails for some \(\lambda >1/2\).

2 Preliminaries

Recall that Bernstein basis functions satisfy the following properties [2]

$$\begin{aligned}& b_{n,j} ( x ) =0,\quad \text{if }j>n\text{ or }j< 0, \\& b_{n,j} ( x ) = \biggl( 1-\frac {j}{n+1} \biggr) b_{n+1,j} ( x ) +\frac {j+1}{n+1}b_{n+1,j+1} ( x ) , \end{aligned}$$
(3)
$$\begin{aligned}& \frac {d}{dx}b_{n,j} ( x ) =n \bigl[ b_{n-1,j-1} ( x ) -b_{n-1,j} ( x ) \bigr] . \end{aligned}$$
(4)

Definition 2.1

([2])

Let \(x_{1},x_{2},\ldots,x_{r}\in [ 0,1 ] \) be distinct points and f be a real-valued function on \([ 0,1 ] \). Then, the divided difference of f with order \((r-1)\) is defined as

$$ [ x_{1},x_{2},\ldots,x_{r}:f ] :=\sum _{j=1}^{r} \frac {f ( x_{j} ) }{ ( x_{j}-x_{1} ) ( x_{j}-x_{2} ) \cdots ( x_{j}-x_{j-1} ) ( x_{j}-x_{j+1} ) \cdots ( x_{j}-x_{r} ) }. $$

Fix \(r\in \mathbb{N}\) and \(f: [ 0,1 ] \rightarrow \mathbb{R}\). We say that f is a convex (respectively, concave) function of order r, if all its divided differences with order \((r+1)\) are positive (respectively, negative).

Theorem 2.1

([2])

The identity

$$ \frac {d^{r}}{dx^{r}}B_{n} ( f;x ) = \frac {n!r!}{ ( n-r ) !n^{r}}\sum _{j=0}^{n-r}b_{n-r,j} ( x ) \biggl[ \frac{j}{n},\frac{j+1}{n},\ldots, \frac{j+r}{n} :f \biggr] , $$
(5)

holds for any \(f: [ 0,1 ] \rightarrow \mathbb{R}\) and \(r\in \{ 0,1,\ldots,n \} \).

Corollary 2.1

([2])

Bernstein operators preserve convexities of all orders. In particular, \(B_{n} ( f ) \) is decreasing (increasing) for every n whenever f is a decreasing (increasing) function on \([ 0,1 ] \), respectively. Similarly, \(B_{n} ( f ) \) is convex (concave) for every n whenever f is a convex (concave) function on \([ 0,1 ] \), respectively.

Theorem 2.2

([2])

Bernstein operators satisfy the identity

$$ B_{n+1} ( f;x ) -B_{n} ( f;x ) =- \frac{x ( 1-x ) }{n ( n+1 ) } \sum_{j=0}^{n-1}b_{n-1,j} ( x ) \biggl[ \frac{j}{n}, \frac{j+1}{n+1},\frac{j+1}{n}:f \biggr] $$

for \(f: [ 0,1 ] \rightarrow \mathbb{R}\), \(n\in \mathbb{N}\), \(x \in [ 0,1 ] \).

Corollary 2.2

([2])

If \(f: [ 0,1 ] \rightarrow \mathbb{R}\) is convex, then \(B_{n+1} ( f;x ) \leq B_{n} ( f;x ) \) for all \(n\in \mathbb{N}\), \(x\in [ 0,1 ] \).

Lemma 2.1

([3])

λ-Bernstein operators satisfy

$$\begin{aligned}& B_{n,\lambda } ( 1;x ) =1,\\& B_{n,\lambda } ( t;x ) =x+\lambda \frac{1-2x+x^{n+1}- ( 1-x ) ^{n+1}}{n ( n-1 ) },\\& B_{n,\lambda } \bigl( t^{2};x \bigr) =x^{2}+ \frac{x ( 1-x ) }{n}+\lambda \biggl[ \frac{2x-4x^{2}+2x^{n+1}}{n ( n-1 ) }+ \frac{x^{n+1}+ ( 1-x ) ^{n+1}-1}{n^{2} ( n-1 ) } \biggr] . \end{aligned}$$

Theorem 2.3

([3])

If \(f\in C [ 0,1 ] \) and \(\lambda \in [ -1,1 ] \), then \(B_{n,\lambda } ( f;x ) \) converges to \(f(x)\) uniformly on \([ 0,1 ] \) as \(n\rightarrow \infty \).

3 Main results

From now on, we will use the notation \(f_{j}:=f ( \frac{j}{n} ) \) for \(j=0,1,2,\ldots,n\).

Lemma 3.1

We can write \(B_{n,\lambda } ( f;x ) \) in the following form

$$ B_{n,\lambda } ( f;x ) =B_{n} ( f;x ) +\lambda \sum _{j=1}^{n}\frac {n-2j+1}{n^{2}-1}b_{n+1,j} ( x ) [ f_{j} -f_{j-1} ] . $$
(6)

Proof

By definition of λ-Bernstein operators, we have

$$\begin{aligned} B_{n,\lambda } ( f;x ) &=\sum_{j=0}^{n}b_{n,j} ( x ) f_{j} +\lambda \sum_{j=1}^{n} \frac {n-2j+1}{n^{2}-1}b_{n+1,j} ( x ) f_{j} \\ &\quad{} -\lambda \sum_{j=0}^{n-1} \frac {n-2j-1}{n^{2}-1}b_{n+1,j+1} ( x ) f_{j} \\ &=B_{n} ( f;x ) +\lambda \sum_{j=1}^{n} \frac {n-2j+1}{n^{2}-1}b_{n+1,j} ( x ) f_{j} \\ &\quad{} -\lambda \sum_{j=1}^{n} \frac {n-2j+1}{n^{2}-1}b_{n+1,j} ( x ) f_{j-1}. \end{aligned}$$

The last equation easily implies (6) and the proof is completed. □

Lemma 3.2

λ-Bernstein operators satisfy the identity

$$\begin{aligned} \frac {d}{dx}B_{n,\lambda } ( f;x ) &= \sum _{j=0}^{n-1} [ f_{j+1} -f_{j} ] b_{n,j} ( x ) \biggl[ n-j+ \lambda \frac {n-2j-1}{n-1} \biggr] \\ &\quad {}+\sum_{j=0}^{n-1} [ f_{j+1} -f_{j} ] b_{n,j+1} ( x ) \biggl[ j+1-\lambda \frac {n-2j-1}{n-1} \biggr], \end{aligned}$$
(7)

for all \(f: [ 0,1 ] \rightarrow \mathbb{R}\) and \(\lambda \in [ -1,1 ]\).

Proof

Differentiating the expression (6) and using (4) and (5), we obtain

$$\begin{aligned} \frac {d}{dx}B_{n,\lambda } ( f;x ) &=\sum _{j=0}^{n-1}b_{n-1,j} ( x ) \biggl[ \frac{j}{n},\frac{j+1}{n}:f \biggr] \\ &\quad {}+\lambda \sum_{j=1}^{n} \frac {n-2j+1}{n-1} \bigl( b_{n,j-1} ( x ) -b_{n,j} ( x ) \bigr) ( f_{j}-f_{j-1} ). \end{aligned}$$

Using the property (3), we obtain

$$\begin{aligned} \frac {d}{dx}B_{n,\lambda } ( f;x ) &=n\sum _{j=0}^{n-1} \biggl[ \biggl( 1-\frac {j}{n} \biggr) b_{n,j} ( x ) + \frac {j+1}{n}b_{n,j+1} ( x ) \biggr] ( f_{j+1}-f_{j} ) \\ &\quad {}+\lambda \sum_{j=0}^{n-1} \frac {n-2j-1}{n-1} \bigl( b_{n,j} ( x ) -b_{n,j+1} ( x ) \bigr) ( f_{j+1}-f_{j} ), \end{aligned}$$

which gives (7) and completes the proof. □

Remark 3.1

Taking \(\lambda =0\) in equation (7), we arrive at equation (5) for \(r=1\).

Theorem 3.1

λ-Bernstein operators preserve monotonic functions for all \(\lambda \in [ -1,1 ] \), i.e., \(B_{n,\lambda } ( f ) \) is decreasing (increasing) for all \(n\in \mathbb{N}\) and \(\lambda \in [ -1,1 ] \) whenever \(f: [ 0,1 ] \rightarrow \mathbb{R} \) is decreasing (increasing), respectively.

Proof

Let \(f: [ 0,1 ] \rightarrow \mathbb{R} \) be an increasing function. Then, for all distinct points \(u,v\in [ 0,1 ] \), one has

$$ [ u, v:f ] = \frac {f ( v ) -f ( u ) }{v-u}>0. $$
(8)

Since \(0\leq j\leq n-1 \), it easily follows that \(-1\leq 1-\frac{2j}{n-1}\leq 1 \). Using \(-1\leq \lambda \leq 1 \), one easily obtains \(-1\leq -\lambda ( 1-\frac{2j}{n-1} ) \leq 1 \). As a result, we can write

$$ 0\leq n-j-1\leq n-j+\lambda \biggl( 1-\frac{2j}{n-1} \biggr), $$
(9)

and

$$ 0\leq ( j+1 ) -1\leq ( j+1 ) -\lambda \biggl( 1- \frac{2j}{n-1} \biggr). $$
(10)

Using Lemma 3.2, it follows from (8), (9), and (10) that \(\frac {d}{dx}B_{n,\lambda } ( f;x ) >0\) and thus \(B_{n,\lambda } ( f;x ) \) is increasing. Analogously, one can prove that if f is decreasing, then so is \(B_{n,\lambda } ( f;x )\). □

Lemma 3.3

λ-Bernstein operators satisfy

$$\begin{aligned} \frac {d^{2}}{dx^{2}}B_{n,\lambda } ( f;x ) &=\lambda \frac {n ( n+1 ) }{n-1} \bigl\{ b_{n-1,0} ( x ) ( f_{0}-f_{1} ) +b_{n-1,n-1} ( x ) ( f_{n}-f_{n-1} ) \bigr\} \\ &\quad{} +n\sum_{j=0}^{n-2} ( f_{j+2}-2f_{j+1}+f_{j} ) b_{n-1,j} ( x ) \biggl( n-j-1+\lambda \frac {n-2j-3}{n-1} \biggr) \\ &\quad{} +n\sum_{k=0}^{n-2} ( f_{j+2}-2f_{j+1}+f_{j} ) b_{n-1,j+1} ( x ) \biggl( j+1-\lambda \frac {n-2j-1}{n-1} \biggr), \end{aligned}$$

for all \(f: [ 0,1 ] \rightarrow \mathbb{R}\) and \(\lambda \in [ -1,1 ]\).

Proof

Differentiating (7) and using (4) one has

$$\begin{aligned} \frac {d^{2}}{dx^{2}}B_{n,\lambda } ( f;x ) ={}&n\sum_{j=0}^{n-1} ( f_{j+1}-f_{j} ) \bigl( b_{n-1,j-1} ( x ) -b_{n-1,j} ( x ) \bigr) \biggl( n-j+ \lambda \frac {n-2j-1}{n-1} \biggr) \\ & {} +n\sum_{j=0}^{n-1} ( f_{j+1}-f_{j} ) \bigl( b_{n-1,j} ( x ) -b_{n-1,j+1} ( x ) \bigr) \biggl( j+1- \lambda \frac {n-2j-1}{n-1} \biggr) . \end{aligned}$$

The last equation can be written as

$$\begin{aligned} \frac {d^{2}}{dx^{2}}B_{n,\lambda } ( f;x ) &=n\sum _{j=0}^{n-2} ( f_{j+2}-f_{j+1} ) b_{n-1,j} ( x ) \biggl( n-j-1+\lambda \frac {n-2j-3}{n-1} \biggr) \\ &\quad{} +n\sum_{j=0}^{n-1} ( f_{j}-f_{j+1} ) b_{n-1,j} ( x ) \biggl( n-j-1+ \lambda \frac {n-2j-3}{n-1} \biggr) \\ &\quad{} +n\sum_{j=0}^{n-1} ( f_{j+1}-f_{j} ) b_{n-1,j} ( x ) \biggl( j-\lambda \frac {n-2j+1}{n-1} \biggr) \\ &\quad{} +n\sum_{j=0}^{n-2} ( f_{j}-f_{j+1} ) b_{n-1,j+1} ( x ) \biggl( j+1- \lambda \frac {n-2j-1}{n-1} \biggr). \end{aligned}$$

Similarly, shifting the index in the third sum completes the proof. □

Remark 3.2

Taking \(\lambda =0\) in Lemma 3.3, we obtain (5) for \(r=2 \). Moreover, if \(0 \leq j\leq n-2 \), then it is obvious that

$$ -1\leq 1-\frac{2 ( j+1 ) }{n-1}\leq 1. $$

Since \(-1\leq \lambda \leq 1 \), it immediately follows that

$$ -1\leq \lambda \biggl( 1-\frac{2 ( j+1 ) }{n-1} \biggr) \leq 1, $$

and thus

$$ 0\leq n-j-2\leq n-j-1+\lambda \frac {n-2j-3}{n-1}. $$

Similarly, one can show that

$$ 0\leq j+1-\lambda \frac {n-2j-1}{n-1}. $$

Let f \(: [ 0,1 ] \rightarrow \mathbb{R} \) be a convex function. Then, all divided differences \([ x_{1},x_{2},x_{3}:f ] \) are positive. It easily follows that

$$ \frac{2}{n^{2}} \biggl[ \frac{j}{n}, \frac{j+1}{n}, \frac{j+2}{n}:f \biggr] =f_{j+2}-2f_{j+1}+f_{j}>0. $$

As a result

$$\begin{aligned} &n\sum_{j=0}^{n-2} ( f_{j+2}-2f_{j+1}+f_{j} ) \biggl[ b_{n-1,j} ( x ) \biggl( n-j-1+\lambda \frac {n-2j-3}{n-1} \biggr) \\ &\quad{} +b_{n-1,j+1} ( x ) \biggl( j+1-\lambda \frac {n-2j-1}{n-1} \biggr) \biggr] >0. \end{aligned}$$

However, the term

$$ \lambda \frac {n ( n+1 ) }{n-1} \biggl\{ b_{n-1,0} ( x ) \biggl[ f ( 0 ) -f \biggl( \frac{1}{n} \biggr) \biggr] +b_{n-1,n-1} ( x ) \biggl[ f ( 1 ) -f \biggl( \frac{n-1}{n} \biggr) \biggr] \biggr\} $$

can be negative or positive (since \(-1\leq \lambda \leq 1\)), which may cause \(\frac {d^{2}}{dx^{2}}B_{n,\lambda } ( f;x ) <0\). We demonstrate this with an example.

Example 3.1

Consider the convex function \(f(t)=t^{2}\) on \([ 0,1 ] \). From Lemma 2.1, we obtain

$$ \frac {d^{2}}{dx^{2}}B_{n,\lambda } \bigl( t^{2};x \bigr) =2- \frac{2}{n} +\lambda \frac{-8+ ( n+1 ) ( 2n+1 ) x^{n-1}+ ( n+1 ) ( 1-x ) ^{n-1}}{n ( n-1 ) }. $$
(11)

Taking \(\lambda =1\) and \(n=2\) in the last equation, we have

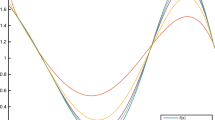
$$ \frac {d^{2}}{dx^{2}}B_{2,1} \bigl( t^{2};x \bigr) =6x- \frac{3}{2}, $$

and it is obvious that \(B_{2,1} ( t^{2};x ) \) is convex on the interval \(( \frac {1}{4},1 ) \), whereas it is concave on the interval \(( 0,\frac {1}{4} ) \). Therefore, \(B_{n,1} ( f;x ) \) does not preserve convexity. Similarly, taking \(\lambda =-1\) in equation (11), we give the intervals where \(B_{n,-1} ( t^{2};x ) \) is convex in Table 1 for different values of n. From the table, it can be observed that \(B_{n,-1} ( t^{2};x ) \) is not convex on \([ 0,1 ] \) for \(n\leq 50\) and thus \(B_{n,-1} ( f ) \) does not preserve convexity. We can see this in Fig. 1 for \(n=2, 3, 4, 5, \text{and } 10\).

Figure 1
figure 1

Graphs of \(B_{n,-1} ( t^{2};x ) \) for \(n=2, 3, 4, 5, \text{and } 10\)

Full size image
Table 1 The intervals where \(B_{n,-1} ( t^{2};x ) \) is convex for corresponding values of n
Full size table

Solving the inequality

$$ \frac {d^{2}}{dx^{2}}B_{n,\lambda } \bigl( t^{2};x \bigr) >0 $$

for different values of λ and n, we see more examples in which \(B_{n,\lambda } ( t^{2};x ) \) is not convex on \([ 0,1 ] \). We collect these examples in Table 2, which shows the intervals where \(B_{n,\lambda } ( t^{2};x ) \) is convex for different values of λ and n.

Table 2 The intervals where \(B_{n,\lambda } ( t^{2};x ) \) is convex for the corresponding values of λ and n
Full size table

The numerical data shows us that for \(\lambda =-\frac{1}{2}\), \(B_{n,\lambda } ( t^{2};x ) \) is convex on \([ 0,1 ] \) only for \(n\geq 5 \), for \(\lambda =\frac{1}{2}\), \(B_{n,\lambda } ( t^{2};x ) \) is convex on \([ 0,1 ] \) only for \(n\geq 3\). Similarly, we see that \(B_{n,\lambda } ( f ) \) does not preserve convexity for \(\lambda =-\frac{15}{16}\) and \(\lambda =-\frac{35}{36}\) when we look at the simple example \(f(t)=t^{2}\). Therefore, we conclude the next result.

Remark 3.3

λ-Bernstein operators do not preserve convexity of functions for certain \(\lambda \in [ -1,1 ] \).

We have seen that λ-Bernstein operators do not preserve convexity in general. However, we see that in some special cases, they preserve convexity as a result of the representation of \(\frac {d^{2}}{dx^{2}}B_{n,\lambda } ( f;x ) \) given in Lemma 3.3.

Theorem 3.2

If \(f: [ 0,1 ] \rightarrow \mathbb{R} \) is a convex function that is nonincreasing on \(( 0,x_{0} ) \) and nondecreasing on \(( x_{0},1 ) \) for an interior point \(x_{0}\in ( 0,1 ) \), then \(B_{n,\lambda } ( f ) \) is also convex for all \(\lambda \in [ 0,1 ] \) and \(n>n_{0}\) where \(n_{0}\) is dependent on \(x_{0}\).

Proof

From Remark 3.2, it is enough to show that

$$ \lambda \frac {n ( n+1 ) }{n-1} \biggl\{ b_{n-1,0} ( x ) \biggl[ f ( 0 ) -f \biggl( \frac{1}{n} \biggr) \biggr] +b_{n-1,n-1} ( x ) \biggl[ f ( 1 ) -f \biggl( \frac{n-1}{n} \biggr) \biggr] \biggr\} \geq 0. $$
(12)

If \(x_{0}<\frac{1}{2}\), then we can choose n such that \(\frac{1}{n}< x_{0}\). Then, f is nonincreasing on the interval \(( 0,\frac{1}{n} ) \) and nondecreasing on the interval \(( \frac{n-1}{n},1 ) \) for all such \(n\in \mathbb{N}\) and thus

$$ f ( 0 ) -f \biggl( \frac{1}{n} \biggr) \geq 0, \qquad f ( 1 ) -f \biggl( \frac{n-1}{n} \biggr) \geq 0. $$
(13)

Therefore, we have the inequality (12) for all n such that \(\frac{1}{n}< x_{0}\) and for all \(\lambda \in [ 0,1 ] \). Similarly if \(x_{0}>\frac{1}{2}\), then we can choose n such that \(1-\frac{1}{n}>x_{0}\). Then, f is nonincreasing on \(( 0,\frac{1}{n} ) \) and nondecreasing on \(( \frac{n-1}{n},1 ) \) for all such \(n\in \mathbb{N}\), which yields the inequality (12) for \(\lambda \in [ 0,1 ] \). Finally, if \(x_{0}=\frac{1}{2}\), then the inequality (12) holds for all \(n\geq 2\) and \(\lambda \in [ 0,1 ] \). □

Definition 3.1

([17])

Let \(f: [ 0,1 ] \rightarrow \mathbb{R} \) be continuous. f is called quasiconvex on \([ 0,1 ] \) if

$$ f \bigl( \eta u+ ( 1-\eta ) v \bigr) \leq \max \bigl\{ f(u),f(v) \bigr\} ,\quad \forall u,v,\eta \in [ 0,1 ] . $$

f is quasiconvex on \([ 0,1 ] \) iff f is nonincreasing and nondecreasing on the intervals \([ 0,c ] \) and \([ c,1 ] \), respectively, where \(c\in [ 0,1 ] \). Obviously, every nondecreasing, nonincreasing or convex function is quasiconvex on \([ 0,1 ] \).

Remark 3.4

Note that in the hypothesis of the last theorem, we have excluded the cases \(x_{0}=0\) or \(x_{0}=1\). This is because if f is nondecreasing or nonincreasing on \([ 0,1 ] \), we can not have both inequalities in (13). If f is a function that satisfies the hypothesis of the last theorem, then f is a quasiconvex function. Therefore, the assertion of the last theorem does not hold for all quasiconvex functions.

Now, we investigate the monotonicity of \(B_{n,\lambda } ( f;x ) \) with n. Namely, we try to answer the question “is the inequality \(B_{n+1,\lambda } ( f;x ) \leq B_{n,\lambda } ( f;x ) \) satisfied for every \(n\in \mathbb{N}\) and \(x\in [ 0,1 ] \) for fixed \(\lambda \in [ -1,1 ] \) if \(f: [ 0,1 ] \rightarrow \mathbb{R} \) is an arbitrary convex function?” Again, we consider \(f(t)=t^{2}\) and check if this property is satisfied. Basically, from Lemma 2.1 the problem reduces to checking when the inequality

$$\begin{aligned} &\frac{x ( 1-x ) }{n+1}+\lambda \biggl[ \frac{2x-4x^{2}+2x^{n+2}}{n ( n+1 ) }+ \frac{x^{n+2}+ ( 1-x ) ^{n+2}-1}{ ( n+1 ) ^{2}n} \biggr] \\ &\quad \leq \frac{x ( 1-x ) }{n}+\lambda \biggl[ \frac{2x-4x^{2}+2x^{n+1}}{n ( n-1 ) }+ \frac{x^{n+1}+ ( 1-x ) ^{n+1}-1}{n^{2} ( n-1 ) } \biggr] \end{aligned}$$
(14)

is satisfied. We solve this inequality using computer algebra and obtain the data given in Table 3. We have observed that for different negative values of λ, the inequality (14) holds for all \(n\in \mathbb{N}\) and \(x\in [ 0,1 ] \). As for the positive values of λ, we have seen that the inequality (14) is satisfied for all \(n\in \mathbb{N}\) and \(x\in [ 0,1 ] \) if \(\lambda \leq 1/2\). However, if \(\lambda >1/2\), then the inequality (14) does not hold for some x. In Table 3, we give the solutions of the inequality (14) for the corresponding values of n and λ.

Table 3 Solutions of the inequality (14) for the corresponding values of n and λ
Full size table

From these observations, the next result easily follows.

Remark 3.5

λ-Bernstein operators do not have monotonicity property with n for some \(\lambda >1/2\). Namely, the inequality

$$ B_{n+1,\lambda } ( f;x ) \leq B_{n,\lambda } ( f;x ) $$

does not hold for all \(n\in \mathbb{N}\) and \(x\in [ 0,1 ] \) for some fixed \(1/2<\lambda \leq 1\) and arbitrary convex function \(f\in C [ 0,1 ] \).

4 Conclusion

In this study, the shape-preserving properties of recently introduced λ-Bernstein operators \(B_{n,\lambda } ( f;x ) \) have been revealed. These properties are fundamental for the applications in computer graphics and computer-aided design. It has been seen that the monotonicity-preserving property is satisfied for every \(\lambda \in [ -1,1 ] \). However, it has been demonstrated with a counter example that the convexity-preserving property fails for some \(\lambda \in [ -1,1 ] \). In this case, it has been proven that for a special class of convex functions, \(B_{n,\lambda } ( f;x ) \) is convex for \(\lambda \in [ 0,1 ] \) and \(n>n_{0}\) (see Theorem 3.2). Furthermore, it has been shown with a counter example that the monotonicity of λ-Bernstein operators with n also fails for \(\lambda > 1/2 \). For further studies, a special class of functions for which λ-Bernstein operators preserve convexity for every \(\lambda \in [ -1,1 ] \) can be investigated. Moreover, as for the monotonicity property of λ-Bernstein operators with n, we have shown that this property is not satisfied, at least for some \(\lambda > 1/2 \). However, we were not able to obtain results for the other cases of λ. For this reason, it could be interesting to investigate whether this property is satisfied for \(-1 \leq \lambda \leq 1/2\) or not.