Abstract
In this paper, we introduce a new type λ-Bernstein operators with parameter \(\lambda\in[-1,1]\), we investigate a Korovkin type approximation theorem, establish a local approximation theorem, give a convergence theorem for the Lipschitz continuous functions, we also obtain a Voronovskaja-type asymptotic formula. Finally, we give some graphs and numerical examples to show the convergence of \(B_{n,\lambda }(f;x)\) to \(f(x)\), and we see that in some cases the errors are smaller than \(B_{n}(f)\) to f.
Similar content being viewed by others
1 Introduction
In 1912, Bernstein [1] proposed the famous polynomials called nowadays Bernstein polynomials to prove the Weierstrass approximation theorem as follows:
where \(x\in[0,1]\), \(n=1,2,\ldots\) , and Bernstein basis functions \(b_{n,k}(x)\) are defined as:
Based on this, there are many papers about Bernstein type operators [2–9]. In 2010, Ye et al. [10] defined new Bézier bases with shape parameter λ by
where \(\lambda\in[-1,1]\). When \(\lambda=0\), they reduce to (2). It must be pointed out that we have more modeling flexibility when adding the shape parameter λ.
In this paper, we introduce the new λ-Bernstein operators,
where \(\tilde{b}_{n,k}(\lambda;x)\) (\(k=0,1,\ldots,n\)) are defined in (3) and \(\lambda\in[-1,1]\).
This paper is organized as follows: In the following section, we estimate the moments and central moments of these operators (4). In Sect. 3, we investigate a Korovkin approximation theorem, establish a local approximation theorem, give a convergence theorem for the Lipschitz continuous functions, and obtain a Voronovskaja-type asymptotic formula. In Sect. 4, we give some graphs and numerical examples to show the convergence of \(B_{n,\lambda}(f;x)\) to \(f(x)\) with different parameters.
2 Some preliminary results
Lemma 2.1
For λ-Bernstein operators, we have the following equalities:
Proof
From (4), it is easy to prove \(\sum_{k=0}^{n}\tilde {b}_{n,k}(\lambda;x)=1\), then we can obtain (5). Next,
as is well known, the Bernstein operators (1) preserve linear functions, that is to say, \(B_{n}(at+b;x)=ax+b\). We denote the latter two parts in the bracket of the last formula by \(\triangle_{1}(n;x)\) and \(\triangle_{2}(n;x)\), then we have
Now, we will compute \(\triangle_{1}(n;x)\) and \(\triangle_{2}(n;x)\),
and
Combining (10), (11) and (12), we have
Hence, (6) is proved. Finally, by (4), we have
since \(B_{n}(t^{2};x)=\sum_{k=0}^{n}\frac{k^{2}}{n^{2}}b_{n,k}(x)=x^{2}+\frac {x(1-x)}{n}\), and we denote the latter two parts in the bracket of last formula by \(\triangle_{3}(n;x)\) and \(\triangle_{4}(n;x)\), then we have
On the one hand,
On the other hand,
Combining (13), (14) and (15), we obtain
therefore, we get (7). Thus, Lemma 2.1 is proved.
Similarly, we can obtain (8) and (9) by some computations, here we omit these. □
Corollary 2.2
For fixed \(x\in[0,1]\) and \(\lambda\in[-1,1]\), using Lemma 2.1 and by some easy computations, we have
Remark 2.3
For \(\lambda\in[-1,1]\), \(x\in[0,1]\), λ-Bernstein operators possess the endpoint interpolation property, that is,
Proof
We can obtain (21) easily by using the definition of λ-Bernstein operators (4) and
Remark 2.3 is proved. □
Example 2.4
The graphs of \(\tilde{b}_{3,k}(\lambda;x)\) with \(\lambda= -1, 0, -1\) are shown in Fig. 1(left). The corresponding \(B_{3,\lambda}(f;x)\) with \(f(x) = 1 - \cos(4e^{x})\) are shown in Fig. 1(right). The graphs show the λ-Bernstein operators’ endpoint interpolation property, which is based on the interpolation property of \(\tilde{b}_{n,k}(\lambda, x)\).
3 Convergence properties
As we know, the space \(C{[0,1]}\) of all continuous functions on \([0,1]\) is a Banach space with sup-norm \(\|f\|:=\sup_{x\in[0,1]}|f(x)|\). Now, we give a Korovkin type approximation theorem for \(B_{n,\lambda}(f;x)\).
Theorem 3.1
For \(f\in C{[0,1]}\), \(\lambda\in[-1,1]\), λ-Bernstein operators \(B_{n,\lambda}(f;x)\) converge uniformly to f on \([0,1]\).
Proof
By the Korovkin theorem it suffices to show that
We can obtain these three conditions easily by (5), (6) and (7) of Lemma 2.1. Thus the proof is completed. □
The Peetre K-functional is defined by \(K_{2}(f;\delta):=\inf_{g\in C ^{2}{[0,1]}}\{\|f-g\|+\delta\|g''\|\}\), where \(\delta>0\) and \(C^{2}{[0,1]}:=\{g\in C{[0,1]}: g', g''\in C{[0,1]}\}\). By [11], there exists an absolute constant \(C>0\) such that
where \(\omega_{2}(f;\delta):=\sup_{0< h\leq\delta}\sup_{x,x+h,x+2h\in [0,1]}|f(x+2h)-2f(x+h)+f(x)|\) is the second order modulus of smoothness of \(f\in C{[0,1]}\). We also denote the usual modulus of continuity of \(f\in C{[0,1]}\) by \(\omega(f;\delta):=\sup_{0< h\leq\delta}\sup_{x,x+h\in [0,1]}|f(x+h)-f(x)|\).
Next, we give a direct local approximation theorem for the operators \(B_{n,\lambda}(f;x)\).
Theorem 3.2
For \(f\in C{[0,1]}\), \(\lambda\in[-1,1]\), we have
where C is a positive constant, \(\phi_{n}(x)\) and \(\psi_{n}(x)\) are defined in (16) and (17).
Proof
We define the auxiliary operators
From (5) and (6), we know that the operators \(\widetilde{B}_{n,\lambda}(f;x)\) are linear and preserve the linear functions:
Let \(g\in C^{2}{[0,1]}\), by Taylor’s expansion,
and (25), we get
Hence, by (24) and (17), we have
On the other hand, by (24), (5) and (4), we have
Hence, taking infimum on the right hand side over all \(g\in C^{2}{[0,1]}\), we get
By (22), we have
where \(\phi_{n}(x)\) and \(\psi_{n}(x)\) are defined in (16) and (17). This completes the proof of Theorem 3.2. □
Remark 3.3
For any \(x\in[0,1]\), we have \(\lim_{n\rightarrow\infty}\phi_{n}(x)=0\) and \(\lim_{n\rightarrow\infty}\psi_{n}(x)=0\), these give us a rate of pointwise convergence of the operators \(B_{n,\lambda}(f;x)\) to \(f(x)\).
Now, we study the rate of convergence of the operators \(B_{n,\lambda }(f;x)\) with the help of functions of Lipschitz class \(\operatorname{Lip}_{M}(\alpha )\), where \(M>0\) and \(0<\alpha\leq1\). A function f belongs to \(\operatorname{Lip}_{M}(\alpha)\) if
We have the following theorem.
Theorem 3.4
Let \(f\in \operatorname{Lip}_{M}(\alpha)\), \(x\in[0,1]\) and \(\lambda\in [-1,1]\), then we have
where \(\psi_{n}(x)\) is defined in (17).
Proof
Since \(B_{n,\lambda}(f;x)\) are linear positive operators and \(f\in \operatorname{Lip}_{M}(\alpha)\), we have
Applying Hölder’s inequality for sums, we obtain
Thus, Theorem 3.4 is proved. □
Finally, we give a Voronovskaja asymptotic formula for \(B_{n,\lambda}(f;x)\).
Theorem 3.5
Let \(f(x)\) be bounded on \([0,1]\). Then, for any \(x\in(0,1)\) at which \(f''(x)\) exists, \(\lambda\in[-1,1]\), we have
Proof
Let \(x\in[0,1]\) be fixed. By the Taylor formula, we may write
where \(r(t;x)\) is the Peano form of the remainder, \(r(t;x)\in C{[0,1]}\), using L’Hopital’s rule, we have
Applying \(B_{n,\lambda}(f;x)\) to (29), we obtain
By the Cauchy–Schwarz inequality, we have
since \(r^{2}(x;x)=0\), then we can obtain
by (31) and (20). Finally, using (18), (19), (32) and (30), we get
Theorem 3.5 is proved. □
4 Graphical and numerical analysis
In this section, we give several graphs and numerical examples to show the convergence of \(B_{n,\lambda}(f;x)\) to \(f(x)\) with different values of λ and n.
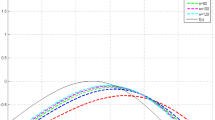
Let \(f(x) = 1 - \cos(4e^{x})\), the graphs of \(B_{n,-1}(f;x)\) and \(B_{n,1}(f;x)\) with different values of n are shown in Figs. 2 and 3. In Table 1, we give the errors of the approximation of \(B_{n,\lambda}(f;x)\) to \(f(x)\). We can see from Table 1 that in some special cases (such as \(n=10, 20\) and \(\lambda>0\)), the errors of \(\|f-B_{n,\lambda}(f)\|_{\infty}\) are smaller than \(\|f-B_{n,0}(f)\|_{\infty}\) (where \(B_{n,0}(f;x)\) are classical Bernstein operators). Figure 4 shows the graphs of \(B_{n,\lambda}(f;x)\) with \(n = 10\) and different values of λ.
References
Bernstein, S.N.: Démonstration du théorème de Weierstrass fondée sur la calcul des probabilités. Commun. Soc. Math. Charkow Sér. 2 t. 13, 1–2 (1912)
Ditzian, Z., Ivanov, K.: Bernstein-type operators and their derivatives. J. Approx. Theory 56(1), 72–90 (1989)
Guo, S., Li, C., Liu, X., Song, Z.: Pointwise approximation for linear combinations of Bernstein operators. J. Approx. Theory 107(1), 109–120 (2000)
Zeng, X.-M., Cheng, F.: On the rates of approximation of Bernstein type operators. J. Approx. Theory 109(2), 242–256 (2001)
Phillips, G.M.: Bernstein polynomials based on the q-integers. Ann. Numer. Math. 4, 511–518 (1997)
Gupta, V.: Some approximation properties of q-Durrmeyer operators. Appl. Math. Comput. 197, 172–178 (2008)
Agrawal, P.N., Gupta, V., Kumar, A.S.: On q-analogue of Bernstein–Schurer–Stancu operators. Appl. Math. Comput. 219(14), 7754–7764 (2013)
Nowak, G.: Approximation properties for generalized q-Bernstein polynomials. J. Math. Anal. Appl. 350, 50–55 (2009)
Mursaleen, M., Ansari, K.J., Khan, A.: On \((p, q)\)-analogue of Bernstein operators. Appl. Math. Comput. 266, 874–882 (2015)
Ye, Z., Long, X., Zeng, X.-M.: Adjustment algorithms for Bézier curve and surface. In: International Conference on Computer Science and Education, pp. 1712–1716 (2010)
DeVore, R.A., Lorentz, G.G.: Constructive Approximation. Springer, Berlin (1993)
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant Nos. 11601266 and 11626201), the Natural Science Foundation of Fujian Province of China (Grant No. 2016J05017) and the Program for New Century Excellent Talents in Fujian Province University. We also thank Fujian Provincial Key Laboratory of Data Intensive Computing and Key Laboratory of Intelligent Computing and Information Processing of Fujian Province University.
Author information
Authors and Affiliations
Contributions
QBC, BYL and GZ carried out the molecular genetic studies, participated in the sequence alignment and drafted the manuscript. QBC, BYL and GZ carried out the immunoassays. QBC. BYL and GZ participated in the sequence alignment. QBC, BYL and GZ participated in the design of the study and performed the statistical analysis. QBC, BYL and GZ conceived of the study, and participated in its design and coordination and helped to draft the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Cai, QB., Lian, BY. & Zhou, G. Approximation properties of λ-Bernstein operators. J Inequal Appl 2018, 61 (2018). https://doi.org/10.1186/s13660-018-1653-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-018-1653-7