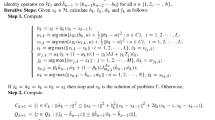1 Introduction

The triplet \((\Xi ,\langle \cdot ,\cdot \rangle ,\|\cdot \|)\) represents a real Hilbert space, the inner product, and the induced norm, respectively. For an operator \(U:K\rightarrow K\), \(\operatorname{Fix}(U)\) denotes the set of all fixed points of the operator U, where K is a nonempty closed convex subset of Ξ. Recall that the operator U is called η-demimetric [46], where \(\eta \in (-\infty ,1)\), if \(\operatorname{Fix}(U) \neq \emptyset \) and

$$ \bigl\langle p-q, (Id-U)p \bigr\rangle \geq \frac{1}{2}(1-\eta ) \bigl\Vert (Id-U)p \bigr\Vert ^{2} \quad \text{for all } p \in K \text{ and } q\in \operatorname{Fix}(U), $$

where Id denotes the identity operator.

The η-demimetric operator is equivalently defined by

$$ \Vert Up-q \Vert ^{2}\leq \Vert p-q \Vert ^{2}+ \eta \Vert p-Up \Vert ^{2} \quad \text{for all } p \in K \text{ and } q\in \operatorname{Fix}(U). $$

The class of η-demimetric operators plays a prominent role in metric fixed point theory and has been analyzed in various instances of fixed point problems [47, 48, 50]. We remark that various nonlinear operators have been analyzed in connections with variational inequality problems, fixed point problems, equilibrium problems, convex feasibility problems, signal processing, and image reconstruction [3–6, 11, 12, 14–19, 23, 24, 26, 28–30, 32, 34, 35, 37, 42, 43, 53–57]. In 2007, Aoyama et al. [2] suggested a Halpern [33] type approximants for an infinite family of nonexpansive operators satisfying the AKTT-Condition \(\sum^{\infty}_{k=1}\sup_{p\in X}\Vert U_{k+1}p-U_{k}p\Vert < \infty \) for any bounded subset X of Ξ. The following construction of operator \(S_{k}\) for a countably infinite family of η-demimetric operators does not require the AKTT-Condition and hence improves the performance of the approximants:

$$\begin{aligned}& Q_{k,k+1} = Id, \\& Q_{k,k} = \lambda _{k} U^{\prime }_{k} Q_{k,k+1}+(1-\lambda _{k})Id, \\& Q_{k,k-1} = \lambda _{k-1}U^{\prime }_{k-1}Q_{k,k}+(1- \lambda _{k-1})Id, \\& \vdots \\& Q_{k,m} = \lambda _{m}U^{\prime }_{m}Q_{k,m+1}+(1- \lambda _{m})Id, \\& \vdots \\& Q_{k,2} = \lambda _{2}U^{\prime }_{2}Q_{k,3}+(1- \lambda _{2})Id, \\& S_{k} = Q_{k,1} = \lambda _{1}U^{\prime }_{1}Q_{k,2}+(1- \lambda _{1})Id, \end{aligned}$$

where \(0\leq \lambda _{m}\leq 1\) and \(U^{\prime }_{m}=\rho p+(1-\rho )((1-\gamma )Id+\gamma U_{m})p\) for all \(p \in K\) with \(U_{m}\) being η-demimetric operator, \(\rho \in (0 , 1) \), and \(0<\gamma < 1-\eta \). It is well known in the context of operator \(S_{k}\) that each \(U^{\prime }_{m}\) is nonexpansive and the limit \(\lim_{k\rightarrow \infty}Q_{k,m}\) exists. Moreover,

$$ Sp=\lim_{k\rightarrow \infty}S_{k}p=\lim_{k\rightarrow \infty}Q_{k,1}p \quad \text{for all } p\in K. $$

This implies that \(\operatorname{Fix}(S)=\bigcap^{\infty}_{k=1}\operatorname{Fix}(S_{k})\) [36, 49].

The following concept of a split convex feasibility problem (SCFP) is presented in [20]:

Let H and W be nonempty closed convex subsets of real Hilbert spaces \(\Xi _{1}\) and \(\Xi _{2}\), respectively. In SCFP, we compute

$$ p \in H \quad \text{such that } Vp \in W, $$
(1.1)

where \(V: \Xi _{1} \rightarrow \Xi _{2}\) is a bounded linear operator. The SCFP is a particular case of the following split common null point problem (SCNPP) of maximal monotone operators:

Let \(A_{1}\subseteq \Xi _{1} \times \Xi _{1}\) and \(A_{2}\subseteq \Xi _{2} \times \Xi _{2}\) be two monotone operators such that \(\Gamma =A_{1}^{-1}(0)\cap V^{-1}(A_{2}^{-1}(0))\neq \emptyset \). In SCNPP, we compute \(p \in \Gamma \). Some interesting results on the SCNPP via iterative approximants can be found in [13, 21, 22, 44]. It is worth mentioning that the concept of SCNPP has been extended to the concept of a generalized split common null point problem (GSCNPP) in Hilbert spaces [39, 40]. In GSCNPP, we compute

$$ p \in \Gamma :=A^{-1}_{1}(0)\cap V^{-1}_{1} \bigl(A^{-1}_{2}(0) \bigr)\cap \cdots \cap V^{-1}_{1} \bigl(V^{-1}_{2} \cdots \bigl(V^{-1}_{N-1} \bigl(A^{-1}_{N}(0) \bigr) \bigr) \bigr), $$
(1.2)

where \(A_{j}:\Xi _{j} \rightarrow 2^{\Xi _{j}}\), \(j \in \{1,2,\ldots ,N\}\), is a finite family of maximal monotone operators, and \(V_{j}: \Xi _{j} \rightarrow \Xi _{j+1}\), \(j \in \{1,2,\ldots ,N-1\}\), is a finite family of bounded linear operators such that \(V_{j} \neq 0\).

From the perspective of optimization, problem (1.2) has been analyzed via different iterative approximants. A variant of the classical CQ-algorithm, essentially due to Byrne [13], is employed in [39], whereas shrinking projection approximants are analyzed in [40] to obtain the strong convergence results in Hilbert spaces. It is therefore natural to ask whether we can device strongly convergent approximants to compute a solution of GSCNPP and fixed point point problem of an infinite family of operators without employing the AKTT-Condition.

To answer the above question, we consider the following GSCNPP and FPP:

$$ p \in \Omega =\Gamma \cap \operatorname{Fix}(S) \neq \emptyset . $$
(1.3)

For the computation of a solution of problem (1.3), we employ hybrid shrinking approximants embedded with the inertial extrapolation technique, essentially due to Polyak [38] (see also [1, 7–10]), in Hilbert spaces.

The rest of the paper is organized as follows: In Sect. 2, we present mathematical preliminaries. We establish strong convergence results of the approximants and their variant, namely the Halpern-type approximants in Sect. 3. In Sect. 4, we elaborate the adaptability of the approximants for various extensively analyzed theoretical problems in this framework. Section 6 provides a numerical experiment to analyze the viability of the approximants in comparison with the existing results.

2 Preliminaries

We start this section with mathematical preliminary notions. We always assume that K is a nonempty closed convex subset of a real Hilbert space \(\Xi _{1}\).

Recall the nearest point projector \(\Pi ^{\Xi _{1}}_{K}\) of \(\Xi _{1}\) onto \(K\subset \Xi _{1}\) is defined so that for every \(p \in \Xi _{1}\), we have a unique \(\Pi ^{\Xi _{1}}_{K}p\) in K such that

$$ \bigl\Vert p-\Pi ^{\Xi _{1}}_{K}p \bigr\Vert \leq \Vert p-q \Vert \quad \text{for all } q \in K. $$

Note here that the nearest point projector has the following properties:

  1. (i)

    \(\|\Pi ^{\Xi _{1}}_{K}p-\Pi ^{\Xi _{1}}_{K}q\|^{2}\leq \langle p-q, \Pi ^{\Xi _{1}}_{K}p-\Pi ^{\Xi _{1}}_{K}q\rangle\) for all p, \(q \in K\) (firmly nonexpansive);

  2. (ii)

    \(\langle p-\Pi ^{\Xi _{1}}_{K}p,\Pi ^{\Xi _{1}}_{K}p-q\rangle \geq 0\) for all \(p \in \Xi _{1}\) and \(q \in K\) (characterization property).

Let the sets \(\mathcal{D}(A_{1})=\{p \in \Xi _{1}\mid A_{1}p \neq \emptyset \}\), \(\mathcal{R}(A_{1})=\{ u \in \Xi _{1}\mid (\exists p \in \Xi _{1}) u \in A_{1}p\}\), \(\mathcal{G}(A_{1})=\{(p,u) \in \Xi _{1}\times \Xi _{1}\mid u \in A_{1}p \}\), and \(\mathcal{Z}(A_{1})=\{p \in \Xi _{1}\mid 0 \in A_{1}p\}\) denote the domain, range, graph, and zeros of a set-valued operator \(A_{1}\subseteq \Xi _{1} \times \Xi _{1}\), respectively. If a set-valued operator \(A_{1}\) satisfies \(\langle p-q,t-w\rangle \geq 0\) for all \((p,t), (q,w) \in \operatorname{gra}(A_{1})\), then \(A_{1}\) is called monotone. Recall also that a monotone operator \(A_{1}\) is called maximal monotone if its graph is not strictly contained in the graph of any other monotone operator on \(\Xi _{1}\). The well-defined single-valued operator \(\mathcal{J}^{A_{1}}_{\theta}:=(Id+\theta A_{1})^{-1}:\mathcal{R}(Id+ \theta A_{1})\rightarrow \mathcal{D}(A_{1})\) is known as the resolvent of \(A_{1}\), where \(\theta >0\). The resolvent operator \(\mathcal{J}^{A_{1}}_{\theta}\) is closely related to \(A_{1}\) as \(q \in A_{1}^{-1}(0)\) if and only if \(q=\mathcal{J}^{A_{1}}_{\theta}(q)\).

Lemma 2.1

([46])

Let \(K\subset \Xi _{1}\), and let \(U: K \rightarrow \Xi _{1}\) be an η-demimetric operator with \(\eta \in (-\infty ,1)\). Then \(\operatorname{Fix}(U)\) is closed and convex.

Lemma 2.2

([50])

Let \(K\subset \Xi _{1}\), and let \(U: K \rightarrow \Xi _{1}\) be an η-demimetric operator with \(\eta \in (-\infty ,1)\) and \(\operatorname{Fix}(U)\neq \emptyset \). Let γ be a real number such that \(0<\gamma < 1-\eta \) and set \(M=(1-\gamma )Id+\gamma U\). Then M is a quasinonexpansive operator of K into \(\Xi _{1}\).

Lemma 2.3

([45])

Let \(\Xi _{1}\) be a real Hilbert space, and let \((d_{k})\) be a sequence in \(\Xi _{1}\). Then:

  1. (i)

    If \(d_{k}\rightharpoonup d\) and \(\Vert d_{k}\Vert \rightarrow \Vert d \Vert \) as \(k \rightarrow \infty \), then \(d_{k} \rightarrow d\) as \(k \rightarrow \infty \) (the Kadec–Klee property);

  2. (ii)

    If \(d_{k} \rightharpoonup d\) as \(k \rightarrow \infty \), then \(\Vert d\Vert \leq \lim \inf_{k \rightarrow \infty}\Vert d_{k}\Vert \).

Lemma 2.4

([27])

Let \(A_{1}\subseteq \Xi _{1} \times \Xi _{1}\) be a maximal monotone operator. Then for \(\theta \geq \tilde{\theta}>0\), we have

$$ \bigl\Vert p-\mathcal{J}^{A_{1}}_{\tilde{\theta}}p \bigr\Vert \leq 2 \bigl\Vert p- \mathcal{J}^{A_{1}}_{\theta}p \bigr\Vert \quad \textit{for all } p \in \Xi _{1}. $$

Lemma 2.5

([31])

Let \(K\subset \Xi _{1}\). Then the operator \(Id-U\) satisfies the demiclosedness principle with respect to the origin, that is, \((Id-U)(d)=0\), provided that there exists a sequence \((d_{k})\) in K that converges weakly to some d and \(((Id-U)d_{k})\) converges strongly to 0.

Lemma 2.6

([52])

Let \(K\subset \Xi _{1}\), and let \((U^{\prime }_{m})\) be a sequence of nonexpansive operators such that \(\bigcap^{\infty}_{k=1}\operatorname{Fix}(U^{\prime }_{k}) \neq \emptyset \) and \(0\leq \beta _{m}\leq b<1\). Then for a bounded subset D of K, we have

$$ \lim_{k\rightarrow \infty}\sup_{p\in D} \Vert Sp-S_{k}p \Vert =0. $$

3 Convergence analysis of the approximants

For the computation of a solution of (1.3), we propose the following approximants:

We assume the following control conditions on the approximants:

  1. (C1)

    \(\sum^{\infty}_{k=1}\mu _{k}\|d_{k-1}-d_{k}\|<\infty \);

  2. (C2)

    \(0 < a \leq \rho _{k} \leq b <1\);

  3. (C3)

    \(\liminf_{k \rightarrow \infty} \tau _{k} > 0\);

  4. (C4)

    \(\min_{j}\{\inf_{k}\{\theta _{j,k}\}\} \geq m > 0\).

Theorem 3.1

Any approximants defined via Algorithm 1, under control conditions (C1)–(C4), converge strongly to an element in Ω.

Algorithm 1
figure a

Hybrid Shrinking Approximants (Algo.1)

Full size image

Proof

We divide the proof into different steps for understanding.

Step 1. We show that the approximants \((d_{k})\) defined in Algorithm 1 are stable.

Claim: \(H_{k}\) and \(W_{k}\) are closed and convex subsets of \(\Xi _{1}\) for all \(k \geq 0\).

Consider, for each \(k \geq 0\), the following representation of the subsets \(H_{k}\) and \(W_{k}\):

$$\begin{aligned}& \begin{aligned} H_{k}&= \biggl\{ p \in \Xi _{1}: \\ &\quad \langle b_{k}-d_{k},p\rangle \leq \frac{1}{2} \bigl( \Vert b_{k} \Vert ^{2}- \Vert d_{k} \Vert ^{2}+\mu ^{2}_{k} \Vert d_{k}-d_{k-1} \Vert ^{2}+2\mu _{k}\langle d_{k}-p,d_{k}-d_{k-1} \rangle \bigr) \biggr\} , \end{aligned} \\& \begin{aligned} W_{k}&= \biggl\{ p \in \Xi _{1}:\langle \bar{V}_{j-1}b_{k}-c_{k}, \bar{V}_{j-1}p\rangle \leq \frac{1}{2} \bigl( \Vert \bar{V}_{j-1}b_{k} \Vert ^{2}- \Vert c_{k} \Vert ^{2} \bigr) \biggr\} , \\ &= \biggl\{ p \in \Xi _{1}: \bigl\langle \bar{V}^{\ast}_{j-1}( \bar{V}_{j-1}b_{k}-c_{k}),p \bigr\rangle \leq \frac{1}{2} \bigl( \Vert \bar{V}_{j-1}b_{k} \Vert ^{2}- \Vert c_{k} \Vert ^{2} \bigr) \biggr\} . \end{aligned} \end{aligned}$$

The claim follows from the above representations of closed and convex subsets \(H_{k}\) and \(W_{k}\) of \(\Xi _{1}\) for all \(k \geq 1\). Further, the sets Γ and \(\operatorname{Fix}(S)\) (from Lemma 2.1) are closed and convex. Hence we have that Ω is nonempty, closed, and convex. Let \(q \in \Omega \), \(\Omega \subset H_{0} = \Xi _{1}\). Now it follows from Algorithm 1 that

$$\begin{aligned} \Vert a_{k}-q \Vert ^{2} =&\bigl\Vert (1+\mu _{k})d_{k}-\mu _{k}(d_{k-1}-q) \bigr\Vert ^{2} \\ \leq & \Vert d_{k}-q \Vert ^{2}+\mu ^{2}_{k} \Vert d_{k}-d_{k-1} \Vert ^{2}+2\mu _{k}\langle d_{k}-q,d_{k}-d_{k-1} \rangle . \end{aligned}$$
(3.1)

From (3.1) and Lemma 2.2 we obtain

$$\begin{aligned} \Vert b_{k}-q \Vert ^{2} =& \bigl\Vert \rho _{k}a_{k}+(1-\rho _{k})S_{k}a_{k}-q \bigr\Vert ^{2} \\ \leq &\rho _{k} \Vert a_{k}-q \Vert ^{2}+(1-\rho _{k}) \Vert S_{k}a_{k}-q \Vert ^{2}-\rho _{k}(1-\rho _{k}) \bigl\Vert (Id-S_{k})a_{k} \bigr\Vert ^{2} \\ \leq &\rho _{k} \Vert a_{k}-q \Vert ^{2}+(1-\rho _{k}) \Vert a_{k}-q \Vert ^{2}-\rho _{k}(1-\rho _{k}) \bigl\Vert (Id-S_{k})a_{k} \bigr\Vert ^{2} \\ \leq & \Vert a_{k}-q \Vert ^{2}-\rho _{k}(1-\rho _{k}) \bigl\Vert (Id-S_{k})a_{k} \bigr\Vert ^{2} \\ \leq & \Vert d_{k}-q \Vert ^{2}+\mu ^{2}_{k} \Vert d_{k}-d_{k-1} \Vert ^{2}+2 \mu _{k}\langle d_{k}-q,d_{k}-d_{k-1} \rangle . \end{aligned}$$
(3.2)

This shows that Ω is contained in \(H_{k}\) for all \(k \geq 1\). Now assume that \(\Omega \subset W_{k}\) for some \(k \geq 1\). Using the nonexpansiveness of \(\mathcal{J}^{A_{j}}_{\theta _{j,k}}\), (3.1), and (3.2), we get

$$\begin{aligned} \Vert c_{k}-\bar{V}_{j-1}q \Vert ^{2} =& \bigl\Vert \tau _{k}(\bar{V}_{j-1}b_{k}- \bar{V}_{j-1}q)+(1-\tau _{k}) \bigl(\mathcal{J}^{A_{j}}_{\theta _{j,k}}( \bar{V}_{j-1}b_{k})-\bar{V}_{j-1}q \bigr) \bigr\Vert ^{2} \\ \leq & \tau _{k} \Vert \bar{V}_{j-1}b_{k}- \bar{V}_{j-1}q \Vert ^{2}+ (1- \tau _{k}) \bigl\Vert \mathcal{J}^{A_{j}}_{\theta _{j,k}}(\bar{V}_{j-1}b_{k})- \mathcal{J}^{A_{j}}_{\theta _{j,k}}(\bar{V}_{j-1}q) \bigr\Vert ^{2} \\ \leq & \tau _{k} \Vert \bar{V}_{j-1}b_{k}- \bar{V}_{j-1}q \Vert ^{2}+ (1- \tau _{k}) \Vert \bar{V}_{j-1}b_{k}-\bar{V}_{j-1}q \Vert ^{2} \\ \leq & \Vert \bar{V}_{j-1}b_{k}-\bar{V}_{j-1}q \Vert ^{2}. \end{aligned}$$
(3.3)

It follows from estimate (3.3) that \(\Omega \subset W_{k+1}\), and hence \(\Omega \subset H_{k+1}\cap W_{k+1}\). Consequently, by Step 1 the approximants \((d_{k})\) defined in Algorithm 1 are stable.

Step 2. We next show that \(\lim_{k\rightarrow \infty }\Vert d_{k}-d_{1}\Vert \) exists.

Observe that

$$ \Vert d_{k+1}-d_{1} \Vert \leq \Vert q-d_{1} \Vert \quad \text{for all } q \in \Omega \subset H_{k+1},$$

since \(d_{k+1}=\Pi ^{\Xi _{1}}_{H_{k+1}\cap W_{k+1}}d_{1}\). In particular,

$$ \Vert d_{k+1}-d_{1} \Vert \leq \bigl\Vert \Pi ^{\Xi _{1}}_{\Omega }d_{1}-d_{1} \bigr\Vert .$$

These estimates establish the boundedness of the approximants \((\Vert d_{k}-d_{1}\Vert )\). Since \(d_{k}=\Pi ^{\Xi _{1}}_{H_{k}\cap W_{k}}d_{1}\) and \(d_{k+1}=\Pi ^{\Xi _{1}}_{H_{k+1}\cap W_{k+1}}d_{1} \in H_{k+1}\), we have

$$ \Vert d_{k}-d_{1} \Vert \leq \Vert d_{k+1}-d_{1} \Vert . $$

This yields that the approximants \((\Vert d_{k}-d_{1}\Vert )\) are nondecreasing, and hence

$$ \lim_{k\rightarrow \infty } \Vert d_{k}-d_{1} \Vert \text{ exists}. $$
(3.4)

Step 3. We now show that \(\tilde{q}\in \Omega \).

We first compute

$$\begin{aligned} \Vert d_{k+1}-d_{k} \Vert ^{2} =& \Vert d_{k+1}-d_{1} \Vert ^{2}+ \Vert d_{k}-d_{1} \Vert ^{2}-2 \langle d_{k}-d_{1},d_{k+1}-d_{1} \rangle \\ =& \Vert d_{k+1}-d_{1} \Vert ^{2}+ \Vert d_{k}-d_{1} \Vert ^{2}-2 \langle d_{k}-d_{1},d_{k+1}-d_{k}+d_{k}-d_{1} \rangle \\ =& \Vert d_{k+1}-d_{1} \Vert ^{2}- \Vert d_{k}-d_{1} \Vert ^{2}-2 \langle d_{k}-d_{1},d_{k+1}-d_{k} \rangle \\ \leq & \Vert d_{k+1}-d_{1} \Vert ^{2}- \Vert d_{k}-d_{1} \Vert ^{2}. \end{aligned}$$

By (3.3) the above computation yields

$$ \lim_{k\rightarrow \infty } \Vert d_{k+1}-d_{k} \Vert =0. $$
(3.5)

In view of the control condition (C1), we get

$$ \lim_{k\rightarrow \infty } \Vert a_{k}-d_{k} \Vert =\lim_{k \rightarrow \infty }\mu _{k} \Vert d_{k}-d_{k-1} \Vert =0. $$
(3.6)

As a consequence of estimates (3.5) and (3.6), we also obtain that

$$ \lim_{k \rightarrow \infty} \Vert a_{k}-d_{k+1} \Vert =0. $$
(3.7)

Since \(d_{k+1} \in H_{k+1}\), we have

$$ \Vert b_{k}-d_{k+1} \Vert \leq \Vert d_{k}-d_{k+1} \Vert ^{2}+\mu ^{2}_{k} \Vert d_{k}-d_{k-1} \Vert ^{2}+2\mu _{k}\langle d_{k}-d_{k+1},d_{k}-d_{k-1} \rangle . $$

This estimate, in the light of estimate (3.5) and the control condition (C1), yields that

$$ \lim_{k \rightarrow \infty} \Vert b_{k}-d_{k+1} \Vert = 0. $$
(3.8)

Similarly, we infer from estimates (3.5) and (3.8) that

$$ \lim_{k \rightarrow \infty} \Vert b_{k}-d_{k} \Vert =0, $$
(3.9)

and from the estimates (3.6) and (3.9) that

$$ \lim_{k \rightarrow \infty} \Vert b_{k}-a_{k} \Vert =0. $$
(3.10)

In view of the control condition (C2), consider the variant of estimate (3.2)

$$\begin{aligned} a(1-b) \bigl\Vert (Id-S_{k})a_{k} \bigr\Vert ^{2} \leq & \Vert d_{k}-q \Vert ^{2}- \Vert b_{k}-q \Vert ^{2} \\ \leq & \bigl( \Vert d_{k}- q \Vert + \Vert b_{k}-q \Vert \bigr) \Vert d_{k}-b_{k} \Vert . \end{aligned}$$

Letting \(k \rightarrow \infty \) and using (3.9) and (C2), we have

$$ \lim_{k \rightarrow \infty} \Vert a_{k}-S_{k}a_{k} \Vert = 0. $$
(3.11)

Observe that

$$\begin{aligned} \Vert b_{k}-S_{k}b_{k} \Vert \leq & \Vert b_{k}-a_{k} \Vert + \Vert a_{k}-S_{k}a_{k} \Vert + \Vert S_{k}a_{k}-S_{k}b_{k} \Vert \\ \leq & 2 \Vert b_{k}-a_{k} \Vert + \Vert a_{k}-S_{k}a_{k} \Vert . \end{aligned}$$

The above computation, in view of estimates (3.10) and (3.11), yields

$$ \lim_{k \rightarrow \infty} \Vert b_{k}-S_{k}b_{k} \Vert =0. $$
(3.12)

Note that \(d_{k+1}=\Pi ^{\Xi _{1}}_{H_{k}\cap W_{k}}(d_{1}) \in W_{k}\). Therefore we have

$$ \Vert c_{k}-\bar{V}_{j-1}d_{k+1} \Vert \leq \Vert \bar{V}_{j-1} b_{k}- \bar{V}_{j-1}d_{k+1} \Vert \leq \Vert \bar{V}_{j-1} \Vert \Vert b_{k}-d_{k+1} \Vert . $$

Employing estimate (3.8), the above computation yields

$$ \lim_{k\rightarrow \infty } \Vert c_{k}-\bar{V}_{j-1}d_{k+1} \Vert =0. $$
(3.13)

Reasoning as above, we infer from estimates (3.8) and (3.13) that

$$ \lim_{k \rightarrow \infty} \Vert c_{k}-\bar{V}_{j-1}b_{k} \Vert =0 $$
(3.14)

and from estimates (3.9) and (3.14) that

$$ \lim_{k\rightarrow \infty } \Vert c_{k}-\bar{V}_{j-1}d_{k} \Vert =0. $$
(3.15)

Since \((d_{k})\) is bounded, there exists a subsequence \((d_{k_{t}})\) of \((d_{k})\) such that \(d_{k_{t}} \rightharpoonup \tilde{q} \in \Xi _{1}\) as \(t \rightarrow \infty \). Therefore \(b_{k_{t}} \rightharpoonup \tilde{q}\) and \(c_{k_{t}}\rightharpoonup \bar{V}_{j-1}\tilde{q}\) as \(t \rightarrow \infty \). From the definition of \(\bar{V}_{j-1}\) we have \(\bar{V}_{j-1}d_{k_{t}}\rightharpoonup \bar{V}_{j-1}\tilde{q}\) as \(t \rightarrow \infty \) for all \(j \in \{1,2,\ldots ,N\}\).

Using (3.14), we estimate that

$$ \lim_{t \rightarrow \infty } \bigl\Vert \bar{V}_{j-1}c_{k_{t}}- \mathcal{J}^{A_{j}}_{ \theta _{j,k}}(\bar{V}_{j-1}c_{k_{t}}) \bigr\Vert = 0 $$

for all \(j \in \{1,2,\ldots ,N\}\). Then from Lemma 2.4 and (C4) we obtain the inequality

$$ \bigl\Vert \bar{V}_{j-1}c_{k_{t}}-\mathcal{J}^{A_{j}}_{\theta}( \bar{V}_{j-1}c_{k_{t}}) \bigr\Vert \leq 2 \bigl\Vert \bar{V}_{j-1}c_{k_{t}}-\mathcal{J}^{A_{j}}_{\theta _{j,k}}( \bar{V}_{j-1}c_{k_{t}}) \bigr\Vert . $$

This estimate implies that

$$ \lim_{t \rightarrow \infty } \bigl\Vert \bar{V}_{j-1}c_{k_{t}}- \mathcal{J}^{A_{j}}_{ \theta}(\bar{V}_{j-1}c_{k_{t}}) \bigr\Vert = 0 $$
(3.16)

for all \(j \in \{1,2,\ldots ,N\}\). By Lemma 2.5 we have \(\bar{V}_{j-1}\tilde{q} \in \operatorname{Fix}(\mathcal{J}^{A_{j}}_{\theta})\) for all \(j \in \{1,2,\ldots ,N\}\), that is, \(\tilde{q} \in \Gamma \). It remains to show that \(\tilde{q} \in \operatorname{Fix}(S)\). Observe that

$$\begin{aligned} \Vert b_{k}-Sb_{k} \Vert \leq & \Vert b_{k}-S_{k}b_{k} \Vert + \Vert S_{k}b_{k}-Sb_{k} \Vert \\ \leq & \Vert b_{k}-S_{k}b_{k} \Vert + \sup_{p\in D} \Vert S_{k}p-Sp \Vert . \end{aligned}$$

Using (3.12) and Lemma 2.6, this estimate implies that \(\lim_{k\rightarrow \infty}\Vert b_{k}-Sb_{k}\Vert =0\). This, together with the fact that \(b_{k_{t}} \rightharpoonup \tilde{q}\), implies by Lemma 2.5 that \(\tilde{q} \in \operatorname{Fix}(S)= \bigcap^{\infty}_{k=1}\operatorname{Fix}(S_{k})\). Hence \(\tilde{q} \in \Omega \).

Step 4. The final part is showing that \(d_{k}\rightarrow q=\Pi ^{\Xi _{1}}_{\Omega }d_{1}\).

Since \(q=\Pi ^{\Xi _{1}}_{\Omega}d_{1}\) and \(\tilde{q} \in \Omega \), Lemma 2.3 implies that

$$\begin{aligned} \Vert q-d_{1} \Vert \leq& \Vert \tilde{q}-d_{1} \Vert \leq \liminf_{t \rightarrow \infty} \Vert d_{k_{t}}-d_{1} \Vert \\ \leq &\limsup_{t \rightarrow \infty} \Vert d_{k_{t}}-d_{1} \Vert \leq \Vert q-d_{1} \Vert . \end{aligned}$$

Using the uniqueness of q yields the equality \(\tilde{q}=q\). From Step 2 it follows that \(\Vert d_{k_{t}}-d_{1}\Vert \leq \Vert q-d_{1}\Vert \), and from Lemma 2.3 we obtain \(\lim_{k\rightarrow \infty }d_{k}=\tilde{q}=q=\Pi ^{\Xi _{1}}_{ \Omega }d_{1}\). □

We first apply Theorem 3.1 to the following problem:

$$ \Omega :=\bigcap^{s}_{j=1}A^{-1}_{j}(0) \cap V^{-1} \Biggl(\bigcap^{N}_{\ell =s+1}A^{-1}_{ \ell}(0) \Biggr)\cap \operatorname{Fix}(S), $$

where \(A_{j}\subseteq \Xi _{1} \times \Xi _{1}\), \(j\in \{1,2,\ldots ,s\}\), and \(A_{\ell}\subseteq \Xi _{1} \times \Xi _{1}\), \(\ell =\{s+1,s+2,\ldots ,N\}\), are finite families of maximal monotone operators, and \(S_{k}:\Xi _{1} \rightarrow \Xi _{1}\) is an infinite family of η-demimetric operators.

Corollary 3.2

Assume that \(\Omega \neq \emptyset \). Then the approximants initialized by arbitrary \(d_{0}, d_{1} \in \Xi _{1}\) and \(H_{0}= W_{0} = \Xi _{1}\) with the nonincreasing sequences \(\rho _{k},\tau _{k} \subset (0,1)\), \(\mu _{k} \in [0,1)\), and \(\gamma _{k} \in (0, \infty )\) for \(k\geq 1\) defined as

$$ \textstyle\begin{cases} a_{k}=(1+\mu _{k})d_{k}-\mu _{k}d_{k-1}, \\ b_{k}=\rho _{k}a_{k}+(1-\rho _{k})S_{k}a_{k}, \\ c_{k}=\tau _{k}\bar{V}_{j-1}b_{k}+(1-\tau _{k})(\mathcal{J}^{A_{j}}_{ \theta _{j,k}}(\bar{V}_{j-1}b_{k})); \\ H_{k+1}=\{p \in \Xi _{1}: \\ \hphantom{H_{k+1}={}}{}\Vert b_{k}-p \Vert ^{2} \leq \Vert d_{k}-p \Vert ^{2}+\mu ^{2}_{k} \Vert d_{k}-d_{k-1} \Vert ^{2}+2 \mu _{k}\langle d_{k}-p,d_{k}-d_{k-1}\rangle \}, \\ W_{k+1}=\{p \in \Xi _{1}: \Vert c_{k}-\bar{V}_{j-1}p \Vert \leq \Vert \bar{V}_{j-1} b_{k}-\bar{V}_{j-1}p \Vert \}, \\ d_{k+1}=\Pi ^{\Xi _{1}}_{H_{k+1}\cap W_{k+1}}d_{1}\quad \forall k \geq 1, \end{cases} $$
(3.17)

under the control conditions (C1)–(C4), converge strongly to an element in Ω.

We now consider the following Halpern-type variant of Algorithm 1:

Theorem 3.3

Any approximants defined via Algorithm 2, under the control conditions (C1)–(C4), converge strongly to an element in Ω.

Algorithm 2
figure b

Hybrid Shrinking Halpern Approximants (Algo.2)

Full size image

Proof

Observe that for each \(k \geq 1\), the subsets \(H_{k}\) have the following form:

$$\begin{aligned} H_{k} =& \bigl\{ p \in \Xi _{1}: \Vert b_{k}-p \Vert ^{2}\leq \rho _{k} \Vert t-p \Vert ^{2}+(1-\rho _{k}) \bigl( \Vert d_{k}-p \Vert ^{2}+\mu ^{2}_{k} \Vert d_{k}-d_{k-1} \Vert ^{2} \\ &{}+2\mu _{k}\langle d_{k}-z,d_{k}-d_{k-1} \rangle \bigr) \bigr\} . \end{aligned}$$

Arguing similarly as in the proof of Theorem 3.1 (Steps 1–2), we deduce that Ω, \(H_{k}\), and \(W_{k}\) are closed and convex. Moreover, \(\Omega \subset H_{k+1}\cap W_{k+1}\) for all \(k \geq 1\). Furthermore, the sequence \((d_{k})\) is bounded, and

$$ \lim_{k \rightarrow \infty} \Vert d_{k+1} - d_{k} \Vert = 0. $$
(3.18)

Since \(d_{k+1}=\Pi ^{\Xi _{1}}_{H_{k}\cap W_{k}}(t) \in H_{k}\), we have

$$\begin{aligned}& \Vert b_{k}-d_{k+1} \Vert ^{2} \\& \quad \leq \rho _{k} \Vert t-d_{k+1} \Vert ^{2}+(1- \rho _{k}) \bigl( \Vert d_{k}-d_{k+1} \Vert ^{2}+\mu ^{2}_{k} \Vert d_{k}-d_{k-1} \Vert ^{2}+2\mu _{k}\langle d_{k}-z,d_{k}-d_{k-1} \rangle \bigr). \end{aligned}$$

Letting \(k \rightarrow \infty \), using (3.18) along (C1)–(C2), and the boundedness of \((d_{k})\), we obtain

$$ \lim_{k \rightarrow \infty} \Vert b_{k}-d_{k+1} \Vert =0. $$

Similarly, we get

$$ \lim_{k \rightarrow \infty} \Vert b_{k}-d_{k} \Vert = 0. $$

Let \(b_{k}=\rho _{k}t+(1-\rho _{k})S_{k}a_{k}\). An easy calculation along (C1)–C2) implies that

$$ \Vert S_{k}a_{k}-a_{k} \Vert \leq \frac{1}{(1-\rho _{k})} \Vert b_{k}-a_{k} \Vert + \frac{\rho _{k}}{(1-\rho _{k})} \Vert t-a_{k} \Vert . $$

This estimate implies that

$$ \lim_{k \rightarrow \infty} \Vert S_{k}a_{k}-a_{k} \Vert =0. $$

The rest of the proof of Theorem 3.3 follows immediately from the proof of Theorem 3.1 and is therefore omitted. □

4 Applications

Our main result in the previous section has various interesting applications of great importance in the field. We present some of these applications.

4.1 Generalized split feasibility problems

In the context of generalized split feasibility problems [20], we recall that the indicator function \(j_{K}\) is a proper lower semicontinuous convex function (PCLS), where \(K\subset \Xi _{1}\). Therefore \(\partial j_{K}\), the subdifferential of \(j_{K}\), satisfies the maximal monotonicity such that \(\partial j_{K}(p)=N_{p}^{K}\), where \(N_{p}^{K}\) denotes the normal cone of K at u. From this we can deduce that \(\partial j_{K}\) coincides with \(\Pi _{K}^{\Xi _{1}}\). Assume that

$$ \Theta :=K_{1} \cap V^{-1}_{1}(K_{2}) \cap \cdots \cap V^{-1}_{1} \bigl(V^{-1}_{2} \cdots \bigl(V^{-1}_{N-1}(K_{N}) \bigr) \bigr) \neq \emptyset ,$$

where \(K_{j}\subset \Xi _{j}\), \(j \in \{1,2,\ldots ,N\}\).

Theorem 4.1

Assume that \(\Omega = \Theta \cap \operatorname{Fix}(S)\neq \emptyset \). Then the approximants initialized by arbitrary \(d_{0}, d_{1} \in \Xi _{1}\) and \(H_{0}= W_{0}=\Xi _{1}\) with the nonincreasing sequences \(\rho _{k},\tau _{k} \subset (0,1)\), \(\mu _{k} \in [0,1)\), and \(\gamma _{k} \in (0, \infty )\) for \(k\geq 1\) defined as

$$ \textstyle\begin{cases} a_{k}=(1+\mu _{k})d_{k}-\mu _{k}d_{k-1}, \\ b_{k}=\rho _{k}a_{k}+(1-\rho _{k})S_{k}a_{k}, \\ c_{k}=\tau _{k}\bar{V}_{j-1}b_{k}+(1-\tau _{k})(\Pi ^{\Xi _{j}}_{K_{j}} (\bar{V}_{j-1}b_{k})), \\ H_{k+1}=\{z \in \Xi _{1}: \\ \hphantom{H_{k+1}={}}{}\Vert b_{k}-z \Vert ^{2} \leq \Vert d_{k}-z \Vert ^{2}+\mu ^{2}_{k} \Vert d_{k}-d_{k-1} \Vert ^{2}+2 \mu _{k}\langle d_{k}-z,d_{k}-d_{k-1}\rangle \}, \\ W_{k+1}=\{z \in \Xi _{1}: \Vert c_{k}-\bar{V}_{j-1}z \Vert \leq \Vert \bar{V}_{j-1} b_{k}-\bar{V}_{j-1}z \Vert \}, \\ d_{k+1}=\Pi ^{\Xi _{1}}_{H_{k+1}\cap W_{k+1}}d_{1} \quad \forall k \geq 1, \end{cases} $$
(4.1)

under the control conditions (C1)–(C4), converge strongly to an element in Ω.

4.2 Generalized split variational inequality problems

The well-known variational inequality problem deals with computation of a point \(p \in K\) such that

$$ \langle \mathcal{A}p,q-p \rangle \geq 0\quad \forall q \in K, $$

where \(\mathcal{A}:K \rightarrow \Xi _{1}\) is a nonlinear monotone operator defined with respect to \(K\subset \Xi _{1}\). By \(\operatorname{Sol}(K,\mathcal{A})\) we denote the set of all solutions associated with the variational inequality problem. We consider the following problem:

$$ \Theta :=\operatorname{Sol}(K_{1},\mathcal{A}_{1}) \cap V^{-1}_{1} \bigl(\operatorname{Sol}(K_{2}, \mathcal{A}_{2}) \bigr)\cap \cdots \cap V^{-1}_{1} \bigl(V^{-1}_{2}\cdots \bigl(V^{-1}_{N-1} \bigl(\operatorname{Sol}(K_{N}, \mathcal{A}_{N}) \bigr) \bigr) \bigr) \neq \emptyset .$$

Theorem 4.2

Assume that \(\Omega = \Theta \cap \operatorname{Fix}(S)\neq \emptyset \). Then the approximants initialized by arbitrary \(d_{0}, d_{1} \in \Xi _{1}\) and \(H_{0}= W_{0}=\Xi _{1}\) with the nonincreasing sequences \(\rho _{k},\tau _{k} \subset (0,1)\), \(\mu _{k} \in [0,1)\), and \(\gamma _{k} \in (0, \infty )\) for \(k\geq 1\) defined as

$$ \textstyle\begin{cases} a_{k}=(1+\mu _{k})d_{k}-\mu _{k}d_{k-1}, \\ b_{k}=\rho _{k}a_{k}+(1-\rho _{k})S_{k}a_{k}; \\ c_{k}=\tau _{k}\bar{V}_{j-1}b_{k}+(1-\tau _{k})\Pi _{K_{j}}(Id- \theta _{j,k} \mathcal{A}_{j})\bar{V}_{j-1}b_{k}, \\ H_{k+1}=\{z \in \Xi _{1}: \\ \hphantom{H_{k+1}={}}{} \Vert b_{k}-z \Vert ^{2} \leq \Vert d_{k}-z \Vert ^{2}+\mu ^{2}_{k} \Vert d_{k}-d_{k-1} \Vert ^{2}+2 \mu _{k}\langle d_{k}-z,d_{k}-d_{k-1}\rangle \}, \\ W_{k+1}=\{z \in \Xi _{1}: \Vert c_{k}-\bar{V}_{j-1}z \Vert \leq \Vert \bar{V}_{j-1} b_{k}-\bar{V}_{j-1}z \Vert \}, \\ d_{k+1}=\Pi ^{\Xi _{1}}_{H_{k+1}\cap W_{k+1}}d_{1}\quad \forall k \geq 1, \end{cases} $$
(4.2)

under the control conditions (C1)–(C4), converge strongly to an element in Ω.

Proof

Let \(h_{\mathcal{A}_{j}}\subset \Xi _{j} \times \Xi _{j}\) be defined by

$$ h_{\mathcal{A}_{j}}p= \textstyle\begin{cases} \mathcal{A}_{j}p+N_{K_{j}}(p) & \text{if } p \in K_{j}, \\ \emptyset & \text{if } p \notin K_{j}, \end{cases} $$

where \(N_{K_{j}}(p):=\{q \in \Xi _{j}:\langle t-p, q\rangle \leq 0 \text{ for all } t \in K_{j}\}\), \(j=\{1,2,\ldots ,N\}\).

Note that \(h_{\mathcal{A}_{j}}\) is maximal monotone [41] such that

$$ 0 \in h_{\mathcal{A}_{j}}(p)\quad \iff \quad p \in \operatorname{Sol}(K_{j}, \mathcal{A}_{j}) \quad \iff \quad p=\Pi _{K_{j}} \bigl(p-\theta _{j,k} \mathcal{A}_{j}(p) \bigr).$$

The rest of the proof now follows from Theorem 3.1. □

4.3 Generalized split minimization problems

Let the set of minimizers associated with the function \(\phi : \Xi _{1} \rightarrow (-\infty ,\infty ]\) be denoted as

$$ \operatorname*{arg\,min}(\phi ):= \bigl\{ p \in \Xi _{1}: \phi (p)\leq \phi (q) \text{ for all } q \in \Xi _{1} \bigr\} . $$

If ϕ is a proper convex lower semicontinuous (PCLS) function, then ∂ϕ is a maximal monotone operator. Moreover, \(q \in (\partial \phi )^{-1}0 \Leftrightarrow 0 \in \partial \phi (q)\) (see [25]). Now observe that

$$\begin{aligned} \Theta := & \operatorname*{arg\,min}_{x \in \Xi _{1}}\phi _{1}(x)\cap V^{-1}_{1} \bigl( \operatorname*{arg\,min}_{x \in \Xi _{2}}\phi _{2}(x) \bigr)\cap \cdots \\ &{}\cap V^{-1}_{1} \bigl(h^{-1}_{2} \cdots \bigl(V^{-1}_{N-1} \bigl( \operatorname*{arg\,min}_{x \in \Xi _{N}} \phi _{N}(x) \bigr) \bigr) \bigr) \neq \emptyset , \end{aligned}$$

where \(\phi _{j}: \Xi _{j} \rightarrow (-\infty ,\infty ]\) is as defined above.

Theorem 4.3

Assume that \(\Omega = \Theta \cap \operatorname{Fix}(S) \neq \emptyset\). Then the approximants initialized by arbitrary \(d_{0}, d_{1} \in \Xi _{1}\) and \(H_{0}= W_{0}=\Xi _{1}\) with the nonincreasing sequences \(\rho _{k},\tau _{k} \subset (0,1)\), \(\mu _{k} \in [0,1)\), and \(\gamma _{k} \in (0, \infty )\) for \(k\geq 1\) defined as

$$ \textstyle\begin{cases} a_{k}=(1+\mu _{k})d_{k}-\mu _{k}d_{k-1}, \\ b_{k}=\rho _{k}a_{k}+(1-\rho _{k})S_{k}a_{k}, \\ c_{k}=\tau _{k}\bar{V}_{j-1}b_{k}+(1-\tau _{k})\mathcal{J}^{ \partial \phi _{j}}_{\theta _{j,k}}\bar{V}_{j-1}b_{k}, \\ H_{k+1}=\{p \in \Xi _{1}: \\ \hphantom{H_{k+1}={}}{}\Vert b_{k}-p \Vert ^{2} \leq \Vert d_{k}-p \Vert ^{2}+\mu ^{2}_{k} \Vert d_{k}-d_{k-1} \Vert ^{2}+2 \mu _{k}\langle d_{k}-p,d_{k}-d_{k-1}\rangle \}, \\ W_{k+1}=\{p \in \Xi _{1}: \Vert c_{k}-\bar{V}_{j-1}p \Vert \leq \Vert \bar{V}_{j-1} b_{k}-\bar{V}_{j-1}p \Vert \}, \\ d_{k+1}=\Pi ^{\Xi _{1}}_{H_{k+1}\cap W_{k+1}}d_{1}\quad \forall k \geq 1, \end{cases} $$
(4.3)

under the control conditions (C1)–(C4), converge strongly to an element in Ω.

4.4 Signal processing

This subsection deals with the case of signal recovery problem, which we aim to solve by applying Theorem 4.1. The following underdetermined formalism denotes the signal recovery problem:

$$ V d=\kappa -\vartheta , $$
(4.4)

where \(\kappa \in \mathbb{R}^{M}\) is the measured noise data with noise ϑ, \(d \in \mathbb{R}^{N}\) is the sparse original data for recovery, and \(V:\mathbb{R}^{N} \rightarrow \mathbb{R}^{M}\) (\(M < N\)) is the bounded linear observation matrix. Formalism (4.4) is equivalent to the well-known least absolute shrinkage and selection operator (LASSO) problem [51] in the following convex constrained optimization formalism:

$$ \min_{d \in \mathbb{R}^{N}} \biggl\{ \frac{1}{2} \Vert V d-\kappa \Vert ^{2} \biggr\} \quad \text{subject to } t\geq \Vert d \Vert _{1}. $$
(4.5)

If we set \(\Theta = K_{1}\cap V^{-1}(K_{2}) \neq \emptyset \) with \(K_{1}=\{d \mid t\geq \Vert d\Vert _{1} \}\) and \(K_{2}=\{\kappa \}\), then the LASSO problem can be easily solved via Theorem 4.1. To conduct the numerical experiment, we generate (i) the matrix \(V^{N \times M}\) from the standard normal distributions with zero mean and unit variance, (ii) d having \(m\ll N\) nonzero elements via a uniform distribution in \([-2,2]\), and (iii) κ from a Gaussian noise with signal-to-noise ratio \(\mathrm{SNR} =40\). The approximants are initiated with randomly chosen \(d_{0}\), \(d_{1}\) and abort when the following mean square error is satisfied:

$$ E_{k}=\frac{1}{N} \bigl\Vert d_{k}-d^{\ast} \bigr\Vert < 10^{-4}. $$

Here \(d^{\ast}\) is called the estimated signal of d.

For Theorem 4.1, we choose \(\mu _{k} =\frac{1}{(100 \times k+1)^{1.04}}\), \(\rho _{k} =\frac{1}{k^{1.02}}\), \(t=m-0.001\), and \(\vartheta =0\).

We recover the signals for the following two tests:

Numerical Test 1

Choose \(N=512\), \(M=256\), and \(m=15\).

Numerical Test 2

Choose \(N=1024\), \(M=512\), and \(m=30\).

From Table 1 and Figs. 1 and 2 we conclude that IGSNPP as in Theorem 4.1 reconstruct the original signal (A) faster than the algorithm for GSNPP as in Theorem 4.4 [40] in the compressed sensing. Moreover, the graph of error function values (B) and objective function values (C) generated by IGSNPP as in Theorem 4.1 converge faster as compared to the algorithm for GSNPP as in Theorem 4.4 [40].

Figure 1
figure 1

Comparison of two algorithms for Numerical Test 1

Full size image
Figure 2
figure 2

Comparison of two algorithms for Numerical Test 2

Full size image
Table 1 Comparison of Theorems 4.1 and 4.4 (Reich et al. [40])
Full size table

5 Numerical experiment and results

In this section, we focus on numerical implementation of our proposed algorithm. Comparison with Reich et al. [40]) shows the effectiveness and efficiency of our proposed algorithm. All codes were written in MATLAB R2020a and performed on a laptop Intel(R) Core(TM) i3-3217U @ 1.80 GHz, RAM 4.00 GB.

Example 5.1

Let \(\Xi _{1} = \mathbb{R}^{2}\) and \(\Xi _{2} = \mathbb{R}^{4}\) with the inner product defined by \(\langle x, y\rangle = xy\), for all \(x , y \in \mathbb{R}^{2},\mathbb{R}^{4}\) and the induced usual norm \(|\cdot |\).

Consider the following problem: find an element \(q \in \mathbb{R}^{2}\) such that

$$ q \in \Omega = \Theta _{1}\cap V^{-1}(\Theta _{2})\cap \operatorname{Fix}(S)\neq \emptyset , $$

where

$$ \Theta _{1} = \bigl\{ x \in \mathbb{R}^{2}\mid \Vert x-a_{1} \Vert ^{2}\leq R^{2}_{1} \bigr\} , \qquad \Theta _{2} = \bigl\{ x \in \mathbb{R}^{4}\mid \Vert x-a_{2} \Vert ^{2} \leq R^{2}_{2} \bigr\} ,$$

and \(V:\mathbb{R}^{2}\rightarrow \mathbb{R}^{4}\) is a bounded linear matrix randomly generated in the closed interval \([-5,5]\). Let the operators \(S_{k}: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}\) be defined by \(S_{k}(x)= (-(k+1)x_{1},-(k+1)x_{2})\) for \(k=1,2\). Then \(S_{k}\) is a η-demimetric operator with \(\eta _{1}=\frac{1}{3}\) and \(\eta _{2}=\frac{1}{2}\), respectively. It is easy to observe that \(\bigcap_{k=1}^{2} \operatorname{Fix}(S_{k})=\{0\}\) and \(\Theta := \{\Theta _{1}\cap V^{-1}(\Theta _{2})\}=0\). Hence \(\Omega = \Theta \cap \operatorname{Fix}(S) = 0\). Furthermore, the coordinate of the center a is randomly generated in the closed interval \([-1,1]\), and the radii \(R_{1}\) and \(R_{2}\) are randomly generated in the closed intervals \([5,9]\) and \([9,17]\), respectively. The coordinates of the initial point \(d_{0}\), \(d_{1}\) are randomly generated in the closed interval \([-5,5]\). Choose \(\mu =0.9\), \(m=0.01\), \(\rho _{k} =\frac{1}{100k+1}\), and \(\beta _{1} =\frac{1}{100k+1}\). We provide a numerical test of the hybrid shrinking approximants defined in Theorem 4.1 (i.e., Theorem 4.1 with \(\mu _{k}\neq 0\)) with the noninertial variant of Theorem 4.4 (i.e., Theorem 4.4, Reich et al. [40]). It is remarked that the function \(E_{k}\) is defined by

$$ E_{k} = \frac{1}{2} \bigl[ \bigl\Vert d_{k}-\Pi ^{\mathbb{R}^{2}}_{\Theta _{1}}(d_{k}) \bigr\Vert ^{2}+ \bigl\Vert Vd_{k}-\Pi ^{\mathbb{R}^{4}}_{\Theta _{2}}(Vd_{k}) \bigr\Vert ^{2} \bigr] \quad \text{for } k \geq 1. $$

Note that at the kth step, \(E_{k}=0\), and then \(d_{k}\in \Theta \), which implies that \(d_{k}\) is a solution of this problem. The stopping criterion is defined as \(E_{k} < 10^{-5}\). The different choices of \(d_{0}\), \(d_{1}\) are given as follows:

  1. Case I:

    \(d_{0}=[6,8]^{T}\), \(d_{1}=[3,7]^{T}\).

  2. Case II:

    \(d_{0}=[6.5,7.2]^{T}\), \(d_{1}=[-1.4,-9.7]^{T}\).

  3. Case III:

    \(d_{0}=[3,-4.7]^{T}\), \(d_{1}=[1.2,4]^{T}\).

Remark 5.2

  1. (i)

    The example presented above serves for two purposes:

    • impact of different values of \(\mu _{k}\) on our proposed algorithm

    • comparison with the noninertial (\(\mu _{k} = 0\)) type algorithm proposed by Reich et al. [40] given in Theorem 4.4.

  2. (ii)

    The numerical results presented in Table 2 and Figs. 3–5 indicate that our proposed approximants are efficient, easy to implement, and do well for any values of \(\mu _{k}\neq 0\) in both number of iterations and CPU time required.

    Figure 3
    figure 3

    Example 5.1: Case I

    Full size image
    Figure 4
    figure 4

    Example 5.1: Case II

    Full size image
    Figure 5
    figure 5

    Example 5.1: Case III

    Full size image
    Table 2 Comparison of Theorems 4.1 and 4.4 (Reich et al. [40]) with different values of \(\mu _{k}\)
    Full size table
  3. (iii)

    We observe that the CPU time of Theorem 4.1 increases, but the number of iterations decreases as the parameter μ approaches 1.

  4. (iv)

    We observe from the numerical implementation above and our proposed algorithm outperformed the noninertial version proposed by Reich et al. [40] given in Theorem 4.4 both in the number of iterations and CPU time required to reach the stopping criterion.

6 Conclusions

The problem for computing a common solution via unifying approximants, of a finite family of GSCNPP and the FPP for a countably infinite family of nonlinear operators has its own importance in the fields of monotone operator theory and fixed point theory. We proved that the approximants perform in an effective and efficient way when compared with the existing approximants, in particular, those studied in Hilbert spaces. The theoretical framework of the algorithm has been strengthened with an appropriate numerical example. Moreover, this framework has also been implemented to various instances of the split inverse problems. We would like to emphasize that the above mentioned problems occur naturally in many applications. Therefore iterative algorithms are inevitable in this field of investigation. As a consequence, our theoretical framework constitutes an important topic of future research.