Double controlled metric-like spaces

Abstract

In this paper, we introduce a new extension of the double controlled metric-type spaces, called double controlled metric-like spaces, by assuming that the “self-distance” may not be zero On the other hand, if the value of the metric is zero, then it has to be a “self-distance” (i.e., we replace $[\varsigma(g,h)=0 \Leftrightarrow g=h]$ by $[\varsigma(g,h)=0 \Rightarrow g=h]$). Using this new type of metric spaces, we generalize many results in the literature. We prove fixed point results along with examples illustrating our theorems. Also, we present double controlled metric-like spaces endowed with a graph along with an open question.

1 Introduction

In 1922, Banach [1] proved the existence and uniqueness of a fixed point for self-contractive mapping in metric spaces. That was the starting point for researchers in the field of analysis to generalize his result, whether by changing the contractions or by generalizing the type of metric spaces covering a wider class of metrics, for example, extension of metric spaces to partial metric spaces or b-metric spaces; see [2–17].

One interesting extension of metric spaces is b-metric spaces introduced by Bakhtin [18]. Recently, several extensions of b-metric spaces were introduced, such as extended b-metric spaces, which were initiated by Kamran et al. [19]. In 2018, Mlaiki et al. [20] gave an extension of the extended b-metric spaces, the so-called controlled metric-type spaces. Also, in 2018, Abdeljawad et al. [21], introduced the concept of double controlled metric-type spaces. As an extension of all the types of metric spaces mentioned, we introduce a new class, the so-called double controlled metric-like spaces.

2 Preliminaries

We begin our preliminaries by recalling the definition of extended b-metric spaces.

Definition 2.1

([19])

Consider the set $\mathcal{F}\neq\emptyset$ and a function $\hbar: \mathcal{F}\times\mathcal{F}\rightarrow[1,\infty)$. Suppose that a function $\varsigma:\mathcal{F}\times\mathcal{F}\rightarrow\mathbb {\mathbb{R}}^{+}$ satisfies the following conditions for all $g,h,w \in \mathcal{F}$:

• (1) $\varsigma(g,h)=0 \Longleftrightarrow g=h$;

• (2) $\varsigma(g,h) = \varsigma(h,g)$;

• (3) $\varsigma(g,h) \leq\hbar(g,h) [\varsigma(g,w) + \varsigma(w,h)]$.

Then the pair $(\mathcal{F}, \varsigma)$ is called an extended b-metric space.

Next, we present the definition of controlled metric-type spaces.

Definition 2.2

([20])

Given a nonempty set $\mathcal{F}$ and a function $\varpi: \mathcal {F}^{2}\rightarrow[1,\infty)$, suppose that a function $\rho: \mathcal{F}^{2}\rightarrow[0,\infty)$ satisfies the following conditions for all $g,h,w\in\mathcal{F}$:

($\rho_{1}$):

$\rho(g,h)=0\Leftrightarrow g=h$;

($\rho_{2}$):

$\rho(g,h)=\rho(h,g)$;

($\rho_{3}$):

$\rho(g,h)\leq\varpi(g,w) \rho(g,w)+\varpi(w,h) \rho (w,h)$.

Then the pair $(\mathcal{F},\rho)$ is called a controlled metric-type space.

The following definition is a generalization of controlled metric-type spaces to double controlled metric-type spaces.

Definition 2.3

([21])

$(DCMTS)$ Consider a set $\mathcal{F}\neq\emptyset$ and noncomparable functions $\varpi,\varepsilon: \mathcal{F}\times \mathcal{F}\rightarrow[1,\infty)$. Suppose that a function $\varsigma : \mathcal{F}^{2}\rightarrow[0,\infty)$ satisfies the following conditions for all $g,h,w\in\mathcal{F}$:

• (1) $\varsigma(g,h)=0$ if and only if $g=h$;

• (2) $\varsigma(g,h)=\varsigma(h,g)$;

• (3) $\varsigma(g,h)\leq\varpi(g,w) \varsigma(g,w)+\varepsilon(w,h) \varsigma(w,h)$.

Then the pair $(\mathcal{F},\varsigma)$ is called a double controlled metric-type space.

Now we present our generalization of the double controlled metric-type spaces.

Definition 2.4

$(DCMLS)$ Consider a set $\mathcal{F}\neq\emptyset$ and noncomparable functions $\varpi,\varepsilon: \mathcal{F}\times \mathcal{F}\rightarrow[1,\infty)$. Suppose that a function $\varsigma : \mathcal{F}\times \mathcal{F}\rightarrow[0,\infty)$ satisfies the following conditions for all $g,h,w\in\mathcal{F}$:

($\varsigma_{1}$):

$\varsigma(g,h)=0\Rightarrow g=h$;

($\varsigma_{2}$):

$\varsigma(g,h)=\varsigma(h,g)$;

($\varsigma_{3}$):

$\varsigma(g,h)\leq\varpi(g,w) \varsigma (g,w)+\varepsilon(w,h) \varsigma(w,h)$.

Then the pair $(\mathcal{F},\varsigma)$ is called a double controlled metric-like space $(DCMLS)$.

We denote double controlled metric-type spaces by $(DCMTS)$ and double controlled metric-like spaces by $(DCMLS)$.

Remark 2.5

Note that any $(DCMTS)$ is a $(DCMLS)$. However, the converse is not always true.

Example 2.6

Let $\mathcal{F}=\mathbb{R}^{+}$. Take $\varsigma:\mathcal{F} \times \mathcal{F} \to\mathbb{R}^{+}$ defined as

$$\varsigma(g,h)= \textstyle\begin{cases} 0 &\Rightarrow g=h,\\ \frac{1}{2} &\text{if $g= 0$ and $h=0$},\\ \frac{1}{g} &\text{if $g\geq1$ and $h\in[0,1)$},\\ \frac{1}{h} &\text{if $h\geq1$ and $g\in[0,1)$},\\ 1 &\textrm{otherwise}. \end{cases} $$

Consider the following $\varpi,\varepsilon: \mathcal{F}\times \mathcal{F}\rightarrow[1,\infty)$:

$$\varpi(g,h)= \textstyle\begin{cases} g &\text{if }g,h\geq1,\\ 1 &\text{otherwise}, \end{cases}\displaystyle \quad\mbox{and}\quad \varepsilon(g,h)= \textstyle\begin{cases} 1 &\text{if }g,h< 1,\\ \max\{g,h\} &\text{otherwise}. \end{cases} $$

It is not difficult to see that ($\varsigma_{1}$) and ($\varsigma_{2}$) are satisfied. Next, we show that condition ($\varsigma_{3}$) is satisfied.

Case 1: If $w=g$ or $w=h$, then ($\varsigma_{3}$) is satisfied.

Case 2: If $w\neq g$ and $w\neq h$, note that if $g=h$, then we are done. So, without loss of generality, we may assume that $g\neq h$. Thus $g\neq h\neq w$. It is not difficult to see that if ($g\geq1$ and $0\le h < 1$) or ($h\geq1$ and $0\le g < 1$), then ($\varsigma_{3}$) holds. Now we consider the following subcases:

Subcase 1: $g,h\geq1$.

If $w\geq1$, then we are done. Also, if $0\le w < 1$, then we get

$$1\leq\frac{1}{g}+h.\frac{1}{h}, $$

and hence $(\varsigma_{3})$ holds.

Subcase 2: $g,h< 1$.

If $0\le w < 1$, then we are done. On the other hand, if $w\geq1$, then we have

$$1\leq\frac{1}{w}+w.\frac{1}{w}, $$

and thus $(\varsigma_{3})$ is satisfied. Therefore $(\mathcal{F}, \varsigma)$ is a $(DCMLS)$.

Moreover,

$$\varsigma(0,0)\neq0, $$

and thus $(\mathcal{F}, \varsigma)$ is not a $(DCMTS)$.

Example 2.7

Let $\mathcal{F}=\{0,1,2\}$. Define ς by

$$\varsigma(0,0)=\varsigma(1,1)=0, \qquad\varsigma(2,2)=\frac{1}{10}, $$

and

$$\varsigma(0,1)=\varsigma(1,0)=1,\qquad\varsigma(0,2)=\varsigma (2,0)= \frac{1}{2},\qquad\varsigma(1,2)=\varsigma(2,1)=\frac{2}{5}. $$

Take $\varpi,\varepsilon: \mathcal{F}\times \mathcal{F}\rightarrow[1,\infty)$ to be symmetric and defined by

$$\varpi(0,0)=\varpi(1,1)=\varpi(2,2)=\varpi(0,2)=1, \qquad\varpi (1,2)= \frac{5}{8}, \qquad\varpi(0,1)=\frac{11}{10}, $$

and

$$\varepsilon(0,0)=\varepsilon(1,1)=\varepsilon(2,2)=1,\qquad\varepsilon (0,2)= \frac{3}{2}, \qquad\varepsilon(1,2)=\frac{5}{4}, \qquad \varepsilon (0,1)=\frac{11}{10}. $$

Note that $(\mathcal{F}, \varsigma)$ is a $(DCMLS)$. Also, we have;

$$\varsigma(2,2)=\frac{1}{10}\neq0. $$

Thus $(\mathcal{F}, \varsigma)$ is not a $(DCMTS)$.

Next, we present the topology of the controlled metric-like spaces.

Definition 2.8

Let $(F,\varsigma)$ be a $(DCMLS)$, and let $\{g_{n}\}_{n\ge0}$ be a sequence in F.

• (1) $\{g_{n}\}$ is convergent to g in F if and only if

  $$\lim_{n\rightarrow\infty}\varsigma(g_{n},g)=\varsigma(g,g). $$

  In this case, we write $\lim_{n \rightarrow\infty}{g_{n}=g}$.

• (2) $\{g_{n}\}$ is ς-Cauchy if and only if $\lim_{n,m\rightarrow\infty}\varsigma(g_{n},g_{m})$ exists and is finite.

• (3) $(F,\varsigma)$ is said to be complete if for each ς-Cauchy sequence $\{g_{n}\}$, there is $g\in F$ such that

  $$\lim_{n\rightarrow\infty}\varsigma(g_{n},g)=\varsigma(g,g)=\lim _{n,m\rightarrow\infty}\varsigma(g_{n},g_{m}). $$

Definition 2.9

Let $(F,\varsigma)$ be a $(DCMLS)$. For $g\in F$ and $\tau>0$:

• (i) An open ball $\mathbb{B}(g,\tau)$ in $(F,\varsigma)$ is

  $$\mathbb{B}(g,\tau)=\bigl\{ y\in F, \bigl\vert \varsigma(g,h)-\varsigma(g,g) \bigr\vert < \tau\bigr\} . $$

• (ii) The mapping $\aleph:F\rightarrow F$ is said to be continuous at $g\in F$ if for all $\varepsilon>0$, there exists $\delta>0$ such that $\zeta(\mathbb{B}(g,\delta))\subseteq\mathbb{B}(\aleph(g),\varepsilon )$. Thus if ℵ is continuous at g, then for any sequence $\{ g_{n}\}$ converging to g, we have $\lim_{n \rightarrow\infty}\aleph g_{n}=\aleph g$, that is,

  $$\lim_{n\rightarrow\infty}\varsigma(\aleph g_{n},\aleph g)= \varsigma (\aleph g,\aleph g). $$

3 Main results

In our first theorem, we prove the Banach contraction type theorem in $(DCMLS)$.

Theorem 3.1

Let$(\mathcal{F},\varsigma)$be a complete$(DCMLS)$defined by functions$\varpi,\varepsilon:\mathcal{F}^{2}\rightarrow[1,\infty)$. Let$\aleph :\mathcal{F}\rightarrow\mathcal{F}$be a mapping such that

$$ \varsigma(\aleph g,\aleph h)\leq k\varsigma(g,h) $$

(3.1)

for all$g,h\in\mathcal{F}$, where$k\in(0,1)$. For$g_{0}\in\mathcal {F}$, take$g_{n}=\aleph^{n}g_{0}$. Suppose that

$$ \sup_{m\geq1}\lim_{i\rightarrow\infty} \frac{\varpi (g_{i+1},g_{i+2})}{\varpi(g_{i},g_{i+1})}\varepsilon(g_{i+1},g_{m})< \frac {1}{k}. $$

(3.2)

Also, assume that for every$g\in\mathcal{F}$, we have

$$ \lim_{n\rightarrow\infty}\varpi(g,g_{n}) \quad\textit{and} \quad\lim_{n\rightarrow \infty}\varepsilon(g_{n},g)\quad \textit{exist and are finite}. $$

(3.3)

Then ℵ has a unique fixed point.

Proof

Let $\{g_{n}=\aleph^{n}g_{0}\}$ in $\mathcal{F}$ be a sequence that satisfies the conditions of our theorem. By using (3.1) we get

$$ \varsigma(g_{n},g_{n+1})\le k^{n}\varsigma(g_{0},g_{1})\quad\mbox{for all } n\geq0. $$

(3.4)

Let $n,m \in\mathbb{N}$ be such that $n< m$. Then

$$\begin{aligned} \varsigma(g_{n},g_{m})&\le\varpi(g_{n},g_{n+1}) \varsigma (g_{n},g_{n+1})+\varepsilon(g_{n+1},g_{m}) \varsigma(g_{n+1},g_{m}) \\ &\le\varpi(g_{n},g_{n+1})\varsigma(g_{n},g_{n+1})+ \varepsilon (g_{n+1},g_{m})\varpi(g_{n+1},g_{n+2}) \varsigma(g_{n+1},g_{n+2}) \\ &\quad+\varepsilon(g_{n+1},g_{m})\varepsilon(g_{n+2},g_{m}) \varsigma (g_{n+2},g_{m}) \\ &\le \varpi(g_{n},g_{n+1})\varsigma(g_{n},g_{n+1})+ \varepsilon (g_{n+1},g_{m})\varpi(g_{n+1},g_{n+2}) \varsigma(g_{n+1},g_{n+2}) \\ &\quad+\varepsilon(g_{n+1},g_{m})\varepsilon(g_{n+2},g_{m}) \varpi (g_{n+2},g_{n+3})\varsigma(g_{n+2},g_{n+3}) \\ &\quad+\varepsilon(g_{n+1},g_{m})\varepsilon(g_{n+2},g_{m}) \varepsilon (g_{n+3},g_{m})\varsigma(g_{n+3},g_{m}) \\ &\le\cdots \\ &\le\varpi(g_{n},g_{n+1})\varsigma(g_{n},g_{n+1})+ \sum_{i=n+1}^{m-2} \Biggl(\prod _{j=n+1}^{i}\varepsilon(g_{j},g_{m}) \Biggr)\varpi(g_{i},g_{i+1}) \varsigma(g_{i},g_{i+1}) \\ &\quad+\prod_{k=n+1}^{m-1} \varepsilon(g_{k},g_{m})\varsigma(g_{m-1},g_{m}) \\ &\le \varpi(g_{n},g_{n+1})k^{n} \varsigma(g_{0},g_{1})+\sum _{i=n+1}^{m-2} \Biggl(\prod _{j=n+1}^{i}\varepsilon(g_{j},g_{m}) \Biggr)\varpi(g_{i},g_{i+1}) k^{i} \varsigma(g_{0},g_{1}) \\ &\quad+\prod_{i=n+1}^{m-1} \varepsilon(g_{i},g_{m})k^{m-1}\varsigma (g_{0},g_{1}) \\ &\le \varpi(g_{n},g_{n+1})k^{n} \varsigma(g_{0},g_{1})+\sum _{i=n+1}^{m-2} \Biggl(\prod _{j=n+1}^{i}\varepsilon(g_{j},g_{m}) \Biggr)\varpi(g_{i},g_{i+1}) k^{i} \varsigma(g_{0},g_{1}) \\ &\quad+ \Biggl(\prod_{i=n+1}^{m-1} \varepsilon(g_{i},g_{m}) \Biggr)k^{m-1}\varpi (g_{m-1},g_{m})\varsigma(g_{0},g_{1}) \\ &= \varpi(g_{n},g_{n+1})k^{n} \varsigma(g_{0},g_{1})+\sum _{i=n+1}^{m-1} \Biggl(\prod _{j=n+1}^{i}\varepsilon(g_{j},g_{m}) \Biggr)\varpi(g_{i},g_{i+1}) k^{i} \varsigma(g_{0},g_{1}) \\ &\leq \varpi(g_{n},g_{n+1})k^{n} \varsigma(g_{0},g_{1})+\sum _{i=n+1}^{m-1} \Biggl(\prod _{j=0}^{i}\varepsilon(g_{j},g_{m}) \Biggr)\varpi (g_{i},g_{i+1}) k^{i} \varsigma(g_{0},g_{1}). \end{aligned}$$

Note that we are using the fact that $\varpi(g,h) \geq1$. Let

$$\varOmega_{p} = \sum_{i=0}^{p} \Biggl(\prod_{j=0}^{i}\varepsilon (g_{j},g_{m}) \Biggr)\varpi(g_{i},g_{i+1})k^{i}. $$

Then we have

$$ \varsigma(g_{n},g_{m})\leq \varsigma(g_{0},g_{1}) \bigl[ k^{n} \varpi (g_{n},g_{n+1})+(\varOmega_{m-1}- \varOmega_{n}) \bigr]. $$

(3.5)

By condition (3.2), using the ratio test, we see that $\lim_{n\rightarrow\infty}\varOmega_{n}$ exists, and hence the real sequence $\{\varOmega_{n}\}$ is ς-Cauchy. Finally, if we take the limit in inequality (3.5) as $n,m\rightarrow\infty$, we deduce that

$$ \lim_{n,m\rightarrow\infty}\varsigma(g_{n},g_{m})=0. $$

(3.6)

Hence the sequence $\{g_{n}\}$ is ς-Cauchy in $(\mathcal {F},\varsigma)$, which is a complete $(DCMLS)$, so $\{g_{n}\}$ converges to some $g\in\mathcal{F}$, that is,

$$ \lim_{n\rightarrow\infty}\varsigma(g_{n},g)= \varsigma(g,g)=\lim_{n,m\rightarrow\infty}\varsigma(g_{n},g_{m})=0. $$

(3.7)

Then $\varsigma(g,g)=0$. Next, we show that $\aleph g=g$. The triangle inequality of $DCMLS$ implies that

$$\varsigma(g,g_{n+1})\leq\varpi(g,g_{n})\varsigma(g, g_{n})+ \varepsilon (g_{n},g_{n+1}) \varsigma(g_{n},g_{n+1}). $$

Using (3.3) and (3.6), we deduce that

$$ \lim_{n\rightarrow\infty}\varsigma(g,g_{n+1})=0. $$

(3.8)

By the triangle inequality and (3.1) we have

$$\begin{aligned} \varsigma(g,\aleph g)&\leq\varpi(g,g_{n+1})\varsigma(g, g_{n+1})+ \varepsilon(g_{n+1},\aleph g) \varsigma(g_{n+1}, \aleph g) \\ &\le\varpi(g,g_{n+1})\varsigma(g, g_{n+1})+ k\varepsilon (g_{n+1},\aleph g)\varsigma(g_{n}, g). \end{aligned}$$

Taking the limit as $n\rightarrow\infty$, by (3.3) and (3.8) we deduce that $\varsigma(g,\aleph g)=0$, that is, $\aleph g=g$. Finally, assume that ℵ has two fixed points, say α and β. Then

$$\varsigma(\alpha,\beta)=\varsigma(\aleph\alpha,\aleph\beta)\le k \varsigma( \alpha,\beta)< \varsigma(\alpha,\beta), $$

which leads us to a contradiction. Therefore $\varsigma(\alpha,\beta )=0$, so $\alpha=\beta$. Hence ℵ has a unique fixed point. □

Remark 3.2

Note that condition (3.3) in Theorem 3.1 can be changed by the assumption that ℵ and the $(DCMLS)$ς are continuous. To see this, the continuity gives us that if $g_{n}\rightarrow u$, then $\aleph g_{n}\rightarrow\aleph u$, and hence we have

$$\lim_{n\rightarrow\infty} \varsigma(\aleph g_{n}, \aleph u)=0= \lim_{n\rightarrow\infty} \varsigma(\aleph g_{n+1}, \aleph u)= \varsigma (u,\aleph u), $$

and thus $\aleph u=u$.

Now we illustrate Theorem 3.1 by the following example.

Example 3.3

Consider $\mathcal{F}=\{0,1,2\}$. Let ς be symmetric and defined by

$$\begin{gathered} \varsigma(g,g)=0\quad\mbox{for } g\in\{0,1\}, \\ \varsigma(2,2)=\frac{1}{100},\end{gathered} $$

and

$$\varsigma(0,1)=1,\qquad\varsigma(0,2)=\frac{2}{5},\qquad\varsigma (1,2)= \frac{6}{25}. $$

Take $\varpi,\varepsilon: \mathcal{F}\times \mathcal{F}\rightarrow[1,\infty)$ to be symmetric and defined by

$$\begin{gathered} \varpi(0,0)=\varpi(1,1)=\varpi(2,2)=1,\qquad\varpi(0,2)=\frac{151}{100}, \\\varpi(1,2)=\frac{8}{5}, \qquad\varpi(0,1)=\frac{6}{5},\end{gathered} $$

and

$$\varepsilon(0,0)=\varepsilon(1,1)=\varepsilon(2,2)=1,\qquad\varepsilon (0,2)= \frac{8}{5}, \qquad\varepsilon(1,2)=\frac{33}{20}, \qquad \varepsilon(0,1)=\frac{6}{5}, $$

Now define the self-mapping ℵ on $\mathcal{F}$ as follows:

$$\aleph0=2 \quad\mbox{and}\quad\aleph1=\aleph2=1. $$

Choose $k=\frac{3}{5}$. Clearly, (3.1) holds. For any $g_{0}\in \mathcal{F}$, (3.2) holds, along with conditions of Theorem 3.1. Therefore the mapping ℵ admits a unique fixed point, which is $g=1$.

Definition 3.4

Let $\aleph:\mathcal{F} \longrightarrow\mathcal{F}$. For some $g_{0}\in \mathcal{F}$, consider $\textit{O}(g_{0})=\{g_{0},\aleph g_{0},\aleph ^{2}g_{0},\ldots\}$ to be the orbit of $g_{0}$. We say that a function $G:\mathcal{F}\longrightarrow\mathbb{R}$ is ℵ-orbitally lower semicontinuous at $w\in\mathcal{F}$ if for $\{g_{n}\}\subset\textit {O}(g_{0})$ such that $g_{n}\longrightarrow w$, we have $G(w)\leq \lim_{n\rightarrow\infty}\inf G(g_{n})$.

Inspired by [19], we are going to use Definition 3.4 to present a nice consequence of Theorem 3.1, which is a generalization of Theorem 1 in [22].

Corollary 3.5

Let$(\mathcal{F},\varsigma)$be the complete$(DCMLS)$defined by functions$\varpi,\varepsilon:\mathcal{F}^{2}\rightarrow[1,\infty)$. Let$\aleph :\mathcal{F}\rightarrow\mathcal{F}$, Let$g_{0}\in\mathcal{F}$and$0< k<1$be uch that

$$ \varsigma\bigl(\aleph w,\aleph^{2}w\bigr)\leq k\varsigma(w,\aleph w)\quad \textit{for each } w\in O(g_{0}). $$

(3.9)

Take$g_{n}=\aleph^{n}g_{0}$. Suppose that

$$ \sup_{m\geq1}\lim_{i\rightarrow\infty} \frac{\varpi (g_{i+1},g_{i+2})}{\varpi(g_{i},g_{i+1})}\varepsilon(g_{i+1},g_{m})< \frac{1}{k}. $$

(3.10)

Then$\lim_{n\rightarrow\infty}g_{n}= w \in\mathcal{F}$. Also, $\aleph w=w\Leftrightarrow g\mapsto\varsigma(g,\aleph g)$is ℵ-orbitally lower semicontinuous atw.

Next, we present the nonlinear case.

Theorem 3.6

Let$(\mathcal{F},\varsigma)$be a complete$(DCMLS)$defined by functions$\varpi,\varepsilon:\mathcal{F}^{2}\rightarrow[1,\infty)$. Consider a map$\aleph:\mathcal{F}\rightarrow\mathcal{F}$and assume that there exists a nondecreasing and continuous function$\phi:\mathbb {R}^{+}\rightarrow\mathbb{R}^{+}$such that

$$\begin{aligned}& \phi^{i}(g)\rightarrow0 \quad\textit{as } n\rightarrow\infty, g>0, \\& \varsigma(\aleph g,\aleph h)\leq\phi\bigl(\Delta(g,h)\bigr),\quad \Delta(g,h)=\max\bigl\{ \varsigma(g,h),\varsigma(g,\aleph g),\varsigma(h,\aleph h) \bigr\} \end{aligned}$$

(3.11)

for all$g,h\in\mathcal{F}$. Moreover, assume that for each$g_{0} \in\mathcal{F}$, we have

$$ \sup_{m\geq1}\lim_{i\rightarrow\infty} \frac{\varpi (g_{i+1},g_{i+2})}{\varpi(g_{i},g_{i+1})}\varepsilon(g_{i+1},g_{m}) \frac{\phi^{i+1}(\varsigma(g_{1},g_{0}))}{\phi^{i}(\varsigma(g_{1},g_{0}))}< 1, $$

(3.12)

where$g_{n}=\aleph^{n} g_{0}$, $n\in\mathbb{N}$. If the$(DCMLS)$ςand ℵ are continuous, then ℵ admits a unique fixed point$w \in\mathcal{F}$with$\aleph^{n} s\rightarrow w$for each$g \in\mathcal{F}$.

Proof

Let $\{g_{n}\}$ and $g_{0}$ be as in the hypothesis of the theorem. Assume that there exists $m\in\mathbb{N}$ such that $g_{m}=g_{m+1}=\aleph g_{m}$, which implies that $g_{m}$ is a fixed point. So we may assume that $g_{n+1}\neq g_{n}$ for each n. From condition (3.11) we have

$$ \varsigma(g_{n},g_{n+1})=\varsigma( \aleph g_{n},\aleph g_{n-1})\leq\phi \bigl( \Delta(g_{n-1},g_{n})\bigr), $$

(3.13)

where $\Delta(g_{n-1},g_{n})=\max\{\varsigma(g_{n-1},g_{n}), \varsigma (g_{n},g_{n+1})\}$. If for some n, we accept that $\Delta (g_{n-1},g_{n})=\varsigma(g_{n},g_{n+1})$, then by (3.13) and the fact that we have $\phi(t)< t$ for all $t>0$, we deduce that

$$ 0< \varsigma(g_{n},g_{n+1})\leq\phi \bigl(\varsigma(g_{n},g_{n+1})\bigr)< \varsigma (g_{n},g_{n+1}), $$

(3.14)

which is a contradiction. Thus, for all $n\in\mathbb{N}$, we obtain $\Delta(g_{n-1},g_{n})=\varsigma(g_{n-1},g_{n})$. It follows that $0<\varsigma(g_{n},g_{n+1})\leq\phi(\varsigma(g_{n-1},g_{n}))$. By using induction we easily see that for all $n\geq0$,

$$0< \varsigma(g_{n}, g_{n+1})\leq\phi^{n} \bigl(\varsigma(g_{0},g_{1})\bigr). $$

By the properties of ϕ we can easily deduce that

$$\varsigma(g_{n},g_{n+1})\rightarrow0\quad \text{as } n \rightarrow\infty. $$

Using the argument in the proof of Theorem 3.1, for $n,m \in\mathbb{N}$ such that $n< m$, we can easily deduce that

$$ \begin{aligned}[b] \varsigma(g_{n},g_{m})\leq{}& \varpi(g_{n},g_{n+1}) \phi^{n} \bigl(\varsigma (g_{0},g_{1})\bigr)\\&+ \sum_{i=n+1}^{m-1} \Biggl(\prod_{j=0}^{i}\varepsilon (g_{j},g_{m}) \Biggr)\varpi(g_{i},g_{i+1}) \phi^{i}\bigl(\varsigma(g_{0},g_{1})\bigr).\end{aligned} $$

(3.15)

By condition (3.12), using the ratio test, we can easily deduce that the sequence $\{g_{n}\}$ is ς-Cauchy. Since $(\mathcal{F},\varsigma)$ is a complete $(DCMLS)$, if $g_{n}\rightarrow w\in\mathcal{F}$ as $n\rightarrow\infty$, then $\lim_{n\rightarrow\infty} \varsigma(g_{n},w)=0$. Hence by Remark 3.2 we conclude that $\aleph w=w$. Finally, assume that w and u are two fixed points of ℵ such that $w\neq u$. From assumption (3.11) we have

$$\varsigma(w,u)=\varsigma(\aleph w, \aleph u)\leq\phi\bigl(\Delta(w,u)\bigr)= \phi\bigl(\varsigma(w,u)\bigr)< \varsigma(w,u), $$

which leads to a contradiction. Therefore $w=u$, as desired. □

Remark 3.7

Note that if $\phi(g)=kg$, $0< k<1$, then condition (3.11) in Theorem 3.6 becomes

$$ \varsigma(\aleph g,\aleph h)\leq k \max\bigl\{ \varsigma(g,h), \varsigma (g,\aleph g),\varsigma(h,\aleph h)\bigr\} . $$

(3.16)

Next, we prove the following result for mappings satisfying Kannan-type contraction.

Theorem 3.8

Let$(\mathcal{F},\varsigma)$be the complete$(DCMLS)$defined by functions$\varpi,\varepsilon:\mathcal{F}^{2}\rightarrow[1,\infty)$. Let$\aleph :\mathcal{F}\rightarrow\mathcal{F}$be a Kannan mapping defined as follows:

$$ \varsigma(\aleph g,\aleph h)\leq a \bigl[\varsigma(g,\aleph g)+\varsigma (h, \aleph h)\bigr] $$

(3.17)

for$g,h\in\mathcal{F}$, where$a\in(0,\frac{1}{2})$. For$g_{0}\in \mathcal{F}$, take$g_{n}=\aleph^{n}g_{0}$. Suppose that

$$ \sup_{m\geq1}\lim_{i\rightarrow\infty} \frac{\varpi (g_{i+1},g_{i+2})}{\varpi(g_{i},g_{i+1})}\varepsilon(g_{i+1},g_{m})< \frac{1-a}{a}. $$

(3.18)

Also, assume that for every$g\in\mathcal{F}$, we have

$$ \lim_{n\rightarrow\infty}\varpi(g,g_{n})\quad \textit{exists and is finite}, \textit{ and }\quad \lim_{n\rightarrow\infty} \varepsilon(g_{n},g)< \frac{1}{a} . $$

(3.19)

Then ℵ has a fixed point. Moreover, if for every fixed pointw, we have$\varsigma(w,w)=0$, then the fixed point is unique.

Proof

Consider the sequence $\{g_{n}=\aleph g_{n-1}\}$ in $\mathcal{F}$ satisfying hypotheses (3.18) and (3.19). From (3.17) we obtain

$$\begin{aligned} \varsigma(g_{n},g_{n+1}) = & \varsigma(\aleph g_{n-1},\aleph g_{n}) \\ \leq& a\bigl[\varsigma(g_{n-1},\aleph g_{n-1})+ \varsigma(g_{n},\aleph g_{n})\bigr] \\ = & a\bigl[\varsigma(g_{n-1},g_{n})+ \varsigma(g_{n},g_{n+1})\bigr]. \end{aligned}$$

Then $\varsigma(g_{n},g_{n+1}) \leq\frac{a}{1-a}\varsigma (g_{n-1},g_{n})$. By induction we get

$$ \varsigma(g_{n},g_{n+1}) \leq\biggl(\frac{a}{1-a} \biggr)^{n}\varsigma(g_{1},g_{0}),\quad \forall n \geq0 . $$

(3.20)

Next, we show that $\{g_{n}\}$ is a ς-Cauchy sequence. For two natural numbers $n< m$, we have

$$ \varsigma(g_{n},g_{m}) \leq \varpi(g_{n},g_{n+1}) \varsigma (g_{n},g_{n+1})+\varepsilon(g_{n+1},g_{m}) \varsigma(g_{n+1},g_{m}). $$

Similarly to the proof of Theorem 3.1, we get

$$\begin{aligned} \varsigma(g_{n},g_{m}) &\leq \varpi(g_{n},g_{n+1}) \varsigma (g_{n},g_{n+1})+\sum _{i=n+1}^{m-2} \Biggl(\prod _{j=n+1}^{i}\varepsilon (g_{j},g_{m}) \Biggr)\varpi(g_{i},g_{i+1}) \varsigma(g_{i},g_{i+1}) \\ & \quad+ \prod_{k=n+1}^{m-1} \varepsilon(g_{k},g_{m})\varsigma (g_{m-1},g_{m}) \\ & \leq \varpi(g_{n},g_{n+1}) \biggl(\frac{a}{1-a} \biggr)^{n}\varsigma (g_{0},g_{1})\\&\quad+\sum _{i=n+1}^{m-2} \Biggl(\prod _{j=n+1}^{i}\varepsilon (g_{j},g_{m}) \Biggr)\varpi(g_{i},g_{i+1}) \biggl(\frac{a}{1-a} \biggr)^{i}\varsigma(g_{0},g_{1}) \\ &\quad+\prod_{i=n+1}^{m-1} \varepsilon(g_{i},g_{m}) \biggl(\frac {a}{1-a} \biggr)^{m-1}\varsigma(g_{0},g_{1}). \end{aligned}$$

Since $0\leq a <\frac{1}{2}$, we have $0<\frac{a}{1-a}<1$, and similarly to the argument in the proof of Theorem 3.1, we obtain that $\{g_{n}\}$ is a ς-Cauchy sequence in the complete $(DCMLS)$$(\mathcal{F},\varsigma)$. Thus $\{g_{n}\}$ converges to some $w\in\mathcal{F}$. Suppose that $\aleph w\neq w$. Then

$$\begin{aligned} 0< \varsigma(w,\aleph w) \leq& \varpi(w,g_{n+1}) \varsigma (w,g_{n+1})+\varepsilon(g_{n+1}, \aleph w) \varsigma(g_{n+1}, \aleph w) \\ \leq& \varpi(w,g_{n+1})\varsigma(w,g_{n+1})+ \varepsilon(g_{n+1}, \aleph w)\bigl[a \varsigma(g_{n},g_{n+1})+a \varsigma(w,\aleph w)\bigr]. \end{aligned}$$

Taking the limit in both sides of these inequalities and using (3.19), we deduce that $0<\varsigma(w,\aleph w)< \varsigma(w,\aleph w)$, which is a contradiction. Hence $\aleph w=w$. Now assume that for every fixed point w, we have $\varsigma(w,w)=0$ and suppose that ℵ has more than one fixed point, say w and λ. Then

$$\begin{aligned} \varsigma(w,\lambda)=\varsigma(\aleph w,\aleph\lambda) \leq& a \bigl[ \varsigma(w,\aleph w)+\varsigma(\lambda,\aleph\lambda)\bigr] \\ = & a \bigl[\varsigma(w,w)+\varsigma(\lambda,\lambda)\bigr]=0. \end{aligned}$$

Thereby $w=\lambda$, as required. □

4 Conclusion

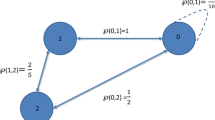
In this section, we present an open question on $(DCMLS)$ endowed with a graph. First, Fig. 1 is an example of a $(DCMLS)$ endowed with a graph.

Figure 1

$(DCMLS)$ as in Example 2.7

Let ς be a $(DCMLS)$ on a set $\mathcal{F}\neq\emptyset$. Let Δ be the diagonal of $\mathcal{F}^{2}$. A graph G is defined by the pair $(V,E)$, where V is a set of vertices coinciding with $\mathcal{F}$, and E is the set of its edges with $\Delta\subset E$. From now on, assume that G has no parallel edges.

Definition 4.1

Let t and g be two vertices in a graph G. A path in G from t to g of length q ($q\in\mathbb{N}\cup\{0\}$) is a sequence $(k_{i})_{i=0}^{q}$ of $q+1$ distinct vertices such that $k_{0}=t$, $k_{n}=g$, and $(k_{i},k_{i+1})\in E(G)$ for $i=1,2,\ldots,q$.

The graph G may be converted to a weighted graph by assigning to each edge the distance given by the $(DCMLS)$ between its vertices.

Notation

Let $\mathcal{F}^{\aleph}=\{x\in\mathcal{F}/ (x,\aleph x)\in E(G) \mbox{ or } (\aleph x,x)\in E(G)\}$.

Definition 4.2

Let $(\mathcal{F},\varsigma)$ be a complete $(DCMLS)$ endowed with a graph G. The mapping $\aleph:\mathcal{F}\rightarrow\mathcal {F}$ is said to be a $G_{\phi}$-contraction if

• $$ \mbox{for all } t,g\in\mathcal{F},\quad (t,g)\in E(G) \Longrightarrow (\aleph t, \aleph g)\in E(G); $$

  (4.1)

• there is a function $\phi:\mathbb{R^{+}}\longrightarrow\mathbb {R^{+}}$ such that

  $$ \xi\bigl(\aleph t,\aleph^{2}t\bigr)\leq\phi\bigl(\xi(t,\aleph t) \bigr),\quad \forall t\in\mathcal {F}^{\aleph}, $$

  (4.2)

  where ϕ is a nondecreasing function, and $\{\phi^{n}(t)\}_{n\in \mathbb{N}}$ converges to 0 for each $t>0$.

Definition 4.3

The mapping $\aleph:\mathcal{F}\longrightarrow\mathcal{F}$ is called orbitally G-continuous if for all $a,b\in X$ and any positive sequence $\{g_{n}\}_{n\in\mathbb{N}}$,

$$ \aleph^{g_{n}}a\longrightarrow b, \bigl(\aleph^{g_{n}}a, \aleph^{g_{n+1}}a\bigr)\in E(G) \Longrightarrow\aleph\bigl( \aleph^{g_{n}}a\bigr)\longrightarrow\aleph b \quad\mbox{as } n\rightarrow \infty. $$

Conjecture 4.4

Let$(\mathcal{F},\varsigma, G)$be a complete$(DCMLS)$with a graphG. Let$\aleph:\mathcal{F}\rightarrow\mathcal{F}$be a$G_{\phi }$-contraction that is orbitallyG-continuous. Suppose the following property holds:

$(P)$:

for any$\{t_{n}\}_{n\in\mathbb{N}}$in$\mathcal{F}$, if$t_{n}\longrightarrow t$and$(t_{n},t_{n+1})\in E(G)$, then there is a subsequence$\{t_{k_{n}}\}_{n\in\mathbb{N}}$with$(t_{k_{n}},t)\in E(G)$.

Moreover, suppose that, for each$g\in\mathcal{F}$,

$$ \sup_{m\geq1}\lim_{i\rightarrow\infty} \frac{\varpi (g_{i+1},g_{i+2})}{\varpi(g_{i},g_{i+1})}\varepsilon(g_{i+1},g_{m})< M;\quad M>1. $$

Also, assume that for every$g\in\mathcal{F}$, we have that

$$ \lim_{n\rightarrow\infty}\varpi(g,g_{n}) \quad\textit{and} \quad\lim _{n\rightarrow \infty}\varepsilon(g_{n},g) \quad\textit{exist and are finite}. $$

Then the restriction of$\aleph_{|[g]_{\tilde{G}}}$to$[g]_{\tilde {G}}$possesses a fixed point.