Abstract
In this paper, we establish that every controlled metric space \((X, d_{\alpha })\) induces a Hausdorff controlled metric \((\textit{H}_{\alpha }, \textit{CLD}(X))\) on the class of closed subsets of X which is also complete if \((X, d_{\alpha })\) is complete. Furthermore, we define multivalued almost F-contractions on Hausdorff controlled metric spaces and prove some fixed point results.
Similar content being viewed by others
1 Introduction and preliminaries
We denote by \(\textit{P}(X)\), \(\textit{CLB}( X)\), \(\textit{CLD}(X)\) and by \(\textit{K}(X)\) the class of all nonempty subsets of X, the class of all nonempty closed and bounded subsets of X, the class of all nonempty closed subsets of X, and the class of all nonempty compact subsets of X. For \(\mathcal{A}, \mathcal{B} \in \textit{CLB}( X)\), let
where \(d(a, \mathcal{B}) = \inf \{d( a, b) : b\in \mathcal{B}\}\). Then H is a metric on \(\textit{CLB}( X)\), which is called the Pompeiu–Hausdorff metric induced by d. In 1969, Nadler [1] proved that every multivalued contraction on a complete metric space has a fixed point. Since then, many researchers extended it multi-directionally (see, for example [2–14]). Berinde and Berinde in [15] introduced the idea of multivalued almost contractions (originally called multivalued \((\delta , {L})\)-weak contractions) and proved the following fixed point theorem.
Theorem 1.1
([15])
Let \(\mathit{{T}} : X\rightarrow \textit{CLB}(X)\)be a multivalued almost contraction mapping on a complete metric space \((X, \textit{d})\), that is, there exist two constants \(0 < \mathcal{ \delta } < 1\)and \({L} \geq 0\)such that, for all \({x}, {y} \in X\), it satisfies
ThenThas a fixed point.
Wardowski [16] extended the Banach contraction principle by introducing F-contractions and established fixed point theorems in metric spaces as follows.
Definition 1.1
([16])
Let us consider a function \(\mathit{{F}} : (0, \infty ) \rightarrow \mathbb{R}\) and the following axioms:
- (F1)
F is strictly non-decreasing;
- (F2)
for each sequence \(\{ a_{n}\} \subset (0, \infty )\) of positive real numbers, \(\lim_{n \rightarrow \infty } a_{n} = 0\) if and only if \(\lim_{n \rightarrow \infty } \mathit{{F}}(a_{n}) = -\infty \);
- (F3)
for each sequence \(\{ a_{n}\} \subset (0, \infty )\) of positive real numbers, \(\lim_{n \rightarrow \infty } a_{n} = 0\), there exists \(l \in (0, 1)\) such that \(\lim_{n \rightarrow \infty } ( a_{n})^{l} \mathit{{F}}(a_{n}) = 0\);
- (F4)
\(\mathit{{F}}(\inf \mathcal{A}) = \inf \mathit{{F}}(\mathcal{A})\) for all \(\mathcal{A} \subset (0, \infty )\) with \(\inf \mathcal{A} > 0\).
We denote by \(\mathcal{F}\) the family of all functions F satisfying (F1)–(F3), and by \(\mathcal{F}^{*}\) the family of all functions F satisfying (F1)–(F4).
Example 1.1
([16])
Let \(\mathit{{F}} : (0, \infty ) \rightarrow \mathbb{R}\) be defined by
- (i)
\(\mathit{{F}}(\alpha ) = \ln \alpha \);
- (ii)
\(\mathit{{F}}(\alpha ) = \alpha + \ln \alpha \).
Clearly, F in (i) and (ii) satisfies (F1)–(F4).
Definition 1.2
([16])
A mapping \(\mathit{{T}} : X\rightarrow X\) on a metric space \(( X, d)\) is called F-contraction, if \(\mathit{{F}} \in \mathcal{F}\) and there exists \(\mathcal{\tau } > 0\) such that
for all \({x}, {y} \in X\) with \(d({x}, {y}) > 0\).
If we take \(\mathit{{F}}(\alpha ) = \ln \alpha \) in (2), we obtain
Clearly for \({x}, {y} \in X\) such that \(\mathit{{T}} {x} = \mathit{{T}} {y}\), the inequality \(d(\mathit{{T}} {x}, \mathit{{T}} {y}) \leq e^{-\mathcal{\tau }} d({x}, {y})\) also holds. Thus, T is an ordinary contraction with contractive constant \(\textit{c} = e^{-\mathcal{ \tau }}\), but its converse is not true in general.
By combining the ideas of Wardowski and Nadler, Altun et al. [17] introduced the idea of multivalued F-contractions and obtained some fixed point results for this type of mappings on complete metric spaces.
Definition 1.3
([17])
Let \(\mathit{{T}} : X\rightarrow \textit{CLB}(X)\) be a multivalued mapping on a metric space \((X, d)\). Then T is called a multivalued F-contraction, if \(\mathit{{F}} \in \mathcal{F}\) and there exists \(\mathcal{\tau } > 0\) such that
for all \({x}, {y} \in X\) with \(\textit{H}({x}, {y}) > 0\).
By putting \(\mathit{{F}}(a) = \ln a\), then every multivalued contraction in the sense of Nadler is also a multivalued F-contraction.
Theorem 1.2
([17])
Let \(\mathit{{T}} : X\rightarrow \textit{K}( X)\)be a multivaluedF-contraction on a complete metric space \((X, d)\). ThenThas a fixed point inX.
Theorem 1.3
([17])
Let \(\mathit{{T}} : X\rightarrow \textit{CLB}(X)\)be a multivaluedF-contraction on a complete metric space \((X, d)\). If \(\mathit{{F}} \in \mathcal{F}^{*}\), thenThas a fixed point inX.
Altun et al. [18] established the concept of multivalued almost F-contractions and proved some fixed point results as follows.
Definition 1.4
([18])
A multivalued mapping \(\mathit{{T}} : X\rightarrow \textit{CLB}(X)\) on a metric space \((X, d)\) is called a multivalued almost F-contraction, if \(\mathit{{F}} \in \mathcal{F}\) and there exist two constants \(\mathcal{\tau } > 0\) and \(\gamma \geq 0\) such that
for all \({x}, {y} \in X\) with \(\textit{H}({x}, {y}) > 0\).
By putting \(\mathit{{F}}(a) = \ln a\), then every multivalued almost contraction (1) is a multivalued almost F-contraction.
Theorem 1.4
([18])
Let \(\mathit{{T}} : X\rightarrow \textit{CLB}(X)\)be a multivalued almostF-contraction on a complete metric space \((X, d)\). If \(\mathit{{F}} \in \mathcal{F} ^{*}\), thenThas a fixed point inX.
Remark 1.1
Theorem 1.4 generalized Theorem 1.1 and Theorem 1.3, because
- (i)
If we take \(\mathit{{F}}( a) = \ln a\), \(\mathcal{\tau } = - \ln \mathcal{\delta }\) and \(\gamma = \frac{1}{\mathcal{\delta }}\), where \(\mathcal{\delta } \in (0, 1)\) in equation (5). Then we get equation (1).
- (ii)
If we take \(\gamma = 0\) in equation (5), we get equation (4).
In recent times, Kamran et al. in [19] established the idea of extended b-metric spaces, which generalized b-metric spaces (see [20, 21]) simply by replacing a constant s by a function depending on the left hand side of the triangle inequality.
Definition 1.5
([19])
Let X be a nonempty set and \(\mathcal{ \theta } : X\times X\rightarrow [1, \infty )\). Then a mapping \(d_{\mathcal{\theta }} : X\times X\rightarrow [0, \infty )\) is called an extended b-metric, if for all \({x}, {y}, {z} \in X\), it satisfies the following axioms:
- (i)
\(d_{\mathcal{\theta }}({x}, {y}) = 0\) iff \({x} = {y}\),
- (ii)
\(d_{\mathcal{\theta }}({x}, {y}) = d_{\mathcal{\theta }}({y}, {x})\),
- (iii)
\(d_{\mathcal{\theta }}({x}, {z}) \leq \mathrm{\mathcal{\theta }}({x}, {z})[d_{\mathcal{ \theta }}({x}, {y}) + d_{\mathcal{\theta }}({y}, {z})]\).
The pair \((X, d_{\mathcal{\theta }})\) is called an extended b-metric space.
Since then, many authors proved several fixed point results in the context of extended b-metric spaces; see [22–31]. In [32], Mlaiki et al. introduced the concept of controlled type metric spaces as a generalization of b-metric spaces, which is different from extended b-metrics space and is very useful to prove existence and uniqueness theorems for different types of integral and differential equations.
Definition 1.6
([32])
Let X be a nonempty set and \(\alpha : X\times X\rightarrow [1, \infty )\). Then a mapping \(d_{\alpha } : X\times X\rightarrow [0, \infty )\) is called a controlled metric, if for all \({x}, {y}, {z} \in X\), it satisfies the following axioms:
- (i)
\(d_{\alpha }({x}, {y}) = 0\) iff \({x} = {y}\),
- (ii)
\(d_{\alpha }({x}, {y}) = d_{\alpha }({y}, {x})\),
- (iii)
\(d_{\alpha }({x}, {z}) \leq \alpha ({x}, {y})d_{\alpha }( {x}, {y}) + \alpha ({y}, {z}) d _{\alpha }({y}, {z})\).
The pair \((X, d_{\alpha })\) is called a controlled metric space.
Remark 1.2
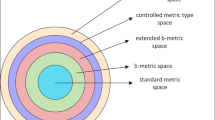
Every b-metric space is a controlled metric space, if we take \(\alpha ({x}, {y}) = s \geq 1\) for all \({x}, {y} \in X\). Generally, a controlled metric space is not an extended b-metric space [32], if we take same functions \(\alpha = \mathcal{\theta }\) as follows.
Example 1.2
([32])
Let \(X= \{1, 2, \ldots \}\). Define \(d_{\alpha } : X\times X\rightarrow [0, \infty )\) as:
Hence \((X, d_{\alpha })\) is a controlled metric space, where \(\alpha : X\times X\rightarrow [1, \infty )\) is defined as:
Clearly, \(d_{\alpha }\) is not an extended b-metric for the same function \(\alpha = \mathcal{\theta }\).
In this paper, we define a generalized Hausdorff metric on the class of nonempty closed subsets of controlled metric spaces. Also we prove that if \((X, d_{\alpha })\) is complete, then \((\textit{H}_{\alpha }, \textit{CLD}(X))\) is complete, too. Moreover, we define multivalued almost F-contractions on controlled metric spaces and prove some fixed point results, which generalize many pre-existing results in the literature.
2 Main results
We denote by \(\alpha ({x}, \mathcal{A}) = \inf_{a\in \mathcal{A}} \alpha ( {x}, a)\), and \(d_{\alpha }( {x}, \mathcal{A}) = \inf_{a\in \mathcal{A}} d_{\alpha }({x}, a)\), for \(\mathcal{A} \subset X\).
Lemma 2.1
Let \((X, d_{\alpha })\)be a controlled metric space. Then
for all \({x}_{1}\), \({x}_{2} \in X\)and \(a\in \mathcal{A} \subset X\), where \(\alpha ({x}_{2}, \mathcal{A}) = \inf_{a\in \mathcal{A}}\alpha ( {x}_{2}, a)\).
Proof
From axiom of definition, we have
By taking infimum of both sides over \(\mathcal{A}\), we get
Since \(\alpha ({x}_{2}, \mathcal{A}) = \inf_{a\in \mathcal{A}}\alpha ( {x}_{2}, a)\),
□
Now we will introduce the Pompeiu–Hausdorff metric.
Definition 2.1
Let \((X, d_{\alpha })\) be a controlled metric space. Then the function \(\textit{H}_{\alpha } : \textit{CLD}(X) \times \textit{CLD}(X) \rightarrow [0, \infty )\) is defined by
where \(\mathcal{A}, \mathcal{B} \in \textit{CLD}(X)\).
Lemma 2.2
For all \(\mathcal{A}, \mathcal{B}, \mathcal{C} \subset \textit{CLD}( X)\), we have
Proof
Assume that \(\textit{H}_{\alpha }(\mathcal{A}, \mathcal{B})\) and \(\textit{H}_{\alpha }(\mathcal{B}, \mathcal{C})\) are finite. From Lemma 2.1 for \(a\in \mathcal{A}\), \(b\in \mathcal{B}\), we have
As \(d_{\alpha }(b, \mathcal{C}) \leq \textit{H}_{\alpha }(\mathcal{B}, \mathcal{C})\), therefore we have
Hence by taking supremum over \(a\in \mathcal{A}\), we get
Analogously,
So
Therefore, by Definition 2.1, we get
Moreover, if \(\textit{H}_{\alpha }(\mathcal{A}, \mathcal{B})\) or \(\textit{H}_{\alpha }(\mathcal{B}, \mathcal{C})\) is infinite, the condition is obvious. □
Theorem 2.1
Let \((X, d_{\alpha })\)be a controlled metric space, then the function \(\textit{H}_{\alpha } : \textit{CLD}(X) \times \textit{CLD}( X) \rightarrow [0, \infty ]\)is a generalized controlled metric space in \(\textit{CLD}(X)\).
Proof
Let \(\textit{H}_{\alpha }(\mathcal{A}, \mathcal{B}) = 0\), for \(\mathcal{A}, \mathcal{B} \in \textit{CLD}(X)\). This implies
Then \(d_{\alpha }(a, \mathcal{B}) = 0\) for all \(a\in \mathcal{A}\), hence \(a\in \mathcal{B}\), i.e., \(\mathcal{A} \subset \mathcal{B}\). In the same way, we see that \(\mathcal{B} \subset \mathcal{A}\) and consequently \(\mathcal{A} = \mathcal{B}\). Conversely, if \(\mathcal{A} = \mathcal{B}\), then \(\textit{H}_{\alpha }(\mathcal{A}, \mathcal{B}) = 0\). Of course \(\textit{H}_{\alpha }( \mathcal{A}, \mathcal{B}) = \textit{H}_{\alpha }( \mathcal{B}, \mathcal{A})\) for all \(\mathcal{A}, \mathcal{B} \in \textit{CLD}(X)\). Finally, in view of Lemma 2.2, the proof is complete. □
Definition 2.2
\(a\in \bar{\mathcal{A}}\), where \(\bar{\mathcal{A}}\) is the closure of a set \(\mathcal{A} \subset X\), if and only if there exists a sequence \(\{a_{n}\}\) in \(\mathcal{A}\) such that \(a= \lim_{n \rightarrow \infty } a_{n}\), for \(n = 0, 1, 2, \ldots \) .
Denote for \(\varepsilon > 0\) and \(\mathcal{A} \subset X\),
Lemma 2.3
If \({x} \in \overline{\mathcal{A}_{\varepsilon }}\), then \(d_{\alpha }({x}, \mathcal{A}) \leq \lim_{n \rightarrow \infty } \alpha ({x}_{n}, \mathcal{A})\varepsilon \), where
Proof
Let \({x} \in \overline{\mathcal{A}_{\varepsilon }}\), then there exists a sequence \(\{{x}_{n}\}\) in \(\mathcal{A}_{\varepsilon }\) such that \(\lim_{n \rightarrow \infty }{x}_{n} = {x}\), for \(n = 0, 1, 2, \ldots \) . From Lemma 2.1, we have
By letting \(n \rightarrow \infty \) in the above inequality, we get
It proves the lemma. □
Definition 2.3
The upper topological limit of a sequence \(\{\mathcal{A}_{l}\}\), for \(l = 1, 2, \ldots \) in controlled metric space X is denoted by \(\overline{{Lt}}\mathcal{A}_{l}\) determined by
Theorem 2.2
A point \(a\in \overline{{Lt}}\mathcal{A} _{l}\), if and only if there exists a subsequence \(\{a_{n_{l}}\} \subset \mathcal{A}\)such that \(\lim_{l \rightarrow \infty } a_{n_{l}} = a\)and \(a_{n_{l}} \in \mathcal{A}_{n_{l}}\), for \(l = 1, 2, 3, \ldots \) .
Proof
First, let us suppose that \(a\in \overline{ {Lt}}\mathcal{A}_{l}\), then there exists a subsequence \(\{\mathcal{A}_{n_{l}}\}\) of \(\mathcal{A}_{l}\) such that \(\lim_{l \rightarrow \infty }d_{\alpha }(a, \mathcal{A}_{n_{l}}) = 0\). Hence for every l there exists a strictly increasing sequence of positive integers \(\{p_{l}\}\) with
Therefore, we can find a sequence \(\{a_{n_{l}}\}\) of points such that \(a_{n_{l}} \in \mathcal{A}_{n_{l}}\) and \(d_{\alpha }(a, a_{n_{l}}) < \frac{1}{l}\), for \(p_{l} \leq n < p_{l + 1}\). Hence \(\lim_{l \rightarrow \infty }a_{n_{l}} = a\).
Conversely, let us assume that \(a_{n_{l}} \rightarrow a\) and \(a_{n_{l}} \in \mathcal{A} _{n_{l}}\), \(l = 1, 2, 3, \ldots \) . Hence
and \(\lim_{l \rightarrow \infty }\inf d_{\alpha }( a, \mathcal{A}_{l}) = 0\). This implies that \(a\in \overline{{Lt}}\mathcal{A}_{l}\). □
Theorem 2.3
\(L = \overline{{Lt}}\mathcal{A}_{l}\)is closed.
Proof
Suppose that x is a limit point of L. Then there exists a sequence \({x}_{m} \in L - \{{x}\}\) that converges to x. By Theorem 2.2 for \({x} _{m} \in L\), there exists a subsequence \(\{{x}_{m_{l}}\} \subset \mathcal{A}\) such that \(\lim_{l \rightarrow \infty } {x}_{m_{l}} = {x}_{l}\) and \({x}_{m_{l}} \in \mathcal{A}_{m_{l}}\), for \(l = 1, 2, 3, \ldots \) . Now by the triangular inequality, we have
Clearly \(\lim_{l \rightarrow \infty }{x}_{m_{l}} = {x}\). It follows that \(\{{x}_{m_{l}}\}\) converges to x and \({x}_{m_{l}} \in \mathcal{A}_{m_{l}}\), for \(l = 1, 2, 3, \ldots \) . Therefore, by Theorem 2.2, \({x} \in L\). Hence L is closed. □
Corollary 2.1
Proof
First, let us assume that \({x} \in \overline{{Lt}} \mathcal{A}_{l}\), then there exists \(\{{x}_{n_{l}}\} \subset \mathcal{A}\) such that \(\lim_{l \rightarrow \infty }{x}_{n_{l}} = {x}\) and \({x}_{n_{l}} \in \mathcal{A}_{n_{l}}\), for \(l = 1, 2, 3, \ldots \) . Hence for every p
This implies that
Conversely let us assume that, for every p, \({x} \in \overline{ \bigcup_{n = 0}^{\infty }\mathcal{A}_{p + n}}\). Then there is a sequence \(\{{x}_{n_{l}}^{p}\} \subset \bigcup_{n = 0}^{\infty } \mathcal{A}_{p + n}\) such that \({x}_{n_{l}^{p}} \rightarrow {x}\) as \(l \rightarrow \infty \) for every natural. Let there exists \({x}_{1} = {x}_{n_{1}}^{1}\) such that \({x}_{n_{1}}^{1} \in \mathcal{A}_{p_{1}}\) and \(d_{\alpha }({x}_{n_{1}}^{1}, {x}) < 1\). Similarly, let \({x}_{2} = {x}_{n_{2}}^{l_{1} + 1}\) such that \(p_{2} > p_{1}\) and \(d_{\alpha }({x}_{n_{2}}^{l_{1} + 1}, {x}) < \frac{1}{2}\), \({x}_{n_{2}}^{l_{1} + 1} \in \mathcal{A}_{p_{2}}\). By continuing this process, we have \({x}_{l + 1} = {x}_{n_{l + 1}}^{l_{l} + 1}\) such that \(d_{\alpha }({x}_{n_{l + 1}}^{l_{l} + 1}, {x}) < \frac{1}{l + 1}\) and \({x}_{n_{l + 1}}^{l_{l} + 1} \in \mathcal{A}_{p_{l + 1}}\), \(p_{l} < p_{l + 1}\). Thus, we have \({x}_{l} \rightarrow {x}\) as \(l \rightarrow \infty \) and \({x}_{l} \in \mathcal{A}_{l}\) for \(l = 1, 2, 3, \ldots \) . Hence by Theorem 2.2, \({x} \in \overline{{Lt}} \mathcal{A}_{l}\). It completes the proof. □
Corollary 2.2
Proof
Let us assume that \(a\in \overline{\overline{ {Lt}}\mathcal{A}_{l}}\), then there is a sequence \(a_{n} \in \overline{{Lt}}\mathcal{A}_{l}\) for \(n = 1, 2, 3, \ldots \) such that \(a_{n} \rightarrow a\) as \(n \rightarrow \infty \). Consequently, there exists an integer \(p_{l_{1}}\) such that \(a_{l_{1}} \in \mathcal{A}_{l_{1}}\) and \(d_{\alpha }( a_{l_{1}}, a_{1}) < 1\). Similarly, there exists an integer \(p_{l_{2}} > p_{l_{1}}\) such that \(d_{\alpha }(a_{l_{2}}, a_{2}) < \frac{1}{2}\). Continuing this process, we can find an increasing sequence \(\{p_{l_{n}}\}\) of integers with \(a_{l_{n}} \in \mathcal{A}_{l_{n}}\) for \(n = 1, 2, 3, \ldots \) such that
Thus, by the triangle inequality, we get
Note that, as we take n to infinity, the distance between \(\{a_{l_{n}}\}\) and a converges to zero, so it follows that \(\{a_{l_{n}}\}\) converges to a. Hence, by Theorem 2.2, \(a\in \overline{{Lt}}\mathcal{A}_{l}\). It follows that
Conversely, let us assume that \(a\in \overline{ {Lt}}\mathcal{A}_{l}\), then, in a similar way,
From Eqs. (7) and (8), we have
The remaining part of the theorem can be verified by the similar way. □
Theorem 2.4
If \((X, d_{\alpha })\)be a complete controlled metric space with \(\lim_{n, m \rightarrow \infty }\alpha ({x}_{n}, {x}_{m})\kappa < 1\), for all \({x}_{n}, {x}_{m} \in X\), where \(\kappa \geq 1\). Then \((\textit{CLD}( X), H_{\alpha })\)is complete.
Proof
Let \(\{\mathcal{A}_{n}\}\), \(n = 1, 2, \ldots \) be a Cauchy sequence in \(\textit{CLD}( X)\). Then, by the definition, for each \(\varepsilon > 0\), there exists a positive integer \(N \in \mathbb{N}\) such that
Let \(\mathcal{A} = \overline{lt}\mathcal{A}_{n}\). We will prove that \(\mathcal{A} \in \textit{CLD}(X)\) and \(\mathcal{A} _{n} \rightarrow \mathcal{A}\). From Theorem 2.3, \(\mathcal{A} \in \textit{CLD}(X)\). Next, we will show that \(\{\mathcal{A}_{n}\}\) converges to \(\mathcal{A}\), i.e. there exists a positive integer N such that \(\textit{H}_{\alpha }( \mathcal{A}_{n}, \mathcal{A}) < \varepsilon \) for all \(n \geq N\). By the triangle inequality for all \(n, m \geq N\),
For \(n, m \geq N\), we have from (9)
Now, we will prove that
For this purpose, we will show the following inequalities:
From (9), we get
Next from Corollary 2.1, we have
hence from Lemma 2.3, we get, for \(a^{*} \in \mathcal{A}\),
Thus, condition (12) is fulfilled.
Now, we have to prove (11). Since \(\{\mathcal{A}_{n}\}\) is a Cauchy sequence in \(\textit{CLD}(X)\), we can find a strictly increasing sequence of positive integers \(\{n_{r}\} = \{\varepsilon l^{-r}\}\) for \(r = 1, 2, 3, \ldots \) such that \(n_{r} > N\), where \(N \in \mathbb{N}\) and \(\textit{H}_{\alpha }(\mathcal{A}_{n}, \mathcal{A}_{m}) < \varepsilon l^{-r}\), for all \(n, m \geq n_{r}\). Take arbitrary \(a_{m} \in \mathcal{A}_{m}\), where \(a_{m} = a_{n_{0}}\). Since \(\textit{H}_{\alpha }( \mathcal{A}_{n}, \mathcal{A}_{n_{0}}) < \varepsilon \), for \(n > n_{0}\), there exists \(a_{n_{1}} \in \mathcal{A}_{n_{1}}\) such that \(d_{\alpha }(a_{n_{0}}, a_{n_{1}}) < \varepsilon \), for \(n = n_{1} > n_{0}\). Similarly, \(\textit{H}_{\alpha }(\mathcal{A}_{n}, \mathcal{A}_{n_{1}}) < \frac{\varepsilon }{l}\), so there exists \(a_{n_{2}} \in \mathcal{A}_{n_{2}}\) such that \(d_{\alpha }(a_{n_{1}}, a_{n_{2}}) < \frac{\varepsilon }{l}\), for \(n = n_{2} > n_{1}\). By continuing this process, we can form a sequence \(\{a_{n_{r}}\}\) with \(a_{n_{r}} \in \mathcal{A}_{n_{r}}\), for \(r = 0, 1, 2, \ldots \) and
Next, we will verify that \(\{a_{n_{r}}\}\) is a Cauchy sequence, from the triangle inequality, we have
From Eq. (13), we have
As \(\lim_{n, m \rightarrow \infty } \alpha ({x}_{n}, {x}_{m})\kappa < 1\), for all \({x}_{n}, {x}_{m} \in X\). Thus the series
converges by the ratio test. By taking the limit \(r \rightarrow \infty \) in Eq. (14), we get
Hence, we conclude that \(\{a_{n _{r}}\}\) is a Cauchy sequence. Since \((X, d_{\alpha })\) is complete, there exists \(a_{*} \in X\) such that \(a_{n_{r}} \rightarrow a_{*} \in X\), and clearly \(a_{*} \in \mathcal{A}\). Again, by the triangle inequality, we have
From Eq. (13), we have
As \(\lim_{n, m \rightarrow \infty } \alpha ({x}_{n}, {x}_{m})\kappa < 1\), for all \({x}_{n}, {x}_{m} \in X\). Thus, the series
converges by the ratio test. By taking the limit \(r \rightarrow \infty \) in Eq. (15), we get
Next, from the triangle inequality, we have
Hence, \(d_{\alpha }(a^{*}, a_{m}) \leq \alpha (a_{n_{r}}, a_{m})\varepsilon \), when \(r \rightarrow \infty \). So the condition (11) is fulfilled.
Hence, from (10), we obtain
Since \(\lim_{n, m \rightarrow \infty } \alpha ({x} _{n}, {x}_{m})\kappa < 1\), for all \({x}_{n}, {x} _{m} \in X\), by taking the limit \(n, m \rightarrow \infty \) in the above inequality, we get a positive real number on right side. Hence \(\mathcal{A}_{n}\) approaches \(\mathcal{A}\), which completes the proof. □
Next, we will prove some fixed point results over controlled Hausdorff metric spaces.
Lemma 2.4
Let \(\mathcal{A}, \mathcal{B} \in \textit{CLD}( X)\), then for all \(\epsilon > 0\)and \(b\in \mathcal{B}\)there exists \(a\in \mathcal{A}\)such that
Proof
From Definition 2.1, for \(\mathcal{A}, \mathcal{B} \in \textit{CLD}(X)\) and for any \({b} \in \mathcal{B}\), we have
By definition of infimum, we may assume a sequence \({{a}_{n}}\) in \(\mathcal{A}\) such that
Since \(\mathcal{A}\) is closed, there exists \({a} \in \mathcal{A}\) such that \({a} _{n} \rightarrow {a}\). Therefore, by (17), we have
□
Theorem 2.5
Let \(\mathit{{T}} : X\rightarrow \textit{CLD}(X)\)be a mapping on a complete controlled metric space \((X, d_{\alpha })\). IfTsatisfies the inequality
where \(\kappa \in [0, 1)\)is a real constant such that \(\lim_{n, m \rightarrow \infty }\alpha ({x}_{n}, {x}_{m})\kappa < 1\), for all \({x}_{n}, {x}_{m} \in X\). ThenThas a fixed point.
Proof
Let us consider \(\kappa > 0\), \({x}_{0}\in X\) and choose \({x}_{1} \in \mathit{{T}} {x}_{0}\). As \(\mathit{{T}} {x}_{0}, \mathit{{T}} {x}_{1}\in \textit{CLD}(X)\) and \({x}_{1} \in \mathit{{T}} {x}_{0}\), then, by Lemma 2.4, there exists \({x}_{2} \in \mathit{{T}} {x}_{1}\) such that
Now since \(\mathit{{T}} {x}_{1}, \mathit{{T}} {x}_{2} \in \textit{CLD}X)\) and \({x}_{2} \in \mathit{{T}} {x}_{1}\), there exists \({x}_{3} \in \mathit{{T}} {x}_{2}\) such that
Continuing in this fashion, we obtain a sequence \(\{{x}_{n}\}\) of elements of X such that \({x}_{n + 1} \in \mathit{{T}} {x}_{n}\), for \(n = 0, 1, 2, \ldots \) and
From Eq. (18), we have
Continuing in this way, we have
From the triangle inequality and Eq. (19) for \(m > n\), we have
This implies that
Since \(\lim_{n, m \rightarrow \infty }\alpha ({x} _{n}, {x}_{m})\kappa < 1\) for all \({x}_{n}, {x} _{m} \in X\), \(\alpha ({x}_{n}, {x}_{m})\) is finite and the series \(\sum_{n = 1}^{\infty }\kappa ^{n}\prod_{i = 1}^{n}\alpha ( {x}_{i}, {x}_{m})\alpha ({x}_{i}, {x}_{i + 1})\) converges by the ratio test for each \(m \in \mathbb{N}\). If we take \(S_{n} = \kappa ^{n}\prod_{i = 1}^{n}\alpha ({x}_{i}, {x}_{m})\alpha ({x}_{i}, {x}_{i + 1})\) and \(S_{n + 1} = \kappa ^{n + 1}\prod_{i = 1}^{n + 1}\alpha ({x}_{i}, {x}_{m})\alpha ({x}_{i}, {x}_{i + 1})\), then \(\frac{S_{n + 1}}{S_{n}} < 1\), when \(n \rightarrow \infty \). By the same procedure \(\sum_{n = 1}^{\infty }n \kappa ^{n}\prod_{i = 1}^{n}\alpha ({x}_{i}, {x}_{m})\alpha ({x} _{i}, {x}_{i + 1})\) is convergent. Let
and
Thus, for \(m > n\), we have
By letting \(n \rightarrow \infty \), we conclude that \(\{{x}_{n}\}\), for \(n = 0, 1, 2, \ldots \) is a Cauchy sequence. Since X is complete, there exists \({x}_{*} \in X\) such that \(\lim_{n \rightarrow \infty }{x}_{n} = {x}_{*}\). Now by the triangle inequality
Since \(\lim_{n, m \rightarrow \infty }\alpha ({x} _{n}, {x}_{m})\kappa < 1\) for all \({x}_{n}, {x} _{m} \in X\), \(\alpha ({x}_{n}, {x}_{m})\) is finite. Thus, by taking the limit \(n \rightarrow \infty \) in the above inequality, we get
T is closed, therefore \({x}_{*} \in \mathit{{T}} {x}_{*}\). Hence \({x}_{*}\) is a fixed point of T. □
Definition 2.4
([18])
A multivalued mapping \(\mathit{{T}} : X\rightarrow \textit{CLD}(X)\) on a controlled metric space \((X, d _{\alpha })\) is said to be a multivalued almost F-contraction, if \(\mathit{{F}} \in \mathcal{F}\) and there exist two constants \(\mathcal{\tau } > 0\) and \(\gamma \geq 0\) such that
for all \({x}, {y} \in X\) with \(\textit{H}_{\alpha }( \mathit{{T}} {x}, \mathit{{T}} {y}) > 0\).
By putting \(\mathit{{F}}(\alpha ) = \ln \alpha \), then every multivalued almost contraction (1) is also a multivalued almost F-contraction.
Theorem 2.6
Let \(\mathit{{T}} : X\rightarrow \textit{CLD}(X)\)be a multivalued almostF-contraction on a complete controlled metric space \((X, d_{\alpha })\)with \(\lim_{n, m \rightarrow \infty }\alpha ( {x}_{n}, {x}_{m})\kappa < 1\), for all \({x}_{n}, {x}_{m} \in X\), where \(\kappa \geq 1\). If \(\mathit{{F}} \in \mathcal{F}^{*}\), thenThas a fixed point inX.
Proof
Let \({x}_{0}\in X\). Since Tx is nonempty for all \({x} \in X\), we may choose \({x}_{1} \in \mathit{{T}} {x}_{0}\). If \({x}_{1} \in \mathit{{T}} {x}_{1}\), then \({x}_{1}\) is a fixed point of T. Therefore let us suppose that \({x}_{1} \notin \mathit{{T}} {x}_{1}\). Since \(\mathit{{T}} {x}_{1}\) is closed, \(d_{\alpha }({x}_{1}, \mathit{{T}} {x} _{1}) > 0\), and also \(d_{\alpha }({x}_{1}, \mathit{{T}} {x}_{1}) \leq \textit{H}_{\alpha }( \mathit{{T}} {x}_{0}, \mathit{{T}} {x}_{1})\). From axiom (F1) of Definition 1.1, we have
From Eq. (20), we obtain
As \(d_{\alpha }({x}_{1}, \mathit{{T}} {x}_{0}) = d_{\alpha }({x}_{1}, {x} _{1}) = 0\), from above inequality, we have
From condition (F4), we can write
Thus, from Eq. (21), we have
From Eq. (22), there exists \({x} _{2} \in \mathit{{T}} {x}_{1}\) such that
If \({x}_{2} \in \mathit{{T}} {x}_{2}\), then the proof is complete, otherwise in the same way there exists \({x}_{3} \in \mathit{{T}} {x}_{2}\) such that
By continuing the same procedure recursively, we get a sequence \(\{{x}_{n}\}\) in X, for \(n = 0, 1, 2, \ldots \) such that \({x}_{n + 1} \in \mathit{{T}} {x}_{n}\) and
If \({x}_{n} \in \mathit{{T}} {x}_{n}\), then \({x}_{n}\) is a fixed point of T. Therefore, suppose that for every \(n \in \mathbb{N}\) \({x}_{n} \notin \mathit{{T}} {x}_{n}\). Denote by \(\mathcal{A}_{n} = d _{\alpha }({x}_{n}, {x}_{n + 1})\), for \(n = 0, 1, 2, \ldots \) . Thus, for all \(n = 0, 1, 2, \ldots \) , \(d_{\alpha }({x}_{n}, {x}_{n + 1}) > 0\). From Eq. (23), we get
By taking the limit \(n \rightarrow \infty \) in Eq. (24), we get \(\lim_{n \rightarrow \infty } \mathit{{F}}(\mathcal{A}_{n}) = - \infty \). Thus, from condition \((\mathit{{F}}2)\) of Definition 1.1, we have
Also from condition \((\mathit{{F}}3)\), there exists \(l \in (0, 1)\) such that
From Eq. (24), for all \(n \in \mathbb{N}\), the following holds:
By letting \(n \rightarrow \infty \) in (25), we obtain
From Eq. (26), there exists \(n_{1} \in \mathbb{N}\) such that \(n \mathcal{A}_{n}^{l} \leq 1\) for all \(n \geq n_{1}\). Thus, for all \(n \geq n_{1}\), we have
From the triangle inequality and Eq. (27) for \(m > n \geq n_{1}\), we have
Since \(\lim_{n, m \rightarrow \infty }\alpha ({x} _{n + 1}, {x}_{m})\kappa < 1\) for all \({x}_{n}, {x}_{m} \in X\), the series \(\sum_{i = 1}^{\infty } (\prod_{j = 1}^{i}\alpha ( {x}_{j}, {x}_{m}) ) \alpha ({x} _{i}, {x}_{i + 1})\frac{1}{i^{\frac{1}{l}}}\) converges by the ratio test for each \(m \in \mathbb{N}\). Therefore, by taking the limit \(n \rightarrow \infty \) in the above inequality, we get \(d_{\alpha }({x}_{n}, {x}_{m}) \rightarrow 0\). Since X is complete, there exists \({x}_{*} \in X\) such that \(\lim_{n \rightarrow \infty } {x}_{n} = {x}_{*}\). Now, we prove that \({x}_{*}\) is a fixed point of T. From the construction of \(\{{x}_{n}\}\) for \(n = 0, 1, 2, \ldots \) , there is a subsequence \(\{{x}_{p}\}\) such that
Since \(\lim_{p \rightarrow \infty }{x}_{p} = {x}_{*}\), we have
From Lemma 2.1 and (20), we have
Since \(\lim_{n, m \rightarrow \infty }\alpha ({x} _{n}, {x}_{m})\kappa < 1\) for all \({x}_{n}, {x} _{m} \in X\), \(\alpha ({x}_{n}, {x}_{m})\) is finite. Thus by taking the limit \(p \rightarrow \infty \) in the above inequality and from (29), we get \(d_{\alpha }({x}_{*}, \mathit{{T}} {x} _{*}) = 0\). Hence \({x}_{*} \in \mathit{{T}} {x} _{*}\), and \({x}_{*}\) is a fixed point of T. □
Remark 2.1
Theorem 2.6 is a generalization of Theorem 1.1 and Theorem 1.3.
Example 2.1
Let \(X= [0, \infty )\). Define \(d_{\alpha } : X\times X\rightarrow [0, \infty )\) as
Hence \((X, d_{\alpha })\) is a complete controlled metric space, where \(\alpha : X\times X\rightarrow [1, \infty )\) is defined as
Define a mapping \(\mathit{{T}} : X\rightarrow \textit{CLD}(X)\) by
Now, consider the mapping F defined by \(\mathit{{F}}(\mathcal{A}) = \ln \mathcal{A}\). Then T is multivalued almost F-contraction with \(\mathcal{\tau } = \ln 2\) and \(\gamma = 10\). As \(\textit{H}_{\alpha }(\mathit{{T}} {x}, \mathit{{T}} {y}) > 0\) for \({x} \neq {y}\). So (20) is equivalent to the following equation:
and so
Now, we will consider the following cases:
- Case (1)
If \({x}, {y} \in [0, 1)\), then
$$ \textit{H}_{\alpha }(\mathit{{T}} {x}, \mathit{{T}} {y}) = 1 = d_{\alpha }({x}, {y}), $$and hence (30) is satisfied.
- Case (2)
If \({x}, {y} \geq 1\), then
$$ \textit{H}_{\alpha }(\mathit{{T}} {x}, \mathit{{T}} {y}) = 1 = d_{\alpha }({x}, {y}) = d_{\alpha }( {y}, \mathit{{T}} {x}). $$Clearly, (30) is satisfied.
- Case (3)
If \({x} \geq 1\) and \({y} \in [0, 1)\), then
$$ \textit{H}_{\alpha }(\mathit{{T}} {x}, \mathit{{T}} {y}) = \frac{1}{{x}} = d_{\alpha }({x}, {y}) = d_{\alpha }({y}, \mathit{{T}} {x}). $$Equation (30) is satisfied.
- Case (4)
If \({y} \geq 1\) and \({x} \in [0, 1)\), then
$$ \textit{H}_{\alpha }(\mathit{{T}} {x}, \mathit{{T}} {y}) = \frac{1}{{y}} = d_{\alpha }({x}, {y}) = d_{\alpha }({y}, \mathit{{T}} {x}). $$Hence (30) is satisfied.
3 Conclusion
In the present study, we defined the concept of a Pompeiu–Hausdorff metric on the class of nonempty closed subsets of controlled metric spaces and we showed that if \((X, d_{\alpha })\) is complete, then \((\textit{H}_{\alpha }, \textit{CLD}(X))\) is also complete. Also, we analyzed some topological properties of such spaces. Then we established some fixed point results for multivalued mappings satisfying almost F-contractive condition on controlled metric spaces which generalize many existing results in the literature. We think that different versions of contractive conditions can be considered in such spaces by using a Pompeiu–Hausdorff metric. Also, this new working area will be a powerful tool for the existence solution of the systems of integral inclusions and fractional differential inclusions.
References
Nadler, S.B.: Multi-valued contraction mappings. Not. Am. Math. Soc. 14, 930 (1967)
Aydi, H., Abbas, M., Vetro, C.: Partial Hausdorff metric and Nadler’s fixed point theorem on partial metric spaces. Topol. Appl. 159, 3234–3242 (2012)
Aydi, H., Abbas, M., Vetro, C.: Common fixed points for multivalued generalized contractions on partial metric spaces. Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 108, 483–501 (2014)
Aydi, H., Felhi, A., Karapinar, E., Sahmim, S.: A Nadler-type fixed point theorem in dislocated spaces and applications. Miskolc Math. Notes 19(1), 111–124 (2018)
Mizoguchi, N., Takahashi, W.: Fixed point theorem for multivalued mappings on complete metric space. J. Math. Anal. Appl. 141, 177–188 (1989)
Sintamarian, A.: Integral inclusions of Fredholm type relative to multivalued φ-contraction. Semin. Fixed Point Theory Cluj-Napoca 3, 361–368 (2002)
Feng, Y., Liu, S.: Fixed point theorems for multi-valued contractive mappings and multi-valued Caristi type mappings. J. Math. Anal. Appl. 317, 103–112 (2006)
Suzuki, T.: Mizoguchi–Takahashi’s fixed point theorem is a real generalization of Nadler’s. J. Math. Anal. Appl. (2007). https://doi.org/10.1016/j.jmaa.2007.08.022
Klim, D., Wardowski, D.: Fixed point theorems for set-valued contractions in complete metric spaces. J. Math. Anal. Appl. 334, 132–139 (2007)
Kamran, T.: Mizoguchi–Takahashi’s type fixed point theorem. Comput. Math. Appl. 57, 507–511 (2009)
Işık, H., Ionescu, C.: New type of multivalued contractions with related results and applications. UPB Sci. Bull., Ser. A 80(2), 13–22 (2018)
Saleem, N., Vujaković, J., Baloch, W.U., Radenović, S.: Coincidence point results for multivalued Suzuki type mappings using θ-contraction in b-metric spaces. Mathematics 7, 1017 (2019)
Işık, H., Parvaneh, V., Mohammadi, B., Altun, I.: Common fixed point results for generalized Wardowski type contractive multi-valued mappings. Mathematics 7(11), 1130 (2019)
Kaddouri, H., Işık, H., Beloul, S.: On new extensions of F-contraction with application to integral inclusions. UPB Sci. Bull., Ser. A 81(3), 31–42 (2019)
Berinde, M., Berinde, V.: On a general class of multivalued weakly Picard mappings. J. Math. Anal. Appl. 326, 772–782 (2007)
Wardowski, D.: Fixed points of a new type of contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2012, 94 (2012)
Altun, I., Minak, G., Dag, H.: Multivalued F-contractions on complete metric space. J. Nonlinear Convex Anal. 16, 659–666 (2015)
Altun, I., Durmaz, G., Minak, G., Romaguera, S.: Multivalued almost F-contraction on complete metric spaces. Filomat 30, 441–448 (2016)
Kamran, T.: A generalization of b-metric space and some fixed point theorems. Mathematics 5, 1–7 (2017)
Czerwik, S.: Contraction mappings in b-metric spaces. Acta Math. Inform. Univ. Ostrav. 1, 5–11 (1993)
Bakhtin, I.A.: The contraction mapping principle in almost metric spaces. Funct. Anal. 30, 26–37 (1989)
Subashi, L.: Some topological properties of extended b-metric space. In: Proceedings of the 5th International Virtual Conference on Advanced Scientific Results, vol. 5, pp. 164–167 (2017)
Subashi, L., Gjini, N.: Fractals in extended b-metric space. J. Progressive Res. Math. 12, 2057–2065 (2017)
Subashi, L., Gjini, N.: Some results on extended b-metric spaces and Pompeiu–Hausdorff metric. J. Progressive Res. Math. 12, 2021–2029 (2017)
Alqahtani, B., Fulga, A., Karapinar, E.: Non-unique fixed point results in extended b-metric space. Mathematics 6, 1–11 (2018)
Shatanawi, W., Mukheimer, A., Abodayeh, K.: Some fixed point theorems in extended b-metric spaces. Sci. Bull. “Politeh.” Univ. Buchar., Ser. A, Appl. Math. Phys. 80, 71–78 (2018)
Kiran, Q., Alamgir, N., Mlaiki, N., Aydi, H.: On some new fixed point results in complete extended b-metric spaces. Mathematics 7, 476 (2019)
Alamgir, N., Kiran, Q., Aydi, H., Mukheimer, A.: A Mizoguchi–Takahashi type fixed point theorem in complete extended b-metric spaces. Mathematics 7, 478 (2019)
Asim, M., Imdad, M., Radenović, S.: Fixed point results in extended rectangular b-metric spaces with an application. UPB Sci. Bull., Ser. A 81, 43–50 (2019)
Patle, P.R., Vujaković, L., Radenović, S., Patel, D.K.: Topology induced by θ-metric and multivalued mappings. Symmetry 7, 144 (2019)
Patle, P.R., Patel, D.K., Aydi, H., Radenović, S.: \(\mathcal{H}^{+} \)-type multivalued contraction and its applications in symmetric and probabilistic spaces. Mathematics 7, 144 (2019)
Mlaiki, N., Aydi, H., Souayah, N., Abdeljawad, T.: Controlled metric type spaces and the related contraction principle. Mathematics 6, 194 (2018)
Acknowledgements
The authors are thankful to the editor and anonymous referees for their valuable comments and suggestions.
Availability of data and materials
The data used to support the findings of this study are available from the corresponding author upon request.
Funding
This research received no external funding.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare to have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alamgir, N., Kiran, Q., Işık, H. et al. Fixed point results via a Hausdorff controlled type metric. Adv Differ Equ 2020, 24 (2020). https://doi.org/10.1186/s13662-020-2491-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-2491-8