Abstract
This paper proposes a new nonlinear stochastic SIVS epidemic model with double epidemic hypothesis and Lévy jumps. The main purpose of this paper is to investigate the threshold dynamics of the stochastic SIVS epidemic model. By using the technique of a series of stochastic inequalities, we obtain sufficient conditions for the persistence in mean and extinction of the stochastic system and the threshold which governs the extinction and the spread of the epidemic diseases. Finally, this paper describes the results of numerical simulations investigating the dynamical effects of stochastic disturbance. Our results significantly improve and generalize the corresponding results in recent literatures. The developed theoretical methods and stochastic inequalities technique can be used to investigate the high-dimensional nonlinear stochastic differential systems.
Similar content being viewed by others
1 Introduction
Mathematical inequalities are widely used in many fields of mathematical analysis, especially differential systems [1–5]. Recently, the inequality technique was applied to stochastic differential systems [6–11], impulsive differential systems [12–21], and impulsive stochastic differential systems [22], thus some new results have been obtained.
As an important factor threatening the safety of human life and property, the investigation of epidemic has received extensive attention from experts in various fields [23–27]. Generally speaking, medical researchers often use observation and experimental methods to study the behavior of epidemics. Recently, however, a number of experts in the field of mathematics have also been interested in the study of epidemics. They have used mathematical methods to analyze the spread and control of epidemics [28–31]. Kermack and McKendrick’s pioneering work on the development of an epidemic disease is one of the typical examples. They established an SIS compartment model and proposed the famous threshold theory, which has laid a solid foundation for the study of the dynamics of infectious diseases [30].
The SIS model based on the deterministic ordinary differential equation is given by
In system (1), \(\beta S(t)\) represents the number of people infected by a patient within a unit time at t. But in reality, the number of people who can be exposed to a patient at a time is limited. To this end, some authors have introduced a saturated infection rate to study the dynamic behavior of the disease [32–34]. In addition, all creatures on the earth are infected by a variety of environmental noises, of course, the disease is no exception. Motivated by this, some scholars have studied the infection system with environmental noises (such as Brownion noise, Markov noise and Lévy noise) [35–38]. Meanwhile, populations may be affected by different kinds of infectious diseases at the same time. Therefore, it is of great significance to study the epidemic model with multiple diseases [39–41].
Recently, Meng et al. [39] considered a novel nonlinear stochastic SIS epidemic model with double epidemic hypothesis as follows:
They obtained the threshold of system (2) for the extinction and the persistence in mean of the epidemic diseases. Based on system (2), recently, Zhang et al. [40] proposed an SIS system with double epidemic diseases driven by Lévy jumps as follows:
In model (3), the authors discussed in detail the conditions for persistence in mean and extinction of each epidemic disease. Therefore, they discussed the persistence in mean of susceptible individuals under different conditions. The above two studies provide a theoretical basis for the study of infectious diseases. But they just discussed the persistence in mean and extinction of epidemic diseases under different conditions. In real life, however, when an epidemic outbreak occurs, we do not sit idly but take measures to control the spread of the epidemic disease. There are many ways to suppress the spread of a disease, for instance, cut off transmission routes, pay attention to food hygiene, vaccination and so on [42, 43]. Vaccination is an effective method of preventing infectious diseases and many scientists have explored the effect of vaccination on diseases [44–47].
Motivated by the above works, in this paper, we propose a stochastic SIVS model with double epidemic diseases and Lévy jumps under vaccination as follows:
where \(S(t)\), \(I_{1}(t)\), \(I_{2}(t)\), \(V(t)\), respectively, stand for the density of susceptible, infective A, infective B and vaccinated individuals at time t, Λ is a constant input of new numbers into the population, q means a fraction of vaccinated for the newborn, \(\beta _{i}\) is the infection rate coefficient from \(I_{i}(t)\) (\(i=1,2\)) to \(S(t)\), respectively. u represents the natural death rate of \(S(t)\), \(I_{1}(t)\), \(I_{2}(t)\), \(V(t)\), p is the proportional coefficient of vaccinated for the susceptible, \(r_{i}\), \(d_{i}\) is the recovery rate and disease-caused death rate of \(I_{i}(t)\), \(i=1,2\), respectively. δ stands for the rate of losing their immunity for vaccinated individuals, \(\alpha_{1}\) and \(\alpha_{2}\) are the so-called half-saturation constants, respectively. \(B(t)=(B_{1}(t),B_{2}(t),B_{3}(t),B_{4}(t))\) is a standard Brownian motion with intensity \(\sigma_{i}>0\) (\(i=1,2,3,4\)).
Throughout this paper, let \((\Omega,\mathcal{F},\{\mathcal{F}\}_{t\geq 0},\mathcal{P})\) be a complete probability space with a filtration \(\{\mathcal{F}_{t}\} _{t\geq0}\) satisfying the usual conditions (i.e. it is increasing and right continuous while \(\mathcal{F}_{0}\) contains all \(\mathcal{P}\)-null sets). Function \(B_{i}(t)\) (\(i=1,2,3,4\)) is a Brownian motion defined on the complete probability space Ω, the intensity of \(B_{i}(t)\) is \(\sigma_{i}\) (\(i=1,2,3,4\)). \(\widetilde{N}(dt,du)=N(dt,du)-\lambda(du)\,dt\), N is a Poisson counting measure on \((0,+\infty)\times\mathbb{Z}\), λ is the characteristic measure of N on a measurable subset \(\mathbb{Z}\), \(\lambda(\mathbb{Z})<+\infty\), \(\gamma_{i}\) (\(i=1,2,3,4\)) is bounded and continuous with respect to λ and is \(\mathcal {B}(\mathbb{Z})\times\mathcal{F}_{t}\)-measurable. For an integrable function \(X(t)\) on \([0,+\infty)\), we define \(\langle X(t)\rangle=\frac {1}{t}\int^{t}_{0}X(s)\,ds\).
The main purpose of this paper is to investigate the threshold dynamics of the stochastic SIVS epidemic model. In this paper, by using the Lyapunov method and the technique of a series of stochastic inequalities, we obtain sufficient conditions for the persistence in mean and extinction of the stochastic system and the threshold which governs the extinction and the spread of the epidemic diseases. Our results significantly improve and generalize the corresponding results in recent literatures. The developed theoretical methods and stochastic inequalities technique can be used to investigate the high-dimensional nonlinear stochastic differential systems. In Section 2, we firstly give some lemmas and recall some necessary notations and definitions. Furthermore, we obtain the main results for stochastic disease-free dynamics and stochastic endemic dynamics which imply the extinction and the spread of the epidemic diseases. Finally, this paper gives the conclusions and numerical simulations investigating the dynamical effects of stochastic disturbance.
2 Main results
The main purpose of this paper is to investigate the threshold dynamics of the stochastic SIVS epidemic model. In this section, by using the technique of a series of stochastic inequalities, we obtain sufficient conditions for the persistence in mean and extinction of the stochastic system and the threshold which governs the extinction and the spread of epidemic diseases.
2.1 Preliminary knowledge
For the sake of notational simplicity, we define
Throughout this paper, suppose that the following two assumptions hold.
Assumption 2.1
The following hold:
-
(i)
\(1+\gamma_{i}(u)>0\);
-
(ii)
\(\int_{\mathbb{Z}} [\gamma_{i}(u)-\ln(1+\gamma_{i}(u)) ]\lambda(du)<\infty\), \(i=1,2,3,4\), \(u\in\mathbb{Z}\).
Remark 2.1
This assumption means that the intensities of Lévy noises are not infinite.
Assumption 2.2
Suppose that there exists some \(\varrho>1\) such that the following inequality holds:
Definition 2.1
[39]
-
(i)
The species \(X(t)\) is said to be extinctive if \(\lim_{t\rightarrow+\infty}X(t)=0\);
-
(ii)
The species \(X(t)\) is said to be persistent in mean if \(\lim_{t\rightarrow+\infty}\langle X(t)\rangle_{*}>0\).
The following elementary inequality will be used frequently in the sequel.
Lemma 2.1
Burkholder-Davis-Gundy inequality [48]
Let \(g\in\mathcal {L}^{2}(R_{+};R^{d\times m})\). For any \(t\geq0\), define
Then, for every \(p>0\), there exist two positive constants \(c_{p}\), \(C_{p}\) such that
where \(c_{p}\), \(C_{p}\) only depend on p.
Lemma 2.2
Chebyshev inequality [48]
For any \(c>0\), \(p>0\), \(X\in L^{p}\), the following inequality holds:
Lemma 2.3
Hölder inequality [48]
For any \(a_{i},b_{i}\in R\) and \(k\geq2\), if \(p,q>1\) and \(\frac{1}{p}+\frac{1}{q}=1\), the following inequality holds:
Lemma 2.4
Doob’s martingale inequality [48]
Let X be a submartingale taking nonnegative real values, either in discrete or continuous time. That is, for all times s and t with \(s< t\),
Then, for any constant \(C>0\),
where P denotes the probability measure on the sample space Ω of the stochastic process \(X: [0,T]\times\Omega\rightarrow[0,+\infty)\) and E denotes the expected value with respect to the probability measure P.
Lemma 2.5
Assume that \(X(t)\in R^{+}\) is an Itô’s-Lévy process of the form
where \(F : R^{n}\times R_{+}\times S\rightarrow R^{n}\), \(G : R^{n}\times R_{+}\times S\rightarrow R^{n}\) and \(H : R^{n}\times R_{+}\times S\times Z\rightarrow R^{n}\) are measurable functions.
Given \(V\in C^{2,1}(R^{n}\times R_{+}\times S; R_{+})\), we define the operator LV by
where
Then the generalized Itô’s formula with Lévy jumps is given by
Lemma 2.6
[51]
Let \(X(t)\in C(\Omega\times[0,+\infty),R_{+})\). We have the following conclusions.
-
(i)
If there exist \(T>0\), \(\lambda_{0}>0\), λ, m, \(n_{i}\) such that when \(t\geq T\),
$$\ln X(t)\leq\lambda t-\lambda_{0} \int_{0}^{t}X(s)\,ds+mB(t)+\sum _{i=1}^{j}n_{i} \int _{0}^{t} \int_{\mathbb{Z}}\ln\bigl(1+\gamma_{i}(u)\bigr) \widetilde{\Gamma}(ds,du)\quad \textit{a.s.}, $$then
$$ \textstyle\begin{cases} \langle X\rangle^{*}\leq\frac{\lambda}{\lambda_{0}}\quad \textit{a.s., if } \lambda\geq 0;\\ \lim_{t\rightarrow+\infty}X(t)=0 \quad \textit{a.s., if } \lambda< 0. \end{cases} $$ -
(ii)
If there exist \(T>0\), \(\lambda_{0}>0\), \(\lambda>0\), m, \(n_{i}\) such that when \(t\geq T\),
$$\ln X(t)\geq\lambda t-\lambda_{0} \int_{0}^{t}X(s)\,ds+mB(t)+\sum _{i=1}^{j}n_{i} \int _{0}^{t} \int_{\mathbb{Z}}\ln\bigl(1+\gamma_{i}(u)\bigr) \widetilde{\Gamma}(ds,du) \quad \textit{a.s.}, $$then \(\langle X\rangle_{*}\geq\frac{\lambda}{\lambda_{0}}\) a.s.
Lemma 2.7
For any initial value \((S(0),I_{1}(0),I_{2}(0),V(0))\in R_{+}^{4}\), the solution \((S(t),I_{1}(t),I_{2}(t), V(t))\) of model (4) has the following property:
Moreover,
Proof
Define
Applying the generalized Itô’s formula to \(Q(X)\), we have
where
Choose a positive constant \(\varrho>1\) that satisfies
For any constant k satisfying \(k\in(0,b\varrho)\), one has
Integrating from 0 to t and taking expectation on both sides of (5), we have
Easily, one has
Therefore
By Lemma 2.1, applying the Burkholder-Davis-Gundy inequality, integrating equation (5) from 0 to t, and for an arbitrarily small positive constant δ, one has
where
and
where \(c_{\varrho}, C_{\varrho}>0\).
So we have
Choose a positive constant δ that satisfies
Combining it with equation (6), one has
Applying the arbitrariness of \(\kappa_{X}>0\) and Lemma 2.2 for Chebyshev’s inequality, one obtains
Applying the Borel-Cantelli lemma [48], for almost all \(\omega\in\Omega\), one has
holds for all but finitely many k. Therefore, for any positive constant \(k\geq k_{0}\) and almost all \(\omega\in\Omega\), there is \(k_{0}(\omega)\) such that equation (7) holds.
Thus, for almost all \(\omega\in\Omega\), once conditions \(k\geq k_{0}\) and \(k\delta\leq t\leq(k+1)\delta\) hold, then we have
Taking the limit superior on both sides of equation (8) and applying the arbitrariness of \(\kappa_{X}>0\), one has
Easily, for any ϱ satisfying \(1<\varrho<1+\frac{2(u-\phi )}{\sigma^{2}}\), one has \(u>\frac{\varrho-1}{2}\sigma^{2}+\phi\). Therefore
That is to say, for any constant τ satisfying \(0<\tau<1-\frac {1}{\varrho}\), there is a constant \(N=N(\omega)\), and once condition \(t\geq N\) holds, then we have
Therefore
So
and
This completes the proof. □
Lemma 2.8
For any initial value \((S(0),I_{1}(0),I_{2}(0),V(0))\in R_{+}^{4}\), the solution \((S(t),I_{1}(t),I_{2}(t), V(t))\) of model (4) has the following property:
Proof
Define
Applying Lemma 2.1 for the Burkholder-Davis-Gundy inequality and Lemma 2.3 for Hölder’s inequality, one has
for \(2<\varrho<1+\frac{2(u-\phi)}{\sigma^{2}}\). Here \(C_{\varrho}= [\frac{\varrho^{\varrho+1}}{2(\varrho-1)^{\varrho-1}} ]^{\frac {\varrho}{2}}>0\) is a constant.
Applying equation (6), we have
For any constant \(\kappa_{X_{1}}>0\), applying Lemma 2.4 for Doob’s martingale inequality, one obtains
Applying the Borel-Cantelli lemma, one has
Taking the limit superior on both sides of equation (9) and applying the arbitrariness of \(\kappa_{X}>0\), one has
That is to say, for any constant τ satisfying \(0<\tau<\frac {1}{2}-\frac{1}{\varrho}\), there is a constant \(N=N(\omega)\), and once \(t\geq N\), \(w\in\Omega_{\tau}\) holds, then we have
Dividing both sides of equation (10) by t and taking the limit superior, we have
Combining it with \(\liminf_{t\rightarrow\infty}\frac{|X_{1}(t)|}{t}\geq0\), one has
Similarly, one obtains
This completes the proof. □
Lemma 2.9
For any initial value \((S(0),I_{1}(0),I_{2}(t),V(0))\in R_{+}^{4}\), model (4) has a unique positive solution \((S(t),I_{1}(t),I_{2}(t),V(t))\in R_{+}^{4}\) on \(t\geq0\) with probability 1.
Proof
The proof is similar to Refs. [9, 44] by defining \(Q(S,I_{1},I_{2},V)=S-1-\ln S+I_{1}-1-\ln I_{1}+I_{2}-1-\ln I_{2}+V-1-\ln V\), and hence is omitted. □
2.2 Stochastic disease-free dynamics
Theorem 2.1
Suppose that conditions \(R_{1}<0\) and \(R_{2}<0\) hold. Then, for any initial value \((S(0),I_{1}(0),I_{2}(0),V(0))\in R_{+}^{4}\), the solution \((S(t),I_{1}(t),I_{2}(t),V(t))\) of model (4) has the following property:
That is to say, the two epidemic diseases go to extinct almost surely.
Proof
By equation (4), one has
Dividing both sides of equation (11) by t and integrating over the time interval 0 to t yield
where
Applying Lemmas 2.7 and 2.8, we obtain that
Applying the generalized Itô’s formula in Lemma 2.5 to \(\alpha_{1}\ln I_{1}(t)+I_{1}(t)\) yields
Dividing both sides of equation (14) by t, integrating over the time interval 0 to t and taking the limit, one obtains that
Combining equations (12) and (15), one obtains
where
Similarly, applying the generalized Itô’s formula in Lemma 2.5 to \(\alpha_{2}\ln I_{2}(t)+I_{2}(t)\) yields
where
Applying Lemmas 2.7 and 2.8, we obtain that
By taking the limit superior of both sides of equation (16) and equation (17), respectively, one has
That is to say,
Applying (13) and (19) into equation (12), we obtain that
By equation (4), one has
Dividing both sides of equation (21) by t, integrating over the time interval \(t=0\) to t and taking the limit, one obtains that
Applying (19), (20), Lemmas 2.7 and 2.8, we have
This completes the proof. □
2.3 Stochastic endemic dynamics
Theorem 2.2
For any initial value \((S(0),I_{1}(0),I_{2}(0),V(0))\in R_{+}^{4}\), the solution \((S(t),I_{1}(t), I_{2}(t),V(t))\) of model (4) has the following property:
-
(i)
If \(R_{1}>0\) and \(R_{2}<0\), then the epidemic disease \(I_{1}(t)\) is persistent in mean and \(I_{2}(t)\) goes extinct, i.e. \(\lim_{t\rightarrow\infty}\langle I_{1}(t)\rangle=\frac{R_{1}}{\Upsilon _{11}}>0\), \(\lim_{t\rightarrow\infty}I_{2}(t)=0\) a.s. Moreover,
$$\begin{aligned}& \lim_{t\rightarrow\infty}\bigl\langle S(t)\bigr\rangle = \frac{(u+\delta-uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+\delta)(u+d_{1})}{u^{2}+u\delta+up}\frac {R_{1}}{\Upsilon_{11}}\quad \textit{a.s.}, \\& \lim_{t\rightarrow\infty}\bigl\langle V(t)\bigr\rangle = \frac{(p+uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+d_{1})p}{u(u+\delta+p)}\frac{R_{1}}{\Upsilon _{11}} \quad \textit{a.s.} \end{aligned}$$ -
(ii)
If \(R_{1}<0\) and \(R_{2}>0\), then the epidemic disease \(I_{1}(t)\) goes extinct and \(I_{2}(t)\) is persistent in mean, i.e. \(\lim_{t\rightarrow\infty}\langle I_{1}(t)\rangle=0\), \(\lim_{t\rightarrow \infty}I_{2}(t)=\frac{R_{2}}{\Upsilon_{21}}>0\) a.s. Moreover,
$$\begin{aligned}& \lim_{t\rightarrow\infty}\bigl\langle S(t)\bigr\rangle = \frac{(u+\delta-uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+\delta)(u+d_{2})}{u^{2}+u\delta+up}\frac {R_{2}}{\Upsilon_{21}}\quad \textit{a.s.}, \\& \lim_{t\rightarrow\infty}\bigl\langle V(t)\bigr\rangle = \frac{(p+uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+d_{2})p}{u(u+\delta+p)}\frac{R_{2}}{\Upsilon _{21}}\quad \textit{a.s.} \end{aligned}$$
Proof
Case (i): From equation (16) we have
where
From Theorem 2.1, when \(R_{2}<0\) one has
Therefore, there exists an arbitrarily small constant \(\varepsilon>0\) such that when t is large enough, we have \(I_{2}(t)<\varepsilon\). Applying this into equation (23) leads to
Applying Lemma 2.6 and the arbitrariness of ε, we obtain
Applying (13), (24) and (25) into equation (12), we obtain that
Applying (24), (25), (26), Lemmas 2.7 and 2.8 into equation (22), we have
Case (ii): From equation (17) we have
where
From Theorem 2.1, when \(R_{1}<0\) one has
Therefore, there exists an arbitrarily small constant \(\varepsilon>0\) such that when t is large enough, we have \(I_{1}(t)<\varepsilon\). Applying this into equation (23) leads to
Applying Lemma 2.6 and the arbitrariness of ε, we obtain
Applying equations (13), (28), (29) into equation (12), we obtain that
Applying (28), (29), (30), Lemmas 2.7 and 2.8 into equation (22), we have
This completes the proof. □
Theorem 2.3
Suppose that conditions \(R_{1}>0\) and \(R_{2}>0\) hold. Let \((S(t),I_{1}(t),I_{2}(t),V(t))\) be the solution of model (4) with the initial value \((S(0),I_{1}(0),I_{2}(0),V(0))\in R_{+}^{4}\).
-
(i)
If \(\Upsilon_{11}R_{2}<\Upsilon_{21}R_{1}\), then the epidemic disease \(I_{1}(t)\) is persistent in mean and \(I_{2}(t)\) goes extinct, i.e. \(\lim_{t\rightarrow\infty}\langle I_{1}(t)\rangle=\frac {R_{1}}{\Upsilon_{11}}>0\), \(\lim_{t\rightarrow\infty}I_{2}(t)=0\) a.s. Moreover,
$$\begin{aligned}& \lim_{t\rightarrow\infty}\bigl\langle S(t)\bigr\rangle = \frac{(u+\delta-uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+\delta)(u+d_{1})}{u^{2}+u\delta+up}\frac {R_{1}}{\Upsilon_{11}} \quad \textit{a.s.}, \\& \lim_{t\rightarrow\infty}\bigl\langle V(t)\bigr\rangle = \frac{(p+uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+d_{1})p}{u(u+\delta+p)}\frac{R_{1}}{\Upsilon _{11}}\quad \textit{a.s.} \end{aligned}$$ -
(ii)
If \(\Upsilon_{22}R_{1}<\Upsilon_{12}R_{2}\), then the epidemic disease \(I_{1}(t)\) goes extinct and \(I_{2}(t)\) is persistent in mean, i.e. \(\lim_{t\rightarrow\infty}\langle I_{1}(t)\rangle=0\), \(\lim_{t\rightarrow\infty}I_{2}(t)=\frac{R_{2}}{\Upsilon_{21}}>0\) a.s. Moreover,
$$\begin{aligned}& \lim_{t\rightarrow\infty}\bigl\langle S(t)\bigr\rangle =\frac{(u+\delta-uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+\delta)(u+d_{2})}{u^{2}+u\delta+up}\frac {R_{2}}{\Upsilon_{21}} \quad \textit{a.s.}, \\& \lim_{t\rightarrow\infty}\bigl\langle V(t)\bigr\rangle =\frac{(p+uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+d_{2})p}{u(u+\delta+p)}\frac{R_{2}}{\Upsilon _{21}}\quad \textit{a.s.} \end{aligned}$$ -
(iii)
If \(\Upsilon_{11}R_{2}>\Upsilon_{21}R_{1}\), \(\Upsilon _{22}R_{1}>\Upsilon_{12}R_{2}\), then the epidemic diseases \(I_{1}\) and \(I_{2}\) are persistent in mean. Moreover,
$$\begin{aligned}& \lim_{t\rightarrow\infty}\bigl\langle I_{1}(t)\bigr\rangle = \frac{\Upsilon _{22}R_{1}-\Upsilon_{12}R_{2}}{\Upsilon_{11}\Upsilon_{22}-\Upsilon _{12}\Upsilon_{21}}, \qquad \lim_{t\rightarrow\infty}\bigl\langle I_{2}(t)\bigr\rangle =\frac{\Upsilon_{11}R_{2}-\Upsilon_{21}R_{1}}{\Upsilon_{11}\Upsilon _{22}-\Upsilon_{12}\Upsilon_{21}}\quad \textit{a.s.}, \\& \lim_{t\rightarrow\infty}\bigl\langle S(t)\bigr\rangle = \frac{(u+\delta-uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+\delta)(u+d_{1})}{u^{2}+u\delta+up}\frac{\Upsilon _{22}R_{1}-\Upsilon_{12}R_{2}}{\Upsilon_{11}\Upsilon_{22}-\Upsilon _{12}\Upsilon_{21}} \\& \hphantom{\lim_{t\rightarrow\infty}\bigl\langle S(t)\bigr\rangle ={}}{}-\frac{(u+\delta)(u+d_{2})}{u^{2}+u\delta+up}\frac{\Upsilon _{11}R_{2}-\Upsilon_{21}R_{1}}{\Upsilon_{11}\Upsilon_{22}-\Upsilon _{12}\Upsilon_{21}}\quad \textit{a.s.}, \\& \lim_{t\rightarrow\infty}\bigl\langle V(t)\bigr\rangle = \frac{(p+uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+d_{1})p}{u(u+\delta+p)}\frac{\Upsilon _{22}R_{1}-\Upsilon_{12}R_{2}}{\Upsilon_{11}\Upsilon_{22}-\Upsilon _{12}\Upsilon_{21}} \\& \hphantom{\lim_{t\rightarrow\infty}\bigl\langle V(t)\bigr\rangle ={}}{}-\frac{(u+d_{2})}{u(u+\delta+p)}\frac{\Upsilon_{11}R_{2}-\Upsilon _{21}R_{1}}{\Upsilon_{11}\Upsilon_{22}-\Upsilon_{12}\Upsilon_{21}}\quad \textit{a.s.} \end{aligned}$$
Proof
Case (i): Note that
there exists an arbitrarily small constant \(\varepsilon>0\) such that when t is large enough, we have
From equation (23) and equation (27), when t is large enough, one has
Since \(\Upsilon_{11}R_{2}<\Upsilon_{21}R_{1}\) and \(\Upsilon_{11}\Upsilon _{22}>\Upsilon_{12}\Upsilon_{21}\), taking the limit superior of both sides of equation (31), applying equation (18) and the arbitrariness of ε, we have
That is to say,
By using the method of Case (ii) in Theorem 2.2, one obtains the persistence in mean of \(I_{1}(t)\), \(S(t)\) and \(V(t)\), and hence is omitted.
Case (ii): The proof of Case (ii) is similar to the proof of Case (i) in this subsection and hence is omitted.
Case (iii): Since \(\Upsilon_{11}R_{2}>\Upsilon_{21}R_{1}\) and \(\Upsilon_{11}\Upsilon_{22}>\Upsilon_{12}\Upsilon_{21}\), using Lemma 2.6 and the arbitrariness of ε for equation (31), one obtains that
Similarly, when \(\Upsilon_{22}R_{1}>\Upsilon_{12}R_{2}\), we have
From equation (32), there exists an arbitrarily small constant \(\varepsilon>0\) such that when t is large enough, we have
Applying equation (23) into equation (34), one obtains that
By using Lemma 2.6 and the arbitrariness of ε, we obtain that
Similarly, one obtains
Applying equations (32), (33), (35) and (36) leads to
Applying (13) and (37) into equation (12), we obtain that
Applying (37), (38), Lemmas 2.7 and 2.8 into equation (22), we have
This completes the proof. □
3 Conclusions and numerical simulations
In this paper, we propose a novel stochastic epidemic system with double epidemic diseases under vaccination. By using stochastic differential equation theory, we study the persistence in mean and extinction of the two diseases. Compared with the existing work in Refs. [39] and [40], the model constructed in this paper also considers the efficiency of vaccination. When all the coefficients related to the vaccination are 0, system (4) is similar to systems (2) and (3) in Refs. [39] and [40], in addition, our conclusion is consistent with them. That is to say, systems (2) and (3) in Refs. [39] and [40] are a special case of our system (4). The theoretical results of this article can be used as a reference for the control of infectious diseases.
To sum up, we have the following conclusions:
- I.:
-
Stochastic disease-free dynamics
When \(R_{1}<0\) and \(R_{2}<0\) hold, we have
$$\begin{aligned}& \lim_{t\rightarrow\infty}I_{i}(t)=0,\quad i=1,2,\qquad \lim _{t\rightarrow\infty }\bigl\langle S(t)\bigr\rangle =\frac{(u+\delta-uq)\Lambda}{u^{2}+u\delta+up}, \\& \lim_{t\rightarrow\infty}\bigl\langle V(t)\bigr\rangle =\frac{(p+uq)\Lambda }{u^{2}+u\delta+up}. \end{aligned}$$That is to say, the two epidemic diseases go to extinct almost surely.
- II.:
-
Stochastic endemic dynamics
-
(i)
If one of the following conditions holds:
-
\(R_{1}>0\), \(R_{2}<0\),
-
\(R_{1}, R_{2}>0\), \(\Upsilon_{11}R_{2}<\Upsilon_{21}R_{1}\),
then we have
$$\begin{aligned}& \lim_{t\rightarrow\infty}\bigl\langle I_{1}(t)\bigr\rangle = \frac{R_{1}}{\Upsilon _{11}}>0,\qquad \lim_{t\rightarrow\infty}I_{2}(t)=0\quad \mbox{a.s.}, \\& \lim_{t\rightarrow\infty}\bigl\langle S(t)\bigr\rangle = \frac{(u+\delta-uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+\delta)(u+d_{1})}{u^{2}+u\delta+up}\frac {R_{1}}{\Upsilon_{11}} \quad \mbox{a.s.}, \\& \lim_{t\rightarrow\infty}\bigl\langle V(t)\bigr\rangle = \frac{(p+uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+d_{1})p}{u(u+\delta+p)}\frac{R_{1}}{\Upsilon _{11}}\quad \mbox{a.s.} \end{aligned}$$That is to say, the epidemic disease \(I_{1}(t)\) is persistent in mean and \(I_{2}(t)\) is extinct.
-
-
(ii)
If one of the following conditions hold:
-
\(R_{1}<0\), \(R_{2}>0\),
-
\(R_{1}, R_{2}>0\), \(\Upsilon_{22}R_{1}<\Upsilon_{12}R_{2}\),
then we have
$$\begin{aligned}& \lim_{t\rightarrow\infty}\bigl\langle I_{1}(t)\bigr\rangle = 0, \qquad \lim_{t\rightarrow \infty}I_{2}(t)=\frac{R_{2}}{\Upsilon_{21}}>0\quad \mbox{a.s.}, \\& \lim_{t\rightarrow\infty}\bigl\langle S(t)\bigr\rangle = \frac{(u+\delta-uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+\delta)(u+d_{2})}{u^{2}+u\delta+up}\frac {R_{2}}{\Upsilon_{21}}\quad \mbox{a.s.}, \\& \lim_{t\rightarrow\infty}\bigl\langle V(t)\bigr\rangle = \frac{(p+uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+d_{2})p}{u(u+\delta+p)}\frac{R_{2}}{\Upsilon _{21}} \quad \mbox{a.s.} \end{aligned}$$That is to say, the epidemic disease \(I_{1}(t)\) is extinct and \(I_{2}(t)\) is persistent in mean.
-
-
(iii)
If \(\Upsilon_{11}R_{2}>\Upsilon_{21}R_{1}\), \(\Upsilon _{22}R_{1}>\Upsilon_{12}R_{2}\) hold, then we have
$$\begin{aligned}& \lim_{t\rightarrow\infty}\bigl\langle I_{1}(t)\bigr\rangle = \frac{\Upsilon _{22}R_{1}-\Upsilon_{12}R_{2}}{\Upsilon_{11}\Upsilon_{22}-\Upsilon _{12}\Upsilon_{21}}, \qquad \lim_{t\rightarrow\infty}\bigl\langle I_{2}(t)\bigr\rangle =\frac{\Upsilon_{11}R_{2}-\Upsilon_{21}R_{1}}{\Upsilon_{11}\Upsilon _{22}-\Upsilon_{12}\Upsilon_{21}} \quad \mbox{a.s.}, \\& \lim_{t\rightarrow\infty}\bigl\langle S(t)\bigr\rangle = \frac{(u+\delta-uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+\delta)(u+d_{1})}{u^{2}+u\delta+up}\frac{\Upsilon _{22}R_{1}-\Upsilon_{12}R_{2}}{\Upsilon_{11}\Upsilon_{22}-\Upsilon _{12}\Upsilon_{21}} \\& \hphantom{\lim_{t\rightarrow\infty}\bigl\langle S(t)\bigr\rangle ={}}{}-\frac{(u+\delta)(u+d_{2})}{u^{2}+u\delta+up}\frac{\Upsilon _{11}R_{2}-\Upsilon_{21}R_{1}}{\Upsilon_{11}\Upsilon_{22}-\Upsilon _{12}\Upsilon_{21}}\quad \mbox{a.s.}, \\& \lim_{t\rightarrow\infty}\bigl\langle V(t)\bigr\rangle = \frac{(p+uq)\Lambda }{u^{2}+u\delta+up}- \frac{(u+d_{1})p}{u(u+\delta+p)}\frac{\Upsilon _{22}R_{1}-\Upsilon_{12}R_{2}}{\Upsilon_{11}\Upsilon_{22}-\Upsilon _{12}\Upsilon_{21}} \\& \hphantom{\lim_{t\rightarrow\infty}\bigl\langle V(t)\bigr\rangle ={}}{}-\frac{(u+d_{2})}{u(u+\delta+p)}\frac{\Upsilon_{11}R_{2}-\Upsilon _{21}R_{1}}{\Upsilon_{11}\Upsilon_{22}-\Upsilon_{12}\Upsilon_{21}} \quad \mbox{a.s.} \end{aligned}$$That is to say, the epidemic diseases \(I_{1}\) and \(I_{2}\) are persistent in mean.
-
(i)
In [39, 41], Meng and Chang et al. obtained the lower boundedness of the persistence in mean for \(I_{1}\) and \(I_{2}\) as follows:
where \(m^{*}\) is a positive constant. However, this paper proves that \(I_{1}\) and \(I_{2}\) have their own limit, that is,
where \(m_{1}^{*}=\frac{\Upsilon_{22}R_{1}-\Upsilon_{12}R_{2}}{\Upsilon _{11}\Upsilon_{22}-\Upsilon_{12}\Upsilon_{21}}\) and \(m_{2}^{*}=\frac {\Upsilon_{11}R_{2}-\Upsilon_{21}R_{1}}{\Upsilon_{11}\Upsilon_{22}-\Upsilon _{12}\Upsilon_{21}}\). Thus this paper contains and significantly improves the results for persistence in mean in [39, 41]. The developed theoretical methods can be used to investigate the high-dimensional nonlinear stochastic differential systems.
To numerically illustrate our results, we employ a numerical method from [52] with ©Matlab2013b to the following discrete equations:
where \(\Delta t=0.01\), \(\Delta W_{ik}\triangleq W(t_{k+1})-W(t_{k})\) (\(i=1,2,3,4\)) obeys the Gaussian distribution \(N(0,\Delta t)\), \(\Delta \Gamma_{ik}\triangleq\Gamma(t_{k+1})-\Gamma(t_{k})\) obeys the Poisson distribution with intensity λ.
To this end, we set \(\Lambda=1\), \(q=0.1\), \(u=0.2\), \(p=0.2\), \(\beta_{1}=0.24\), \(\beta _{2}=0.27\), \(\alpha_{1}=1\), \(\alpha_{2}=1\), \(r_{1}=0.2\), \(r_{2}=0.1\), \(\delta=0.2\), \(d_{1}=0.2\), \(d_{2}=0.4\).
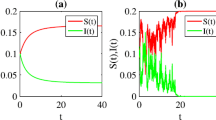
Figure 1(a) is the time sequence diagram of system (4) with \(\sigma_{i}=\gamma_{i}=0\), \(i=1,2,3,4\); Figure 1(b) is the corresponding phase diagram of \(I_{1}(t)\) and \(I_{2}(t)\). In this case, the two epidemic diseases are persistent.
Time sequence diagram and phase diagram of model ( 4 ) without stochastic effects.
In Figure 2, we choose \(\sigma_{1}=0.6\), \(\sigma_{2}=0.8\), \(\sigma_{3}=0.1\), \(\sigma _{4}=0.1\), \(\gamma_{1}=0.2\), \(\gamma_{2}=0.3\), \(\gamma_{3}=0.1\), \(\gamma_{4}=0.2\). In this case, \(R_{1}=-0.0377<0\), \(R_{2}=-0.2026<0\). We see that in the time sequence diagram Figure 2(a) and the corresponding phase diagram Figure 2(b), the two epidemic diseases are extinct.
Time sequence diagram and phase diagram of model ( 4 ) for extinction of two epidemic diseases.
In Figure 3, we choose \(\sigma_{1}=0.2\), \(\sigma_{2}=0.6\), \(\sigma_{3}=0.1\), \(\sigma _{4}=0.1\), \(\gamma_{1}=0.3\), \(\gamma_{2}=0.3\), \(\gamma_{3}=0.1\), \(\gamma_{4}=0.2\). In this case, \(R_{1}=0.1024>0\), \(R_{2}=-0.0626<0\). We see that in the time sequence diagram Figure 3(a) and the corresponding phase diagram Figure 3(b), the epidemic disease \(I_{1}(t)\) is persistent in mean and \(I_{2}(t)\) is extinct.
Time sequence diagram and phase diagram of model ( 4 ) for extinctions of disease 2 and persistence of disease 1.
In Figure 4, we choose \(\sigma_{1}=0.6\), \(\sigma_{2}=0.2\), \(\sigma_{3}=0.1\), \(\sigma _{4}=0.1\), \(\gamma_{1}=0.3\), \(\gamma_{2}=0.3\), \(\gamma_{3}=0.1\), \(\gamma_{4}=0.2\). In this case, \(R_{1}=-0.0576<0\), \(R_{2}=0.0974>0\). We see that in the time sequence diagram Figure 4(a) and the corresponding phase diagram Figure 4(b), the epidemic disease \(I_{2}(t)\) is persistent in mean and \(I_{1}(t)\) is extinct.
Time sequence diagram and phase diagram of model ( 4 ) for extinctions of disease 1 and persistence of disease 2.
In Figure 5, we choose \(\sigma_{1}=0.3\), \(\sigma_{2}=0.14\), \(\sigma_{3}=0.1\), \(\sigma_{4}=0.1\), \(\gamma_{1}=0.1\), \(\gamma_{2}=0.1\), \(\gamma_{3}=0.1\), \(\gamma_{4}=0.1\). In this case, \(R_{1}=0.0123>0\), \(R_{2}=0.0079>0\). We see that in the time sequence diagram Figure 2(a) and the corresponding phase diagram Figure 2(b), the two epidemic diseases are persistent in mean.
Time sequence diagram and phase diagram of model ( 4 ) for persistence of two diseases.
Obviously, the numerical simulation results are consistent with the conclusion of our theorems.
References
Lakshmikantham, V, Vatsala, AS: Theory of Differential and Integral Inequalities with Initial Time Difference and Applications. Springer, Berlin (1999)
Bai, ZB, Zhang, S, Sun, SJ, Yin, C: Monotone iterative method for fractional differential equations. Electron. J. Differ. Equ. 2016, 6 (2016)
Cui, YJ: Uniqueness of solution for boundary value problems for fractional differential equations. Appl. Math. Lett. 51, 48-54 (2016)
Zhang, Y, Dong, HH, Zhang, XE, Yang, HW: Rational solutions and lump solutions to the generalized \((3+1)\)-dimensional shallow water-like equation. Comput. Math. Appl. 73, 246-252 (2017)
Jleli, M, Kirane, M, Samet, B: Lyapunov-type inequalities for fractional partial differential equations. Appl. Math. Lett. 66, 30-39 (2017)
Liu, M, Bai, CZ: Analysis of a stochastic tri-trophic food-chain model with harvesting. J. Math. Biol. 73, 597-625 (2016)
Meng, XZ, Wang, L, Zhang, TH: Global dynamics analysis of a nonlinear impulsive stochastic chemostat system in a polluted environment. J. Appl. Anal. Comput. 6, 865-875 (2016)
Liu, Q, Jiang, DQ, Shi, NZ, Hayat, T, Alsaedi, A: Stochastic mutualism model with Lévy jumps. Commun. Nonlinear Sci. Numer. Simul. 43, 78-90 (2016)
Feng, T, Meng, XZ, Liu, LD, Gao, SJ: Application of inequalities technique to dynamics analysis of a stochastic eco-epidemiology model. J. Inequal. Appl. 2016, 327 (2016)
Liu, Q, Jiang, DQ, Shi, NZ, Hayat, T, Alsaedi, A: Dynamics of a stochastic tuberculosis model with constant recruitment and varying total population size. Phys. A, Stat. Mech. Appl. 469, 518-530 (2017)
Liu, LD, Meng, XZ: Optimal harvesting control and dynamics of two-species stochastic model with delays. Adv. Differ. Equ. 2017, 18 (2017)
Gao, SJ, Zhang, FM, He, YY: The effects of migratory bird population in a nonautonomous eco-epidemiological model. Appl. Math. Model. 37, 3903-3916 (2013)
Zhang, H, Chen, LS, Nieto, JJ: A delayed epidemic model with stage-structure and pulses for pest management strategy. Nonlinear Anal., Real World Appl. 9, 1714-1726 (2008)
Cheng, HD, Zhang, TQ: A new predator-prey model with a profitless delay of digestion and impulsive perturbation on the prey. Appl. Math. Comput. 217, 9198-9208 (2011)
Jiao, JJ, Cai, SH, Zhang, YJ, Zhang, LM: Dynamics of a stage-structured single population system with winter hibernation and impulsive effect in polluted environment. Int. J. Biomath. 9, 277-294 (2016)
Zhao, W, Zhang, T, Chang, Z, Meng, X, Liu, Y: Dynamical analysis of SIR epidemic models with distributed delay. J. Appl. Math. 2013, Article ID 154387 (2013)
Zhang, TQ, Ma, WB, Meng, XZ, Zhang, TH: Periodic solution of a prey-predator model with nonlinear state feedback control. Appl. Math. Comput. 266, 95-107 (2015)
Li, ZX, Chen, LS: Dynamical behaviors of a trimolecular response model with impulsive input. Nonlinear Dyn. 62, 167-176 (2010)
Shi, RQ, Jiang, XW, Chen, LS: A predator-prey model with disease in the prey and two impulses for integrated pest management. Appl. Math. Model. 33, 2248-2256 (2009)
Zhang, TQ, Meng, XZ, Song, Y, Zhang, TH: A stage-structured predator-prey SI model with disease in the prey and impulsive effects. Math. Model. Anal. 18, 505-528 (2013)
Bai, ZB, Dong, XY, Yin, C: Existence results for impulsive nonlinear fractional differential equation with mixed boundary conditions. Bound. Value Probl. 2016, 63 (2016)
Zhang, SQ, Meng, XZ, Zhang, TH: Dynamics analysis and numerical simulations of a stochastic non-autonomous predator-prey system with impulsive effects. Nonlinear Anal. Hybrid Syst. 26, 19-37 (2017)
Pounds, JA, Bustamante, MR, Coloma, LA, Consuegra, JA, Fogden, MP, Foster, PN, La, ME, Masters, KL, Merinoviteri, A, Puschendorf, R: Widespread amphibian extinctions from epidemic disease driven by global warming. Nature 7073, 161-167 (2006)
Hernández-Suárez, CM: A Markov chain approach to calculate \(r_{0}\)in stochastic epidemic models. J. Theor. Biol. 215, 83-93 (2002)
Amador, J: The SEIQS stochastic epidemic model with external source of infection. Appl. Math. Model. 40, 8352-8365 (2016)
Zhao, DL: Study on the threshold of a stochastic SIR epidemic model and its extensions. Commun. Nonlinear Sci. Numer. Simul. 38, 172-177 (2016)
Area, I, Batarfi, H, Losada, J, Nieto, JJ, Shammakh, W, Ángela, T: On a fractional order Ebola epidemic model. Adv. Differ. Equ. 2015, 278 (2015)
Li, HD, Peng, R, Wang, FB: Varying total population enhances disease persistence: qualitative analysis on a diffusive sis epidemic model. J. Differ. Equ. 262, 885-913 (2016)
Teng, ZD, Wang, L: Persistence and extinction for a class of stochastic SIS epidemic models with nonlinear incidence rate. Phys. A, Stat. Mech. Appl. 451, 507-518 (2016)
Kermack, WO, Mckendrick, AG: A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond., Ser. A, Math. Phys. Eng. Sci. 115, 700-721 (1927)
Wang, JL, Muroya, Y, Kuniya, T: Global stability of a time-delayed multi-group SIS epidemic model with nonlinear incidence rates and patch structure. J. Math. Anal. Appl. 425, 415-439 (2015)
Zhang, TQ, Meng, XZ, Zhang, TH: Global analysis for a delayed SIV model with direct and environmental transmissions. J. Appl. Anal. Comput. 6, 479-491 (2016)
Chen, YM, Zou, SF, Yang, JY: Global analysis of an SIR epidemic model with infection age and saturated incidence. Nonlinear Anal., Real World Appl. 30, 16-31 (2016)
Zhou, XY, Cui, JA: Analysis of stability and bifurcation for a SEIR epidemic model with saturated recovery rate. Commun. Nonlinear Sci. Numer. Simul. 16, 4438-4450 (2011)
Roberts, MG, Saha, AK: The asymptotic behaviour of a logistic epidemic model with stochastic disease transmission. Appl. Math. Lett. 12, 37-41 (1999)
Emvudu, Y, Bongor, D, Koïna, R: Mathematical analysis of hiv/aids stochastic dynamic models. Appl. Math. Model. 40, 9131-9151 (2016)
Nieto, JJ, Ouahab, A, Rodríguez-López, R: Random fixed point theorems in partially ordered metric spaces. Fixed Point Theory Appl. 2016, 98 (2016)
Liu, M, Fan, M: Permanence of stochastic Lotka-Volterra systems. J. Math. Anal. Appl. 27, 425-452 (2017)
Meng, XZ, Zhao, SN, Feng, T, Zhang, TH: Dynamics of a novel nonlinear stochastic SIS epidemic model with double epidemic hypothesis. J. Math. Anal. Appl. 433, 227-242 (2016)
Zhang, XH, Jiang, DQ, Hayat, T, Ahmad, B: Dynamics of a stochastic SIS model with double epidemic diseases driven by Lévy jumps. Phys. A, Stat. Mech. Appl. 471, 767-777 (2017)
Chang, ZB, Meng, XZ, Lu, X: Analysis of a novel stochastic SIRS epidemic model with two different saturated incidence rates. Phys. A, Stat. Mech. Appl. 472, 103-116 (2017)
Molyneux, DH: ‘Neglected’ diseases but unrecognised successes - challenges and opportunities for infectious disease control. Lancet 364, 380-383 (2004)
Hinman, AR: Global progress in infectious disease control. Vaccine 16, 1116-1121 (1998)
Zhao, YN, Jiang, DQ, O’Regan, D: The extinction and persistence of the stochastic SIS epidemic model with vaccination. Phys. A, Stat. Mech. Appl. 392, 4916-4927 (2013)
Liu, XS, Dai, BX: Flip bifurcations of an SIR epidemic model with birth pulse and pulse vaccination. Appl. Math. Model. 43, 579-591 (2017)
Gao, SJ, Chen, LS, Nieto, JJ, Torres, A: Analysis of a delayed epidemic model with pulse vaccination and saturation incidence. Vaccine 24, 6037-6045 (2006)
Meng, XZ, Chen, LS, Wu, B: A delay SIR epidemic model with pulse vaccination and incubation times. Nonlinear Anal., Real World Appl. 11, 88-98 (2010)
Friedman, A: Stochastic Differential Equations and Applications. Academic Press, New York (1975)
Zhao, Y, Yuan, SL: Stability in distribution of a stochastic hybrid competitive Lotka-Volterra model with Lévy jumps. Chaos Solitons Fractals 85, 98-109 (2016)
Øksendal, B, Sulem, A: Applied Stochastic Control of Jump Diffusions. Springer, Berlin (2005)
Liu, M, Wang, K: Stochastic Lotka-Volterra systems with Lévy noise. J. Math. Anal. Appl. 410, 750-763 (2014)
Zou, XL, Wang, K: Numerical simulations and modeling for stochastic biological systems with jumps. Commun. Nonlinear Sci. Numer. Simul. 19, 1557-1568 (2014)
Acknowledgements
This research was partially supported by the National Natural Science Foundation of China (11371230, 11501331, 11561004), by the SDUST Research Fund (2014TDJH102), Shandong Provincial Natural Science Foundation, China (ZR2015AQ001, BS2015SF002), by Joint Innovative Center for Safe And Effective Mining Technology and Equipment of Coal Resources, the Open Foundation of the Key Laboratory of Jiangxi Province for Numerical Simulation and Emulation Techniques, Gannan Normal University, China, by SDUST Innovation Fund for Graduate Students (SDKDYC170225).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The work presented in this paper has been accomplished through contributions of all authors. All authors read and approved the final manuscript.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Leng, X., Feng, T. & Meng, X. Stochastic inequalities and applications to dynamics analysis of a novel SIVS epidemic model with jumps. J Inequal Appl 2017, 138 (2017). https://doi.org/10.1186/s13660-017-1418-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-017-1418-8