1 Introduction

Neural networks can be modeled either as a static neural network model or as a local field neural network model according to the modeling approaches [1, 2]. The typical static neural networks are the recurrent back-propagation networks and the projection networks. The Hopfield neural network is a typical example of the local field neural networks. The two types of neural networks have attained broad applications in knowledge acquisition, combinatorial optimization, pattern recognition, and other areas [3]. But these two types of neural networks are not equivalent in general. Static neural networks can be transferred into local field neural networks only under some preconditions. However, the preconditions are usually not satisfied. Hence, it is necessary to study static neural networks.

In practical implementation of neural networks, time delays are inevitably encountered and may lead to instability or significantly deteriorated performances [4]. Therefore, the dynamics of delayed systems which include delayed neural networks has received considerable attention during the past years and many results have been achieved [5–19]. As is well known, the Lyapunov-Krasovskii functional method is the most commonly used method in the investigation of dynamics of the delayed neural networks. The conservativeness of this approach mainly lies in two aspects: the construction of Lyapunov-Krasovskii functional and the estimation of its time-derivative. In order to get less conservative results, a variety of methods were proposed. First of all, several types of Lyapunov-Krasovskii functional were presented such as an augmented Lyapunov-Krasovskii functional [20] and a delay-decomposing Lyapunov-Krasovskii functional [21]. Second, novel integral inequalities were proposed to obtain a tighter upper bound of the integrals occurring in the time-derivative of the Lyapunov-Krasovskii functional. Wirtinger’s integral inequality [22], the free-matrix-based integral inequality [23], the integral inequality including a double integral [24] were typical examples of these integral inequalities.

In a practical situation, it is impossible to completely acquire the state information of all neurons in neural networks because of their complicated structure. So it is worth to investigate the state estimation of neural networks. Recently, some results on the state estimation of neural networks have been obtained [25–27]. In addition, in analog VLSI implementations of neural networks, uncertainties, which can be modeled as an energy-bounded input noise, should be taken into account because of the tolerances of the utilized electronic elements. Therefore, it is of practical significance to study the \(\mathcal{H_{\infty}}\) state estimation of the delayed neural networks. Some significant results on this issue have been reported by some researchers [28–34]. For instance, in [28], the state estimation problem of the guaranteed \(\mathcal{H_{\infty}}\) performance of static neural networks was discussed. In [31], based on the reciprocally convex combination technique and a double-integral inequality, a delay-dependent condition was derived such that the error system was globally exponentially stable and a prescribed \(\mathcal{H_{\infty}}\) performance was guaranteed. In [32], further improved results were proposed by using zero equalities and a reciprocally convex approach [35].

In the above mentioned results [28–33], the lower bound of time-varying delay was always assumed to be 0. However, in the real world, the time-varying delay may be an interval delay, which means that the lower bound of the delay is not restricted to be 0. In this case, the criteria in [28–33] guaranteeing the \(\mathcal{H_{\infty}}\) performance of the state estimation cannot be applied because they did not consider the information of the lower bound of the delay. In [34], by constructing an augmented Lyapunov-Krasovskii functional, the guaranteed \(\mathcal{H_{\infty}}\) performance state estimation problem of static neural networks with interval time-varying delay was discussed. Slack variables were introduced in order to derive less conservative results, but the computational burden was increased at the same time [34]. Thus, there remains room to improve the results reported in [34], which is one of the motivations of this paper.

In this paper, the problem of an \(\mathcal{H_{\infty}}\) state estimation for static neural networks with interval time-varying delay is investigated. The activation function is assumed to satisfy a sector-bounded condition. On one hand, a modified Lyapunov-Krasovskii functional is constructed which takes information of the lower bound of the time-varying delay into account. Compared with the Lyapunov-Krasovskii functional in [34], the one proposed in this paper is simple, since some terms such as \(V_{4}(t)\) in [34] are removed. On the other hand, Wirtinger’s integral inequality, which can provide a tighter upper bound than the ones derived based on Jensen’s inequality, is employed to deal with the integral appearing in the derivative. Based on the constructed Lyapunov-Krasovskii functional and the new integral inequality, an improved delay-dependent criterion is derived such that the resulting error system is globally asymptotically stable with guaranteed \(\mathcal{H_{\infty}}\) performance. Compared with existing relevant conclusions, the criterion in this paper has less conservativeness as well as a lower computational burden. In addition, when the lower bound of the time-varying delay is 0, a new delay-dependent \(\mathcal{H_{\infty }}\) state estimation condition is also obtained, which can provide a better performance than the existing results. Simulation results are provided to demonstrate the effectiveness of the presented method.

Notations

The notations are quite standard. Throughout this paper, \(R^{n}\) and \(R^{n\times m}\) denote respectively, the n-dimensional Euclidean space and the set of all \(n\times m\) real matrices. \(\operatorname{diag}(\cdot)\) denotes the diagonal matrix. For real symmetric matrices X and Y, the notations \(X\geq Y\) (respectively, \(X>Y\)) means that the matrix \(X-Y\) is a positive semi-definite (respectively, positive definite). The symbol ∗ within a matrix represents the symmetric term of the matrix.

2 Problem description and preliminaries

In this paper, the following delayed static neural network subject to noise disturbance was considered:

$$ \begin{aligned} &\dot{x}(t) = -Ax(t)+f\bigl(Wx\bigl(t-h(t) \bigr)+J\bigr)+B_{1}w(t), \\ &y(t) = Cx(t)+Dx\bigl(t-h(t)\bigr)+B_{2}w(t), \\ &z(t) = Hx(t), \\ &x(t) = \psi(t),\quad t\in[-h_{2}, 0], \end{aligned} $$
(1)

where \(x(t)=[x_{1}(t), x_{2}(t), \ldots, x_{n}(t)]^{T}\in R^{n}\) is the state vector of the neural network associated with n neurons, \(y(t) \in R^{m}\) is the network output measurement, \(z(t) \in R^{p}\), to be estimated, is a linear combination of the states, \(w(t) \in R^{q}\) is the noise input belonging to \(\mathcal{L}_{2}[0, \infty)\), \(A=\operatorname{diag}\{a_{1}, a_{2}, \ldots, a_{n}\}>0\) describes the rate with which the ith neuron will reset its potential to the resting state in isolation when disconnected from the networks and external inputs, \(W=[w_{ij}]_{n\times n}\) is the delayed connection weight matrix, \(B_{1}\), \(B_{2}\), C, D, and H are real known constant matrices with appropriate dimensions. \(f(x(t))=[f_{1}(x_{1}(t)), f_{2}(x_{2}(t)), \ldots, f_{n}(x_{n}(t))]^{T}\) denotes the continuous activation function, \(J=[J_{1}, J_{2}, \ldots, J_{n}]^{T}\) is the exogenous input vector. \(\psi(t)\) is the initial condition. \(h(t)\) denotes the time-varying delay satisfying

$$ 0\leq h_{1} \leq h(t) \leq h_{2}, \qquad \dot{h}(t)\leq\mu, $$
(2)

where \(h_{1}\), \(h_{2}\), μ are known constants.

The neuron activation function \(f_{i}(\cdot)\) satisfies

$$ k^{-}_{i}\leq\frac{f_{i}(x)-f_{i}(y)}{x-y}\leq k^{+}_{i}, \quad i=1,2,\ldots ,n, x\neq y, $$
(3)

where \(k^{-}_{i}\), \(k^{+}_{i}\) are some known constants.

Remark 1

Compared with [29, 30, 34], the activation function considered in this paper is more general since \(k^{-}_{i}\), \(k^{+}_{i}\) in (3) may be positive, zero or negative.

For the neural network (1), we construct a state estimator for estimation of \(z(t)\):

$$ \begin{aligned} &\dot{\hat{x}}(t)=-A\hat{x}(t)+f\bigl(W \hat{x}\bigl(t-h(t)\bigr)+J\bigr)+K\bigl(y(t)-\hat {y}(t)\bigr), \\ &\hat{y}(t)=C\hat{x}(t)+D\hat{x}\bigl(t-h(t)\bigr), \\ &\hat{z}(t)=H\hat{x}(t), \\ &\hat{x}(t)=0,\quad t\in[-h_{2}, 0], \end{aligned} $$
(4)

where \(\hat{x}(t)\in R^{n}\) denotes the estimated state, \(\hat{z}(t)\in R^{p}\) denotes the estimated measurement of \(z(t)\), and K is the state estimator gain matrix to be determined.

Define the error by \(r(t)=x(t)-\hat{x}(t)\), and \(\bar{z}(t)=z(t)-\hat{z}(t)\). Then, based on (1) and (4), we can easily obtain the error system of the form

$$ \begin{aligned} &\dot{r}(t) = -(A+KC)r(t)-KDr\bigl(t-h(t) \bigr)+g\bigl(Wr\bigl(t-h(t)\bigr)\bigr) +(B_{1}-KB_{2})w(t), \\ &\bar{z}(t) = Hr(t), \end{aligned} $$
(5)

where \(g(Wr(t))=f(Wx(t)+J)-f(W\hat{x}(t)+J)\).

To proceed, we need the following useful definition and lemmas.

Definition 1

Given a prescribed level of noise attenuation \(\gamma> 0\), find a proper state estimator (4) such that the equilibrium point of the resulting error system (5) with \(w(t)=0\) is globally asymptotically stable, and

$$ \bigl\| \bar{z}(t)\bigr\| _{2}< \gamma\bigl\| w(t)\bigr\| _{2} $$
(6)

under zero-initial conditions for all nonzero \(w(t)\in\mathcal {L}_{2}[0,\infty)\), where \(\|x(t)\|_{2}= \sqrt{\int_{0}^{\infty}x^{T}(t)x(t)\,dt}\). In this case, the error system (5) is said to be globally asymptotically stable with \(\mathcal{H_{\infty}}\) performance γ.

Lemma 1

([35])

Let \(f_{1}, f_{2}, \ldots , f_{N}: R^{m}\rightarrow R\) have positive values in an open subsets D of \(R^{m}\). Then the reciprocally convex combination of \(f_{i}\) over D satisfies

$$ \min_{\{\alpha_{i}|\alpha_{i}>0, \sum _{i}\alpha_{i}=1\} }\sum_{i} \frac{1}{\alpha_{i}}f_{i}(t)=\sum_{i}f_{i}(t)+ \max_{g_{ij}(t)}\sum_{i\neq j}g_{ij}(t) $$
(7)

subject to

$$ \left\{g_{ij}: R^{m}\rightarrow R, g_{j,i}(t)=g_{i,j}(t), \begin{pmatrix} f_{i}(t) & g_{i,j}(t) \\ g_{i,j}(t) & f_{j}(t) \end{pmatrix} \geq0 \right\}. $$
(8)

Lemma 2

([22])

For a given matrix \(R>0\), the following inequality holds for all continuously differentiable function x in \([a,b]\rightarrow R^{n}\):

$$ -(b-a) \int_{a}^{b}\dot{x}^{T}(s)R\dot{x}(s)\,ds \leq -\bigl[x(b)-x(a)\bigr]^{T}R\bigl[x(b)-x(a)\bigr]-3 \Omega^{T}R\Omega, $$
(9)

where \(\Omega=x(b)+x(a)-\frac{2}{b-a}\int_{a}^{b}x(s)\,ds\).

3 Main results

In this section, we first establish a delay-dependent sufficient condition under which system (5) is asymptotically stable with a prescribed \(\mathcal{H_{\infty}}\) performance γ.

Theorem 1

For given scalars \(0< h_{1}< h_{2}\), \(\mu, \gamma>0\), \(K_{1}=\operatorname{diag}\{k^{-}_{1}, k^{-}_{2}, \ldots, k^{-}_{n}\}\), and \(K_{2}=\operatorname{diag}\{k^{+}_{1}, k^{+}_{2}, \ldots, k^{+}_{n}\}\), the error system (5) is globally asymptotically stable with \(\mathcal{H_{\infty}}\) performance γ if there exist real matrices \(P>0\), \(Q>0\), \(Z_{1}>0\), \(Z_{2}>0\), \(Z_{3}>0\), \(Z_{4}>0\), \(R>0\), \(T_{1}=\operatorname{diag}\{t_{11}, t_{12}, \ldots, t_{1n}\}>0\), \(T_{2}=\operatorname{diag}\{t_{21}, t_{22}, \ldots, t_{2n}\}>0\), and matrices \(S_{11}\), \(S_{12}\), \(S_{21}\), \(S_{22}\), M, G with appropriate dimensions such that the following LMIs are satisfied:

$$\begin{aligned}& \Pi^{*}_{[h(t)=h_{1}]}< 0,\quad\quad \Pi^{*}_{[h(t)=h_{2}]}< 0, \end{aligned}$$
(10)
$$\begin{aligned}& \begin{pmatrix} Z_{2} & 0 & S_{11} & S_{12}\\ \ast& 3Z_{2} & S_{21} & S_{22}\\ \ast& \ast& Z_{2} & 0\\ \ast& \ast& \ast& 3Z_{2} \end{pmatrix} >0, \end{aligned}$$
(11)

where

$$\begin{aligned}& P= \begin{pmatrix} P_{11} & P_{12} & P_{13}\\ \ast& P_{22} & P_{23}\\ \ast& \ast& P_{33} \end{pmatrix} ,\quad\quad R= \begin{pmatrix} R_{11} & R_{12}\\ \ast& R_{22} \end{pmatrix} , \\& \Pi_{[h(t)]}^{*}= \begin{pmatrix} \Pi& \hat{H} \\ \ast& -I \end{pmatrix} ,\quad \Pi=[\Pi_{ij}]_{11\times11}, \hat{H}=[H \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0]^{T}, \\& \Pi_{11}=P_{12}+P^{T}_{12}-4Z_{1}+Z_{3}+ \mu R_{11}+R_{12}+R^{T}_{12}+R_{22} \\& \hphantom{\Pi_{11}=}{}-MA -(MA)^{T}-(1-\mu) \bigl(R_{12}+R^{T}_{12} \bigr)-(1-\mu )R_{22}-GC-(GC)^{T} \\& \hphantom{\Pi_{11}=}{} -2W^{T}K_{1}T_{1}K_{2}W, \\& \Pi_{12}=(1-\mu)R_{12}+(1-\mu)R_{22}-GD, \quad\quad\Pi _{13}=-P_{12}+P_{13}-2Z_{1} -R_{12}-R_{22}, \\& \Pi_{14}=-P_{13},\quad\quad \Pi _{15}=W^{T}(K_{1}+K_{2})T_{1}, \quad\quad \Pi_{16}=M,\quad\quad \Pi_{17}=h_{1}P^{T}_{22}+6Z_{1},\\& \Pi _{18}=\bigl(h(t)-h_{1}\bigr)P_{23}, \quad\quad \Pi_{19}=\bigl(h_{2}-h(t)\bigr)P_{23},\quad\quad \Pi_{1,10}=MB_{1}-GB_{2}, \\& \Pi _{1,11}=P_{11}+\bigl(h(t)-h_{1} \bigr)R_{11}+\bigl(h(t)-h_{1}\bigr)R_{12}+ \bigl(h(t)-h_{1}\bigr)R^{T}_{12}+\bigl(h(t)-h_{1}\bigr)R_{22} \\& \hphantom{\Pi_{1,11}=}{} -M-(MA)^{T}-(GC)^{T}, \\& \Pi_{22}=-(1-\mu )R_{22}-8Z_{2}+S_{11}+S^{T}_{11}+S_{12}+S^{T}_{12}-S_{21}-S^{T}_{21}-S_{22}-S^{T}_{22} \\& \hphantom{\Pi_{22}=}{} -2W^{T}K_{1}T_{2}K_{2}W, \\& \Pi_{23}=-2Z_{2}-S^{T}_{11}-S^{T}_{12}-S^{T}_{21}-S^{T}_{22}, \\& \Pi_{24}=Z_{2}-3Z_{2}-S_{11}+S_{12}+S_{21}-S_{22},\quad\quad \Pi _{26}=W^{T}(K_{1}+K_{2})T_{2}, \\& \Pi_{28}=6Z_{2}+2S^{T}_{21}+2S^{T}_{22},\quad\quad \Pi _{29}=6Z_{2}-2S_{12}+2S_{22}, \\& \Pi_{2,11}=-(GD)^{T},\quad\quad \Pi_{33}=-Z_{3}+Z_{4}-4Z_{1}-4Z_{2}+R_{22}, \\& \Pi_{34}=S_{11}-S_{12}+S_{21}-S_{22},\quad\quad \Pi _{37}=-h_{1}P^{T}_{22}+h_{1}P^{T}_{23}+6Z_{1}, \\& \Pi_{38}=-\bigl(h(t)-h_{1}\bigr)P_{23}+ \bigl(h(t)-h_{1}\bigr)P^{T}_{33}+6Z_{2}, \\& \Pi_{39}=-\bigl(h_{2}-h(t)\bigr)P_{23}+ \bigl(h_{2}-h(t)\bigr)P^{T}_{33}+2S_{12}+2S_{22}, \\& \Pi_{44}=-Z_{4}-4Z_{2},\quad\quad \Pi_{47}=-h_{1}P^{T}_{23}, \\& \Pi_{48}=-\bigl(h(t)-h_{1}\bigr)P^{T}_{33}-2S^{T}_{21}+2S^{T}_{22},\quad\quad \Pi _{49}=-\bigl(h_{2}-h(t)\bigr)P^{T}_{33}+6Z_{2}, \\& \Pi_{55}=Q-2T_{1}, \quad\quad\Pi_{66}=-(1- \mu)Q-2T_{2}, \quad\quad\Pi _{6,11}=M^{T}, \\& \Pi_{77}=-12Z_{1},\quad\quad \Pi_{7,11}=h_{1}P^{T}_{12},\quad\quad \Pi_{88}=-12Z_{2},\quad\quad \Pi _{89}=-4S_{22}, \\& \Pi _{8,11}=\bigl(h(t)-h_{1}\bigr)P^{T}_{13}- \bigl(h(t)-h_{1}\bigr)R^{T}_{12}- \bigl(h(t)-h_{1}\bigr)R_{22}, \\& \Pi_{99}=-12Z_{2},\quad\quad \Pi_{9,11}= \bigl(h_{2}-h(t)\bigr)P^{T}_{13}, \quad\quad\Pi _{10,10}=-\gamma^{2}, \\& \Pi_{10,11}=B^{T}_{1}M^{T}-B^{T}_{2}G^{T},\quad\quad \Pi _{11,11}=h^{2}_{1}Z_{1}+(h_{2}-h_{1})^{2}Z_{2}-M-M^{T}. \end{aligned}$$

Moreover, the gain matrix K of the state estimator of (4) can be designed as \(K=M^{-1}G\).

Proof

Construct the following Lyapunov-Krasovskii functional:

$$ V(t)=V_{1}(t)+V_{2}(t)+V_{3}(t)+V_{4}(t)+V_{5}(t), $$
(12)

with

$$\begin{aligned}& V_{1}(t)= \begin{pmatrix} r(t) \\ \int_{t-h_{1}}^{t}r(s)\,ds \\ \int_{t-h_{2}}^{t-h_{1}}r(s)\,ds \end{pmatrix} ^{T} \begin{pmatrix} P_{11} & P_{12} & P_{13}\\ \ast& P_{22} & P_{23}\\ \ast& \ast& P_{33} \end{pmatrix} \begin{pmatrix} r(t) \\ \int_{t-h_{1}}^{t}r(s)\,ds \\ \int_{t-h_{2}}^{t-h_{1}}r(s)\,ds \end{pmatrix} , \\& V_{2}(t)= \int_{t-h(t)}^{t}g^{T}\bigl(Wr(s)\bigr)Qg \bigl(Wr(s)\bigr)\,ds, \\& V_{3}(t)=h_{1} \int_{-h_{1}}^{0} \int_{t+\theta}^{t}\dot {r}^{T}(s)Z_{1} \dot{r}(s)\,ds\,d\theta+h_{12} \int_{-h_{2}}^{-h_{1}} \int _{t+\theta}^{t}\dot{r}^{T}(s)Z_{2} \dot{r}(s)\,ds\,d\theta, \\& V_{4}(t)= \int_{t-h_{1}}^{t}r^{T}(s)Z_{3}r(s)\,ds+ \int _{t-h_{2}}^{t-h_{1}}r^{T}(s)Z_{4}r(s)\,ds, \\& V_{5}(t)= \int_{t-h(t)}^{t-h_{1}} \begin{pmatrix} r(t) \\ \int_{s}^{t}\dot{r}(u)\,du \end{pmatrix} ^{T} \begin{pmatrix} R_{11} & R_{12}\\ \ast& R_{22} \end{pmatrix} \begin{pmatrix} r(t) \\ \int_{s}^{t}\dot{r}(u)\,du \end{pmatrix} \,ds, \end{aligned}$$

where \(h_{12}=h_{2}-h_{1}\).

The time derivative of \(V(t)\) along the trajectory of system (5) is given by

$$ \dot{V}(t)=\dot{V}_{1}(t)+\dot{V}_{2}(t)+ \dot{V}_{3}(t)+\dot {V}_{4}(t)+\dot{V}_{5}(t), $$
(13)

where

$$\begin{aligned} \dot{V}_{1}(t) =&2 \begin{pmatrix} r(t) \\ h_{1}u \\ ((h(t)-h_{1})v_{1} +(h_{2}-h(t))v_{2}) \end{pmatrix} ^{T} \begin{pmatrix} P_{11} & P_{12} & P_{13}\\ \ast& P_{22} & P_{23}\\ \ast& \ast& P_{33} \end{pmatrix} \\ &{}\times \begin{pmatrix} \dot{r}(t) \\ r(t)-r(t-h_{1}) \\ r(t-h_{1})-r(t-h_{2}) \end{pmatrix} \\ =&2r^{T}(t)P_{11} \dot {r}(t)+2r^{T}(t)P_{12}r(t)-2r^{T}(t)P_{12}r(t-h_{1}) \\ &{}+2r^{T}(t)P_{13}r(t-h_{1})-2r^{T}(t)P_{13}r(t-h_{2})+2h_{1}u^{T}P^{T}_{12} \dot {r}(t) \\ &{}+2h_{1}u^{T}P_{22}r(t)-2h_{1}u^{T}P_{22}r(t-h_{1})+2h_{1}u^{T}P_{23}r(t-h_{1}) \\ &{}-2h_{1}u^{T}P_{23}r(t-h_{2})+2 \bigl[h(t)-h_{1}\bigr]v^{T}_{1}P^{T}_{13} \dot {r}(t) \\ &{}+2\bigl[h_{2}-h(t)\bigr]v^{T}_{2}P^{T}_{13} \dot {r}(t)+2\bigl[h_{2}-h(t)\bigr]v^{T}_{2}P^{T}_{23}r(t) \\ &{}+2\bigl[h(t)-h_{1}\bigr]v^{T}_{1}P^{T}_{23}r(t)-2 \bigl[h(t)-h_{1}\bigr]v^{T}_{1}P^{T}_{23}r(t-h_{1}) \\ &{}-2\bigl[h_{2}-h(t)\bigr]v^{T}_{2}P^{T}_{23}r(t-h_{1})+2 \bigl[h(t)-h_{1}\bigr]v^{T}_{1}P_{33}r(t-h_{1}) \\ &{}-2\bigl[h(t)-h_{1}\bigr]v^{T}_{1}P_{33}r(t-h_{2})+2 \bigl[h_{2}-h(t)\bigr]v^{T}_{2}P_{33}r(t-h_{1}) \\ &{}-2\bigl[h_{2}-h(t)\bigr]v^{T}_{2}P_{33}r(t-h_{2}), \end{aligned}$$
(14)

where \(u=\frac{1}{h_{1}}\int_{t-h_{1}}^{t}r(s)\,ds\), \(v_{1}=\frac{1}{h(t)-h_{1}}\int_{t-h(t)}^{t-h_{1}}r(s)\,ds\), \(v_{2}=\frac {1}{h_{2}-h(t)}\int_{t-h_{2}}^{t-h(t)}r(s)\,ds\),

$$\begin{aligned}& \dot{V}_{2}(t) \leq g^{T}\bigl(Wr(t)\bigr)Qg\bigl(Wr(t) \bigr) \\& \hphantom{\dot{V}_{2}(t) \leq}{}-(1-\mu)g^{T}\bigl(Wr\bigl(t-h(t)\bigr)\bigr)Qg\bigl(Wr\bigl(t-h(t) \bigr)\bigr), \end{aligned}$$
(15)
$$\begin{aligned}& \dot{V}_{3}(t) = h^{2}_{1} \dot{r}^{T}(t)Z_{1}\dot {r}(t)+(h_{2}-h_{1})^{2} \dot{r}^{T}(t)Z_{2}\dot{r}(t) \\& \hphantom{\dot{V}_{3}(t) =}{} -h_{1} \int_{t-h_{1}}^{t}\dot{r}^{T}(s)Z_{1} \dot {r}(s)\,ds-(h_{2}-h_{1}) \int_{t-h_{2}}^{t-h_{1}}\dot{r}^{T}(s)Z_{2} \dot{r}(s)\,ds, \end{aligned}$$
(16)

based on Lemma 2, one can have

$$\begin{aligned}& -h_{1} \int_{t-h_{1}}^{t}\dot{r}^{T}(s)Z_{1} \dot{r}(s)\,ds \\& \quad\leq -\bigl[r(t)-r(t-h_{1})\bigr]^{T}Z_{1} \bigl[r(t)-r(t-h_{1})\bigr] \\& \quad\quad{}-\bigl[r(t)+r(t-h_{1})-2u\bigr]^{T}3Z_{1} \bigl[r(t)+r(t-h_{1})-2u\bigr], \end{aligned}$$
(17)

by employing Lemma 1 and Lemma 2, we can derive

$$\begin{aligned}& -(h_{2}-h_{1}) \int_{t-h_{2}}^{t-h_{1}}\dot{r}^{T}(s)Z_{2} \dot {r}(s)\,ds \\& \quad= -(h_{2}-h_{1}) \int_{t-h(t)}^{t-h_{1}}\dot{r}^{T}(s)Z_{2} \dot {r}(s)\,ds-(h_{2}-h_{1}) \int_{t-h_{2}}^{t-h(t)}\dot{r}^{T}(s)Z_{2} \dot{r}(s)\,ds \\& \quad\leq -\alpha _{1}\bigl[r(t-h_{1})-r\bigl(t-h(t)\bigr) \bigr]^{T}Z_{2}\bigl[r(t-h_{1})-r\bigl(t-h(t) \bigr)\bigr] \\& \quad\quad{}-3\alpha _{1}\bigl[r(t-h_{1})+r\bigl(t-h(t) \bigr)-2v_{1}\bigr]^{T}Z_{2}\bigl[r(t-h_{1})+r \bigl(t-h(t)\bigr)-2v_{1}\bigr] \\& \quad\quad{}-\alpha _{2}\bigl[r\bigl(t-h(t)\bigr)-r(t-h_{2}) \bigr]^{T}Z_{2}\bigl[r\bigl(t-h(t)\bigr)-r(t-h_{2}) \bigr] \\& \quad\quad{}-3\alpha _{2}\bigl[r\bigl(t-h(t)\bigr)+r(t-h_{2})-2v_{2} \bigr]^{T}Z_{2}\bigl[r\bigl(t-h(t)\bigr)+r(t-h_{2})-2v_{2} \bigr] \\& \quad\leq -\beta^{T}(t) \begin{pmatrix} Z_{2} & 0 & S_{11} & S_{12}\\ \ast& 3Z_{2} & S_{21} & S_{22}\\ \ast& \ast& Z_{2} & 0\\ \ast& \ast& \ast& 3Z_{2} \end{pmatrix} \beta(t), \end{aligned}$$
(18)

where

$$\begin{aligned}& \alpha_{1}=(h_{2}-h_{1})/ \bigl(h(t)-h_{1}\bigr),\\& \alpha _{2}=(h_{2}-h_{1})/ \bigl(h_{2}-h(t)\bigr), \\& \beta^{T}(t)=\bigl[r^{T}(t-h_{1})-r^{T} \bigl(t-h(t)\bigr), r^{T}(t-h_{1})+r^{T} \bigl(t-h(t)\bigr)-2v^{T}_{1}, \\& \hphantom{\beta^{T}(t)=} r^{T}\bigl(t-h(t)\bigr)-r^{T}(t-h_{2}), r^{T}\bigl(t-h(t)\bigr)+r^{T}(t-h_{2})-2v^{T}_{2} \bigr]. \end{aligned}$$

Calculating \(\dot{V}_{4}(t)\), \(\dot{V}_{5}(t)\) yields

$$\begin{aligned}& \dot{V}_{4}(t) = r^{T}(t)Z_{3}r(t)-r^{T}(t-h_{1})Z_{3}r(t-h_{1}) \\& \hphantom{\dot{V}_{4}(t) =}{}+r^{T}(t-h_{1})Z_{4}r(t-h_{1})-r^{T}(t-h_{2})Z_{4}r(t-h_{2}), \end{aligned}$$
(19)
$$\begin{aligned}& \dot{V}_{5}(t) \leq \begin{pmatrix} r(t)\\ \int_{t-h_{1}}^{t}\dot{r}(u)\,du \end{pmatrix} ^{T} \begin{pmatrix} R_{11} & R_{12}\\ \ast& R_{22} \end{pmatrix} \begin{pmatrix} r(t)\\ \int_{t-h_{1}}^{t}\dot{r}(u)\,du \end{pmatrix} \\& \hphantom{\dot{V}_{5}(t) \leq}{} -(1-\mu) \begin{pmatrix} r(t)\\ \int_{t-h(t)}^{t}\dot{r}(u)\,du \end{pmatrix} ^{T} \begin{pmatrix} R_{11} & R_{12}\\ \ast& R_{22} \end{pmatrix} \begin{pmatrix} r(t)\\ \int_{t-h(t)}^{t}\dot{r}(u)\,du \end{pmatrix} \\& \hphantom{\dot{V}_{5}(t) \leq}{}+2 \int_{t-h(t)}^{t-h_{1}} \begin{pmatrix} r(t) \\ \int_{s}^{t}\dot{r}(u)\,du \end{pmatrix} ^{T} \begin{pmatrix} R_{11} & R_{12}\\ \ast& R_{22} \end{pmatrix} \begin{pmatrix} \dot{r}(t) \\ \dot{r}(t) \end{pmatrix} \,ds \\& \hphantom{\dot{V}_{5}(t) }{}= r^{T}(t)R_{11}r(t)+r^{T}(t)R_{12}r(t)-r^{T}(t)R_{12}r(t-h_{1})+r^{T}(t)R^{T}_{12}r(t) \\& \hphantom{\dot{V}_{5}(t) \leq}{}-r^{T}(t-h_{1})R^{T}_{12}r(t)+r^{T}(t)R_{22}r(t)-r^{T}(t)R_{22}r(t-h_{1}) \\& \hphantom{\dot{V}_{5}(t) \leq}{}-r^{T}(t-h_{1})R_{22}r(t)+r^{T}(t-h_{1})R_{22}r(t-h_{1}) \\& \hphantom{\dot{V}_{5}(t) \leq}{}-(1-\mu)r^{T}(t)R_{11}r(t)-(1-\mu)r^{T}(t)R_{12}r(t) \\& \hphantom{\dot{V}_{5}(t) \leq}{}+(1-\mu)r^{T}(t)R_{12}r\bigl(t-h(t)\bigr)-(1- \mu)r^{T}(t)R^{T}_{12}r(t) \\& \hphantom{\dot{V}_{5}(t) \leq}{}+(1-\mu)r^{T}\bigl(t-h(t)\bigr)R^{T}_{12}r(t)-(1- \mu)r^{T}(t)R_{22}r(t) \\& \hphantom{\dot{V}_{5}(t) \leq}{}+(1-\mu)r^{T}(t)R_{22}r\bigl(t-h(t)\bigr)+(1-\mu )r^{T}\bigl(t-h(t)\bigr)R_{22}r(t) \\& \hphantom{\dot{V}_{5}(t) \leq}{}-(1-\mu)r^{T}\bigl(t-h(t)\bigr)R_{22}r\bigl(t-h(t)\bigr) \\& \hphantom{\dot{V}_{5}(t) \leq}{}+2 \bigl[h(t)-h_{1}\bigr]r^{T}(t)R_{11}\dot {r}(t)+2\bigl[h(t)-h_{1}\bigr]r^{T}(t)R_{12} \dot{r}(t) \\& \hphantom{\dot{V}_{5}(t) \leq}{}+2 \int _{t-h(t)}^{t-h_{1}}\bigl[r(t)-r(s)\bigr]^{T}R^{T}_{12} \dot{r}(t)\,ds+2 \int_{t-h(t)}^{t-h_{1}}\bigl[r(t)-r(s)\bigr]^{T}R_{22} \dot{r}(t)\,ds \\& \hphantom{\dot{V}_{5}(t) }{}= r^{T}(t)\bigl[\mu R_{11}+R_{12}+R^{T}_{12}+R_{22}-(1- \mu ) \bigl(R_{12}+R^{T}_{12}\bigr)-(1-\mu)R_{22}\bigr]r(t) \\& \hphantom{\dot{V}_{5}(t) \leq}{} +(1-\mu)r^{T}(t) (R_{12}+R_{22})r\bigl(t-h(t)\bigr) +(1-\mu )r^{T}\bigl(t-h(t)\bigr) \bigl(R^{T}_{12}+R_{22} \bigr)r(t) \\& \hphantom{\dot{V}_{5}(t) \leq}{}-r^{T}(t) (R_{12}+R_{22})r(t-h_{1})-r^{T}(t-h_{1}) \bigl(R^{T}_{12}+R_{22} \bigr)r(t)+r^{T}(t-h_{1})R_{22}r(t-h_{1}) \\& \hphantom{\dot{V}_{5}(t) \leq}{}+2\bigl[h(t)-h_{1}\bigr]r^{T}(t)\bigl[R_{11}+R_{12}+R^{T}_{12}+R_{22} \bigr]\dot {r}(t) \\& \hphantom{\dot{V}_{5}(t) \leq}{}-2\bigl[h(t)-h_{1}\bigr]v^{T}_{1} \bigl[R^{T}_{12}+R_{22}\bigr]\dot{r}(t). \end{aligned}$$
(20)

According to (3), for any positive definite diagonal matrices \(T_{1}\), \(T_{2}\), the following inequalities hold:

$$\begin{aligned}& -2g^{T}\bigl(Wr(t)\bigr)T_{1}g\bigl(Wr(t) \bigr)+2r^{T}(t)W^{T}(K_{1}+K_{2})T_{1}g \bigl(Wr(t)\bigr) \\& \quad{} -2r^{T}(t)W^{T}K_{1}T_{1}K_{2}Wr(t) \geq0, \end{aligned}$$
(21)
$$\begin{aligned}& -2g^{T}\bigl(Wr\bigl(t-h(t)\bigr)\bigr)T_{2}g\bigl(Wr \bigl(t-h(t)\bigr)\bigr) +2r^{T}\bigl(t-h(t)\bigr)W^{T}(K_{1}+K_{2})T_{2}g \bigl(Wr\bigl(t-h(t)\bigr)\bigr) \\& \quad{}-2r^{T}\bigl(t-h(t)\bigr)W^{T}K_{1}T_{2}K_{2}Wr \bigl(t-h(t)\bigr)\geq0. \end{aligned}$$
(22)

Furthermore, for any matrix M with appropriate dimension, the following equation holds:

$$\begin{aligned}& \bigl(2r^{T}(t)+2\dot{r}^{T}(t)\bigr)M\bigl[-\dot {r}(t)-(A+KC)r(t)-KDr\bigl(t-h(t)\bigr) \\& \quad{}+g\bigl(Wr\bigl(t-h(t)\bigr)\bigr)+(B_{1}-KB_{2})w(t) \bigr]=0. \end{aligned}$$
(23)

Under the zero-initial condition, it is obvious that \(V(r(t))|_{t=0}=0\). For convenience, let

$$ J_{\infty}= \int_{0}^{\infty}\bigl[\bar{z}^{T}(t) \bar{z}(t)-\gamma^{2}w^{T}(t)w(t)\bigr]\,dt. $$
(24)

Then for any nonzero \(w(t)\in\mathcal{L}_{2}[0,\infty)\), we obtain

$$\begin{aligned} J_{\infty} \leq& \int_{0}^{\infty}\bigl[\bar{z}^{T}(t) \bar{z}(t)-\gamma ^{2}w^{T}(t)w(t)\bigr]\,dt+V\bigl(r(t)\bigr) \big|_{t\rightarrow\infty}-V\bigl(r(t)\bigr)\big| _{t=0} \\ =& \int_{0}^{\infty}\bigl[\bar{z}^{T}(t) \bar{z}(t)-\gamma ^{2}w^{T}(t)w(t)+\dot{V}(t)\bigr]\,dt. \end{aligned}$$
(25)

From (13)-(25), one has

$$ \bar{z}^{T}(t)\bar{z}(t)-\gamma^{2}w^{T}(t)w(t)+ \dot{V}(t)\leq\xi ^{T}(t)\Phi\xi(t), $$
(26)

where

$$\begin{aligned} \xi^{T}(t) =&\bigl[r^{T}(t), r^{T}\bigl(t-h(t) \bigr), r^{T}(t-h_{1}), r^{T}(t-h_{2}), \\ &g^{T}\bigl(Wr(t)\bigr),g^{T}\bigl(Wr\bigl(t-h(t)\bigr)\bigr), u^{T}, v^{T}_{1}, v^{T}_{2}, w^{T}(t), \dot {r}^{T}(t)\bigr], \end{aligned}$$

and \(\Phi=[\Phi_{ij}]_{11\times11}\) with \(\Phi_{11}=\Pi_{11}+H^{T}H\), \(\Phi_{ij}=\Pi_{ij} \) (\(i\leq j\), \(1\leq i \leq11\), \(2 \leq j \leq11\)). By applying the Schur complement, \(\Phi<0\) is equivalent to \(\Pi^{*}<0\). Then, if (10) holds, we can ensure the error system (5) with the guaranteed \(\mathcal{H_{\infty}}\) performance defined by Definition 1.

In the sequel, we will show that the equilibrium point of (5) with \(w(t)=0\) is globally asymptotically stable if (10) holds. When \(w(t)=0\), the error system (5) becomes

$$ \dot{r}(t) = -(A+KC)r(t)-KDr\bigl(t-h(t)\bigr)+g\bigl(Wr\bigl(t-h(t)\bigr) \bigr). $$
(27)

We still consider the Lyapunov-Krasovskii functional candidate (12) and calculate its time-derivative along the trajectory of (27). We can easily obtain

$$ \dot{V}(t)\leq\bar{\xi}^{T}(t)\bar{\Pi}^{\ast}\bar{\xi}(t), $$
(28)

where

$$\begin{aligned} \bar{\xi}^{T}(t) =&\bigl[r^{T}(t), r^{T} \bigl(t-h(t)\bigr), r^{T}(t-h_{1}), r^{T}(t-h_{2}), \\ &g^{T}\bigl(Wr(t)\bigr),g^{T}\bigl(Wr\bigl(t-h(t)\bigr)\bigr), u^{T}, v^{T}_{1}, v^{T}_{2}, \dot {r}^{T}(t)\bigr], \end{aligned}$$

and \(\bar{\Pi}^{*}=[\bar{\Pi}^{*}_{ij}]_{10\times10}\) with

$$\begin{aligned}& \bar{\Pi}^{\ast}_{11}=P_{12}+P^{T}_{12}-4Z_{1}+Z_{3}+ \mu R_{11}+R_{12}+R^{T}_{12}+R_{22} \\& \hphantom{\bar{\Pi}^{\ast}_{11}=}{}-MA-(MA)^{T}-(1-\mu) \bigl(R_{12}+R^{T}_{12} \bigr)-(1-\mu )R_{22}-GC-(GC)^{T} \\& \hphantom{\bar{\Pi}^{\ast}_{11}=}{} -2W^{T}K_{1}T_{1}K_{2}W, \\& \bar{\Pi}^{\ast}_{12}=(1-\mu)R_{12}+(1- \mu)R_{22}-GD,\quad\quad \bar{\Pi}^{\ast }_{13}=-P_{12}+P_{13}-2Z_{1} -R_{12}-R_{22}, \\& \bar{\Pi}^{\ast}_{14}=-P_{13},\quad\quad \bar{\Pi}^{\ast }_{15}=W^{T}(K_{1}+K_{2})T_{1},\quad\quad \bar{\Pi}^{\ast}_{16}=M, \\& \bar{\Pi}^{\ast}_{17}=h_{1}P^{T}_{22}+6Z_{1},\quad\quad \bar{\Pi}^{\ast }_{18}=\bigl(h(t)-h_{1} \bigr)P_{23}, \quad\quad\bar{\Pi}^{\ast }_{19}= \bigl(h_{2}-h(t)\bigr)P_{23}, \\& \bar{\Pi}^{\ast }_{1,10}=P_{11}+\bigl(h(t)-h_{1} \bigr)R_{11}+\bigl(h(t)-h_{1}\bigr)R_{12}+ \bigl(h(t)-h_{1}\bigr)R^{T}_{12}+\bigl(h(t)-h_{1}\bigr)R_{22} \\& \hphantom{\bar{\Pi}^{\ast}_{1,10}=}{}-M-(MA)^{T}-(GC)^{T}, \\& \bar{\Pi}^{\ast}_{22}=-(1-\mu )R_{22}-8Z_{2}+S_{11}+S^{T}_{11}+S_{12}+S^{T}_{12}-S_{21}-S^{T}_{21}-S_{22}-S^{T}_{22} \\& \hphantom{ \bar{\Pi}^{\ast}_{22}=}{}-2W^{T}K_{1}T_{2}K_{2}W, \\& \bar{\Pi}^{\ast }_{23}=-2Z_{2}-S^{T}_{11}-S^{T}_{12}-S^{T}_{21}-S^{T}_{22}, \\& \bar{\Pi}^{\ast}_{24}=Z_{2}-3Z_{2}-S_{11}+S_{12}+S_{21}-S_{22},\quad\quad \bar {\Pi}^{\ast}_{26}=W^{T}(K_{1}+K_{2})T_{2}, \\& \bar{\Pi}^{\ast}_{28}=6Z_{2}+2S^{T}_{21}+2S^{T}_{22},\quad\quad \bar{\Pi}^{\ast }_{29}=6Z_{2}-2S_{12}+2S_{22},\quad\quad \bar{\Pi}^{\ast }_{2,10}=-(GD)^{T}, \\& \bar{\Pi}^{\ast}_{33}=-Z_{3}+Z_{4}-4Z_{1}-4Z_{2}+R_{22},\quad\quad \bar{\Pi }^{\ast}_{34}=S_{11}-S_{12}+S_{21}-S_{22}, \\& \bar{\Pi}^{\ast}_{37}=-h_{1}P^{T}_{22}+h_{1}P^{T}_{23}+6Z_{1},\quad\quad \bar {\Pi}^{\ast}_{38}=-\bigl(h(t)-h_{1} \bigr)P_{23}+\bigl(h(t)-h_{1}\bigr)P^{T}_{33} +6Z_{2}, \\& \bar{\Pi}^{\ast }_{39}=- \bigl(h_{2}-h(t)\bigr)P_{23}+\bigl(h_{2}-h(t) \bigr)P^{T}_{33}+2S_{12}+2S_{22}, \\& \bar{\Pi}^{\ast}_{44}=-Z_{4}-4Z_{2},\quad\quad \bar{\Pi}^{\ast }_{47}=-h_{1}P^{T}_{23},\quad\quad \bar{\Pi}^{\ast }_{48}=-\bigl(h(t)-h_{1} \bigr)P^{T}_{33}-2S^{T}_{21}+2S^{T}_{22}, \\& \bar{\Pi}^{\ast}_{49}=-\bigl(h_{2}-h(t) \bigr)P^{T}_{33}+6Z_{2}, \quad\quad\bar{\Pi}^{\ast }_{55}=Q-2T_{1},\quad\quad \bar{\Pi}^{\ast}_{66}=-(1-\mu)Q-2T_{2}, \\& \bar{\Pi}^{\ast}_{6,10}=M^{T},\quad\quad \bar{ \Pi}^{\ast}_{77}=-12Z_{1},\quad\quad \bar { \Pi}^{\ast}_{7,10}=h_{1}P^{T}_{12},\quad\quad \bar{\Pi}^{\ast }_{88}=-12Z_{2}, \\& \bar{\Pi}^{\ast}_{89}=-4S_{22},\quad\quad \bar{ \Pi}^{\ast }_{8,10}=\bigl(h(t)-h_{1} \bigr)P^{T}_{13}-\bigl(h(t)-h_{1} \bigr)R^{T}_{12}-\bigl(h(t)-h_{1} \bigr)R_{22}, \\& \bar{\Pi}^{\ast}_{99}=-12Z_{2}, \quad\quad\bar{ \Pi}^{\ast }_{9,10}=\bigl(h_{2}-h(t) \bigr)P^{T}_{13}, \\& \bar{\Pi}^{\ast }_{10,10}=h^{2}_{1}Z_{1}+(h_{2}-h_{1})^{2}Z_{2}-M-M^{T}. \end{aligned}$$

It is obvious that if \(\Pi^{*}_{[h(t)=h_{1}]}<0\), \(\Pi ^{*}_{[h(t)=h_{2}]}<0\), then \(\bar{\Pi}^{*}_{[h(t)=h_{1}]}<0\), \(\bar{\Pi }^{*}_{[h(t)=h_{2}]}<0\). So system (27) is globally asymptotically stable. Moreover, if (10) holds, the state estimator (4) for the static neural networks (1) has the guaranteed \(\mathcal{H_{\infty}}\) performance and guarantees the globally asymptotically stable of the error system (5). This completes the proof. □

Remark 2

The time-varying delay in [28–33] was always assumed to satisfy \(0\leq h(t)\leq h\), which is a special case of the condition (2) in this paper. Therefore, compared with [28–33], the time-varying delay discussed in this paper is less restrictive. In [30, 31], for the sake of converting a nonlinear matrix inequality into a linear matrix inequality, some inequalities such as \(-PT^{-1}P\leq-2P+T\), which lack freedom and may lead to some conservativeness for the derived results, were utilized in the discussion of the guaranteed \(\mathcal{H}_{\infty}\) performance state estimation problem. In our paper, the zero equality (23) is used to avoid this problem, which can give much flexibility in solving LMIs. In [32], Jensen’s integral inequality, which ignored some terms and may introduce conservativeness to some extent, was employed to estimate the upper bound of the time derivative of the Lyapunov-Krasovskii functional. In this paper, Wirtinger’s integral inequality, which takes information not only on the state and the delayed state of a system, but also on the integral of the state over the period of the delay into account, is exploited to give an estimation of the time derivative of the Lyapunov-Krasovskii functional.

Remark 3

Based on a Lyapunov-Krasovskii functional with triple integrals involving augmented terms, the guaranteed \(\mathcal{H}_{\infty}\) performance state estimation problem of static neural networks with interval time-varying delay was investigated in [34], and a sufficient criterion guaranteeing the globally asymptotical stability of the error system (5) for a given \(\mathcal{H}_{\infty}\) performance index was obtained [34]. Since the augmented Lyapunov-Krasovskii functional contained more information, the criterion derived in [34] had less conservativeness than most of the previous results [28–33]. However, the computational burden increased at the same time because of the augmented Lyapunov-Krasovskii functional. Compared with the results in [34], the advantages of the method used in this paper mainly rely on two aspects. First, the Lyapunov-Krasovskii functional is simpler than that in [34], since the triple integrals and other augmented terms in [34] are not needed, which will reduce the computational complexity. Second, in the proof of Theorem 1, Wirtinger’s integral inequality, which includes Jensen’s integral inequality, and a reciprocally convex approach are employed to estimate the upper bound of the derivative of the Lyapunov-Krasovskii functional, which will yield less conservative results.

When \(0\leq h(t)\leq h\), that is, the lower bound of the time-varying delay is 0, we introduce the Lyapunov-Krasovskii functional as follows:

$$ V(t)=\sum_{i=1}^{5}V_{i}(t), $$
(29)

with

$$\begin{aligned}& V_{1}(t) = \begin{pmatrix} r(t) \\ \int_{t-h}^{t}r(s)\,ds \end{pmatrix} ^{T} \begin{pmatrix} P_{11} & P_{12}\\ \ast& P_{22} \end{pmatrix} \begin{pmatrix} r(t) \\ \int_{t-h}^{t}r(s)\,ds \end{pmatrix} , \\& V_{2}(t) = \int_{t-h(t)}^{t}g^{T}\bigl(Wr(s)\bigr)Qg \bigl(Wr(s)\bigr)\,ds, \\& V_{3}(t) = h \int_{-h}^{0} \int_{t+\theta}^{t}\dot{r}^{T}(s)Z_{2} \dot {r}(s)\,ds\,d\theta, \\& V_{4}(t) = \int_{t-h}^{t}r^{T}(s)Z_{4}r(s)\,ds, \\& V_{5}(t) = \int_{t-h(t)}^{t} \begin{pmatrix} r(t) \\ \int_{s}^{t}\dot{r}(u)\,du \end{pmatrix} ^{T} \begin{pmatrix} R_{11} & R_{12}\\ \ast& R_{22} \end{pmatrix} \begin{pmatrix} r(t) \\ \int_{s}^{t}\dot{r}(u)\,du \end{pmatrix} \,ds. \end{aligned}$$

By a similar method to that employed in Theorem 1, we can obtain the following corollary.

Corollary 1

For given scalars h, μ, and \(\gamma>0\), the error system (5) is globally asymptotically stable with the \(\mathcal{H_{\infty}}\) performance γ if there exist real matrices \(P>0\), \(Q>0\), \(Z_{2}>0\), \(Z_{4}>0\), \(R>0\), \(T_{1}=\operatorname{diag}\{t_{11}, t_{12}, \ldots, t_{1n}\}>0\), \(T_{2}=\operatorname{diag}\{t_{21}, t_{22}, \ldots, t_{2n}\}>0\), and matrices \(S_{11}\), \(S_{12}\), \(S_{21}\), \(S_{22}\), M, G with appropriate dimensions such that the following LMIs are satisfied:

$$\begin{aligned}& \Xi^{*}_{[h(t)=0]}< 0, \quad\quad\Xi^{*}_{[h(t)=h]}< 0, \end{aligned}$$
(30)
$$\begin{aligned}& \begin{pmatrix} Z_{2} & 0 & S_{11} & S_{12}\\ \ast& 3Z_{2} & S_{21} & S_{22}\\ \ast& \ast& Z_{2} & 0\\ \ast& \ast& \ast& 3Z_{2} \end{pmatrix} >0, \end{aligned}$$
(31)

where

$$\begin{aligned}& P= \begin{pmatrix} P_{11} & P_{12} \\ \ast& P_{22} \end{pmatrix} ,\quad\quad R= \begin{pmatrix} R_{11} & R_{12}\\ \ast& R_{22} \end{pmatrix} , \\& \Xi_{[h(t)]}^{*}= \begin{pmatrix} \Xi& \bar{H} \\ \ast& -I \end{pmatrix} , \quad\Xi=[\Xi_{ij}]_{9\times9}, \bar{H}=[H \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 0]^{T}, \\& \Xi_{11}=P_{12}+P^{T}_{12}-4Z_{2}+Z_{4}\\& \hphantom{\Xi_{11}=}{}-MA-(MA)^{T}-GC-(GC)^{T}+ \mu R_{11}-(1-\mu) \bigl(R_{12}+R^{T}_{12}\bigr)-(1-\mu )R_{22} \\& \hphantom{\Xi_{11}=}{} -2W^{T}K_{1}T_{1}K_{2}W, \\& \Xi_{12}=-2Z_{2}-S_{11}-S_{12}-S_{21}-S_{22}-GD+(1- \mu)R_{12}+(1-\mu )R_{22}, \\& \Xi_{13}=-P_{12}+S_{11}-S_{12}+S_{21}-S_{22},\quad\quad \Xi _{14}=W^{T}(K_{1}+K_{2})T_{1}, \\& \Xi_{15}=M,\quad\quad \Xi_{16}=h(t)P^{T}_{22}+6Z_{2},\quad\quad \Xi _{17}=\bigl(h-h(t)\bigr)P^{T}_{22}+2S_{12}+2S_{22}, \\& \Xi_{18}=MB_{1}-GB_{2}, \\& \Xi _{19}=P_{11}-M-(MA)^{T}-(GC)^{T}+h(t)R_{11} +h(t)R_{12}+h(t)R^{T}_{12}+h(t)R_{22}, \\& \Xi _{22}=-8Z_{2}+S_{11}+S^{T}_{11}+S_{12}+S^{T}_{12}-S_{21}-S^{T}_{21}-S_{22}-S^{T}_{22} -(1-\mu)R_{22} \\& \hphantom{\Xi _{22}=}{}-2W^{T}K_{1}T_{2}K_{2}W, \\& \Xi_{23}=-2Z_{2}-S_{11}+S_{12}+S_{21}-S_{22},\quad\quad \Xi _{25}=W^{T}(K_{1}+K_{2})T_{2}, \\& \Xi_{26}=6Z_{2}+2S^{T}_{21}+2S^{T}_{22},\quad\quad \Xi _{27}=6Z_{2}-2S_{12}+2S_{22}, \\& \Xi_{29}=-(GD)^{T},\quad\quad \Xi_{33}=-4Z_{2}-Z_{4},\quad\quad \Xi _{36}=-h(t)P^{T}_{22}-2S^{T}_{21}+2S^{T}_{22}, \\& \Xi_{37}=-\bigl(h-h(t)\bigr)P^{T}_{22}+6Z_{2},\quad\quad \Xi_{44}=Q-2T_{1},\quad\quad \Xi _{55}=-(1- \mu)Q-2T_{2}, \\& \Xi_{59}=M^{T},\quad\quad \Xi_{66}=-12Z_{2},\quad\quad \Xi_{67}=-4S_{22}, \quad\quad\Xi _{69}=h(t)P^{T}_{12}-h(t)R^{T}_{12} -h(t)R_{22}, \\& \Xi_{77}=-12Z_{2},\quad\quad \Xi_{79}=\bigl(h-h(t)\bigr)P^{T}_{12},\quad\quad \Xi _{88}=-\gamma^{2}, \\& \Xi_{89}=(MB_{1})^{T}-(GB_{2})^{T},\quad\quad \Xi _{99}=h^{2}Z_{2}-M-M^{T}. \end{aligned}$$

Moreover, the gain matrix K of the state estimator of (4) can be designed as \(K=M^{-1}G\).

Remark 4

As an effective approach to establish the delay-dependent stability criteria for delayed neural networks, the complete delay-decomposing approach was proposed in [21], which significantly reduced the conservativeness of the derived stability criteria. A novel Lyapunov-Krasovskii functional decomposing the delay in all integral terms was constructed. Since delay information can be taken fully into account by dividing the delay interval into several subintervals, less conservative results may be obtained. The computational burden for the complete delay-decomposing approach will increase with the increasing number of subintervals. In order to get less conservative results as well as less computational burden, the number of the subintervals should be chosen properly. Jensen’s inequality was used to estimate the derivative of the Lyapunov-Krasovskii functional in [21]. The conservativeness of the derived result in this paper can be further reduced by our method with the complete delay-decomposing approach [21].

Remark 5

The integral inequality method and the free-weighting matrix method are two main techniques to deal with the bounds of the integrals that appear in the derivative of Lyapunov-Krasovskii functional for stability analysis of delayed neural networks. A free-matrix-based integral inequality was developed and was applied to a stability analysis of systems with time-varying delay [23]. A free-matrix-based integral inequality implied Wirtinger’s inequality as a special case. The free matrices can provide freedom in reducing the conservativeness of the inequality. This new inequality was used to derive improved delay-dependent stability criteria although the computational burden increased because of the introduction of free-weighting matrices. The free-matrix-based integral inequality in [23] made use of information as regards only a single integral of the system state. Different from the free-matrix-based integral inequality, a new integral inequality was developed basing on information as regards a double integral of the system state in [24]. It also included the Wirtinger-based integral inequality. By employing a free-matrix-based integral inequality [23] or the novel integral inequality in [24], less conservative results than those obtained in our paper may be further derived.

4 Examples

Example 1

Consider the system with the following parameters:

$$\begin{aligned}& A= \begin{pmatrix} 7.0214 & 0 \\ 0 & 7.4367 \end{pmatrix} ,\quad\quad W= \begin{pmatrix} -6.4993 & -12.0257 \\ -0.6867 & 5.6614 \end{pmatrix} , \\& B_{1}= \begin{pmatrix} 0.2 \\ 0.2 \end{pmatrix} , \quad\quad J= \begin{pmatrix} 0 \\ 0 \end{pmatrix} ,\quad\quad H= \begin{pmatrix} 1 & 1 \\ 0 & -1 \end{pmatrix} , \\& C= (\begin{matrix} 1 & 0 \end{matrix}) , \quad\quad D= (\begin{matrix} 2 & 0 \end{matrix}) , \quad\quad B_{2}=-0.1, \\& K_{1}= \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} ,\quad\quad K_{2}= \begin{pmatrix} 0.5 & 0 \\ 0 & 0.5 \end{pmatrix} . \end{aligned}$$

Based on Theorem 1, we can derive the optimal \(\mathcal{H_{\infty}}\) performance index for different \(h_{1}\), \(h_{2}\), and μ. The results are stated in Table 1. From Table 1, it is observed that Theorem 1 in this paper can provide less conservative results than [34]. It is worth pointing out that the criterion in [34] does not work when \(h_{1}=0.5\), \(h_{2}=0.9\), \(\mu=1.2\), but Theorem 1 in our paper can provide a feasible solution of the optimal \(\mathcal{H_{\infty}}\) performance index. It should also be noted that the number of variables involved in [34] is 207, and Theorem 1 only needs 72 variables. Now, let \(h(t)=0.7+0.2\sin(6t)\), \(f(x)=0.5\tanh(x)\), and \(w(t)=\cos(t)e^{-12t}\), then \(0.5\leq h(t) \leq0.9\), \(\dot{h}(t)\leq1.2\). Consider the design of the guaranteed \(\mathcal{H_{\infty}}\) performance state estimator studied above, by employing the MATLAB LMI toolbox to solve the problem, the gain matrix K can be designed as

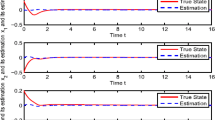
$$ K= \begin{pmatrix} -0.8979 \\ -0.0388 \end{pmatrix} $$

with the optimal \(H_{\infty}\) performance index \(\gamma=0.2555\). Figure 1 represents the responses of the error \(r(t)\) under the initial condition \(r(0)=[-1\ 1]^{T}\). It confirms the effectiveness of the presented approach to the design of the state estimator with \(H_{\infty}\) guaranteed performance for delayed static neural networks.

Figure 1
figure 1

The response of the error \(\pmb{r(t)}\) for given initial value in Example  1 .

Full size image
Table 1 The \(\pmb{\mathcal{H_{\infty}}}\) performance index γ with different \(\pmb{(h_{1}, h_{2}, \mu)}\)
Full size table

Example 2

Consider the system with the following parameters:

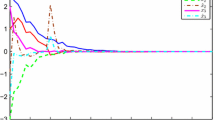
$$\begin{aligned}& A= \begin{pmatrix} 0.96 & 0 & 0 \\ 0 & 0.8 & 0 \\ 0 & 0 & 1.48 \end{pmatrix} ,\quad\quad W= \begin{pmatrix} 0.5 & 0.3 & -0.36 \\ 0.1 & 0.12 & 0.5 \\ -0.42 & 0.78 & 0.9 \end{pmatrix} , \\& H= \begin{pmatrix} 1 & 1 & 0\\ 1 & 0 & -1 \\ 0 & 1 & 1 \end{pmatrix} , \quad\quad J= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} ,\quad\quad B_{1}= \begin{pmatrix} 0.1 \\ 0.2 \\ 0.1 \end{pmatrix} , \\& C= (\begin{matrix} 1 & 0 & -2 \end{matrix}) ,\quad\quad D= (\begin{matrix} 0.5 & 0 & -1 \end{matrix}) ,\quad\quad B_{2}=-0.1, \\& K_{1}= \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix} ,\quad\quad K_{2}= \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} . \end{aligned}$$

For different h and μ, the optimal \(\mathcal{H_{\infty}}\) performance index γ can be obtained by Theorem 1 in [31], Theorem 3.1 in [32], Theorem 3.1 in [34], and Corollary 1 in this paper. The results are summarized in Table 2. From Table 2, it is clear that a better performance can be derived by the approach proposed in our paper. When \(0\leq h(t) \leq1\), \(\dot {h}(t)\leq0.9\), \(\gamma=1.2361\), the state response of the error system under the initial condition \(r(0)=[-1\ 1\ {-}0.5]^{T}\) is shown in Figure 2.

Figure 2
figure 2

The response of the error \(\pmb{r(t)}\) for given initial value in Example  2 .

Full size image
Table 2 The \(\pmb{\mathcal{H_{\infty}}}\) performance index γ with different \(\pmb{(h, \mu)}\)
Full size table

5 Conclusions

In this paper, the problem of delay-dependent \(\mathcal{H_{\infty}}\) state estimation of static neural networks with interval time-varying delay has been investigated. Based on Lyapunov stability theory, Wirtinger’s integral inequality, and a reciprocally convex approach, some improved sufficient conditions which guarantee the globally asymptotical stability of the error system with the guaranteed \(H_{\infty}\) performance have been proposed. The estimator gain matrix can be determined by solving the LMIs. The effectiveness of the theoretical results has been illustrated by two numerical examples. In addition, how to utilize more accurate inequalities such as the integral inequalities in [23, 24] with less computational burden will be investigated in our future work.